Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Holy guacamole! www.integral.mn сайт 2026-01-01-ээс шинэчлэгдэж www.mathminds.club хуудас руу шилжинэ.
Багтаасан адил хажуут трапец
$r$ радиустай тойрог багтаасан адил хажуут трапецийн сууриуд $m:n$ харьцаатай бол хажуу талын урт ямар байх вэ?
A.$\dfrac{2r^2}{\sqrt{mn}}$ B.$\dfrac{r(m+n)}{\sqrt{mn}}$ C.$\dfrac{r|m-n|}{\sqrt{mn}}$ D.$\dfrac{r\sqrt{m^2+n^2}}{m+n}$ E.$\dfrac{r^2}{\sqrt{mn}}$
Бодлогын төрөл:Сонгох
Амжилтын хувь:48.25%
Бодлогыг оруулсан: baysaa41@yahoo.com
Бодолт
Заавар:Тойргийн гаднах цэгээс тойрогт татсан шүргэгчийн уртууд тэнцүү байдаг.
Тойрог багтаасан 4 өнцөгтийн чанар: $$AB+CD=AD+BC$$
Тойрог багтаасан 4 өнцөгтийн чанар: $$AB+CD=AD+BC$$
Бодолт:Суурийн уртуудыг $mx$, $nx$ гэвэл оройгоос шүргэлтийн цэгүүд хүртэлх зай $\dfrac{mx}{2}$, $\dfrac{nx}{2}$ тул хажуу талын урт нь $\dfrac{(m+n)x}{2}$ байна.
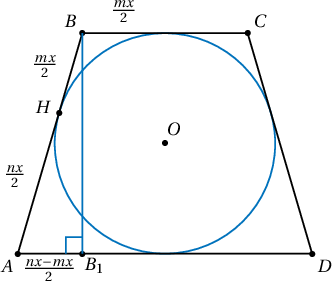Нөгөө талаас трапецийн өндөр нь
$$H=2r=\sqrt{\left(\dfrac{(m+n)x}{2}\right)^2-\left(\dfrac{(m-n)x}{2}\right)^2}=x\sqrt{mn}$$
тул $x=\dfrac{2r}{\sqrt{mn}}$ байна. Иймд
$$\dfrac{(m+n)x}{2}=\dfrac{r(m+n)}{\sqrt{mn}}.$$
Сорилго
2016-05-19 Хавтгайн геометр 1 Сорилго 2 Тойрог, түүнтэй холбоотой бодлогууд багтсан ба багтаасан 4 өнцөгт багтсан ба багтаасан 4 өнцөгт Хавтгайн геометр 1 тестийн хуулбар Геометр /хавтгай/