Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Бодлого №7830
$ABCD$ гүдгэр дөрвөн өнцөгтөд $AB:BC:CD:DA=1:2:5:4$ байжээ. Хэрэв $AC=9$ см бол түүний $ABC$, $CDA$ өнцгийн биссектристэй огтлолцсон цэгээр гурав хуваагдсан хэсгүүд нь ямар ямар урттай вэ?
A. 4 см, 2 см, 3 см
B. 3 см, 1 см, 5 см
C. 2 см, 2 см, 5 см
D. 4 см, 1 см, 4 см
E. 3 см, 2 см, 4 см
Бодлогын төрөл: Сонгох
Амжилтын хувь: 10.00%
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
Заавар: Биссектриссийн чанар:
Гурвалжны өнцгийн биссектрис нь эсрэг орших талаа налсан талуудтай нь пропорционал хэсгүүдэд хуваадаг: $$\dfrac{BC}{BD}=\dfrac{AC}{AD}\Leftrightarrow\dfrac{a}{x}=\dfrac{b}{y}$$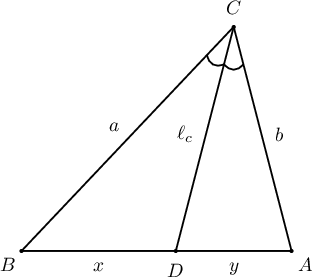
Гурвалжны өнцгийн биссектрис нь эсрэг орших талаа налсан талуудтай нь пропорционал хэсгүүдэд хуваадаг: $$\dfrac{BC}{BD}=\dfrac{AC}{AD}\Leftrightarrow\dfrac{a}{x}=\dfrac{b}{y}$$
Бодолт: 
$ABC$ гурвалжны $BM$ биссектриссийн хувьд биссектриссийн чанар бичвэл $$\dfrac{x}{AM}=\dfrac{2x}{MC}\Leftrightarrow AM=t, MC=2t$$ ба $AM+MC=t+2t=3t=9$ тул $t=3$ буюу $AM=3$, $MC=6$ байна. Яг адилханаар $ADC$ гурвалжны $DN$ биссектриссийн хувьд биссектриссийн чанар бичвэл $$\dfrac{4x}{AN}=\dfrac{5x}{NC}\Leftrightarrow AN=4s, NC=5s$$ ба $AN+NC=4s+5s=9s=9$ тул $s=1$ буюу $AN=4$, $NC=5$ байна. Түүнчлэн $MN=9-3-5=1$ тул 3 см, 1 см, 5 см урттай хэсгүүдэд хуваана.
$ABC$ гурвалжны $BM$ биссектриссийн хувьд биссектриссийн чанар бичвэл $$\dfrac{x}{AM}=\dfrac{2x}{MC}\Leftrightarrow AM=t, MC=2t$$ ба $AM+MC=t+2t=3t=9$ тул $t=3$ буюу $AM=3$, $MC=6$ байна. Яг адилханаар $ADC$ гурвалжны $DN$ биссектриссийн хувьд биссектриссийн чанар бичвэл $$\dfrac{4x}{AN}=\dfrac{5x}{NC}\Leftrightarrow AN=4s, NC=5s$$ ба $AN+NC=4s+5s=9s=9$ тул $s=1$ буюу $AN=4$, $NC=5$ байна. Түүнчлэн $MN=9-3-5=1$ тул 3 см, 1 см, 5 см урттай хэсгүүдэд хуваана.