Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Holy guacamole! www.integral.mn сайт 2026-01-01-ээс шинэчлэгдэж www.mathminds.club хуудас руу шилжинэ.
Фалесийн теорем
$ABCD$ параллелограммын $AB$ талын дундаж $E$, $AD$ талын дундаж $F$ байжээ. $DE$, $CF$ хэрчмүүд $M$ цэгт огтлолцсон бол $DM:ME$ аль нь вэ?
A.$\dfrac12$ B.$\dfrac34$ C.$\dfrac45$ D.$\dfrac23$ E.$\dfrac32$
Бодлогын төрөл:Сонгох
Амжилтын хувь:23.26%
Бодлогыг оруулсан: baysaa41@yahoo.com
Бодолт
Заавар:$E$ цэгийг дайрсан $CF$-тэй параллель шулуун тат. Параллель шулуунуудыг гурав дах шулуунаар огтлоход үүсэх өнцгүүд тэнцүү.
Бодолт: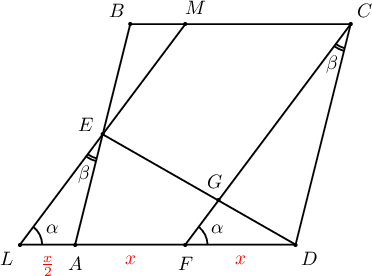
$E$ цэгийг дайруулж $CF$-тэй параллель шулууныг зураг татав. Солбисон өнцгүүд тул $\angle L=\angle F$ ба $\angle D$ ерөнхий тул ӨӨ шинжээр $\triangle LEA\sim\triangle FCD$ байна. Иймд
$$\dfrac{LA}{FD}=\dfrac{EA}{CD}=\dfrac12$$
ба $FD=x$ гэвэл $AF=x$ ба $LA=\dfrac{x}{2}$ болно. Иймд Фалесийн теоремоор
$$\dfrac{DG}{GE}=\dfrac{DF}{FL}=\dfrac{x}{x+\frac{x}{2}}=\dfrac23$$