Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Гүдгэр 4 өнцөгтийн талуудыг бодох
$ABCD$ дөрвөн өнцөгтөд $AB=1$, $\measuredangle ABC=60^{\circ}$, $\measuredangle ACB=45^{\circ}$, $\measuredangle BAD=105^{\circ}$, $\measuredangle ADB=45^{\circ}$ байв. $AC$ диагоналийн урт $\dfrac{\sqrt{\fbox{a}}}{\fbox{b}}$, $\measuredangle ABD=\fbox{cd}^\circ$, $AD=\dfrac{\sqrt{\fbox{e}}}{\fbox{f}}$, $CD=\dfrac{\sqrt{\fbox{g}}}{\fbox{h}}$ болно.
ab = 62
cd = 30
ef = 22
gh = 22
Бодлогын төрөл: Нөхөх
Амжилтын хувь: 39.38%
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
Заавар: Гурвалжны дотоод өнцгүүдийн нийлбэр $180^\circ$ байх чанар болон синус, косинусын теорем ашигла.
Бодолт: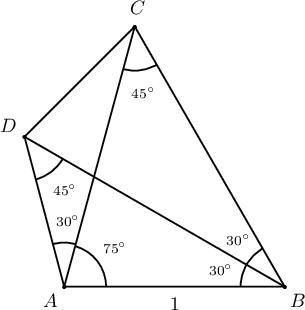 
Синусын теоремоор
$$\dfrac{AC}{\sin60^\circ}=\dfrac{AB}{\sin45^\circ}\Rightarrow AC=\dfrac{1}{\frac{\sqrt2}{2}}\cdot\dfrac{\sqrt3}{2}=\dfrac{\sqrt6}{2}$$
Гурвалжны дотоод өнцгүүдийн нийлбэр $180^\circ$ тул: $$\measuredangle ABD=180^{\circ}-105^\circ-45^\circ=30^\circ$$
Мөн синусын теоремоор $$\dfrac{AD}{\sin30^\circ}=\dfrac{AB}{\sin45^\circ}\Rightarrow AD=\dfrac{1}{\frac{\sqrt2}{2}}\cdot\dfrac{1}{2}=\dfrac{\sqrt2}{2}$$ $\measuredangle CAD=105^\circ-\measuredangle BAC=105^\circ-(180^\circ-60^\circ-45^\circ)=30^\circ$ тул $\triangle ADC$-д косинусын теорем бичвэл $$CD^2=AC^2+AD^2-2\cdot AC\cdot AD\cdot\cos30^\circ\Rightarrow$$ $$CD=\sqrt{\dfrac64+\dfrac{2}{4}-2\cdot\dfrac{\sqrt6}{2}\cdot\dfrac{\sqrt2}{2}\cdot\dfrac{\sqrt3}{2}}=\dfrac{\sqrt2}{2}$$
Гурвалжны дотоод өнцгүүдийн нийлбэр $180^\circ$ тул: $$\measuredangle ABD=180^{\circ}-105^\circ-45^\circ=30^\circ$$
Мөн синусын теоремоор $$\dfrac{AD}{\sin30^\circ}=\dfrac{AB}{\sin45^\circ}\Rightarrow AD=\dfrac{1}{\frac{\sqrt2}{2}}\cdot\dfrac{1}{2}=\dfrac{\sqrt2}{2}$$ $\measuredangle CAD=105^\circ-\measuredangle BAC=105^\circ-(180^\circ-60^\circ-45^\circ)=30^\circ$ тул $\triangle ADC$-д косинусын теорем бичвэл $$CD^2=AC^2+AD^2-2\cdot AC\cdot AD\cdot\cos30^\circ\Rightarrow$$ $$CD=\sqrt{\dfrac64+\dfrac{2}{4}-2\cdot\dfrac{\sqrt6}{2}\cdot\dfrac{\sqrt2}{2}\cdot\dfrac{\sqrt3}{2}}=\dfrac{\sqrt2}{2}$$