Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Гурвалжны биссектрисс ба медиан
$ABC$ гурвалжны $AL$ биссектрисс $CM$ медиантай $O$ цэгт огтлолцоно. $AC=4$, $AB=6$ бол $\dfrac{CO}{CM}=\dfrac{\fbox{a}}{\fbox{b}}$, $BO$ шулууны $AC$ талтай огтлолцох цэгийг $N$ гэвэл $\dfrac{ON}{BN}=\dfrac{\fbox{c}}{\fbox{d}}$ болох бөгөөд $BL=\dfrac{12}{5}$ үед $BN=\dfrac{\fbox{e}}{\fbox{f}}\sqrt{14}$ байна.
ab = 47
cd = 27
ef = 65
Бодлогын төрөл: Нөхөх
Амжилтын хувь: 25.00%
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
Заавар: Лемм. $AB$ хэрчмийг $CD$ шулуун $E$ цэгт огтолдог байв. Тэгвэл
$$\dfrac{AE}{BE}=\dfrac{S_{\triangle ACD}}{S_{\triangle BCD}}$$
байна.
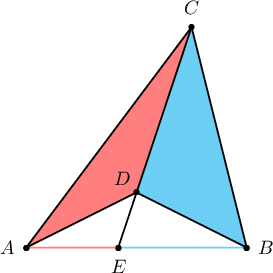Ижил өндөртэй гурвалжны талбайн харьцаа сууриудын харьцаатай тэнцүү тул
$$\dfrac{AE}{BE}=\dfrac{S_{\triangle ACE}}{S_{\triangle BCE}}=\dfrac{S_{\triangle ADE}}{S_{\triangle BDE}}$$
ба эндээс пропорцийн чанараар
$$\dfrac{AE}{BE}=\dfrac{S_{\triangle ACE}-S_{\triangle ADE}}{S_{\triangle BCE}-S_{\triangle BDE}}=\dfrac{S_{\triangle ACD}}{S_{\triangle BCD}}$$
болж батлагдав.
Бодолт: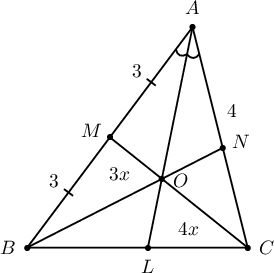 
$AO$ нь $\triangle AMC$-ийн биссектрисс болох тул биссектриссийн чанараар $CO=4x$, $OM=3x$ тул $$\dfrac{CO}{OM}=\dfrac{4x}{7x}=\dfrac{4}{7}$$
Зааварт баталсан лемм ёсоор $$\dfrac{S_{AOC}}{S_{BOC}}=\dfrac33=1\Rightarrow S_{AOC}=S_{BOC}$$
Биссектриссийн чанар ёсоор $$\dfrac{CL}{LB}=\dfrac{4}{6}=\dfrac23$$
ба мөн лемм ёсоор $$\dfrac{CN}{NA}=\dfrac{S_{BOC}}{S_{AOB}}=\dfrac{S_{AOC}}{S_{AOB}}=\dfrac{CL}{LB}=\dfrac23$$
байна. $CN=2y$, $NA=3y$ гэвэл $2y+3y=4\Rightarrow 5y=4\Rightarrow y=0.8$ тул $AN=3y=2.4$
болно. Түүнчлэн $AO$ нь $\triangle ANB$-ийн биссектрисс болох тул биссектриссийн чанараар $ON=2.4z$, $OB=6z$ тул $$\dfrac{ON}{BN}=\dfrac{2.4z}{8.4z}=\dfrac{2}{7}$$
$BL=\dfrac{12}{5}$ үед $BL=\dfrac{6}{10}BC$ тул $BC=\dfrac{12}{5}:\dfrac{6}{10}=4$ болно. Иймд $ABC$ нь $AC=BC$ байх адил хажуут гурвалжин болно. Иймд $CM$ нь өндөр болох тул $\cos\angle MBC=\dfrac{3}{4}$ тул косинусын теоремоор $$AL^2=6^2+\dfrac{12^2}{5^2}-2\cdot 6\cdot\dfrac{12}{5}\cdot\dfrac34$$ тул $$AL=\dfrac65\sqrt{14}$$ байна.
$BL=\dfrac{12}{5}$ үед $BL=\dfrac{6}{10}BC$ тул $BC=\dfrac{12}{5}:\dfrac{6}{10}=4$ болно. Иймд $ABC$ нь $AC=BC$ байх адил хажуут гурвалжин болно. Иймд $CM$ нь өндөр болох тул $\cos\angle MBC=\dfrac{3}{4}$ тул косинусын теоремоор $$AL^2=6^2+\dfrac{12^2}{5^2}-2\cdot 6\cdot\dfrac{12}{5}\cdot\dfrac34$$ тул $$AL=\dfrac65\sqrt{14}$$ байна.