Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Хоёр тойргийн огтлолцолд үүсэх дүрс
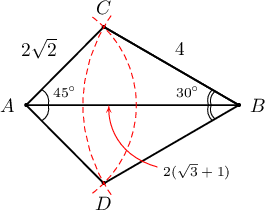
$2(\sqrt{3}+1)$ см урттай $AB$ хэрчмийн $A$ цэгт төвтэй $2\sqrt{2}$ см радиустай тойрог ба $B$ цэгт төвтэй $4$ см радиустай тойргууд $C$, $D$ цэгт огтлолцдог гэе. $\measuredangle CAD =\fbox{ab}^{\circ}$ ба $\measuredangle CBD =\dfrac{\pi}{\fbox{c}}$, дугуйнуудын ерөнхий хэсгийн талбай нь $\dfrac{\fbox{de}}{3}\pi-(4+4\sqrt{3})$ см$^2$ байна.
ab = 90
c = 3
de = 14
Бодлогын төрөл: Нөхөх
Амжилтын хувь: 20.00%
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
Заавар: $\triangle ABC$-д косинусын теорем бичиж $\measuredangle CAB$, $\measuredangle CBA$-г ол.
$R$ радиустай дугуйн $\theta$ төв өнцөгт харгалзах секторын талбай нь $\dfrac{\theta R^2}{2}$, сегментийн талбай нь $\dfrac{(\theta-\sin\theta)R^2}{2}$ байна.
$R$ радиустай дугуйн $\theta$ төв өнцөгт харгалзах секторын талбай нь $\dfrac{\theta R^2}{2}$, сегментийн талбай нь $\dfrac{(\theta-\sin\theta)R^2}{2}$ байна.
Бодолт: $\triangle ABC$-д косинусын теорем бичвэл
$$\cos\measuredangle CAB=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}=\dfrac{(2(\sqrt3+1))^2+(2\sqrt2)^2-4^2}{2\cdot2(\sqrt3+1)\cdot 2\sqrt2}=\dfrac{\sqrt2}{2}$$
$$\cos\measuredangle CBA=\dfrac{AB^2+BC^2-AC^2}{2\cdot AB\cdot BC}=\dfrac{(2(\sqrt3+1))^2+4^2-(2\sqrt2)^2}{2\cdot2(\sqrt3+1)\cdot 4}=\dfrac{\sqrt3}{2}$$
тул $\measuredangle CAB=45^\circ$, $\measuredangle CBA=30^\circ$ байна.
Иймд $\measuredangle CAD=\dfrac{\pi}{2}$ ба $\measuredangle CBD=\dfrac{\pi}{3}$ байна. Бидний олох дүрсийн талбай нь 2 сегментийн талбайн нийлбэр тул
$$S=\dfrac12\Big(\dfrac{\pi}{2}-\sin\dfrac{\pi}{2}\Big)\cdot (2\sqrt2)^2+\dfrac12\Big(\dfrac{\pi}{3}-\sin\dfrac{\pi}{3}\Big)\cdot 4^2=\dfrac{14}{3}\pi-4+4\sqrt3$$