Монгол Бодлогын Сан

Заавар: Гурвалжны медианы урт нь $$m_a=\dfrac12\sqrt{2(b^2+c^2)-a^2}$$ $\triangle ABM_1\sim CA_1M_1$, $\triangle BA_1M_1\sim ACM_1$ ашиглан $A_1B$, $A_1C$ талуудын уртыг ол.

Бодолт: 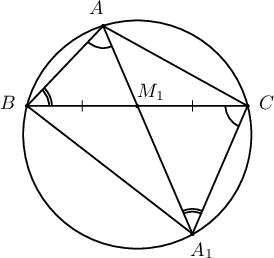$$AM_1=\dfrac12\sqrt{2(2^2+3^2)-4^2}=\dfrac12\sqrt{10}$$ Нэг нумд тулсан өнцгүүд тул $\angle BAA_1=\angle BCA_1$, $\angle ABC=\angle AA_1C$ байна. Иймд $\triangle ABM_1\sim\triangle CA_1M_1$ болно. Иймд $$\dfrac{A_1M_1}{BM_1}=\dfrac{CM_1}{AM_1}\Rightarrow A_1M_1=\dfrac{CM_1\cdot BM_1}{AM_1}=\dfrac{2\cdot 2}{\frac12\cdot\sqrt{10}}=\dfrac{4\sqrt{2}}{\sqrt{5}}$$ Мөн $AB=BM_1$ тул $A_1C=A_1M_1=\dfrac{4\sqrt{2}}{\sqrt{5}}$ байна. Мөн $\triangle BA_1M_1\sim ACM_1$ тул $$\dfrac{A_1B}{AC}=\dfrac{BM_1}{AM_1}\Rightarrow A_1B=\dfrac{BM_1\cdot AC}{AM_1}=\dfrac{2\cdot 3}{\frac12\cdot\sqrt{10}}=\dfrac{6\sqrt2}{\sqrt5}$$ Иймд $A_1BC$ гурвалжны периметр $$4+\dfrac{4\sqrt{2}}{\sqrt{5}}+\dfrac{6\sqrt{2}}{\sqrt{5}}=4+2\sqrt{10}$$ $p=\dfrac{2+3+4}{2}=\dfrac{9}{2}$ тул Героны томьёогоор $$S_{ABC}=\sqrt{\dfrac{9}{2}\cdot \dfrac{5}{2}\cdot \dfrac{3}{2}\cdot \dfrac{1}{2}}=\dfrac{3\sqrt{15}}{4}$$ Мөн $BC$ ерөнхий суурьт буусан өндрүүдийн харьцаа медиануудын харьцаатай тэнцүү тул $$\dfrac{S_{A_1BC}}{S_{ABC}}=\dfrac{A_1M_1}{AM_1}\Rightarrow S_{A_1BC}=\dfrac{\frac{4\sqrt{2}}{\sqrt{5}}}{\frac12\sqrt{10}}\cdot\dfrac{3\sqrt{15}}{4}=\dfrac{6\sqrt{15}}{5}$$