Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Тэгш өнцөгт гурвалжин
$ABC$ гурвалжны талууд $AB=12$, $BC=5$, $AC=13$ ба $AB$ тал дээр ${AC_1}\colon {BC_1}={1}\colon{2}$ байх $C_1$ цэг тэмдэглэв. $BC$ талын дундаж нь $A_1$, $BB_1$ нь $AC$ тал дээр буулгасан өндөр бол $BB_1=\dfrac{\fbox{ab}}{13},$ $S_{AC_1B_1}=\dfrac{\fbox{cdef}}{13^2}$, $S_{CA_1B_1}=\dfrac{\fbox{ghi}}{13^2}$ байна.
ab = 60
cdef = 1440
ghi = 375
Бодлогын төрөл: Нөхөх
Амжилтын хувь: 21.54%
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
Заавар: Өгөгдсөн гурвалжин тэгш өнцөгт гурвалжин болохыг шалга.
Бодолт: $AB^2=144$, $BC^2=25$, $AC^2=169$ тул
$$AB^2+BC^2=AC^2$$
буюу $\angle B=90^\circ$ байна. Иймд
$$2S=AC\cdot BB_1=AB\cdot BC\Rightarrow BB_1=\dfrac{5\cdot 12}{13}=\dfrac{60}{13}$$
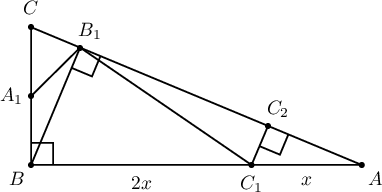$\triangle ABC\sim\triangle AB_1B$ тул төсөөгийн харьцаагаар
$$S_{ABB_1}=\left(\dfrac{AB}{AC}\right)^2 S=\dfrac{12^2}{13^2}\cdot 30$$
болох ба
$$\dfrac{S_{AC_1B_1}}{S_{ABB_1}}=\dfrac{C_1C_2}{BB_1}=\dfrac{x}{3x}=\dfrac{1}{3}$$
тул $S_{AC_1B_1}=\dfrac13\cdot S_{ABB_1}=\dfrac{1440}{13^2}$
$\triangle ABC\sim\triangle BB_1C$ тул төсөөгийн харьцаагаар $$S_{BB_1C}=\left(\dfrac{BC}{AC}\right)^2 S=\dfrac{5^2}{13^2}\cdot 30$$ ба $B_1A_1$ нь $BB_1C$ гурвалжны медиан тул $$S_{CA_1B_1}=\dfrac12 S_{BB_1C}=\dfrac{1}{2}\cdot\dfrac{5^2\cdot 30}{13^2}=\dfrac{375}{13^2}$$
$\triangle ABC\sim\triangle BB_1C$ тул төсөөгийн харьцаагаар $$S_{BB_1C}=\left(\dfrac{BC}{AC}\right)^2 S=\dfrac{5^2}{13^2}\cdot 30$$ ба $B_1A_1$ нь $BB_1C$ гурвалжны медиан тул $$S_{CA_1B_1}=\dfrac12 S_{BB_1C}=\dfrac{1}{2}\cdot\dfrac{5^2\cdot 30}{13^2}=\dfrac{375}{13^2}$$
Сорилго
2017-04-25
geometr
ЭЕШ сорил-1
геометр
2020-12-21 сорил
Гурвалжны өндөр
холимог тест
Пифагорын теором
ААТТШ
ААТТШ тестийн хуулбар