Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Шүргэгч ба хөвчийн урт
$O$ төвтэй тойргийн $T$ цэг дээрх шүргэгч дээр $T$ цэгийн нэг талд байрлах $P$, $Q$ цэгүүд авав ($PT< QT$). $OP$, $OQ$ хэрчмүүдийн тойрогтой огтлолцох цэгийг харгалзан $R$, $S$, $\measuredangle OQT=\theta$ гэвэл
- $\lim \limits _{P\rightarrow T}\dfrac{RS}{PQ}=\dfrac{\sqrt{\fbox{a}}\sin \theta}{\sqrt{1+\sin \theta }}$ болно.
- $\lim \limits _{P\rightarrow T}\dfrac{RS}{PQ}=\dfrac{1}{\sqrt{3}}$ байх үеийн $\theta$-ийн утга нь $\fbox{bc}^{\circ}$ байна.
a = 2
bc = 30
Бодлогын төрөл: Нөхөх
Амжилтын хувь: 15.92%
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
Заавар: $\lim\limits_{P\rightarrow T}\dfrac{RS}{PQ}=\dfrac{TS}{TQ}$ байна.
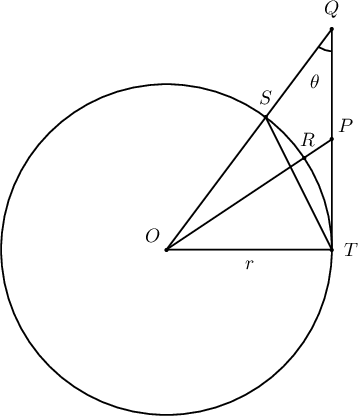
Бодолт: Тойргийн радиусыг $r$ гэвэл $TS=\sqrt{2r^2-2r^2\cos\angle QOT}$, $TQ=r\ctg\theta$ тул
- $\lim\limits_{P\rightarrow T}\dfrac{RS}{PQ}=\dfrac{TS}{TQ}=\dfrac{\sqrt{2}\cdot\sqrt{1-\sin\theta}\cdot\sin\theta}{\cos\theta}$ ба $$\cos\theta=\sqrt{1-\sin^2\theta}=\sqrt{1-\sin\theta}\cdot\sqrt{1+\sin\theta}$$ тул $$\lim\limits_{P\rightarrow T}\dfrac{RS}{PQ}=\dfrac{\sqrt2\sin\theta}{\sqrt{1+\sin\theta}}$$
- $\dfrac{\sqrt2\sin\theta}{\sqrt{1+\sin\theta}}=\dfrac{1}{\sqrt3}\Rightarrow 6\sin^2\theta-\sin\theta-1=0$ тул $$\sin\theta=\dfrac{1\pm\sqrt{1^2-4\cdot 6\cdot(-1)}}{2\cdot 6}=\dfrac{1\pm 5}{12}$$ $\theta<180^\circ$ тул синус эерэг байхыг тооцвол $\sin\theta=\dfrac12$ буюу $\theta=30^\circ$ байна.
Сорилго
2016-09-29
математик101
математик101 тестийн хуулбар
математик101 тестийн хуулбар тестийн хуулбар
математик101 тестийн хуулбар тестийн хуулбар