Монгол Бодлогын Сан

Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.

$ABC$ гурвалжны талууд $AB=5$, $BC=8$, $\measuredangle ABC=60^{\circ}$ байдаг гэе.

$ABC$ гурвалжны талбай $\fbox{ab}\sqrt{\fbox{c}}$,
$AC=\fbox{d}$, $\cos\widehat{ACB}=\dfrac{\fbox{ef}}{\fbox{gh}}$,
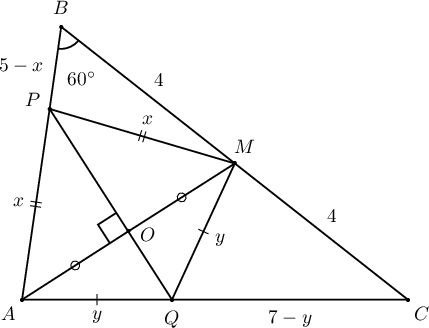
$BC$ талын дунджийг $M$ гээд $AB$, $AC$ талууд дээр $PA=PM$, $QA=QM$ байх $P,Q$ цэгүүд авахад $MP=\dfrac{\fbox{i}}{\fbox{j}}$, $MQ=\dfrac{\fbox{kl}}{\fbox{mn}}$ байна.

abc = 103

d = 7

efgh = 1114

ij = 72

klmn = 4918

Бодлогын төрөл: Нөхөх

Амжилтын хувь: 31.37%

Заавар:

$S=\frac12ac\sin\beta$ томьёог ашигла.
Косинусын теорем ашигла.
$AM$ хэрчмийн дундаж цэгийг дайруулж $AM$-д перпендикуляр шулуун татахад уг шулуун дээр $P$, $Q$ цэгүүд оршино.

Бодолт:

$S=\frac12\cdot 5\cdot 8\sin60^\circ=10\sqrt3$.
Косинусын теоремоор $$AC^2=AB^2+BC^2-2\cdot AB\cdot AC\cdot\cos60^\circ\Rightarrow$$ $$AC=\sqrt{5^2+8^2-2\cdot 5\cdot 8\cdot\dfrac12}=7$$ $$\cos\measuredangle ACB=\dfrac{7^2+8^2-5^2}{2\cdot 7\cdot 8}=\dfrac{11}{14}$$
$PBM$ гурвалжинд косинусын теорем бичвэл $$x^2=4^2+(5-x)^2-2\cdot 4\cdot(5-x)\cdot\dfrac12\Rightarrow$$ $$(10-4)x=21\Rightarrow x=\dfrac72$$ $QCM$ гурвалжинд косинусын теорем ашиглавал
$$y^2=4^2+(7-y)^2-2\cdot 4\cdot(7-y)\cdot\dfrac{11}{14}\Rightarrow$$ $$\left(14-\dfrac{44}{7}\right)y=21\Rightarrow y=\dfrac{49}{18}$$ Түүнчлэн $$\cos\measuredangle ABC=\dfrac{5^2+8^2-7^2}{2\cdot 5\cdot 8}=$$