Монгол Бодлогын Сан

Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.

Дараахь бодлогуудыг бод.

$ABC$ гурвалжны талууд $a=3$, $b=4$, $c=5$ бол $\dfrac{r}{R}=\dfrac{\fbox{a}}{\fbox{b}}$ байна.
$a=3$, $c=7$ ба $\cos \beta =1-\dfrac{r}{R}$ үед $b=\fbox{c}$ ба энэ үед гурвалжны талбай $\dfrac{\fbox{de}}{\fbox{f}}\sqrt{\fbox{g}}$ болно.

ab = 25

c = 5

defg = 1543

Бодлогын төрөл: Нөхөх

Амжилтын хувь: 22.65%

Заавар: $ABC$ гурвалжны $A$ оройгоос багтсан тойрогт татсан шүргэгч хэрчмийн уртыг $$x=\dfrac{b+c-a}{2}$$ томьёогоор олдог.

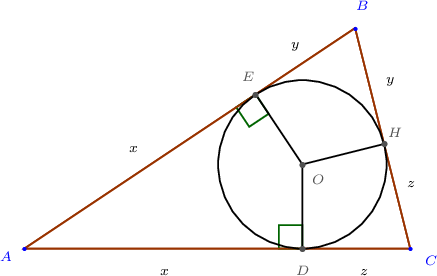Энд $y+z=a$, $x+z=b$, $x+y=c$ байна.

$ABC$ нь ($5^2=3^2+4^2$) тэгш өнцөгт гурвалжин болохыг ашигла.
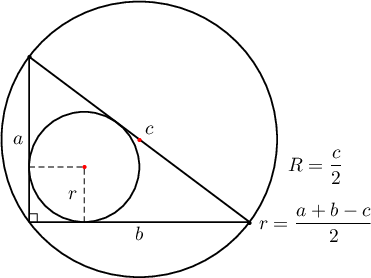
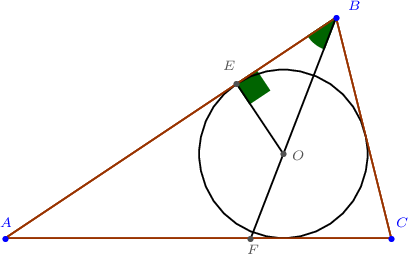
$B$ оройгоос багтаасан тойрогт татсан шүргэгчийн урт $BE=\dfrac{a+c-b}{2}=\dfrac{10-b}{2}\Rightarrow r=\dfrac{10-b}{2}\cdot\tg\dfrac{\beta}{2}$, $R=\dfrac{b}{2\sin\beta}=\dfrac{b}{4\sin\frac{\beta}{2}\cos\frac{\beta}{2}}$-г бодлогын нөхцөлд орлуулж хялбарчлаад $\sin\frac\beta2\neq0$ болохыг тооцож $b$-г ол.
3 талын урт мэдэгдэж байгаа тохиолдолд талбайг Героны $$S=\sqrt{p(p-a)(p-b)(p-c)}$$ томьёог ашиглан олно. Энд $p=\dfrac{a+b+c}{2}$ буюу гурвалжны периметрийн хагас.

Бодолт:

$r=\dfrac{3+4-5}{2}=1$, $R=\dfrac{5}{2}\Rightarrow \dfrac{r}{R}=\dfrac{1}{\frac52}=\dfrac{2}{5}$.
$r=\dfrac{10-b}{2}\cdot\tg\dfrac{\beta}{2}$, $R=\dfrac{b}{2\sin\beta}=\dfrac{b}{4\sin\frac{\beta}{2}\cos\frac{\beta}{2}}$ ба бодлогын нөхцлөөс \begin{align*} \cos\beta&=1-\dfrac{\dfrac{10-b}{2}\cdot\tg\dfrac\beta2}{\dfrac{b}{4\sin\frac\beta2\cos\frac\beta2}}\\ &=1-\frac{10-b}{2b}\cdot\frac{\sin\frac\beta2}{\cos\frac\beta2}\cdot 4\sin\frac\beta2\cos\frac\beta2\\ &=1-\dfrac{2(10-b)}{b}\sin^2\frac\beta2 \end{align*} болох ба $1-\cos\beta=2\sin^2\dfrac\beta2$ тул $$2\sin^2\frac\beta2-\dfrac{2(10-b)}{b}\sin^2\frac\beta2=0\Rightarrow 2b-2(10-b)=0\Rightarrow b=5.$$ $p=\dfrac{3+5+7}{2}=\dfrac{15}{2}$ тул $$S=\sqrt{\tfrac{15}{2}\cdot\big(\tfrac{15}{2}-3\big)\big(\tfrac{15}{2}-5\big)\big(\tfrac{15}{2}-7\big)}=\sqrt{\tfrac{15}2\cdot\tfrac92\cdot\tfrac52\cdot\tfrac12}=\tfrac{15}{4}\sqrt{3}.$$