Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Тэгш өнцөгт гурвалжинд багтсан тойргууд
$AB=1$, $AC=2$ катетууд бүхий тэгш өнцөгт гурвалжинд багтсан тойргийн радиусыг $r$, $AC$ талыг шүргэн гадуур багтсан тойргийн радиусыг $R_{b}$ гэвэл $r=\dfrac{\fbox{a}-\sqrt{\fbox{b}}}{2}$, $R_{b}=\dfrac{\sqrt{\fbox{c}}+1}{\fbox{d}}$ байна. Энэ хоёр тойргийн $BC$ талыг шүргэх цэгүүдийг $E_1$, $E_2$ гэвэл $E_1E_2=\sqrt{\fbox{e}}-\fbox{f}$ болно.
ab = 35
cd = 52
ef = 51
Бодлогын төрөл: Нөхөх
Амжилтын хувь: 48.39%
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
Заавар: Тэгш өнцөгт гурвалжинд багтсан тойргийн төв нь
$$r=\dfrac{a+b-c}{2}$$
байна.
$ABC$ гурвалжны $B$ оройгоос $\angle ABC$-д багтсан гадаад багтсан тойргийн шүргэлтийн цэг хүртэлх зай $p$ байдаг.
$ABC$ гурвалжны $B$ оройгоос $\angle ABC$-д багтсан гадаад багтсан тойргийн шүргэлтийн цэг хүртэлх зай $p$ байдаг.
Бодолт: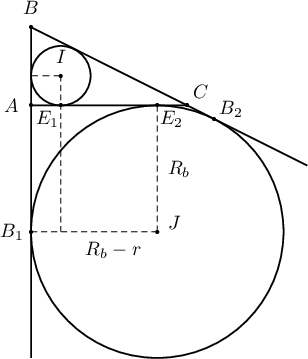 
Пифагорын теоремоор $BC=\sqrt{2^2+1^2}=\sqrt{5}$ тул багтсан тойргийн радиус нь $$r=\dfrac{1+2-\sqrt{5}}{2}=\dfrac{3-\sqrt{5}}{2}$$
$\angle BAC=90^\circ$ тул $R_b=AB_1=BB_1-BA=\dfrac{1+2+\sqrt{5}}{2}-1=\dfrac{\sqrt{5}+1}{2}$ байна. Түүнчлэн
$$E_1E_2=R_b-r=\dfrac{\sqrt{5}+1}{2}-\dfrac{3-\sqrt{5}}{2}=\sqrt5-1.$$