Монгол Бодлогын Сан

Заавар: Ялгаврыг үржвэрт хувиргах томьёо ашигла.

Бодолт: $$\sin x-\sin3x=2\sin\dfrac{x-3x}{2}\cdot\cos\dfrac{x+3x}{x}=-2\sin x\cos 2x,$$ $$\sin 4x-\sin2x=2\sin\dfrac{4x-2x}{2}\cdot\cos\dfrac{4x+2x}{x}=2\sin x\cos 3x$$ тул $$\sin x-\sin3x=\sin4x-\sin2x\Leftrightarrow -\sin x\cos 2x=\sin x\cos 3x$$ буюу $$\sin x\cdot (\cos 2x+\cos 3x)=0\Leftrightarrow$$ $$2\sin x\cdot\cos\dfrac{2x+3x}{2}\cdot\cos\dfrac{2x-3x}{2}=0$$ Иймд $$\left[\begin{array}{c} \sin x=0\\ \cos\dfrac{5x}{2}=0\\ \cos\dfrac{-x}{2}=0\\ \end{array}\right.\Leftrightarrow\left[\begin{array}{c} x=\pi k\\ \dfrac{5}{2}x=\dfrac{\pi}{2}+\pi n\\ -\dfrac{1}{2}x=\dfrac{\pi}{2}+\pi \ell \end{array}\right.\Leftrightarrow\left[\begin{array}{c} x=\pi k\\ x=\dfrac{\pi}{5}+\dfrac{2\pi n}{5}\\ x=-\pi-2\pi \ell \end{array}\right.$$ 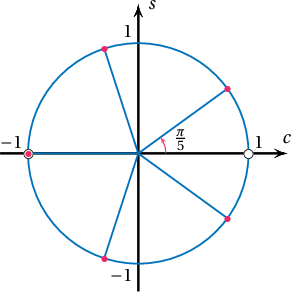Эндээс $x=2\pi m$, $x=\dfrac{\pi}{5}+\dfrac{2\pi n}{5}$ гэсэн ерөнхий шийдтэй.