Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Трапецийн талбай
$ABCD$ трапецийн хувьд $AD$, $BC$ талууд параллель ба $|AB|=5$, $|BC|=7$, $|CD|=6$, $|AD|=4$ байв. Трапецийн $A$ оройгоос $BC$ тал дээр буулгасан өндрийн урт $\dfrac{\fbox{a}\sqrt{14}}{\fbox{b}}$ болох тул талбай нь $\dfrac{\fbox{cd}\sqrt{\fbox{ef}}}{3}$ байна.
ab = 43
cdef = 2214
Бодлогын төрөл: Нөхөх
Амжилтын хувь: 57.44%
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
Заавар: $\theta=\measuredangle ADB=\measuredangle CBD$ гээд $\triangle ADB$, $\triangle CBD$-д косинусын теорем бич.
Бодолт: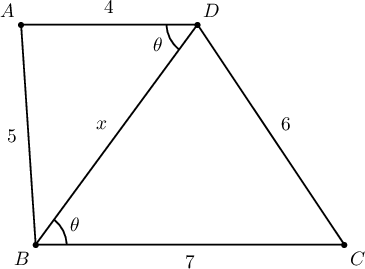 
Косинусын теоремоор
$$
\cos\theta=\dfrac{7^2+x^2-6^2}{2\cdot 7\cdot x}=\dfrac{4^2+x^2-5^2}{2\cdot 4\cdot x}
$$
ба $x\neq0$ тул
$$4(13+x^2)=7(x^2-9)\Rightarrow 3x^2=115\Rightarrow x^2=\dfrac{115}{3}$$
Иймд косинусын теоремоор
$$\cos\measuredangle DCB=\dfrac{7^2+6^2-\dfrac{115}{3}}{2\cdot 6\cdot 7}=\dfrac{5}{9}$$
тул
$$\sin\measuredangle DCB=\sqrt{1-\cos^2\measuredangle DCB}=\dfrac{2\sqrt{14}}{9}$$
байна. Иймд
$$h=CD\cdot\sin\measuredangle DCB=6\cdot\dfrac{2\sqrt{14}}{9}=\dfrac{4\sqrt{14}}{3}$$
ба талбай нь
$$S=\dfrac{AD+BC}{2}\cdot h=\dfrac{4+7}{2}\cdot\dfrac{4\sqrt{14}}{3}=\dfrac{22\sqrt{14}}{3}$$