Монгол Бодлогын Сан

Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.

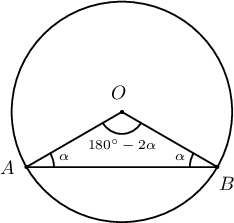
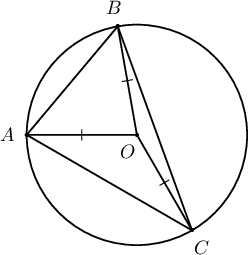
$ABC$ гурвалжныг багтаасан тойргийн төвийг $O$ гэе. $\measuredangle ACB=40^\circ$, $\measuredangle OAC =30^\circ$ үед $\measuredangle OAB= \fbox{ab}^\circ$, $\measuredangle OBC= \fbox{cd}^\circ$ байна.
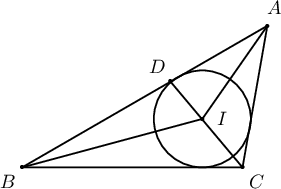
$ABC$ гурвалжинд багтсан тойргийн төвийг $I$ гээд $\measuredangle ABC=30^\circ$, $\measuredangle ACB=100^\circ$ гэе. $IC$ шулуун $AB$ талыг $D$ цэгээр огтолдог бол $\measuredangle BID =\fbox{ef} ^\circ$, $\measuredangle AIC=\fbox{ghi}^\circ$ байна.

ab = 50

cd = 10

ef = 65

ghi = 105

Бодлогын төрөл: Нөхөх

Амжилтын хувь: 10.71%

Заавар:

Бодолт:

$\measuredangle OAC=\measuredangle OCA=30^\circ$ тул $\measuredangle OCB=40^\circ-30^\circ=10^\circ$. Иймд $\measuredangle AOC=180^\circ-2\cdot 30^\circ=120^\circ$, $\measuredangle BOC=180^\circ-2\cdot 10^\circ=160^\circ$. Иймд $$\measuredangle AOB=360^\circ-120^\circ-160^\circ=80^\circ=180^\circ-2\cdot\measuredangle OAB$$ тул $\measuredangle OAB=50^\circ$ байна. Мөн $\measuredangle OBC=\measuredangle OCB=10^\circ$.
$CD$, $BI$ биссектрис тул $\measuredangle BCD=\dfrac{\measuredangle BCA}{2}=50^\circ$, $\measuredangle DBI=\dfrac{\measuredangle ABC}{2}=15^\circ$. Гурвалжны өнцгүүдийн нийлбэр $180^\circ$ тул $$\measuredangle BDI=\measuredangle BDC=180^\circ-30^\circ-50^\circ=100^\circ$$ ба $$\measuredangle BID =180^\circ-15^\circ-100^\circ=65^\circ$$ байна. $$\measuredangle BAC=180^\circ-30^\circ-100^\circ=50^\circ$$ тул $\measuredangle IAC=\dfrac{\measuredangle BAC}{2}=25^\circ$. Түүнчлэн $\measuredangle ACI=\dfrac{\measuredangle ACB}{2}=50^\circ$ тул $$\measuredangle AIC=180^\circ-25^\circ-50^\circ=105^\circ$$ байна.