Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Тойрог ба өнцөг
$4$ радиустай тойрог дээр $A$, $B$, $C$ цэгүүд авчээ. $|AB|=|BC|$, $\measuredangle ABC=110^\circ$ байсан ба $AB$ шулуун $C$ цэгт татсан тойргийн шүргэгчийг $D$ цэгээр огтолж байв. $\measuredangle ADC=\fbox{ab}^\circ$ ба $|AB|=\fbox{c}\sin \fbox{de}^\circ$ болох тул $AB$ богино нумын урт $\dfrac{\fbox{f}}{18} \pi$ байна.
ab = 75
cde = 835
f = 7
Бодлогын төрөл: Нөхөх
Амжилтын хувь: 29.91%
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
Заавар: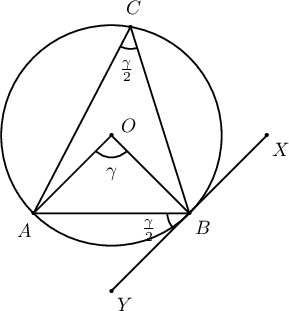 
Тойрогт багтсан өнцгийн чанар:
Тойргийн $\overset{\smile}{AB}$ нумд тулсан аливаа өнцөг нь төв өнцгийнхөө хагастай тэнцүү байна. Мөн $AB$ хэрчмийн үзүүрт татсан шүргэгч ба $AB$ хэрчмийн хооронд үүсэх өнцөг тулсан өнцөгтэй тэнцүү байна. Зурагт үзүүлсэн өнцгүүдийн хувьд $$\angle ACB=\dfrac12\angle AOB=\angle ABY$$
Тойрогт багтсан өнцгийн чанар:
Тойргийн $\overset{\smile}{AB}$ нумд тулсан аливаа өнцөг нь төв өнцгийнхөө хагастай тэнцүү байна. Мөн $AB$ хэрчмийн үзүүрт татсан шүргэгч ба $AB$ хэрчмийн хооронд үүсэх өнцөг тулсан өнцөгтэй тэнцүү байна. Зурагт үзүүлсэн өнцгүүдийн хувьд $$\angle ACB=\dfrac12\angle AOB=\angle ABY$$
Бодолт: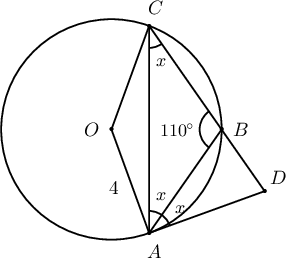 
Тойрогт багтсан өнцгийн чанар ёсоор $x=\angle BCA=\angle BAD$ ба $\triangle ABC$ адил хажуут гурвалжин тул
$$x=\angle BCA=\angle BAC=\dfrac{180^\circ-110^\circ}{2}=35^\circ$$
болно.
Хамар өнцгүүд тул
$$\angle ABC+\angle ABD=180^\circ\Rightarrow \angle ABD=70^\circ$$
Иймд $\triangle ADB$-ээс
$$\angle ADB=180^\circ-70^\circ-35^\circ=75^\circ$$
Синусын теоремоор
$$AB=2R\sin x=8\sin35^\circ$$
$AB$ нумд тулсан өнцөг нь $35^\circ$ тул $\angle AOB=2\cdot35^\circ=70^\circ$ ба $AB$ нумын урт
$$\dfrac{\pi}{180^\circ}\cdot 70^\circ=\dfrac{7}{18}\pi$$