Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Тойрогт багтсан зөв гурвалжин
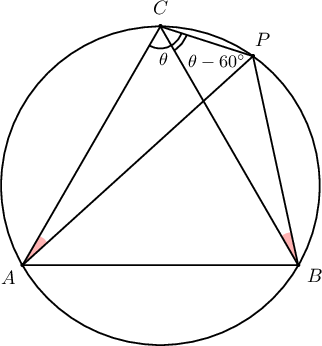
Тойрогт $5$ талтай $ABC$ зөв гурвалжин багтжээ. Уг тойргийн $\measuredangle BAC$ өнцөгт тулсан нум дээр $P$ цэг авчээ. $\measuredangle ACP =\theta$ бол $PA+PB=\fbox{ab}\sin \Big(\theta-\dfrac{\pi}{\fbox{c}}\Big)$ болох ба $S_{PAC}=\dfrac{\fbox{de}}{\sqrt{\fbox{f}}}\sin \Big(\dfrac{\fbox{g}}{\fbox{h}}\pi -\theta\Big)\sin \theta$ байна.
abc = 106
defgh = 25323
Бодлогын төрөл: Нөхөх
Амжилтын хувь: 55.56%
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
Заавар: $\angle BCP=\theta-60^\circ$ байна. $\angle BPC=180^\circ-\angle BAC=120^\circ$ тул $$\angle CBP=180^\circ-120^\circ-(\theta-60^\circ)=120^\circ-\theta$$
байна. Түүнчлэн нэг нумд тулсан өнцгүүд тул
$$\angle CAP=\angle CBP=120^\circ-\theta$$
байна. Синусын теорем ашиглан $AP,\ BP$ утгуудыг ол.
$$\sin\alpha+\sin\beta=2\sin\dfrac{\alpha+\beta}{2}\cos\dfrac{\alpha-\beta}{2}$$
Бодолт: Синусын теоремоор
$$2R=\dfrac{5}{\sin 60^\circ}=\dfrac{AP}{\sin\theta}=\dfrac{BP}{\sin(\theta-60^\circ)}$$
буюу $$AP=\dfrac{10}{\sqrt3}\sin\theta,\ BP=\dfrac{10}{\sqrt3}\sin(\theta-60^\circ)$$
байна. Түүнчлэн
$$\sin\theta+\sin(\theta-60^\circ)=2\sin(\theta-30^\circ)\cos 30^\circ$$
тул
$$AP+BP=\dfrac{10}{\sqrt3}\cdot 2\cdot\dfrac{\sqrt3}{2}\cdot\sin\left(\theta-\frac{\pi}{6}\right)=10\sin\left(\theta-\frac{\pi}{6}\right)$$
байна.
\begin{align*}
S_{\triangle PAC}&=\dfrac12 AC\cdot AP\cdot\sin(120^\circ-\theta)=\\
&=\dfrac12\cdot 5\cdot \dfrac{10}{\sqrt3} \sin\theta\sin\left(\frac{2}{3}\pi-\theta\right)\\
&=\dfrac{25}{\sqrt3}\sin\left(\frac{2}{3}\pi-\theta\right)\sin\theta
\end{align*}