Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Хоёр шулууны хоорондох өнцөг
$ABCA_1B_1C_1$ шулуун призмийн суурь $a$ талтай адил талт гурвалжин, хажуу ирмэгийн урт $\sqrt2a$ бол призмийн талсуудын $A_1B,B_1C$ диагоналиудын хоорондох хурц өнцгийг ол.
A. $45^\circ$
B. $60^\circ$
C. $\arccos\frac14$
D. $\arccos\sqrt{\frac23}$
E. $30^\circ$
Бодлогын төрөл: Сонгох
Амжилтын хувь: 39.47%
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
Заавар: $\overrightarrow{BC_1^\prime}=\overrightarrow{CB_1}$ байх $C_1^\prime$ цэгийг байгуулж косинусын теорем ашиглан $\triangle A_1BC_1^\prime$ гурвалжны талуудыг ол.
Бодолт: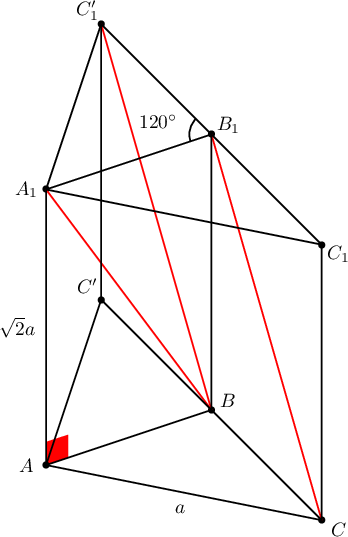 
Пифагорын теоремоор
$$BA_1^2={BC_1^\prime}^2=a^2+(\sqrt2a)^2=3a^2$$
байна. Түүнчлэн $\triangle A_1B_1C_1^\prime$ гурвалжинд косинусын теорем хэрэглэвэл
$${A_1C_1^\prime}^2=a^2+a^2-2a^2\cos120^\circ=3a^2$$
тул $\triangle A_1BC_1^\prime$ гурвалжин адил талт болов. Бидний олох өнцөг $\measuredangle A_1BC_1^\prime=60^\circ$ байна.