Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Holy guacamole! www.integral.mn сайт 2026-01-01-ээс шинэчлэгдэж www.mathminds.club хуудас руу шилжинэ.
Бодлого №7995
Конуст багтсан бөмбөрцөг конусын өндрийг оройгоос 1:4 харьцаагаар хуваана. Конусын байгуулагч суурийн хавтгайтай үүсгэх өнцгийн хэмжээг ол.
A.$75^\circ$ B.$\arccos\dfrac35$ C.$45^\circ$ D.$60^\circ$ E.$\arccos\dfrac23$
Бодлогын төрөл:Сонгох
Амжилтын хувь:24.89%
Бодлогыг оруулсан: baysaa41@yahoo.com
Бодолт
Заавар:Конусын тэнхлэгийг дайрсан огтлол авч үз.
Бодолт:Конусын тэнхлэг огтлол нь
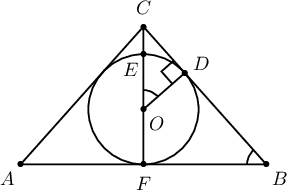байг. $4CE=EF=2r$ тул $CE=0.5r$ болно. Нөгөө талаас $\measuredangle CBF=\measuredangle COD$ ба
$$\cos\measuredangle COD=\dfrac{OD}{CO}=\dfrac{r}{0.5r+r}=\dfrac{2}{3}$$
тул
$$\measuredangle CBF=\arccos\dfrac23$$
болно. Энэ нь конусын $CB$ байгуулагчын суурийн хавтгайтай үүсгэх өнцөг юм.
Сорилго
hw-58-2017-04-20 Огторгуйн геометр 3 Огторгуйн геометр Огторгуйн геометр 2020-04-01 сорил ЭЕШ сорил 1 Эргэлтийн бие