Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Призмийн огтлолын талбай
$ABCA_1B_1C_1$ зөв гурвалжин призмийн суурийн тал 4, призмийн өндөр $\dfrac{\sqrt{42}}{7}$ байв. $AB$, $A_1C_1$, $BB_1$ ирмэгүүдийн дунджийг дайрсан хавтгайгаар призмийг огтлох огтлолыг байгуулав.
- Огтлолын хавтгай ба $(ABC)$ хавтгайн хоорондох өнцөг $\varphi=\arccos \sqrt{\dfrac{\fbox{a}}{\fbox{b}}}$ байна.
- Огтлолын талбай $S=\dfrac{\fbox{cd}\cdot \sqrt{\fbox{e}}}{\fbox{f}}$ байна.
ab = 23
cdef = 1324
Бодлогын төрөл: Нөхөх
Амжилтын хувь: 25.94%
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
Заавар: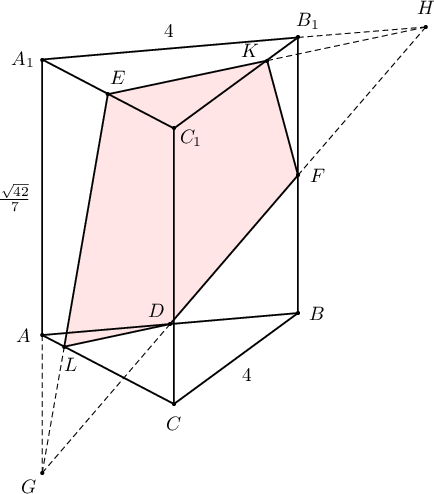 
$AB$, $A_1C_1$, $BB_1$ ирмэгүүдийн дунджийг харгалзан $D$, $E$, $F$ гэе.
$A_1A\cap DF=G$, $A_1B_1\cap DF=H$, $GE\cap AC=L$, $EH\cap B_1C_1=K$ гэвэл огтлол нь $EKFDL$ таван өнцөгт байна. Талбайг нь олохдоо проекц дээр дүрсийн талбайг олоод олсон өнцгийнхөө косинуст хувааж олно.
Бодолт: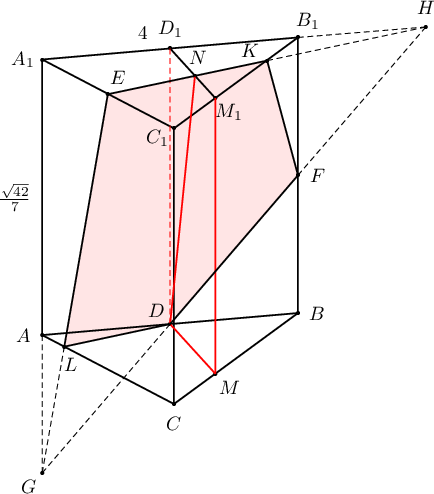 
$A_1B_1$-ийн дундаж $D_1$ цэгээс $EH$-д татсан перпендикулярын суурийг $N$ гэе. Тэгвэл $\varphi=\measuredangle D_1ND$ байна. $\measuredangle DD_1N=90^\circ$ тул $\cos\varphi=\dfrac{ND_1}{ND}$ байна.
$ABB_1A_1$ тэгш өнцөгтийн $AB$, $BB_1$ талуудын дундаж нь $D$, $F$ цэгүүд тул $B_1H=\dfrac{A_1B_1}{2}=2$ байна. $AE=\dfrac{A_1C_1}{2}=2$ ба $\angle EA_1H=60^\circ$ тул $$S_{\triangle EA_1H}=\dfrac{1}{2}\cdot A_1H\cdot A_1E\sin60^\circ=\dfrac{1}{2}\cdot6\cdot 2\cdot\dfrac{\sqrt{3}}{2}=3\sqrt{3}$$ байна.
Мөн косинусын теоремоор $$EH=\sqrt{6^2+2^2-2\cdot 6\cdot 2\cdot\dfrac{1}{2}}=\sqrt{28}=2\sqrt{7}$$ тул $A_1$ оройгоос $EH$-д татсан өндөр $h=\dfrac{2\cdot 3\sqrt3}{2\sqrt7}$ болох тул $D_1N=\dfrac{2}{3}h=\dfrac{2\sqrt{3}}{\sqrt{7}}$ байна. Пифагорын теоремоор $$DN=\sqrt{DD_1^2+DN^2}=\sqrt{\dfrac{42}{49}+\dfrac{12}{7}}=\sqrt{\dfrac{18}{7}}=\dfrac{3\sqrt2}{\sqrt7}$$ Иймд $$\cos\varphi=\dfrac{\dfrac{2\sqrt{3}}{\sqrt{7}}}{\dfrac{3\sqrt2}{\sqrt7}}=\sqrt{\dfrac23}\Rightarrow\varphi=\arccos\sqrt{\dfrac23}$$
Дүрсийг дээрээс нь харвал проекц нь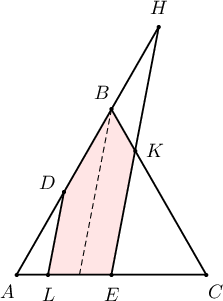
$S=S_{\triangle ABC}$ гэвэл $BK:KC=1:3$ тул $S_{\triangle EKC}=\dfrac{3}{4}\cdot\dfrac{S}{2}=\dfrac{3S}{8}$, $S_{\triangle ADL}=\dfrac{S}{2\cdot 6}=\dfrac{S}{12}$ тул проекцийн талбай нь:
$$S-\dfrac{3S}{8}-\dfrac{S}{12}=\dfrac{(24-9-2)S}{24}=\dfrac{13\cdot 4\sqrt{3}}{24}=\dfrac{13\sqrt{3}}{6}$$
тул $EKFDL$ таван өнцөгтийн талбай:
$$\dfrac{\dfrac{13\sqrt{3}}{6}}{\sqrt{\dfrac23}}=\dfrac{13\sqrt{2}}{4}$$
$ABB_1A_1$ тэгш өнцөгтийн $AB$, $BB_1$ талуудын дундаж нь $D$, $F$ цэгүүд тул $B_1H=\dfrac{A_1B_1}{2}=2$ байна. $AE=\dfrac{A_1C_1}{2}=2$ ба $\angle EA_1H=60^\circ$ тул $$S_{\triangle EA_1H}=\dfrac{1}{2}\cdot A_1H\cdot A_1E\sin60^\circ=\dfrac{1}{2}\cdot6\cdot 2\cdot\dfrac{\sqrt{3}}{2}=3\sqrt{3}$$ байна.
Мөн косинусын теоремоор $$EH=\sqrt{6^2+2^2-2\cdot 6\cdot 2\cdot\dfrac{1}{2}}=\sqrt{28}=2\sqrt{7}$$ тул $A_1$ оройгоос $EH$-д татсан өндөр $h=\dfrac{2\cdot 3\sqrt3}{2\sqrt7}$ болох тул $D_1N=\dfrac{2}{3}h=\dfrac{2\sqrt{3}}{\sqrt{7}}$ байна. Пифагорын теоремоор $$DN=\sqrt{DD_1^2+DN^2}=\sqrt{\dfrac{42}{49}+\dfrac{12}{7}}=\sqrt{\dfrac{18}{7}}=\dfrac{3\sqrt2}{\sqrt7}$$ Иймд $$\cos\varphi=\dfrac{\dfrac{2\sqrt{3}}{\sqrt{7}}}{\dfrac{3\sqrt2}{\sqrt7}}=\sqrt{\dfrac23}\Rightarrow\varphi=\arccos\sqrt{\dfrac23}$$
Дүрсийг дээрээс нь харвал проекц нь