Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Хамгийн их талбайтай адил хажуут гурвалжин
Өгөгдсөн периметртай адил хажуут гурвалжнуудаас хамгийн их талбайтайг нь ол.
Бодлогын төрөл: Уламжлалт
Бодлогыг оруулсан: Балхүүгийн Батбаясгалан
Бодолт
Заавар:
Бодолт: Гурвалжны суурь нь $2x$, хажуу тал нь $y$, периметр нь $4\ell$, талбай нь $S$ гэе. Тэгвэл $x>0$, $y>0$, $2x+2y=4\ell$.
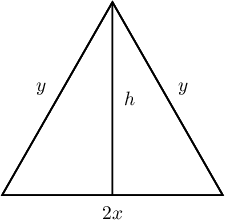Гурвалжны тэнцэтгэл биш ёсоор $y+y>2x$ тул $y>x$ байна. Гурвалжны оройгоос буусан өндрийг $h$ гэвэл $S=\dfrac 12\cdot 2xh=x\sqrt{y^2-x^2}$. Түүнчлэн $y=2\ell-x>x$ тул $0< x< \ell$ байна.
$$S^2=x^2\left((2\ell-x)^2-x^2\right)=x^2(4\ell^2-4\ell x)=4\ell^2 x^2-4\ell x^3, (S^2)^\prime =4\ell x(2\ell-3x)$$ болно. Иймд $S^2$-ийн сэжигтэй цэг нь $x=\frac{2\ell}3$.
Хүснэгтээс $x=\frac{2\ell}3$ нь максимумын цэг болох нь харагдаж байна. Иймд $x=\frac{2\ell}3$ буюу зөв гурвалжин үед хамгийн их талбайтай байна.
| $x$ | $0$ | $\boldsymbol{\ldots}$ | $2\ell/3$ | $\boldsymbol{\ldots}$ | $\ell$ |
| $(S^2)^\prime $ | $+$ | 0 | $-$ | ||
| $S^2$ | $\nearrow$ | $\max$ | $\searrow$ |