Заавар.

Бодолт. Натурал тооны квадратыг $16$-д хуваахад зөвхөн $0,1,4,9$ үлдэгдэл өгнө. Нөгөө талаас $1980=16\cdot 123+12$ юм. $$a+b+c\equiv 12\pmod{16}$$ тэгшитгэл $\{0,1,4,9\}$ олонлогт шийдгүй гэдгийг шууд шалгаж болно. Иймд тэгшитгэл шийдгүй.

Заавар.

Бодолт. $S_k =\displaystyle{\sum_{i=1}^k} a_i-\displaystyle{\sum_{i=k+1}^n} a_j$ гэж тэмдэглэе. $S_n=\displaystyle{\sum_{i=1}^n} a_i>0$ гэж үзье. $S_n<0$ байх тохиолдол нь мөн адилаар бодогдох нь бодолтоос харагдана. Иймд $$S_0 =-S, S_1, S_2,\dots, S_n=S$$ байна. $S_k$ хэмжигдэхүүн нь $S_0=-S<0$ ээс $S_n =S > 0$ хүртэлх бүх утгыг авч байгаа билээ. Иймд $S_k<0$ ба $S_{k+1}\geqslant 0$ байх $k$ дугаар заавал олдоно. Нэгэнт $S_{k+1} = S_k +2x_{k+1}$ тул $$a_{k+1}=\dfrac{S_{k+1}+(-S_k)}{2}=\dfrac{|S_{k+1}|+|S_k|}{2}$$ буюу $a_{k+1} = |a_{k+1} |$ нь $| S_{k+1}|$ ба $|S_k|$-ийн хооронд оршино. Тухайлбал, $| S_{k+1} |< | S_k|$ гэвэл $| a_{k+1} |\geqslant | S_{k+1} |$ болно. Нэгэнт $\max |a_i|\geqslant |a_k|$ тул бодлого бодогдов.

Заавар.

Бодолт. $A_1 A_2 A_3$ нь хамгийн их өнцөг нь $90^\circ$-аас үл хэтрэх гурвалжин байг. $\angle A_1\geqslant \angle A_2\geqslant \angle A_3$ гэж үзэж болно. $O$ нь багтаасан тойргийн, $I$ нь багтсан тойргийн төвүүд, $H_i$ нь $A_i$ оройгоос эсрэг талд буулгасан өндрийн сууриуд, $B_1$ нь багтсан тойргийн $A_2 A_3$ талыг, $B_2$ нь багтсан тойргийн $A_1 A_3$ талыг, $B_3$ нь багтсан тойргийн $A_1 A_2$ талыг шүргэсэн цэг нь байг. 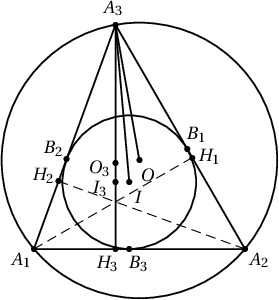Хэрэв $I$ ба $O$ цэг давхацвал $A_1 A_2 A_3$ нь зөв гурвалжин болох ба $r+R = m$ байх нь илэрхий юм. $$| A_2 B_1 |=r\cdot\ctg{\dfrac{\angle A_2}{2}}\leqslant r\cdot\ctg{\dfrac{\angle A_3}{2}}\leqslant |B_1 A_3|$$ \begin{align*} \angle OA_3B_1&=\dfrac{1}{2}(\pi-\angle A_3OA_2)=\dfrac{1}{2}(\pi-2\angle A_1)\\ &\leqslant \dfrac{1}{2}(\pi-\angle A_1-\angle A_2)=\dfrac{\angle A_3}{2}=\angle IA_3B_1 \end{align*} тул $O$ төв нь $B_1A_3I$ гурвалжны дотор юмуу тал дээр нь оршино. $$\angle H_3A_3I=\dfrac{\angle A_3}{2}-\angle A_1A_3H=\dfrac{\angle A_3}{2}-\left(\dfrac{\pi}{2}-\angle A_1\right)=\dfrac{\angle A_3}{2}-\angle OA_3B_1=\angle OA_3I$$ учир $A_3O$ ба $A_3H_3$ нь $A_3I$-ийн хувьд тэгш хэмтэйгээр байрлана. $A_3I$-ийн хувьд $O$-той тэгш хэмтэйгээр $A_3H_3$ дээр орших цэг нь $O_3$ гэвэл $|A_3O_3|=R$ харин $I$ цэгийн $A_3H_3$ дээрх ортогональ проекц нь $I_3$ гэвэл $|I_3H_3|=r$ болно. $\angle O_3IB_3>\dfrac{\pi}{2}$ тул $O_3$ цэг $|A_3I_3|$ хэрчим дээр оршино. Иймд $r+R\leqslant |A_3H_3|=m$

Заавар.

Бодолт. $a^n+b^n=c^n$ гэдгээс $a
$(a+1)^n=a^n+na^{n-1}+\cdots , b < n$ ба $b^{n-1} < a^{n-1}$ байгаа тул $c^n=a^n+b^n<(a+1)^n$ болно. Эндээс $a< c < a+1$ гэж гарах тул $c$ нь бүхэл тоо байж чадахгүй.

Заавар.

Бодолт. \begin{align*} n\sin^{n+1}{x}-n\cdot \sin^n{x}-(\sin^n{x}-1)&=n \sin^n{x}(\sin{x}-1)-(\sin{x}-1)(\sin^{n-1}{x}+\sin^{n-2}{x} +\cdots +1)\\ &=(\sin{x}-1)(n\sin^n{x}-\sin^{n-1}{x}-\cdots-1)=0 \end{align*} болох ба $0<\sin{x}<1$ бол $\sin^n{x}<\sin^{n-1}{x}<\cdots<\sin{x}< 1$ байх тул $$n\sin^n{x}-\sin^{n-1}{x}-\cdots-1\ne 0$$ болно. Иймд $\sin{x}= 1$, $x=\dfrac{\pi}{2}+2k\pi$, $k\in \mathbb{Z}$

Заавар.

Бодолт. $y_k=x_kx_{k+1}x_{k+2}x_{k+3}$, $k=1,2,\ldots, n$ гэж авъя. $y_k$ бүр $1$ юмуу $-1$ утгыг авах ба $y_1+\cdots+y_n=0$ билээ. Эндээс $n=2m$ болох ба $y_k$-уудын $m$ нь $1$-тэй, $m$ нь $-1$-тэй тэнцүү байна. Иймд $$y_1\cdots y_n=(-1)^m$$ болно. Энэ үржвэрт $x_j$ бүр 4 удаа орж байгаа тул $$y_1\cdots y_n=(-1)^m=\big(\prod x_i\big)^4=1.$$ Иймд $m=2p, n=2m=4p$ болж батлагдав.