Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Holy guacamole! www.integral.mn сайт 2026-01-01-ээс шинэчлэгдэж www.mathminds.club хуудас руу шилжинэ.
Геометр хувиргалт
Гомотет
Тэгш өнцөгт параллелепепидийн урт, өргөн, өндрийг нь тус бүр 3 дахин ихэсгэв. Эхлэхүүн нь хэд дахин ихсэх вэ?
A. $3$
B. $6$
C. $9$
D. $18$
E. $27$
$ |2x-1|+|x+5|=10 $ тэгшитгэл бод.
A. $ {-4, -\frac{14}{3}} $
B. $ {-4, 2,\frac{14}{3}}$
C. $ {-4, 2}$
D. $ {2. -\frac{14}{3}$
E. $ {2} $
$A(3; 0 ), B(2; 2), C(3; 2)$ цэгүүдэд оройтой гурвалжныг гомотетоор хувиргахад $ А(1; -2), B(-2; 4), C(1; 4) $ цэгүүдэд оройтой гурвалжин үүсчээ. Гомотетын төвийн координатуудыг олоорой.
A. $(4, 0)$
B. $(3, 1)$
C. $(3, 0)$
D. $(1, 4)$
E. $(4, 1)$
$A(-3; 0 ), B(-4; 2), C(-3; 2)$ цэгүүдэд оройтой гурвалжныг гомотетоор хувиргахад $ А(1; -2), B(-2; 4), C(1; 4) $ цэгүүдэд оройтой гурвалжин үүсчээ. Гомотетын төвийн координатуудыг олоорой.
A. $(5, 1)$
B. $(-5, 1)$
C. $(-5, 0)$
D. $(1, 5)$
E. $(0, 0)$
$A(-3; 0 ), B(-4; 2), C(-3; 2)$ цэгүүдэд оройтой гурвалжныг гомотетоор хувиргахад $ А(-1; -1), B(-3; 3), C(-1; 3) $ цэгүүдэд оройтой гурвалжин үүсчээ. Гомотетын төвийн координатуудыг олоорой.
A. $(5, 1)$
B. $(-5, 1)$
C. $(-5, 0)$
D. $(1, 5)$
E. $(0, 0)$
Параллель зөөлт
Төвийн тэгш хэм
Транвекц
Тэнхлэгийн тэгш хэм
$A(3,2)$ цэгийг координатын эх дээр төвтэй $k=-2$ коэффициенттэй гомотетоор хувиргахад $B$ цэг, харин $y$ тэнхлэгийн хувьд тэгш хэмтэй хувиргахад $C$ цэг үүсэв. $ABC$ гурвалжны талбайг олоорой.
$A(1;3)$ цэгийг $y=x$ шулууны хувьд хувиргахад гарах дүрийн коодинатыг ол.
A. $(3;-1)$
B. $(3;1)$
C. $(-1;3)$
D. $(-3;1)$
E. $(-1;-3)$
$P(3;-2)$ цэгийг $OX$ тэнхлэгийн хувьд тэгш хэмтэй хувиргахад ямар цэг гарах вэ?
A. $(-3;2)$
B. $(-2;-3)$
C. $(-3;-2)$
D. $(-2;3)$
E. $(3;2)$
$A(3;1)$ цэгийг $y=2x$ шулууны хувьд тэгш хэмтэй хувиргахад гарах дүрийн коодинатыг ол.
A. $(3;-1)$
B. $(-3;-1)$
C. $(-1;3)$
D. $(-3;1)$
E. $(-1;-3)$
$A(3;1)$ цэгийг $y=x$ шулууны хувьд хувиргахад гарах дүрийн коодинатыг ол.
A. $(-1;-3)$
B. $(3;-1)$
C. $(1;3)$
D. $(3;1)$
E. $(-1;-3)$
Хувиргалтыг матрицаар илэрхийлэх
$\begin{pmatrix} 0 & 1\\ 1 & 0\end{pmatrix}$ матриц ямар хувиргалт тодорхойлох вэ?
A. эргүүлэлт
B. гомотет
C. тэнхлэгийн тэгш хэм
D. төвийн тэгш хэм
E. параллел зөөлт
$\begin{pmatrix} 0 & -1\\ 1 & \phantom{-}0\end{pmatrix}$ матриц ямар хувиргалт тодорхойлох вэ?
A. төвийн тэгш хэм
B. гомотет
C. тэнхлэгийн тэгш хэм
D. параллел зөөлт
E. эргүүлэлт
$A(1,1)$, $B(1,4)$, $C(3,1)$ цэгүүдэд оройтой гурвалжин өгчээ.
- Энэ гурвалжныг координатын эх дээр төвтэй, цагийн зүүний эсрэг $90^\circ$ өнцгөөр эргүүлэхэд үүсэх $A_1B_1C_1$ гурвалжны цэгүүдийн координатуудыг олбол $A_1(-\fbox{a},1)$ (1 оноо), $B_1(-\fbox{b},1)$ (1 оноо) , $C_1(-1,\fbox{c})$ (1 оноо)
- $A_1$, $B_1$, $C_1$ цэгүүдийн координатуудыг ашиглан хувиргалтын матрицыг олбол $\begin{pmatrix} \fbox{d} & -\fbox{e}\\ \fbox{f} & \phantom{-}\fbox{g} \end{pmatrix}$ (4 оноо)
$A(1,1)$, $B(1,4)$, $C(3,1)$ цэгүүдэд оройтой гурвалжин өгчээ.
- Энэ гурвалжныг координатын эх дээр төвтэй, цагийн зүүний эсрэг $90^\circ$ өнцгөөр эргүүлэхэд үүсэх $A_1B_1C_1$ гурвалжны цэгүүдийн координатуудыг олбол $A_1(-\fbox{a},1)$ (1 оноо), $B_1(-\fbox{b},1)$ (1 оноо) , $C_1(-1,\fbox{c})$ (1 оноо)
- $A_1$, $B_1$, $C_1$ цэгүүдийн координатуудыг ашиглан хувиргалтын матрицыг олбол $\begin{pmatrix} \fbox{d} & -\fbox{e}\\ \fbox{f} & \phantom{-}\fbox{g} \end{pmatrix}$ (4 оноо)
$A(1,1)$, $B(1,4)$, $C(3,1)$ цэгүүдэд оройтой гурвалжин өгчээ.
- Энэ гурвалжныг координатын эх дээр төвтэй, цагийн зүүний эсрэг $90^\circ$ өнцгөөр эргүүлэхэд үүсэх $A_1B_1C_1$ гурвалжны цэгүүдийн координатуудыг олбол $A_1(-\fbox{a},1)$ (1 оноо), $B_1(-\fbox{b},1)$ (1 оноо) , $C_1(-1,\fbox{c})$ (1 оноо)
- $A_1$, $B_1$, $C_1$ цэгүүдийн координатуудыг ашиглан хувиргалтын матрицыг олбол $\begin{pmatrix} \fbox{d} & -\fbox{e}\\ \fbox{f} & \phantom{-}\fbox{g} \end{pmatrix}$ (4 оноо)
$A(2,1)$, $B(2,4)$, $C(4,1)$ цэгүүдэд оройтой гурвалжин өгчээ.
- Энэ гурвалжныг координатын эх дээр төвтэй, цагийн зүүний эсрэг $90^\circ$ өнцгөөр эргүүлэхэд үүсэх $A_1B_1C_1$ гурвалжны цэгүүдийн координатуудыг олбол $A_1(-\fbox{a},2)$ (1 оноо), $B_1(-\fbox{b},2)$ (1 оноо) , $C_1(-1,\fbox{c})$ (1 оноо)
- $A_1$, $B_1$, $C_1$ цэгүүдийн координатуудыг ашиглан хувиргалтын матрицыг олбол $\begin{pmatrix} \fbox{d} & -\fbox{e}\\ \fbox{f} & \phantom{-}\fbox{g} \end{pmatrix}$ (4 оноо)
Хувиргалтыг таних, тодорхойлох
Дараах хувиргалтуудын аль нь $A(2,2)$ цэгийг $B(-2,2)$ цэгт буулгахгүй вэ?
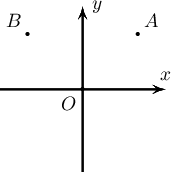

A. $OY$ тэнхлэгийн хувьд тэгш хэм
B. $O$ цэгт төвтэй цагийн зүүний эсрэг чиглэлд $90^\circ$ эргүүлэлт
C. $\overrightarrow{AB}$ векторын дагуу параллел зөөлт
D. Координатын эх дээр төвтэй төвийн тэгш хэм
E. Дээрх хувиргалтууд бүгд $A$ цэгийг $B$ цэгт буулгана
Дараах хувиргалтуудын аль нь $A(2,2)$ цэгийг $B(-2,-2)$ цэгт буулгах вэ?
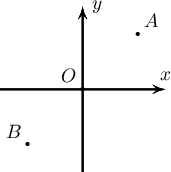

A. $OX$ тэнхлэгийн хувьд тэгш хэм
B. $O$ цэгт төвтэй төвийн тэгш хэм
C. $\overrightarrow{BA}$ векторын дагуу параллел зөөлт
D. $B$ цэгт төвтэй төвийн тэгш хэм
E. $OY$ тэнхлэгийн хувьд тэгш хэм
Дараах хувиргалтуудын аль нь $A$ дүрсийг $B$ дүрсэд буулгах вэ?
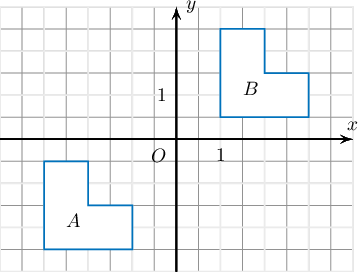

A. $OX$ тэнхлэгийн хувьд тэгш хэм
B. $O$ цэгт төвтэй төвийн тэгш хэм
C. $(4,3)$ векторын дагуу параллел зөөлт
D. $x=-y$ шулууны хувьд тэнхлэгийн тэгш хэм
E. $OY$ тэнхлэгийн хувьд тэгш хэм
$A(1,1)$, $B(1,4)$, $C(3,1)$ цэгүүдэд оройтой гурвалжин өгчээ.
- Энэ гурвалжныг координатын эх дээр төвтэй, цагийн зүүний эсрэг $90^\circ$ өнцгөөр эргүүлэхэд үүсэх $A_1B_1C_1$ гурвалжны цэгүүдийн координатуудыг олбол $A_1(-\fbox{a},1)$ (1 оноо), $B_1(-\fbox{b},1)$ (1 оноо) , $C_1(-1,\fbox{c})$ (1 оноо)
- $A_1$, $B_1$, $C_1$ цэгүүдийн координатуудыг ашиглан хувиргалтын матрицыг олбол $\begin{pmatrix} \fbox{d} & -\fbox{e}\\ \fbox{f} & \phantom{-}\fbox{g} \end{pmatrix}$ (4 оноо)
$A(1,1)$, $B(1,4)$, $C(3,1)$ цэгүүдэд оройтой гурвалжин өгчээ.
- Энэ гурвалжныг координатын эх дээр төвтэй, цагийн зүүний эсрэг $90^\circ$ өнцгөөр эргүүлэхэд үүсэх $A_1B_1C_1$ гурвалжны цэгүүдийн координатуудыг олбол $A_1(-\fbox{a},1)$ (1 оноо), $B_1(-\fbox{b},1)$ (1 оноо) , $C_1(-1,\fbox{c})$ (1 оноо)
- $A_1$, $B_1$, $C_1$ цэгүүдийн координатуудыг ашиглан хувиргалтын матрицыг олбол $\begin{pmatrix} \fbox{d} & -\fbox{e}\\ \fbox{f} & \phantom{-}\fbox{g} \end{pmatrix}$ (4 оноо)
$A(1,1)$, $B(1,4)$, $C(3,1)$ цэгүүдэд оройтой гурвалжин өгчээ.
- Энэ гурвалжныг координатын эх дээр төвтэй, цагийн зүүний эсрэг $90^\circ$ өнцгөөр эргүүлэхэд үүсэх $A_1B_1C_1$ гурвалжны цэгүүдийн координатуудыг олбол $A_1(-\fbox{a},1)$ (1 оноо), $B_1(-\fbox{b},1)$ (1 оноо) , $C_1(-1,\fbox{c})$ (1 оноо)
- $A_1$, $B_1$, $C_1$ цэгүүдийн координатуудыг ашиглан хувиргалтын матрицыг олбол $\begin{pmatrix} \fbox{d} & -\fbox{e}\\ \fbox{f} & \phantom{-}\fbox{g} \end{pmatrix}$ (4 оноо)
$A(2,1)$, $B(2,4)$, $C(4,1)$ цэгүүдэд оройтой гурвалжин өгчээ.
- Энэ гурвалжныг координатын эх дээр төвтэй, цагийн зүүний эсрэг $90^\circ$ өнцгөөр эргүүлэхэд үүсэх $A_1B_1C_1$ гурвалжны цэгүүдийн координатуудыг олбол $A_1(-\fbox{a},2)$ (1 оноо), $B_1(-\fbox{b},2)$ (1 оноо) , $C_1(-1,\fbox{c})$ (1 оноо)
- $A_1$, $B_1$, $C_1$ цэгүүдийн координатуудыг ашиглан хувиргалтын матрицыг олбол $\begin{pmatrix} \fbox{d} & -\fbox{e}\\ \fbox{f} & \phantom{-}\fbox{g} \end{pmatrix}$ (4 оноо)