Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Holy guacamole! www.integral.mn сайт 2026-01-01-ээс шинэчлэгдэж www.mathminds.club хуудас руу шилжинэ.
Бином
Биномын ерөнхий гишүүний томьёо
$\Big(\sqrt{x}+\dfrac{1}{\sqrt[3]{x}}\Big)^{15}$ биномын задаргааны $x^5$-г агуулсан гишүүний дугаар хэд вэ?
A. $10$
B. $8$
C. $9$
D. $4$
E. $5$
$k$ нь 20-оос бага натурал тоо бол $C_{20}^k$ илэрхийлэл аль илэрхийлэлтэй тэнцүү вэ?
A. $\dfrac{20!}{k!}$
B. $A_{20}^k$
C. $A_{21}^{k+1}$
D. $C_{21}^{k+1}$
E. $C_{20}^{20-k}$
$\Big(x+\dfrac2x\Big)^6$-ийн задаргааны $x$-г агуулаагүй гишүүнийг ол.
A. $165$
B. $200$
C. $180$
D. $160$
E. $140$
$(x^2+1)^{2015}$-ийн задаргааны $x^{10}$ өмнөх коэффициент аль нь вэ?
A. $C_{2015}^{10}$
B. $A_{2015}^{2005}$
C. $P_{2005}$
D. $\dfrac{2015!}{5!\cdot 2010!}$
E. $\dfrac{2015!}{5!}$
$\Big(x+\dfrac1{x^2}\Big)^{9}$-ийн задаргааны $x$ агуулаагүй гишүүнийг ол.
A. $C_9^1$
B. $A_9^2$
C. $C_9^6$
D. $C_9^5$
E. $A_9^6$
$(x+y)^{12}$ биномын задаргаа дахь хамгийн их коэффициент аль вэ?
A. $C_{12}^5$
B. $C_{12}^6$
C. $C_{12}^7$
D. $C_{12}^8$
E. $C_{12}^9$
$\Bigl(\sqrt x-\dfrac{\sqrt2}{\sqrt[4]x}\Bigr)^8$ биномын дундаж гишүүн аль вэ?
A. $-70x$
B. $-280x$
C. $280x$
D. $140x$
E. $70x$
$(3x-y)^8$ биномын $x^3y^5$ ба $x^5y^3$-ын өмнөх коэффициентүүдийн нийлбэр аль вэ?
A. $216C_8^3$
B. $-216C_8^3$
C. $270C_8^3$
D. $-270C_8^3$
E. $-135C_8^3$
$(x-2y)^8$ биномын $x^6y^2$ ба $x^2y^6$-ын өмнөх коэффициентүүдийн нийлбэр аль вэ?
A. $60C_8^2$
B. $-60C_8^2$
C. $68C_8^2$
D. $-68C_8^2$
E. $64C_8^2$
$\Bigl(x^5+\dfrac1{x^3}\Bigr)^{50}$ биномын $C_{50}^nx^{10}$
гишүүнд оpж буй $n$-ын утга аль вэ?
A. $22$
B. $24$
C. $25$
D. $30$
E. $40$
$\Bigl(x^5+\dfrac1{x^2}\Bigr)^{21}$ биномын $x$-ийг агуулаагүй гишүүн (сул гишүүн)-ний дугаар хэд вэ?
A. $10$
B. $12$
C. $15$
D. $16$
E. $18$
$\Bigl(2x^3-\dfrac1{4x^2}\Bigr)^9$ биномын эхнээсээ 4-р гишүүн аль вэ?
A. $-84x^{12}$
B. $168x^{18}$
C. $-168x^{18}$
D. $84x^{12}$
E. $-32x^{18}$
$\Bigl(\dfrac x4-2x^{-1}\Bigr)^{10}$ биномын эхнээсээ 7-р гишүүн аль вэ?
A. $210x^{-2}$
B. $-\dfrac{155}{2x^2}$
C. $\dfrac{105}{2x^2}$
D. $-210x^{-2}$
E. $-\dfrac{155}{2x^2}$
$y=(x^2+1)^{100}$ функцийн $y'$ уламжлалын $mx^{41}$ нэмэгдэхүүний коэффициент $m$ аль вэ?
A. $200C_{100}^{20}$
B. $200C_{99}^{20}$
C. $200C_{99}^{21}$
D. $200C_{100}^{21}$
E. $100C_{99}^{20}$
$y=(\sqrt x+1)^{20}$ функцийн уламжлал $y^\prime$-ын $mx^7$ нэмэгдэхүүний коэффициент $m$ аль вэ?
A. $10C_{20}^4$
B. $20C_{19}^4$
C. $10C_{19}^4$
D. $C_{19}^4$
E. $8C_{19}^4$
$(1+x)^n$ биномын задаргааны эхнээсээ 2,3 ба 4-р гишүүдийн коэффициентүүд арифметик прогресс үүсгэх $n$-ийн утгын олонлог аль вэ?
A. $\{10,7\}$
B. $\{9,7\}$
C. $\{8,2\}$
D. $\{2,7\}$
E. $\{7,9\}$
$(1+x)^n$ биномын задаргааны 5,6 ба 7-р гишүүдийн коэффициентүүд арифметик прогресс үүсгэх $n$-ийн утгын олонлог аль вэ?
A. $\{1,14\}$
B. $\{2,14\}$
C. $\{7,2\}$
D. $\{7,14\}$
$\Bigl(2\sqrt[x]{2^{-1}}+\dfrac4{\sqrt[4-x]4}\Bigr)^6$ биномын задаргааны эхнээсээ гурав дахь гишүүн нь 240 бол $x$-ийн утгын олонлог аль вэ?
A. $\{3,0\}$
B. $\{4,3\}$
C. $\{2\}$
D. $\{1,3\}$
E. $\{2,0\}$
$\biggl(\dfrac{\sqrt[5]{a^4}}{a^{\frac{x-1}x}}+a\cdot a^{\frac{x-1}{x+1}}\biggr)^8$ биномын задаргааны эхнээсээ дөрөв дэх гишүүн нь $56a^{5.5}$ бол $x$-ийн утгын олонлог аль вэ?
A. $\{4,2\}$
B. $\{3,5\}$
C. $\{-5,2\}$
D. $\{1,2\}$
$(2x+5)^{10}$ биномын задаргааны $x^5$-ийн өмнөх коэффициентийг ол.
A. $63\cdot 2^3\cdot 5^5$
B. $63\cdot 2^7\cdot 5^5$
C. $63\cdot 2^2$
D. $2^7\cdot 5^5$
E. $63\cdot 2^5\cdot 5^7$
$(2a+3b)^5$-ийн $a^4$-ийг агуулсан гишүүнийг бич.
A. $240a^4b$
B. $5a^4b$
C. $30a^4b$
D. $120a^4b$
E. $60a^4b$
$(3x+2)^{12}$ биномын задаргааны $x^5$-ийн өмнөх коэффициентийг ол.
A. $11\cdot 2^7\cdot 3^9$
B. $11\cdot 2^9\cdot 3^7$
C. $11\cdot 2^9\cdot 3^3$
D. $2^7\cdot 3^5$
E. $11\cdot 2^{10}\cdot 3^7$
$(2x+3)^{8}$ биномын задаргааны $x^4$-ийн өмнөх коэффициентийг ол.
A. $70$
B. $2^4\cdot 3^4$
C. $35\cdot 2^5\cdot 3^4$
D. $70\cdot 3^4$
E. $35\cdot 2^5$
$(2x+1)^{10}$ биномын задаргааны $x^3$-ийн өмнөх коэффициентийг ол.
A. $2^3$
B. $2^{10}$
C. $15\cdot 2^6$
D. $15\cdot 2^{10}$
E. $15\cdot 2^{13}$
$\Big(x-\dfrac2{x^2}\Big)^6$ задаргааны $x$ агуулаагүй тогтмол гишүүнийг ол.
A. $32$
B. $36$
C. $48$
D. $60$
E. $64$
$\Big(2x^2-\dfrac1x\Big)^6$ задаргааны $x$ агуулаагүй тогтмол гишүүнийг ол.
A. 32
B. 36
C. 48
D. 60
E. 64
$y=(\sqrt[3]{x}+1)^{100}$ функцийн уламжлалын $x^{10}$ өмнөх коэффициент нь хэдтэй тэнцүү вэ?
A. $C_{100}^{30}$
B. $10C_{100}^{31}$
C. $11\cdot C_{100}^{11}$
D. $10C_{100}^{33}$
E. $11C_{100}^{33}$
$a>0$ ба $(a+x)^5$-ийн задаргааны $x^4$ ба $x^3$-ын өмнөх коэффицентүүдийн нийлбэр 50 бол $a$-г ол.
A. $1$
B. $2$
C. $3$
D. $4$
E. $5$
$a<0$ ба $(a+x)^5$-ийн задаргааны $x^4$ ба $x^3$-ын өмнөх коэффицентүүдийн нийлбэр 5 бол $a$-г ол.
A. $0$
B. $-1$
C. $-2$
D. $-3$
E. $-4$
$C_{20}^0+5\cdot C_{20}^1+25\cdot C_{20}^2+\dots+5^{19}\cdot C_{20}^{19}+5^{20}\cdot C_{20}^{20}$ нийлбэрийг ол.
A. $3^{20}$
B. $6^{20}$
C. $5^{20}$
D. $4^{20}$
E. $2^{20}$
$3^{100}\cdot C_{100}^{100}-3^{99}\cdot C_{100}^{99}+3^{98}\cdot C_{100}^{98}-\cdots-3^{1}\cdot C_{100}^1+1$ нийлбэрийг олоорой!
A. $2$
B. $3^{100}$
C. $2^{100}$
D. $2^{101}$
E. олох боломжгүй
$3^{50}\cdot C_{50}^{50}-3^{49}\cdot C_{50}^{49}+3^{48}\cdot C_{50}^{48}-\cdots-3^{1}\cdot C_{50}^1+1$ нийлбэрийг олоорой!
A. $2$
B. $3^{50}$
C. $2^{50}$
D. $2^{51}$
E. олох боломжгүй
$2^{100}\cdot C_{100}^{100}-2^{99}\cdot C_{100}^{99}+2^{98}\cdot C_{100}^{98}-\cdots-2^{1}\cdot C_{100}^1+1$ нийлбэрийг олоорой!
A. $2$
B. $1$
C. $2^{100}$
D. $2^{101}$
E. олох боломжгүй
$2^{50}\cdot C_{50}^{50}-2^{99}\cdot C_{50}^{49}+2^{98}\cdot C_{50}^{48}-\cdots-2^{1}\cdot C_{50}^1+1$ нийлбэрийг олоорой!
A. $1$
B. $2$
C. $2^{50}$
D. $2^{51}$
E. олох боломжгүй
$2^{100}\cdot C_{100}^{100}-2^{99}\cdot C_{100}^{99}+2^{98}\cdot C_{100}^{98}-\cdots-2^{1}\cdot C_{100}^1+1$ нийлбэрийг олоорой!
A. $2$
B. $1$
C. $2^{100}$
D. $2^{101}$
E. олох боломжгүй
$\left(2x^2+\dfrac{1}{x}\right)^9$ биномыг задлахад гарах $x$-ийг агуулаагүй гишүүнийг ол.
A. $C_9^3$
B. $2^2\cdot C_9^2$
C. $8C_9^6$
D. $2^6C_9^6$
E. $1$
$(2x+5)^{10}$ биномын задаргааны $x^5$-ийн өмнөх коэффициентийг ол.
A. $63\cdot 2^3\cdot 5^5$
B. $63\cdot 2^7\cdot 5^5$
C. $63\cdot 2^2$
D. $2^7\cdot 5^5$
E. $63\cdot 2^5\cdot 5^7$
$(1-2y+3c)^{35}$-ийн задаргааны коэффициентүүдийн нийлбэрийг олоорой.
A. 1
B. $6^{35}$
C. 2
D. $2^{35}$
$(x-y)^{4}$ биномын задралыг бичээрэй.
A. $x^{4}-4x^{3}y+6x^{2}y^{2}-4xy^{3}+y^{4}$
B. $x^{4}-4x^{3}y-4xy^{3}+y^{4}$
C. $x^{4}4x^{3}y+6x^{2}y^{2}+4xy^{3}+y^{4}$
D. $x^{4}-4x^{3}y-6x^{2}y^{2}-4xy^{3}+y^{4}$
$(a^{2}+2b)^{10}$-ийн задаргааны 4-р гишүүнийг олоорой.
A. $120a^{14}b^{3}$
B. $240a^{14}b$
C. $960a^{14}b^{3}$
D. $960a^{7}b^{3}$
E. $240a^{14}b^3$
$(x-y+c)^{3}$ гурван гишүүнтийн задаргааг олоорой.
A. $x^3+y^3+c^3-3x^2y+3x^2c+3y^2x+3y^2c+3c^2x-3c^2y$
B. $x^3-y^3+c^3-3x^2y+3x^2c+3y^2x+3y^2c+3c^2x-3c^2y-6xyc$
C. $x^3-y^3+c^3-3x^2y+3x^2c+3y^2x+3y^2c-3c^2y-6xyc$
D. $x^3+y^3+c^3-3x^2y+3x^2c+3y^2x+3y^2c+3c^2x-3c^2y+6xyc$
$O(0,0)$ цэгээс $B(3,6)$ цэг хүртэлх богино замын тоог олоорой.
A. 20
B. 72
C. 80
D. 84
$A(3,4)$ цэгээс $B(6,6)$ цэг хүртлэх богино замын тоог олоорой.
A. 10
B. 30
C. 15
D. 40
$\Big(\sqrt{x}+\dfrac{1}{\sqrt[3]{x}}\Big)^{15}$ биномын задаргааны $x^5$-г агуулсан гишүүний дугаар хэд вэ?
A. $10$
B. $8$
C. $9$
D. $4$
E. $5$
$3^{50}\cdot C_{50}^{50}-3^{49}\cdot C_{50}^{49}+3^{48}\cdot C_{50}^{48}-\cdots-3^{1}\cdot C_{50}^1+1$ нийлбэрийг олоорой!
A. $2$
B. $3^{50}$
C. $2^{50}$
D. $2^{51}$
E. олох боломжгүй
$(\sqrt[3]{3}+\sqrt{2})^{5}$ биномын задаргааны рационал гишүүн нь $\fbox{ab}$ байна.
$(\sqrt[3]{2}+\sqrt[4]{3})^{7}$ биномын задаргааны рационал гишүүн нь $\fbox{abc}$ байна.
$\left(x^2+\dfrac 1x\right)^m$ бином задаргааны нэг,
хоёр ба гуравдугаар гишүүний коэффициентуудын нийлбэр 46-тай
тэнцүү бол $m=\fbox{a}$ ба $x$ оролцоогүй гишүүн нь $\fbox{bc}$ байна.
$\left(x\sqrt x+\dfrac{1}{x^2}\right)^m$ бином задаргааны бүх коэффициентуудын нийлбэр 128 бол
$m=\fbox{a}$ ба $x$ оролцоогүй гишүүн нь $\fbox{bc}$ байна.
Комбинаторикийн томьёонууд
$3\cdot C_{x-1}^2+(x-2)P_2=4\cdot A_{x-2}^2$
A. $3$
B. $4$
C. $5$
D. $6$
E. $7$
$n$ нь 10-аас бага натурал тоо бол $C_{10}^{n} $ илэрхийлэл аль илэрхийлэлтэй тэнцүү вэ?
A. $C_{10}^{11-n}$
B. $n!A_{10}^{n}$
C. $C_{10}^{10-n}$
D. $\dfrac{A_{10}^{n} }{(10-n)!} $
E. $C_{11}^{10-n} $
$C_{18}^n=C_{18}^{n+2}$ бол $7\cdot C_n^7=A_{x+1}^2$ тэгшитгэлийн язгуур $x$ хэдтэй тэнцүү вэ?
A. $10$
B. $9$
C. $8$
D. $7$
E. $6$
$A_x^y=156$, $C_x^y=78$ бол $P_{(x-y)}$ нь хэдтэй тэнцүү вэ?
A. $11$
B. $10!$
C. $8!$
D. $11!$
E. $9!$
$(y+1)^6=y^6+6y^5+ay^4+20y^3+by^2+6y+1$ бол $a+b$-г ол.
A. $15$
B. $30$
C. $35$
D. $20$
E. $28$
$8!\cdot C_{10}^2=?$
A. $0$
B. $10\cdot 8!$
C. $C_{10}^8$
D. $A_{10}^2$
E. $A_{10}^8$
$C_7^5=?$
A. 7
B. 14
C. 21
D. 35
E. 42
$A_{n+2}^4=6\cdot P_4\cdot C_{n}^{n-2}$ тэгшитгэл бод.
A. 4
B. 5
C. 6
D. 7
E. 8
$A_6^4$ хэдтэй тэнцүү вэ?
A. $1296$
B. $216$
C. $316$
D. $360$
E. $36$
$n$ нь $15$-аас бага натурал тоо бол $C_{15}^n$ илэрхийлэл аль илэрхийлэлтэй тэнцүү вэ?
A. $A_{16}^{n+1}$
B. $A_{15}^{n}$
C. $C_{16}^{n+1}$
D. $C_{15}^{15-n}$
E. $C_{16}^n$
$C_7^2=?$
A. 7
B. 14
C. 21
D. 35
E. 42
$A_6^4$ хэдтэй тэнцүү вэ?
A. $1296$
B. $216$
C. $316$
D. $360$
E. $36$
$C_8^2=?$
A. 7
B. 14
C. 21
D. 35
E. 28
$7!\cdot C_{10}^3=?$
A. $0$
B. $10\cdot 7!$
C. $C_{10}^7$
D. $A_{10}^3$
E. $A_{10}^7$
$ (\frac{1}{x-1}+\frac{x^2-3x}{x^2-1}) : \frac{2x-2}{x^2-x-2}$ илэрхийллийг хялбарчил.
A. $ \frac{x+2}{2}$
B. $ \frac{(x-1)(x+2)}{2(x+1)}$
C. $ \frac{(x-1)(x-2)}{2(x+1)}$
D. $ \frac{x-2}{2}$
E. $ \frac{x+1}{2}$
$C_{18}^n=C_{18}^{n+2}$ бол $7\cdot C_n^7=A_{x+1}^2$ тэгшитгэлийн язгуур $x$ хэдтэй тэнцүү вэ?
A. $10$
B. $9$
C. $8$
D. $7$
E. $6$
$A_x^y=156$, $C_x^y=78$ бол $P_{(x-y)}$ нь хэдтэй тэнцүү вэ?
A. $11$
B. $10!$
C. $8!$
D. $11!$
E. $9!$
$C_x^7=C_x^5$ байх $x$-ийн хувьд $\dfrac{P_x}{A_x^2}=?$
A. $ \dfrac{1}{10!}$
B. $ {10!}$
C. $12!$
D. $7!$
E. $5!$
$C_x^6=C_x^4$ байх $x$-ийн хувьд $\dfrac{P_x}{A_x^2}=?$
A. ${9!}$
B. $\dfrac{1}{8!}$
C. $10!$
D. $8!$
E. $7!$
$C_x^6=C_x^4$ байх $x$-ийн хувьд $\dfrac{P_x}{A_x^2}=?$
A. $ {9!}$
B. $ \frac{1} {10!}$
C. $10!$
D. $8!$
E. $7!$
$$x_{n}=\dfrac{A_{n+4}^{4}}{P_{n+2}}-\dfrac{143}{4P_{n}}, (n=1, 2, 3, \ldots)$$ дараалал $\fbox{a}$ ширхэг сөрөг гишүүнтэй.
$$x_{n}=C_{n+3}^{2}-\dfrac{48}{187}C_{n+4}^{n} (n=1, 2, 3, \ldots)$$ дараалал $\fbox{a}$ ширхэг эерэг гишүүнтэй.
Паскалийн гурвалжин
$C_{10}^2=45$, $C_{10}^3=\dfrac{10\cdot 9\cdot 8}{3!}=120$ болохыг ашиглан $C_{11}^3$-ийг ол.
A. 85
B. 125
C. 145
D. 165
E. 180
Полиномын задаргаа
$(3a+2b+c)^{27}$ задаргааны $a^4\cdot b^2\cdot c^{21}$ гишүүний коэффициентийг ол.
A. $\dfrac{6\cdot 27!}{4!\cdot 2!\cdot 2!}$
B. $324\cdot C_{27}^2\cdot C_{27}^4\cdot C_{27}^{21}$
C. $\dfrac{324\cdot 27!}{4!\cdot 2!\cdot 21!}$
D. $324\cdot A_{27}^2\cdot A_{27}^4\cdot A_{27}^{21}$
E. $324\cdot P_2\cdot P_4\cdot P_{21}$
$(1+2y+2x)^3$ задаргааны бүх коэффициентүүдийн нийлбэрийг ол.
A. 125
B. $\dfrac{6!}{1!2!3!}$
C. 120
D. 100
E. 80
$(2x+3y+z)^{30}$ олон гишүүнтийн коэффициентүүдийн алгебр нийлбэр аль вэ?
A. $3^{30}$
B. $1$
C. $2^{30}$
D. $5^{30}$
E. $6^{30}$
$(x+y+z)^{10}$ биномын $mx^4y^4z^2$ гишүүний өмнөх коэффициент $m$ аль вэ?
A. $5880$
B. $3150$
C. $9450$
D. $1260$
E. $3200$
$(x-y+z)^8$ биномын $mx^3y^2z^3$-ын өмнөх $m$ коэффициент аль вэ?
A. $560$
B. $-560$
C. $280$
D. $-280$
E. $256$
$(1-2x+3y)^{30}$ биномын коэффициентүүдийн алгебр нийлбэр аль вэ?
A. $3^{30}$
B. $1$
C. $2^{30}$
D. $5^{30}$
E. $6^{30}$
$(-1+2x-3y)^{25}$ биномын коэффициентүүдийн алгебр нийлбэр аль вэ?
A. $2^{25}$
B. $-3^{25}$
C. $-2^{25}$
D. $-1$
E. $3^{25}$
$(1+x+y)^{2015}$-ийн задаргааны бүх коэффициентүүдийн нийлбэр хэдтэй тэнцүү вэ?
A. $2^{2015}$
B. $3^{2015}-2^{2015}$
C. $3^{2015}$
D. $2\cdot 3^{2015}$
E. $1$
$(5a+3b+c)^{27}$ задаргааны $a^2\cdot b^2\cdot c^{23}$ гишүүний коэффициентийг ол.
A. $\dfrac{225\cdot 27!}{2!\cdot 2!\cdot 23!}$
B. $225\cdot C_{27}^2\cdot C_{27}^2\cdot C_{27}^{23}$
C. $\dfrac{15\cdot 27!}{2!\cdot 2!\cdot 23!}$
D. $15\cdot A_{27}^2\cdot A_{27}^4\cdot A_{27}^{21}$
E. $15\cdot P_2\cdot P_4\cdot P_{21}$
$(1-2y-2x)^4$ задаргааны бүх коэффициентүүдийн нийлбэрийг ол.
A. $64$
B. $\dfrac{6!}{1!2!3!}$
C. $120$
D. $36$
E. $81$
$(3a+2b+c)^{27}$ задаргааны $a^4\cdot b^2\cdot c^{21}$ гишүүний коэффициентийг ол.
A. $\dfrac{6\cdot 27!}{4!\cdot 2!\cdot 2!}$
B. $324\cdot C_{27}^2\cdot C_{27}^4\cdot C_{27}^{21}$
C. $\dfrac{324\cdot 27!}{4!\cdot 2!\cdot 21!}$
D. $324\cdot A_{27}^2\cdot A_{27}^4\cdot A_{27}^{21}$
E. $324\cdot P_2\cdot P_4\cdot P_{21}$
$(1-2y-2x)^4$ задаргааны бүх коэффициентүүдийн нийлбэрийг ол.
A. $64$
B. $\dfrac{6!}{1!2!3!}$
C. $120$
D. $36$
E. $81$
$(1+x^2-x^3)^9$ олон гишүүнтийн $x^8$ илэрхийллийг агуулсан гишүүний өмнөх коэффициент $\fbox{abc}$ байна.
$(1+x+\frac{6}{x})^{5}$ олон гишүүнтийн $x$-ийн зэргийг
агуулаагүй гишүүн $\fbox{abcd}$-тэй тэнцүү байна.
Траекторын арга
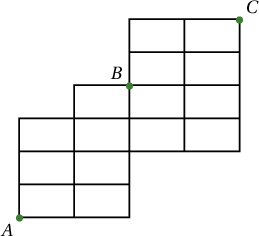
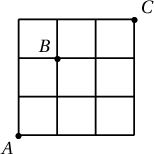
$A$ цэгээс эхлэн эсвэл дээш 1 нэгж, эсвэл баруун тийш 1 нэгж явсаар $B$ цэгийг дайран $C$ цэгт очих бүх ялгаатай замын тоог ол.

A. $9$
B. $8$
C. $10$
D. $11$
E. $12$