Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Тойрог ба дугуй
Дугуйн талбай
Огтлогч шулуун
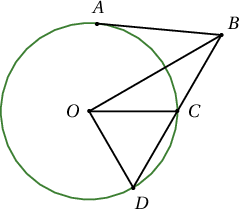
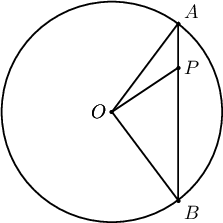
$AB$-шүргэгч, $BD$-огтлогч, $\angle DOC=60^\circ$, $DC=CB$, $AB=\sqrt6$ бол $OB=?$
A. $\sqrt3$
B. $\dfrac{\sqrt3}{2}$
C. $2$
D. $1$
E. $3$
Сектор, сегментийн талбай
$ABCD$ дөрвөн өнцөгтийн $AC$ диагонал $\sqrt2$. Хэрэв $\angle ABC=105^\circ$, $\angle ACD=42^\circ$, $\angle DAC=63^\circ$ бол $ABD$ гурвалжинг багтаасан дугуйн талбайг ол.
$r$ ба $3r$ радиустай тойргууд гадаад байдлаар шүргэлцдэг. Эдгээр тойргуудын ерөнхий шүргэгчүүд ба тойргуудын хооронд үүсэх дүрсийн талбайг ол.
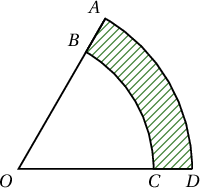
Талын урт нь $a$, хурц өнцөг нь $60^\circ$ байх ромбо өгөгдөв. Түүний их диагоналаар диаметр хийсэн тойрог байгуулав. а) Дугуйн талбайг ол. б) Ромбын талбай ба ромбын гадна орших дугуйн талбайн аль нь их вэ?
$R$ радиустай тойргийн доторх орших $P$ цэгийг дайруулан харилцан перпендикуляр хоёр хөвч татав. Эдгээрийн нэг нь тойргийн төв ба $P$ цэгийг дайрсан шулуунтай $\alpha>0$ өнцөг үүсгэх ба төвөөс $a$ зайтай байв. Эдгээр хөвчүүдээр диагоналаа хийсэн дөрвөн өнцөгтөд дугуй багтсан бол энэ дугуйн талбайг ол.
$64$ см.кв талбайтай дугуйд багтсан квадратын талыг ол.
Ялгаатай радиус бүхий хоёр тойрог $A$ цэгээр гадаад байдлаар шүргэлцэж байв. $AB$ нь жижиг тойргийн диаметр бөгөөд $B$ цэгээс том тойрогт $M$ ба $N$ цэгүүдээр шүргэх шүргэгчүүд татав. $AM$ шулуун бага тойргийг $K$ цэгээр огтлох ба $MK=\sqrt{2-\sqrt{3}}$, $\angle BMA=15^\circ$ байв. $BM, BN$ шүргэгчүүд болон $A$-г агуулаагүй $MN$ нумаар хүрээлэгдсэн дүрсийн талбайг ол.
$3$ ба $4$ катеттай тэгш өнцөгт гурвалжин өгөгдөв. Дугуйн диаметр том катеттай давхцах бол гипотенузаар хуваагдсан дугуйн хэсгүүдийн талбайг ол.
$r$ радиустай тойргийн талбайг $1:2$ харьцаагаар хуваах хөвчийн төгсгөлүүдийг дайруулан уг тойрогт шүргэгч шулуунууд татав. $r$-ын ямар утгад хөвч болон шүргэгч шулуунуудаар үүссэн гурвалжны талбай $12\sqrt3$-тай тэнцүү байх вэ?
$60^\circ$ төв өнцөгтэй секторт дугуй багтав. Секторын радиус хэд байхад тойргийн талбай $\pi$-тэй тэнцэх вэ?
$R$ радиустай хагас тойрогт $R/2$ радиустай тойрог багтав. Хагас тойргийн үлдсэн хэсэгт $R$ радиустай хагас тойрог, $R/2$ радиустай тойрог, хагас тойргийн диаметр гурвыг шүргэх дугуй багтаав. Хэрэв $R=4$ бол сүүлчийн тойргийн радиусыг ол.
Зөв гурвалжны талууд $a$-тай тэнцүү. Түүнтэй ижил төвтэй $a/3$ радиустай тойрог татав. Тойргийн гадна байрлах гурвалжны хэсгүүдийн талбайг тодорхойл.
Дугуйн радиус $R=6/\sqrt{4\pi-3\sqrt3}$. Энэ дугуйг түүнд багтсан зөв гурвалжны талтай тэнцүү урттай хөвчөөр 2 сегментэд хуваав. Жижиг сегментийн талбайг ол.
$1$ радиустай дугуйд $AB=\sqrt{2}$ ба $BC=\dfrac{10}{7}$ хөвчүүд татав. Хэрэв $BAC$ нь хурц өнцөг бол дугуйн $ABC$ өнцөг доторх хэсгийн талбайг ол.
Тулга ямаагаа 5 м урттай уяагаар $2\times 3$ м хэмжээтэй тэгш өнцөгт хэлбэртэй хашааны гадна талд, аль нэг тэгш өнцөгийн оройгоос нь уяжээ. Тэгвэл ямааны өвс идэж чадах талбайн хэмжээг ол.
A. $10\pi$
B. $20\pi$
C. $22\pi$
D. $25\pi$
E. $30\pi$
A. $\pi$
B. $2\pi$
C. $\dfrac72\pi$
D. $\dfrac{13}{3}\pi$
E. $\dfrac{16}{3}\pi$
$8$ см талтай квадратад тойрог багтсан бол зурагт үзүүлсэн будагдсан хэсгийн талбайг ол.
A. $(32\pi-64)$ см.кв
B. $(64-8\pi)$ см.кв
C. $16\pi$ см.кв
D. $(64-16\pi)$ см.кв
E. $64$ см.кв
Квадратын талбайг уг квадратыг багтаасан дугуйн талбайд харьцуулсан харьцаа аль нь вэ?
A. $\dfrac{1}{\pi}$
B. $\dfrac{\pi}{2}$
C. $\dfrac{2}{\pi}$
D. $\dfrac{4}{\pi}$
E. $\dfrac{\pi}{4}$
4см талтай квадратад тойрог багтсан бол зурагт үзүүлсэн будагдсан хэсгийн талбайг ол.
A. $(8\pi-16)$ см.кв
B. $(16-2\pi)$ см.кв
C. $16$ см.кв
D. $(16-4\pi)$ см.кв
E. $4\pi$ см.кв
A. $9\pi$
B. $10\pi$
C. $11\pi$
D. $12\pi$
E. $13\pi$
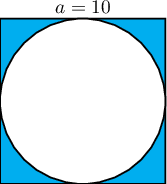
$10$ см талтай квадратад тойрог багтсан бол зурагт үзүүлсэн будагдсан хэсгийн талбайг ол.
A. $(50\pi-100)$ см.кв
B. $(100-25\pi)$ см.кв
C. $50\pi$ см.кв
D. $100$ см.кв
E. $25\pi$ см.кв
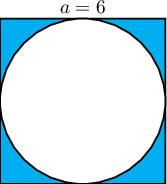
$6$ см талтай квадратад тойрог багтсан бол зурагт үзүүлсэн будагдсан хэсгийн талбайг ол.
$10$ см талтай квадратад тойрог багтсан бол зурагт үзүүлсэн будагдсан хэсгийн талбайг ол.
A. $(18\pi-6)$ см.кв
B. $(36+9\pi)$ см.кв
C. $9\pi$ см.кв
D. $(36-9\pi)$ см.кв
E. $36$ см.кв
Тойрогт багтсан зөв 6 өнцөгтийн периметр 24 бол зурагт дүрслэгдсэн будагдсан хэсгийн талбайг ол.
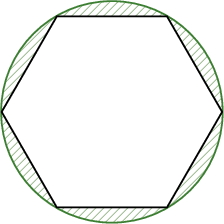
A. $2\pi+\sqrt3$
B. $8\pi-12\sqrt3$
C. $4\pi-2\sqrt3$
D. $16\pi-24\sqrt3$
E. $24\pi-12\sqrt3$
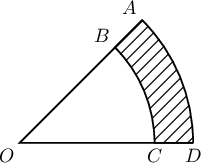
A. $7\pi$
B. $8\pi$
C. $5\pi$
D. $4\pi$
E. $2\pi$
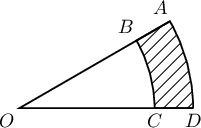
A. $7\pi$
B. $3\pi$
C. $\dfrac{8\pi}{3}$
D. $\dfrac{16\pi}{3}$
E. $5\pi$
Тулга ямаагаа 5 м урттай уяагаар $1\times 4$ м хэмжээтэй хашааны гадна нэг өнцгөөс уяжээ. Тэгвэл ямааны өвс идэж болох талбай ямар хэмжээтэй байх вэ?
A. $10\pi$
B. $20\pi$
C. $22\pi$
D. $23\pi$
E. $30\pi$
Дараах зурагт $O$ цэг тойргийн төв. $OA=OB=5$ см (радиусууд) бол будагдсан хэсгийн талбайг ол.
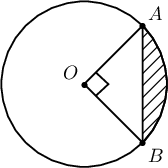
A. $6.25\pi-12.5$
B. $25\pi-25$
C. $25\pi$
D. $12.5\pi-25$
E. $25\pi-12.5$
A. $18$
B. $20$
C. $22$
D. $24$
E. $26$
$4$ см урттай $AB$ хэрчмийн $A$ цэгт төвтэй
$2(\sqrt{3}-1)$ см радиустай тойрог ба $B$ цэгт төвтэй
$2\sqrt{2}$ см радиустай тойргууд $C$, $D$ цэгт огтлолцдог гэе.
$\measuredangle CAD =\dfrac{\pi}{\fbox{a}}$ ба $\measuredangle CBD
=\dfrac{\pi}{\fbox{b}}$, дугуйнуудын ерөнхий хэсгийн талбай нь
$\dfrac{\pi}{3}(\fbox{c}-2\sqrt{\fbox{d}} )-(\fbox{e}\sqrt{3}-2)$ см$^2$
байна.
Харилцан перпендикуляр $OA$, $OB$ шулуунууд ба төв $O_1$ нь $OA$
шулуун дээр орших $\sqrt{2}$ радиус бүхий тойрог өгөв.
$OO_1=5\sqrt{2}+3\sqrt{6}$ бол $AOB$ өнцөгт багтан өгсөн тойргийг
шүргэх бага тойргийн радиус $\fbox{a}\sqrt{2}+2\sqrt{\fbox{b}}$
байна. Энэ үед уг хоёр тойрог ба $OA$ шулуунуудаар хүрээлэгдсэн
дүрсийн талбай
$7\sqrt{3}+\fbox{cd}-2\sqrt{3}\pi-\dfrac{\fbox{ef} \pi}{6}$ болно.
Харилцан перпендикуляр $OA$, $OB$ шулуунууд ба төв $O_1$ нь $OA$
шулуун дээр орших $\sqrt{3}$ радиус бүхий тойрог өгөв.
$OO_1=5\sqrt{3}+9$ бол $AOB$ өнцөгт багтан өгсөн тойргийг шүргэх
бага тойргийн радиус $\fbox{a}\sqrt{3}+\sqrt{\fbox{b}}$ байна. Энэ
үед уг хоёр тойрог ба $OA$ шулуунуудаар хүрээлэгдсэн дүрсийн
талбай
$\dfrac{\fbox{cd}}{2}\sqrt{3}+18-3\sqrt{3}\pi-\dfrac{\fbox{ef} \pi}{4}$
байна.
Нэгж радиустай, $O$ цэгт төвтэй, төвийн өнцөг нь $\dfrac{2}{3}\pi$
байх $OAB$ секторт багтсан тойргийн радиус
$\sqrt{\fbox{a}}(\fbox{b}-\sqrt{3})$ байна. Энэхүү тойргийн $OA$,
$OB$ хэрчмийг шүргэсэн цэгүүдийг харгалзан $A_1$, $B_1$, $AB$
нумыг шүргэсэн цэгийг $O_1$ гэе. $A_1B_1$ богино нум ба $OA_1$,
$OB_1$ хэрчмүүдээр хүрээлэгдсэн дүрсийн талбай $\dfrac{\fbox{cd}
-2\pi}{2}+\dfrac{2\pi-\fbox{ef}}{3}\sqrt{3}$ болно.
$\sqrt{3}$ радиустай, $O$ цэгт төвтэй, төвийн өнцөг нь
$\dfrac{\pi}{3}$ байх $OAB$ секторт багтсан тойргийн радиус
$\fbox{a}(\fbox{b}-\sqrt{3})$ байна. Энэхүү тойргийн $OA$, $OB$
хэрчмийг шүргэсэн цэгүүдийг харгалзан $A_1$, $B_1$, $AB$ нумыг
шүргэсэн цэгийг $O_1$ гэе. $A_1B_1$ богино нум ба $OA_1$, $OB_1$
хэрчмүүдээр хүрээлэгдсэн дүрсийн талбай $\fbox{cd}\sqrt{3}\pi
+3\sqrt{3}-\fbox{ef}$ болно.
$ABC$ гурвалжны $AC$ тал болон $AB$, $BC$ талын үргэлжлэлийг
шүргэсэн тойргийн радиус $\sqrt{3}$ байв. $ABC$ гурвалжны талбай
$\sqrt{3}(2-\sqrt{3})$ ба $\measuredangle BAC=60^{\circ}$ байсан
бол $AB=\sqrt{\fbox{a}}-\fbox{b}$, $\measuredangle
BCA=\dfrac{\pi}{\fbox{c}}$, $BC=\fbox{d}-\sqrt{\fbox{e}}$ болно.
Тойргийн төвөөс $AB$, $BC$ талуудад буулгасан перепендикулярууд,
$AB$, $BC$ талуудын үргэлжлэл болон $AC$ талаар хүрээлэгдсэн
дүрсийн талбай $\fbox{f}-\fbox{g}\sqrt{3}$ болно.
$ABC$ гурвалжны $AC$ тал болон $AB$, $BC$ талын үргэлжлэлийг
шүргэсэн тойргийн радиус $\sqrt{6}$, $ABC$ гурвалжны талбай
$2\sqrt{3}(2-\sqrt{3})$ ба $\measuredangle BAC=30^{\circ}$ байсан
бол $AB=\sqrt{\fbox{a}}-\sqrt{\fbox{b}}$, $\measuredangle
BCA=\dfrac{\pi}{\fbox{c}}$ ба
$BC=3\sqrt{\fbox{d}}-\sqrt{\fbox{e}}$ болно. Тойргийн төвөөс $AB$,
$BC$ талуудад буулгасан перепендикулярууд, $AB$, $BC$ талуудын
үргэлжлэл болон $AC$ талаар хүрээлэгдсэн дүрсийн талбай
$\fbox{fg}-\fbox{h}\sqrt{3}$ болно.
$AB$, $AC$ нь нэгж радиустай тойргийн харилцан перепендикуляр
радиусиуд бөгөөд $P$ цэг $BC$ нум дээр оршино. $P$ цэгийн $AC$
хэрчим дээрх перепендикулярын суурийг $Q$ гээд $C$ цэг нь $Q$, $R$
хоёрын хооронд оршиж байхаар $PQRS$ квадратыг байгуулав. $PS$,
$SR$, $CR$ хэрчмүүд болон $PC$ нумаар хүрээлэгдсэн дүрсийн талбай
$S$ нь хамгийн их байх үед квадратын талын урт
$\dfrac{\fbox{a}}{\fbox{b}}$ байна. Энэ үед
$S=\sqrt{\fbox{c}}\dfrac{1+2\sqrt{3}}{ \fbox{d}}$ байна.
$S=\dfrac{3}{4}-\dfrac{\pi}{8}$ үед $PQ=\dfrac{1}{\fbox{e}}$ ба
$\measuredangle PAQ=\dfrac{\pi}{\fbox{f}}$ болно.
Тойргийн $AB$ ба $AC$ хоёр хөвч ижил урттай ба хоорондох өнцөг нь $\dfrac{\pi}{3}$ хэмжээтэй юм.
- Тойргийн төв $O$ гэвэл $\measuredangle BOC=\dfrac{2\pi}{\fbox{a}}$ ба $\measuredangle BOA=\dfrac{\fbox{b}\pi}{\fbox{c}}$ байна.
- $AB$ ба $AC$ шулууны хооронд хашигдсан дугуйн хэсгийг дугуйн нийт талбайд харьцуулсан харьцаа $\dfrac{\fbox{d}\pi+3\sqrt{3}}{\fbox{e}\pi}$
- $AB$ талын уртыг тойргийн радиуст харьцуулсан харьцаа $\sqrt{\fbox{f}}$ байна.
Тойргийн гадна оройтой өнцөг
Тойргийн урт
Тойргийн хөвч
$R$ ба $\frac{R}{2}$ радиустай тойргууд гадаад байдлаар шүргэлцэж байв. Хэрвээ тойргийн төвүүдийг холбосон хэрчимтэй $30^\circ$ өнцөг үүсгэдэг, $2R$ урттай хэрчмийн нэг төгсгөл жижиг тойргийн төвтэй давхцаж байсан бол энэ хэрчмийн тойргуудын гадна байрлах хэсгийн уртыг нийт хэрчмийн уртад харьцуулсан харьцааг ол.
$Q$ талбайтай цагираг өгөгдөв. Бага тойргийг шүргэх том тойргийн хөвчийн уртыг ол.
Огтлолцсон $2$ тойргийн радиусууд $13$ ба $15$, тэдгээрийн ерөнхий хөвчийн урт $24$ байв. Хэрэв эдгээр тойргийн төвүүд нөгөөгийнхөө гадна байрладаг гэвэл төвүүдийн хоорондох зайг ол.
$6$ радиустай тойрог дотор орших цэг түүнийг дайрсан хөвчийг $5$ ба $4$ урттай хэсгүүдэд хуваадаг бол уг цэгээс тойрог хүртэл ямар зайтай вэ?
Тойргийн $AB$ ба $CD$ хөвчүүд перпендикуляр бөгөөд өөр хоорондоо огтлолцдог. $AD=m$, $BC=n$ бол тойргийн диаметрийг ол.
Тойргийн хөвчийн урт $10$ см. Уг хөвчийн нэг төгсгөлийг дайруулан тойргийн шүргэгч шулуун ба нөгөө төгсгөлийг дайруулан түүнтэй параллель шулуун татав. Хэрэв энэ шулуунаар үүсэх хөвчийн урт $12$ см бол тойргийн радиусыг ол.
A. $6.5$ см
B. $6.25$ см
C. $7$ см
D. $7.5$ см
E. $7.25$ см
Параллел 2 хөвчийн урт 40 ба 48, хоорондох зай 22 бол тойргийн радиусыг ол. (Тойргийн төв хөвчүүдийн хооронд оршино гэж үзнэ.)
A. $25$
B. $33$
C. $\dfrac{142}{11}$
D. $\dfrac{315}{11}$
E. $\dfrac{355}{11}$
$BC$ хөвчийн дундаж цэгээс $AB$ диаметр хүртэлх зай 1-тэй тэнцүү ба $\angle BAC=30^\circ$ бол $AC$ хөвчийн уртыг ол.
A. $1$
B. $2$
C. $4$
D. $2\sqrt{3}$
E. $4\sqrt{3}$
$ABC$ гурвалжны $BC$ талын медианы үргэлжлэл багтаасан
тойрогтой $D$ цэгт огтлолцжээ. Хэрэв $BC=a$ тал медиантайгаа ижил
урттай бол $AD$-ийн урт аль нь вэ?
A. $\dfrac23a$
B. $\dfrac34a$
C. $\dfrac54a$
D. $\dfrac65a$
E. $\dfrac32a$
$r$ радиустай тойргийн хөвчийн нэг үзүүр, нөгөө үзүүрт татсан
шүргэгчээс $a$ зайтай байжээ. Хөвчийн урт ямар байх вэ?
A. $\dfrac12\sqrt{ar}$
B. $\dfrac{a^2+r^2}{2r}$
C. $2\sqrt{r(a-r)}$
D. $\sqrt{2ar}$
E. $2\sqrt{ar}$
$P$ цэг 11 см радиустай тойргийн төвөөс 7 см зайд байв. $P$ цэгийг дайрсан 18 см урттай хөвчийн $P$ цэгээр хуваагдах хоёр хэсгийн аль их урттайг нь ямар урттай байх вэ?
A. 10
B. 11
C. 12
D. 13
E. 14
Тойргийн $AB$ хөвчийн дундаж цэг $M$-ийг дайруулан түүнд перпендикуляр $\ell$ шулуун татав. Энэ шулууны тойргийг огтлох цэгүүд нь $C$, $D$ ба $MC=8$, $MD=2$ бол $AB$ хэрчмийн уртыг ол.
A. $5$
B. $6$
C. $\sqrt{51}$
D. $4\sqrt{3}$
E. $8$
A. $20$
B. $17$
C. $15$
D. $12$
E. $10$
Тойргийн $AB$ ба $AC$ хоёр хөвч ижил урттай ба хоорондох өнцөг нь $\dfrac{\pi}{3}$ хэмжээтэй юм.
- Тойргийн төв $O$ гэвэл $\measuredangle BOC=\dfrac{2\pi}{\fbox{a}}$ ба $\measuredangle BOA=\dfrac{\fbox{b}\pi}{\fbox{c}}$ байна.
- $AB$ ба $AC$ шулууны хооронд хашигдсан дугуйн хэсгийг дугуйн нийт талбайд харьцуулсан харьцаа $\dfrac{\fbox{d}\pi+3\sqrt{3}}{\fbox{e}\pi}$
- $AB$ талын уртыг тойргийн радиуст харьцуулсан харьцаа $\sqrt{\fbox{f}}$ байна.
Тойргийн шүргэгч
$O$ төвтэй тойргийн гадна оршиж байгаа $K$ цэгээс $MK$, $NK$ гэсэн 2 шүргэгч шулуун татав ($M$ ба $N$ нь шүргэлтийн цэгүүд цэг). $MN$ хөвч дээр $C$ ($MC< CN$) цэг авч $C$ цэгийг дайруулан $OC$-тэй перпендикуляр шулуун татахад $NK$-тэй $B$ цэгт огтлолцов. Хэрэв тойргийн радиус $R$, $\angle MKN=\alpha$, $MC=b$ бол $CB$ хэрчмийн уртыг ол.
Радиусын харьцаа $2/3$-тай тэнцүү $2$ тойрог дотоод байдлаар шүргэлцэнэ. Жижиг тойргийн төвийг дайруулан төвүүдийг дайрсан шулуунтай перпендикуляр шулуун шугам татав. Энэ шулууны том тойрогтой огтлолцсон цэгээс жижиг тойрогт шүргэгч шулуунууд татав. Энэ шүргэгчүүдийн хоорондох өнцгийг ол.
Тойргийн гадна талд тойргийн төвөөс диаметртэй тэнцүү зайд байрлах цэгээс тойрогт татсан шүргэгчүүдийн хоорондох өнцгийг ол.
Гадаад байдлаар шүргэлцсэн хоёр тойргийн радиусууд $3$ ба $4$ байв. Хэрвээ $\ell$ шулуун тойргуудыг $A$ ба $B$ $(A\neq B)$ цэгүүдэд шүргэх бол $AB$ хэрчмийн урт аль нь вэ?
A. $7$
B. $12$
C. $5$
D. $4\sqrt{3}$
E. $5\sqrt{2}$
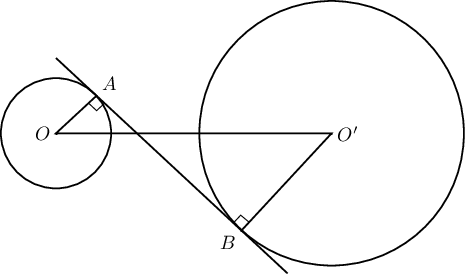
$5$ ба $12$ радиустай тойргуудын төвүүд хоорондоо 25 зайтай байв. Тойргуудын дотоод ерөнхий шүргэгчийн уртыг ол.
A. $16$
B. $2\sqrt{17}$
C. $5\sqrt{15}$
D. $17$
E. $4\sqrt{21}$
Хэрэв квадратын 2 орой нь $R$ радиустай $C$ тойрог дээр, үлдсэн хоёр орой нь $C$ тойрогт татсан нэгэн шүргэгч шулуун дээр орших бол квадратын талыг ол.
A. $2R$
B. $\dfrac{\sqrt2}{2}R$
C. $\dfrac{8\pi}{5}$
D. $\dfrac{8\pi}{3}$
E. $4R$
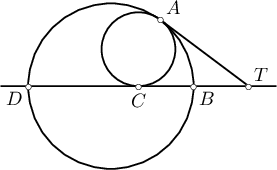
Зурагт өгөгдсөн дотоод байдлаар шүргэлцсэн хоёр тойргийн $TA$ нь ерөнхий шүргэгч, $TC$ том тойргийн огтлогч, жижиг тойргийн шүргэгч болно. $DC=2$, $CB=1$ бол $TA$-г ол.
A. $1$
B. $3$
C. $2$
D. $4$
E. $3.5$
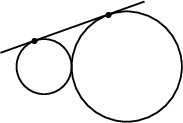
Гадаад шүргэлцсэн тойргуудын радиусууд нь 3 см ба 5 см байв. Эдгээр тойргуудад татсан шүргэлцлийн цэгийг нь дайраагүй ерөнхий шүргэгч шулууны шүргэлтийн цэгүүдээр үүсэх хэрчмийн уртыг ол.
A. $4\sqrt{3}$
B. $8$
C. $2\sqrt{15}$
D. $4\sqrt{15}$
E. $5\sqrt{5}$
Гадаад шүргэлцсэн тойргуудын радиусууд нь 2 см ба 4 см байв. Эдгээр тойргуудад татсан шүргэлцлийн цэгийг нь дайраагүй ерөнхий шүргэгч шулууны шүргэлтийн цэгүүдээр үүсэх хэрчмийн уртыг ол.
A. $3\sqrt{3}$
B. $6$
C. $4$
D. $4\sqrt{2}$
E. $\sqrt{15}$
Зурагт өгөгдсөн дотоод байдлаар шүргэлцсэн хоёр тойргийн $TA$ нь ерөнхий шүргэгч, $TC$ том тойргийн огтлогч, жижиг тойргийн шүргэгч болно. $DC=3$, $CB=2$ бол $TA$-г ол.
A. $8$
B. $5.5$
C. $5$
D. $4$
E. $6$
$O$ төвтэй тойргийн $T$ цэг дээрх шүргэгч дээр $T$
цэгийн нэг талд байрлах $P$, $Q$ цэгүүд авав ($PT< QT$). $OP$, $OQ$
хэрчмүүдийн тойрогтой огтлолцох цэгийг харгалзан $R$, $S$,
$\measuredangle OQT=\theta$ гэвэл
- $\lim \limits _{P\rightarrow T}\dfrac{RS}{PQ}=\dfrac{\sqrt{\fbox{a}}\sin \theta}{\sqrt{1+\sin \theta }}$ болно.
- $\lim \limits _{P\rightarrow T}\dfrac{RS}{PQ}=\dfrac{1}{\sqrt{3}}$ байх үеийн $\theta$-ийн утга нь $\fbox{bc}^{\circ}$ байна.
Тойрог ба гурвалжин
$R$ радиустай тойргийн диаметр нь зөв гурвалжны нэг тал болно. Гурвалжны тойрог доторх хэсгийн талбайг ол.
Ижил радиустай хоёр тойрог $C$ цэгээр гадаад байдлаар шүргэлцэнэ. Үүнээс гадна энэ 2 тойрог $A$ ба $B$ цэгээр $6,5$ радиустай $3$ дахь тойрогтой гадаад байдлаар шүргэлцэнэ. $AB=5$ бол $ABC$ гурвалжны талбайг ол.
$R$ радиустай тойрогт адил хажуут $ABC$ ($AB=BC$) адил хажуут гурвалжин багтах ба $\angle BAC=\alpha$. $ABC$ гурвалжинд багтсан тойргийн радиусыг ол.
Тойрог $O$ оройтой өнцгийг $A, B$ цэгүүдээр шүргэнэ. Энэ тойрог дээр $AOB$ гурвалжин дотор $C$ цэг авав. $C$ цэгээс $A$ ба $B$ цэгүүд хүртэлх зайнууд харгалзан $a$ ба $b$ бол $C$ цэгээс $AB$ хөвч хүртэлх зайг ол.
$K, L, M, N, P$ цэгүүд $2\sqrt {2}$ радиустай тойрог дээр дээрх дарааллаараа байрласан байв. Хэрэв $LM\parallel KN$, $KM\parallel NP$, $MN\parallel LP$, $\angle LOM=45^{\circ}$ ба $O$ нь $LN$ ба $MP$ хөвчүүдийн огтолцлын цэг бол $KLM$ гурвалжны талбайг ол.
$A$ ба $B$ цэгүүдэд төвтэй харгалзан $2$ ба $1$ радиустай 2 тойрог бие биенээ шүргэж байв. Энэ 2 тойргийг зэрэг шүргэх шулуун дээр $C$ цэг байрласан ба $AB$ хэрчмийн дунджаас $\dfrac{3\sqrt{3}}{2\sqrt{2}}$ зайд байв. Хэрэв $S>2$ бол $ABC$ гурвалжны талбай $S$-г ол.
Тойргийн диаметр $MN$-ийн урт 16. Энэ тойргийн $M$ цэгт татсан шүргэгч шулуун дээр $MP$ хэрчмийн урт 15-аас их байхаар $P$ цэг авав. $P$ цэгийг дайруулан өөр нэг шүргэгч шулуун татахад тэр нь $MN$ шулуунтай $Q$ цэгт огтлолцов. Хэрэв $MPQ$ гурвалжны периметр 72 бол түүний талбайг ол.
$O$ төвтэй тойрогт $ABCD$ трапец багтав. $AD\parallel BC$, $AD=7$, $BC=3$, $\angle BCD=120^{\circ}$, $BM$ хөвч нь $AD$ хэрчмийг $N$ цэгт огтолж $ND=2$ байв. $BOM$ гурвалжны талбайг ол.
$O$ төвтэй тойрогт $ABCD$ трапец багтжээ. $AB\parallel DC$, $AB=5$, $DC=1$, $\angle ABC=60^{\circ}$. Мөн $K$ цэг $AB$ хэрчид харъяалагдах ба $AK=2$ байв. $CK$ шулуун тойргийг $C$-ээс гадна $F$ цэгээр огтлох бол $OFC$ гурвалжны талбайг ол.
$ABCD$ ба $ACDE$ трапецуудын $AC$ ба $AD$ их сууриуд тэнцүү бөгөөд эдгээр трапецууд нэг тойрогт багтсан байв. Хэрэв $ABCD$ трапецийн диагоналуудын огтлолцлын цэг нь $O$ ба $ADE$ гурвалжны талбай $1+\sqrt {3}$, $\angle COD=60^{\circ}$ бол тойргийн радиусыг ол.
$ABC$ гурвалжны $AB$ тал дээр орших $M$ ба $N$ цэгүүдэд төвтэй 2 тойрог бие биенээ шүргэнэ. Эдгээр тойргууд $AC$ ба $BC$ талуудыг харгалзан $A, P$ ба $B, Q$ цэгүүдээр огтлох ба $AM=PM=2$, $BN=QN=5$ байв. Хэрэв $AQN$ гурвалжны талбайг $MPB$ гурвалжны талбайд харьцуулсан харьцаа $15\dfrac{\sqrt{3}}{8}$ ба $AP=\dfrac25QB\sqrt{\dfrac{2+\sqrt3}{3}}$ бол $ABC$ гурвалжныг багтаасан тойргийн радиусыг ол.
2 тойрог $K$ ба $L$ цэгүүдээр огтлолцох ба тойргийн төвүүд нь $KL$ шулууны нэг талд нь байрлана. $A$ ба $B$ цэгүүд өөр өөр тойрог дээр орших бөгөөд $AK$ шулуун нь нэг тойргийг нь $K$ цэгт шүргэх ба $BK$ шулуун нөгөө тойргийг нь мөн адил $K$ цэгт шүргэнэ. $AL$ хэрчмийн урт 3, $BL$ хэрчмийн урт 6 ба $AKB$ өнцгийн тангенс $-0.5$ бол $AKB$ гурвалжны талбайг ол.
2 тойрог $A$ ба $K$ цэгүүдээр огтлолцох ба тойргийн төвүүд нь $AK$ шулууны өөр өөр талд нь байрлана. $B$ ба $C$ цэгүүд өөр өөр тойрог дээр орших бөгөөд $AB$ шулуун нь нэг тойргийг нь $A$ цэгт шүргэх ба $AC$ шулуун нөгөө тойргийг нь мөн адил $A$ цэгт шүргэнэ. $BK$ хэрчмийн урт 1, $CK$ хэрчмийн урт 4 ба $CAB$ өнцгийн тангенс $\dfrac{1}{\sqrt{15}}$ бол $ABC$ гурвалжны талбайг ол.
Төвүүд нь $MPN$ гурвалжны $MN$ тал дээр байрлах, бие биеэ гадаад байдлаар шүргэх тойргууд $MP$ ба $PN$ талуудыг харгалзан $M, D$ ба $N, C$ цэгүүдээр огтолно. Тойргуудын төвүүд нь харгалзан $O_1$, $O_2$ ба $MO_1=O_1D=3$, $NO_2=CO_2=6$ байв. Хэрэв $MCO_2$ гурвалжны талбайг $O_1DN$ гурвалжны талбайд харьцуулсан харьцаа $\dfrac85\sqrt3$ ба $PN=MP\sqrt{2-\sqrt3}$ бол $MNP$ гурвалжны талбайг ол.
$r$ ба $R$ ($r< R$) радиустай 2 тойргийн нэг дотоод ерөнхий шүргэгч нь нэг гадаад ерөнхий шүргэгчид перпенпикуляр байв. Эдгээр шүргэгчүүд ба өөр нэг дотоод ерөнхий шүргэгчээр үүсэх гурвалжны талбайг ол.
5 нэгж радиустай тойрог багтаасан тэгш өнцөгт гурвалжны
гипотенуз шүргэлтийн цэгээр 10, 15 нэгж урт хэсгүүдэд хуваагдсан
бол өндрийн сууриар ямар урттай хэсгүүдэд хуваагдах вэ?
A. 12, 13
B. 11, 14
C. 10, 15
D. 9, 16
E. 8, 1
15, 20 нэгж урт катетуудтай тэгш өнцөгт гурвалжинд багтсан
тойргийн төвөөс гипотенузэд буулгасан өндөр хүртэлх зай аль нь
вэ?
A. 1
B. 2
C. 4
D. 5
E. 6
$ABC$ гурвалжины багтаасан тойргийн радиус $R$, багтсан тойргийн төв $J$, $\measuredangle CAB=\alpha$, $\measuredangle ABC=\beta$, $\measuredangle BCA=\gamma$ бол $AJ$ хэрчмийн урт ямар байх вэ?
A. $2R\cos\alpha$
B. $R\sin\alpha$
C. $4R\cos\frac{\beta}2\cos\frac{\gamma}2$
D. $4R\sin\frac{\beta}2\sin\frac{\gamma}2$
E. $2R\sin\alpha$
$ABC$ гурвалжны багтаасан тойргийн радиус $R$,
$\measuredangle CAB=\alpha$, $\measuredangle ABC=\beta$,
$\measuredangle BCA=\gamma$ бол $A$ оройгоос $B$, $C$ хоёр оройн
гадаад өнцгийн биссектрисийн огтлолцол хүртэлх зай аль нь вэ?
A. $4R\cos\frac{\beta}2\cos\frac{\gamma}2$
B. $2R\sin\frac{\alpha}2$
C. $2R\cos\frac{\alpha}2$
D. $4R\sin\frac{\beta}2\sin\frac{\gamma}2$
$ABC$ гурвалжны багтаасан тойргийн радиус $R$,
$\measuredangle CAB=\alpha$, $\measuredangle ABC=\beta$,
$\measuredangle BCA=\gamma$ байжээ. Хэрэв $B$, $C$ орой дахь
гадаад өнцгийн биссектрисийн огтлолцсон цэг $J_1$ бол $BJ_1$
хэрчмийн урт ямар байх вэ?
A. $4R\sin\frac{\alpha}2\cos\frac{\gamma}2$
B. $4R\sin\frac{\gamma}2\cos\frac{\alpha}2$
C. $2R\cos\frac{\beta}2$
D. $2R\sin\frac{\alpha}2$
$R$ радиустай тойрогт багтсан $ABC$ гурвалжны
$\measuredangle CAB\mbox{=}\alpha$, $\measuredangle ABC=\beta$,
$\measuredangle BCA=\gamma$ бол багтсан тойргийн радиус ямар байх
вэ?
A. $2R\sin\alpha\sin\beta\sin\gamma$
B. $2R\cos\alpha\cos\beta\cos\gamma$
C. $4R\sin\frac{\alpha}2\sin\frac{\beta}2\sin\frac{\gamma}2$
D. $4R\cos\frac{\alpha}2\cos\frac{\beta}2\cos\frac{\gamma}2$
$R$ радиустай тойрогт багтсан $ABC$ гурвалжны $\measuredangle
CAB=\alpha$, $\measuredangle ABC=\beta$, $\measuredangle
BCA=\gamma$ бол $BC$ талын гадуур багтсан тойргийн радиусын урт
аль вэ?
A. $4R\sin\frac{\alpha}2\cos\frac{\beta}2\cos\frac{\gamma}2$
B. $4R\cos\frac{\alpha}2\sin\frac{\beta}2\sin\frac{\gamma}2$
C. $4R\tg\frac{\alpha}2$
D. $4R\ctg\frac{\alpha}2$
$ABC$ гурвалжны $C$ оройгоос, багтсан тойргийн $AC$ талыг
шүргэсэн цэг хүртэлх зай $p-c$, $\measuredangle CBA=\beta$ бол
$BC$ талын гадуур багтсан тойргийн радиус аль вэ?
A. $(p-c)\ctg\frac{\beta}2$
B. $(p-c)\tg\frac{\beta}2$
C. $(p-c)\sin\frac{\beta}2$
D. $(p-c)\cos\frac{\beta}2$
$ABC$ гурвалжинд багтсан тойрог $AB$ талыг $M$ цэгт шүргэнэ.
Хэрэв гурвалжны талбай 60 кв.нэгж, $AM:MB=8:5$, $AB=AC$ бол $A$
оройгоос багтсан тойргийн төв хүртэлх зай хэд байх вэ?
A. 18
B. $\frac{35}2$
C. $\frac{26}3$
D. $\frac{84}5$
$BC>CA=AB$ байх $ABC$ гурвалжинд багтсан $\frac{4\sqrt5}5$
радиустай тойрог $AB$ талыг $AM:MB=1:2$ байх $M$ цэгт шүргэсэн бол
$A$ оройн дотоод өнцгийн биссектрисийн урт хэд байх вэ?
A. $4\sqrt5$
B. 6
C. $3\sqrt2$
D. $2\sqrt5$
$ABC$ гурвалжинд багтсан тойргийн төв $J$, багтаасан тойргийн
радиус $R$ байжээ. Хэрэв $\measuredangle BAC=\alpha$ бол $BC$
талын гадуур багтсан тойргийн төвөөс $J$ хүртэлх зай аль вэ?
A. $4R\sin\frac{\alpha}2$
B. $4R\sin\alpha$
C. $2R\cos\alpha$
D. $2R\cos\frac{\alpha}2$
$ABC$ гурвалжны багтаасан тойргийн радиус $R$,
$\measuredangle ABC=\beta$, $\measuredangle BCA=\gamma$,
$\measuredangle CAB=60^\circ$, $BC$ талын гадуур багтсан тойргийн
төв $J$ бол $JBC$ гурвалжны талбай аль вэ?
A. $3R^2\cos\frac{\beta}2\cos\frac{\gamma}2$
B. $\sqrt3R^2\cos\frac{\beta}2\cos\frac{\gamma}2$
C. $3R^2\sin\frac{\beta}2\sin\frac{\gamma}2$
D. $\sqrt3R^2\sin\frac{\beta}2\sin\frac{\gamma}2$
$ABC$ гурвалжны $BC$ талыг шүргэсэн $R$ радиустай хагас
тойргийн $AB$, $AC$ хоёр талтай огтлолцсон цэг нь $BC$ талтай
параллель диаметрийн хоёр үзүүр байжээ. Хэрэв $h:R=m:n$, үүнд $h$
нь $BC$ талд буусан өндөр бол $BC$ талын урт ямар байх вэ?
A. $\frac{mR}{m+n}$
B. $\frac{2mR}{|m-n|}$
C. $\frac{2mR}{m+n}$
D. $\frac{mR}{|m-n|}$
$ABC$ гурвалжны $BC$ талыг шүргэсэн тойргийн $AB$, $AC$
талтай огтлолцсон цэгүүд нь $BC$ талтай параллель диаметрийн хоёр
үзүүр байжээ. Хэрэв $BC=a$, түүнд буусан өндрийн урт $h$ байсан
бол тойргийн радиус ямар байх вэ?
A. $\frac{ah}{a+2h}$
B. $\frac{ah}{a+h}$
C. $\frac{ah}{|a-h|}$
D. $\frac{ah}{2a-h}$
$ABC$ гурвалжны $BC$ талын медианы суурь $M$, $AB=10$, $AC=6$
бол $ABM$, $ACM$ хоёр гурвалжинд багтсан тойргийн $AM$-ийг
шүргэсэн цэгүүдийн хоорондох зайг ол.
A. 2
B. 3
C. 4
D. 5
$AB=AC$ гурвалжны $BC$ талыг $M$ цэг 5, 9 урттай хэсгүүдэд
хуваасан бол $ABM$, $ACM$ хоёр гурвалжинд багтсан тойргийн $AM$
талтай шүргэлцсэн цэгүүдийн хоорондох зайг ол.
A. 2
B. 3
C. 4
D. 5
E. 6
20 дм периметртэй $ABC$ гурвалжинд багтсан тойргийн $BC$
талтай параллель шүргэгчийн, гурвалжин дотор орших хэрчмийн урт
24 см бол $BC$ талын урт аль вэ?
A. 3 дм, 60 см
B. 40 см, 6 дм
C. 8 дм, 4 дм
D. 6 дм, 8 дм
$ABC$ гурвалжинд багтсан тойргийн $AB$ талтай параллель
шүргэгч $CA$, $BC$ хоёр талыг $M$, $N$ цэгт огтолжээ. Хэрэв $MCN$
гурвалжны периметр 24 см, $MN=6$ см бол $AB$ талын урт хэдэн см
байх вэ?
A. 9
B. 10
C. 11
D. 12
24 см суурьтай адил хажуут гурвалжинд багтсан тойрогт,
гурвалжны тал тус бүртэй параллель шүргэгч татахад үүссэн гурван
жижиг гурвалжны периметрийн нийлбэр 9.6 дм бол хажуу талын урт нь
хэдэн см байх вэ?
A. 40
B. 38
C. 36
D. 34
E. 32
Гурвалжны $60^\circ$ өнцгийн эсрэг орших тал 16 см, багтсан
тойргийн радиус 4 см бол талбай нь хэд вэ?
A. $64+\frac{16}{\sqrt3}$
B. $64+16\sqrt3$
C. $64$
D. ийм гурвалжин байхгүй
3 нэгж радиустай тойрог багтаасан гурвалжны талбай
36 кв.нэгж бол $2\arctg\frac12$ өнцгийн эсрэг орших тал хэдэн нэгж
байх вэ?
A. $\frac{15}2$
B. $\frac{21}2$
C. 8
D. 6
3 нэгж радиустай тойрог багтаасан тэгш өнцөгт гурвалжны
гипотенуз 15 нэгж бол хурц өнцгүүд нь хэд хэд вэ?
A. $\arcsin\frac35, \arcsin\frac45$
B. $\arcsin\frac5{13}, \arcsin\frac{12}{13}$
C. $\arctg\frac34, \arctg\frac{12}5$
D. $\arctg\frac43, \arctg\frac5{12}$
$BC=10$, $CA=7$, $AB=9$ талтай гурвалжны $BC$ тал дээр $D$
цэгийг $ABD$, $ACD$ хоёр гурвалжинд багтсан тойрог шүргэлцэж
байхаар авсан бол $BD$ хэрчмийн урт ямар байх вэ?
A. 6
B. 5
C. 7
D. 4
$BC=13$, $AB=15$ гурвалжны $BC$ тал дээр $D$ цэгийг $ABD$,
$ACD$ гурвалжинд багтсан тойргууд шүргэлцэж байхаар авахад $CD=4$
байсан бол $AC$ талын урт аль нь вэ?
A. 8
B. 10
C. 5
D. 4
$R$ радиустай тойрогт багтсан хурц өнцөгт $ABC$ гурвалжны $A$
оройгоос татсан $AH$ өндрийн үргэлжлэл багтаасан тойрогтой $A_1$
цэгт огтлолцжээ. Хэрэв $\measuredangle ABC=\beta$, $\measuredangle
ACB=\gamma$ бол $AA_1$ хэрчмийн урт аль нь вэ?
A. $2R\sin\beta\sin\gamma$
B. $2R\cos(\gamma-\beta)$
C. $2R\sin(\beta+\gamma)$
D. $2R\sin(\beta-\gamma)$
$R$ радиустай тойрогт багтсан хурц өнцөгт $ABC$ гурвалжны
$A$ оройгоос татсан өндрийн үргэлжлэл багтаасан тойрогтой $D$ цэгт
огтлолцжээ. Хэрэв орто төвөөс $D$ цэг хүртэлх зай $2R\cos\gamma$
байсан бол $\measuredangle ABC$ аль нь вэ?
A. $60^\circ$
B. $30^\circ$
C. $45^\circ$
D. $36^\circ$
Тэгш өнцөгт гурвалжны $AB$ гипотенуз $2\sqrt{\sqrt3+1}$,
түүнд налсан өнцгүүд $30^\circ$, $60^\circ$, багтсан тойргийн төв
$J$ бол $JAB$ гурвалжны талбай ямар байх вэ?
A. 1
B. 2
C. 3
D. 4
$ABC$ гурвалжны $\measuredangle BAC=\alpha$, багтаасан
тойргийн радиус $R$, багтсан тойргийн төв $J$ бол $JBC$ гурвалжныг
багтаасан тойргийн радиус аль нь вэ?
A. $2R\cos\frac{\alpha}2$
B. $R\sin\frac{\alpha}2$
C. $R\tg\alpha$
D. $2R\sin\frac{\alpha}2$
10 см радиустай тойрогт багтсан адил хажуут гурвалжны суурь,
түүнд буусан өндөр хоёрын нийлбэр диаметртэй нь тэнцүү бол суурь
нь хэдэн см вэ?
A. 13
B. 14
C. 15
D. 16
Гурвалжныг багтаасан тойргийн нэг диаметр талыг 4 см, 6 см
хэсгүүдэд хувааж, уг талтай $60^\circ$ өнцөг үүсгэсэн бол тойргийн
радиус хэдэн см вэ?
A. $2\sqrt5$
B. 5
C. $2\sqrt{3}$
D. 9
E. $2\sqrt7$
Тэгш өнцөгт гурвалжны богино катет диаметр нь болсон хагас
тойрог, тэр катетад налсан хурц өнцгийн биссектрисийг 3:1
харьцаатай хэсгүүдэд хуваасан бол энэ өнцөг аль нь вэ?
A. $60^\circ$
B. $30^\circ$
C. $75^\circ$
D. $45^\circ$
Тэгш өнцөгт гурвалжны богино катет диаметр нь болсон тойрог
гипотенузийг 3:1 харьцаатай хэсгүүдэд хуваасан бол энэ катетад
налсан хурц өнцөг аль нь вэ?
A. $60^\circ$
B. $30^\circ$
C. $75^\circ$
D. $45^\circ$
$ABC$ гурвалжны $A,B,C$ оройн дотоод өнцгийн биссектрис
багтаасан тойрогтой харгалзан $A_1,B_1,C_1$ цэгт огтлолцжээ. Хэрэв
$\overset{\smile}{B_1C_1}:\overset{\smile}{C_1A_1}:\overset{\smile}{A_1B_1}=15:14:7$ бол багтсан тойргийн төвөөс гурвалжны талууд
ямар ямар өнцгөөр харагдах вэ?
A. $105^\circ, 110^\circ, 145^\circ$
B. $100^\circ, 115^\circ, 145^\circ$
C. $105^\circ, 115^\circ, 135^\circ$
D. $110^\circ, 120^\circ, 130^\circ$
$ABC$ гурвалжны $BC$, $CA$, $AB$ талд тулсан багтаасан
тойргийн нумууд $5:15:12$ харьцаатай бол багтсан тойргийн төвөөс
тал тус бүрийн харагдах өнцөг хэдэн градус вэ?
A. $120^\circ30', 122^\circ30', 135^\circ$
B. $105^\circ, 110^\circ, 145^\circ$
C. $140^\circ30', 110^\circ30', 145^\circ$
D. $123^\circ45', 104^\circ3'45'', 132^\circ11'15''$
6 см, $3\sqrt5$ см катеттай гурвалжны тэгш өнцгийн орой дээр
төвтэй 6 см радиустай тойргийн гипотенуз дээр орших хөвчийн урт
хэдэн см вэ?
A. 8
B. 7
C. $4\sqrt3$
D. $2\sqrt5$
Тэгш өнцөгт $ABC$ гурвалжны катетууд $BC=a< b=AC$ байжээ. $C$
төв, $a$ радиустай тойрог гипотенузийг $D$ цэгт огтолсон бөгөөд
$ADC$, $BDC$ гурвалжнууд адил хажуутай байсан бол $ABC$ гурвалжны
хурц өнцгүүдийн хэмжээ аль вэ?
A. $15^\circ, 75^\circ$
B. $20^\circ, 70^\circ$
C. $25^\circ, 65^\circ$
D. $30^\circ, 60^\circ$
$ABC$ гурвалжны хамгийн богино тал $BC=a$ байжээ. $C$ төвтэй
$a$ радиустай тойрог $AB$ талыг $D$ цэгт огтолно. $AD$ нь $ABC$
гурвалжныг багтаасан тойргийн радиустай тэнцүү байсан бол дотоод
гурван өнцгийн хамаарал аль нь вэ?
A. $7\alpha-5\beta+\gamma=0$
B. $5\alpha-2\beta+\gamma=0$
C. $3\alpha-2\beta+2\gamma=0$
D. $4\alpha-3\beta+\gamma=0$
E. $4\alpha+3\beta+\gamma=0$
$R$ радиустай тойрогт багтсан $ABC$ гурвалжны $BC=a$,
$\measuredangle CAB=\alpha$, $\measuredangle ABC=\beta$ байжээ.
Хэрэв $AB$ тал дээр $AD=2R\sin(\beta-\alpha)$ байхаар $D$ цэг
авсан бол $CD$ ямар урттай вэ?
A. $2a\cos\beta$
B. $R\cos\beta-a$
C. $a\cos\beta$
D. $a$
15 см гипотенузтэй тэгш өнцөгт гурвалжны талбай
$54 \mbox{см}^2$ бол багтсан тойргийн диаметрын урт аль нь вэ?
A. 8
B. 7
C. 6
D. 5
3 см радиустай тойрог багтаасан тэгш өнцөгт гурвалжны
гипотенузэд буусан өндөр 80 мм бол гипотенузийн урт аль нь вэ?
A. 12 см
B. 11 мм
C. 6 см
D. 90 мм
Тэгш өнцөгт $ABC$ гурвалжинд багтсан тойрог $AC$ катетыг
$AD:DC=2:1$ харьцаагаар хуваах $D$ цэгт шүргэжээ. $AB=10$ нэгж бол
$AC$ хэдэн нэгж вэ?
A. 6
B. $2\sqrt3$
C. 4
D. $3\sqrt2$
Тэгш өнцөгт $ABC$ гурвалжинд багтсан тойрог $BC$, $CA$
катетуудыг харгалзан $D$, $E$ цэгт шүргэжээ. Хэрэв $AE:EC=5:3$ бол
$CD:DB$ ямар байх вэ?
A. 1:4
B. 3:2
C. 2:1
D. 4:3
Зөв $ABC$ гурвалжин багтаасан $R$ радиустай тойргийн төвийг
дайрсан $\ell$ шулуун татахад, гурвалжны гурван оройгоос $\ell$
шулуун хүртэлх зайн квадратуудын нийлбэр тогтмол байдаг бол тэр
нийлбэрийг $R=2$ см байхад ол.
A. 6
B. 9
C. 12
D. 8
Тойргийн аль ч цэгээс түүнд багтсан зөв гурвалжны гурван
орой хүртэлх зайн нэг нь нөгөө хоёрын нийлбэртэй тэнцдэг.
$R=\sqrt6-\sqrt2$ радиустай тойрогт багтсан зөв $ABC$ гурвалжин
өгсөн бол $\overset{\smile}{BP}:\overset{\smile}{PC}=1:3$ байх $P$
цэг авахад $BP+PC$ аль нь вэ?
A. 5
B. 3
C. 2
D. 1
Адил хажуут гурвалжны суурь 6, хажуу тал 10 нэгж бол багтсан
тойргийн хоёр хажуу талыг шүргэсэн цэгийн хоорондох зай хэдэн нэгж
вэ?
A. 5
B. 4.2
C. 4.8
D. 4
Адил хажуут гурвалжны талууд 5, 5, 6 бол багтсан тойргийн
хоёр хажуу талыг шүргэсэн цэгийг холбоход үүссэн жижиг гурвалжны
талбай хэдэн кв.нэгж вэ?
A. 3
B. 1.92
C. 2.8
D. 1.52
E. 1.44
$AB=6$, $AC=4$ талтай гурвалжинд багтсан тойргийн төв $J$,
$S_{JCA}=S_B$, $S_{JAB}=S_C$ гэвэл $S_B:(S_B+S_C)$ ямар байх вэ?
A. 2:3
B. 2:5
C. 3:5
D. 1:4
$BC=a$, $CA=b$, $AB=c$ гурвалжинд багтсан тойргийн төв $J$,
$S_{JBC}=S_A$ байхад $S_A=\frac13S_{ABC}$ бол гурвалжны талуудын
хамаарал аль нь вэ?
A. $a^2=bc$
B. $\frac2a=\frac1b+\frac1c$
C. $2a=b+c$
D. $3a=b+c$
$CA=CB$ байх $ABC$ гурвалжны $A$ оройд төвтэй $AB$ радиустай
тойрог $BC$ талыг $D$ цэгт огтолжээ. Хэрэв $\measuredangle
DAC=18^\circ$ бол $\measuredangle BCA$ аль нь вэ?
A. $40^\circ$
B. $45^\circ$
C. $50^\circ$
D. $48^\circ$
Ерөнхий $AC$ талтай $ABC$, $ADC$ хоёр гурвалжны $AD$ тал
$BAC$ өнцгийн, $BC$ тал $ACD$ өнцгийн биссектрис байв. Хэрэв $BC$,
$AD$ талууд $E$ цэгт огтлолцсон бөгөөд $\measuredangle
ABC=40^\circ$, $\measuredangle CEA=80^\circ$ бол $\measuredangle
CDA$ хэдэн градус вэ?
A. $20^\circ$
B. $50^\circ$
C. $45^\circ$
D. $40^\circ$
216 см$^2$ талбайтай
гурвалжны хоёр өндөр 18 см, 24 см бол үлдсэн өндөр хэдэн см вэ?
A. 24.5
B. 26.4
C. 14.4
D. 27
$ABC$ гурвалжны $BC$, $CA$ талын гадуур багтсан хоёр
тойргийн радиус 2 см, 6 см бол $AB$ талд буусан өндөр хэдэн см
вэ?
A. 4
B. 3
C. 2
D. 1
Гурвалжны гурван өндөр 40 см, 45 см, 72 см бол гадуур багтсан
гурван тойргийн радиус хэд хэдэн см вэ?
A. 30, 40, 60
B. 40, 60, 90
C. 30, 40, 90
D. 30, 60, 90
Гурвалжны гадуур багтсан гурван тойргийн радиус 8 см, 12 см,
24 см бол гурван өндөр хэд хэдэн см вэ?
A. $\frac{25}2, 12, 16$
B. $\frac{24}5, 14, 16$
C. $\frac{48}5, 12, 16$
D. $\frac{48}5, 12, 14$
$10$ нэгж радиустай тойргийн диаметр дээр $C$ цэг өгсөн ба $AB$
хөвч нь уг диаметртэй параллель байв. Хэрэв $\measuredangle
ACB=90^{\circ}$, $\measuredangle CAB=75^{\circ}$ байсан бол $C$
цэгээс $AB$ хэрчим хүртлэх зай $h=\fbox{a}\sqrt{\fbox{b}}$ болно.
Мөн $ABC$ гурвалжны талбай $\fbox{cd}$,
$AB=\fbox{e}\sqrt{\fbox{f}}$ байна.
$4\sqrt{7}$ нэгж радиустай тойргийн диаметр дээр $C$ цэг өгсөн ба
$AB$ хөвч нь уг диаметртэй параллель байв. Хэрэв $\measuredangle
ACB=90^{\circ}$, $\measuredangle CAB=60^{\circ}$ байсан бол $C$
цэгээс $AB$ хэрчим хүртлэх зай $h=\fbox{a}\sqrt{\fbox{b}}$ болно.
Мөн $ABC$ гурвалжны талбай $\fbox{cd}\sqrt{\fbox{e}}$,
$AB=\fbox{fg}$ байна.
$ABC$ гурвалжны $AB$ талын урт $4$ ба $AB$ тал дээр $O$
төв нь орших, $AC$, $BC$ талуудыг $O_1$, $O_2$ цэгт шүргэх тойргийн
радиус $\dfrac{3}{10}\sqrt{15}$, $AO=\dfrac{12}{5}$ бол
$\cos\measuredangle{ABC}=\dfrac{\fbox{ab}}{\fbox{cd}}$,
$\dfrac{S_{BOO_2}}{S_{AOO_1}}=\dfrac{\fbox{ef}}{21}$ байна. Мөн
$\sin\measuredangle{BAC}=\dfrac{\sqrt{15}}{\fbox{g}}$,
$CO=\dfrac{\fbox{h}}{\fbox{i}}\sqrt{6}$ болно.
$ABC$ гурвалжины $AC$ талын урт $3$ ба төв $O$ нь $AC$ тал дээр
оршин $AC$ тал ба $BC$ талыг $O_1$, $O_2$ цэгт шүргэх тойргийн
радиус $\dfrac{\sqrt{15}}{4}$, $AO=2$ бол
$\cos\widehat{BCA}=\dfrac{\fbox{a}}{\fbox{b}}$,
$\dfrac{S_{COO_2}}{S_{AOO_1}}=\dfrac{\fbox{c}}{\fbox{d}}$ байна.
Мөн $\sin\widehat{BAC}=\dfrac{\sqrt{\fbox{ef}}}{\fbox{g}}$,
$CO=\dfrac{\fbox{h}}{\fbox{i}}\sqrt{10}$ болно.
$AB=1$, $AC=3$ катетууд бүхий тэгш өнцөгт гурвалжинд багтсан
тойргийн радиусыг $r$, $AC$ талыг шүргэн гадуур багтсан тойргийн
радиусыг
$R_{b}$ гэвэл $r=3(\fbox{a}-\sqrt{\fbox{bc}} )/4$, $R_{b}=13(\sqrt{\fbox{de}}+2)/{6}$ байна.
Энэ хоёр тойргийн $BC$ талыг шүргэх цэгүүдийг $E_1$, $E_2$ гэвэл
$E_1E_2=\dfrac{\fbox{fg}\sqrt{10}+\fbox{hi}}{12}$ болно.
$AC$ нь $O$ цэгт төвтэй, нэгж радиустай тойргийн диаметр ба
тойргийн $А$, $C$-ээс ялгаатай $P$ цэгийг авав. $O$, $Q$ цэгүүд
$PC$ хэрчмийн хоёр талд орших ба $PQC$ нь зөв гурвалжин үүсгэж
байв. $PQ$, $CQ$ хэрчмүүд болон $PC$ нумаар хүрээлэгдсэн дүрсийн
талбай $S$ хамгийн их байх үед гурвалжны талын урт
$\sqrt{\fbox{a}}$ байна. Энэ үед $S=\sqrt{\fbox{b}}-\dfrac{\pi}{
\fbox{c}}$ байна. $S=\sqrt{3}/2-1/2-\pi/12$ үед
$PQ=\sqrt{\fbox{d}-\sqrt{\fbox{e}}}$ ба $\measuredangle
PAC=\dfrac{\pi}{\fbox{f}}$ болно.
$4$ радиустай тойрог дээр $A$, $B$, $C$ цэгүүд авчээ. $|AB|=|BC|$,
$\measuredangle ABC=100^\circ$ байсан ба $AB$ шулуун $C$ цэгт
татсан тойргийн шүргэгчийг $D$ цэгээр огтолж байв. $\measuredangle
ADC=\fbox{ab}^\circ$ ба $|AB|=\fbox{c}\sin \fbox{de}^\circ$ болох
тул $AB$ богино нумын урт $\dfrac{\fbox{fg}}{9} \pi$ байна.
$4$ радиустай тойрог дээр $A$, $B$, $C$ цэгүүд авчээ. $|AB|=|BC|$,
$\measuredangle ABC=110^\circ$ байсан ба $AB$ шулуун $C$ цэгт
татсан тойргийн шүргэгчийг $D$ цэгээр огтолж байв. $\measuredangle
ADC=\fbox{ab}^\circ$ ба $|AB|=\fbox{c}\sin \fbox{de}^\circ$ болох
тул $AB$ богино нумын урт $\dfrac{\fbox{f}}{18} \pi$ байна.
Тойрог ба дөрвөн өнцөгт
Дугуй ба квадрат ерөнхий төвтэй бөгөөд ижил талбайтай. Квадратын тал $1$ бол тойргийн квадрат доторх хэсгүүдийн нийлбэр уртыг ол.
Тойрогт багтсан $ABCD$ дөрвөн өнцөгтийн диагоналууд $E$ цэгт огтлолцоно. $AC$ шулуун дээр $M$ цэг авахад $\angle DME=80^\circ$, $\angle ABD=60^\circ$, $\angle CBD=70^\circ$ байв. $M$ цэг $AC$ диагонал дээр үү, эсвэл түүний үргэлжлэл дээр байрлах уу? Хариултаа үндэслэ.
Тойрогт багтсан $PQRS$ дөрвөн өнцөгтийн диагоналууд $D$ цэгт огтлолцоно. $PR$ шулуун дээр $A$ цэг авахд $\angle SAD=50^\circ$, $\angle PQS=70^\circ$, $\angle RQS=60^\circ$ байв. $A$ цэг хаана байрлах вэ? $PR$ диагонал дээр үү, эсвэл түүний үргэлжлэл дээр үү? Хариултыг үндэслэ.
$\sqrt5$ радиустай хагас дугуй дотор $2$ орой нь хагас тойргийн диаметр дээр байх квадрат багтав. Квадратын талын уртыг ол.
$120^\circ$ нумаар үүсэх дугуйн сегментэд $\sqrt{19}-2$ радиустай квадрат багтав. Дугуйн радиусыг ол.
$r$ радиустай тойрог багтаасан адил хажуут трапецийн сууриуд
$m:n$ харьцаатай бол хажуу талын урт ямар байх вэ?
A. $\dfrac{2r^2}{\sqrt{mn}}$
B. $\dfrac{r(m+n)}{\sqrt{mn}}$
C. $\dfrac{r|m-n|}{\sqrt{mn}}$
D. $\dfrac{r\sqrt{m^2+n^2}}{m+n}$
E. $\dfrac{r^2}{\sqrt{mn}}$
$r$ радиустай тойрог багтаасан адил хажуут трапецийн сууриуд
$m:n$ харьцаатай бол дундаж шугамын урт аль нь вэ?
A. $\dfrac{r(m+n)}{\sqrt{mn}}$
B. $\dfrac{r(m+n)}{2\sqrt{mn}}$
C. $\dfrac{r\sqrt{m^2+n^2}}{2(m+n)}$
D. $r\cdot\dfrac{|m-n|}{\sqrt{mn}}$
E. $\dfrac{r\sqrt{mn}}{2(m+n)}$
Квадратыг багтаасаан тойргийн уртыг, уг квадратад багтсан тойргийн уртад харьцуулсан харьцааг ол.
A. $2$
B. $\sqrt2$
C. $\dfrac{1}{\sqrt2}$
D. $2\sqrt2$
E. $\dfrac12$
Тойрогт багтсан $ABCD$ дөрвөн өнцөгтийн $|AB|=2$, $|BC|=3$, $|CD|=1$, $\angle ABC=60^\circ$ бол $ABCD$ дөрвөн өнцөгтийн талбайг ол.
A. $3\sqrt{3}$
B. $\dfrac{5\sqrt{3}}{2}$
C. $2\sqrt{3}$
D. $\dfrac{3\sqrt{3}}{2}$
E. $\sqrt{3}$
$ABC$ зөв гурвалжны талын урт нь $7$. Багтаасан тойргийн $AC$ нум дээр $AD=2DC$ байхаар $D$ цэг авав.
- $DC=\sqrt{\fbox{a}}$ тул $AD=\fbox{b}\sqrt{\fbox{a}}$ байна.
- $BD=\fbox{c}\sqrt{\fbox{d}}$ байна.
- $ABCD$ дөрвөн өнцөгтийн талбай $\dfrac{\fbox{ef}\sqrt{3}}{4}$ байна.
$ABC$ зөв гурвалжны талын урт нь $\sqrt{7}$. Багтаасан тойргийн $AC$ нум дээр $2AD=DC$ байхаар $D$ цэг авав.
- $AD=\fbox{a}$ тул $DC=\fbox{b}$ байна.
- $BD=\fbox{c}$ байна.
- $ABCD$ дөрвөн өнцөгтийн талбай $\dfrac{\fbox{d}\sqrt{3}}{\fbox{e}}$ байна.
Тойрог ба өнцөг
Тойрогт 2 хөвч $C$ цэгт огтлолцдог бол $x+y$ нь хэдэн градус байх вэ?
A. $40^\circ$
B. $50^\circ$
C. $60^\circ$
D. $160^\circ$
E. $320^\circ$
$A$, $B$, $C$ цэгүүд нь тойргийг $2:4:6$ харьцаатай нумуудад хуваадаг бол эдгээр цэгүүдээр үүсэх өнцгүүд нь аль вэ?
A. $15^\circ$, $45^\circ$, $120^\circ$
B. $30^\circ$, $50^\circ$, $100^\circ$
C. $30^\circ$, $60^\circ$, $90^\circ$
D. $20^\circ$, $40^\circ$, $60^\circ$
E. $30^\circ$, $70^\circ$, $80^\circ$
Тойргийг $1:2:3$ харьцаатай нумуудад хуваав. Хамгийн бага нумд тулсан төв өнцгийг ол.
A. $20^\circ$
B. $180^\circ$
C. $30^\circ$
D. $120^\circ$
E. $60^\circ$
$A$, $B$, $C$ цэгүүд нь хагас тойргийг $1:3:8$ харьцаатай нумуудад хуваадаг бол эдгээр цэгүүдээр үүсэх өнцгүүд нь аль вэ?
A. $15^\circ$, $45^\circ$, $120^\circ$
B. $30^\circ$, $50^\circ$, $100^\circ$
C. $10^\circ$, $30^\circ$, $80^\circ$
D. $20^\circ$, $40^\circ$, $60^\circ$
E. $30^\circ$, $70^\circ$, $80^\circ$
Тойрог ба шулуун
$r$ радиустай тойргийн төвөөс $2r$ зайд байрлах $A$ цэгийг дайруулан тойргийн төвөөс $r/2$ зайтай шулуун татав. Энэ шулуун тойргийг $B, C$ цэгээр огтолсон бол $AB, AC$-г ол.
$O$ цэгт төвтэй $R=6+4\sqrt2$ радиустай тойрог өгөгдсөн шулууныг $A$ цэгт шүргэнэ. Тойрог дээр $AOB$ өнцөг $45^\circ$ байхаар $B$ цэг авав. Тойргийг $B$ цэгт шүргэдэг бөгөөд өгөгдсөн шулууныг шүргэх тойргийн радиусыг ол.
$AB$ нь $O$ цэгт төвтэй 2 радиустай тойргийн диаметр байв. Зурагт үзүүлсэн $PT$ шүргэгч шулуун татахад $\angle BAT=30^\circ$ байв.
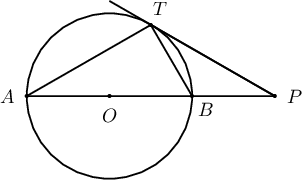$PB=BT=\fbox{a}$ ба $PT=\sqrt{\fbox{bc}}$ байна.
Тойрог багтаасан дөрвөн өнцөгт
Тойрогт багтсан дөрвөн өнцөгт
$ \frac{dy}{dx}=4x-3$ ба $ P(-1,1) $ цэгийг дайрах муруйг ол.
A. $ y=2x^2-1 $
B. $ y=2x^2-3x-4$
C. $ y=4x^2-3x-6$ см
D. $ y=2x^2-3x+2 $ см
E. $ y=4x^2-3x $ см
$ABCD$ дөрвөн өнцөгт тойрогт багтжээ. Хэрэв $BC = 12 $ см, $CD = 20$ см, $\measuredangle BAD = 60^\circ$ бол $BD$ хэрчмийн уртыг олно уу?
A. $ 24$ см
B. $ 28$ см
C. $ 26$ см
D. $ 32$ см
E. $ 30$ см
$ABCD$ дөрвөн өнцөгт тойрогт багтжээ. Хэрэв $BC = 8 $ см, $CD = 7$ см, $\measuredangle BAD = 60^\circ$ бол $BD$ хэрчмийн уртыг олно уу?
A. $ 13$ см
B. $ 11$ см
C. $ 10$ см
D. $ 12$ см
E. $ 14$ см
$ABCD$ дөрвөн өнцөгт тойрогт багтжээ. Хэрэв $BC = 8 $ см, $CD =7$ см, $\measuredangle BAD = 60^\circ$ бол $BD$ хэрчмийн уртыг олно уу?
A. $ 13$ см
B. $ 11$ см
C. $ 10$ см
D. $ 12$ см
E. $ 14$ см
Хоёр тойргийн харицлан байршил
Хөвч ба шүргэгчийн хоорондох өнцөг
Шүргэлцсэн тойргууд
Хоёр тойрог дотоод байдлаар шүргэлцэнэ. Жижиг тойргийн төвийг дайрсан шулуун том тойргийг $A$ ба $D$ цэгт огтолно ба жижиг тойргийг В ба С цэгт огтолно. Хэрэв $AB:BC:CD=2:4:3$ бол том тойргийн радиусийг жижиг тойргийн радиуст харьцуулсан харьцааг ол.
$O_1$ ба $O_2$ төвтэй $32$ радиустай $2$ тойргууд огтлолцох ба $O_1O_2$ хэрчмийг огтлох цэгүүд нь уг хэрчмийг гурван тэнцүү хэсэгт хуваана. Өгөгдсөн хоёр тойргийг дотор талаас нь шүргэх тойрог $O_1O_2$ хэрчмийг ч мөн шүргэх бол энэ тойргийн радиусыг ол.
$R$ ба $r$ радиустай тойргууд гадаад байдлаар $A$ цэгт шүргэлцэж байв. Уг хоёр тойргийн ерөнхий шүргэгч $AD$ ба $BC$ шулуунууд нь $D$ цэгт огтлолцох бол $AD^2=Rr$ гэж батал.
Гурван тойрог хос хосоороо гадаад байдлаар шүргэлцэнэ. Тойргийн төвүүдийн хоорондох зай $7, 8, 9$ см. Тойргуудын радиусыг ол.
A. $3, 4, 5$
B. $4, 5, 6$
C. $3, 4, 6$
D. $4, 4, 3$
E. $4, 5, 7$
Гадна талаараа шүргэлцсэн 2 тойргийн ерөнхий цэгийг дайрсан шулуун дээр орших хоёр хөвчийн нэг нь нөгөөгийн $\dfrac{m}{n}$ байжээ. Хэрэв 2 тойргийн төвийн хоорондох зай $a$ бол радиусууд ямар байх вэ?
A. $\sqrt{an}, \sqrt{am}$
B. $\dfrac{am}{m+n} , \dfrac{an}{m+n}$
C. $\dfrac{a(m+n)}{m} , \dfrac{a(m+n)}{n}$
D. $\dfrac{am}{|m-n|} , \dfrac{an}{|m-n|} $
E. $\sqrt{m^2-a^2} , \sqrt{n^2-a^2}$
2см ба 18см радиустай 2 тойрог гадаад байдлаар шүргэлцжээ. Тэдгээрийн шүргэлтийн цэгийг дайрахгүй ерөнхий шүргэгч шулууны шүргэлтийн цэгүүд болон уг тойргийн төвүүд дээр оройтой 4-н өнцөгтийн талбайг олоорой.
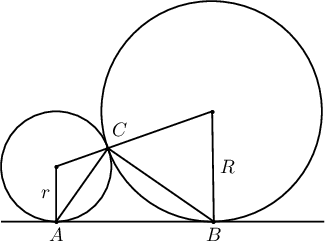
A. $125$
B. $120$
C. $100$
D. $150$
E. $120$
4см ба 16см радиустай 2 тойрог гадаад байдлаар шүргэлцжээ. Тэдгээрийн шүргэлтийн цэгийг дайрахгүй ерөнхий шүргэгч шулууны шүргэлтийн цэгүүд болон уг тойргийн төвүүд дээр оройтой 4-н өнцөгтийн талбайг олоорой.
A. $165$
B. $168$
C. $160$
D. $150$
E. $156$
4см ба 1см радиустай 2 тойрог гадаад байдлаар шүргэлцжээ. Тэдгээрийн шүргэлтийн цэгийг дайрахгүй ерөнхий шүргэгч шулууны шүргэлтийн цэгүүд болон уг тойргийн төвүүд дээр оройтой 4-н өнцөгтийн талбайг олоорой.
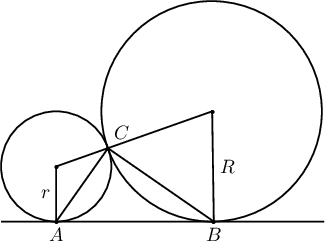
A. $12.5$
B. $7.5$
C. $10$
D. $5$
E. $15$
4см ба 9см радиустай 2 тойрог гадаад байдлаар шүргэлцжээ. Тэдгээрийн шүргэлтийн цэгийг дайрахгүй ерөнхий шүргэгч шулууны шүргэлтийн цэгүүд болон уг тойргийн төвүүд дээр оройтой 4-н өнцөгтийн талбайг олоорой.
A. $72.5$
B. $78$
C. $80$
D. $65$
E. $91$
4см ба 1см радиустай 2 тойрог гадаад байдлаар шүргэлцжээ. Тэдгээрийн шүргэлтийн цэгийг дайрахгүй ерөнхий шүргэгч шулууны шүргэлтийн цэгүүд болон уг тойргийн төвүүд дээр оройтой 4-н өнцөгтийн талбайг олоорой.
A. $12.5$
B. $7.5$
C. $10$
D. $5$
E. $15$
$3r$ радиустай $C_1$ тойрог, $r$ радиустай $C_2$ тойрогтой гадаад байдлаар $A$ цэгт шүргэлцэнэ. $A$ цэгийг үл дайрах $\ell$ шулуун $C_1$ тойргийг $B$ цэгт, $C_2$ тойргийг $C$ цэгт шүргэх бол
- $BC=\fbox{a}\sqrt{\fbox{b}}r$;
- $\measuredangle BAC=\dfrac{\pi}{\fbox{c}}$;
- $AB=\fbox{d}r$;
- $AC=\sqrt{\fbox{e}}r$;
- $S_{ABC}=\dfrac{\fbox{f}\sqrt{\fbox{g}}}{\fbox{h}}r^2$