Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Holy guacamole! www.integral.mn сайт 2026-01-01-ээс шинэчлэгдэж www.mathminds.club хуудас руу шилжинэ.
Функц
Давхар функц
$f(x)=x^2+1$, $g(x)=2x-7$ бол $g(f(-2))$ утгыг ол.
A. $-5$
B. $-3$
C. $-1$
D. $1$
E. $3$
$f(x)=2x+3$, $g(x)=1-x$ бол $f(g(1))=?$
A. $0$
B. $1$
C. $2$
D. $3$
E. $4$
Зэрэгт функц
Дараах нөхцөлүүдийг зэрэг хангах квадрат функц $f(x)$-ийг ол.
- $\int f(x)\,\mathrm{d}x$-ийн $x^3$-ийн болон $x$-ийн өмнөх коэффициентүүдийн нийлбэр нь $x^2$-ийн коэффициентээс 2 дахин их.
- $g(x)=(x-1)f(x)$ гэвэл $g^\prime(x)$-ийн $x$-ийн коэффициент нь бусад коэффициентүүдийн нийлбэрээс 2 дахин бага.
- $f(1)=12$
Илтгэгч функц
- $y=\left(\dfrac 12\right)^{2x}-8\cdot\left(\dfrac12\right)^x+10, (-3\leq x\leq 0)$ функцийн хамгийн их ба хамгийн бага утгыг ол.
- $8^{x+1}-R\cdot 4^x+2^{x+1}=0$ тэгшитгэл хоёр шийдтэй байх $R$ параметрийн утгын мужийг ол.
$a>0$, $a\neq 1$ бол $\frac12(a^x+a^y)$ ба $a^{\frac{x+y}{2}}$ тоонуудыг жиш.
Функцийн хамгийн их ба хамгийн бага утгыг ол.
- $y=\log_2x\quad (1\leq x\leq 16)$
- $y=\log_{\frac12 }x\quad (\frac14\leq x\leq 4)$
- $y=\log_{\frac12}(x-1)+\log_{\frac12}(5-x)$
Квадрат функц
$y=x^2-2x+c, (-2\leq x\leq 2)$ функцийн хамгийн их ба хамгийн бага утгыг ол.
$y=x^2-2x, (a\leq x\leq a+1)$ функцийн хамгийн их ба хамгийн бага утгыг дараах тохиолдлуудад бод.
- $a\leq 0$
- $0< a< \dfrac12$
- $a=\dfrac12$
- $\dfrac12< a< 1$
- $1\leq a$
$f(x)=(x-a)^2+2a-1, (0\leq x\leq 1)$ функцийн хамгийн бага
утга $0$ бол $a$ тоог ол.
$y=x^2+2x-1$ функцийн өгөгдсөн $(-2\leq x\leq 1)$ завсар дахь хамгийн их ба хамгийн бага утгыг ол.
$y=-x^2-4x+2$ функцийн өгөгдсөн $(0\leq x< 3)$ завсар дахь хамгийн их ба хамгийн бага утгыг ол.
$y=-x^2+2bx, (0\leq x\leq 5)$ функц өгөгдөв. $b$ нь $0< b<2$ байх тогтмол тоо.
- Функц хамгийн бага утгаа авах $x$-г ол.
- Функцийн хамгийн бага утга $-10$ бол $b$ тоог ол.
Дараах параболуудыг байгуул.
- $y=x^2+2$
- $y=-2x^2-3$
- $y=4x^2+4x+1$
- $y=-3x^2-6x+2$
- $a$-ийн ямар утгуудад $(a+1)x^2-(2a-3)x+a=0$ тэгшитгэл бодит шийдгүй вэ?
- $a$-ийн ямар утгуудад $y=2x^2-x-a$ парабол $y=3x-1$ шулуунтай ерөнхий цэгтэй байх вэ?
- $a$-ийн ямар утгуудад $y=x^2-ax-3$, $y=2x^2-a$ параболууд хоёр ерөнхий цэгтэй байх вэ?
Дараах тохиолдолуудад $f(x)=ax^2+bx+c$ квадрат функц хоёр бодит язгууртай болохыг батал.
- Ямар нэг $\alpha$, $\beta$ тоонуудын хувьд $f(\alpha)f(\beta)<0$,
- Ямар нэг $\alpha$ тооны хувьд $af(\alpha) < 0$,
- $a(a+b+c) < 0$,
- $c(a-b+c) < 0$.
$a$, $b$, $c$ бодит тоонууд бол $(x-a)(x-b)+(x-b)(x-c)+(x-c)(x-a)$ тэгшитгэл бодит шийдтэй гэж батал.
$2-\sqrt{3}$ тоо нэг язгуур нь болох квадрат тэгшитгэл зохио.
- $a$-ийн ямар утгуудад $ax^2-(a^2+3)x+2=0$ тэгшитгэл хоёр ялгаатай тэмдэгтэй шийдтэй байх вэ?
- $a$-ийн ямар утгуудад $ax^2-(3a-3)x+4a-4=0$ тэгшитгэлийн нэг бодит шийд 1-ээс их, нөгөө бодит шийд 1-ээс бага байх вэ?
- $a$-ийн ямар утгуудад $[1,2]$ хэрчмийн тоо бүр $x^2+(a-2)x-a \le 0$ тэнцэтгэл бишийн шийд болох вэ?
- $a$-ийн ямар утгуудад $2x^2+ax-5>0$ тэнцэтгэл бишийн ядаж нэг шийд $|x| < 1$ нөхцөлийг хангах вэ?
- $a$-ийн ямар утгуудад $x^2+ax-1=0$ тэгшитгэл хоёр шийд хоёулаа 3-аас бага байх вэ?
- $a$-ийн ямар утгуудад $x^2-ax+2a\le 0$ тэнцэтгэл биш ядаж нэг 1-ээс их шийдтэй байх вэ?
- $a$-ийн ямар утгуудад $[-1,1]$ хэрчмийн тоо бүр $ax^2+2(a+1)x+a-4\le 0$ тэнцэтгэл бишийн шийд болох вэ?
$y=x^2+4x+a+5$ функцийн хамгийн бага утга нь $6$ бол $a$ тоог ол.
A. $8$
B. $7$
C. $6$
D. $5$
E. $4$
$f(x)=2x^2-4x+3$ функцийн хамгийн бага утгыг ол.
A. $-2$
B. $-1$
C. $0$
D. $1$
E. $2$
$y=-x^2+4x-12$ функцийн дүрийг ол.
A. $]-\infty;+\infty[$
B. $[2;+\infty[$
C. $]-\infty;-12]$
D. $]-\infty;-8[$
E. $]-\infty;-8]$
$f(x)=2x^2-4x+1$ функцийн дүрийг ол.
A. $[-1;+\infty)$
B. $(-\infty;1]$
C. $[1;+\infty)$
D. $(-\infty;2]$
E. $(-\infty;+\infty)$
$f(x)=3x^2-6x+1$ функцийн утгын мужийг ол.
A. $[1;+\infty)$
B. $(-\infty;1]$
C. $[-2;+\infty)$
D. $(-\infty;2]$
E. $(-\infty;+\infty)$
$y=x^2$ параболыг $\vec{p}=(-3,4)$ векторын дагуу параллель зөөхөд гарах параболын тэгшитгэл аль нь вэ?
A. $y+3=(x-4)^2$
B. $y=(x-3)^2+4$
C. $y=(x+3)^2-4$
D. $y=(x+3)^2+4$
E. $y-3=(x+4)^2$
$f(x)=ax^2+bx+c$ функц тэгш функц бол аль нөхцөл биелэх вэ?
A. $c=0$
B. $f(x)=0$
C. $a=0$
D. $b=0$
E. $f(-x)=-f(x)$
$f(x)=ax^2+bx+c$ функц сондгой функц бол аль нөхцөл биелэх вэ?
A. $c\neq0$
B. $f(x)=0$
C. $a>0$
D. $b=0$
E. $f(-x)=-f(x)$
$f(x)=\left\{\begin{array}{c}
\frac12x^2, 0\le x \le 2\\
\frac12x+1, 2 < x \le 6
\end{array}\right.$ функцийн дүрийг ол.
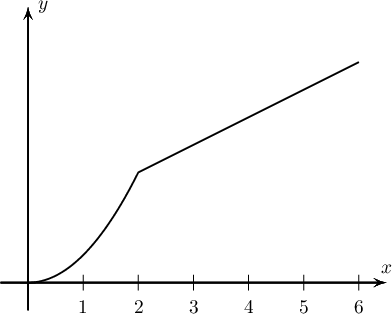

A. $[0,6]$
B. $[0,2]$
C. $[2,4]$
D. $[2,6]$
E. $[0,4]$
$y=x^2-2mx+(m+1)^2, 0< m< 1$ параболын оройн цэгийн
абсциссийн хувьд $\fbox{a}< x_0< \fbox{b}$, ординатын хувьд
$\fbox{c}< y_0< \fbox{d}$ тэнцэтгэл биш биелнэ.
$y=x^2-2(m+1)x+m^2, 0< m< 2$ параболын оройн цэгийн
абсциссийн хувьд $\fbox{a}< x_0< \fbox{b}$, ординатын хувьд
$\fbox{cd}< y_0< \fbox{ef}$ тэнцэтгэл биш биелнэ.
$y=x^2-2ax+1$, $-1\leq x\leq 3$ функц нь
$a\leq \fbox{a}$ бол $x=\fbox{b}$ цэг дээр хамгийн их
$y=\fbox{cd}a+\fbox{ef}$ утгаа авах ба $a>\fbox{a}$ бол
$x=\fbox{gh}$ цэг дээр хамгийн их $y=\fbox{i}a+\fbox{j}$ утгаа
авна.
$y=x^2-6ax+2$, $1\leq x\leq 5$ функц нь
$a\leq \fbox{a}$ бол $x=\fbox{b}$ цэг дээр хамгийн их
$y=\fbox{cd}-\fbox{еf}a$ утгаа авах ба $a>\fbox{a}$ бол
$x=\fbox{g}$ цэг дээр хамгийн их $y=\fbox{h}-\fbox{i}a$ утгаа
авна.
$y=1-x$ ба $|y|=x+1$ тэгшитгэлтэй муруйнуудын
огтлолцлын цэг $(\fbox{a},\fbox{b})$ дээр оройтой $(1,3)$ цэгийг
дайрсан параболын тэгшитгэл $y=\fbox{c}x^2+\fbox{d}x+\fbox{e}$
байна.
$y=2x-1$ ба $y=|x|+1$ тэгшитгэлтэй муруйнуудын
огтлолцлын цэг $(\fbox{a},\fbox{b})$ цэгийг дайрсан $(1,2)$ дээр
оройтой параболын тэгшитгэл $y=x^2+\fbox{cd}x+\fbox{e}$ байна.
$y=x^2-2x,$ $0\leq x\leq 3$ функц
$x=\fbox{a}$ цэг дээр $y=\fbox{b}$ хамгийн их утгаа авах ба
$x=\fbox{c}$ цэг дээр $y=\fbox{de}$ хамгийн бага утгаа авна.
$y=x^2-4x-1$ $-1\leq x\leq 4$ бол $\fbox{fg}\leq
y\leq\fbox{h}$ байна.
$y=x^2+6x,$ $-4\leq x\leq 1$ функц
$x=\fbox{ab}$ цэг дээр $y=\fbox{cd}$ хамгийн бага утгаа авах ба
$x=\fbox{e}$ цэг дээр $y=\fbox{f}$ хамгийн их утгаа авна.
$y=-x^2+2x+3$ $-2\leq x\leq 2$ бол $\fbox{gh}\leq
y\leq\fbox{i}$ байна.
$f(x)=x^2-2ax+2a+3, 0\leq x\leq 4 , a\geq 0$
функцийн хамгийн их утгыг $M(a),$ хамгийн бага утгыг $m(a)$ гэе.
Тэгвэл $0\leq a< \fbox{a}$ бол $M(a)=-\fbox{b}a+\fbox{cd}, a\geq
\fbox{a}$ бол $M(a)=\fbox{e}a+\fbox{f}$ байна. Харин $0\leq
a< \fbox{g}$ бол $m(a)=-a^2+\fbox{h}a+\fbox{i}, a\geq \fbox{g}$ бол
$m(a)=\fbox{j}a+\fbox{k}$ байна.
$f(x)=ax^2+ax+4, -1\leq x\leq 2 , a< 2$ функцийн
хамгийн их утгыг $M(a),$ хамгийн бага утгыг $m(a)$ гэе. Тэгвэл
$-\fbox{a}\leq a< 2 $ бол $M(a)=\fbox{b}a+\fbox{c}, a< -\fbox{a}$
бол $M(a)=\fbox{de}a+\fbox{f}$ байна. Харин $-\fbox{g}\leq a< 2$
бол $m(a)=-\dfrac{a^2}{\fbox{h}}+\fbox{i}, a< -\fbox{g}$ бол
$m(a)=\fbox{j}a+\fbox{k}$ байна.
Квадрат функцийн график
Зурагт $y=\log_ax$ функцийн графикийг үзүүлэв. $a$, $b$, $c$-г ол.
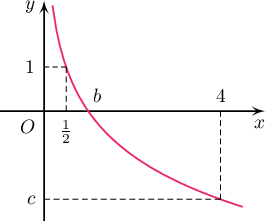

\[y = {x^2}\] график байгуул
Дараах параболуудыг байгуул.
- $y=x^2+2$
- $y=-2x^2-3$
- $y=4x^2+4x+1$
- $y=-3x^2-6x+2$
$y=-x^2+4x+5$ параболын оройн цэг аль нь вэ?
A. $(2,1)$
B. $(-2,1)$
C. $(-2,9)$
D. $(2,9)$
E. $(0,5)$
$y=x^2$ параболыг $\vec{p}=(3,-4)$ векторын дагуу параллель зөөхөд гарах параболын тэгшитгэл аль нь вэ?
A. $y+3=(x-4)^2$
B. $y=(x-3)^2+4$
C. $y=(x-3)^2-4$
D. $y=(x+3)^2-4$
E. $y-3=(x+4)^2$
$y=x^2$ парабол $y=a(x-1)$ шулуунтай яг хоёр цэгээр огтлолцдог байх $a$-ийн бүх бодит тоон утгын олонлогийг ол.
A. $]-\infty;0]\cup[4;+\infty[$
B. $]-\infty;-4]\cup[0;+\infty[$
C. $[0;4]$
D. $]-\infty;0[\cup]4;+\infty[$
E. $]-\infty;-4[\cup]0;+\infty[$
$f(x)=x^2+ax+8$ функцийн график $OX$ тэнхлэгийг шүргэдэг байх $a$ параметрын эерэг утгыг ол.
A. $2$
B. $2\sqrt2$
C. $4$
D. $3\sqrt2$
E. $4\sqrt2$
$y=ax^2$ парабол $y=ax+1$ шулуунтай яг хоёр цэгээр огтлолцдог байх $a$-ийн бүх бодит тоон утгын олонлогийг ол.
A. $]-\infty;-4[\cup]0;+\infty[$
B. $]-\infty;-4]\cup[0;+\infty[$
C. $[-4;0]$
D. $]-\infty;0]\cup[4;+\infty[$
E. $]-\infty;0[\cup]4;+\infty[$
$y=ax^2+bx+c$ функцийн графикийг абсцисс
тэнхлэгийн дагуу $-1$, ординат тэнхлэгийн дагуу $3$ нэгжээр зөөхөд
$y=2x^2$ функцийн график гардаг бол $a=\fbox{a}$, $ b=-\fbox{b},
c=\fbox{cd}$ байна. $y=ax^2+bx+c$ функцийн графикийг ординат
тэнхлэгийн дагуу $\fbox{e}$ нэгжээр зөөвөл абсцисс тэнхлэгийг
шүргэнэ.
$y=ax^2+bx+c$ функцийн графикийг абсцисс
тэнхлэгийн дагуу $-2$, ординат тэнхлэгийн дагуу $5$ нэгжээр зөөхөд
$y=3x^2+1$ функцийн график гардаг бол $a=\fbox{a}$, $b=-\fbox{bc}$, $c=\fbox{d}$ байна. $y=ax^2+bx+c$ функцийн графикийг ординат
тэнхлэгийн дагуу $\fbox{e}$ нэгжээр зөөвөл абсцисс тэнхлэгийг
шүргэнэ.
$y=ax^2-(a+3)x+3$ параболын оройн цэг
$$\left(\dfrac{a+\fbox{a}}{2a};-\dfrac{a^2+\fbox{bc}a+\fbox{d}}{4a}\right)$$ байна.
Оройн цэгийн абсцисс $[2;3]$ мужид ордог бол
$\dfrac{\fbox{e}}{\fbox{f}}\leq a\leq\fbox{g}$ байна.
$y=(a+1)x^2-(a-2)x+2$ параболын оройн цэг
$$\left(\dfrac{a+\fbox{ab}}{2(a+1)};-\dfrac{a^2-\fbox{cd}a-\fbox{e}}{4(a+1)}\right)$$
байна. Оройн цэгийн абсцисс $[1;3]$ мужид ордог бол $-\fbox{f}\leq
a\leq-\dfrac{\fbox{g}}{\fbox{h}}$ байна.
$f(x)=2x^2$ функцийн графикийг абсцисс тэнхлэгийн
дагуу $-1$, ординат тэнхлэгийн дагуу $2$ нэгжээр зөөвөл $\varphi
(x)=\fbox{a}x^2+\fbox{b}x+\fbox{c}$ функцийн график гарна.
$\varphi (x)$ функцийн графикийг ординат тэнхлэгийн хувьд тэгш
хэмээр хувиргавал $\psi (x)=\fbox{a}x^2+\fbox{de}x+\fbox{c}$
функцийн график гарна. Хэрэв $0\leq x\leq 1$ бол $\fbox{f}\leq
\varphi(x)\leq \fbox{gh}$, $\fbox{i}\leq \psi(x)\leq
\fbox{j}$ тэнцэтгэл бишүүд биелнэ.
$f(x)=3x^2+1$ функцийн графикийг абсцисс
тэнхлэгийн дагуу $1$, ординат тэнхлэгийн дагуу $-2$ нэгжээр зөөвөл
$\varphi (x)=\fbox{a}x^2-\fbox{b}x+\fbox{c}$ функцийн график
гарна. $\varphi (x)$ функцийн графикийг ординат тэнхлэгийн хувьд
тэгш хэмээр хувиргавал $\psi
(x)=\fbox{a}x^2-\fbox{de}x+\fbox{c}$ функцийн график гарна. Хэрэв
$0\leq x\leq 1$ бол $-\fbox{f}\leq \varphi(x)\leq \fbox{g}$
$\fbox{h}\leq \psi(x)\leq \fbox{ij}$ тэнцэтгэл бишүүд
биелнэ.
Логарифм функц
$x>0, y>0$ ба $x+2y=8$ бол $\log_{10}x+\log_{10}y$-ийн хамгийн их утгыг ол.
$f(x)=(\log_2\frac x2)\cdot (\log_2 \frac x8),(\frac12 \leq
x\leq 8)$ илэрхийллийн хамгийн их ба хамгийн бага утгыг ол.
Модультай функц
Функцийн график байгуул.
- $y=|x|$
- $y=|2x-3|$
- $y=|x+1|+2$
- $y=|x-1|+|x+2|-3x+1$
- $y=|x-3|+|2x+5|-8$
- $y=|||x|-1|-1|$
Монотон функц
$a=(0.5)^5$, $b=(0.5)^{\frac15}$, $c=(0.5)^2$, $d=(0.5)^{0.1}$ тоонуудыг багаас нь их рүү эрэмбэл.
A. $a< c< b< d$
B. $a< b< c< d$
C. $b< d< c< a$
D. $d< c< b< a$
E. $d< b< c< a$
$a=(0.2)^8$, $b=(0.2)^{\frac14}$, $c=(0.2)^2$, $d=(0.2)^{0.2}$ тоонуудыг багаас нь их рүү эрэмбэл.
A. $a< c< b < d$
B. $d< c< b < a$
C. $b< d< c < a$
D. $a< b< c < d$
E. $d< b< c < a$
$a=(0.2)^3$, $b=(0.2)^{\frac13}$, $c=(0.2)^2$, $d=(0.2)^{0.3}$ тоонуудыг багаас нь их рүү эрэмбэл.
A. $a< c< b< d$
B. $a< b< c< d$
C. $b< c< d< a$
D. $d< b< c< a$
E. $d< b< c< a$
$a=(0.5)^4$, $b=(0.5)^{\frac14}$, $c=(0.5)^3$, $d=(0.5)^{0.15}$ тоонуудыг багаас нь их рүү эрэмбэл.
A. $a< c< b< d$
B. $a< b< c< d$
C. $b< d< c< a$
D. $d< c< b< a$
E. $d< b< c< a$
Тригонометр функцийн график
- $y=\sin \theta+\sqrt{3}\cos\theta$ функцийн графикийг зур.
- $f(x)=6\sin^2 x+2\sqrt{3}\sin x\cdot \cos x+8\cos^2x$ функцийн минимум, максимумыг $(0^{\circ}\leq x\leq 180^{\circ})$ ол. Мөн максимум, минимум утгаа авах үеийн $x$-ийн утгыг ол.
Дараах функцүүдийн графикийг зур.
- $y=3\sin \theta$
- $y=\cos^2 \theta$
- $y=\dfrac 12\tg \theta$
- $y=\sin(\theta-30^{\circ})$
- $y=\tg(45^{\circ}-\theta)$
- $y=2\cos(180^{\circ} -\theta)$
Дараах функцийн графикийг зур.
- $y=\sin(2\theta-180^{\circ})$
- $y=\dfrac12\cos(2\theta-60^{\circ})$
Дараах функцийн үеийг олж, графикийг зур.
- $y=\cos^2\theta$
- $y=\sin^2\theta-\cos^2\theta$
- $y=\sin\theta\cdot \cos\theta$
Дараах функцийн графикийг зур.
- $y=\sin \theta+\cos \theta$
- $y=\sin\theta-\sqrt{3}\cos \theta.$
График байгуул.
- $y=\log_4x$
- $y=\log_4(x-2)$
- $y=\log_{\frac14}x$
- $y=\log_4\frac1x$
- $y=\log_4x-1$
- $y=\log_4 4x$
$46^\circ < x \le 90^\circ$ бол $\sin x$ ба $\cos x$-ийг жишээрэй.
A. $\sin x<\cos x$
B. $\sin x\le\cos x$
C. $\sin x>\cos x$
D. $\sin x\ge\cos x$
E. $\sin x=\cos x$
$0^\circ \le x < 45^\circ$ бол $\sin x$ ба $\cos x$-ийг жишээрэй.
A. $\sin x=\cos x$
B. $\sin x\le\cos x$
C. $\sin x>\cos x$
D. $\sin x\ge\cos x$
E. $\sin x<\cos x$
Тригонометр функцийн ХИ, ХБ утга
- $y=\sin^2\theta$ функцийн үеийг олж, графикийг зур.
- $y=\cos^2x+2\sin x+3$, $(0^{\circ}\leq x< 360^{\circ})$ функцийн максимум, минимум утгыг ол.
- $0^{\circ} \leq \theta\leq 180^{\circ}$ үед $\sin 2\theta\leq 2\sin \theta$ тэнцэтгэл бишийг батал.
$f(\theta)=4\sin^2\theta-4\cos\theta+1$ $(0^{\circ}\leq \theta< 360^{\circ})$ функцийн хамгийн их, хамгийн бага утгыг ол.
$y=x^2+4ax+8a$ функц өгөв.
- функцийн хамгийн бага утга $M$-ийг $a$-аар илэрхийл.
- $a$ ямар үед $M$ хамгийн их утгатай байх вэ?
- $y=\sin \theta+\sqrt{3}\cos\theta$ функцийн графикийг зур.
- $f(x)=6\sin^2 x+2\sqrt{3}\sin x\cdot \cos x+8\cos^2x$ функцийн минимум, максимумыг $(0^{\circ}\leq x\leq 180^{\circ})$ ол. Мөн максимум, минимум утгаа авах үеийн $x$-ийн утгыг ол.
$0^{\circ}\leq \theta< 360^{\circ}$ үед $(\sin\theta+\cos \theta+1)^2\cdot (\sin \theta+\cos\theta-1)^2-2\sqrt{3}\cdot \sin \theta\cdot \cos \theta+1$-ийн хамгийн
их, хамгийн бага утгыг ол.
$f(x)=7\sin x - 24 \cos x $ функцийн хамгийн их ба хамгийн бага утгуудын ялгаврыг ол.
A. 25
B. 24
C. 48
D. 49
E. 50
$y=\sin^2x+\cos x-1$ функцийн авч болох хамгийн бага утгыг ол.
A. $\dfrac12$
B. $0$
C. $-2$
D. $-1$
E. $-\dfrac34$
$y=9-12\sin 2x-2\cos^2 2x$ функцийн утгын мужийг ол.
A. $-11\le y\le 21$
B. $-3\le y\le 21$
C. $-11\le y\le 9$
D. $-11\le y\le 11$
E. $-3\le y\le 11$
$y=\cos^2x-4\cos x+1$ функцийн хамгийн бага утгыг ол.
A. $-4$
B. $-3$
C. $-5$
D. $-2$
E. $-6$
$\dfrac{\sin x-1}{2}$ илэрхийллийн хамгийн их утга нь:
A. $-2$
B. $-1$
C. $0$
D. $1$
E. $2$
$y=2\cos 3x-9\sin^23x$ функцийн утгын мужийг ол.
A. $\left[-\dfrac{80}{9};3\right]$
B. $\left[-\dfrac{82}{9};2\right]$
C. $[-9;2]$
D. $\left[-\dfrac{82}{81};2\right]$
E. $[-11;11]$
$y=4\sin^22x-2\cos 2x+3$ функцийн утгын мужийг ол.
A. $\left[5;\dfrac{29}{4}\right]$
B. $\left[1;\dfrac{29}{16}\right]$
C. $\left[6;\dfrac{27}{4}\right]$
D. $\left[1;\dfrac{29}{4}\right]$
E. $\left[0;\dfrac{29}{4}\right]$
$y=6-4\sin 2x+3\cos 2x$ функцийн утгын мужийг ол.
A. $[5;13];$
B. $[5;7];$
C. $[1;13];$
D. $[1;11];$
$y=-3+6\cos x-8\sin x$ функцийн утгын мужийг ол.
A. $[-17;6];$
B. $[-3;11];$
C. $[-13;7];$
D. $[-11;6];$
$f(x)=\sin \left(x+\dfrac{\pi}{8}\right)\cdot \cos \left(x-\dfrac{\pi}{24}\right)$ функцийн утгын мужийг ол.
A. $\left[-\frac{1}{4};\frac{1}{2}\right];$
B. $\left[-\frac{1}{3};\frac{2}{3}\right];$
C. $\left[-\frac{1}{4};\frac{3}{4}\right];$
D. $\left[-\frac{1}{4};\frac{3}{4}\right[;$
$f(x)=\sin\left(x-\dfrac{\pi}{3}\right)\cdot \sin\left(x+\dfrac{\pi}{3}\right)$ функцийн утгын мужийг ол.
A. $\left[-\frac{1}{4};\frac{3}{4}\right];$
B. $\left[-\frac{3}{4};\frac{1}{4}\right];$
C. $\left[-\frac{1}{2};\frac{2}{3}\right];$
D. $\left[-\frac{1}{3};\frac{1}{4}\right];$
$y=-\dfrac 12\cos \left(x-\dfrac{\pi}{6}\right)$ функцийн $\left[\dfrac{2\pi}{3};\dfrac{5\pi}{3}\right[$ завсар дахь хамгийн бага ба хамгийн их утгыг ол.
A. $-\frac 13,\frac 13;$
B. $-\frac
12,\frac 13;$
C. $0,\frac 12;$
D. $-\frac 14,\frac 12;$
$y=\dfrac 32\sin\left(2x-\dfrac{\pi}{4}\right)$ функцийн $\left[0;\dfrac{3\pi}{4}\right[$ завсар дахь хамгийн бага ба хамгийн их утгыг ол.
A. $-\frac{3\sqrt{2}}{4},\frac32;$
B. $-\frac 34,\frac 32;$
C. $-\frac{3\sqrt{2}}{4},1;$
D. $-1;1.$
$y=3+5\cos2x-12\sin2x$ функцийн утгын мужийг ол.
A. $[2;4]$
B. $[-10;16]$
C. $[-14;20]$
D. $[0;26]$
E. $[-4;14]$
$y=\sin x+\cos2x$ функцийн утгын мужийг ол.
A. $[-2;2]$
B. $[-\sqrt{2};\sqrt{2}]$
C. $\big[-2;1\frac18\big]$
D. $\big]-\infty;1\frac18\big]$
E. $[-2;\sqrt{2}]$
$f(x)=12\sin x + 5 \cos x $ функцийн хамгийн их ба хамгийн бага утгуудын ялгаврыг ол.
A. 25
B. 24
C. 26
D. 49
E. 50
$x^2+y^2=1$ бол $x+\sqrt{3}y$ илэрхийллийн хамгийн бага утгыг ол.
A. $-2\sqrt2$
B. $-1$
C. $-\sqrt3$
D. $-\sqrt2$
E. $-2$
$x^2+y^2=1$ бол $\sqrt{3}x+y$ илэрхийллийн хамгийн их утгыг ол.
A. $2\sqrt2$
B. $2$
C. $\sqrt3$
D. $\sqrt2$
E. $1$
$y=a\cos x+b\sin x$ функц өгөгдөв.
1) Хэрэв $a=1$ ба $b=0$ бол $y\Bigl(\dfrac{\pi}{2}\Bigr)=\fbox{a}, y(0)+y'\Bigl(\dfrac{\pi}{2}\Bigr)=\fbox{b}$ байна.
2) Хэрэв $a=1$ ба $b=1$ бол функцийн хамгийн их утга $y_{\max}=\sqrt{\fbox{c}}$ ба $y=0$ тэгшитгэлийн хамгийн бага эерэг шийд $x=\dfrac{\fbox{e}}{\fbox{d}}\cdot \pi$ байна.
1) Хэрэв $a=1$ ба $b=0$ бол $y\Bigl(\dfrac{\pi}{2}\Bigr)=\fbox{a}, y(0)+y'\Bigl(\dfrac{\pi}{2}\Bigr)=\fbox{b}$ байна.
2) Хэрэв $a=1$ ба $b=1$ бол функцийн хамгийн их утга $y_{\max}=\sqrt{\fbox{c}}$ ба $y=0$ тэгшитгэлийн хамгийн бага эерэг шийд $x=\dfrac{\fbox{e}}{\fbox{d}}\cdot \pi$ байна.
$y=6\sin\dfrac{\pi}{x^2+ax+b}+1$ функцийн хувьд
1) $a=-2, b=7$ үед функцийн утгын муж $]\fbox{a};\fbox{b}]$ байна. Функц хамгийн их утгаа $x=\fbox{c}$ үед авна.
2) $a=0, b=1$ үед $y'(\sqrt{3})=\fbox{d}\dfrac{3\cdot \sqrt{\fbox{f}}}{\fbox{e}}\cdot \pi$ байна.
1) $a=-2, b=7$ үед функцийн утгын муж $]\fbox{a};\fbox{b}]$ байна. Функц хамгийн их утгаа $x=\fbox{c}$ үед авна.
2) $a=0, b=1$ үед $y'(\sqrt{3})=\fbox{d}\dfrac{3\cdot \sqrt{\fbox{f}}}{\fbox{e}}\cdot \pi$ байна.
$y=\sin\Bigl(\dfrac{\pi a^{|x|}}{6}\Bigr)$ функцийн хувьд
1) $0< a< 1$ үед функцийн хамгийн их утга: $y_{\max}=\dfrac{\fbox{b}}{\fbox{a}}$ байна.
2) $a=6$ үед $y=0$ тэгшитгэлийн хамгийн бага эерэг хоёр шийдийн нийлбэр $\fbox{c}+\log_6\fbox{d}$-тэй тэнцүү.
3) $a=6$ үед $y=1$ тэгшитгэлийн хамгийн бага эерэг шийд $x=\log_{\fbox{e}}\fbox{f}$ байна.
1) $0< a< 1$ үед функцийн хамгийн их утга: $y_{\max}=\dfrac{\fbox{b}}{\fbox{a}}$ байна.
2) $a=6$ үед $y=0$ тэгшитгэлийн хамгийн бага эерэг хоёр шийдийн нийлбэр $\fbox{c}+\log_6\fbox{d}$-тэй тэнцүү.
3) $a=6$ үед $y=1$ тэгшитгэлийн хамгийн бага эерэг шийд $x=\log_{\fbox{e}}\fbox{f}$ байна.
$y=2\cos 2x\cdot \cos x+1-4\sin^2x\cdot \cos x$ бол
1) $y\Bigl(\dfrac{\pi}{9}\Bigr)=\fbox{a},$
2) $y_{\max}=\fbox{b}, y_{\min}=\fbox{cd},$
3) Үндсэн үе $T=\dfrac{\fbox{f}}{\fbox{e}}\cdot \pi,$
4) $y=0$ тэгшитгэл бодвол $x=\pm \dfrac{2\pi}{\fbox{g}}+\dfrac 23\pi k (k\in \mathbb Z).$
1) $y\Bigl(\dfrac{\pi}{9}\Bigr)=\fbox{a},$
2) $y_{\max}=\fbox{b}, y_{\min}=\fbox{cd},$
3) Үндсэн үе $T=\dfrac{\fbox{f}}{\fbox{e}}\cdot \pi,$
4) $y=0$ тэгшитгэл бодвол $x=\pm \dfrac{2\pi}{\fbox{g}}+\dfrac 23\pi k (k\in \mathbb Z).$
$y=12\sin 2x\cos 2x\cdot \cos x+7+6\cos 4x\sin x$ бол
1) $x=\dfrac{\pi}{30}$ үед $y=\fbox{ab},$
2) $y_{\max}=\fbox{cd}, y_{\min}=\fbox{e},$
3) Үндсэн үе $T=\dfrac{\fbox{g}}{\fbox{f}}\pi,$
4) $y=1$ тэгшитгэл бодвол $x=-\dfrac{\pi}{\fbox{hi}}+\dfrac{2}{5}\pi k.$
1) $x=\dfrac{\pi}{30}$ үед $y=\fbox{ab},$
2) $y_{\max}=\fbox{cd}, y_{\min}=\fbox{e},$
3) Үндсэн үе $T=\dfrac{\fbox{g}}{\fbox{f}}\pi,$
4) $y=1$ тэгшитгэл бодвол $x=-\dfrac{\pi}{\fbox{hi}}+\dfrac{2}{5}\pi k.$
$y=\sin x+\sin 3x-1$ функцийн
1) $y_{\max}=\dfrac{\fbox{b}}{\fbox{a}}\sqrt{3}-\fbox{c},$
2) $y=-\sqrt{2}-1$ тэгшитгэл бодвол $\left[ % \begin{array}{l} x=(-1)^{k+1}\cdot \dfrac{\pi}{\fbox{d}}+k\pi \\[2mm] x=(-1)^k\arcsin\dfrac{\sqrt{\fbox{e}}-\sqrt{\fbox{fg}}}{4}+k\pi, \\ \end{array} % \right. (k\in \mathbb Z)$.
1) $y_{\max}=\dfrac{\fbox{b}}{\fbox{a}}\sqrt{3}-\fbox{c},$
2) $y=-\sqrt{2}-1$ тэгшитгэл бодвол $\left[ % \begin{array}{l} x=(-1)^{k+1}\cdot \dfrac{\pi}{\fbox{d}}+k\pi \\[2mm] x=(-1)^k\arcsin\dfrac{\sqrt{\fbox{e}}-\sqrt{\fbox{fg}}}{4}+k\pi, \\ \end{array} % \right. (k\in \mathbb Z)$.
$f(x)=3\cos 3x+4\cos 6x$ функц өгөгдөв.
- $\varphi(x)=4\cos 6x-4\sin 3x$ бол $f(x)-\varphi(x)=\fbox{a}\sin \left(\fbox{b}x+\alpha\right)$ болох ба $\alpha =\arccos \dfrac{\fbox{c}}{\fbox{d}}$ байна.
- $f(x)=7$ тэгшитгэл $[0;4\pi]$ завсарт $\fbox{e}$ ширхэг шийдтэй ба тэдгээрийн нийлбэр нь $\fbox{f}\pi$, квадратуудын нийлбэр нь $\fbox{gh}\pi^{\fbox{i}}$ байна.
$y=\cos 3x-\cos x$ функцийн
- $y_{\max}=\dfrac{\fbox{a}}{\fbox{b}}\sqrt{3}$
- $y=-1.5$ тэгшитгэл бодвол $$x=\pm\dfrac{\pi}{\fbox{c}}+2\pi k,\, x=\pm\arccos\dfrac{\sqrt{\fbox{de}}-1}{4}+2\pi n$$ шийдүүд гарна.
$$f(\theta)=(\sin\theta+\cos\theta+1)^3(\sin\theta+\cos\theta-1)^3-6\sin\theta\cdot\cos\theta+a$$
функцийн $0^\circ\leq \theta\leq 90^\circ$ завсар дахь хамгийн бага утга $0$ бол $a$ болон хамгийн бага утгаа авах $\theta$-г ольё.
$$(\sin\theta+\cos\theta+1)(\sin\theta+\cos\theta-1)=(\sin\theta+\cos\theta)^2-1=\sin\fbox{a}\theta$$
учир $\sin\fbox{a}\theta=t$ орлуулга хийвэл $\fbox{b}\leq t\leq\fbox{c}$ ба $f(\theta)$ функц $g(t)=t^3-\fbox{d}t+a$ функц болно. Иймд манай бодлого $g(t)$ функцийн $\fbox{b}\leq t\leq\fbox{c}$ завсар дахь хамгийн бага утга $0$ байх $a$-г олох бодлого болно. $g^\prime(t)>0$ тэнцэтгэл бишийг бодон өсөх завсарыг олбол $]-\infty;-\fbox{e}[\cup]\fbox{f};+\infty[$ болно. Иймд $g(t)$ функц $t_0=\fbox{g}$ үед хамгийн бага утгаа авах ба $g(t_0)=0$ нөхцлөөс $a=\fbox{h}$ болно. Энэ үед $\theta=\fbox{ij}^\circ$ болно.
Тригонометрийн урвуу функцүүд
$\cos(\arcsin x)=\sqrt{1-x^2}$ томьёог батлаж биелэх мужийг заа.
$\sin(\arccos x)=\sqrt{1-x^2}$ томьёог батлаж биелэх мужийг заа.
$\tg(\arcsin x)=\dfrac{x}{\sqrt{1-x^2}}$, $\tg(\arccos x)=\dfrac{\sqrt{1-x^2}}{x}$ томьёог батлаж биелэх мужийг заа.
$\sin\Big(\dfrac12\arccos x\Big)=\sqrt{\dfrac{1-x}{2}}$ томьёог батлаж биелэх мужийг заа.
$\cos\Big(\dfrac12\arccos x\Big)=\sqrt{\dfrac{1+x}{2}}$ томьёог батлаж биелэх мужийг заа.
$\tg(\arcctg x)=\dfrac1x$, $\ctg(\arcctg x)=\dfrac1x$ томьёог батлаж биелэх мужийг заа.
$\cos(\arcctg x)=\dfrac{1}{\sqrt{1+x^2}}$, $\sin(\arcctg x)=\dfrac{1}{\sqrt{1+x^2}}$ томьёог батлаж биелэх мужийг заа.
$\sin(\arctg x)=\dfrac{x}{\sqrt{1+x^2}}$ томьёог батлаж биелэх мужийг заа.
$0.2(6)$ үет бутархайг энгийн бутархай болго
A. $\dfrac{26}{9}$
B. $\dfrac{24}{90}$
C. $\dfrac{4}{15}$
D. $\dfrac{8}{3}$
E. $\dfrac{20}{99}$
Дараах функцүүдээс аль нь $[ -\frac{\pi}{2}, \frac{\pi}{2}]$ завсарт $ y=\sin x $ функцийн урвуу нь болох вэ?
A. $\arcsin x$
B. $\cos x$
C. $\arccos x$
D. $\dfrac{1}{\sin x}$
E. $-\sin x$
$0.2(6)$ үет бутархайг энгийн бутархай болго
A. $\dfrac{26}{9}$
B. $\dfrac{24}{90}$
C. $\dfrac{4}{15}$
D. $\dfrac{8}{3}$
E. $\dfrac{20}{99}$
Дараах функцүүдээс аль нь $ [ 0, \pi]$ завсарт $ y=\cos x $ функцийн урвуу нь болох вэ?
A. $ \sin x$
B. $ \arccos x$
C. $ \arcsin x$
D. $\dfrac{1}{\cos x}$
E. $-\cos x$
$y=\arcsin \dfrac{x-7}{2}.$
1) Функцийн тодорхойлогдох муж $x\in \Bigl[\fbox{a};\fbox{b}\Bigr],$
2) $\pi +y(6)=\dfrac{\fbox{d}}{\fbox{c}}\pi$
3) $\arcsin \sin 95^{\circ}=\fbox{ef}^{\circ}$ байна.
1) Функцийн тодорхойлогдох муж $x\in \Bigl[\fbox{a};\fbox{b}\Bigr],$
2) $\pi +y(6)=\dfrac{\fbox{d}}{\fbox{c}}\pi$
3) $\arcsin \sin 95^{\circ}=\fbox{ef}^{\circ}$ байна.
$y=\arcsin^2(4x)-\arcsin (4x)+2$ функцийн
1) Тодорхойлогдох муж $|x|\leq \dfrac{\fbox{b}}{\fbox{a}},$
2) Утгын муж $\Bigl[\fbox{c,de};\dfrac{\pi^2+\fbox{f}\pi+\fbox{g}}{4}\Bigr]$ байна.
1) Тодорхойлогдох муж $|x|\leq \dfrac{\fbox{b}}{\fbox{a}},$
2) Утгын муж $\Bigl[\fbox{c,de};\dfrac{\pi^2+\fbox{f}\pi+\fbox{g}}{4}\Bigr]$ байна.
Урвуу пропорционал хамаарал
Урвуу функц, харилцан нэг утгатай функц
Дараах функцүүдийн урвуу $f^{-1}(x)$-г ол.
- $f(x)=x^2+1$, $x\in]-\infty,0[$
- $y=1+\dfrac{1}{x}$
- $y=\sqrt[4]{x}$
Дараах функцүүдийн урвуу функцтэйгээ давхцах параметрийн утгыг ол.
- $f(x)=ax+b$
- $y=x^{\alpha}$
- $y=\dfrac{ax+b}{cx+d}$, $c\neq 0$
Хэрэв $f(x)=\dfrac{x-1}{3x+2}$ бол $f$-ийн урвуу функц $f^{-1}(x)$-ийг ол.
A. $\dfrac{3x+2}{x-1}$
B. $\dfrac{x+1}{3x-2}$
C. $\dfrac{2x+1}{1-3x}$
D. $\dfrac{1-3x}{2x+1}$
E. $\dfrac{-x+1}{2x+3}$
$y=\dfrac{x^2+16}{8x}$ функийн $]0;4[$ завсар дахь урвуу функцийг ол.
A. $y=4x-4\sqrt{x^2-1}$
B. $y=4x+4\sqrt{x^2-1}$
C. $y=-4x+4\sqrt{x^2-1}$
D. $y=-4x-4\sqrt{x^2-1}$
E. $y=-4x-4\sqrt{1-x^2}$
$f(x)=\dfrac{x^2+4}{4x}$ функцийн $[2;+\infty[$ завсар дахь урвуу функцийг ол.
A. $f^{-1}(x)=2x-2\sqrt{x^2-1}$
B. $f^{-1}(x)=2x+2\sqrt{x^2-1}$
C. $f^{-1}(x)=-2x+2\sqrt{x^2+1}$
D. $f^{-1}(x)=-2x-2\sqrt{x^2+1}$
E. $f^{-1}(x)=-x-2\sqrt{x^2+1}$
$f(x)=\dfrac{x+3}{x+1}$ функцийн урвуу функц аль нь вэ?
A. $f^{-1}(x)=\dfrac{3-x}{1-x}$
B. $f^{-1}(x)=\dfrac{x+1}{x+3}$
C. $f^{-1}(x)=\dfrac{3-x}{x-1}$
D. $f^{-1}(x)=-\dfrac{x+3}{x+1}$
E. $f^{-1}(x)=\dfrac{1}{x}$
$y=2^{-x}+2$ функцийн урвуу функцийг ол.
A. $y=\log_2x-2$
B. $y=\log_x2-2$
C. $y=-\log_2(x-2)$
D. $y=\dfrac{1}{2^{-x}+2}$
E. Урвуу функц нь оршихгүй.
$f(x)=\log_2(x+1)$ бол $f^{-1}(3)=?$
A. $0$
B. $6$
C. $7$
D. $9$
E. $8$
$y=2-3x$ функцийн урвуу функц аль нь вэ?
A. $y=2-\dfrac{x}{3}$
B. $y=\dfrac{2+x}{3}$
C. $y=\dfrac{2-x}{3}$
D. $y=\dfrac23-x$
E. $y=3x-2$
$f(x)=4^{8x-5}+36$ функцийн хувьд $f^{-1}(100)$ хэдтэй тэнцүү вэ?
A. $2$
B. $\dfrac12$
C. $1$
D. $\dfrac{1}{4^{225}+36}$
E. $\dfrac{1}{4}$
$f(x)=5^{3x-1}-25$ функцийн хувьд $f^{-1}(100)$ хэдтэй тэнцүү вэ?
A. $2$
B. $\dfrac43$
C. $1.3$
D. $\dfrac{1}{5^{299}-25}$
E. $\dfrac{1}{3}$
$f(x)=2^{5x-3}-28$ функцийн хувьд $f^{-1}(100)$ хэдтэй тэнцүү вэ?
A. $7$
B. $\dfrac12$
C. $2$
D. $\dfrac{1}{2^{497}-28}$
E. $\dfrac{1}{7}$
$f(x)=3^{4x-1}-8$ функцийн хувьд $f^{-1}(19)$ хэдтэй тэнцүү вэ?
A. $1$
B. $\dfrac32$
C. $3$
D. $\dfrac{1}{2^{497}-28}$
E. $\dfrac{1}{4}$
$f(x)=2^{5x-3}-28$ функцийн хувьд $f^{-1}(100)$ хэдтэй тэнцүү вэ?
A. $7$
B. $\dfrac12$
C. $2$
D. $\dfrac{1}{2^{497}-28}$
E. $\dfrac{1}{7}$
$f(x)=\dfrac{x+3}{x+1}$ функцийн урвуу функц аль нь вэ?
A. $f^{-1}(x)=\dfrac{3-x}{1-x}$
B. $f^{-1}(x)=\dfrac{x+1}{x+3}$
C. $f^{-1}(x)=\dfrac{3-x}{x-1}$
D. $f^{-1}(x)=-\dfrac{x+3}{x+1}$
E. $f^{-1}(x)=\dfrac{1}{x}$
$f(x)=\dfrac{x-2}{x+2}$ функцийн урвуу функц аль нь вэ?
A. $f^{-1}(x)=\dfrac{x+2}{x-2}$
B. $f^{-1}(x)=-\dfrac{x-2}{x+3}$
C. $f^{-1}(x)=\dfrac{3-x}{x-1}$
D. $f^{-1}(x)=-\dfrac{2x+2}{x-1}$
E. $f^{-1}(x)=\dfrac{1}{x}$
$0.2(6)$ үет бутархайг энгийн бутархай болго
A. $\dfrac{26}{9}$
B. $\dfrac{24}{90}$
C. $\dfrac{4}{15}$
D. $\dfrac{8}{3}$
E. $\dfrac{20}{99}$
$y=3x+1$ функцийн урвуу функц аль нь вэ?
A. $y=\dfrac{x-1}{3}$
B. $y=\dfrac{1}{3x+1}$
C. $x=\dfrac{y-1}{3}$
D. $y=3x-1$
E. $y=\dfrac{x+1}{3}$
$x\ge m$ үед $f(x)=3x^2+6x-1$ гэж тодорхойлогдсон функц харилцан нэгэн утгатай бол $m$-ийн хамгийн бага утгыг олоорой.
A. $\dfrac13$
B. $1$
C. $2$
D. $3$
E. $-1$
$y=2x+1$ функцийн урвуу функц аль нь вэ?
A. $y=\dfrac{x-1}{2}$
B. $y=\dfrac{1}{2x+1}$
C. $x=\dfrac{y-1}{2}$
D. $y=2x-1$
E. $y=\dfrac{x+1}{2}$
$x\ge m$ үед $f(x)=3x^2-6x+2$ гэж тодорхойлогдсон функц харилцан нэгэн утгатай бол $m$-ийн хамгийн бага утгыг олоорой.
A. $3$
B. $-1$
C. $2$
D. $1$
E. $\dfrac13$
Дараах функцүүдээс аль нь $[ -\frac{\pi}{2}, \frac{\pi}{2}]$ завсарт $ y=\sin x $ функцийн урвуу нь болох вэ?
A. $\arcsin x$
B. $\cos x$
C. $\arccos x$
D. $\dfrac{1}{\sin x}$
E. $-\sin x$
$0.2(6)$ үет бутархайг энгийн бутархай болго
A. $\dfrac{26}{9}$
B. $\dfrac{24}{90}$
C. $\dfrac{4}{15}$
D. $\dfrac{8}{3}$
E. $\dfrac{20}{99}$
Дараах функцүүдээс аль нь $ [ 0, \pi]$ завсарт $ y=\cos x $ функцийн урвуу нь болох вэ?
A. $ \sin x$
B. $ \arccos x$
C. $ \arcsin x$
D. $\dfrac{1}{\cos x}$
E. $-\cos x$
$f(x)=\sqrt{x^2-8x+12}$ функцийн монотон өсөх завсар нь
$[\fbox{a};+\infty[$ ба энэ завсар дээрх урвуу функц нь
$f^{-1}(x)=\fbox{b}+\sqrt{\fbox{c}x^2+\fbox{d}}$ болно.
$f(x)=\sqrt{x^2-9x+18}$ функцийн монотон буурах завсар нь
$]-\infty;\fbox{a}]$ ба энэ завсар дээрх урвуу функц нь
$f^{-1}(x)=\dfrac{\fbox{b}-\sqrt{\fbox{c}x^2+\fbox{d}}}{2}$ болно.
$f(x)=x^2 - 4x +6$ функц өгөв. $ x >2, y >2 $ үед урвуу функцийг олбол $f^{-1}(x) = \fbox{a}+\sqrt{x-\fbox{b}}$ байна. $f(x)$, $f^{-1}(x)$ функцийн график $A(\fbox{c},\fbox{d})$, $B(\fbox{e},\fbox{f})$ цэгүүдэд огтлолцох бөгөөд тэдгээрийн хоорондох зай нь $\sqrt{\fbox{g}}$ байна.
$f(x)=x^2 - 4x +6$ функц өгөв. $ x >2, y >2 $ үед урвуу функцийг олбол $f^{-1}(x) = \fbox{a}+\sqrt{x-\fbox{b}}$ байна. $f(x)$, $f^{-1}(x)$ функцийн график $A(\fbox{c},\fbox{d})$, $B(\fbox{e},\fbox{f})$ цэгүүдэд огтлолцох бөгөөд тэдгээрийн хоорондох зай нь $\sqrt{\fbox{g}}$ байна.
$f(x)=x^2 - 4x +6$ функц өгөв. $ x >2, y >2 $ үед урвуу функцийг олбол $f^{-1}(x) = \fbox{a}+\sqrt{x-\fbox{b}}$ байна. $f(x)$, $f^{-1}(x)$ функцийн график $A(\fbox{c},\fbox{d})$, $B(\fbox{e},\fbox{f})$ цэгүүдэд огтлолцох бөгөөд тэдгээрийн хоорондох зай нь $\sqrt{\fbox{g}}$ байна.
$f(x)=x^2 - 6x +12$ функц өгөв. $ x >3, y >3 $ үед урвуу функцийг олбол $f^{-1}(x) = \fbox{a}+\sqrt{x-\fbox{b}}$ байна. $f(x)$, $f^{-1}(x)$ функцийн график $A(\fbox{c},\fbox{d})$, $B(\fbox{e},\fbox{f})$ цэгүүдэд огтлолцох бөгөөд тэдгээрийн хоорондох зай нь $\sqrt{\fbox{g}}$ байна.
Функцийн график
$y=\dfrac{|\sin x|}{\sin x}$ функцийн график байгуул.
$y=\dfrac{\sin|x|}{\sin x}-x$ функцийн график байгуул.
$y=\dfrac{\sin x}{\sin x}\cdot x^2$ функцийн график байгуул.
$y=\dfrac{\sin x-\dfrac12}{\sin x-0.5}$ функцийн график байгуул.
$y=\arcsin(\sin x)$ функцийн график байгуул.
$y=\lg(-\cos x)$ функцийн график байгуул.
$\sin x=\dfrac14 x$ тэгшитгэлийг графикийн аргаар бод.
$f(x) = 2 - 3x^{2} - x^{3}$ функцийг шинжилж графикийг байгуул.
$f\left( {x} \right) = \left( {x - 1} \right)^{2}\left( {x + 3} \right)$ функцийг шинжилж графикийг байгуул.
$f\left( {x} \right) = {\frac{{x^{3}}}{{3}}} - 2x^{2} + 3x$ функцийг шинжилж графикийг байгуул.
$f\left( {x} \right) = x^{4} - 5x^{2} + 4$ функцийг шинжилж графикийг байгуул.
$f\left( {x} \right) = {\left| {x - 1} \right|} + {\frac{{x^{2}}}{{2}}}$ функц өгөгдөв. $f'\left( {x} \right)$ функцийн графикийг байгуул.
$y = \sqrt {1 + 2x + x^{2}} + \sqrt {x^{2} - 2x + 1} $ функцийн сэжигтэй цэгүүдийг олж, түүний графикийг байгуул
$y = x^{5} - 5x^{4} + 5x^{3} - 1$ функцийг шинжилж графикийг байгуул.
$y=3\cos(2 \theta+60^{\circ})$ функцийн графикийг зур.
Дараах функцийн графикийг зур. Мөн $y=\sin\theta$-ийн график ба хамаарлыг ол.
- $y=\sin \theta+1$
- $y=\sin(\theta-60^{\circ})$
- $y=2\sin\theta$
- $y=\sin2\theta$
$f(x)=2x^3+12x^2+18x+9$ функцийн графикийг $x$ тэнхлэгийн дагуу $p$, $y$ тэнхлэгийн дагуу $q$ нэгжээр зөөхөд координатын эхийн хувьд тэгш хэмтэй муруй гарсан бол $p$, $q$-г ол.
- $y=\sin \theta+\sqrt{3}\cos\theta$ функцийн графикийг зур.
- $f(x)=6\sin^2 x+2\sqrt{3}\sin x\cdot \cos x+8\cos^2x$ функцийн минимум, максимумыг $(0^{\circ}\leq x\leq 180^{\circ})$ ол. Мөн максимум, минимум утгаа авах үеийн $x$-ийн утгыг ол.
$x$ нь $t$-ээс хамаарахгүй бол дараах функцүүдын график зур.
- $y=\int\limits_{-1}^{2}(3t^2-2xt)\,dt$
- $y=\int\limits_{0}^{x}(2t-3t^2)\,dt$
- $y=\int\limits_{0}^{x}|t-1|\,dt$
Дараах функцүүдийн графикыг зур.
- $f(x)=\mathop{\int\limits_{0}^{1}}(t-x)\,\mathrm{d}t$
- $f(x)=\mathop{\int\limits_{0}^{1}}|t-x^2|\,\mathrm{d}t$
Зурагт $y=\log_ax$ функцийн графикийг үзүүлэв. $a$, $b$, $c$-г ол.


- $f(x)=4x-3$, $g(x)=-3x^2$ бол дараах утгуудыг ол. $$f\left(\dfrac32\right), f(-2), f(a+2), g(-1+\sqrt3), g(a-2), g(a^2)$$
- Дараах цэгүүд координатын хавтгайн аль мужид орших вэ?
- $(2,3)$
- $(-1,-5)$
- $(-3,2)$
- $(4,-3)$
- $f(x)=-3x+2$, $g(x)=x^2-3x+2$ бол дараах утгуудыг ол. $$f(0), f(-1), f(a+1), g(2), g(a-2), g(2a-1)$$
- $x=2$ бол $(3x-1,3-2x)$ цэг координатын хавтгайн аль мужид орших вэ? Мөн $(3x-1,-2)$ цэг III мужид орших бол $x<\ebox{}$ байна.
$y=|x-2|$ функцийн графикийг байгуул.
Хэрэв $f(x)=kx^2+(k+1)x$ функцийн график дээр $A(1;5)$ цэг оршдог бол $k$-ийн утга хэд байх вэ?
A. $-2$
B. $-1$
C. $0$
D. $1$
E. $2$

Зурагт долоо хоногийн турш орсон хур тундасны хэмжээг графикаар үзүүлэв. Хэвтээ тэнхлэгийн дагуу өдрүүд, босоо тэнхлэгийн дагуу тухайн өдөр унасан хур тундасны хэмжээг мм-ээр илэрхийлэв. Долоо хоногийн турш нийт хэдэн мм хур тундас унасан бэ?
A. 23 мм
B. 30 мм
C. 7 мм
D. 10 мм
E. 16 мм
$y=x^2$ параболыг $Ox$ тэнхлэгийн дагуу $3$ нэгж, $Oy$ тэнхлэгийн дагуу $4$ нэгж зөөхөд гарах параболын тэгшитгэл аль нь вэ?
A. $y=(x-3)^2-4$
B. $y=(x+3)^2-4$
C. $y=(x-3)^2-4$
D. $y=(x-3)^2+4$
E. $x=(y-3)^2+4$
$g(x)=f(x+a)+2b$ бол $f(x)$ функцийн график нь $g(x)$ функцийн графикийг ямар векторын дагуу зөөхөд гарах вэ?
A. $\vec{p}=(a;2b)$
B. $\vec{p}=(-a;2b)$
C. $\vec{p}=(a;-2b)$
D. $\vec{p}=(-a;-2b)$
E. $\vec{p}=(2a;b)$
Зурагт $f(x)$ функцийн график дүрслэгджээ. $f(x)\ge0$ тэнцэтгэл бишийн шийд аль нь вэ?
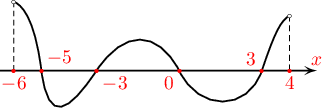

A. $[-6;0]$
B. $[-6;-5]\cup[-3;0]\cup[3;4]$
C. $[0;4]$
D. $[5;-3]\cup[0;3]$
E. $[5;-3]\cup[0;2]$
$y=f(x)$ функц $(-6;4)$ завсарт тодорхойлогдсон байв. Зураг дээр энэхүү функцийн уламжлалын графикийг дүрсэлжээ. $y=f(x)$ функцийн минимумын цэг нь аль вэ?
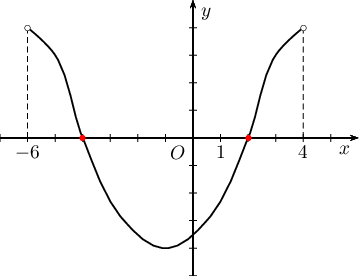

A. $-6$
B. $-4$
C. $-1$
D. $2$
E. $4$
Зураг дээр сарын гуравнаас арван тавны өдрүүдийн хур тунадсаны хэмжээг тэмдэглэсэн байна. Хэвтээ тэнхлэгийн дагуу сарын өдрүүд, босоо тэнхлэгийн дагуу хоногт унасан хур тунадасны хэмээг миллиметрээр тэмдэглэсэн байна. Эдгээр өдрүүдээс хэдэд нь 2-оос илүүгүй мм-ээс бага хур тунадас орсон, эсвэл огт хур тунадас ороогүй байна вэ?


A. 7
B. 8
C. 9
D. 10
E. 11
Дараах график аль функцийн график вэ?
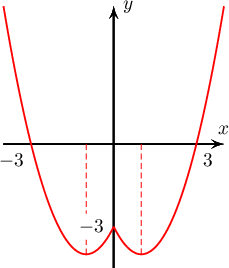

A. $y=|x^2-2x-3|$
B. $y=x^2-2|x|-3$
C. $y=|x^2+2x-3|$
D. $y=x^2+2|x|-3$
E. $y=-x^2-|x|-3$
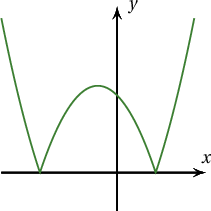
A. $y=x^2+x-2$
B. $y=x^2-x-2$
C. $y=x^2+|x|-2$
D. $y=|x^2+x-2|$
E. $y=|x^2+x|-2$
$f(x)=\dfrac{2x+1}{x}$ функцийн график координатын хавтгайн аль аль мөчид зурагдаж вэ?
A. I, III, IV
B. I, III
C. I, II, IV
D. II, IV
E. I, II, III
$g(x)=f(x-2a)-b$ бол $f(x)$ функцийн график нь $g(x)$ функцийн графикийг ямар векторын дагуу зөөхөд гарах вэ?
A. $\vec{p}=(2a,b)$
B. $\vec{p}=(-2a;b)$
C. $\vec{p}=(2a,-b)$
D. $\vec{p}=(-2a,-b)$
E. $\vec{p}=(a,-b)$
1.Дараах функцийн графикийг байгуул.
- $y=|\log_{0.5}{x}|$
- $y= 2^{|x|}$
- $y=|x-2|^\frac{1}{3}$
- $y=\arccos|x|$
- $y=-x^2-2|x|+3$
- $y = \frac{2x-1}{x+2}$
- $y=0.5\cdot \arcctg4x$
- $y = -2\cos(3x-\frac{\pi}{2}$
- $y=|3\sin(2x-\frac{\pi}{3}+1|$
1.Дараах функцийн графикийг байгуул.
- $y=|\log_{0.5}{x}|$
- $y= 2^{|x|}$
- $y=|x-2|^\frac{1}{3}$
- $y=\arccos|x|$
- $y=-x^2-2|x|+3$
- $y = \frac{2x-1}{x+2}$
- $y=0.5\cdot \arcctg4x$
- $y = -2\cos(3x-\frac{\pi}{2}$
- $y=|3\sin(2x-\frac{\pi}{3}+1|$
$f(x)=x^2-6x+a$ функцийн график $(2,3)$ цэгийг
дайрдаг бол $a=\fbox{ab}$ байна. Иймд $f(x)$ функцийн хамгийн бага
утга нь $\fbox{c}$ байна.
$f(x)=x^2-4x+a$ функцийн график $(3,2)$ цэгийг
дайрдаг бол $a=\fbox{a}$ байна. Иймд $f(x)$ функцийн хамгийн бага
утга нь $\fbox{b}$ байна.
$y=ax^3-3ax^2+(2-a)x+3a-1$ функцийн график $a$-ийн
ямарч утганд $(\fbox{ab},\fbox{cd}), (\fbox{e},\fbox{f}),
(\fbox{g},\fbox{h})$ цэгүүдийг дайрна.$(\fbox{e}< \fbox{g})$
$y=ax^3-4ax^2+(3-4a)x+16a-2$ функцийн график
$a$-ийн ямарч утганд $(\fbox{ab},\fbox{cd}),
(\fbox{e},\fbox{f}), (\fbox{g},\fbox{hi})$ цэгүүдийг дайрна.
$y=1-x$ ба $|y|=x+1$ тэгшитгэлтэй муруйнуудын
огтлолцлын цэг $(\fbox{a},\fbox{b})$ дээр оройтой $(1,3)$ цэгийг
дайрсан параболын тэгшитгэл $y=\fbox{c}x^2+\fbox{d}x+\fbox{e}$
байна.
$y=2x-1$ ба $y=|x|+1$ тэгшитгэлтэй муруйнуудын
огтлолцлын цэг $(\fbox{a},\fbox{b})$ цэгийг дайрсан $(1,2)$ дээр
оройтой параболын тэгшитгэл $y=x^2+\fbox{cd}x+\fbox{e}$ байна.
$y=(a+1)x^2-(a-2)x+2$ параболын оройн цэг
$$\left(\dfrac{a+\fbox{ab}}{2(a+1)};-\dfrac{a^2-\fbox{cd}a-\fbox{e}}{4(a+1)}\right)$$
байна. Оройн цэгийн абсцисс $[1;3]$ мужид ордог бол $-\fbox{f}\leq
a\leq-\dfrac{\fbox{g}}{\fbox{h}}$ байна.
Функцийн графикийн хувиргалт
Зурагт $y=a+b\cos x$ функцийн график өгөгджээ. Зураг ашиглан $a\cdot b$ үржвэрийг олоорой.


A. $-2$
B. $1$
C. $8$
D. $2$
E. $-4$
Зурагт $y=a+b\cos x$ функцийн график өгөгджээ. Зураг ашиглан $a\cdot b$ үржвэрийг олоорой.


A. $-2$
B. $1$
C. $8$
D. $2$
E. $-4$
Функцийн тодорхойлогдох муж, утгын муж, дүр
$y = {\frac{{2}}{{\sqrt { - x^{2} + 7x - 10}} }}$
$f(x) = \sqrt {{\frac{{x^{2} + 3x + 4}}{{x - 3}}}} $
$y = \sqrt {{\frac{{3x + 2}}{{2x - 1}}} + 2} $
$y = \sqrt {{\frac{{x^{2} - 5x + 6}}{{x - 4}}}} $
$y = {\frac{{1}}{{\sqrt {2 - \sqrt {x + 1}} } }}$
$y = \lg \left( {3x^{2} + 7x + 2} \right)$
$y = \lg \left( {10x^{2} - x} \right) + \sqrt {3 + 5x} $
$f\left( {x} \right) = {\frac{{\sqrt {3 + 2x - x^{2}}} }{{\log _{2}
x - 1}}}$
$y = \dfrac{\sqrt {x + 30 - x^{2}} }{\log _{2} \left( {x + 2}
\right)}$ функцийн тодорхойлогдох мужийн бүх бүхэл тоонуудын нийлбэрийг ол.
$y = {\frac{{1}}{{\lg \left( {6 - x} \right)}}} + \sqrt {x - 1} $
тодорхойлогдох мужийн бүхэл утгуудын нийлбэрийг ол.
$y = \log _{6} \log _{0.5} \left( {4 - x} \right)$ тодорхойлогдох
мужийн урт ба дундаж цэгийг ол.
$y = \sqrt {\log _{{\frac{{1}}{{2}}}} \left( {3x^{2} - 2x} \right)}
$
$y = \sqrt {\log _{{\frac{{1}}{{3}}}} \left( {x^{2} +
{\frac{{8}}{{3}}}x} \right)} $
$f(x) = \sqrt {\log _{{\frac{{2}}{{3}}}} \left( {7 - x} \right) - 1}
$
$f\left( {x} \right) = \sqrt {1 + \log _{{\frac{{1}}{{2}}}} x} $
$y = \sqrt {2 - \log _{0.5} x} + \sqrt {x^{2} - 9} $
$f\left( {x} \right) = \sqrt {\log _{2} \left( {4 - x} \right)\left(
{x - 1} \right) - 1} $
$y = \sqrt {\log _{0.3} {\frac{{x - 1}}{{x + 5}}}} $
$y = \sqrt {\log _{{\frac{{1}}{{2}}}} {\frac{{5x - 2}}{{x + 2}}} +
3} $
$y = \log _{x - 1} \left( {7 - x} \right)$ тодорхойлогдох мужийн
бүхэл утгуудын нийлбэрийг ол.
$y = \log _{x + 2} \left( {5 - x} \right)$ тодорхойлогдох мужийн
бүхэл утгуудын нийлбэрийг ол.
$y = \log _{x} \left( {x^{2} + 3x + 2} \right)$
$f\left( {x} \right) = \sqrt {5x^{2} - 3x + 23} + \lg \left( {x^{2}
- 10x + 16} \right) + {\frac{{1}}{{x}}}$
$y = \log _{5} \left( {4 + 5x} \right) + \sqrt {7^{2x} - 2401} $
$f\left( {x} \right) = \sqrt {{\frac{{x^{2} - 7x + 6}}{{3 - x}}}} +
\log _{\sqrt {3}} \left( {7x - 3} \right)$
$y = \sqrt {\left( {{\frac{{1}}{{5}}}} \right)^{x^{2} - 3} - \left(
{{\frac{{1}}{{25}}}} \right)^{x}} $
$y = \sqrt {7x - x^{2} - 6} \cdot \log _{5} {\frac{{x - 7}}{{2 -
x}}}$ тодорхойлогдох мужийн бүхэл утгуудын нийлбэрийг ол.
$f\left( {x} \right) = \sqrt {{\frac{{\log _{{\frac{{1}}{{2}}}}
x}}{{3 - x}}}} $
$f(x) = \sqrt {\dfrac{\log _{2} \left({x + 1}
\right)}{x - 1}}$
$f(x) = \sqrt {\dfrac{{12 + x - x^{2}}}{\log_{\frac{1}{2}} x}}$
$f(x) = \sqrt {\log _{\frac{1}{2}}\log _{3}
\dfrac{x + 1}{x - 1}}$ функцийн тодорхойлогдох мужийг ол.
$y=\sqrt{\left({64-x^{2}}\right)\cdot{\left|{x-10}\right|}}$ функцийн тодорхойлогдох мужийг ол.
$y=\sqrt{\left({x^{2}-3x-10}\right)\cdot\lg{\left|{x-3}\right|}}$ функцийн тодорхойлогдох мужийг ол.
$y=\sqrt{\log_{5-x}\left({x^{2}-9}\right)}$ функцийн тодорхойлогдох мужийг ол.
$f\left({x}\right)=\sqrt{1-{\dfrac{{\lg ^{2}x-3\lg x+3}}{{\lg x-1}}}}$ функцийн тодорхойлогдох мужийг ол.
$f(x)=\log_{\frac{1}{5}}\left({\log_{5}x-\log_{125}\left({3x-2}\right)}\right)$ функцийн тодорхойлогдох мужийг ол.
$y=\sqrt{\left({x^{4}-11x^{2}+18}\right)\cdot{\left|{2x-5}\right|}}$ функцийн тодорхойлогдох мужийг ол.
$f\left({x}\right)=\sqrt{\left({\log_{2}^{2}4x-\log_{2}x^{2}-3}\right)^{-1}}$ функцийн тодорхойлогдох мужийг ол.
$y={\dfrac{{1}}{{\sqrt{\cos\left({-x}\right)}}}}+\log_{\frac{1}{4}}\left({15x-2x^{2}-13}\right).$ Функцийн тодорхойлогдох мужийн бүхэл утгуудын нийлбэрийг ол.
$y=\sqrt{\log_{4}\left({1+6x}\right)+{\left|{\log_{\frac{1}{8}}\left({1+7x}\right)}\right|}}$ функцийн тодорхойлогдох мужийг ол.
$(0,0)$; $(6,-2)$ цэгүүдийг дайрах $y=\log_{\frac12}(x-a)+b$ функц ба $y=\log_2(-x+p)$ функцүүдийн график 2 өөр цэгээр огтолцох үед $a, b$ ба $p$-ын утгын мужийг ол.
$t\geq 0$, $\ell_t:y=3t^2x-2t^3$ байг. $\ell_t$ муруйнууд дээр орших цэгүүдийн олонлогийг $A$ гэе. $P(a, b)$ цэг $A$ олонлогт харъяалагдах зайлшгүй бөгөөд хүрэлцээтэй нөхцлийг тогтоо.
$f(x)=\dfrac{3x+p}{x^2+5x+7}$ функцийн утгын муж нь $(-1;3]$ завсарыг бүхлээр нь агуулж байх $p$ параметрийн утгын мужийг ол.
$f\colon X\to Y$ инъектив функц бол $f(A\cap B)=f(A)\cap f(B)$ гэж батал.
Дараах функцүүдийн тодорхойлогдох муж ол.
- $y=x^3+1$
- $y=\dfrac{x^2-1}{x-1}$
- $y=\sqrt{x-5}$
- $y=\sqrt[3]{x-4}$
- $y=\sqrt[4]{-x}$
- $y=\sqrt{4-x^2}$
$y=x^3$ функцийн хялбар шинжилгээ хийж график байгуул.
$y = \dfrac{\sqrt{x + 3}}{3x+x^2-4}$ функцийн тодорхойлогдох мужийг ол.
A. $[-3;1[\cup]1;+\infty[$
B. $\big[-3;\frac{-3+\sqrt{27}}{2}\big[\cup\big]\frac{-3+\sqrt{27}}{2};+\infty\big[$
C. $\big[-3;\frac{-3-\sqrt{27}}{2}\big[\cup\big]\frac{-3+\sqrt{27}}{2};+\infty\big[$
D. $]1;+\infty[$
E. $[-3;+\infty[$
$y = \sqrt{\dfrac{x - 4}{x^{2} - 4}}$ функцийн тодорхойлогдох мужийг ол.
A. $(-2;2)$
B. $[4;+\infty)$
C. $(-2;2)\cup[4;+\infty)$
D. $(-2;4]$
E. $(2;4]$
$y=9-12\cos7x-2\sin^27x$ функцийн утгын мужийг ол.
A. $-11\le y\le 21$
B. $-3\le y\le 21$
C. $-11\le y<9$
D. $-11\le y\le 11$
E. $-3\le y\le 11$
$y=\log_{x^2-2x+3}4$ функцийн утгын мужийг ол.
A. $\Big]0;\dfrac23\Big[$
B. $]0; 1]$
C. $]0; 3]$
D. $]0; 2]$
E. $\Big]0; \dfrac53\Big]$
$y=\dfrac{\arcsin(2x+9)}{\sqrt{x(x-9)}}$ функцийн тодорхойлогдох мужийг ол.
A. $\big[-5; -\frac92\big]$
B. $\big[-\frac92; -\frac{13}{2}\big]$
C. $\big[-5; -\frac{14}{3}\big]$
D. $\big[-\frac{14}{3}; -4\big]$
E. $[-5; -4]$
$y=\sqrt{(x-1)\left(\tg\frac{11}{36}\pi-\tg1\right)}$ функцийн тодорхойлогдох мужийг ол.
A. $]-\infty;1[$
B. $]-\infty;1]$
C. $]-\infty;\infty[$
D. $]1;+\infty[$
E. $[1;+\infty[$
$y=\dfrac{\arcsin\big(\frac x2-1\big)}{\sqrt{1-x^2}}$ функцийн тодорхойлогдох мужийг ол.
A. $]0;4]$
B. $]-1:4]$
C. $[0;1[$
D. $[1;4[$
E. $[0;2[$
$f(x)=\arccos\left(\dfrac x4\right)+\sqrt{(5+x)(3-x)}$ функцийн тодорхойлогдох мужийг ол.
A. $]-\infty;-4]\cup[3;+\infty[$
B. $[-4;3]$
C. $]-\infty;-5]\cup[3;+\infty[$
D. $[3;4]$
E. $[0;3]$
$y=\sqrt{\log_{5-x}\left({x^{2}-9}\right)}$ функцийн тодорхойлогдох мужийг ол.
A. $(-3;3)$
B. $(-\infty;-5]$
C. $(-\infty;-5]\cup(-3;3)$
D. $[\sqrt{10};4)$
E. $(-\infty;-\sqrt{10}]\cup[\sqrt{10};4)$
Функцийн тодорхойлогдох мужийг ол.
$$y=\dfrac{\log_{x+1}(4-x^2)}{\sqrt{3-5x-2x^2}}$$
A. $[-3;-2)$
B. $(-1;\frac12)$
C. $(-1;0)\cup(0;\frac12)$
D. $(-1;0)\cup[0;\frac12)$
E. $(-2;2)$
$y=\sqrt{\log_{x-1}x}$ функцийн тодорхойлогдох мужийг ол.
A. $1< x\le 2$
B. $x\ge 2$
C. $2< x$
D. $x>0$
E. $1< x$
$\log_{x-1}[x(x-2)]$ функцийн тодорхойлогдох мужийг ол.
A. $x>1$
B. $x\neq2$
C. $x>2$
D. $x<0\cup x>2$
E. $x<0$
$f(x)=\dfrac{x}{5}-3$ функцийн тодорхойлогдох муж $-5< x< 15$ бол функцийн дүр нь:
A. $(-5, 15)$
B. $(2, 10)$
C. $(-5, 7)$
D. $(-3, 3)$
E. $(-4, 0)$
Хэрэв $f(x)=\dfrac{x}{5}-3$ функцийн тодорхойлогдох муж $-5< x< 15$ бол функцийн утгын мужийг ол.
A. $-5< f(x)<15$
B. $0< f(x)<10$
C. $-5< f(x)<7$
D. $-3< f(x)<3$
E. $-4< f(x)<0$
$y=\log_2 {(-x^2+4x-3)}$ функцийн тодорхойлогдох мужыг ол.
A. $[1;3]$
B. $(1;3)$
C. $(-\infty;1) \cup (3; +\infty)$
D. $(-\infty;1] \cup [3;+\infty)$
E. $ [3;+\infty)$
$\dfrac{x^2+9}{3x^2+6x}$ бутархайн тодорхойлогдох мужийг ол.
A. $x\neq0$
B. $x\not=\pm 2$
C. $x\neq0$, $x\neq-2$
D. $x\neq-2$
E. $x\neq 0$, $x\neq\pm2$
$\displaystyle\frac{x^2-25}{5x^2-10x}$ бутархайн тодорхойлогдох мужийг ол.
A. $x\not=0$, $x\not=2$
B. $x\not=\pm 5$
C. $x\not =2$
D. $x\not=5$, $x\not=2$
E. $\mathbb R$
$y=\sqrt{(x-3)(4x^2-16x+15)}+\dfrac1{\sqrt[3]{x-2}}$ функцийн тодорхойлогдох мужийг ол.
A. $[1.5;2.5]\cup[3;\infty[$
B. $]2;2.5]\cup[3;\infty[$
C. $[1.5;2[\cup]2;2.5]\cup[3;\infty[$
D. $]2;\infty[$
E. $]3;\infty[$
$y=\sqrt{(2x+1)(9x^2-15x-14)}+\dfrac1{\sqrt[3]{x-4}}$ функцийн тодорхойлогдох мужийг ол.
A. $[-\dfrac 23;-\dfrac 12]\cup[\dfrac73;\infty[$
B. $]4;\infty[$
C. $]-\infty;-\dfrac 23]\cup[-\dfrac12;\dfrac73]\cup]4;\infty[$
D. $[-\dfrac 23;-\dfrac12]\cup[\dfrac73;4[\cup]4;\infty[$
$f(x)=\sqrt{\lg(\sin x)}$ функцийн тодорхойлогдох мужийг ол.
A. $\frac{\pi}{4}+\pi
k<x<\frac{\pi}{2}+\pi k;$
B. $x=\frac{5\pi}{2}k$
C. $x=\frac{\pi}{2}+2\pi k$
D. $\frac{\pi}{2}+2\pi <x<\pi+2\pi k; k\in Z$
$f(x)=\sqrt{\lg(\cos (2\pi x))}$ функцийн тодорхойлогдох мужийг ол.
A. $x=k;$
B. $x=2k;$
C. $x=2k-1;$
D. $\{\emptyset\} (k\in
\mathbb Z)$
$f(x)=\dfrac{\arcsin \left(\frac{2x+1}{3}\right)}{\log_2x}$ функцийн тодорхойлогдох мужийг ол.
A. $0< x<1$
B. $0< x<\frac 23\lor 2< x<\frac 52$
C. $1< x<2$
D. $0< x<1\lor 1< x<2$
E. $-1< x<2$
$f(x)=\dfrac{\log_3x}{\arccos\big(\frac{x-3}{4}\big)}$ функцийн тодорхойлогдох мужийг ол.
A. $0 < x \leq 7$
B. $1 < x <2$
C. $1 < x < 7$
D. $0 < x <1$
E. $0 < x <7$
$y=2\cos 3x-9\sin^23x$ функцийн утгын мужийг ол.
A. $\left[-\dfrac{80}{9};3\right]$
B. $\left[-\dfrac{82}{9};2\right]$
C. $[-9;2]$
D. $\left[-\dfrac{82}{81};2\right]$
E. $[-11;11]$
$y=4\sin^22x-2\cos 2x+3$ функцийн утгын мужийг ол.
A. $\left[5;\dfrac{29}{4}\right]$
B. $\left[1;\dfrac{29}{16}\right]$
C. $\left[6;\dfrac{27}{4}\right]$
D. $\left[1;\dfrac{29}{4}\right]$
E. $\left[0;\dfrac{29}{4}\right]$
$y=6-4\sin 2x+3\cos 2x$ функцийн утгын мужийг ол.
A. $[5;13];$
B. $[5;7];$
C. $[1;13];$
D. $[1;11];$
$y=-3+6\cos x-8\sin x$ функцийн утгын мужийг ол.
A. $[-17;6];$
B. $[-3;11];$
C. $[-13;7];$
D. $[-11;6];$
$f(x)=\sin \left(x+\dfrac{\pi}{8}\right)\cdot \cos \left(x-\dfrac{\pi}{24}\right)$ функцийн утгын мужийг ол.
A. $\left[-\frac{1}{4};\frac{1}{2}\right];$
B. $\left[-\frac{1}{3};\frac{2}{3}\right];$
C. $\left[-\frac{1}{4};\frac{3}{4}\right];$
D. $\left[-\frac{1}{4};\frac{3}{4}\right[;$
$f(x)=\sin\left(x-\dfrac{\pi}{3}\right)\cdot \sin\left(x+\dfrac{\pi}{3}\right)$ функцийн утгын мужийг ол.
A. $\left[-\frac{1}{4};\frac{3}{4}\right];$
B. $\left[-\frac{3}{4};\frac{1}{4}\right];$
C. $\left[-\frac{1}{2};\frac{2}{3}\right];$
D. $\left[-\frac{1}{3};\frac{1}{4}\right];$
$y=\lg\Big(\dfrac{x+3}{x-4}\Big)+\arcsin(x+5)$ функцийн тодорхойлогдох мужийг ол.
A. $[-6;-4]$
B. $]4;+\infty[$
C. $]-\infty;-3]$
D. $]-\infty;-6]$
E. $[-4;+\infty[$
$y=\sqrt{\lg x-2}$ функцийн тодорхойлогдох мужийг ол.
A. $]0;2]$
B. $[100;+\infty[$
C. $]2;100]$
D. $[2;+\infty[$
E. $(0;+\infty)$
$y=\sqrt{x-1}$ функцийн тодорхойлогдох мужийг ол.
A. $x=1$
B. $x<1$
C. $x\ge1$
D. $x\neq 1$
E. $x>1$
$y=\lg (x^2-2x+1)$ функцийн тодорхойлогдох мужийг ол.
A. $x>0$
B. $x\neq -1$
C. $x>1$
D. $x<-1$
E. $x\neq 1$
$y=\lg\Big(\dfrac{x-3}{x+2}\Big)+\arcsin(x+2)$ функцийн тодорхойлогдох мужийг ол.
A. $[-3;-2[$
B. $]-\infty;-2[\cup]3;+\infty[$
C. $]-2;-1]$
D. $]-\infty;-2[$
E. $]-2;+\infty$
$y=3\log_2(x^2-2x-8)+\sqrt[6]{\dfrac{9-x}{x+5}}$ функцийн тодорхойлогдох мужийг ол.
A. $[-5;-2]\cup]4;9]$
B. $]-5;-2[\cup]4;9]$
C. $[-5;-2]\cup[4;9]$
D. $]-5;-2]\cup[4;9[$
E. $]-5;9]$
$y=\lg\Big(\dfrac{x-2}{x+3}\Big)+\arccos(x-2)$ функцийн тодорхойлогдох мужийг ол.
A. $[1;3]$
B. $]2;3]$
C. $[-3;3]$
D. $]-\infty;-3]$
E. $[2;+\infty[$
$y=\lg\Big(\dfrac{x+5}{x-7}\Big)+\arccos(x-7)$ функцийн тодорхойлогдох мужийг ол.
A. $[8;+\infty]$
B. $]7;8]$
C. $]-5;8]$
D. $]-\infty;-5[$
E. $[6;8]$
$y=\dfrac{\arccos\Big(\dfrac{x}{2}-1\Big)}{\sqrt{2-x^2}}$ функцийн тодорхойлогдох муж ол.
A. $]0;1]$
B. $]-\sqrt2;0]$
C. $[0;4[$
D. $[0;\sqrt2[$
E. $[0;2[$
$y=\sqrt{ax^2-2ax+4}$ функц бүх тоон шулуун дээр тодорхойлогддог байх $a$ параметрийн утгыг ол.
A. $0< a\le4$
B. $a\ge 4$
C. $-4\le a\le0$
D. $a\le 4$
E. $a>0$
$f(x)=\arcsin\left(\dfrac{x+1}{4}\right)+\sqrt{(6+x)(2-x)}$ функцийн тодорхойлогдох мужийг ол.
A. $[-6;3]$
B. $[-5;2]$
C. $]-\infty;-6]\cup[3;+\infty[$
D. $]-\infty;-5]\cup[2;+\infty[$
E. $[-1;3]$
$f(x)=\lg\dfrac{\big(\frac13\big)^x-27}{10^x+4}$ функцийн тодорхойлогдох мужийг ол.
A. $]3;+\infty[$
B. $]-\infty;-3[$
C. $]1;\frac13[$
D. $]-\infty;+\infty[$
E. $]-\infty;3[$
$y=-x^2+4x-12$ функцийн дүрийг ол.
A. $]-\infty;+\infty[$
B. $[2;+\infty[$
C. $]-\infty;-12]$
D. $]-\infty;-8[$
E. $]-\infty;-8]$
$y=|x-1|+\sqrt{x^2-2x+10}$ функцийн хамгийн бага утгыг ол.
A. $0$
B. $1$
C. $2$
D. $3$
E. $4$
$f(x)=2x^2-4x+1$ функцийн дүрийг ол.
A. $[-1;+\infty)$
B. $(-\infty;1]$
C. $[1;+\infty)$
D. $(-\infty;2]$
E. $(-\infty;+\infty)$
Хэрэв $f(x)=7x^2+3$, $g(x)=2x-9$ бол $g(f(2))=?$
A. $28$
B. $0$
C. $31$
D. $19$
E. $53$
$y=\lg\bigg(\dfrac{x^2+8x+7}{x^2+7}\bigg)$ функцийн тодорхойлогдох мужийг ол.
A. $x\le -7$
B. $x>-1$
C. $x<-7\lor x>-1$
D. $-7\le x\le -1$
E. $]-\infty;+\infty[$
$f(x)=\dfrac{\sin x+\cos x}{\tg 2x+\ctg 2x}$ функцийн тодорхойлогдох мужийг ол.
A. $x\neq\dfrac{\pi k}{4}$
B. $x\neq\dfrac{\pi k}{8}$
C. $x\neq\dfrac{\pi}{8}+\dfrac{\pi k}{4}$
D. $]-\infty;+\infty[$
E. $\tg x+\ctg x\neq 0$
$f(x)=3x^2-6x+1$ функцийн утгын мужийг ол.
A. $[1;+\infty)$
B. $(-\infty;1]$
C. $[-2;+\infty)$
D. $(-\infty;2]$
E. $(-\infty;+\infty)$
$y=3+5\cos2x-12\sin2x$ функцийн утгын мужийг ол.
A. $[2;4]$
B. $[-10;16]$
C. $[-14;20]$
D. $[0;26]$
E. $[-4;14]$
$y=\sin x+\cos2x$ функцийн утгын мужийг ол.
A. $[-2;2]$
B. $[-\sqrt{2};\sqrt{2}]$
C. $\big[-2;1\frac18\big]$
D. $\big]-\infty;1\frac18\big]$
E. $[-2;\sqrt{2}]$
$y=\dfrac{\sqrt{5x-x^2}}{\log_{\frac12}(5-3x)}$ функцийн тодорхойлогдох муж аль нь вэ?
A. $\big[0;1\frac23\big[\cup]1\frac23;5[$
B. $\big]-\infty;0\big]\cup]1\frac23;5[$
C. $\big]\frac43;\frac53\big[$
D. $\big]0;1\frac13\big[$
E. $\big[0;1\frac13\big[\cup\big]1\frac13;1\frac23\big[$
$\sqrt{5-x}$ илэрхийлэл утгатай байх $x$-ийн утгын олонлогийг ол.
A. $x=5$
B. $x\ge 5$
C. $x\neq5$
D. $x\le 5$
E. $x<5$
$y=\sqrt{-\dfrac{9}{x}+1}$ функцийн тодорхойлогдох мужийг ол.
A. $]-\infty;-9]\cup[0;\infty[$
B. $]-\infty;0[\cup[9;\infty[$
C. $]0;9]$
D. $[-9;0[$
E. $]-\infty;-9]\cup]0;\infty[$
$y=\sqrt{-\dfrac{8}{x}+2}$ функцийн тодорхойлогдох мужийг ол.
A. $]-\infty;-4]\cup]0;\infty[$
B. $]-\infty;0[\cup[4;\infty[$
C. $]0;4]$
D. $[-4;0[$
E. $]-\infty;-4]\cup]0;\infty[$
$y=\sqrt{-\dfrac{7}{x}-1}$ функцийн тодорхойлогдох мужийг ол.
A. $]-\infty;-7]\cup[0;\infty[$
B. $]-\infty;0[\cup[7;\infty[$
C. $]0;7]$
D. $[-7;0[$
E. $]-\infty;-7]\cup]0;\infty[$
$y=\sqrt{-\dfrac{5}{x}-1}$ функцийн тодорхойлогдох мужийг ол.
A. $]-\infty;-5]\cup[0;\infty[$
B. $]-\infty;0[\cup[5;\infty[$
C. $]0;5]$
D. $]-\infty;-5]\cup]0;\infty[$
E. $[-5;0[$
$y=\sqrt{-\dfrac{7}{x}-1}$ функцийн тодорхойлогдох мужийг ол.
A. $]-\infty;-7]\cup[0;\infty[$
B. $]-\infty;0[\cup[7;\infty[$
C. $]0;7]$
D. $[-7;0[$
E. $]-\infty;-7]\cup]0;\infty[$
$f(x)=\dfrac{\arcsin \left(-\frac{5}{x}+4\right)}{x}$ функцийн тодорхойлогдох мужийг ол.
A. $-2.5< x<2.5$
B. $1\le x\le \dfrac 53$
C. $1< x<2$
D. $\dfrac53\le x$
E. $x\le -\dfrac53\lor \dfrac53\le x$
$f(x)=\dfrac{\arccos \left(-\frac{6}{x}+5\right)}{x}$ функцийн тодорхойлогдох мужийг ол.
A. $-1.5< x<1.5$
B. $1\le x\le \dfrac 53$
C. $1\le x\le \dfrac 32$
D. $\dfrac32\le x$
E. $x\le -\dfrac32\lor \dfrac32\le x$
$y=\sqrt{\log_{x^{2}-9}\left({5-x}\right)}$ функцийн тодорхойлогдох мужийг ол.
A. $]-\infty;-\sqrt{10}[\cup]\sqrt{10};4]$
B. $[-3;3]$
C. $]-\infty;-5]\cup]-3;3[$
D. $]\sqrt{10};4]$
E. $]-\infty;-5[$
$y=2\sin 3x-9\cos^23x$ функцийн утгын мужийг ол.
A. $\left[-\dfrac{80}{9};3\right]$
B. $\left[-\dfrac{82}{9};2\right]$
C. $[-9;2]$
D. $\left[-\dfrac{82}{81};2\right]$
E. $[-11;11]$
$y=\lg (x^2-4x+4)$ функцийн тодорхойлогдох мужийг ол.
A. $x>0$
B. $x\neq -2$
C. $x>2$
D. $x<-2$
E. $x\neq 2$
$y=5\cos x-6\sin^2x$ функцийн утгын мужийг ол.
A. $\left[-\dfrac{80}{9};5\right]$
B. $\left[-1;2\right]$
C. $[-9;2]$
D. $\left[-7\dfrac{1}{24};5\right]$
E. $[-11;11]$
$y=\lg (x^2-6x+9)$ функцийн тодорхойлогдох мужийг ол.
A. $x>0$
B. $x\neq -3$
C. $x>3$
D. $x<-3$
E. $x\neq 3$
$f(x)=ax+b$ шугаман функцийн тодорхойлогдох муж нь нь $D=\{x\mid -1\le x\le 1\}$ ба дүр нь $E=\{y\mid 0\le y\le 2\}$ бол $a+b$ хэдтэй тэнцүү байх вэ?
A. $1$
B. $2$
C. $0$ эсвэл $2$
D. $-1$ эсвэл $1$
E. Хэдтэй ч тэнцэж болно.
$f(x)=\dfrac{x}{3}-3$ функцийн тодорхойлогдох муж $-6 < x < 15$ бол дүр нь:
A. $(-5, 15)$
B. $(2, 10)$
C. $(-5, 2)$
D. $(-3, 3)$
E. $(-4, 0)$
$ M= \begin{pmatrix}
10 & 6\\
3 & 2\\
\end{pmatrix}$ бол $ M^{-1}$ = ?
A. $ \begin{pmatrix} 1 & 3 \\ -1.5 & -5\\ \end{pmatrix}$
B. $ \begin{pmatrix} -5 & 1.5 \\ 3 & -1\\ \end{pmatrix}$
C. $ \begin{pmatrix} 10 & 3 \\ 6 & 2\\ \end{pmatrix}$
D. $ \begin{pmatrix} 2 & -6 \\ -3 & 10 \\ \end{pmatrix}$
E. $ \begin{pmatrix} 1 & -3 \\ 1.5 & 5\\ \end{pmatrix}$
$f(x)=\left\{\begin{array}{ll}
x^2, & 0\le x\le 1\\
\dfrac12x+\dfrac12, & 1< x\le 5
\end{array}\right.$ функцийн дүрийг (функцийн авч болох утгуудын олонлог) олоорой.
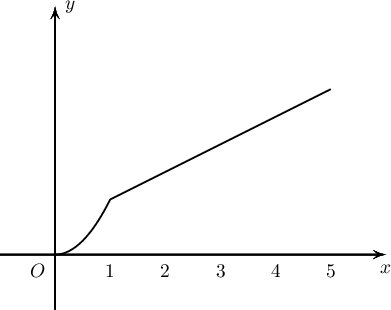

A. $[0;1]$
B. $[0;1[\cup]1;3]$
C. $[0;3]$
D. $]0;3[$
E. $]1;3]$
$f(x)=x^2-4x+3$, $0\le x\le \dfrac72$ функцийн дүрийг (функцийн авч болох утгуудын олонлог) олоорой.
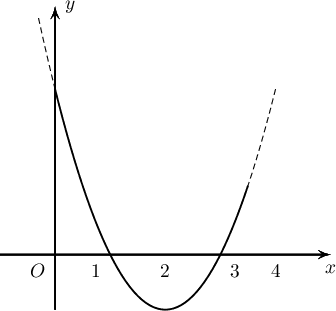

A. $[1.25;3]$
B. $[0;3.5]$
C. $[-1;3]$
D. $[0;3]$
E. $]-1;3[$
$f(x)=\left\{\begin{array}{ll}
\dfrac12x^2, & 0\le x\le 2\\
\dfrac12x+1, & 2< x\le 6
\end{array}\right.$ функцийн дүрийг (функцийн авч болох утгуудын олонлог) олоорой.
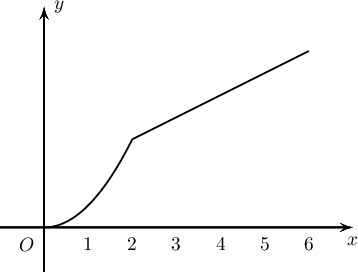

A. $[0;2]$
B. $[0;2[\cup]2;4]$
C. $[0;4]$
D. $]0;4[$
E. $]2;4]$
Дараах функцийн утгын мужийг ол.
- $ f(x) = \dfrac{1-x^2}{1+x^2}$
- $ f(x) = \sqrt {2x-x^2-1}$
- $ f(x) = \sin x - 5\cos x $
- $ f(x) = \log_3x +\log_x3$
- $ f(x)=(\sin x +\cos x)^2$
- $ f(x)=4^x - 2^x +1$
$y=\sqrt{\dfrac{3x+2}{5-x}}$ функцийн тодорхойлогдох мужийг олно уу?
A. $\left]-5;\dfrac{2}{3}\right]$
B. $\left[-\dfrac{3}{2}; 5\right[$
C. $\left[-\dfrac{2}{3}; 5\right[$
D. $\left]-\infty;-\dfrac{2}{3}\right]\cup]5;\infty[$
E. $\left]-\infty; -\dfrac{2}{3}\right]$
$y=\sqrt{\dfrac{5x+3}{2-x}}$ функцийн тодорхойлогдох мужийг олно уу?
A. $\left]-2;\dfrac{3}{5}\right]$
B. $\left[-\dfrac{5}{3}; 2\right[$
C. $\left[-\dfrac{3}{5};2\right[$
D. $\left]-\infty;-\dfrac{3}{5}\right]\cup]2;\infty[$
E. $\left]-\infty; -\dfrac{3}{5}\right]$
$y=\sqrt{\dfrac{5x+3}{2-x}}$ функцийн тодорхойлогдох мужийг олно уу?
A. $\left]-2;\dfrac{3}{5}\right]$
B. $\left[-\dfrac{5}{3}; 2\right[$
C. $\left[-\dfrac{3}{5}; 2\right[$
D. $\left]-\infty;-\dfrac{3}{5}\right]\cup]2;\infty[$
E. $\left]-\infty; -\dfrac{3}{5}\right]$
$f(x)=\left\{\begin{array}{c}
\frac12x^2, 0\le x \le 2\\
\frac12x+1, 2 < x \le 6
\end{array}\right.$ функцийн дүрийг ол.


A. $[0,6]$
B. $[0,2]$
C. $[2,4]$
D. $[2,6]$
E. $[0,4]$
$\dfrac{\sqrt{x^2-3x+5}+8x-3}{4x}\ge2$ тодорхойлогдох мужийг олбол $$x\in]-\infty;\fbox{a}[\cup]\fbox{b};+\infty[$$ болно. Иймд иррациональ тэнцэтгэл бишийн шийдийг интервалын аргаар олбол $x\in[-\fbox{c};\fbox{d}[\cup[\fbox{e};+\infty[$ болно.
$f(x)=\sqrt{-x^2+6x-8}+\sqrt{-x^2+8x-15}$ функцийн тодорхойлогдох муж нь $\left[\fbox{a},\fbox{b}\right],$ харин $\varphi(x)=\sqrt{(-x^2+6x-8)(-x^2+8x-15)}$ функцийн тодорхойлогдох муж нь $\left]-\infty,\fbox{c}\right]\bigcup \left[\fbox{a},\fbox{b}\right]\bigcup\left[\fbox{d},+\infty\right]$ олонлог болно.
$f(x)=\sqrt[4]{\dfrac{x-6}{4-x}}+\sqrt{\dfrac{7-x}{x-5}}$ функцийн тодорхойлогдох муж нь $\left]\fbox{a},\fbox{b}\right]$, харин $\varphi(x)=\sqrt{\dfrac{(x-6)(7-x)}{(4-x)(x-5)}}$ функцийн тодорхойлогдох муж нь $\left]-\infty,\fbox{c}\right]\bigcup \left[\fbox{a},\fbox{b}\right]\bigcup\left[\fbox{d},+\infty\right]$ олонлог болно.
$f(x)=\sqrt{5+4x-x^2}$ функцийн тодорхойлогдох муж нь $D(f)=\left[\fbox{ab};\fbox{c}\right],$ утгын муж нь $E(f)=\left[\fbox{d};\fbox{e}\right]$ байна.
$f(x)=\sqrt{-x^2+6x-8}$ функцийн тодорхойлогдох муж нь $D(f)=\left[\fbox{a};\fbox{b}\right],$ утгын муж нь $E(f)=\left[\fbox{c};\fbox{d}\right]$ байна.
$f(x)=\sqrt{1-4x}$ функцийн тодорхойлогдох муж нь $\left]-\infty;\dfrac{\fbox{a}}{\fbox{b}}\right]$ байна. Иймд $[1;5]$ завсар дахь язгуурын тоо нь $\fbox{c}$ болно. Харин $f(x)=3$ тэгшитгэл $x=\fbox{de}$ шийдтэй.
$f(x)=\sqrt{2x+11}$ функцийн тодорхойлогдох муж нь $\Bigl[-\dfrac{\fbox{ab}}{\fbox{c}};+\infty\Bigr[$ байна. Иймд $[-13;-6]$ завсар дахь язгуурын тоо нь $\fbox{d}$ болно. Харин $f(x)=5$ тэгшитгэл $x=\fbox{e}$ шийдтэй.
$\varphi(x)=\dfrac{1}{\sqrt{x^2-12x+35}}$ функцийн тодорхойлогдох мужийн $[\sqrt{2}+\sqrt{3};\sqrt{10}+\sqrt{26}]$ хэрчимд орших бүхэл цэгүүд нь $x_1=\fbox{a}, x_2=\fbox{b}$ ба $x_1, x_2$ гэсэн язгууруудтай квадрат гурван гишүүнт $f(x)=x^2-\fbox{cd}x+\fbox{ef}$ хэлбэртэй байна (a< b).
$f(x)=\sqrt{(a-3)x^2-2(a-5)x+3a-15}$ функцийн тодорхойлогдох муж нь $D(f)=]-\infty;\infty[$ байх $a$ параметрийн утгын олонлог нь $\left[\fbox{a},+\infty\right[$ энэ үед $f$ функцийн утгын муж нь $\left[\dfrac{6}{\sqrt{5}};+\infty\right[$ байхын тулд $a=\fbox{b}$ байна.
$f(x)=\sqrt{(a+6)x^2-2(a+4)x+3a+12}$ функцийн тодорхойлогдох муж нь $D(f)=]-\infty;\infty[$ байх $a$ параметрийн утгын олонлог нь $\left[\fbox{ab},+\infty\right[$ энэ үед $f$ функцийн утгын муж нь $\left[\dfrac{3}{2}\sqrt{6};+\infty\right[$ байхын тулд $a=\fbox{b}$ байна.
$y=2\ln{(3+5x)}-\ln{(4+9x)^2} $ функц нь $-\dfrac{\fbox{a}}{\fbox{b}}< x< -\dfrac{\fbox{c}}{\fbox{d}}, x>-\dfrac{\fbox{e}}{\fbox{f}} $ мужид тодорхойлогдоно.
$y=\log_{0.3}{(5x+4)}+\log_{0.3}{(8x+7)}-x $ функц нь $ x>-\dfrac{\fbox{a}}{\fbox{b}} $ мужид тодорхойлогдоно.
$y=\log_{3}{(x(x-3))}-\log_{3}{x} $ функц нь $x>\fbox{a} $ мужид тодорхойлогдоно.
$y=\dfrac{\lg(\sqrt{x^2-5x+4}+3-x)}{|x^2-3x-6|-2x}$ функцийн тодорхойлогдох муж
$\left\{ %
\begin{array}{l}
\sqrt{x^2-5x+4}+3-x>0 \\
|x^2-3x-6|-2x\ne 0
\end{array}
\right.$ системээс олдох ба $x\leq \fbox{a},$ $x>\fbox{b},$ $x\ne\fbox{c}$ гэж олдоно.
$y=\dfrac{\lg(\sqrt{x^2-x-2}+1-x)}{|x^2+x-8|-2x-4}$ функцийн тодорхойлогдох муж
$\left\{ %
\begin{array}{l}
\sqrt{x^2-x-2}+1-x>0 \\
|x^2+x-8|-2x-4\ne 0 \\
\end{array} %
\right.$ системээс олдох ба $x\leq -\fbox{a},$ $x>\fbox{b},$
$x\ne \fbox{c}$ гэж олдоно.
$y=\dfrac{\lg(\sqrt{x^2+5x+4}-x-2)}{1-\log_3 15+\log_3(8^{\sqrt{x}}+1)}$ функцийн тодорхойлогдох муж
$\left\{ %
\begin{array}{l}
\sqrt{x^2+5x+4}-x-2>0 \\
1-\log_315+\log_3(8^{\sqrt{x}}+1)\ne 0 \\
\end{array} %
\right.$ системээс олдох ба $x>\fbox{a},$ $x\ne
\dfrac{\fbox{b}}{\fbox{c}}$ гэж олдоно.
$y=\dfrac{\lg(\sqrt{x^2-x-2}-x+1)}{3-\lg(991+3^{\sqrt{0,5x}})}$ функцийн тодорхойлогдох муж
$\left\{ %
\begin{array}{l}
\sqrt{x^2-x-2}-x+1>0 \\
3-\lg(991+3^{\sqrt{0,5x}})\ne 0\\
\end{array} %
\right.$ системээс олдох ба $x>\fbox{a},$ $x\ne \fbox{b}$ гэж
олдоно.
$y=\dfrac{\sqrt{6-|x^2-5x|}}{\lg\sqrt{5^{x(13-x)}}+11\lg 2-11}$ функцийн тодорхойлогдох муж
$\left\{ %
\begin{array}{l}
6-|x^2-5x|\geq 0 \\
\lg\sqrt{5^{x(13-x)}}+11\lg 2-11\ne 0 \\
\end{array} %
\right.$ системээс олдох ба $-\fbox{a}\leq x< \fbox{b},$\\
$\fbox{c}\leq x\leq \fbox{d}$ гэж олдоно.
$y=\dfrac{\sqrt{6-|x^2-7x+6|}}{\log_6\sqrt[7]{3^{x(15-x)}}+8\log_62-8}$ функцийн тодорхойлогдох муж
$\left\{ %
\begin{array}{l}
6-|x^2-7x+6|\geq 0 \\
\log_6\sqrt[7]{3^{x(15-x)}}+8\log_62-8\ne 0 \\
\end{array} %
\right.$ системээс олдох ба $\fbox{a}\leq x\leq \fbox{b},$
$\fbox{c}\leq x< \fbox{d}$ гэж олдоно.
$y=\arccos\dfrac{x^2-1}{24}$ функцийн
- Тодорхойлогдох муж $x\in \Bigl[\fbox{ab};\fbox{c}\Bigr]$;
- $x=-\sqrt{13}$ үед $y=\dfrac{\pi}{\fbox{d}}$;
- Утгын муж $\Bigl[\fbox{e};\pi-\arccos\dfrac1{24}\Big]$;
- Өсөх муж нь $x\in [\fbox{fg};\fbox{h}]$ байна.
$y=\dfrac{4\arcsin (x^2-4x+2)}{\pi}+5$ функцийн
- Тодорхойлогдох муж $x\in \Bigl[\fbox{a}-\sqrt{3};\fbox{b}\Bigr]\cup \Bigl[\fbox{c};\fbox{d}+\sqrt{3}\Bigr],$
- Утгын муж $\Bigl[\fbox{e};\fbox{f}\Bigr],$
- $x=2+\sqrt{\dfrac52}$ үед $\dfrac 1y=\dfrac{\fbox{g}}{\fbox{hi}}$.
$y(x)=\dfrac{8}{\pi}\arcsin x^2-8x^2+16x+5$ функцийн хувьд
1) $y(0)=\fbox{a},$
2) Тодорхойлогдох муж $|x|\leq \fbox{b},$
3) $y_{\max}=\fbox{cd}.$
1) $y(0)=\fbox{a},$
2) Тодорхойлогдох муж $|x|\leq \fbox{b},$
3) $y_{\max}=\fbox{cd}.$
$y(x)=\dfrac{2}{\pi}\arctg\Bigl(\dfrac{2}{\pi}\arcsin
x^2\Bigr)+x^2+7$ функцийн хувьд
1) $y(1)=\fbox{a,b},$
2) Тодорхойлогдох муж $|x|\leq \fbox{c},$
3) $y_{\min}=\fbox{d}.$
1) $y(1)=\fbox{a,b},$
2) Тодорхойлогдох муж $|x|\leq \fbox{c},$
3) $y_{\min}=\fbox{d}.$
$y=\arcsin \left(\dfrac{x^2-3}{6}\right)$ функцийн
1) Тодорхойлогдох муж $|x|\leq \fbox{a},$
2) $x=-\sqrt{6}$ үед $y=\dfrac{\pi}{\fbox{b}},$
3) Функцийн өсөх завсар $x\in [\fbox{c};\sqrt{\fbox{d}}],$
4) Функцийн утгын муж $x\in \left[-\arcsin\dfrac1{\fbox{e}};\dfrac{\pi}{\fbox{f}}\right]$ байна.
1) Тодорхойлогдох муж $|x|\leq \fbox{a},$
2) $x=-\sqrt{6}$ үед $y=\dfrac{\pi}{\fbox{b}},$
3) Функцийн өсөх завсар $x\in [\fbox{c};\sqrt{\fbox{d}}],$
4) Функцийн утгын муж $x\in \left[-\arcsin\dfrac1{\fbox{e}};\dfrac{\pi}{\fbox{f}}\right]$ байна.
$y=2-\arcsin \dfrac{x^2+4}{22}$ функцийн
1) Тодорхойлогдох муж $|x|\leq \fbox{a}\sqrt{\fbox{b}},$
2) $x=\sqrt{7}$ үед $y=\dfrac{\fbox{cd}-\pi}{\fbox{e}},$
3) Функцийн өсөх завсар $x\in [-\sqrt{\fbox{fg}};\fbox{h}],$
4) Функцийн утгын муж $x\in \left[2-\arcsin\dfrac{\fbox{i}}{\fbox{jk}};2+\dfrac{\pi}{\fbox{l}}\right]$ байна.
1) Тодорхойлогдох муж $|x|\leq \fbox{a}\sqrt{\fbox{b}},$
2) $x=\sqrt{7}$ үед $y=\dfrac{\fbox{cd}-\pi}{\fbox{e}},$
3) Функцийн өсөх завсар $x\in [-\sqrt{\fbox{fg}};\fbox{h}],$
4) Функцийн утгын муж $x\in \left[2-\arcsin\dfrac{\fbox{i}}{\fbox{jk}};2+\dfrac{\pi}{\fbox{l}}\right]$ байна.
$y=\sqrt{4+3x-x^2}$ функц болон түүний уламжлалын тодорхойлогдох (D) болон утгын (E) муж нь
байна.
| $y(x)$ | $y'(x)$ | |
| D | $-\fbox{a}\leq x\leq \fbox{b}$ | $-\fbox{e}< x< \fbox{f}$ |
| E | $\fbox{c}\leq x\leq \displaystyle\frac{\fbox{d}}{2}$ | $\fbox{g}\infty< x< +\infty$ |
$y=\sqrt{x^2+2x-15}$ функц болон түүний уламжлалын тодорхойлогдох (D) болон утгын (E) муж нь
байна.
| $y(x)$ | $y'(x)$ | |
| D | $]-\infty;-\fbox{a}]\cup [\fbox b;+\infty[$ | $]-\infty,-\fbox{d}[\cup]\fbox{e},+\infty[$ |
| E | $[\fbox c,\infty[$ | $]-\infty,-\fbox{f}[\cup]\fbox{g},+\infty[$ |
$y = \dfrac{\sqrt {x + 30 - x^{2}} }{\log _{2} \left({x + 2}\right)}$ функц тодорхойлогдох боломжтой бүх бүхэл тоонуудын нийлбэрийг олъё.
Тодорхойлолтоос
$$\left\{\begin{array}{c}
x+30-x^2\ge\fbox{a}\\
x+2>\fbox{b}\\
x+2\neq\fbox{c}
\end{array}\right.$$
байна. Иймд $]-\fbox{d};-\fbox{e}[\cup]-\fbox{e};\fbox{f}]$ мужид тодорхойлогдох ба энэ мужид орох бүхэл тоонуудын нийлбэр $\fbox{gh}$ байна.
Функцийн тэгш, сондгой чанар
Дараах функцүүдээс аль нь тэгш, аль нь сондгой функц вэ?
- $f(x)=\dfrac{x^2+1}{x^3}$
- $f(x)=4x^3-x+1$
- $f(x)=\sqrt[5]{x^3}$
- $f(x)=\dfrac{x^4+1}{x^2-1}$
- $f(x)=|x|-x^2$
- $f(x)=(x-3)^2-(x+3)^2$
Хоёр функцийн үржвэрийн тэгш, сондгойг тогтоо.
- хоёулаа тэгш функц,
- хоёулаа сондгой функц,
- нэг нь тэгш, нөгөө нь сондгой.
Функцүүдийн аль нь тэгш вэ?
A. $f(x)=\ctg x-x\cos x$
B. $f(x)=\dfrac{\ctg x}{\tg 2x+\sin 2x}$
C. $f(x)=\dfrac{x^4\ctg x}{x^2-4}$
D. $f(x)=\dfrac{\sin x+\cos 2x}{x^2-x}$
E. $f(x)=\dfrac{\sin x+\sin 2x}{x^2-x}$
Дараах функцүүдийн аль нь сондгой вэ?
A. $f(x)=\frac{(\tg x+\ctg
x)^2}{\sin x\cdot \cos x};$
B. $f(x)=\sin x^2;$
C. $f(x)=\sin x\cdot \cos x-1;$
D. $f(x)=\frac{\tg x^2+2x}{\sin x};$
Аль нь сондгой функц болох вэ?
A. $f(x)=\frac{\sin x\cdot
\cos x}{\tg x+\ctg x};$
B. $f(x)=\sin 2x-\cos 2x;$
C. $f(x)=x^5+\ctg x;$
D. $f(x)=\frac{2\ctg x}{x^3};$
Аль нь тэгш функц вэ?
A. $f(x)=x^3+\sin x+\tg 2x;$
B. $f(x)=\frac{1-\sin 2x}{x};$
C. $f(x)=\frac{\tg x+\sin x}{\ctg x};$
D. $f(x)=\tg^3x+\ctg x^3;$
Тэгш ч биш, сондгой ч биш функц аль нь вэ?
A. $f(x)=\frac{\sin x-\tg
x}{\sin x+x};$
B. $f(x)=\sin^2 x+\cos x;$
C. $f(x)=\ctg^2x-x^4;$
D. $f(x)=\frac{1-\sin 2x}{1+\sin 2x};$
Тэгш ч биш, сондгой ч биш функц аль нь вэ?
A. $f(x)=\sin 2x+\cos 2x;$
B. $f(x)=x^2-\cos 2x;$
C. $f(x)=\frac{x+\sin x}{x-\sin x};$
D. $f(x)=\sin^3x+\ctg^5x;$
Аль нь тэгш функц вэ?
A. $y=3\cos2x+2x^4$
B. $y=53\sin x+4x^2$
C. $y=7\tg x+5x$
D. $y=33\cos x-25x^3$
E. $y=4\sin x-30\cos x$
Аль нь тэгш функц вэ?
A. $y=3\cos x+2x^2$
B. $y=5\sin x+x^2$
C. $y=7\tg x+5x$
D. $y=3\cos x-2x^3$
E. $y=4\sin x-3\cos x$
Аль нь тэгш функц вэ?
A. $y=3\cos x-8x^3$
B. $y=6\sin x+x^2$
C. $y=7\tg x+6x$
D. $y=3\cos x+\sin x^2$
E. $y=4\sin x-5\cos x$
Аль нь тэгш функц вэ?
A. $y=5\cos x+2\tan^2x$
B. $y=5\sin x+x^2$
C. $y=7\tg x+5x$
D. $y=3\cos x- 2x^3$
E. $y=4\sin x-3\cos x$
$f(x)=x+\sin x$, $g(x)=x\cdot\sin x$, $h(x)=x+\cos x$ функцүүдийн аль нь тэгш функц вэ?
A. Зөвхөн $f(x)$
B. Зөвхөн $g(x)$
C. Зөвхөн $h(x)$
D. $g(x)$ ба $h(x)$
E. Аль нь ч биш
$f(x)=\dfrac{e^{x}-e^{-x}}{2}$, $g(x)=x\cdot\cos x$, $h(x)=1+\cos x$ функцүүдийн аль нь сондгой функц вэ?
A. Зөвхөн $f(x)$
B. Зөвхөн $g(x)$
C. Зөвхөн $h(x)$
D. $f(x)$ ба $g(x)$
E. Бүгдээрээ сондгой функц
$y=\cos x+x^2$ функц дараах чанаруудын алийг нь хангах вэ?
A. тэгш
B. сондгой
C. өсдөг
D. тэгш ч биш, сондгой ч биш
E. буурдаг
$f(x)=(2-x)^2-mx+3m$ функц $m$-ийн ямар утганд тэгш функц байх вэ?
A. $-2$
B. $-1$
C. $2$
D. $-3$
E. $-4$
$y=x+\sin x$ функц аль чанарыг хангах вэ?
A. тэгш функц
B. сондгой функц
C. тэгш ч биш сондгой ч биш
D. үет функц
E. тэгш сондгойг нь тодорхойлох боломжгүй
$f(x)=(2^x+2^{-x})\cdot x$, $g(x)=(2^x-2^{-x})\cdot\sin x$, $s(x)=1+\sin x$, $t(x)=1+\cos x$ функцүүдийн аль нь сондгой функц вэ?
A. Зөвхөн $f(x)$
B. Зөвхөн $g(x)$
C. Зөвхөн $f(x)$ ба $s(x)$
D. Зөвхөн $g(x)$ ба $t(x)$
E. аль нь ч биш
$f(x)=(2^x+2^{-x})\cdot x$, $g(x)=(2^x-2^{-x})\cdot\sin x$, $s(x)=1+\sin x$, $t(x)=1+\cos x$ функцүүдийн аль нь тэгш функц вэ?
A. Зөвхөн $f(x)$
B. Зөвхөн $g(x)$
C. Зөвхөн $f(x)$ ба $s(x)$
D. Зөвхөн $g(x)$ ба $t(x)$
E. аль нь ч биш
$f(x)=ax^2+bx+c$ функц тэгш функц бол аль нөхцөл биелэх вэ?
A. $c=0$
B. $f(x)=0$
C. $a=0$
D. $b=0$
E. $f(-x)=-f(x)$
$f(x)=ax^2+bx+c$ функц сондгой функц бол аль нөхцөл биелэх вэ?
A. $c\neq0$
B. $f(x)=0$
C. $a>0$
D. $b=0$
E. $f(-x)=-f(x)$
Дараах функцүүдийн аль нь тэгш вэ?
A. $y=\dfrac{\sin 2x}{3\tg x}$
B. $y=\dfrac{\cos 2x}{\tg x}$
C. $y=\sin\Big(2x+\dfrac{\pi}{3}\Big)$
D. $y=x\cos x$
E. $y=\cos\Big(3x-\dfrac{\pi}{6}\Big)$
Функцийн үе
- $y=\sin^2\theta$ функцийн үеийг олж, графикийг зур.
- $y=\cos^2x+2\sin x+3$, $(0^{\circ}\leq x< 360^{\circ})$ функцийн максимум, минимум утгыг ол.
- $0^{\circ} \leq \theta\leq 180^{\circ}$ үед $\sin 2\theta\leq 2\sin \theta$ тэнцэтгэл бишийг батал.
$y=\sin 8x$ функцийн үе $\ebox^{\circ}$, $y=\cos 6x$ функцийн үе
$\ebox^{\circ}$, харин $y=\sin8x+\cos 6x$ функцийн үе $\ebox^{\circ}$
байна.
Дараах функцийн үеийг олж, графикийг зур.
- $y=\cos^2\theta$
- $y=\sin^2\theta-\cos^2\theta$
- $y=\sin\theta\cdot \cos\theta$
Дараах функцүүд үелэх эсэхийг шинжил.
- $y=x^2+1$
- $y=2\tg\dfrac{x}{2}+4\tg\dfrac{x}{3}$
- $y=\dfrac{\sin x}{[x/\pi]+1}$
$f(x)=\sin\dfrac 45x+3\cos \dfrac 78x+\cos \left(5x-\dfrac52\right)$ функцийн үндсэн үеийг ол.
A. $40\pi$
B. $60\pi$
C. $80\pi$
D. $120\pi$
E. $160\pi$
$f(x)=2\sin4x-3\sin 5x-7\cos \left(\dfrac x3+3\right)$ фунцкийн үндсэн үеийг ол.
A. $2\pi$
B. $3\pi$
C. $\pi$
D. $6\pi$
$f(x)= \sqrt{\tg 6x}+\sqrt[3]{\ctg 5x}$ функцийн үндсэн үеийг ол.
A. $2\pi$
B. $\dfrac{\pi}{30}$
C. $\pi$
D. $\dfrac{\pi}{6}$
$f(x)=\sqrt{\tg\dfrac x6}+\sqrt{\ctg\dfrac x5}$ функцийн үндсэн үеийг ол.
A. $30\pi$
B. $5\pi$
C. $\dfrac{\pi}{6}$
D. $\frac{2\pi}{5}$
$f(x)=3\cos^4(x+1)+\sin\left(2x+\dfrac{\pi}{3}\right)$ функцийн үндсэн үеийг ол.
A. $\dfrac{2\pi}{3}$
B. $\dfrac{\pi}{3}$
C. $\pi$
D. $2\pi$
$f(x)=\sin^2\left(x-\dfrac{\pi}{6}\right)-2\cos^4(2x-2)$ функцийн үндсэн үеийг ол.
A. $\frac{3\pi}{2}$
B. $\pi$
C. $\frac{\pi}{2}$
D. $3\pi; k\in Z$
$f(x)=\sin\Big(\dfrac{4x}{7}-2\Big)$ функцийн хамгийн бага эерэг үеийг ол.
A. $2\pi$
B. $\dfrac{7\pi}{2}$
C. $\dfrac{25\pi}{6}$
D. $\dfrac{8\pi}{7}$
E. $7\pi$
$f(x)=\sqrt{\tg\dfrac{x}{4}}+\sqrt{\ctg\dfrac{x}{3}}$ функцийн үндсэн үеийг ол.
A. $3\pi$
B. $4\pi$
C. $6\pi$
D. $12\pi$
E. $24\pi$
$y=x+\sin x$ функц аль чанарыг хангах вэ?
A. тэгш функц
B. сондгой функц
C. тэгш ч биш сондгой ч биш
D. үет функц
E. тэгш сондгойг нь тодорхойлох боломжгүй
$f(x)=\sin\Big(\dfrac{7x}{4}+2\Big)$ функцийн хамгийн бага эерэг үеийг ол.
A. $2\pi$
B. $\dfrac{7\pi}{2}$
C. $\dfrac{25\pi}{6}$
D. $\dfrac{8\pi}{7}$
E. $7\pi$
Функционал хамаарал, функцийн утга олох
$f(x)=\log_2 x,g(x)=\log_{\frac12} x,h(x)=\log_2 (2x),R(x)=\log_8 (x+2)^3$ гэвэл
- $g(x),h(x),R(x)$-ыг $f(x)$-ээр илэрхийл.
- $0< x< 1$ үед $g(x),h(x),f(x)$-ыг жиш.
Дурын бодит $x$ тооны хувьд
$f(x)=\sin^3x+k\sin x\cdot \cos x+\cos^3x$, $\sin x+\cos x=t$ байг.
$k$-тогтмол тоо.
- $f(x)$-ийг $t$-ээс хамаарсан функц $g(t)$-ээр илэрхийл.
- $t$-ийн утгын мужийг ол.
- $g(t)$ нь ямарч $k$-ийн утгын хувьд язгууртай гэдгийг батал.
- $f(x)=4x-3$, $g(x)=-3x^2$ бол дараах утгуудыг ол. $$f\left(\dfrac32\right), f(-2), f(a+2), g(-1+\sqrt3), g(a-2), g(a^2)$$
- Дараах цэгүүд координатын хавтгайн аль мужид орших вэ?
- $(2,3)$
- $(-1,-5)$
- $(-3,2)$
- $(4,-3)$
- $f(x)=-3x+2$, $g(x)=x^2-3x+2$ бол дараах утгуудыг ол. $$f(0), f(-1), f(a+1), g(2), g(a-2), g(2a-1)$$
- $x=2$ бол $(3x-1,3-2x)$ цэг координатын хавтгайн аль мужид орших вэ? Мөн $(3x-1,-2)$ цэг III мужид орших бол $x<\ebox{}$ байна.
$f(x)$-нь 2-р зэргийн олон гишүүнт $f(x+1)-f(x)=6x+8$ ба $f(1)=16$ бол $f(2)$ хэд вэ?
A. $30$
B. $60$
C. $20$
D. $18$
E. $22$
$f(x)=\dfrac{x+3}{x-2}$ ба $g(f(x))=x$ бол $g(2)$ хэд вэ?
A. $3$
B. $4$
C. $7$
D. $2$
E. $1$
$f(x)=2x^2+4$, $g(x)=x-3$ бол $f(x)=f(g(x))$ илэрхийллийг ямар тоо хангах вэ?
A. $5$
B. $\frac32$
C. $\frac34$
D. $-4$
E. $10$
$f(x)=\dfrac{x+2}{x-3}$ ба $g(f(x))=x$ бол $g(2)=?$
A. $2$
B. $4$
C. $7$
D. $8$
E. $9$
$f(x)=x^2+1$, $g(x)=2x+1$ бол $f(g(x))=?$
A. $4x^2+4x+1$
B. $2x^2+3$
C. $2x^2+2$
D. $4x^2+1$
E. $4x^2+4x+2$
$f(x)=\sin x$, $g(x)=(2x+1)\pi$ бол $f(g(3))=?$
A. $0$
B. $1$
C. $-1$
D. $\dfrac12$
E. $-\dfrac12$
Хэрэв $f(x)=2x+1$ ба $g(x)=3x-5$ бол $f(g(2))=?$
A. $0$
B. $1$
C. $2$
D. $3$
E. $5$
Хэрэв $f(x)=3x^2-x+5$ бол $f(3)=?$
A. $15$
B. $17$
C. $23$
D. $27$
E. $29$
Хэрэв $f(x)=x^2+x$ ба $f(a-1)=-\dfrac14$ бол $a=?$
A. $-\dfrac12$
B. $-\dfrac14$
C. $\dfrac14$
D. $\dfrac12$
E. $\dfrac34$
$f(x)=\dfrac{1-x}{x}$ бол $f(2)=?$
A. $0$
B. $0.5$
C. $1$
D. $-1$
E. $-0.5$
$f(2x-1)=x+3$ бол $f(x)=?$
A. $f(x)=\dfrac{x+1}{2}$
B. $f(x)=\dfrac{x+7}{2}$
C. $f(x)=\dfrac{x+4}{2}$
D. $f(x)=x+4$
E. $f(x)=x+7$
$f(x)=x^2+3; g(x)=2x-3$ бол $f(g(-5))-g(f(-5))=$
A. $-105$
B. $98$
C. $111$
D. $-111$
E. $119$
$f(x)=\log_2(x+1)$ бол $f^{-1}(3)=?$
A. $0$
B. $6$
C. $7$
D. $9$
E. $8$
$f(x)=3x+p$ ба $g(x)=-7x+2$-ийн хувьд $(f\circ g)(x)=(g\circ f)(x)$ нөхцөл биелэдэг бол $p$-г ол.
A. $-2$
B. $2$
C. $\dfrac12$
D. $-\dfrac12$
E. $-\dfrac27$
$f(x)=(3-2x)^2-3mx+4m$ функц $m$-ийн ямар утганд тэгш функц байх вэ?
A. $-2$
B. $2$
C. $4$
D. $-4$
E. $8$
$f(2x+1)=x-3$ бол $f(x)=?$
A. $f(x)=\dfrac{x+5}{2}$
B. $f(x)=\dfrac{x-5}{2}$
C. $f(x)=2x+3$
D. $f(x)=2x+4$
E. Олох боломжгүй
$f(x)=4^{8x-5}+36$ функцийн хувьд $f^{-1}(100)$ хэдтэй тэнцүү вэ?
A. $2$
B. $\dfrac12$
C. $1$
D. $\dfrac{1}{4^{225}+36}$
E. $\dfrac{1}{4}$
$f(x)=5^{3x-1}-25$ функцийн хувьд $f^{-1}(100)$ хэдтэй тэнцүү вэ?
A. $2$
B. $\dfrac43$
C. $1.3$
D. $\dfrac{1}{5^{299}-25}$
E. $\dfrac{1}{3}$
$f(x)=2^{5x-3}-28$ функцийн хувьд $f^{-1}(100)$ хэдтэй тэнцүү вэ?
A. $7$
B. $\dfrac12$
C. $2$
D. $\dfrac{1}{2^{497}-28}$
E. $\dfrac{1}{7}$
$f(x)=3^{4x-1}-8$ функцийн хувьд $f^{-1}(19)$ хэдтэй тэнцүү вэ?
A. $1$
B. $\dfrac32$
C. $3$
D. $\dfrac{1}{2^{497}-28}$
E. $\dfrac{1}{4}$
$f(x)=2^{5x-3}-28$ функцийн хувьд $f^{-1}(100)$ хэдтэй тэнцүү вэ?
A. $7$
B. $\dfrac12$
C. $2$
D. $\dfrac{1}{2^{497}-28}$
E. $\dfrac{1}{7}$
$y=-\sqrt{x^2-4}$ функц аль нөхцөлийг хангах вэ?
A. $y^2-x^2=4$
B. $x^2-y^2=4$
C. $x^2+y^2+4=0$
D. $x^2+y^2=4$
E. $x^2-y^2+4=0$
$f(x)=2x+3$, $g(x)=1-x$ бол $f(g(1))=?$
A. $0$
B. $1$
C. $2$
D. $3$
E. $4$
Хялбар рационал функцийн график
Шугаман функц
Дараах шугаман функцийн графикийг өгөгдсөн мужид байгуулж хамгийн их ба хамгийн бага утгыг ол.
- $y=-2x+1\quad(-1\le x\le 2)$
- $y=2x-4\quad(0\le x< 3)$
Дараах шугаман функцийн графикийг өгөгдсөн мужид байгуулж хамгийн их ба хамгийн бага утгыг ол.
- $y=5x-2\quad(0\le x\le 3)$
- $y=-3x+1\quad(-1< x\le 2)$
$f(x)=5-3x$ бол дараах олонлогуудыг ол.
- $f([-1,3])$
- $f((-\infty, 2))$
- $f^{-1}([0,2])$
- $f^{-1}((-1,+\infty))$