Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Holy guacamole! www.integral.mn сайт 2026-01-01-ээс шинэчлэгдэж www.mathminds.club хуудас руу шилжинэ.
Олон өнцөгт
Гүдгэр олон өнцөгтийн гадаад өнцгүүдийн нийлбэр
Гүдгэр олон өнцөгтийн дотоод өнцгүүдийн нийлбэр
Дөрвөн өнцөгт
$32$ см.кв талбайтай $ABCD$ трапецийн $AD$ ба $BC$ сууриудын харьцаа $5:1$. $M$ ба $N$ нь харгалзан $AB$, $CD$ хажуу талуудын дундаж цэгүүд. $AN$ ба $DM$ хэрчмүүд $K$ цэгт, $BN$ ба $CM$ хэрчмүүд $E$ цэгт огтлолцдог бол $MENK$ дөрвөн өнцөгтийн талбайг ол.
$ABCD$ параллельограммын $AC$ диагонал дээр $AE$-ын урт нь $AC$-ын уртын $1/3$-тэй тэнцүү байхаар $E$ цэг, $AD$ тал дээр $AF$-ын урт нь $AD$-ын уртын $1/4$-тэй тэнцүү байхаар $F$ цэг авчээ. Хэрэв $G$ нь $FE$ шулуун ба $BC$ талын огтолцлолын цэг бөгөөд $ABGE$ дөрвөн өнцөгтийн талбай $8$ бол $ABCD$ параллельограммын талбайг ол.
Гүдгэр 4 өнцөгтийн диагоналууд түүнийг 4 гурвалжинд хуваана. Эдгээр гурвалжнуудыг багтаасан тойргуудын радиусууд бүгд $2$-той тэнцүү бол $4$ өнцөгтийн талуудын уртыг ол.
Гүдгэр дөрвөн өнцөгтийн диагоналууд $2$ см ба $4$ см. Эсрэг талуудын дунджийг холбосон хэрчмүүд тэнцүү бол дөрвөн өнцөгтийн талбайг ол.
$1$ диаметртэй тойрогт $D$ өнцөг нь тэгш ба $AB=BC$ байх $ABCD$ дөрвөн өнцөгт багтав. $ABCD$ дөрвөн өнцөгтийн периметр $9\sqrt{2}/5$ бол түүний талбайг ол.
$5$ радиустай тойрогт $D$ өнцөг нь тэгш бөгөөд $AB:BC=3:4$ байх $ABCD$ дөрвөн өнцөгт багтжээ. Хэрэв $ABCD$ дөрвөн өнцөгтийн талбайн нь $44$ бол түүний периметрийг ол.
$ABCD$ дөрвөн өнцөгтийг багтаасан тойргийн төв $O$. $AOB$ ба $COD$ өнцгүүдийн нийлбэрийг градусаар илэрхийл.
$ABCD$ гүдгэр дөрвөн өнцөгтийн $AB$ ба $CD$ талуудын дунджуудыг холбосон хэрчмийн урт $1$ метртэй тэнцүү. $BC$ ба $AD$ шулуунууд перпендикуляр бол $AB$ ба $CD$ диагоналуудын дунджуудыг холбосон хэрчмийн уртыг ол.
$ABCD$ гүдгэр дөрвөн өнцөгтийн диагоналуудын дунджуудыг холбосон хэрчмийн урт нь $AD$ ба $BC$ талуудын дунджуудыг холбосон хэрчимтэй тэнцүү бол $AB$ ба $CD$ шулуунуудын хоорондох өнцгийг ол.
Тойрогт багтсан $KLMN$ дөрвөн өнцөгт өгөгдөв. Түүний оройнуудыг дайруулан тойрогт шүргэгч шулуунууд татаж багтаасан дөрвөн өнцөгт үүсгэв. Хэрэв түүний периметр нь $p$ ба $\dfrac{MN}{ML}=2$, $\dfrac{MN}{KL}=8$ бол $KLMN$ дөрвөн өнцөгтийн талбайг ол.
$ABCD$ гүдгэр дөрвөн өнцөгтийн $A$ ба $C$ эсрэг 2 өнцөг нь тэгш байв. $AC$ диагонал дээр $BE$ ба $DF$ перпендикуляруудыг буулгажээ. $CE=FA$ болохыг батал.
Тойрогт багтсан ба тойрог багтаасан $ABCD$ дөрвөн өнцөгт өгөгдөв. $AD$ ба $BC$ талуудын уртын ялгавар нь $AB$ ба $CD$ талуудын уртын ялгавартай тэнцүү бол $AC$ диагонал нь багтаасан тойргийн диаметр болно гэдгийг батал.
Тойргийн $4$ цэг нь $A, B, C, D$ дараалалтай байв. $AB$ ба $CD$ хөвчүүдийн үргэлжлэлүүд харгалзан $B$ ба $C$ цэгийн талд $E$ цэгт огтлолцох бөгөөд $AED$ өнцөг нь $60^\circ$, $ABD$ өнцөг $BAC$ өнцгөөс гурав дахин их бол $AD$ нь тойргийн диаметр болохыг батал.
$ABCD$ трапецийн талбай $36$ см.кв. $A$ оройг дайруулан $BD$ диагоналыг $K$ цэгт, $BC$ суурийг $L$ цэгт шүргэх тойрог татав. Хэрэв $BK:KD=1:3$, $BL:LC=2:1$ бол $DKLC$ дөрвөн өнцөгтийн талбайг ол.
$ABCD$ ромбын $B$ орой дахь мохоо өнцгөөс $BM$ ба $BN$ өндөр татав. $BMDN$ дөрвөн өнцөгтөд 1 см радиустай тойрог багтах ба $\angle ABC=2\arcctg2$ бол ромбын талыг ол.
13 радиустай тойрогт дөрвөн өнцөгт багтав. Түүний диагоналуудын хоорондох нэг өнцөг нь $120^{\circ}$ ба диагоналуудын урт нь 10 ба 24 бол дөрвөн өнцөгтийн их талын уртыг ол.
$ABCD$ дөрвөн өнцөгтийн $AC$ ба $BD$ диагоналууд нь перпендикуляр ба $P$ цэгт огтлолцоно. $C$ оройг $AD$ талын дундаж $M$ цэгтэй холбосон хэрчмийн урт $\dfrac{5}{4}$. $P$ цэгээс $BC$ хэрчим хүртэлх зай нь $\dfrac{1}{2}$ ба $AP=1$. Хэрэв $ABCD$ дөрвөн өнцөгт тойрогт багтах $AD$ хэрчмийн уртыг ол.
$ABCD$ гүдгэр дөрвөн өнцөгтийн $AB$ талын урт $a$, $AC$ талын урт $b$ байв. $B$ ба $C$ оройгоос $AD$ диагонал руу $BK$ ба $CN$ перпендикулярууд татахад $AK< AN$ байв. Хэрэв дөрвөн өнцөгтийн диагоналуудын огтлолцлын цэг $O$ ба $AK=k$, $AN=n$ бол $OC:OA$ харьцааг ол.
Дөрвөн өнцөгтийн диагоналууд $\sqrt{7}$ ба $4$ урттай бөгөөд дөрвөн өнцөгтийг талбайнууд нь арифметик прогресс үүсгэх хэсгүүдэд хуваажээ. Дөрвөн өнцөгтийн их диагонал нь хамгийн бага талтай үүсгэх өнцөг $\dfrac{\pi}{6}$ бол дөрвөн өнцөгтийн талбайг ол.
Тойрог багтаасан $ABCD$ дөрвөн өнцөгт $AC$ диагоналиараа $ABC$ ба $ACD$ гурвалжинуудад хуваагдна. Эдгээр гурвалжнуудад багтсан тойргийн радиусууд харгалзан $1$ ба $\dfrac{3}{\sqrt {15}}$. Хэрэв $ABC$ ба $ACD$ гурвалжнуудын талбай нь харгалзан $6$ ба $\sqrt{15}$ бол дөрвөн өнцөгтийн талууд ба $BD$ диагоналыг ол.
$KLMN$ гүдгэр дөрвөн өнцөгтийн $KN, LM$ талуудын үргэлжлэл $P$ цэгт, $KL, MN$ талуудын үргэлжлэл $Q$ цэгт огтлолцоно. $PQ$ хэрчим $KQN$ өнцгийн биссектрист перпендикуляр. $KQ=12$, $NQ=8$ ба $KLMN$ дөрвөн өнцөгтийн талбай $LQM$ гурвалжны талбайтай тэнцүү бол $KL$ талын уртыг ол.
$ABCD$ гүдгэр дөрвөн өнцөгтийн $C$ оройг $AD$ тал дээр байрлах $M$ цэгтэй холбосон $CB$ хэрчим нь $BD$ диагоналтай $K$ цэгт огтлолцдог. $CK:KM=2:1$, $CD:DK=5:3$ ба $\angle ABC+\angle ACD=180^{\circ}$ бол $AB$ талыг $AC$ диагоналд харьцуулсан харьцааг ол.
$KLMN$ гүдгэр дөрвөн өнцөгтийн $M$ оройг $KN$ тал дээр байрлах $S$ цэгтэй холбосон $MS$ хэрчим $LN$ диагоналтай $O$ цэгт огтлолцоно. $KL:MN=6:7$, $KM:ON=2:1$ ба $\angle KLN=\angle KMN=180^{\circ}$ бол $MO:OS$ харьцааг ол.
$KLMN$ гүдгэр дөрвөн өнцөгтийн $KN$ ба $LM$ талуудын үргэлжлэл $P$ цэгт, $KL, MN$ талуудын үргэлжлэл $Q$ цэгт огтлолцоно. $PQ$ хэрчим $KQN$ өнцгийн биссектрист перпендикуляр. $KQ=6$, $NQ=4$ ба $KLMN$ дөрвөн өнцөгтийн талбай $LQM$ гурвалжны талбайтай тэнцүү бол $MN$ талын уртыг ол.
$ABCD$ гүдгэр дөрвөн өнцөгтийн $AD$ ба $BC$ талуудын үргэлжлэл $M$ цэгт, $AB, CD$ талуудын үргэлжлэл $O$ цэгт огтлолцоно. $MO$ хэрчим $A$ өнцгийн биссектрист перпендикуляр. $OA=12$, $OD=8$, $CD=2$ бол $AOD$ гурвалжны талбайг $ABCD$ дөрвөн өнцөгтийн талбайд харьцуулсан харьцааг ол.
$K, L, M$ цэгүүд $ABCD$ гүдгэр дөрвөн өнцөгтийн талуудыг $AK:BK=CL:BL=CM:DM=1:2$ байхаар хуваана. $KLM$ гурвалжныг багтаасан тойргийн радиус $5/2$, $KL=4$, $LM=3$. Хэрэв $KM< KL$ бол $ABCD$ гурвалжны талбайг ол.
Гүдгэр дөрвөн өнцөгтийн талууд ба диагоналуудын урт нь рационал тоонууд. Дөрвөн өнцөгтийн диагоналиуд түүнийг рационал тоон талуудтай гурвалжинуудад хувааж болох уу? Хариултаа тайлбарла.
$ABCD$ гүдгэр 4 өнцөгтийн диагоналиуд
нь $M$ цэгт огтлолцоно. $ACD$ єнцгийн биссектрис $AB$ талын үргэлжлэлийг $A$ оройн талд $K$ цэгт огтлов. Хэрэв $MA\cdot MC+MA\cdot CD=MB\cdot MD$ бол $\angle BKC=\angle BDC$ гэж батал.
Тойрогт багтсан $ABCD$ дөрвөн өнцөгтийн талууд $AB=2$, $BC=3$,
$CD=1$ ба $\measuredangle ABC=60^{\circ}$ байв. Тэгвэл
- $AC$, багтаасан тойргийн радиус $R$ ба $\sin\widehat{BAC}$-г ол.
- $BD$, $\sin\widehat{BCD}$ ба $S_{BCD}$-г ол.
$ABCD$ трапецийн талбай $48$, $AD$ болон $BC$ сууриудын уртын харьцаа $3:1$. $BC$ суурийн дундаж цэг $N$, $AD$ суурийн дундаж цэг $M$. $AN$ ба $BM$ нь $E$ цэгт, $DN$ ба $CM$ нь $K$ цэгт огтлолцдог бол $ENKM$ дөрвөн өнцөгтийн талбайг ол.
A. $6$
B. $7$
C. $8$
D. $9$
E. $10$
$ABCD$ дөрвөн өнцөгтийн $AC$, $BD$ диагоналиуд нь харгалзан $2$ ба $3$ нэгж урттай, хоорондох өнцгийн косинус нь $\frac{\sqrt{11}}{6}$ бол $ABCD$ дөрвөн өнцөгтийн талбайг ол.
A. $5$
B. $6$
C. $2$
D. $3.5$
E. $2.5$
$ABCD$ гүдгэр дөрвөн өнцөгт багтаасан тойргийн
$\overset{\smile}{AB}:\overset{\smile}{BC}:\overset{\smile}{CD}:\overset{\smile}{DA}=2:3:4:9$ бол $AC$,
$BD$ хоёр диагоналийн хоорондох мохоо өнцөг аль вэ?
A. $150^\circ$
B. $170^\circ$
C. $120^\circ$
D. $130^\circ$
E. $100^\circ$
$ABCD$ дөрвөн өнцөгтийн $A,B,C,D$ орой дахь дотоод өнцгүүд
$1:2:5:4$ харьцаатай бол $AC:BD$ хэд байх вэ?
A. $\sqrt3:\sqrt2$
B. $\sqrt3:1$
C. $2:\sqrt3$
D. $3:2$
E. $4:\sqrt3$
$ABCD$ гүдгэр дөрвөн өнцөгтөд $AB:BC:CD:DA=1:2:5:4$ байжээ.
Хэрэв $AC=9$ см бол түүний $ABC$, $CDA$ өнцгийн биссектристэй
огтлолцсон цэгээр гурав хуваагдсан хэсгүүд нь ямар ямар урттай
вэ?
A. 4 см, 2 см, 3 см
B. 3 см, 1 см, 5 см
C. 2 см, 2 см, 5 см
D. 4 см, 1 см, 4 см
E. 3 см, 2 см, 4 см
$a$ талтай зөв дөрвөн өнцөгт багтаасан тойрогт багтсан зөв
найман өнцөгтийн талбай аль нь вэ?
A. $8\sqrt2a^2$
B. $4\sqrt2a^2$
C. $2\sqrt2a^2$
D. $\sqrt3a^2$
E. $\sqrt2a^2$
Өндөр нь 5см байх $ABCDA_1B_1C_1D_1$ зөв дөрвөн өнцөгт призмийн $ABCD$ суурийн тал 10см. $M$ цэг нь $AB$ тал дээр оршино.
- $\left(\dfrac{|A_1M|}{|MC_1|}\right)^2=\dfrac{1}{\fbox{a}}$ бол $|AM|=|MB|$ байна.
- Энэ тохиолдолд $(A_1MC_1)$ хавтгай нь $BC$ талыг $N$ цэгээр огтлох ба $S_{A_1MNC_1}=\fbox{bc}\cdot\dfrac{\sqrt3}{2}$ байна.
Тойрогт багтсан $ABCD$ дөрвөн өнцөгтийн $AD=\sqrt3$, $AB=1$ ба $\angle ADB=30^\circ$, $\angle CAD=75^\circ$ бол
- багтаасан тойргийн радиус $R=\fbox{a}$,
- $\angle BDC=\fbox{bc}^\circ$,
- $AC^2=\fbox{d}$ байна.
Тойрогт багтсан $ABCD$ дөрвөн өнцөгтийн $AD=\sqrt{3}$, $CD=\sqrt{2} $ ба $\angle ADB=30^\circ$, $\angle CAD=45^\circ$ бол
a) багтаасан тойргийн радиус $R=\fbox{a}$,
б) $\angle BDC=\fbox{bc}^\circ $
в) $AB=\fbox{d}$ байна.
a) багтаасан тойргийн радиус $R=\fbox{a}$,
б) $\angle BDC=\fbox{bc}^\circ $
в) $AB=\fbox{d}$ байна.
Тойрогт багтсан $ABCD$ дөрвөн өнцөгтийн талууд $AB=2$, $BC=3$,
$CD=1$ ба $\measuredangle ABC=60^{\circ}$ байв. Тэгвэл
- $AC=\sqrt{\fbox{a}}$, багтаасан тойргийн радиус $R=\dfrac{\sqrt{\fbox{bc}}}{3}$ ба $\sin\widehat{BAC}=\dfrac{\fbox{d}\sqrt{\fbox{ef}}}{14}$ байна.
- $BD=\dfrac{\fbox{g}\sqrt{\fbox{h}}}{\fbox{m}}$, $\sin\widehat{BCD}=\dfrac{\fbox{i}\sqrt{\fbox{j}}}{7} $ болохыг тогтоож $S_{BCD}=\dfrac{\fbox{k}\sqrt{\fbox{l}}}{\fbox{m}}$ гэж ол.
$ABCD$ дөрвөн өнцөгт тойрогт багтсан бөгөөд
$AB=3$, $BC=7$, $CD=7$, $DA=5$ бол
- $\measuredangle A = \fbox{abc}^{\circ}$, $BD=\fbox{d}$, $AC=\fbox{e}$, $ABCD$-ийн талбай $\fbox{fg}\sqrt{\fbox{h}}$ болно.
- $AC$ ба $BD$ диагоналиудын огтлолцлын цэгийг $E$ гэвэл $\displaystyle \sin\widehat{AEB}=\dfrac{\fbox{i}\sqrt{\fbox{j}}}{\fbox{k}}$, багтаасан тойргийн радиус $\dfrac{\fbox{l}\sqrt{\fbox{m}}}{3}$ байна.
$ABCD$ дөрвөн өнцөгт тойрогт багтсан бөгөөд $AB=3$,
$BC=CD=\sqrt{3}$,
$\cos\widehat{ABC}=\displaystyle\dfrac{\sqrt{3}}{6}$ байсан бол
$AC=\fbox{a}$, $AD=\fbox{b}$ болно. Багтаасан тойргийн радиус
$\displaystyle \dfrac{\fbox{c}\sqrt{\fbox{de}}}{11}$ ба $
\dfrac{S_{ABD}}{S_{BCD}}=\fbox{f}$ байна.
Тойрогт багтсан $ABCD$ дөрвөн өнцөгтийн талууд $AB=BC=2\sqrt{2}$,
$BD=2\sqrt{3}$, $\measuredangle ABC=120^{\circ}$ ба $AD>CD$ бол
$AC=\fbox{a}\sqrt{\fbox{b}}$, $\measuredangle
BDC=\fbox{cd}^{\circ}$ болох бөгөөд $AD=\fbox{e}+\sqrt{\fbox{f}}$
байна. Энэ үед $S_{ABCD}=\fbox{g}\sqrt{3}$ болно.
$ABCD$ дөрвөн өнцөгт $S$ тойрогт багтжээ. $2AB=BC$, $CD=2$, $DA=1$
ба $\cos\widehat{ABC}=\dfrac{5}{8}$ нөхцөл биелэгдэж байв. Энэ үед
$AC=\dfrac{\sqrt{\fbox{ab}}}{\fbox{c}}$, $S$ тойргийн радиус
$\dfrac{2}{13}\sqrt{\fbox{def}}$, $AB=\sqrt{\fbox{g}}$ гэж олдоно.
Бас $BD=\dfrac{4}{5}\sqrt{\fbox{hi}}$,
$\cos\widehat{BCD}=\frac{2}{5}\sqrt{\fbox{j}}$ байна.
Тойрогт
багтсан $ABCD$ дөрвөн өнцөгтийн $\measuredangle ABC$ өнцөг нь хурц
ба $AB=2$, $BC=\sqrt{6}$, $\sin\widehat{ABC}=\dfrac{1}{\sqrt{3}}$
ба $AC \perp BD$ байсан гэе. $AC=\fbox{a}\sqrt{\fbox{b}}$,
тойргийн радиус $\dfrac{\fbox{c}\sqrt{\fbox{d}}}{\fbox{e}}$ ба
$\sin\widehat{CAB}=\dfrac{\fbox{f}}{\fbox{g}}$,
$\sin\widehat{ACB}= \dfrac{\sqrt{\fbox{h}}}{\fbox{i}}$ байна. $AC,
BD$-ийн огтлолцлын цэгийг $H$ гэвэл $DH=\fbox{jk}BH$ болно.
Тойрогт багтсан $ABCD$ дөрвөн өнцөгтийн талууд $AB=3$,
$AC=\dfrac{55}{7}$, $CD=5$, $BD=7$ байв.
- $BC=\fbox{a}$, $AD=\fbox{b}$ ба $BC$ тал дээр уг талыг $5\colon 3$ харьцаагаар хуваах $E$ цэг авбал $\measuredangle DEB=\fbox{cde}^{\circ}$ байна.
- Багтаасан тойргийн радиус $\dfrac{\fbox{f}}{\sqrt{\fbox{g}}}$ байна.
$R=\dfrac{16}{\sqrt{15}}$ радиустай тойрогт багтсан $ABCD$ дөрвөн
өнцөгтийн диагоналиуд харилцан перепендикуляр ба эдгээр нь
$E$ цэгт огтлолцдог байг. $AB=4$, $AD=6$ бол $BD=\fbox{a}$ ба
$\cos\widehat{BDC}=\dfrac{\fbox{b}\sqrt{15}}{\fbox{cd}}$,
$AE=\dfrac{\fbox{e}}{\fbox{f}}\sqrt{15}$ байна. $KE$ нь $ABE$
гурвалжны өндөр ба $M$ нь $KE$ шулууны $CD$ талтай огтлолцох цэг
бол $EM=\dfrac{\fbox{gh}}{15}\sqrt{15}$ болно.
$R=10$ радиустай тойрогт багтсан $ABCD$ дөрвөн өнцөгтийн
диагоналиуд харилцан перепендикуляр ба эдгээр нь $E$ цэгт
огтлолцдог байг. $AB=8$, $BC=6$ бол
$AC={\sqrt{\fbox{a}}}(6\sqrt{3}+4\sqrt{13})/{\fbox{b}}$ ба
$\cos\widehat{BCA}={\sqrt{21}}/{\fbox{c}}$,
$BE={\fbox{de}}/{\fbox{f}}$ байна. $KE$ нь $BCE$ гурвалжны өндөр
ба $M$ нь $KE$ шулууны $CD$ талтай огтлолцох цэг бол
$EM=\sqrt{\fbox{gh}}$ болно.
$O$ цэгт төвтэй $5$ радиустай $S_1$, $4$ радиустай $S_2$ тойргууд
өгөгдөв. Харилцан перепендикуляр диагоналиудтай, эдгээрийн
огтлолцол нь $S_2$ тойрог дээр орших $S_1$-д багтсан дөрвөн
өнцөгтүүд дотроос талбайгаараа хамгийн их байх дөрвөн өнцөгтийг
$ABCD$ гэвэл $O$ цэгээс $BD$ диагональ хүртэлх зай
$2\sqrt{\fbox{a}}$, $BD=2\sqrt{\fbox{bc}}$ байна. Энэ үед
$S_{ABCD}=\fbox{de}$ ба
$AD=\sqrt{\fbox{f}} \bigl(\sqrt{\fbox{gh}}+\sqrt{\fbox{i}} \bigr)$
байна. Энд $AB< DC$ гэж үзнэ.
$O$ цэгт төвтэй $7$ радиустай $S_1$, $6$ радиустай $S_2$ тойргууд
өгөгдөв. Харилцан перепендикуляр диагоналиудтай, эдгээрийн
огтлолцол нь $S_2$ тойрог дээр орших $S_1$-д багтсан дөрвөн
өнцөгтүүд дотроос талбайгаараа хамгийн их байх дөрвөн өнцөгтийг
$ABCD$ гэвэл $O$ цэгээс $AC$ диагональ хүртэлх зай
$\fbox{a}\sqrt{2}$, $AC=2\sqrt{\fbox{bc}}$ байна. Энэ үед
$S_{ABCD}=\fbox{de}$ байна.
$AB=\sqrt{\fbox{f}} \bigl(\sqrt{\fbox{gh}}-\sqrt{\fbox{i}} \bigr)$
байна. Энд $AB< DC$ гэж үзнэ.
Тойрогт багтсан $ABCD$ дөрвөн өнцөгтийн $AD=\sqrt3$, $CD=\sqrt2$ ба $\angle ADB=60^\circ$, $\angle CAD=45^\circ$ бол
- багтаасан тойргийн радиус $R=\fbox{a}$
- $\angle BDC=\fbox{bc}^\circ$
- $AB^2=\fbox{d}$ байна.
1 радиустай тойрогт багтсан $ABCD$ дөрвөн өнцөгтийн хувьд $\angle BCD=75^\circ, \angle CDA=120^\circ, |AB|=\sqrt3$ бол
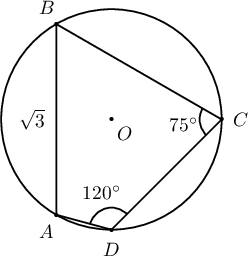
- $\angle BCA=\fbox{ab}^\circ$ /2 оноо/
- $\angle CBD=\fbox{cd}^\circ$ /1 оноо/
- $|CD|=\sqrt{\fbox{e}}$ /2 оноо/
- $|BD|=\dfrac{\sqrt{\fbox{f}}+\sqrt{\fbox{g}}}{\fbox{h}}\,\,\, (\fbox{f}<\fbox{g})$ /2 оноо/

1 радиустай тойрогт багтсан $ABCD$ дөрвөн өнцөгтийн хувьд $\angle ABC=60^\circ, \angle DAB=105^\circ, |BC|=\sqrt3$ бол
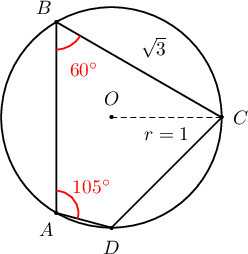
- $\angle BCA=\fbox{ab}^\circ$ /1 оноо/
- $\angle CAD=\fbox{cd}^\circ$ /2 оноо/
- $|CD|=\sqrt{\fbox{e}}$ /2 оноо/
- $|AD|=\dfrac{\sqrt{\fbox{f}}-\sqrt{\fbox{e}}}{\fbox{h}}\,\,\, $ /2 оноо/

$ABCD$ дөрвөн өнцөгт тойрогт багтсан бөгөөд $AB=33$,
$BC=CD=11\sqrt{3}$, $\cos\measuredangle ABC=\dfrac{\sqrt{3}}{6}$ байсан бол $AC=\fbox{ab}$, $AD=\fbox{cd}$ болно. Багтаасан тойргийн радиус $\fbox{e}\sqrt{\fbox{fg}}$ ба $\dfrac{S_{ABD}}{S_{BCD}}=\fbox{h}$ байна.
$ABCD$ дөрвөн өнцөгт тойрогт багтсан бөгөөд $AB=12$,
$BC=CD=10$, $\cos\measuredangle ABC=\dfrac15$ байсан бол $AC=\fbox{ab}$, $AD=\fbox{c}$ болно. Багтаасан тойргийн радиус $\dfrac{\fbox{de}\sqrt{\fbox{f}}}{12}$ ба $\dfrac{S_{ABD}}{S_{BCD}}=\dfrac{\fbox{gh}}{25}$ байна.
Зөв олон өнцөгт
Зөв $6$ өнцөгтийн талын урт $14$ см. Түүнтэй эн чацуу зөв гурвалжны тал ба энэ гурвалжинд багтсан тойргийн талбайг ол.
$O$ төвтэй $A_1A_2\ldots A_{30}$ зөв $30$ өнцөгт өгөгджээ. $OA_3$ ба $A_1A_4$ шулуунуудын хоорондох өнцгийг ол.
A. $64^\circ$
B. $80^\circ$
C. $84^\circ$
D. $76^\circ$
E. $108^\circ$
3 радиустай тойрогт багтсан зөв 8 өнцөгтийн талбай хэд вэ?
A. $24$
B. $12$
C. $36\sqrt2$
D. $18\sqrt2$
E. $18\sqrt3$
Хоёр зөв олон өнцөгтийн талуудын тоо $2:3$, оройн өнцгүүдийнх нь хэмжээ $6:7$ харьцаатай байсан бол талуудын тоо нь хэд вэ?
A. 4, 6
B. 6, 9
C. 8, 12
D. 10, 15
E. 10, 25
2 нэгж талтай зөв зургаан өнцөгтийн нэг оройг $P$ гэв. $P$
оройгоос гарсан нэг талын, мөн оройгоос гарсан бүх диагональ дээрх
проекцийн нийлбэр ямар байх вэ?
A. $2\sqrt3$
B. $3$
C. $1+\sqrt3$
D. $2+\sqrt3$
E. $2-\sqrt3$
1 нэгж талтай зөв зургаан өнцөгтийн нэг талын, түүнтэй
ерөнхий оройгүй бүх диагональ дээрх проекцийн нийлбэр аль нь вэ?
A. $2\sqrt3$
B. $3$
C. $1+\sqrt3$
D. $2+\sqrt3$
Зөв найман өнцөгтийн диагоналиудыг түүнийг багтаасан тойргийн
радиусаар илэрхийлбэл аль нь бүгд зөв бэ?
A. $2R, \sqrt2R, \sqrt{2-\sqrt2}R$
B. $2R, \sqrt3R, \sqrt{2+2\sqrt2}R$
C. $2R, \sqrt3R, \sqrt{2-\sqrt2}R$
D. $2R, \sqrt3R, \sqrt{2-\sqrt2}R$
E. $2R, \sqrt2R, \sqrt{2+\sqrt2}R$
Зөв найман өнцөгтийн диагоналиудыг түүний талын урт $a$-гаар
илэрхийлбэл аль нь бүгд зөв бэ?
A. $\sqrt{2+\sqrt2}a, (1+\sqrt2)a, \sqrt{2-\sqrt2}a$
B. $\sqrt{2+\sqrt2}a, (3-\sqrt2)a, \sqrt{4+\sqrt2}a$
C. $\sqrt{2+\sqrt2}a, (1+\sqrt2)a, \sqrt{4+2\sqrt2}a$
D. $\sqrt{2+\sqrt2}a, \sqrt{3+2\sqrt2}a, \sqrt{4-\sqrt2}a$
E. $\sqrt{2-\sqrt2}a, (3-\sqrt2)a, \sqrt{4+\sqrt2}a$
$R$ радиустай тойрогт багтсан зөв зургаан өнцөгтийн талуудын
дундаж дээр оройтой гүдгэр зургаан өнцөгтийн талуудыг тойргийн
радиусаар илэрхийлбэл аль нь зөв бэ?
A. $\sqrt3R$
B. $\dfrac13R$
C. $\dfrac32R$
D. $\dfrac{\sqrt3}2R$
E. $\dfrac23R$
Зөв найман өнцөгт багтаасан тойргийн $R$ радиусаар,
талуудынх нь дундаж дээр оройтой гүдгэр олон өнцөгтийн талуудыг
илэрхийлбэл аль нь зөв бэ?
A. $\dfrac{\sqrt3}3R$
B. $\dfrac34R$
C. $\dfrac R{\sqrt2}$
D. $(\sqrt2-1)R$
E. $(\sqrt3-1)R$
Нэгж радиустай тойрогт багтсан зөв 12 өнцөгтийн талбай аль нь вэ?
A. $1$
B. $2$
C. $2\sqrt3$
D. $2\sqrt2$
E. $3$
Зөв зургаан өнцөгтийг багтаасан тойргийн радиусыг уг зургаан өнцөгтөд багтсан тойргийн радиуст харьцуулсан харьцааг ол.
A. $3:2$
B. $\sqrt{3}:2$
C. $2:3$
D. $2:\sqrt3$
E. $1:\sqrt3$
Зөв найман өнцөгтийн гадаад өнцөг хэдэн градус байх вэ?
A. $15^\circ$
B. $20^\circ$
C. $30^\circ$
D. $45^\circ$
E. $60^\circ$
Дараах зургаас $x$-ийн утгыг олоорой. Энд $ABCDE$ зөв таван өнцөгт, $M$ нь $AB$, $DC$ талуудын үргэлжлэлийн огтлолын цэг.
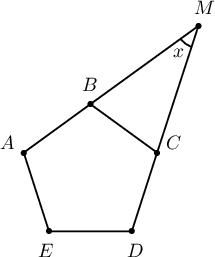

A. $36^\circ$
B. $60^\circ$
C. $66^\circ$
D. $72^\circ$
E. $144^\circ$
$ABCDEFGH$ зөв найман өнцөгтийн талын урт $4$; $AC$, $BD$ диагоналиудын хоорондох өнцөг $\fbox{ab.c}^\circ$, $ABCDE$ таван өнцөгтийн талбай $\fbox{de}\sqrt{2}$, $ABCD$ дөрвөн өнцөгтийн талбай $\fbox{fg}\sqrt{2}$ байна.
Квадрат
Нэг квадратын оройн цэгүүд нь нөгөө квадратын талууд дээр байрлана. Квадратуудын талбайн харьцаа $p$ бол $1$ дэх квадратын оройн цэгүүд $2$ дахь квадратын талуудыг ямар харьцаагаар хуваах вэ?
$ABCD$ квадрат өгөгдөв. $AB$, $CD$-гийн дундаж цэгүүд нь харгалзан $E$, $F$ ба $ABCD$ квадратын тал нь $a$. $K$ цэг $CF$ хэрчим дээр, $N$ цэг $AD$ хэрчимд харъяалагдах бөгөөд $EF$, $KN$ хэрмчмүүд $M$ цэгээр огтлолцоно. Хэрвээ $CK:KF=1:5$ ба $EMNA$ трапецийн талбай нь $3/10$ бол $KMF$ гурвалжны талбайг ол.
$MNPQ$ квадратын $NP$ тал дээр $A$ цэг, $PQ$ тал дээр $B$ цэг авсан ба $NA:AP=PB:BQ=2:3$. $L$ цэг нь $MA$, $NB$ хэрчмүүдийн огтлолцлын цэг болно. $L$ цэг $MA$ хэрчмийг ямар харьцаанд хуваах вэ?
$ABCD$ квадратын талын урт нь $a$. $M$ цэг $AC$ диагоналыг $AM:MC=3:1$ харьцаагаар хуваана. $M$ цэг $AB$ тал дээр орших ба $\angle NMD=90^\circ$ бол $AN$ хэрчмийн уртыг ол.
$18$ см.кв талбайтай квадратад тэгш өнцөгт багтаажээ. Квадратын тал бүр дээр тэгш өнцөгтийн орой байрлана. Тэгш өнцөгтийн талуудын харьцаа нь $1:2$ бол тэгш өнцөгтийн талбайг ол.
$24$ см.кв талбайтай квадратад тэгш өнцөгт багтжээ. Квадратын тал бүр дээр тэгш өнцөгтийн орой байрлана. Тэгш өнцөгтийн талуудын харьцаа нь $1:3$ бол тэгш өнцөгтийн талбайг ол.
Квадратад багтсан тойргийн радиус нь $6$ см. Квадратын талбайг ол.
Трапецийн гадна талд, түүний $AB$ ба $CD$ сууриуд дээр квадрат байгуулав. Тэдгээрийн төвийг холбож байгаа хэрчим трапецийн диагоналуудын огтлолцлын цэгийг дайрахыг батал.
Трапецийн параллель талуудын квадратуудын нийлбэр $288$. Эдгээр талуудтай параллель трапецийн талбайг хагаслан хуваах хэрчмийн уртыг ол.
$ABCD$ квадрат өгөгдөв. Тойрог нь $AC$ шулууныг $C$ цэг шүргэх ба түүний төв ба $D$ цэг $AC$ шулууны нэг талд оршино. $D$ цэгээс тойрогт татсан шүргэгчүүдийн хоорондох өнцөг $120^\circ$ бол квадратын талбайг уг тойргоор хүрээлэгдсэн дугуйн талбайд харьцуулсан харьцааг ол.
Трапецийн диагоналуудын квадратуудын нийлбэр нь хажуу талуудын квадратуудын нийлбэр дээр сууриудын үржвэрийг 2 дахин нэмсэнтэй тэнцүү болохыг батал.
Тойрогт харилцан перпенпикуляр, огтлолцсон $AB$ ба $CD$ хөвчүүд өгөгдөв. Хэрэв $AB=AC=CD$ бол тойргийн талбай ба $AB$ талтай квадратын талбайн аль нь их вэ?
$a$ талтай квадратын өнцгүүдийг тайрч зөв найман өнцөгт үүсгэв. Энэ найман өнцөгтийн талбайг ол.
A. $\dfrac{3a^2}{4}$
B. $2(\sqrt2-1)a^2$
C. $\dfrac{\sqrt2a^2}{2}$
D. $(\sqrt2-1)a^2$
E. $(2-\sqrt2)a^2$
Дугуй ба уг дугуйд багтсан квадрат хоёрын талбайн ялгавар нь $2\sqrt{3}(\pi-2)$. Энэ дугуйд багтсан зөв зургаан өнцөгтийн талбайг ол.
A. $4$
B. $9$
C. $6$
D. $7$
E. $10$
4 м талтай $ABCD$ квадратын $AB$ талын дундаж, квадратын төв, $C$ оройг дайрсан тойргийн радиусыг ол.
A. $4\sqrt5$
B. $2\sqrt2$
C. $4\sqrt2$
D. $2\sqrt{10}$
E. $\sqrt{10}$
$7$ см талтай $ABCD$ квадратын $AD$ талын дундаж цэг $K$ болно. $CK$ шулууны дагуу цаасыг нугалж тэр хоёр талст өнцгийг $60^\circ$ болгов. $B$ ба $D$ цэгүүдийн хоорондох зайг ол.
A. $14\sqrt{5}$
B. $7\sqrt5$
C. $\frac{14\sqrt5}{5}$
D. $\frac{7\sqrt5}{5}$
E. $\frac{2\sqrt5}{5}$
Параллелограммын нэг диагоналийн урт 6, талуудынх нь квадратуудын нийлбэр нь 50 бол нөгөө диагоаналийн уртыг ол.
A. $2$
B. $4$
C. $6$
D. $8$
E. $10$
$ABCD$ квадратын талын урт 3 бол түүнийг багтаасан тойргийн урт нь
A. $12\pi$
B. $4\pi\sqrt3$
C. $2\pi\sqrt{10}$
D. $6\pi\sqrt2$
E. $3\pi\sqrt2$
$ABCD$ квадратын $BA$ талын дундаж $E$, $BC$ талын дундаж $F$
байжээ. $CE$, $DF$ хэрчмүүдийн огтлолцол $M$, квадратын талын урт
$a$ бол $S_{CMF}$ аль нь вэ?
A. $\frac{a^2}{16}$
B. $\frac{a^2}{18}$
C. $\frac{a^2}{20}$
D. $\frac{a^2}{24}$
$ABCD$ квадратын $BA$ талын дундаж $E$, $BC$ талын дундаж
$F$ цэгүүдийг харгалзуулан $C$, $D$ оройтой холбосон хэрчмүүд $M$
цэгт огтлолцжээ. Хэрэв квадратын талбай $S$ бол $S_{AEMD}$ аль нь
вэ?
A. $\frac{11}{20}S$
B. $\frac58S$
C. $\frac12S$
D. $\frac34S$
Квадратын төвийг дайрсан, нэг талтай нь $60^\circ$ өнцөг
үүсгэдэг шулуун тэр талаа ямар харьцаатай хэсгүүдэд хуваах вэ?
A. $\sqrt3:2$
B. $(2\pm\sqrt3):1$
C. $(3+\sqrt2):1$
D. $1:\sqrt3$
$d$ диагональтай квадратын төвийг дайрсан шулуун нэг талтай
нь $60^\circ$ өнцөг үүсгэсэн бол квадрат дотор орших, тэр шулууны
хэрчмийн урт ямар байх вэ?
A. $\frac d{\sqrt2}$
B. $\frac d{\sqrt3}$
C. $\frac d{\sqrt5}$
D. $\frac{2d}{\sqrt6}$
$6$ см талтай квадратад тойрог багтсан бол зурагт үзүүлсэн будагдсан хэсгийн талбайг ол.
$10$ см талтай квадратад тойрог багтсан бол зурагт үзүүлсэн будагдсан хэсгийн талбайг ол.
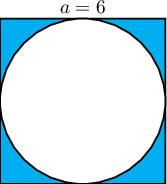

A. $(18\pi-6)$ см.кв
B. $(36+9\pi)$ см.кв
C. $9\pi$ см.кв
D. $(36-9\pi)$ см.кв
E. $36$ см.кв
3; 4 урттай талуудтай квадрат зурагт үзүүлснээр өгчээ. Будагдсан хэсгийн талбайг ол.
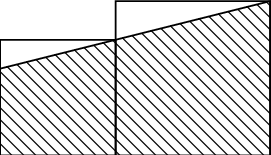

A. $25$
B. $12$
C. $3\dfrac18$
D. $20\dfrac78$
E. $21\dfrac78$
5 талбайтай квадратын диагональтай тэнцүү талтай квадратын талбайг ол.
A. $8.25$
B. $10$
C. $12.5$
D. $25$
E. $20$
2; 3 урттай талуудтай квадрат зурагт үзүүлснээр өгчээ. Будагдсан хэсгийн талбайг ол.
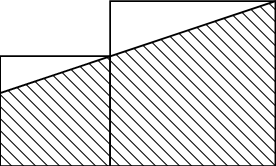

A. $10$
B. $10\dfrac56$
C. $10\dfrac16$
D. $11\dfrac14$
E. $11\dfrac15$
Ромбын диагоналиудын үржвэр нь талын квадратаас $\sqrt3$ дахин их бол өнцгүүд нь аль вэ?
A. $15^\circ,\ 165^\circ$
B. $30^\circ,\ 150^\circ$
C. $45^\circ,\ 135^\circ$
D. $60^\circ,\ 120^\circ$
E. $75^\circ,\ 105^\circ$
Ромбын диагоналиудын үржвэр нь талын квадратаас $\sqrt2$ дахин их бол өнцгүүд нь аль вэ?
A. $15^\circ,\ 165^\circ$
B. $30^\circ,\ 150^\circ$
C. $45^\circ,\ 135^\circ$
D. $60^\circ,\ 120^\circ$
E. $75^\circ,\ 105^\circ$
Квадратын хувьд дараах өгүүлбэрүүдийн аль нь биелэхгүй вэ?
A. Диагональ нь оройн өнцгийн биссектрис болно
B. Диагоналиуд нь харилцан перпендикуляр
C. Эсрэг талууд нь хос хосоороо параллель
D. Диагоналиуд нь тэнцүү
E. Дотоод өнцгүүдийн нийлбэр нь $180^\circ$
Аливаа ромбын хувьд дараах өгүүлбэрүүдийн аль нь биелэхгүй вэ?
A. Бүх талууд нь тэнцүү
B. Бүх өнцгүүд нь тэнцүү
C. Эсрэг талууд нь хос хосоороо параллель
D. Хөрш өнцгүүдийн нийлбэр $180^\circ$
E. Диагоналиуд нь харилцан перпендикуляр
Аливаа параллелограммын хувьд дараах өгүүлбэрүүдийн аль нь биелэхгүй вэ?
A. Хөрш өнцгүүдийн нийлбэр $180^\circ$
B. Дотоод өнцгүүдийн нийлбэр $360^\circ$
C. Эсрэг талууд нь хос хосоороо параллель
D. Эсрэг өнцгүүд нь тэнцүү
E. Диагоналиуд нь харилцан перпендикуляр
Аливаа параллелограммын хувьд дараах өгүүлбэрүүдийн аль нь заавал биелэх вэ?
A. Бүх талууд нь тэнцүү
B. Бүх өнцгүүд нь тэнцүү
C. Эсрэг талууд нь хос хосоороо параллель
D. Эсрэг өнцгүүдийн нийлбэр $180^\circ$
E. Диагоналиуд нь харилцан перпендикуляр
$ABCD$ квадратын $AC$ диагоналийг $M$ цэг $AM=5$, $MC=9$ байхаар хуваажээ. $BM$-ийн уртыг ол.
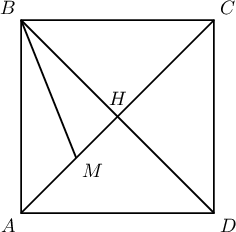

A. $4\sqrt3$
B. $3\sqrt5$
C. $4\sqrt2$
D. $7$
E. $\sqrt{53}$
$ABCD$ квадратын $AC$ диагоналийг $M$ цэг $AM=5$, $MC=7$ байхаар хуваажээ. $BM$-ийн уртыг ол.
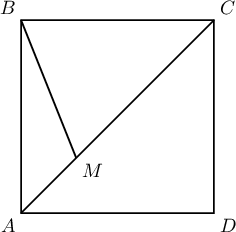

A. $6$
B. $5\sqrt2$
C. $4\sqrt3$
D. $\sqrt{37}$
E. $3\sqrt{3}$
Ромбо дотор тойрог, тойрог дотор квадрат багтав. Хэрэв квадратын талбай ромбын талбайгаас 4 дахин бага бол ромбын бага өнцөг нь $\fbox{ab}^\circ$, их өнцөг нь $\fbox{cde}^\circ$ байна.
$2$ нэгж талтай квадратыг түүний төв $O$ цэгийг тойруулан $\alpha$
өнцгөөр эргүүлэн $A^{\prime}B^{\prime}C^{\prime}D^{\prime}$
квадрат үүсгээд $t=\tg \alpha /2$ гэе. Энэ хоёр квадратын талуудын
огтлолцол дээр оройтой найман өнцөгтийн талбай
$S=S(t)=\dfrac{\fbox{a} (1+t^{\fbox{b}})}{(\fbox{c}+t^{\fbox{d}})}$
байна. $S=S(t)$-ийн утга $\alpha ={\pi}/{\fbox{e}}$ үед хамгийн
бага $S(\pi /{\fbox{e}} )=\fbox{f} (\sqrt{\fbox{g}}-1)$ утгатай
байна.
$3$ нэгж талтай квадратыг түүний төв $O$ цэгийг тойруулан $\alpha$
өнцгөөр эргүүлэн $A^{\prime}B^{\prime}C^{\prime}D^{\prime}$
квадрат үүсгээд $t=\tg \alpha /2$ гэе. Энэ хоёр квадратын талуудын
огтлолцол дээр оройтой найман өнцөгтийн периметр
$P=P(t)=\dfrac{\fbox{ab}(1+t^{\fbox{c}})}{(1+t^{\fbox{d}})}$
байна. $P=P(t)$ нь $\alpha ={\pi}/{\fbox{e}}$ үед хамгийн бага
$P({\pi}/{\fbox{e}} )=\fbox{fg} (\sqrt{2}-1)$ утгатай байна.
Олон өнцөгт
Нэгж талуудтай $ABCDE$ гүдгэр таван өнцөгтийн $AB, CD$ талуудын дундаж цэгүүд нь харгалзан $P, Q$ ба $BC, DE$ талуудын дундаж цэгүүд нь харгалзан $S, T$ байв. $PQ$ ба $ST$ хэрчмүүдийн дундаж цэгүүд $M, N$ бол $MN$ хэрчмийн уртыг ол.
$O$ төвтэй нэг радиустай тойрог дээр $P_1$, $P_2$, $P_3$, $P_4$, $P_5$ цэгүүдийг
$\angle P_1OP_2=\angle P_4OP_5=30^{\circ}$, $\angle P_2OP_3=\angle P_3OP_4=75^{\circ}$ байхаар авчээ. $P_1$, $P_2$, $P_3$, $P_4$, $P_5$-аас хоёр цэгийг авч $O$ цэгтэй холбоход үүсэх гурвалжнуудын талбайн нийлбэрийг ол.
Гүдгэр 6 өнцөгтийн дотоод өнцгүүдийн нийлбэр хэд вэ?
A. $180^\circ$
B. $360^\circ$
C. $540^\circ$
D. $720^\circ$
E. $900^\circ$
Гүдгэр 5 өнцөгтийн гадаад өнцгүүдийн нийлбэр хэд вэ?
A. $180^\circ$
B. $360^\circ$
C. $540^\circ$
D. $720^\circ$
E. $900^\circ$
$R=6$ радиустай тойрогт багтсан $ABCDE$ таван өнцөгтийн $AB=6\sqrt{2}$, $\measuredangle ABE=45^\circ$, $\measuredangle EBD=30^\circ$ ба $BC=CD$ бол таван өнцөгтийн талбайг ол.
Бодолт. Синусын теоремоор $AE=2R\sin45^\circ$ гэдгээс $AE=6\sqrt{\fbox{a}}$. Иймд $ABE$ гурвалжны талбай $S_1=3\fbox{b}$. Цаашилбал $\measuredangle BDE=\fbox{c}0^\circ$ гэдгээс $BD=6\sqrt{\fbox{d}}$, $DE=\fbox{e}$. Иймээс $BDE$ гурвалжны талбай $S_2=18\sqrt{\fbox{d}}$. Харин $BCDE$ дөрвөн өнцөгт тойрогт багтсан гэдгээс $C$ оройн өнцгийг тооцоолж болно. Иймд $BCD$ гурвалжны өндөр $CF=\fbox{f}$ ба түүний талбай $S_3=9\sqrt{\fbox{g}}$. Эдгээрээс таван өнцөгтийн талбай $S=S_1+S_2+S_3$ болно.
Бодолт. Синусын теоремоор $AE=2R\sin45^\circ$ гэдгээс $AE=6\sqrt{\fbox{a}}$. Иймд $ABE$ гурвалжны талбай $S_1=3\fbox{b}$. Цаашилбал $\measuredangle BDE=\fbox{c}0^\circ$ гэдгээс $BD=6\sqrt{\fbox{d}}$, $DE=\fbox{e}$. Иймээс $BDE$ гурвалжны талбай $S_2=18\sqrt{\fbox{d}}$. Харин $BCDE$ дөрвөн өнцөгт тойрогт багтсан гэдгээс $C$ оройн өнцгийг тооцоолж болно. Иймд $BCD$ гурвалжны өндөр $CF=\fbox{f}$ ба түүний талбай $S_3=9\sqrt{\fbox{g}}$. Эдгээрээс таван өнцөгтийн талбай $S=S_1+S_2+S_3$ болно.
$R=4$ радиустай тойрогт багтсан $ABCDE$ таван өнцөгтийн $AB=4\sqrt{2}$, $\measuredangle ABE=45^\circ$, $\measuredangle EBD=30^\circ$ ба $BC=CD$ бол таван өнцөгтийн талбайг ол.
Бодолт. Синусын теоремоор $AE=2R\sin45^\circ$ гэдгээс $AE=4\sqrt{\fbox{a}}$. Иймд $ABE$ гурвалжны талбай $S_1=1\fbox{b}$. Цаашилбал $\measuredangle BDE=\fbox{c}0^\circ$ гэдгээс $BD=4\sqrt{\fbox{d}}$, $DE=\fbox{e}$. Иймээс $BDE$ гурвалжны талбай $S_2=8\sqrt{\fbox{d}}$. Харин $BCDE$ дөрвөн өнцөгт тойрогт багтсан гэдгээс $C$ оройн өнцгийг тооцоолж болно. Иймд $BCD$ гурвалжны өндөр $CF=\fbox{f}$ ба түүний талбай $S_3=4\sqrt{\fbox{g}}$. Эдгээрээс таван өнцөгтийн талбай $S=S_1+S_2+S_3$ болно.
Бодолт. Синусын теоремоор $AE=2R\sin45^\circ$ гэдгээс $AE=4\sqrt{\fbox{a}}$. Иймд $ABE$ гурвалжны талбай $S_1=1\fbox{b}$. Цаашилбал $\measuredangle BDE=\fbox{c}0^\circ$ гэдгээс $BD=4\sqrt{\fbox{d}}$, $DE=\fbox{e}$. Иймээс $BDE$ гурвалжны талбай $S_2=8\sqrt{\fbox{d}}$. Харин $BCDE$ дөрвөн өнцөгт тойрогт багтсан гэдгээс $C$ оройн өнцгийг тооцоолж болно. Иймд $BCD$ гурвалжны өндөр $CF=\fbox{f}$ ба түүний талбай $S_3=4\sqrt{\fbox{g}}$. Эдгээрээс таван өнцөгтийн талбай $S=S_1+S_2+S_3$ болно.
Олон өнцөгтийн периметр
Параллелограмм
$\alpha$, $\beta$ нь параллелограммын хөрш өнцгүүд ба $\dfrac{\sqrt3}{2}(\sin\alpha+\sin\beta)=\sin(\alpha-\beta)$ бол $\alpha$, $\beta$-г ол.
$ABCD$ параллельограм өгөгдөв. $\angle BCD=\pi/3$, $AB=a$, $BCD$ өнцгийн биссектрис нь $AD$ талыг $N$ цэгт огтолно. $NCD$ гурвалжны талбайг ол.
$ABCD$ параллельограмын $AD$ талын урт $8$. $ADC$ өнцгийн биссектрис $AB$ шулууныг $E$ цэгт огтолно. $ADE$ гурвалжинд $O$ төвтэй тойрог багтсан ба уг тойрог нь $AE$ талыг $K$ цэгт, $AD$ талыг $L$ цэгт шүргэнэ. $KL=2$ бол $KOL$ өнцгийг ол.
Параллелограмын диагонал нь $3$ ба $5$, хурц өнцөг нь $60^\circ$ бол талбайг ол.
$ABCD$ параллельограмын $AB$ тал нь $BD$ диагоналтай перпендикуляр. $BD=6$, $AC$ диагоналын урт $2\sqrt{22}$ бол $AD$-г ол.
$ABCD$ параллелограммын $B$ мохоо өнцгийн биссектрис $AD$ талыг $F$ цэгт огтолно. $AB=12$, $AF:FD=4:3$ бол параллелограммын периметрийг ол.
4 өнцөгтийн оройн цэгүүдээс түүний диагоналд нь параллель шулуунууд татав. Эдгээр шулуунуудаар үүссэн параллельограмм болон өгөгдсөн 4 өнцөгтийн талбайн харьцааг ол.
Параллелограммын периметр нь $90$ см, хурц өнцөг нь $60^\circ$. Параллелограммын диагонал нь түүний мохоо өнцгийг $1:3$ хэмжээтэй хуваах бол параллелограммын талуудыг ол.
Параллелограммын хурц өнцөг $45^\circ$. Диагоналуудын огтолцлолын цэгээс тэнцүү биш талууд хүртэлх зай $2$ ба $3$. Параллелограммын талбайг ол.
Параллелограммын периметрийг их талд харьцуулсан харьцаа нь $k$, $k>2$. Хэрэв их диагонал нь параллельограммын өнцгийг $1:2$ харьцаанд хуваадаг бол параллельограммын өнцгүүдийг ол.
Параллелограммын дотор $6$ радустай $2$ тойрог өгөгдөв. Эдгээр тойргууд нь тус бүрдээ параллелограммын $1$ хажуу, $2$ суурь ба нөгөө тойргоо шүргэнэ. Хэрэв хажуу талууд нь шүргэлтийн цэгээр $9:4$ харьцаанд хуваагдах бол параллелограммын талбайг ол.
$ABCD$ параллелограмын дотор $CKD$ нь зөв гурвалжин байхаар $K$ цэг сонгов. $K$ цэгээс $AD$, $AB$, $BC$ шулуун хүртэлх зайнууд нь харгалзан $3$, $6$ ба $5$ байв. Параллелограммын периметрийг ол.
$ABCD$ параллелограммын $BCD$ өнцөг $150^{\circ}$, $AD$ суурь нь $8$. $CD$ шулууныг шүргэж, $AD$ хэрчмийг $A$ цэг ба $D$ оройгоос $2$ зайд орших цэгээр огтлох тойргийн радиусыг ол.
Параллелограммын талууд нь $4$ см ба $6$ см. Их талын дундажаас параллель тал нь $45^{\circ}$ өнцгөөр харагдана. Параллелограммын талбайг ол.
Параллелограммын $B$ ба $C$ өнцгүүдийн биссектрисүүд $O$ цэгт огтлолцоно. Хэрэв $\angle A=2\arcsin\dfrac{2}{\sqrt{13}}$, $OA=2\sqrt{10}$, $OD=5$ бол параллелограммын талбайг ол. (Бүх боломжит шийдийг ол).
Параллелограммын хоёр талын урт 3 ба 7, нэг диагоналийн урт 9 бол нөгөө диагоналийн уртыг ол.
A. $7$
B. $9$
C. $\sqrt{35}$
D. $\sqrt{23}$
E. $9.5$
Параллелограммын хоёр талын урт $3$ ба $5$, нэг диагоналийн урт $7$ бол нөгөө диагоналийн уртыг ол.
A. $19$
B. $7$
C. $7.5$
D. $\sqrt{19} $
E. $\sqrt{15} $
$O$ нь $ABCD$ параллелограммын диагоналиудын огтлолцолын цэг байг. Параллелограммын периметр нь 12-той тэнцүү ба $BOC$ ба $COD$ гурвалжны периметрүүдийн ялгавар 2-той тэнцүү бол параллелограммын талуудын уртыг ол.
A. 2 ба 4
B. 5 ба 7
C. 4 ба 8
D. 3 ба 6
E. 1 ба 5
Параллелограммын нэг диагоналийн урт 6, талуудынх нь квадратуудын нийлбэр нь 50 бол нөгөө диагоаналийн уртыг ол.
A. $2$
B. $4$
C. $6$
D. $8$
E. $10$
Параллелограммын хагас периметр 15 см, диагоналиуд 9 см,
12 см бол талбай хэдэн см.кв вэ?
A. $48$
B. $50$
C. $52$
D. $54$
E. $56$
Параллелограммын хоёр диагоналийн нийлбэр $5+\sqrt{97}$ см, талууд
$5$ см, $6$ см бол талбай нь хэдэн см.кв вэ?
A. $24$
B. $26$
C. $28$
D. $30$
E. $36$
$ABCD$ параллелограммын $AB$ талын дундаж $E$, $AD$ талын
дундаж $F$ байжээ. $DE$, $CF$ хэрчмүүд $M$ цэгт огтлолцсон бол
$DM:ME$ аль нь вэ?
A. $\dfrac12$
B. $\dfrac34$
C. $\dfrac45$
D. $\dfrac23$
E. $\dfrac32$
$ABCD$ параллелограммын $AB$, талын дундаж $E$, $AD$ талын
дундаж $F$ байжээ. $CF$, $DE$ хоёр хэрчмийн огтлолцол $M$ бол
$S_{DMF}:S_{AED}$ аль нь вэ?
A. $\frac12$
B. $\frac15$
C. $\frac13$
D. $\frac25$
50 м периметртэй параллелограммын нэг диагональ өндөр нь
болох бөгөөд талуудын ялгавар 1 м байсан бол диагоналиуд нь аль
вэ?
A. 4 м, 20 м
B. 5 м, $\sqrt{601}$ м
C. 4 м, $\sqrt{601}$ м
D. 5 м, 20 м
Параллелограммын нэг тал 12 см, диагоналиуд 10 см, 26 см бол
талбай нь аль вэ?
A. $130 \mbox{см}^2$
B. $60 \mbox{см}^2$
C. $120 \mbox{см}^2$
D. $78 \mbox{см}^2$
$ABCD$ параллелограммын $AB$ талын үргэлжлэл дээр орших $F$
цэг $D$ орой хоёрыг дайрсан шулуун $AC$ диагоналийг $AE:EC=m:n$
байх $E$ цэгт огтолжээ. Хэрэв $AB=a$ бол $BF$-ийн урт аль нь вэ?
A. $\frac{a(m+n)}{m-n}$
B. $\frac{a(m-n)}m$
C. $\frac{a(m-n)}{n}$
D. $\frac{a(m-n)}{m+n}$
$ABCD$ параллелограммын диагоналиудын огтлолцлын цэгээс $BC$
талд буулгасан перпендикуляр $BC$ талыг $E$, $AB$ талын
үргэлжлэлийг $F$ цэгт тус тус огтолжээ. Хэрэв $AB=a$, $BC=b$,
$BF=c$ бол $BE$ хэрчмийн урт аль нь вэ? ($A$ нь хурц өнцөг).
A. $\frac{ac}b$
B. $\frac{ac}{b+c}$
C. $\frac{bc}{a+2c}$
D. $\frac{bc}{a+c}$
Параллелограммын нэг талд налсан хоёр өнцгийн биссектрис
эсрэг тал дээр нь огтлолцсон бол өндрүүдийн харьцаа аль нь байх
вэ?
A. 1:3
B. 3:5
C. 3:4
D. 1:2
48 нэгж периметртэй параллелограммын өндрүүд 5:7 харьцаатай
бол талуудын урт хэд хэд байх вэ?
A. 11, 13
B. 15, 9
C. 7, 17
D. 10, 14
$P=14$ см байх параллелограммын нэг тал нь 4 см, нэг өнцөг нь $120^\circ$ байв. Талбайг ол.
A. $3\sqrt3$
B. $6$
C. $7$
D. $6\sqrt3$
E. $7\sqrt3$
Параллелограммын талууд нь $3$, $4$ ба мохоо өнцөг нь $120^\circ$ бол талбайг нь ол.
A. $6$
B. $6\sqrt3$
C. $-6\sqrt3$
D. $3\sqrt3$
E. $12$
$P=14$ см байх параллелограммын нэг тал нь 3 см, нэг өнцөг нь $60^\circ$ байв. Талбайг ол.
A. $3\sqrt3$
B. $6$
C. $7$
D. $6\sqrt3$
E. $7\sqrt3$
Параллелограммын хоёр талын урт 2 ба 7, нэг диагоналийн урт 8 бол нөгөө диагоналийн уртыг ол.
A. $8$
B. $8.5$
C. $\sqrt{42}$
D. $10$
E. $\sqrt{11}$
$P=14$ см байх параллелограммын нэг тал нь $4$ см, нэг өнцөг нь $120^\circ$ байв. Талбайг ол.
A. $3\sqrt3$
B. $6$
C. $7$
D. $6\sqrt3$
E. $7\sqrt3$
$ABCD$ параллелограммын $AB$ тал $y=3x+1$ тэгшитгэлтэй, $AD$ тал $4y=x+15$ тэгшитгэлтэй. $AC$ ба $BD$ диагоналиуд нь $E(6.5,7.5)$ цэгт огтлолцдог бол $C$ цэгийн координатыг олоорой.
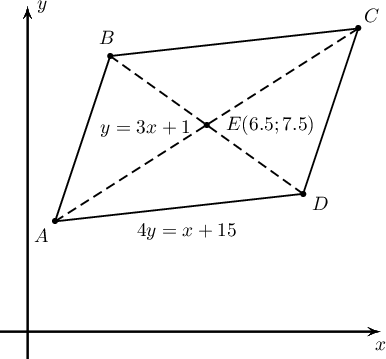

A. $(8;10)$
B. $(1;3)$
C. $(6;8)$
D. $(13;15)$
E. $(12;11)$
$ABCD$ параллелограммын $AB$ тал $y=3x+1$ тэгшитгэлтэй, $AD$ тал $4y=x+15$ тэгшитгэлтэй. $AC$ ба $BD$ диагоналиуд нь $E(6.5,7.5)$ цэгт огтлолцдог бол $C$ цэгийн координатыг олоорой.
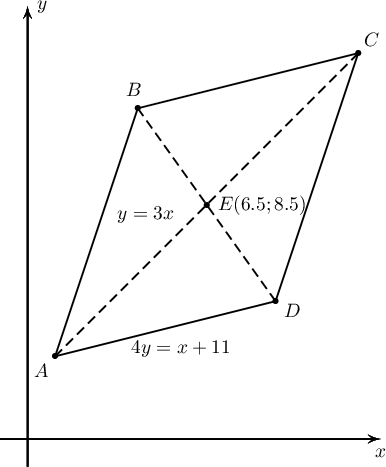

A. $(13;17)$
B. $(1;3)$
C. $(6;8)$
D. $(12;14)$
E. $(8;10)$
$ABCD$ нь $AB=4$, $AD=3$ байх параллелограмм байв. Мөн
$\cos\measuredangle BAD=\dfrac{1}{8}$ байжээ. $\measuredangle BAD$
өнцгийн биссектрисс нь $CD$ талыг $L$ цэгээр, $BC$ талын
үргэлжлэлийг $M$ цэгээр тус тус огтолдог байв.
$AM=\fbox{a}$, $CML$ гурвалжинд багтсан тойргийн радиус
$\dfrac{\fbox{b}\sqrt{\fbox{c}}}{\fbox{de}}$ ба $ADL$ гурвалжны
талбай $\dfrac{\fbox{fg}}{\fbox{hi}}\sqrt{7}$ болно. $BD$
диагональ ба $AL$ хэрчмийн огтлолцлын цэгийг $O$ гэвэл
$\dfrac{BO}{DO}=\dfrac{\fbox{j}}{\fbox{k}}$ байна.
$ABCD$ нь $AB=5$, $AD=3$ байх параллелограмм байв. Мөн
$\cos\widehat{BAD}=\dfrac{1}{8}$ байжээ. $\measuredangle BAD$
өнцгийн биссектрисс нь $CD$ талыг $L$ цэгээр, $BC$ талын
үргэлжлэлийг $M$ цэгээр тус тус огтолдог байв.
$AM=\dfrac{\fbox{a}}{\fbox{b}}\sqrt{7}$ ба $ADL$ гурвалжинд
багтсан тойргийн радиус
$\sqrt{7}\dfrac{\fbox{c}-\sqrt{7}}{\fbox{d}}$, $CML$ гурвалжны
талбай $\dfrac{\fbox{e}\sqrt{\fbox{f}}}{4}$ болно. $BD$ диагональ
ба $AL$ хэрчмийн огтлолцлын цэгийг $O$ гэвэл
$\dfrac{BO}{DO}=\dfrac{\fbox{g}}{\fbox{h}}$ байна.
$A$ оройтой өнцөгт тойрог багтсан ба уг тойрог
дээр орших $C$ цэгээс талуудтай параллель $BC$, $DC$ хэрчмийг
татан $ABCD$ параллелограмм үүсгэв. Дээрх хэрчмүүдийн тойрогтой
огтлолцох цэгүүдийг харгалзан $L$, $M$ гэвэл $\dfrac{CL}{BL}=8$,
$\dfrac{CM}{DM}=3$, $AD=6$ ба $AB>AD$ үед $AB=\fbox{ab}$ байна.
Хэрэв $\cos\hat A=\dfrac{1}{4}$ бол өгсөн тойргийн радиус
$\dfrac{\fbox{cd}}{\fbox{e}}\sqrt{15}$ болно. Мөн
$S_{CLM}=\fbox{f}\sqrt{15}$ байна.
$A$ оройтой өнцөгт тойрог багтсан ба уг тойрог дээр орших $C$
цэгээс талуудтай параллель $BC$, $DC$ хэрчмийг татан $ABCD$
параллелограмм үүсгэв. Дээрх хэрчмүүдийн тойрогтой огтлолцох
цэгүүдийг харгалзан $L$, $M$ гэвэл $\dfrac{CL}{BL}=\dfrac{5}{9}$,
$\dfrac{CM}{DM}=\dfrac{3}{4}$, $AD=4$ ба $AB>AD$ үед $AB=\fbox{a}$
байна. Хэрэв $\cos\hat A=\dfrac{1}{4}$ бол өгсөн тойргийн радиус
$\fbox{b}\sqrt{\fbox{cd}}$ болно. Мөн $S_{CLM}=\fbox{ef}\sqrt{15}$
байна.
$ABCD$ параллелограммын мохоо өнцөгтэй $B$ оройгоос татсан биссектрис $AD$ талыг $F$ цэгт огтолно. $AF:FD=4:3$ ба $AB=12$ бол периметр нь $\fbox{ab}$ байна. Хэрэв $AB=BF$ бол талбай нь $\fbox{cde}\sqrt3$ байна.
$ABCD$ параллелограмын $A$ оройгоос $BC$ талд татсан $AK$ өндөр 4 нэгж, $DC$ талд татсан $AN$ өндөр 4 нэгж ба $KB$ хэрчмийн урт 3 нэгж бол
- $AB$ талын урт $\fbox{a}$
- Гурвалжин $S_{AKB}=\fbox{b}$
- $S_{AKCD}=\fbox{cd}$
- $\dfrac{S_{AKD}}{S_{ABCD}}=\dfrac{\fbox{e}}{\fbox{f}}$
Параллелограмм ба трапецийн талбай
Ромбо
$20$ талтай ромбо өгөгдөв. Хэрвээ ромбын нэг диагонал нь нөгөө диагоналаасаа $\dfrac43$ дахин их бол ромбод багтсан дугуйн талбайг ол.
$ABCD$ ромбо өгөгдөв. $ABD$ гурвалжныг багтаасан тойргийн радиус $R$. Энэ тойрог нь $CBD$ гурвалжинд багтсан тойргийн төвийг дайрна. Ромбын талбайг ол.
Ромбын талууд багтсан дугуйн шүргэлтийн цэгүүдээр $a$ ба $b$ урттай хэрчмүүдэд хуваагджээ. Багтсан дугуйн талбайг ол.
Ромбод багтсан дугуйн талбай нь ромбын талбайгаас 2 дахин бага бол ромбын өнцгүүдийг ол.
Ромбын хурц өнцөг нь $\alpha$. Ромбод багтсан тойргийн талбай нь ромбын талбайн ямар хэсэгтэй тэнцэх вэ?
Ромбын бага диагоналын урт, талын урт ба их диагоналын урт геометр прогресс үүсгэнэ. Ромбын өнцгүүдийг ол.
Ромбын мохоо өнцөг нь хурц өнцгөөсөө $5$ дөхин их. Тэгвэл ромбын тал нь ромбод багтсан тойргийн радиусаас хэд дахин их вэ?
$ABCD$ ромбын $A$ өнцөг нь $\pi/3$. $N$ цэг $AB$ талыг $AN:NB=2:1$ харьцаагаар хуваана. $DNC$ өнцгийн тангенсийг ол.
$KLMN$ ромбын $MN$ тал дээр $C$ цэг оршино. $CN=2$ см, $\angle MNK=120^\circ$, $CKN$ ба $CLM$ өнцгүүдийн косинусын харьцааг ол.
$Q$ талбайтай ромбод $S$ талбайтай тойрог багтсан бол ромбын өнцгүүдийг ол.
$ABCD$ ромбын $B$ орой дахь мохоо өнцгөөс $BM$ ба $BN$ өндөр татав. $BMDN$ дөрвөн өнцөгтөд 1 см радиустай тойрог багтах ба $\angle ABC=2\arcctg2$ бол ромбын талыг ол.
$ABCD$ ромбын $AD$ талын үргэлжлэл дээр $D$ цэгийн талд $K$ оршино. $AC$ ба $BK$ шулуун $Q$ цэгт огтлолцоно. $AK=14$ ба $A, B, Q$ цэгүүд $AK$ хэрчмийн дундаж дээр төвтэй $6$ радиустай тойрог дээр байрлах бол $BK$ хэрчмийг ол.
Ромбын диагоналиудын нийлбэрийг түүний периметрт харьцуулсан харьцаа $1:\sqrt2$-тай тэнцүү бол ромбын хурц өнцгийг ол.
A. $\arccos\frac54$
B. $\arcsin\frac{\sqrt5}{9}$
C. $90^\circ$
D. $\arcsin\frac34$
E. $\arcsin\frac14$
Ромбын диагоналиуд $6, 8$ урттай бол ромбын талын уртыг ол.
A. $6$
B. $\sqrt{14}$
C. $7$
D. $5$
E. $10$
Тал нь диагоналиудынхаа арифметик дундажаас $\sqrt{1.5}$
дахин бага ромбын өнцгүүдийг ол.
A. $45^\circ, 135^\circ$
B. $72^\circ, 108^\circ$
C. $30^\circ, 150^\circ$
D. $60^\circ, 120^\circ$
E. $54^\circ, 126^\circ$
Тал нь диагоналиудынхаа геометр дундаж болдог ромбын
өнцгүүдийг ол.
A. $45^\circ, 135^\circ$
B. $80^\circ, 100^\circ$
C. $60^\circ, 120^\circ$
D. $30^\circ, 150^\circ$
E. $15^\circ, 165^\circ$
Ромбын нэг талын дундаж, орой хоёрыг дайрсан шулуунаар
периметрийн хуваагдсан хоёр хэсгийн нэг 15 см байжээ. Хэрэв
ромбын нэг диагональ 12 см, эсвэл 14 см байсан гэвэл ямар
диагональ, ямар талтай ромбо байж болох вэ?
A. 6, 12
B. 6, 14
C. 6, 10; 6, 14
D. 10, 12; 10, 14
$r$ радиустай тойрог багтаасан $a$ талтай ромбыг $(r,a)$ гэж
тэмдэглэв. Дараахь хосуудын аль нь тийм ромбо тодорхойлох вэ?
A. (4,9)
B. (3,5)
C. (5,8)
D. (9,16)
$Q$ талбайтай ромбын хоёр диагоналийн нийлбэр $m$ бол талын
урт ямар байх вэ?
A. $\sqrt{Q-m^2}$
B. $2\sqrt{Q+m^2}$
C. $\dfrac12\sqrt{m^2-4Q}$
D. $\dfrac12\sqrt{4Q-m^2}$
E. $\sqrt{m^2-Q}$
Диагоналиуд нь $m:n$ харьцаатай ромбын талбай $Q$ бол тал нь
аль вэ?
A. $\sqrt{\dfrac{m^2+n^2}{2mn}Q}$
B. $\dfrac12\sqrt{\dfrac{|m^2-n^2|}{mn}Q}$
C. $\dfrac1m\sqrt{(m^2+n^2)Q}$
D. $\sqrt{\dfrac{m^2+n^2}{mn}Q}$
E. $\sqrt{Q}$
Ромбын диагоналиуд 24 ба 10 бол талын урт нь аль вэ?
A. 26
B. 17
C. 34
D. 13
E. 12
Ромбын диагоналиудын үржвэр нь талын квадратаас $\sqrt3$ дахин их бол өнцгүүд нь аль вэ?
A. $15^\circ,\ 165^\circ$
B. $30^\circ,\ 150^\circ$
C. $45^\circ,\ 135^\circ$
D. $60^\circ,\ 120^\circ$
E. $75^\circ,\ 105^\circ$
Ромбын диагоналиудын үржвэр нь талын квадратаас $\sqrt2$ дахин их бол өнцгүүд нь аль вэ?
A. $15^\circ,\ 165^\circ$
B. $30^\circ,\ 150^\circ$
C. $45^\circ,\ 135^\circ$
D. $60^\circ,\ 120^\circ$
E. $75^\circ,\ 105^\circ$
Квадратын хувьд дараах өгүүлбэрүүдийн аль нь биелэхгүй вэ?
A. Диагональ нь оройн өнцгийн биссектрис болно
B. Диагоналиуд нь харилцан перпендикуляр
C. Эсрэг талууд нь хос хосоороо параллель
D. Диагоналиуд нь тэнцүү
E. Дотоод өнцгүүдийн нийлбэр нь $180^\circ$
Аливаа ромбын хувьд дараах өгүүлбэрүүдийн аль нь биелэхгүй вэ?
A. Бүх талууд нь тэнцүү
B. Бүх өнцгүүд нь тэнцүү
C. Эсрэг талууд нь хос хосоороо параллель
D. Хөрш өнцгүүдийн нийлбэр $180^\circ$
E. Диагоналиуд нь харилцан перпендикуляр
Аливаа параллелограммын хувьд дараах өгүүлбэрүүдийн аль нь биелэхгүй вэ?
A. Хөрш өнцгүүдийн нийлбэр $180^\circ$
B. Дотоод өнцгүүдийн нийлбэр $360^\circ$
C. Эсрэг талууд нь хос хосоороо параллель
D. Эсрэг өнцгүүд нь тэнцүү
E. Диагоналиуд нь харилцан перпендикуляр
Аливаа параллелограммын хувьд дараах өгүүлбэрүүдийн аль нь заавал биелэх вэ?
A. Бүх талууд нь тэнцүү
B. Бүх өнцгүүд нь тэнцүү
C. Эсрэг талууд нь хос хосоороо параллель
D. Эсрэг өнцгүүдийн нийлбэр $180^\circ$
E. Диагоналиуд нь харилцан перпендикуляр
Ромбо дотор тойрог, тойрог дотор квадрат багтав. Хэрэв квадратын талбай ромбын талбайгаас 4 дахин бага бол ромбын бага өнцөг нь $\fbox{ab}^\circ$, их өнцөг нь $\fbox{cde}^\circ$ байна.
Ромбо дотор $r$ радиустай тойрог, тойрог дотор квадрат багтав. Хэрэв квадратын талбай ромбын талбайгаас 4 дахин бага бол ромбын бага өнцөг нь $\fbox{ab}^{\circ}$ (7 оноо) байна.
Төсөөтэй дүрсүүдийн периметр ба талбайн харьцаа
Трапец
Адил хажуут трапецийн талбай $S$. Хажуу талуудын эсрэг орших, диагоналуудын хоорондох өнцөг $\alpha$ бол трапецийн өндрийг ол.
Адил хажуут трапецад $r$ радиустай тойрог багтав. Бага суурийн урт нь өндрөөс хоёр дахин бага бол талбайг ол.
$ABCD$ трапецийн $AD$ суурьт налсан өнцгүүдийн нийлбэр $90^\circ$. Суурийн уртууд $7$ ба $3$ бол сууриудын дунджуудыг холбосон хэрчмийн уртыг ол.
Трапецийн сууриуд нь $a$, $b$. Түүний диагоналиудын огтолцлыг дайрсан суурьтай параллель шулууны хажуу талуудтай огтолцход үүсэх хэрчмийн уртыг ол.
Суурийн өнцгүүд нь $\alpha$, $\beta$ байх трапец тойрогт багтав. Трапецийн талбайг тойргийн талбайд харьцуулсан харьцааг ол.
Адил хажуут трапецийн периметр түүнд багтсан тойргийн уртаас хоёр дахин их. Трапецийн суурийн өнцгийг ол.
$ABCD$ трапецийн $AC, BD$ диагоналууд $F$ цэгт огтлолцоно. $C$ оройг дайруулан $AD$ хажуутай параллель шулуун татахад $BD$ талтай $L$ цэгт огтлолцов. $DF=BL$ бол $AB:CD$-г ол.
$a$, $b$ сууриудтай тэгш өнцөгт трапецад багтсан дугуйн талбайг ол.
Тэгш өнцөгт трапецад багтсан тойргийн төвөөс түүний налуу хажуугийн төгсгөлүүд хүртэл $1$ см ба $2$ см зайтай. Трапецийн талбайг ол.
Трапецийн сууриуд $6$ см ба $11$ см, нэг хажуу нь $4$ см. Хэрэв нэг суурьт нь налсан өнцгүүдийн нийлбэр нь $\pi/2$ бол талбайг ол.
$R$ радиустай тойрог багтаасан трапецийн их суурь дахь өнцгүүд $\alpha, \beta$ нь хурц өнцгүүд байв. Трапецийн талбайг ол.
Адил хажуут трапецийн бага суурь нь өндөртэй тэнцүү $h$ байв. Трапецийн хурц өнцөг нь $\alpha$ бол периметрийг нь ол.
Адил хажуут трапецийн сууриуд $a$, $b$ ба диагоналиуд перпендикуляр бол талбайг ол.
Адил хажуут трапецийн хурц өнцөг нь $\alpha$ ба периметр нь $p$. Трапецийн өндөр $h$ бол талбайг нь ол.
Тойрогт багтсан трапецийн нэг тал нь багтаасан тойргийн диаметр болж байв. Хэрэв мохоо өнцөг нь $\alpha$ бол багтаасан дугуйн талбайг трапецийн талбайд харьцуулсан харьцааг ол.
Адил хажуут $ABCD$ трапецийн $AB$ хажуу тал болон $BC$ бага суурийн урт $a=2$ см, $BD$ нь $AB$-тэй перпиндикуляр байв. Трапецийн талбайг ол.
Адил хажуут трапецийн сууриуд нь 21 ба 9, өндөр нь 8 бол багтаасан тойргийн радиусыг ол.
Адил хажуут трапецад 2 радиустай тойрог багтав. Хэрэв хажуу талуудын урт нь 10 бол талбайг нь ол.
Хурц өнцөг нь $30^\circ$ байх адил хажуут трапецад багтсан тойргийн радиус $2$ см байв. Трапецийн дундаж шугамын уртыг ол.
Трапецийн диагоналууд нь $7$ см, $8$ см, сууриуд нь $3$ см, $9$ см бол талбайг ол.
Трапецийн сууриудын урт $10$ ба $24$, хажуу талуудын урт $13$ ба $15$ бол түүний талбайг ол.
Адил хажуут трапецийг багтаасан тойргийн радиус $R$, хажуу талыг их суурьт харьцуулсан харьцаа өгөгдсөн $k$ тоотой тэнцүү бол бага суурийн уртыг ол.
Адил хажуут трапецийн хажуу талын урт $c$, диагоналын урт нь $l$ бөгөөд талбайг $3:5$ харьцаанд хуваадаг. Трапецийн сууриудыг ол.
Трапецийн $AB$, $CD$ хажуу талуудын үргэлжилж $E$ цэгт огтлолцдог. $O$ цэг нь $ADE$ гурвалжныг багтаасан тойргийн төв. Хэрэв $A$, $B$, $C$, $D$, $O$ цэгүүд нэг тойрог дээр байрладаг бөгөөд уг тойргийн радиус нь багтаасан тойргийн радиусаас $\sqrt3$ дахин бага бол трапецийн хурц өнцөг $A$-ийн хэмжээг ол.
$4$ см, $16$ см сууриудтай трапецад тойрог багтсан бол трапецийн талбайг ол.
Адил хажуут трапец тойрогт багтсан бөгөөд дундаж шугамын урт $5$, хурц өнцгийн синус нь $0,8$-тай тэнцүү. Трапецийн талбайг ол.
Трапецийн дунд шугам $10$-тай тэнцүү бөгөөд трапецийн талбайг $3:5$ харьцаагаар хуваадаг. Трапецийн сууриудын уртыг ол.
Трапецийн суурийн уртууд $a$ ба $b$ $(a>b)$, их суурь ба хажуу талуудын хоорондох өнцөг $\alpha$, $\beta$ бол трапецийн талбайг ол.
$S=20$ см.кв талбайтай трапецад $r=2$ см радиустай тойрог багтсан байв. Трапецийн талуудын уртыг ол.
Тэгш өнцөгт трапецад багтсан тойргийн төв нь хажуу талын төгсгөлөөс $4$ ба $8$ см-ээр алслагдсан бол трапецийн дундаж шугамыг ол.
$r=4$ радиустай тойрогт адил хажуут трапец багтсан ба трапецийн дундаж шугамын урт $10$ см. Трапецийн хажуу талуудын уртыг ол.
Тойрог багтаасан адил хажуут трапецийн сууриуд нь $8$ см ба $2$ см. Багтсан тойргийн уртыг ол.
Адил хажуут трапецийн дундаж шугам $d$. Харин диагоналиуд нь харилцан перпендиклер бол трапецийн талбайг ол.
$ABCD$ трапецийн $AB$ хажуу талын урт $4$, $BAD$-ийн өнцгийн биссектрис нь $BC$ шулууныг $E$ цэгт огтолно. $ABE$ гурвалжинд багтсан тойргийн төв $O$ бөгөөд уг тойрог $AB$ талыг $M$, $BE$ талын $N$ цэгт шүргэнэ. $MN=2$ бол $MNO$ өнцгийн хэмжээг ол.
Хэрэв багтаасан адил хажуут трапецийн периметр $2$ см, хурц өнцөг нь $30^\circ$ бол уг трапецад багтсан тойргийн радиусыг ол.
Трапецийн параллель талууд $25$ ба $4$-тэй тэнцүү. Параллель биш талууд нь $20$ ба $13$ бол трапецийн өндрийг ол.
Адил хажуут трапецийн диогналиуд нь харилцан перпендикуляр, өндөр нь $10$ бол талбайг ол.
Тэгш өнцөгт трапецийн талбай нь $S$. Хурц өнцөг нь $\alpha$. Хэрэв бага диагонал нь их, суурьтайгаа тэнцүү бол өндрийг ол.
$2$ см радиустай тойргийг $20$ см.кв талбайтай адил хажуут трапец багтаасан бол трапецийн талуудыг ол.
Трапецийн сууриуд $4$ см ба $10$ см, нэг хажуу тал нь бага суурьтайгаа $150^\circ$-ын өнцөг үүсгэнэ. Трапецийн талбай $S=21$ см.кв бол уг хажуу талыг ол.
Тэгш өнцөгт трапецийн их диагонал нь $24$ ба хурц өнцгийн биссектрис болно. Хэрэв мохоо өнцгийн оройгоос диагонал хүртэлх зай $9$ см бол трапецийн талбайг ол.
Тэгш өнцөгт трапецын дундаж шугам $13,5$. Бага диагонал нь мохоо өнцөгийн биссектрис бөгөөд урт нь $12$ бол трапецын талуудыг ол.
Адил хажуут трапецийн диагонал $5$, талбай $S=12$ см.кв бол өндрийг ол.
$ABCD$ трапецийн сууриуд $BC, AD$ ба $\angle ACD=\angle ABC$-тэй тэнцүү. $BC=12$, $AD=27$ бол $AC$-г ол.
Трапецийн сууриуд нь 15 ба 5 см, хажуу талууд нь 8 ба 6 см бол талбайг ол.
Тойрог багтаасан адил хажуут трапецийн 2 диагонал $AD$ суурьтай тэнцүү. Суурийн өнцгийг ол.
$32$ см.кв талбайтай $ABCD$ трапецийн $AD$ ба $BC$ сууриудын харьцаа $5:1$. $M$ ба $N$ нь харгалзан $AB$, $CD$ хажуу талуудын дундаж цэгүүд. $AN$ ба $DM$ хэрчмүүд $K$ цэгт, $BN$ ба $CM$ хэрчмүүд $E$ цэгт огтлолцдог бол $MENK$ дөрвөн өнцөгтийн талбайг ол.
Трапецийн хажуу талуудын урт $1$ ба $15$. Энэ трапецад тойрог багтааж болно. Дундаж шугам нь трапецыг талбайнуудынх нь харьцаа $5/11$-тай тэнцүү хэсгүүдэд хуваана. Сууриудын уртыг ол.
Адил хажуут трапецийн дундаж шугам $5$ см ба трапецийн талбайг $7/13$ харьцаатай хэсгүүдэд харьцана. Хэрэв уг трапецад тойрог багтааж болох бол өндрийг ол.
Адил хажуут трапецийн хажуу талын урт нь дундаж шугамтай тэнцүү, периметр нь $48$ см бол хажуу талын уртыг ол.
Тойрог багтаасан адил хажуут трапецийн талбай $32$ см.кв, суурийн өнцөг нь $30^\circ$ бол хажуу талуудын уртыг ол.
Адил хажуут трапецийн бага суурийн урт $1$-тэй тэнцүү ба түүнд багтсан тойргийн радиус $1$ бол талбайг ол.
Адил хажуут трапецийн хажуу талууд нь бага сууриас $3$ дахин урт. Энэ трапецийн мохоо өнцгийн биссектрисүүд нь суурь дээр орших цэгээр огтлолцоно. Трапецийн талбай ба бага суурь ба дээрх биссектрисүүдээр үүсэх гурвалжны талбайн харьцааг ол.
Адил хажуут трапецийн сууриуд $BC=18$, $AD=32$ ба уг трапецад тойрог багтдаг бол трапец ба багтсан дугуйн талбайг ол.
$3$ радиустай тойрог багтаасан адил хажуут трапецийн хурц өнцөг нь $60^\circ$ бол трапецийн дундаж шугамыг ол.
Трапецийн сууриудын уртын ялгавар $14$, хажуу талуудын урт $13$ ба $15$. Энэ трапецад тойрог багтсан бол трапецийн талбайг ол.
Тойрог багтаасан адил хажуут трапецийн талбай $S$, суурийн хурц өнцөг нь $\alpha$ бол дундаж шугамыг ол.
Багтаасан тойргийн төв нь трапецийн их суурь дээр оршдог бол $12$ ба $15$ см сууриудтай адил хажуут трапецийн хажуу тал ба диагоналыг ол.
$15$ см диаметртэй тойрог багтаасан адил хажуут трапецийн хажуу талууд нь $17$ см бол сууриудыг ол.
Адил хажуут трапецийн өндөр нь $5$, диагонал нь $15$ бол талбайг ол.
$6$ см радиустай тойрог багтаасан адил хажуут трапецийн сууриудын харьцаа нь $9:16$. Трапецийн хажуу талыг ол.
Тэгш өнцөгт трапецад багтсан тойргийн төв нь хажуу талын төгсгөлөөс $8$ ба $4$ см зайтай бол трапецийн дундаж шугамыг ол.
$ABCD$ трапецийн $AB$ хажуу тал дээр $M$ цэг оршино. $BD$ диагонал ба $CM$ хэрчмийн огтлолцол $O$. Хэрэв $AM=MB$, $CD=4OM$ ба $BOM$ гурвалжны талбай $1$ бол $COD$ гурвалжны талбайг ол.
$AD$ ба $BC$ суурьтай $ABCD$ трапец $6$ радиустай тойрогт багтав. Багтаасан тойргийн төв нь $AD$ суурь дээр орших ба $BC=4$ бол трапецийн талбайг ол.
$LM, KN$ сууриудтай $KLMN$ трапец тойрогт багтсан ба тойргийн төв нь $KN$ суурь дээр оршино. $LN=4$, $\angle MNK=60^\circ$ бол трапецийн $LM$ суурийн уртыг ол.
KN ба LM сууриудтай KLMN трапецууд тойрог багтсан. Тойргийн төв KN суурь дээр оршино. Трапецийн KM=4, KL=3 бол LM суурийн уртыг ол.
Тэгш өнцөгт трапецад тойрог багтав. Сууриуд нь $2$ ба $3$ бол тойргийн радиусыг ол.
Трапецийн сууриуд $3$ см ба $4$ см. $6$ см урттай диагонал нь нэг өнцгийнхөө биссектрис болно. Энэ трапец адил хажуут байж болох уу?
Адил хажуут трапецийн диагонал нь $8$ см урттай ба нэг өнцгийнхөө биссектрис болно. Хэрэв нэг суурийн урт нь $5$ бол нөгөөгийх нь урт $4$-өөс бага байж болох уу?
Трапецийн дундаж шугамын урт $20$ ба түүгээр трапецийн талбай $3:5$ харьцаатай хэсгүүдэд хуваагдана. Сууриудыг ол.
Трапецийн диагоналуудын огтлолцлын цэгийг дайруулан суурьтай параллель шулуун татахад тэр нь хажуу талуудыг $E$ ба $F$ цэгүүдээр огтолно. $EF=2$ ба трапецийн сууриудын харьцаа $4$-тэй тэнцүү бол сууриудыг ол.
Трапецийн диогналиудын огтлолцлын цэг $O$-г дайруулан суурьтай нь параллель шулуун татав. Хэрэв дундаж шугамын урт $4/3$ ба $O$ цэг нь трапецийн диогналыг $1:3$ харьцаанд хуваасан бол дээрх шулууны трапецийн хажуу талуудын хоорондох хэсгийн уртыг ол.
Багтаасан адил хажуут трапецийн хажуу тал нь $12$ см бол түүний периметрийг ол.
$ABCD$ трапецийн өндөр нь $7$, $AD$ болон $BC$ сууриудын урт нь $8$ ба $6$. $CD$ тал дээр орших $E$ цэгээс $BE$ рүү шулуун татахад $BE$ шулуун нь $AC$ диагоналыг $AO:OC=3:2$ харьцаагаар $O$ цэгээр огтолно. $OEC$ гурвалжны талбайг ол.
$ABCD$ трапецийн $AD$, $BC$ сууриудын урт харгалзан $4$, $3$ ба $AB=CD$ байв. $M$ ба $N$ цэгүүд $BD$ диагоналд харъяалагдах ба $M$ нь $B$, $N$-ийн хооронд оршино. Түүнчлэн $AM$ ба $CN$ хэрчмүүд перпендикуляр ба $BM:DN=2/3$ бол $CN$ хэрчмийн уртыг ол.
Адил хажуут трапецид $4$ радиустай тойрог багтжээ. Трапецийн хажуу тал $9$ бол талбайг ол.
$28$ см.кв талбайтай адил хажуут трапецид $2$ см радиустай тойрог багтжээ. Трапецийн хажуу талыг ол.
$20$ талбайтай адил хажуут трапеци $2$ радиустай тойрог багтаажээ. Трапецийн хажуу талыг ол.
Диагоналууд нь хоорондоо перпендикуляр трапецийн өндөр нь $4$. Хэрвээ нэг диагонал нь $5$ бол трапецийн талбайг ол.
Адил хажуут трапеци тойрог багтаажээ. $b/a=k$ ба $a$-бага суурь, $b$-хажуу тал бол трапецийн өнцгүүдийн болон $k$-ийн байж болох утгуудыг ол.
Адил хажуут $ABCD$ трапецийн бага суурь болох $BC$-ын дундаж цэг нь $O$ нь $A$ өнцгийн биссектрис болно. $AD=15$ ба өндөр нь $6$ бол трапецийн талбайг ол.
Адил хажуут трапецийн диагонал нь $8$ ба нэг хажуу талтайгаа перпендикуляр. Хэрвээ их суурь нь $10$ бол бага суурийг ол.
Трапецийн их суурь 24 см, диагоналуудын дундаж цэгүүдийн хоорондох зай $4$ см бол бага суурийг ол.
$24$ см радиустай тойрог трапецийн их суурь ба хоёр хажууг шүргэдэг. Хэрэв хажуу талуудын үргэлжлэлийн огтлолцлын цэгээс уг тойргийн төв хүртэл $40$ см бол трапецийн их суурийг ол.
$ABCD$ трапецийн бага суурь $BC=7$ см. $A, C, D$ оройнуудыг дайрсан тойрог $BC$ суурийн үргэлжлэлийг $E$ цэг огтолно. $ED=7\sqrt3$, $\angle EDA=30^\circ$ бол $AB$ хажуу талын уртыг ол.
$ABCD$ тэгш өнцөгт трапец өгөгдөв. $AD$ их суурь нь $24$ ба хурц өнцгийн биссектрис болно. Мохоо өнцгийн оройн цэгээс диагонал хүртэлх зай нь $9$ см бол трапецийн талбайг ол.
Адил хажуут трапецийн хурц өнцөг нь $\alpha$, бага суурь нь хажуу талтай тэнцүү $a$ бол талбайг ол.
Тэгш өнцөгт трапецийн талбай $S\text{ см}^2$. Хэрэв трапецийн хурц өнцөг нь $\alpha$ бөгөөд бага диагонал нь их суурьтай тэнцүү бол трапецийн өндрийг ол.
Адил хажуут трапецийн сууриуд нь $12$ см ба $20$ см. Багтаасан тойргийн төв нь трапецийн их суурь дээр оршино. Трапецийн талбайг ол.
$ABCD$ квадрат өгөгдөв. $AB$, $CD$-гийн дундаж цэгүүд нь харгалзан $E$, $F$ ба $ABCD$ квадратын тал нь $a$. $K$ цэг $CF$ хэрчим дээр, $N$ цэг $AD$ хэрчимд харъяалагдах бөгөөд $EF$, $KN$ хэрмчмүүд $M$ цэгээр огтлолцоно. Хэрвээ $CK:KF=1:5$ ба $EMNA$ трапецийн талбай нь $3/10$ бол $KMF$ гурвалжны талбайг ол.
$ABCD$ трапецийн $AB$ талын дундаж $E$. $ECD$ гурвалжны талбай нь $ABCD$ трапецийн талбайн хагастай тэнцүү болохыг батал.
$a$ ба $b$ суурьтай адил хажуут трапец өгөгджээ. Хэрэв энэ трапецад тойрог багтдаг бол түүний диаметр $\sqrt{ab}$-тэй тэнцүү гэдгийг батал.
Трапецийн гадна талд, түүний $AB$ ба $CD$ сууриуд дээр квадрат байгуулав. Тэдгээрийн төвийг холбож байгаа хэрчим трапецийн диагоналуудын огтлолцлын цэгийг дайрахыг батал.
Трапецийн параллель талуудын нэг дээр $A$ цэг нөгөө дээр $B$ цэг авчээ. $AB$ хэрчим трапецийн дундаж шугамаар таллан хуваагдахыг батал.
$ABCD$ трапецийн $AD$ суурийн урт нь $a$ ба $BC$ сууриас 2 дахин урт, $\angle A=45^\circ$. Хэрэв түүний хажуу талуудаар диаметрээ хийсэн тойргууд бие биенээ шүргэх бол трапецийн талбайг ол.
$ABCD$ трапецийн $AB$, $CD$ хажуу талуудын урт нь харгалзан $8$ см ба $10$ см, $BC$ суурийн урт $2$ см. $ADC$ өнцгийн биссектрис $AB$ талын дунджийг дайрах бол трапецийн талбайг ол.
Адил хажуут трапецад тойрог багтав. Уг тойргийн төвөөс трапецийн диагоналиудын огтолцлын цэг хүртэлх зайг тойргийн радиуст харьцуулсан харьцаа $3:5$. Трапецийн периметрийг багтсан тойргийн уртад харьцуулсан харьцааг ол.
Хэрэв адил хажуут трапецийн өндөр нь $h$, түүнийг багтаасан тойргийн төвөөс хажуу талууд нь $60^\circ$ өнцгөөр харагдах бол талбайг нь ол.
$ABCD$ трапецийн $\angle BAD=90^\circ$, $\angle ADC=30^\circ$. $AD$ хэрчим дээр төвтэй тойрог $AB$, $BC$, $CD$ талуудыг шүргэнэ. Хэрэв энэ тойргийн радиус $R$ бол трапецийн талбайг ол.
Адил хажуут $ABCD$ трапецийн диагонал нь хажуу талдаа перпендикуляр, их суурь нь $a$, бага суурь ба хажуу талын нийлбэр $\dfrac{3a}{4}$. Бага суурийг ол.
Адил хажуут $ABCD$ трапецийн $AC$ диагонал $CD$ хажууд перпендикуляр байв. Хэрэв $AD=a$, $AB^2+BC^2=\dfrac{11}{16}a^2$ бол $BC$-г ол.
$ABCD$ трапецийн их суурь $AD$-ээр диаметрээ хийсэн тойрог $CD$ шулууныг $D$ цэгт шүргэх ба $AB$ талыг $L$ цэгээр огтлох ба $AB=\dfrac{4}{\sqrt3}AL$ байв. Тойргийн радиус $R$, $\angle CAD=45^\circ$ бол трапецийн талбайг ол.
Трапецийн нэг диагонал нь дундаж шугамаа $k$ харьцаанд хуваадаг. Дундаж шугамаар хуваагдсан хэсгүүдийн багынх нь талбай $S$ бол трапецийн талбайг ол.
$ABCD$ трапецийн сууриуд нь $AD$ ба $BC$. $BAD$ өнцөгийн биссектрис $CD$ талын дундаж $M$ цэгийг дайрах ба $AB=5$, $AM=4$ бол $BM$ хэрчмийн уртыг ол.
$M$ ба $N$ цэгүүд нь $ABCD$ трапецийн $BC$ суурь ба $CD$ хажуу дээр орших цэгүүд. $AM$ ба $BN$ шулуунууд $K$ цэгт огтлолцох ба $AK=3KM$, $KN=2BK$ байв. $CN:ND$-г ол.
$ABCD$ трапецийн $AD$ ба $BC$ сууриуд нь $9$ ба $3$. $AB$ талын дундаж $E$, $CD$ талын дундаж $F$. Трапецийн $EF$ дундаж шугам $BAD$ өнцөгийн биссектриcтэй $P$ цэгт, $ADC$ өнцөгийн биссектристэй $Q$ цэгт огтлолцоно. $EQ$, $PQ$ ба $PF$ хэрчмүүд ижил урттай бол трапецийн талбайг ол.
Трапецийн $2$ суурийн уртуудын нийлбэр $9$, харин диагоналууд нь $5$ ба $34$. Их суурьд налсан өнцгүүд нь хурц бол трапецийн талбайг ол.
Трапецийн диагоналын уртууд нь $2\sqrt{61}$ ба $3\sqrt{41}$, суурийн уртууд $10$ ба $15$ байв. Трапецийн талбайг ол. Энэ трапецид тойрог багтааж болох уу? Энэ трапецийг тойрогт багтааж болох уу?
$ABCD$ трапецийн $AB$ суурь нь $CD$ суурь ба $AD$ талаас 2 дахин урт. $AC$ диагоналын урт $a$, $BC$ талын урт $b$ бол трапецийн талбайг ол.
Трапецийн параллель талуудын квадратуудын нийлбэр $288$. Эдгээр талуудтай параллель трапецийн талбайг хагаслан хуваах хэрчмийн уртыг ол.
Адил хажуут $ABCD$ трапецийн $AD$ суурийн урт $14$ ба $BC$ суурийн урт $2$. $AB$, $BC$, $CD$ талуудыг шүргэх тойрог нь хажуу талуудыг шүргэлтийн цэгээр $1:9$ харьцаанд хуваах бол уг тойргийн радиусыг ол.
$\angle D=90^{\circ}$, $BC\parallel AD$ байх $ABCD$ тэгш өнцөгт трапецийн $BD$ диагонал дээр $BQ:QD=1:3$ байхаар $Q$ цэг авав. $Q$ цэгт төвтэй тойрог нь $AD$ шулууныг шүргэж, $BC$ шулууныг $P$ ба $M$ цэгээр огтолно. Хэрэв $BC=9$, $AD=8$, $PM=4$ бол $AB$ талын уртыг ол.
Адил хажуут биш трапецийн $12$ см урттай тал нэг суурьтайгаа $60^\circ$ өнцөг үүсэгдэг. Трапецийн суурийн урт $16$ см ба $40$ см. Сууриудын дундаж цэгүүдийг холбосон хэрчмийн уртыг ол.
< p>< /p>Бодолтыг харах
$AD$ ба $BC$ суурьтай $ABCD$ трапецийн $A$ оройг дайруулан татсан шулуун $BD$ диагоналыг $BE:ED=1:2$ байх $E$ цэгт, $CD$ талыг $CK:KD=1:4$ байх $K$ цэгт огтолсон бол трапецийн сууриудын харьцааг ол.
$AD$ ба $BC$ суурьтай $ABCD$ трапецийн $AC$ ба $BD$ диагоналууд $E$ цэгт огтлолцоно. $EBC$ гурвалжныг багтаасан тойргийн $E$ цэгт татсан шүргэгч шулуун $AD$ талыг $F$ цэгт огтолно. $AF=a$, $AD=b$ ба $A$ цэг $AF$ хэрчимд харъяалагдана гэвэл $EF$-ийг ол.
$ABCD$ трапецийн сууриуд $AD=4$, $BC=1$ ба $\angle A=\arcctg 2$, $\angle D=\arcctg 4$. $E$ диагоналиудын огтлолцлын цэг бол $CBE$ гурвалжинд багтсан тойргийн радиусыг ол.
$ABCD$ трапецийн $AB$ тал нь $BC$ суурьтай перпендикуляр. $C, D$ цэгүүдийг дайрч $AB$ шулууныг $E$ цэгт шүргэх тойрог татав. Хэрэв $AD=4$, $BC=3$ бол $E$ цэгээс $CD$ шулуун хүртэлх зайг ол.
$ABCD$ трапецийн талбай $36$ см.кв. $A$ оройг дайруулан $BD$ диагоналыг $K$ цэгт, $BC$ суурийг $L$ цэгт шүргэх тойрог татав. Хэрэв $BK:KD=1:3$, $BL:LC=2:1$ бол $DKLC$ дөрвөн өнцөгтийн талбайг ол.
$ABCD$ трапецийн $AD$ ба $BC$ сууриудын харьцаа $2:1$. $AB$ хажуу тал дээр $AK:KB=1:2$ байх $K$ цэг, $CD$ тал дээр $CL:LD=1:2$ байх $L$ цэг авав. $KL$ хэрчим $BD$ диагоналыг ямар харьцаагаар хуваах вэ?
$AD$ ба $BC$ суурьтай $ABCD$ трапецийн $A$ өнцгийн биссектрис $CD$ талыг $E$ цэгт огтолно. Хэрэв $AD=2BC$, $AD=AB$ ба трапецийн талбай $18$ см.кв бол $ABE$ гурвалжны талбайг ол.
$ABCD$ трапецийн $CD$ хажуу тал дээр $E$ цэг авав. $BD$ диагонал ба $AE$ хэрчмийн огтлолцлын цэг $O$. Хэрэв $DE:CE=1:2$, $AO=2OE$ ба $AOB$ гурвалжны талбай $1$ бол $DOE$ гурвалжны талбайг ол.
$KLMN$ трапецийн $KN$ суурь, $KM$ диагонал ба $KL$ талын уртууд $a$, харин $LN$ диагоналын урт $b$ байв. $MN$ хажуу талыг ол.
$ABCD$ трапецийн $BD$ диагоналын урт $m$, харин $AD$ хажуу талын урт $n$. Хэрэв $C$ оройгоос гарсан суурь, диагонал, хажуу талын уртууд өөр хоорондоо тэнцүү бол $CD$ суурийн уртыг ол.
$AD$ ба $BC$ суурьтай трапецийг багтаасан тойргийн радиус $5$ см. Хэрэв багтаасан тойргийн төв $AD$ суурь дээр байрлах ба $BC=6$ см бол $AC$ диагоналын уртыг ол.
Тойрог багтааж болох тэгш өнцөгт трапецийн талбай нь 2 суурийнхаа үржвэртэй тэнцүү болохыг батал.
Трапецийн диагоналуудын квадратуудын нийлбэр нь хажуу талуудын квадратуудын нийлбэр дээр сууриудын үржвэрийг 2 дахин нэмсэнтэй тэнцүү болохыг батал.
Трапецийн нэг хажуу тал нь 2 суурьтайгаа перпендикуляр ба урт нь $2a$. Энэ талаар диаметрээ хийсэн тойрог нөгөө хажууг 3 хэсэгт хуваажээ. Энэ хэрчмүүд бага сууриас тооцоход $1:2:2$ харьцаатай байв. Трапецийн талбайг ол.
$ABCD$ адил хажуут трапецийн $AD$ суурийн өнцөг $30^{\circ}$, $AC$ диагонал нь $BAD$ өнцгийн биссектрис. $BCD$ өнцгийн биссектрис $AD$ суурьтай $M$ цэгт огтлолцох ба $BM$ хэрчим $AC$ диагоналтай $N$ цэгт огтлолцоно. Хэрэв $ABCD$ трапецийн талбай $(2+\sqrt{3})$ см.кв бол $ANM$ гурвалжны талбайг ол.
$ABCD$ тэгш өнцөгтийн $C$ орой нь $ABKM$ ($BK\parallel AM$) адил хажуут трапецийн $KM$ тал дээр байв. $AM$ ба $CD$ хэрчмүүд $P$ цэгт огтлолцоно. Хэрэв $AB=2BC$, $AP=3BK$ бол трапецийн өнцөг болон тэгш өнцөгтийн талбайг трапецийн талбайд харьцуулсан харьцааг ол.
$MNPQ$ ($MQ\parallel NP$) трапецийн $NPM$ өнцөг нь $NQM$ өнцгөөс 2 дахин их. $NP=MP=\dfrac{13}{2}$, $MQ=12$ бол трапецийн талбайг ол.
$ABCD$ ($BC\parallel AD$) трапецийн $A$ ба $B$ өнцгийн биссектрисүүд $O$ цэгт огтлолцов. Хэрэв $\angle A=2\arccos\sqrt{\dfrac{5}{6}}$, $OC=\sqrt{7}$, $OD=3\sqrt{15}$, $AD=5BC$ бол $AB$ ба $BC$ талуудын уртыг ол.
Радиус нь 4 байх тойргийг багтаасан тэгш өнцөгт трапецийн хувьд $AD-BC=6$ бол $P_{ABCD}$ периметрийг олоорой.


$ABCD$ трапецийн талбай $48$, $AD$ болон $BC$ сууриудын уртын харьцаа $3:1$. $BC$ суурийн дундаж цэг $N$, $AD$ суурийн дундаж цэг $M$. $AN$ ба $BM$ нь $E$ цэгт, $DN$ ба $CM$ нь $K$ цэгт огтлолцдог бол $ENKM$ дөрвөн өнцөгтийн талбайг ол.
A. $6$
B. $7$
C. $8$
D. $9$
E. $10$
Тойрогт багтаж болох ба түүнийг багтааж болох трапецийн сууриуд 25 ба 9 бол түүний талбайг ол.
A. $255$
B. $256$
C. $257$
D. $258$
E. $259$
Адил хажуут трапецийн диагональ нь хурц өнцгөө таллан хуваадаг ба сууриудын харьцаа $1:2$ бол хурц өнцөг нь хэдэн градус вэ?
A. $75^\circ$
B. $30^\circ$
C. $72^\circ$
D. $45^\circ$
E. $60^\circ$
Адил хажуут трапецийн сууриуд 8 ба 16 нэгж урттай бөгөөд диагональ нь суурийн өнцгөө таллан хуваадаг бол трапецийн талбайг ол.
A. $48\sqrt3$
B. $56\sqrt2$
C. $72$
D. $72\sqrt3$
E. $80$
$ABCD$ трапецийн $AB, CD$ сууриудын урт харгалзан 4 ба 6 см бөгөөд диагоналиуд $O$ цэгт огтолцоно. Хэрэв $AOB$ гурвалжны талбай 4 см.кв бол $AOD$ гурвалжны талбай ол.
A. олох боломжгүй
B. 9
C. 4
D. 6
E. 8
Трапецийн хоёр диагоналиуд хоорондоо перпендикуляр ба тэдгээрийн нэг нь 6 урттай ба нөгөө диагональ нь сууриудтай $30^{\circ}$ өнцөг үүсгэх бол дундаж шугамын уртыг ол.
A. $3$
B. $3\sqrt3$
C. $6$
D. $6\sqrt2$
E. $12$
Трапецийн сууриуд нь 1 ба 3, диагоналиуд нь перпендикуляр бол талбайн боломжит хамгийн их утгыг ол.
A. 3
B. 4
C. 2
D. 6
E. 8
Адил хажуут трапецийн их суурь нь бага сууриасаа 2 дахин урт бөгөөд суурийн өнцөг нь $60^\circ$ бол диагоналиудын хооронд үүсэх хурц өнцгийг ол.
A. $30^\circ$
B. $36^\circ$
C. $45^\circ$
D. $60^\circ$
E. $72^\circ$
$ABC$ тэгш өнцөгт гурвалжны $AB$ катеттай параллел шулуун татахад уг шулуун нөгөө нөгөө катет болон $BC$ гипотенузыг харгалзан $E$, $F$ цэгүүдэд огтлов. $AEFB$ трапецад 1 радиустай тойрог багтах ба $B$ оройгоос татсан шүргэгчийн урт $2$ байсан бол трапецийн талбайг ол.
A. $4$
B. $4.5$
C. $5$
D. $6$
E. $3.5$
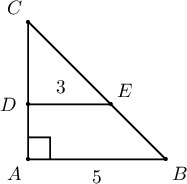
A. $2$
B. $4$
C. $6$
D. $16$
E. $8$
$ABCD$ трапецийн $A,B,C$ гурван орой $D$ төвтэй тойрог дээр
орших бөгөөд $AD^2=AB\cdot BC$ байсан бол $\measuredangle ABC$
өнцөг аль нь вэ? үүнд: $AB\ne BC$ гэж бод.
A. $60^\circ,$
B. $72^\circ$
C. $108^\circ$
D. $120^\circ$
Трапецийн хажуу талууд 1 см, 5 см, нэг суурь 4 см бол нөгөө
суурийн бүхэл утга хэдэн см байж болох вэ?
A. $9$
B. $8$
C. $7$
D. $6$
E. $5$
Трапецийн талууд 2, 3, 4, 5 нэгж бол суурь болж чадах хос нь
аль вэ?
A. $(3,5)$
B. $(4,5)$
C. $(2,5)$
D. $(3,4)$
Тойрогт багтсан трапецийн хажуу тал бага суурьтай тэнцүү
бөгөөд их суурь дахь өнцөг $51^\circ20'$ бол хоёр хажуу болон бага
суурьт тулсан нум хэдэн градус вэ?
A. $77^\circ$
B. $304^\circ$
C. $154^\circ$
D. $231^\circ$
$R$ радиустай тойрогт багтсан $ABCD$ трапецийн диагоналиудын
огтлолцол $M$, түүнээс богино $BC$ суурь хүртэлх зай $a$,
$\measuredangle AMB=60^\circ$ бол богино $BC$ нумын дунджаас $BC$
суурь хүртэлх зай аль нь вэ?
A. $R-\sqrt{R^2-4a^2}$
B. $R-\sqrt{R^2-3a^2}$
C. $R+a-\sqrt{R^2-4a^2}$
D. $a-\sqrt{R^2-4a^2}$
$ABCD$ трапецийн сууриуд $BC$, $AD$. Хэрэв $AB=3$, $BC=4$,
$CD=5$, $DA=8$ байхад $A,B$ оройн дотоод өнцгийн биссектрисүүд $P$
цэгт, $C$, $D$ оройн дотоод өнцгийн биссектрисүүд $Q$ цэгт
огтлолцсон бол $PQ$ зай ямар байх вэ?
A. 2
B. 3
C. 4
D. 5
$ABCD$ трапецийн $AD$ суурь 8 нэгж, хажуу тал $AB=3$ нэгж
урттай бол $D$ оройгоос $B$ оройн дотоод өнцгийн биссектрисийн
$AD$ суурьтай огтлолцсон цэг хүртэлх зай аль нь вэ?
A. 3
B. 4
C. 5
D. 6
$a,b$ сууриудтай тэгш өнцөгт трапецэд багтсан тойргийн
радиусын урт аль нь вэ?
A. $\dfrac{ab}{a+b}$
B. $\dfrac{a^2+b^2}{a+b}$
C. $\dfrac{a^2+ab+b^2}{a+b}$
D. $\dfrac{a^3-b^3}{(a+b)^2}$
E. $\dfrac{a^3+b^3}{(a+b)^2}$
30 дм радиустай тойрог багтаасан тэгш өнцөгт трапецийн хажуу тал $\dfrac{82}3$ м бол сууриудын урт аль нь вэ?
A. $\dfrac{10}3$ м, 40 м
B. 10 м, 30 м
C. $\dfrac{10}3$ м, 30 м
D. 20 м, 40 м
E. 30 м, 40 м
Адил хажуут трапецийн сууриуд 36 см, 1 м бол түүнд багтсан
тойргийн радиусын урт хэд вэ?
A. 16 дм
B. 36 см
C. 3 дм
D. 0.16 м
12 см радиустай тойрог багтаасан адил хажуут трапецийн хажуу
тал 2.5 дм бол сууриудын урт хэд хэд вэ?
A. 18 см, 32 дм
B. 9 см, 16 см
C. 1.8 дм, 32 см
D. 12 см, 24 см
$AB$, $CD$ суурьтай $ABCD$ трапецын диагоналиудын огтлолцлын цэг $O$ байг. $BO=4$, $OD=8$ ба $AB=10$ бол трапецын дундаж шугамын уртыг ол.
A. $7.5$
B. $20$
C. $30$
D. $15$
E. $25$
$AB$, $CD$ суурьтай $ABCD$ трапецын диагоналиудын огтлолцлын цэг $O$ байг. $BO=4$, $OD=8$ ба $AB=20$ бол трапецын дундаж шугамын уртыг ол.
A. 40
B. 20
C. 30
D. 15
E. 25
Трапецийн сууриудын урт нь $3$ ба $10$ нэгж, хоёр хажуу нь $6$ ба $8$ нэгж байсан бол трапецийн өндрийг ол.
A. $\dfrac32\sqrt{15}$
B. $5$
C. $\dfrac{48}{7}$
D. $\sqrt{15}$
E. $\dfrac34\sqrt{15}$
Тойрогт багтаж болох ба тойргийг багтааж болох трапецийн сууриуд $9$ ба $16$ бол түүний талбайг ол.
A. 140
B. 150
C. 160
D. 170
E. 180
$AB$, $CD$ суурьтай $ABCD$ трапецын диагоналиудын огтлолцлын цэг $O$ байг. $BO=4$, $OD=10$ ба $AB=20$ бол трапецын дундаж шугамын уртыг ол.
A. $35$
B. $50$
C. $30$
D. $15$
E. $25$
$AB$, $CD$ суурьтай $ABCD$ трапецын диагоналиудын огтлолцлын цэг $O$ байг. $BO=4$, $OD=6$ ба $AB=20$ бол трапецын дундаж шугамын уртыг ол.
A. $40$
B. $20$
C. $30$
D. $15$
E. $25$
Адил хажуут трапецийн сууриуд 8 ба 4 нэгж урттай бөгөөд диагональ нь суурийн өнцгөө тааллан хуваадаг бол трапецийн талбай хэдэн кв.нэгж байх вэ?
A. $12\sqrt5$
B. $15\sqrt3$
C. $12$
D. $12\sqrt3$
E. $14$
$\angle BAD=90^\circ$ байх тэгш өнцөгт трапецид багтсан тойрог $CD$ хажуу талыг $E$ цэгээр шүргэх бөгөөд $|CE|=4, |DE|=7$ бол тойргийн радиусыг ол.


A. $3\sqrt3$
B. $3\sqrt2$
C. $6$
D. $4\sqrt7$
E. $2\sqrt7$
Тэгш өнцөгт трапецийн бага суурийн урт $\sqrt2$, налуу хажуу ирмэг нь их суурьтай $45^\circ$ өнцөг үүсгэх бөгөөд 4 нэгж урттай байв. Трапецийн талбайг ол.
A. $4$
B. $8$
C. $12$
D. $16$
E. $20$
Адил хажуут $ABCD$ ($AB=CD$) трапецийн периметр $50$, $BC=9$, $AD=21$ байв. $AC$ диагоналын уртыг ол.
A. $13$
B. $14$
C. $15$
D. $16$
E. $17$
Трапецийн талууд 4, 6, 8, 10 нэгж урттай бол сууриудын урт нь аль нь вэ?
A. $(4,6)$
B. $(4,8)$
C. $(4,10)$
D. $(6,8)$
E. $(6,10)$
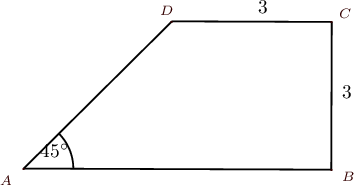
A. $12$
B. $12+3\sqrt2$
C. $9+3\sqrt2$
D. $12+2\sqrt3$
E. $15$
Трапецийн сууриуд нь 4 см болон 18 см-тай тэнцүү, хажуу талууд нь 13 ба 15 см урттай бол трапецийн талбайг ол.
A. $84$
B. $168$
C. $132$
D. $139$
E. $100$
$AD\parallel BC$ байх трапецийн $AB=5$, $BC=9$, $BD=7$, $AD=3$ байв. Трапецийн талбайг ол.
A. $20$
B. $10\sqrt{2}$
C. $15$
D. $30\sqrt{3}$
E. $15\sqrt{3}$
$AD$, $BC$ суурьтай $ABCD$ трапецийн $A$ ба $B$ оройн биссектрисүүдийн огтлолцлын цэг $K$ байв. $ABK$ гурвалжныг багтаасан тойргийн радиус $R=5$ бол $AB$ талын уртыг ол.
A. $10$
B. $2\sqrt{5}$
C. $5$
D. $25$
E. $20$
$AD$, $BC$ суурьтай $ABCD$ трапецийн $A$ ба $B$ оройн биссектрисүүдийн огтлолцлын цэг $K$ байв. $AB$ талын урт $20$ бол $ABK$ гурвалжныг багтаасан тойргийн радиусыг ол.
A. $10$
B. $2\sqrt{5}$
C. $5$
D. $25$
E. $20$
Трапецийн сууриуд $2$, $4$ ба диагоналиуд перпендикуляр бол талбай нь хамгийн ихдээ хэд байх вэ?
A. 3
B. 9
C. 10
D. 8
E. 5
$AD$, $BC$ суурьтай $ABCD$ трапецийн $A$ ба $B$ оройн биссектрисүүдийн огтлолцлын цэг $K$ байв. $ABK$ гурвалжныг багтаасан тойргийн радиус $R=3$ бол $AB$ талын уртыг ол.
A. $3$
B. $2\sqrt{3}$
C. $6$
D. $9$
E. $12$
$ABCD$ трапецийн $AB$, $CD$ хажуу талууд дээр харгалзан $E$, $F$
цэгүүдийг $EF\parallel AD$ байхаар авсан ба $AD=4$, $BC=2$ байв.
$\dfrac{BE}{EA}=3$ бол $EF=\dfrac{\fbox{a}}{\fbox{b}}$ болох ба
$EF$ хэрчим трапецийн талбайг хагаслан хуваах үед
$EF=\sqrt{\fbox{cd}}$ байна. Сүүлийн тохиолдолд трапецийн өндөр
1 бол $S_{APD}=\fbox{e}$ болно. Энд $P$ нь $AB$, $CD$ шулуунуудын
огтлолцлын цэг юм.
$ABCD$ трапецийн $AB$, $CD$ хажуу талууд дээр
харгалзан $E$, $F$ цэгүүдийг $EF\|AD$ байхаар авсан ба $AD=4$,
$BC=2$ байв. $EF$ хэрчим трапецийн диагоналиудын огтлолцлын цэгийг
дайрдаг бол $EF=\dfrac{\fbox{a}}{\fbox{b}}$ болох ба $EF$ хэрчим
трапецийн талбайг хагаслан хуваах үед $EF=\sqrt{\fbox{cd}}$ байна.
Сүүлийн тохиолдолд трапецийн өндөр 1 бол $S_{APD}=\fbox{e}$ болно.
Энд $P$ нь $AB$, $CD$ шулуунуудын
огтлолцлын цэг юм.
$ABCD$ трапецийн хувьд $AD$, $BC$ талууд параллель ба $|AB|=7$,
$|BC|=9$, $|CD|=8$, $|AD|=4$ байв. Трапецийн $A$ оройгоос $BC$ тал
дээр буулгасан өндрийн урт $\fbox{a}\sqrt{\fbox{b}}$ болох тул
талбай нь $\fbox{cd}\sqrt{\fbox{e}}$ байна.
$AB$, $CD$ суурьтай $ABCD$ трапецын талууд $AB=27$, $BC=20$, $CD=2$ ба $DA=15$ байг.
- Трапецын дундаж шугамын урт $\dfrac{\fbox{ab}}{2}$;
- Трапецын өндөр $\fbox{cd}$;
- Трапецын талбай $\fbox{efg}$.
$AB$, $CD$ суурьтай $ABCD$ трапецийн талууд $AB=30$, $BC=20$, $CD=5$ ба $DA=15$ байг.
- Трапецийн дундаж шугамын урт $\dfrac{\fbox{ab}}{2}$
- Трапецийн өндөр $\fbox{cd}$
- Трапецийн талбай $\fbox{efg}$
$AB$, $CD$ суурьтай $ABCD$ трапецын талууд $AB=29$, $BC=20$, $CD=4$ ба $DA=15$ байг.
- Трапецын дундаж шугамын урт $\dfrac{\fbox{ab}}{2}$ /2 оноо/;
- Трапецын өндөр $\fbox{cd}$ /3 оноо/;
- Трапецын талбай $\fbox{efg}$ /2 оноо/.
$AB$, $CD$ суурьтай $ABCD$ трапецын талууд $AB=28$, $BC=20$, $CD=3$ ба $DA=15$ байг.
- Трапецын дундаж шугамын урт $\dfrac{\fbox{ab}}{2}$ /2 оноо/;
- Трапецын өндөр $\fbox{cd}$ /3 оноо/;
- Трапецын талбай $\fbox{efg}$ /2 оноо/.
$ABCD$ трапецийн сууриуд $BC=2x$, $AD=3x$ урттай бай трапецийн талбай $S_{ABCD}=S$-тэй тэнцүү. Хэрэв $AD$, $BC$ диагоналиуд $M$ цэгт огтлолцох бол
- $S_{ADM}=\dfrac{\fbox{a}}{\fbox{bc}}S$
- $S_{BCM}=\dfrac{\fbox{d}}{\fbox{bc}}S$
- $S_{ABM}=\dfrac{\fbox{e}}{\fbox{bc}}S$
Трапецийн сууриуд $8$ ба $16$, хажуу талууд нь $6$, $10$ бол трапецийн өндөр $\fbox{a}$, дундаж шугам нь $\fbox{bc}$, талбай нь $\fbox{de}$ байна.
$AB$, $CD$ суурьтай $ABCD$ трапецын талууд $AB=27$, $BC=20$, $CD=2$ ба $DA=15$ байг.
- Трапецын дундаж шугамын урт $\dfrac{\fbox{ab}}{2}$;
- Трапецын өндөр $\fbox{cd}$;
- Трапецын талбай $\fbox{efg}$.
Тэгш өнцөгт
$a$, $b$ сууриудтай тэгш өнцөгт трапецад багтсан дугуйн талбайг ол.
Тэгш өнцөгт трапецад багтсан тойргийн төвөөс түүний налуу хажуугийн төгсгөлүүд хүртэл $1$ см ба $2$ см зайтай. Трапецийн талбайг ол.
Тэгш өнцөгт трапецад багтсан тойргийн төв нь хажуу талын төгсгөлөөс $4$ ба $8$ см-ээр алслагдсан бол трапецийн дундаж шугамыг ол.
Тэгш өнцөгт трапецийн талбай нь $S$. Хурц өнцөг нь $\alpha$. Хэрэв бага диагонал нь их, суурьтайгаа тэнцүү бол өндрийг ол.
Тэгш өнцөгт трапецийн их диагонал нь $24$ ба хурц өнцгийн биссектрис болно. Хэрэв мохоо өнцгийн оройгоос диагонал хүртэлх зай $9$ см бол трапецийн талбайг ол.
Тэгш өнцөгт трапецын дундаж шугам $13,5$. Бага диагонал нь мохоо өнцөгийн биссектрис бөгөөд урт нь $12$ бол трапецын талуудыг ол.
Тэгш өнцөгт трапецад багтсан тойргийн төв нь хажуу талын төгсгөлөөс $8$ ба $4$ см зайтай бол трапецийн дундаж шугамыг ол.
Тэгш өнцөгт трапецад тойрог багтав. Сууриуд нь $2$ ба $3$ бол тойргийн радиусыг ол.
$ABCD$ тэгш өнцөгт трапец өгөгдөв. $AD$ их суурь нь $24$ ба хурц өнцгийн биссектрис болно. Мохоо өнцгийн оройн цэгээс диагонал хүртэлх зай нь $9$ см бол трапецийн талбайг ол.
Тэгш өнцөгт трапецийн талбай $S\text{ см}^2$. Хэрэв трапецийн хурц өнцөг нь $\alpha$ бөгөөд бага диагонал нь их суурьтай тэнцүү бол трапецийн өндрийг ол.
$ABCD$ тэгш өнцөгтийн $AB$ тал $6$, $BC$ тал $8$. $AB$ ба $BC$ талууд дээр $MN$ нь $AC$-тэй параллель байхаар $M, N$ цэгүүдийг авав. $AMNCD$ олон өнцөгтийн периметрийг $MBN$ гурвалжны периметрт харьцуулахад $7/3$ гардаг бол $MN$ хэрчмийн уртыг ол.
$ABCD$ тэгш өнцөгт талууд $AB=a$, $AD=b$. $\angle AED=\angle CED$ байхаар $AB$ тал дээр $E$ цэгийг ол.
Тэгш өнцөгтийн талууд $a$ ба $b$. $a$ урттай талаар диаметрээ хийсэн тойрог байгуулав. Уг тойрог тэгш өнцөгтийн диагоналыг ямар урттай хэрчмүүдэд хуваах вэ?
$18$ см.кв талбайтай квадратад тэгш өнцөгт багтаажээ. Квадратын тал бүр дээр тэгш өнцөгтийн орой байрлана. Тэгш өнцөгтийн талуудын харьцаа нь $1:2$ бол тэгш өнцөгтийн талбайг ол.
$24$ см.кв талбайтай квадратад тэгш өнцөгт багтжээ. Квадратын тал бүр дээр тэгш өнцөгтийн орой байрлана. Тэгш өнцөгтийн талуудын харьцаа нь $1:3$ бол тэгш өнцөгтийн талбайг ол.
$\angle D=90^{\circ}$, $BC\parallel AD$ байх $ABCD$ тэгш өнцөгт трапецийн $BD$ диагонал дээр $BQ:QD=1:3$ байхаар $Q$ цэг авав. $Q$ цэгт төвтэй тойрог нь $AD$ шулууныг шүргэж, $BC$ шулууныг $P$ ба $M$ цэгээр огтолно. Хэрэв $BC=9$, $AD=8$, $PM=4$ бол $AB$ талын уртыг ол.
$ABCD$ тэгш өнцөгтийн $A$ ба $B$ оройг тойрог дайрна. Тойргийн диаметр $\sqrt {10}$, $C$ оройгоос уг тойрогт татсан шүргэгчий урт $3$ ба $AB=1$. $BC$-ийн боломжит бүх утгыг ол.
Тойрог багтааж болох тэгш өнцөгт трапецийн талбай нь 2 суурийнхаа үржвэртэй тэнцүү болохыг батал.
$ABCD$ тэгш өнцөгтийг багтаасан тойргийн радиус $R$ бол тойргийн дээрх дурын $M$ цэгийн хувьд $MA^2+MB^2+MC^2+MD^2=8R^2$ болохыг батал.
$ABCD$ тэгш өнцөгтийн $C$ орой нь $ABKM$ ($BK\parallel AM$) адил хажуут трапецийн $KM$ тал дээр байв. $AM$ ба $CD$ хэрчмүүд $P$ цэгт огтлолцоно. Хэрэв $AB=2BC$, $AP=3BK$ бол трапецийн өнцөг болон тэгш өнцөгтийн талбайг трапецийн талбайд харьцуулсан харьцааг ол.
$ABC$ тэгш өнцөгт гурвалжны $AB$ катеттай параллел шулуун татахад уг шулуун нөгөө нөгөө катет болон $BC$ гипотенузыг харгалзан $E$, $F$ цэгүүдэд огтлов. $AEFB$ трапецад 1 радиустай тойрог багтах ба $B$ оройгоос татсан шүргэгчийн урт $2$ байсан бол трапецийн талбайг ол.
A. $4$
B. $4.5$
C. $5$
D. $6$
E. $3.5$

A. $2$
B. $4$
C. $6$
D. $16$
E. $8$
Зурагт өгсөн $CDEF$ тэгш өнцөгтийн талбай $ABCF$ тэгш өнцөгтийнхөөс 2 дахин их байв. Хэрэв $CD=2x+2$ бол $AE=?$
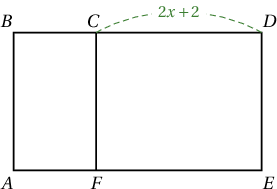

A. $2x+3$
B. $2x+4$
C. $4x+6$
D. $3x+3$
E. $3x+2$
$ABCD$ тэгш өнцөгтийн богино тал $AB=10$ см, диагоналиудын
огтлолцлоос түүний харагдах өнцөг $60^\circ$ бол урт $BC$ талд
тулсан ($A$ цэгийн оршихгүй) $BC$ нумын дунджаас $B$ орой хүртэлх
зай аль нь вэ?
A. 4
B. 6
C. 8
D. 10
$a,b$ сууриудтай тэгш өнцөгт трапецэд багтсан тойргийн
радиусын урт аль нь вэ?
A. $\dfrac{ab}{a+b}$
B. $\dfrac{a^2+b^2}{a+b}$
C. $\dfrac{a^2+ab+b^2}{a+b}$
D. $\dfrac{a^3-b^3}{(a+b)^2}$
E. $\dfrac{a^3+b^3}{(a+b)^2}$
30 дм радиустай тойрог багтаасан тэгш өнцөгт трапецийн хажуу тал $\dfrac{82}3$ м бол сууриудын урт аль нь вэ?
A. $\dfrac{10}3$ м, 40 м
B. 10 м, 30 м
C. $\dfrac{10}3$ м, 30 м
D. 20 м, 40 м
E. 30 м, 40 м
$\angle BAD=90^\circ$ байх тэгш өнцөгт трапецид багтсан тойрог $CD$ хажуу талыг $E$ цэгээр шүргэх бөгөөд $|CE|=4, |DE|=7$ бол тойргийн радиусыг ол.


A. $3\sqrt3$
B. $3\sqrt2$
C. $6$
D. $4\sqrt7$
E. $2\sqrt7$
Тэгш өнцөгт трапецийн бага суурийн урт $\sqrt2$, налуу хажуу ирмэг нь их суурьтай $45^\circ$ өнцөг үүсгэх бөгөөд 4 нэгж урттай байв. Трапецийн талбайг ол.
A. $4$
B. $8$
C. $12$
D. $16$
E. $20$
$ABCD$ тэгш өнцөгт, $AB=AE=ED$ бол $\angle COD=?$

A. $\dfrac{\pi}{18}+\arctg\dfrac12$
B. $45^\circ$
C. $100^\circ$
D. $\dfrac{\pi}{4}+\arctg\dfrac12$
E. $60^\circ$

A. $12$
B. $12+3\sqrt2$
C. $9+3\sqrt2$
D. $12+2\sqrt3$
E. $15$
Аливаа тэгш өнцөгтийн хувьд дараах өгүүлбэрүүдийн аль нь биелэхгүй вэ?
A. Диагоналиуд нь огтлолцлын цэгээрээ хагаслан хуваагдана
B. Диагоналиуд нь харилцан перпендикуляр
C. Эсрэг талууд нь хос хосоороо параллель
D. Диагоналиуд нь тэнцүү
E. Дотоод өнцгүүдийн нийлбэр нь $360^\circ$
Тэгш өнцөгт гурвалжны катетуудаар талаа хийсэн тэгш өнцөгтийн талбай 36 бол катетуудын үржвэрийг ол.
A. $18$
B. $9$
C. $6$
D. $36$
E. $12$
Тэгш өнцөгтийн урт, өргөний харьцаа $3:2$ ба талбай нь $150$ бол талуудыг ол.
A. $50;3$
B. $15;10$
C. $75;2$
D. $30;5$
E. $30;20$
$AB=10$, $BC=8$ байх тэгш өнцөгтийн $BC$, $CD$ талууд дээр $CE=5$,
$CF=4$ байх $E,F$ цэгүүдийг тэмдэглээд $EF$ хэрчим дээр $Q$ цэг
авч $AB$, $AD$ талууд дээр харгалзан $QP$, $QR$ перепендикулярууд
буулгав. $AP=\dfrac{\fbox{ab}}{\fbox{c}}$ үед $APQR$ тэгш
өнцөгтийн талбай $\dfrac{\fbox{def}}{\fbox{gh}}$ гэсэн хамгийн их
утгатай болно. $Q$ цэгээс $BC$, $DC$ талуудад буулгасан
перепендикулярийн суурийг харгалзан $R_1$, $P_1$ гэвэл
$S_{APQR}+S_{QR_1CP_1}$ хамгийн их байх үед
$QR_1=\dfrac{\fbox{ij}}{\fbox{kl}}$ байна.
$AB=12$, $BC=9$ байх тэгш өнцөгтийн $BC$, $CD$ талууд дээр $CE=6$,
$CF=4$ байх $E,F$ цэгүүдийг тэмдэглээд $EF$ хэрчим дээр $Q$ цэг
авч $BC$, $CD$ талууд дээр харгалзан $QP$, $QR$ перепендикулярууд
буулгав. $CP=\fbox{a}$ үед $CPQR$ тэгш өнцөгтийн талбай хамгийн их
утгаа авах ба энэ утга нь $\fbox{b}$ болно. $Q$ цэгээс $AC$, $AD$
талуудад буулгасан перепендикулярийн суурийг харгалзан $P_1$,
$R_1$ гэвэл $S_{AP_1QR_1}+S_{QRCP}$ хамгийн их байх үед
$P_1R_1=\dfrac{\fbox{c}\sqrt{\fbox{def}}}{\fbox{g}}$ байна.