Монгол Бодлогын Сан

$\sqrt3(1-2\sin^2735^{\circ})$ илэрхийллийн утгыг ол.

A.

$-1.5$ B.

$-1$ C.

$0$ D.

$1$ E.

$1.5$

Универсал орлуулга

$\tg\Big(\dfrac{3\pi}{2}+\alpha\Big)=\dfrac12$ бол

$\sin2\alpha$ илэрхийллийн утгыг ол.

A.

$\dfrac45$ B.

$\dfrac14$ C.

$-\dfrac45$ D.

$-\dfrac14$ E.

$\dfrac15$

ЭЕШ 2011 A №15

Хэрэв

$\cos\beta=\dfrac{10}{11}$ ба

$270^\circ\le\beta\le360^\circ$ бол

$\sin2\beta\cdot\cos\beta$ тоон утгыг ол.

A.

$\dfrac{200\sqrt{21}}{1331}$ B.

$\dfrac{100\sqrt{21}}{121}$ C.

$\dfrac{200\sqrt{21}}{121}$ D.

$-\dfrac{200\sqrt{21}}{1331}$ E.

$-\dfrac{100\sqrt{21}}{121}$

ЭЕШ 2011 B №10

$8\cdot\cos10^\circ\cdot\cos20^\circ\cdot\cos40^\circ$ хялбарчил.

A.

$\tg 10^\circ$ B.

$2\tg10^\circ$ C.

$2\ctg10^\circ$ D.

$\frac12\ctg10^\circ$ E.

$\ctg10^\circ$

Косинусыг хагас өнцгийн тангесаар илэрхийлэх

$\tg\alpha=\dfrac12$ бол

$\cos 2\alpha=?$

A.

$0.6$ B.

$\dfrac{3}{4}$ C.

$\dfrac{4}{3}$ D.

$\dfrac{4}{5}$ E.

$-\dfrac{4}{5}$

Универсаль орлуулга

$\tg 20^\circ=a$ бол

$\cos 40^\circ$ аль нь вэ?

A.

$\dfrac{2a}{1+a^2}$ B.

$\dfrac{1-a^2}{1+a^2}$ C.

$\dfrac{1}{\sqrt{1-a^2}}$ D.

$\dfrac{1}{\sqrt{1+a^2}}$ E.

$\dfrac{1}{1+a^2}$

$\sin22.5^\circ$

$\sin22.5^\circ$ -ийн утгыг ол.

A.

$\sqrt2-1$ B.

$\dfrac{\sqrt{2-\sqrt2}}{2}$ C.

$\dfrac{\sqrt{2+\sqrt2}}{2}$ D.

$0.67$ E.

$\sqrt{3}-\sqrt{2}$

Бодлого №5673

$\sin^440^\circ-\cos^440^\circ=?$

A.

$\cos80^\circ$ B.

$\sin80^\circ$ C.

$\cos100^\circ$ D.

$\sin100^\circ$ E.

$1$

Илэрхийллийг хялбарчлах

$\dfrac{1-\cos 25^{\circ}+\cos 50^{\circ}}{\sin 50^{\circ}-\sin 25^{\circ}}-\tg 65^{\circ}$ илэрхийллийг хялбарчил.

A.

$0$ B.

$-1$ C.

$1$ D.

$0.5$ E.

$-0.5$

Универсаль орлуулга

$\dfrac{\pi}{4}< x< \dfrac{\pi}{2}$ ба

$\sin 2x=\dfrac 35$ бол

$\tg x=?$

A.

$3$ B.

$2$ C.

$\dfrac 32$ D.

$\dfrac 52$ E.

$1$

Бодлого №6764

$\pi< x< \dfrac{5\pi}{4}$ ба

$\tg 2x=\dfrac 34$ бол

$\cos x=?$

A.

$-\frac3{\sqrt{10}};$ B.

$-\frac 2{\sqrt{5}};$ C.

$-\frac4{\sqrt{10}};$ D.

$-\frac 3{2\sqrt{5}};$

Бодлого №6814

$8\cos^4x-\cos 4x=1$ тэгшитгэл

$-\dfrac 43< x< 5$ нөхцөлийг хангадаг хэдэн шийдтэй вэ?

A.

$5$ B.

$4$ C.

$3$ D.

$2$ E.

$1$

ЭЕШ 2013 A №4

$\dfrac{1-(\sin 20^\circ-\cos20^\circ)^2}{\cos40^\circ+\sin^220^\circ}$ илэрхийллийг хялбарчлаарай.

A.

$3\tg20^\circ$ B.

$2\ctg20^\circ$ C.

$2\ctg40^\circ$ D.

$2\tg20^\circ$ E.

$2\tg40^\circ$

Тангес тодорхойлолт, давхар өнцгийн томьёо

$2\sin^215^\circ\cdot\ctg15^\circ=?$

A.

$\dfrac12$ B.

$\dfrac{\sqrt3}2$ C.

$\dfrac14$ D.

$\dfrac{\sqrt3}4$ E.

$1$

Хагас өнцгийн тангес

$\alpha$ нь

$180^\circ<\alpha<270^\circ$ ба

$\sin\alpha=-\dfrac{\sqrt5}{3}$ байх өнцөг бол

$\tg\dfrac{\alpha}{2}$ хэд вэ?

A.

$\dfrac{1-\sqrt5}{2}$ B.

$-\sqrt5$ C.

$\dfrac{\sqrt5-1}{2}$ D.

$\sqrt5$ E.

$3$

Давхар өнцгийн синус

$\sin\alpha+\cos\alpha=m$ бол

$\sin2\alpha=?$

A.

$m^2$ B.

$m^2-1$ C.

$\dfrac{m^2-1}{2}$ D.

$-\dfrac{m^2-1}{2}$ E.

$1-m^2$

$\cos2\alpha$

$\sin^2\dfrac{3\pi}{8}-\cos^2\dfrac{3\pi}{8}=?$

A.

$\dfrac{\sqrt2}{2}$ B.

$-1$ C.

$0$ D.

$-\dfrac{\sqrt2}{2}$ E.

$1$

Тангес тодорхойлолт, давхар өнцгийн томьёо

$2\cos^215^\circ\cdot\tg15^\circ=?$

A.

$\dfrac12$ B.

$\dfrac{\sqrt3}2$ C.

$\dfrac14$ D.

$\dfrac{\sqrt3}4$ E.

$1$

Хагас өнцгийн тангес

$\alpha$ нь

$180^\circ<\alpha<270^\circ$ ба

$\cos\alpha=-\dfrac{1}{\sqrt{5}}$ байх өнцөг бол

$\tg\dfrac{\alpha}{2}$ хэд вэ?

A.

$\dfrac{\sqrt5+1}{2}$ B.

$-\dfrac{\sqrt5+1}{2}$ C.

$\dfrac{\sqrt5-1}{2}$ D.

$\dfrac{1-\sqrt5}{2}$ E.

$3$

Давхар өнцгийн косинус

$\sin\alpha=\dfrac23$ бол

$\cos2\alpha=?$

A.

$\dfrac13$ B.

$\dfrac19$ C.

$-\dfrac13$ D.

$-\dfrac19$ E.

$\dfrac29$

$\cos\theta-\sin\theta$ олох

$\cos\theta\cdot\sin\theta=-\dfrac14$ ,

$45^\circ <\theta<135^\circ$ бол

$\cos\theta-\sin\theta$ ол.

A.

$\dfrac{\sqrt3}{\sqrt2}$ B.

$-\dfrac{\sqrt6}{2}$ C.

$0$ D.

$1$ E.

$\dfrac23$

Давхар өнцгийн синус

$4\sin\varphi\cos\varphi\cos2\varphi$ хялбарчил.

A.

$\cos4\varphi$ B.

$\sin2\varphi$ C.

$\cos2\varphi$ D.

$\sin4\varphi$ E.

$\frac12\sin4\varphi$

Тангесийн утга олох

$\dfrac{\pi}2\leq\theta\leq\pi$ байх

$\theta$ -ийн хувьд

$\cos^2\theta-\sin^2\theta=\dfrac13$ бол

$\tg\theta$ -г ол.

A.

$\sqrt2$ B.

$\dfrac1{\sqrt2}$ C.

$1$ D.

$-\dfrac1{\sqrt2}$ E.

$-\sqrt2$

tan utga oloh

$\dfrac{\pi}2\leq\theta\leq\pi$ байх

$\theta$ -ийн хувьд

$\sin^2\theta-\cos^2\theta=\dfrac13$ бол

$\tan\theta$ -г ол.

A.

$\sqrt2$ B.

$\frac1{\sqrt2}$ C.

$1$ D.

$-\frac1{\sqrt2}$ E.

$-\sqrt2$

ЭЕШ 2016 C №9

$2\cos^222.5^\circ-1$ илэрхийллийн утгыг тооцоолоорой.

A.

$\dfrac{\sqrt3}{2}$ B.

$\dfrac{\sqrt2}{2}$ C.

$\dfrac{1}{2}$ D.

$\dfrac{1-\sqrt2}{4}$ E.

$\dfrac{1+\sqrt2}{4}$

ЭЕШ 2016 D №9

$1-2\sin^222.5^\circ$ илэрхийллийн утгыг тооцоолоорой.

A.

$\dfrac{\sqrt3}{2}$ B.

$\dfrac{\sqrt2}{2}$ C.

$\dfrac{1}{2}$ D.

$\dfrac{1-\sqrt2}{4}$ E.

$\dfrac{1+\sqrt2}{4}$

ЭЕШ 2016 A №9

$1-2\sin^215^\circ$ илэрхийллийн утгыг тооцоолоорой.

A.

$\dfrac{1}{2}$ B.

$\dfrac{\sqrt2}{2}$ C.

$\dfrac{\sqrt3}{2}$ D.

$\dfrac{1+\sqrt3}{2}$ E.

$\dfrac{1-\sqrt3}{2}$

ЭЕШ 2016 B №9

$2\cos^215^\circ-1$ илэрхийллийн утгыг тооцоолоорой.

A.

$\dfrac{\sqrt3}{2}$ B.

$\dfrac{\sqrt2}{2}$ C.

$\dfrac{1}{2}$ D.

$\dfrac{1-\sqrt3}{2}$ E.

$\dfrac{1+\sqrt3}{2}$

Хагас өнцгийн томьёо

$1-2\sin^215^\circ$ илэрхийллийн утгыг тооцоолоорой.

A.

$\dfrac{1}{2}$ B.

$\dfrac{\sqrt2}{2}$ C.

$\dfrac{\sqrt3}{2}$ D.

$\dfrac{1+\sqrt3}{2}$ E.

$\dfrac{1-\sqrt3}{2}$

$2\sqrt3(1-2\sin^2735^{\circ})$ илэрхийллийн утгыг ол.

A.

$-3$ B.

$3$ C.

$0$ D.

$2$ E.

$-2$

$2\sqrt3(1-2\cos^2735^{\circ})$ илэрхийллийн утгыг ол.

A.

$-3$ B.

$-2$ C.

$0$ D.

$2$ E.

$3$

Бодлого №24

$2\cos^275^\circ\cdot\tg75^\circ=?$

A.

$\dfrac12$ B.

$\dfrac{\sqrt3}2$ C.

$1$ D.

$\dfrac{\sqrt3}4$ E.

$\dfrac14$

Бодлого №24

$2\cos^222.5^\circ\cdot\tg22.5^\circ=?$

A.

$1$ B.

$\dfrac{\sqrt2}2$ C.

$\dfrac12$ D.

$\dfrac{\sqrt3}4$ E.

$\dfrac14$

Бодлого №13865

$90^\circ<\alpha< 180^\circ$

$\cos \alpha=-\dfrac{4}{5}$ бол

$\sin 2\alpha$ ол.

A.

$1$ B.

$\dfrac{3}{5}$ C.

$-\dfrac{24}{25}$ D.

$\dfrac{24}{25}$ E.

$-\dfrac{3}{5}$

Бодлого №15536

$\sin^480^\circ-\cos^480^\circ=?$

A.

$\cos20^\circ$ B.

$\sin20^\circ$ C.

$\cos80^\circ$ D.

$\sin80^\circ$ E.

$0$

Бодлого №6858

$\bar{a}(2;3)$ ба

$\bar{b}(4;-8)$ векторуудын хоорондох өнцөг

$\alpha$ гэвэл

$1+\cos2\alpha=\dfrac{\fbox{cd}}{\fbox{ab}}$ байна.

Бодлого №12522

$\tg\alpha=3$ бол

$\dfrac{2\sin2\alpha-3\cos2\alpha}{4\sin2\alpha+5\cos2\alpha}$ илэрхийллийн утгыг ол.

Үржвэрийг хялбарчил

$A=\sin\dfrac{\pi}{7}\cdot\sin\dfrac{2\pi}{7}\cdot\sin\dfrac{3\pi}{7}$ илэрхийллийн утгыг ол.

ЭЕШ 2010 A №4

$\dfrac{1-\tg2\alpha+\tg^22\alpha}{1-\ctg2\alpha+\ctg^22\alpha}$ илэрхийллийг хялбарчил.

A.

$\tg^22\alpha$ B.

$\sin2\alpha$ C.

$\cos2\alpha$ D.

$\ctg\alpha$ E.

$1$

ЭЕШ 2014 A №26

$(3+\sqrt5)\sin^218^\circ=?$

A.

$\dfrac12$ B.

$\dfrac{\sqrt3}{2}$ C.

$\dfrac14$ D.

$2\sqrt3$ E.

$1$

$\cos^235^{\circ}+\cos^225^{\circ}-\cos^25^{\circ}$ илэрхийллийн утгыг ол.

A.

$\dfrac 12$ B.

$\dfrac 23$ C.

$\dfrac 34$ D.

$\dfrac 13$ E.

$\dfrac 14$

ЭЕШ 2015 D №31

$\dfrac{\sin10^\circ+\sin20^\circ}{1+\cos 10^\circ+\cos 20^\circ}\cdot\ctg10^\circ$ -ийг хялбарчил.

A.

$\sin10^\circ$ B.

$\tg^210^\circ$ C.

$\dfrac12$ D.

$1$ E.

$\dfrac32$

ЭЕШ 2015 A №31

$\dfrac{\sin36^\circ+\sin18^\circ}{1+\cos18^\circ+\cos36^\circ}\cdot\ctg18^\circ$ хялбарчил.

A.

$\sin18^\circ$ B.

$\tg^218^\circ$ C.

$\dfrac12$ D.

$1$ E.

$\dfrac32$

ЭЕШ 2015 B №31

$\dfrac{\sin72^\circ+\sin36^\circ}{1+\cos 36^\circ+\cos 72^\circ}\cdot\ctg36^\circ$ -ийг хялбарчил.

A.

$\sin36^\circ$ B.

$\tg^236^\circ$ C.

$\dfrac12$ D.

$1$ E.

$\dfrac32$

ЭЕШ 2015 C №31

$\dfrac{\sin14^\circ+\sin7^\circ}{1+\cos 7^\circ+\cos 14^\circ}\cdot\ctg7^\circ$ -ийг хялбарчил.

A.

$\sin7^\circ$ B.

$\tg^27^\circ$ C.

$\dfrac12$ D.

$1$ E.

$\dfrac32$

ЭЕШ 2014 B №26

$(7+3\sqrt5)\sin^418^\circ=?$

A.

$1$ B.

$\dfrac{\sqrt3}{2}$ C.

$\dfrac14$ D.

$\dfrac12$ E.

$\dfrac18$

Бодлого №24

$2\cos^275^\circ\cdot\tg75^\circ=?$

A.

$\dfrac12$ B.

$\dfrac{\sqrt3}2$ C.

$1$ D.

$\dfrac{\sqrt3}4$ E.

$\dfrac14$

Бодлого №24

$2\cos^222.5^\circ\cdot\tg22.5^\circ=?$

A.

$1$ B.

$\dfrac{\sqrt2}2$ C.

$\dfrac12$ D.

$\dfrac{\sqrt3}4$ E.

$\dfrac14$

ЭЕШ 2010 B №4

$\dfrac{\sin2\alpha+\sin6\alpha+\sin10\alpha}{\cos2\alpha+\cos6\alpha+\cos10\alpha}$ илэрхийллийг хялбарчил.

A.

$\tg6\alpha$ B.

$0$ C.

$\cos2\alpha$ D.

$2$ E.

$\sin10\alpha$

Бодлого №13859

$\dfrac{\sqrt{2} \cos\alpha -2\cos(45^\circ +\alpha)}{2\sin (45^\circ +\alpha)-\sqrt{2}\sin\alpha}$ хялбарчил.

A.

$0$ B.

$10$ C.

$1$ D.

$\ctg \alpha$ E.

$\tg \alpha$

Бодлого №622

$\alpha$ ,

$\beta$ нь параллелограммын хөрш өнцгүүд ба

$\dfrac{\sqrt3}{2}(\sin\alpha+\sin\beta)=\sin(\alpha-\beta)$ бол

$\alpha$ ,

$\beta$ -г ол.

Бодлого №790

$\sin\left(x-\dfrac\pi6\right)-\sin\left(x+\dfrac{2\pi}3\right)=\cos\left(x+\dfrac\pi4\right)$ тэгшитгэлийг бод.

Бодлого №791

$\sin3x+\sin7x=2\sin5x$ тэгшитгэлийг бод.

Бодлого №792

$\sin x+\sin3x=\sin2x$ тэгшитгэлийг бод.

Бодлого №793

$\sin3x=\cos x-\sin x$ тэгшитгэлийг бод.

Бодлого №794

$\sin x-\sin3x=\sin4x-\sin2x$ тэгшитгэлийг бод.

Бодлого №795

$\sin x-\sin3x-\sin5x+\sin7x=0$ тэгшитгэлийн

$[0^\circ,360^\circ]$ муж дахь шийдийн тоог ол.

Бодлого №796

$\cos x-\sin\left(5x+\dfrac{3\pi}2\right)=\sqrt3\cos(3x+\pi)$ тэгшитгэлийг бод.

Бодлого №797

$\cos5x-\sin\left(3x-\dfrac\pi2\right)=\sqrt2\cos(4x+3\pi)$ тэгшитгэлийг бод.

Бодлого №798

$\sin3x-\sin7x=\sqrt3\sin2x$ тэгшитгэлийг бод.

Бодлого №799

$\cos8x-4\sin6x-\cos4x=0$ тэгшитгэлийн

$\big[\dfrac\pi2,\dfrac{5\pi}4\big]$ муж дахь шийдүүдийн нийлбэрийг градусаар илэрхийл.

Бодлого №800

$\sin x+\cos x=\sin3x+\cos3x=0$ тэгшитгэлийн хамгийн их сөрөг шийдийг градусаар илэрхийл.

Бодлого №801

$\sin x+\sin2x+\sin3x+\sin4x=0$ тэгшитгэлийг бод.

Бодлого №802

$\cos 2x+\cos4x+\cos x=0$ тэгшитгэлийг бод.

Бодлого №803

$\sin2x+\sin3x+\sin5x=1$ тэгшитгэлийг бод.

Бодлого №804

$\sin(x+30^\circ)+\cos(x=60^\circ)=1+\cos2x$ тэгшитгэлийг бод.

Бодлого №805

$\cos5x-\cos3x+\sin2x=0$ тэгшитгэлийг бод.

Бодлого №806

$\sin x+\sin2x+\sin3x=\cos x+\cos2x+\cos3x$ тэгшитгэлийг бод.

Бодлого №807

$\sin3x=\sin2x+\sin x, \dfrac\pi2< x< \pi$ тэгшитгэлийг бод.

Бодлого №808

$\cos5x+\cos7x=\cos(\pi+6x)$ тэгшитгэлийг бод.

Бодлого №809

$\sqrt{3}\sin2x+\cos x=\cos9x$ тэгшитгэлийн

$\big[0,\dfrac{\pi}3\big]$ муж дахь шийдийн тоог ол.

Бодлого №810

$\sin3x-\sin4x-\cos7x=1$ тэгшитгэлийг бод.

Бодлого №811

$\sin(3\pi2^x)=\cos(\pi2^x)-\sin(\pi2^x)$ тэгшитгэлийг бод.

Бодлого №812

$\cos6x=2\sin\left(\dfrac{3\pi}2+2x\right)$ тэгшитгэлийг бод.

Бодлого №813

$\sin9x=2\sin3x$ тэгшитгэлийг бод.

Бодлого №814

$\dfrac{\cos x-\sin2x}{\cos3x}=1$ тэгшитгэлийг бод.

Нийлбэр, ялгавар, үржвэрийн томьёонууд

Дараах утгыг ол.

$\cos 15^{\circ}-\cos 75^{\circ}$
$\sin40^{\circ}\cdot\cos70^{\circ}\cdot \sin 80^{\circ}$

Бодлого №10579

Нийлбэр, үржвэрийн томъёог хэрэглэж, дараах утгыг ол.

$\sin 75^{\circ}\cdot \cos 15^{\circ}$
$\cos 45^{\circ}\cdot \sin 75^{\circ}$
$\sin 105^{\circ}\cdot \sin 45^{\circ}$
$\cos45^{\circ}\cdot \cos 75^{\circ}$
$\sin 75^{\circ}+\sin 15^{\circ}$
$\sin 75^{\circ}-\sin 15^{\circ}$
$\cos 105^{\circ}+\cos 15^{\circ}$
$\cos 105^{\circ}-\cos 15^{\circ}$

Бодлого №10580

Илэрхийллийг хялбарчил.

$\sin20^{\circ}\cdot \sin 40^{\circ}\cdot \sin80^{\circ}$
$\cos 10^{\circ}+\cos 110^{\circ}+\cos 230^{\circ}$

Синусуудын нийлбэр

$\sin75^\circ+\sin15^\circ=?$

A.

$\dfrac{\sqrt6}{2}$ B.

$\dfrac{\sqrt{3}}{4}$ C.

$1$ D.

$\dfrac{\sqrt6+1}{2}$ E.

$\dfrac{\sqrt{3}+1}{4}$

Нийлбэрийг үржвэрт задлах

$\sin 87^{\circ}-\sin 59^{\circ}-\sin93^{\circ}+\sin61^{\circ}$ -илэрхийллийг хялбарчил.

A.

$\sin89^{\circ}$ B.

$\sin 1^{\circ}$ C.

$\cos29^{\circ}$ D.

$\cos61^{\circ}$ E.

$1$

Хялбарчил

$\cos115^{\circ}-\cos 35^{\circ}+\cos65^{\circ}+\cos 25^{\circ}$ илэрхийллийг хялбарчил.

A.

$\cos5^{\circ}$ B.

$\sin5^{\circ}$ C.

$\cos15^{\circ}$ D.

$\sin 35^{\circ}$ E.

$\sin105^\circ$

Арифметик прогрессийн дараалсан гишүүд

$1+\sin x, \sin^2 x, 1+\sin 3x$ нь

$x$ -ийн ямар утганд арифметик прогрессийн дараалсан гурван гишүүн болох вэ?

A.

$\dfrac{\pi}{2}+2\pi k, \pm\dfrac{\pi}{3}+2\pi k$ B.

$(-1)^{k}\dfrac{\pi}{6}+\pi k, \dfrac{\pi}{2}+\pi k$ C.

$(-1)^{k+1}\dfrac{\pi}{3}+\pi k; \pi +2\pi k$ D.

$\dfrac{\pi}{2}+\pi k, \dfrac{\pi}{6}+\pi k$ E.

$\dfrac{\pi}{2}+\pi k, (-1)^{k+1}\dfrac{\pi}{6}+\pi k$

Бодлого №6794

$1+\cos x, \cos^2 x, 1-\cos 3x$ нь

$x$ -ийн ямар утганд арифметик прогрессийн дараалсан гурван гишүүн болох вэ?

A.

$2\pi k, \pm \frac{\pi}{3}+2\pi k;$ B.

$\pi k, \pm\frac{2\pi}{3}+2\pi k;$ C.

$\frac{\pi}{2}+\pi k, (-1)^k\frac{\pi}{6}+\pi k;$ D.

$(-1)^{k+1}\frac{\pi}{3}+\pi k, \pi+2\pi k; (k\in Z)$

Ялгаврыг үржвэрт задлах

$\cos15^\circ-\sin15^\circ=?$

A.

$\dfrac{\sqrt2}{2}$ B.

$\dfrac{\sqrt3-2}{2}$ C.

$\dfrac{\sqrt2-1}{2}$ D.

$\dfrac{\sqrt2+1}{2}$ E.

$\dfrac{\sqrt6}{2}$

Ялгаврыг үржвэрт хувиргах томьёо

$\sin75^\circ-\sin15^\circ=?$

A.

$\dfrac12$ B.

$\dfrac{\sqrt3}{4}$ C.

$\dfrac{\sqrt2}2$ D.

$\dfrac{\sqrt6-2}{2}$ E.

$\dfrac{\sqrt3-1}{4}$

Бодлого №6893

$\sin x+\sin 2x+\sin 3x+\sin 4x=0$ бодвол

$x_1=\dfrac{\fbox{a}}{\fbox{b}}\pi k$ ,

$x_2=\pi(\fbox{c}k+1)$ ,

$x_3=\dfrac{\pi}{2}(\fbox{d}k+1) (k\in \mathbb Z)$ болно.

Бодлого №551

$\sin\alpha=-\dfrac{1}{3},\cos\beta=-\dfrac23$ ба

$\pi< \alpha,\beta< \dfrac{3\pi}{2}$ бол

$\sin(\alpha+\beta)$ -г ол.

Бодлого №559

$\sin\alpha=\dfrac{8}{17},\sin\beta=\dfrac{15}{17}$ ба

$\alpha$ ,

$\beta\in\big(\frac{\pi}{2};\pi\big)$ бол

$\sin(\alpha+\beta)$ илэрхийллийн утгыг ол.

Бодлого №573

$\sin\alpha=\dfrac45$ ба

$\dfrac{\pi}{2}< \alpha< \pi$ бол

$\cos\Big(\dfrac{\pi}{3}+\alpha\Big)$ илэрхийллийн утгыг ол.

Бодлого №577

$\sin\alpha=a$ ба

$\alpha\in\Big[\dfrac{\pi}{2};\pi\Big]$ бол

$\cos\Big(\alpha+\dfrac{\pi}{4}\Big)$ илэрхийллийн утгыг ол.

Бодлого №578

$\cos\alpha=a$ ба

$\alpha\in\Big(0;\dfrac{\pi}{4}\Big)$ бол

$\sin2\alpha$ ,

$\cos\Big(2\alpha+\dfrac{\pi}{4}\Big)$ илэрхийллийн утгыг ол.

Бодлого №603

$\dfrac{\cos(\alpha+\beta)}{\cos(\alpha-\beta)}=\dfrac13$ бол

$\tg\alpha\tg\beta$ илэрхийллийн утгыг ол.

Бодлого №679

$\dfrac{\sin50^{\circ}\cdot\cos12^{\circ}-\sin40^{\circ}\cos78^{\circ}}{\cos68^{\circ}-\sqrt3\sin68^{\circ}}$ тооцоол.

Бодлого №782

$\cos x\cos2x-\sin x\sin2x=1$ тэгшитгэлийн

$[0, 5]$ муж дахь

$\sin2x>0$ байх шийдийн тоог ол.

Бодлого №783

$\sin\dfrac x2\cos\dfrac{3x}2-\dfrac1{\sqrt3}\sin2x=\sin\dfrac{3x}2\cos\dfrac x2$ тэгшитгэлийг бод.

Бодлого №785

$\cos x\cos2x=\cos3x, 0^\circ< x< 180^\circ$ тэгшитгэлийг бод.

Бодлого №786

$\sin x\sin5x=\cos4x$ тэгшитгэлийг бод.

Бодлого №787

$\dfrac{\cos3x}{\sin2x}+\sin x=0$ тэгшитгэлийг бод.

Бодлого №788

$\dfrac{\sin6x}{\sin x+\cos x}=\dfrac{\cos6x}{\cos x-\sin x}, 0< x< \dfrac\pi2$ тэгшитгэлийг бод.

Бодлого №789

$\left(\sin\Big(x+\dfrac\pi6\Big)+\cos\Big(x+\dfrac\pi3\Big)\right)^2=0,5(1+2\sin^2x)$ тэгшитгэлийн

$x^2-2\pi x\le 0$ байх бүх шийдийг ол.

Бодлого №909

$5\sin x+12\cos x=13$ тэгшитгэлийг бод.

Бодлого №10106

$0^\circ< x< 45^\circ$ нөхцлийг хангах дурын

$x$ -ийн хувьд

$\sin 3x+t\sin 2x>0$ тэнцэтгэл биш биелэх

$t$ -ийн утгын мужийг ол.

Бодлого №10565

Дараах утгыг ол.

$\cos75^{\circ}$ , $\tg75^{\circ}$
$\sin15^{\circ}$ , $\tg15^{\circ}$
$\cos165^{\circ}$ , $\tg165^{\circ}$

Бодлого №10566

$\alpha$ нь I мужийн өнцөг ба

$\sin\alpha=\dfrac5{13}$ ,

$\beta$ нь III мужийн өнцөг ба

$\cos\beta=-\dfrac 35$ гэе.

$\sin(\alpha-\beta)=\ebox$ ,

$\cos(\alpha+\beta)=\ebox$ ,

$\cos(\alpha-\beta)=\ebox.$

Бодлого №10578

$\sin\theta=s$ ,

$\cos\theta=c$ ,

$\tg\theta=t$ гэвэл

$\cos4\theta$ , $\cos5\theta$ -ийг $c$ -ээр илэрхийл.
$\sin 5\theta$ -ийг $s$ -ээр илэрхийл.
$\tg 3\theta$ , $\tg 4\theta$ -ийг $t$ -ээр илэрхийл.

Бодлого №784

$\sin7x\cos x=\sin 6x$ тэгшитгэлийг бод.

A.

$x=\pi n$ B.

$x_1=\dfrac{\pi}{7}+\dfrac{2\pi n}7$ ,

$x_2=2\pi n$ C.

$x_1=\dfrac{\pi}{14}+\dfrac{\pi n}7$ ,

$x_2=\pi n$ D.

$x=\dfrac{\pi}{14}+\dfrac{\pi n}7$ E.

$x=(-1)^k\arcsin\dfrac{6}{7}+\pi k$

ЭЕШ 2006 A №9

$1-2(\sin72^\circ\cos12^\circ-\sin18^\circ\cos78^\circ)^2$ илэрхийллийн утгыг ол.

A.

$0.5$ B.

$1$ C.

$-1$ D.

$0$ E.

$-0.5$

ЭЕШ 2006 C №6

$32\cdot(\cos121^\circ\cdot\cos1^\circ+\sin59^\circ\cdot\cos89^\circ)$ илэрхийллийн утгыг ол.

A.

$32$ B.

$-16$ C.

$16$ D.

$8$ E.

$-8$

ЭЕШ 2007 A1 №24

$\arccos\dfrac35+\arccos\dfrac5{13}=\arccos a$ бол

$a$ -г ол.

A.

$\dfrac{12}{13}$ B.

$\dfrac45$ C.

$\dfrac23$ D.

$-\dfrac{37}{65}$ E.

$-\dfrac{33}{65}$

Нийлбэр ба ялгаврын томьёо

$\sin 76^\circ\cos14^{\circ}-\cos76^\circ\sin 14^\circ=?$

A.

$\cos 62^\circ$ B.

$0$ C.

$1$ D.

$\cos 28^\circ$ E.

$\sin 28^\circ$

Ялгавар өнцгийн косинусын томьёо

$\cos75^\circ\cos15^\circ+\sin 75^\circ\sin15^\circ=?$

A.

$\dfrac{\sqrt3}2$ B.

$\dfrac{\sqrt2}2$ C.

$\dfrac12$ D.

$0$ E.

$-0.5$

Бодлого №5056

$\cos(30^{\circ}+45^{\circ})=\cos 75^{\circ}$ -ийг ашиглан

$\cos 75^\circ$ -ийг ол.

A.

$\displaystyle\frac{\sqrt{6}+\sqrt{2}}{4}$ B.

$\displaystyle\frac{\sqrt{6}-\sqrt{2}}{4}$ C.

$\displaystyle\frac{\sqrt{3}-\sqrt{2}}{2}$ D.

$\displaystyle\frac{\sqrt{3}-\sqrt{1}}{\sqrt{2}}$ E.

$\frac12$

Нийлбэр өнцгийн косинус

$\cos24^\circ\cdot\cos36^\circ-\sin 24^\circ\cdot\sin 36^\circ=?$

A.

$0.5$ B.

$\dfrac{\sqrt2}{2}$ C.

$\cos 12^\circ$ D.

$\dfrac{\sqrt3}{2}$ E.

$\sin 12^\circ$

$\sin 75^\circ$

$\sin75^\circ$ илэрхийллийн утгыг ол.

A.

$\dfrac{\sqrt2}{2}$ B.

$\dfrac{\sqrt{5}}{2}$ C.

$\dfrac{\sqrt6+\sqrt2}{4}$ D.

$\dfrac{\sqrt6-\sqrt2}{4}$ E.

$\dfrac{\sqrt3-\sqrt2}{4}$

Ялгавар өнцгийн синусын томьёо

$\dfrac{\sin3x}{\sin x}-\dfrac{\cos3x}{\cos x}=?$

A.

$-3$ B.

$-1$ C.

$0$ D.

$2$ E.

$3$

Бодлого №6769

$\dfrac{\pi}{2}< \alpha< \pi,$

$\dfrac{\pi}{2}< \beta< \pi,$

$\sin\alpha=\dfrac 45,$

$\cos\beta=-\dfrac{15}{17}$ бол

$\sin(\alpha+\beta)=?$

A.

$-\frac{84}{85};$ B.

$-\frac{7}{17};$ C.

$-\frac{28}{85};$ D.

$-\frac{12}{17};$

Нийлбэрийн косинусын томьёо

$0< \alpha< \dfrac{\pi}{2}$ ,

$\dfrac{3\pi}{2}< \beta< 2\pi$ ,

$\sin\alpha=\dfrac{9}{41}$ ,

$\sin\beta=-\dfrac{40}{41}$ бол

$\cos(\alpha+\beta)=?$

A.

$\dfrac{1600}{1681}$ B.

$\dfrac{720}{1681}$ C.

$\dfrac{360}{1681}$ D.

$\dfrac{369}{1681}$ E.

$\dfrac{365}{1681}$

Косинусын нийлбэр ялгаврын томьёо

$\cos(\alpha+\beta)=\dfrac 13,$

$\cos(\alpha-\beta)=\dfrac 15$ бол

$\tg\alpha\cdot \tg\beta$ -г ол.

A.

$\dfrac 12$ B.

$\dfrac 13$ C.

$-\dfrac12$ D.

$-\dfrac14$ E.

$-\dfrac13$

Ялгавар өнцгийн косинус

$\sin\alpha+\sin\beta=1,$

$\cos\alpha+\cos\beta=\sqrt{2}$ бол

$\cos(\alpha-\beta)=?$

A.

$\dfrac 13$ B.

$\dfrac 12$ C.

$\dfrac{1-\sqrt{2}}{2}$ D.

$\dfrac{\sqrt{2}}{4}$ E.

$-\dfrac12$

ЭЕШ 2011 D №3

Зурагт дүрсэлсэн өнцгийн косинус хэд вэ?

A.

$0$ B.

$\dfrac{1}{\sqrt5}$ C.

$-\dfrac{\sqrt2}{2}$ D.

$\dfrac{\sqrt3}{2}$ E.

$1$

ЭЕШ 2007 A №13

$\cos2\alpha=\dfrac{2}{3}$ бол

$\sin^3\alpha\cdot\sin3\alpha+\cos^3\alpha\cdot\cos3\alpha$ илэрхийллийн утгыг ол.

A.

$\dfrac49$ B.

$\dfrac12$ C.

$\dfrac8{27}$ D.

$\dfrac13$ E.

$\dfrac23$

ЭЕШ 2014 B №22

$\sin2x\cdot\cos4x-\cos2x\cdot\sin4x=0.5$ тэгшитгэлийн хамгийн их сөрөг шийд аль нь вэ?

A.

$-15^\circ$ B.

$-1^\circ$ C.

$-30^\circ$ D.

$-75^\circ$ E.

$-1^\circ$

$\sec$ функц

$\alpha$ ,

$\beta$ нь хурц өнцөг болно.

$\cos\alpha=\dfrac{15}{17}$ ба

$\cos\beta=\dfrac{3}{5}$ бол

$\sin(\alpha+\beta)=?$

A.

$\dfrac{84}{85}$ B.

$\dfrac{56}{57}$ C.

$\dfrac{7}{8}$ D.

$\dfrac{37}{38}$ E.

$\dfrac{99}{100}$

Нийлбэрийн томьёо ба үндсэн адилтгалыг хэрэглэх

$x$ ба

$y$ нь II мужийн өнцгүүд ба

$\sin x=\dfrac{2}{\sqrt{5}}$ ,

$\sin y=\dfrac{3}{5}$ бол

$\sin(x-y)$ хэдтэй тэнцүү вэ?

A.

$-\dfrac{2\sqrt{5}}{25}$ B.

$-\dfrac{\sqrt{5}}{25}$ C.

$-\dfrac{2}{25}$ D.

$-\dfrac{\sqrt{5}}{5}$ E.

$-\dfrac{22}{25}$

$\sec$ функц

$\alpha$ ,

$\beta$ нь хурц өнцөг болно.

$\cos\alpha=\dfrac{15}{17}$ ба

$\cos\beta=\dfrac{3}{5}$ бол

$\cos(\alpha+\beta)=?$

A.

$-\dfrac{13}{85}$ B.

$-\dfrac{16}{57}$ C.

$-\dfrac{3}{8}$ D.

$-\dfrac{17}{38}$ E.

$-\dfrac{33}{100}$

Үндсэн адилтгал, ялгавар өнцгийн синус

$\sin\alpha=-\dfrac{12}{13}$ ,

$\cos\beta=\dfrac{24}{25}$ ба

$0<\beta<\dfrac{\pi}{2}$ ,

$\pi<\alpha<\dfrac{3\pi}{2}$ бол

$\sin(\alpha-\beta)=-0.\fbox{abc}\dots$ байна.

Нийлбэр ялгавар өнцгийн синусын томьёо

$\alpha$ нь I мужийн өнцөг ба

$\sin\alpha=\dfrac{5}{13}$ ,

$\beta$ нь III мужийн өнцөг ба

$\cos\beta=-\dfrac{3}{5}$ гэе.

$\sin(\alpha-\beta)=\dfrac{\fbox{ab}}{\fbox{cd}}$ ,

$\sin(\alpha+\beta)=-\dfrac{\fbox{ef}}{\fbox{gh}}$ .

Бодлого №6861

$\sin\alpha=-\dfrac 35 \Bigl(|\alpha|< \dfrac{\pi}{2}\Bigr), \cos\beta=\dfrac{5}{13} \Bigl(-\pi< \beta< 0\Bigr)$ бол

$\sin(\alpha-\beta)=\dfrac{\fbox{ab}}{\fbox{cd}}$ байна.

Бодлого №6862

$\sin\alpha=-\dfrac 45 \Bigl(|\alpha|< \dfrac{\pi}{2}\Bigr),$

$\sin \beta=-\dfrac{12}{13} \left(\dfrac{\pi}{2}< |\beta|< \pi\right)$ бол

$\cos(\alpha+\beta)=-\dfrac{\fbox{cd}}{\fbox{ab}}$ байна.

Бодлого №6887

$2\sin 17x\cdot \sin 2x=\sqrt{a}-3-\cos 19x$ тэгшитгэл өгөгдөв.

1) Тэгшитгэлийг шийдтэй байлгах

$a$ параметрийн утга нь

$a\in [\fbox{a};\fbox{bc}]$ байна.

2)

$a=16$ үед тэгшитгэлийн шийд нь

$x=\dfrac{\fbox{d}}{\fbox{ef}}k\pi$ болох ба

$[0.5;1.5]$ завсар дахь шийдүүдийн нийлбэр

$\dfrac{\fbox{g}}{\fbox{h}}\pi$ байна.

Бодлого №6888

$2\cos 15x\cdot \cos 3x=\sqrt{a}-2+\cos 18x$ тэгшитгэл өгөгдөв.

1) Тэгшитгэлийг шийдтэй байлгах

$a$ параметрийн утга нь

$a\in [\fbox{a};\fbox{b}]$ байна.

2)

$a=9$ үед тэгшитгэлийн шийд нь

$x=\dfrac{\fbox{c}}{\fbox{d}}k\pi$ болох ба

$[0.4;2.2]$ завсарт шийдүүдийн нийлбэр

$\dfrac{\fbox{e}}{\fbox{f}}\pi$ байна.

Систем тэгшитгэл

$\left\{\begin{array}{c}\sin x\cos y=\dfrac{\sqrt2}{4}\\ \cos x\sin y=\dfrac{\sqrt2}{4}\end{array}\right.$ систем тэгшитгэлийг бодъё:

$\sin(x+y)=\dfrac{\sqrt{\fbox{a}}}{\fbox{b}},\ \sin(x-y)=\fbox{c}$ тул

$x+y=\dfrac{(-1)^n\pi}{\fbox{d}}+\pi n,\ x-y=\pi k$ болно. Эндээс

$x=\dfrac{(-1)^n\pi}{\fbox{e}}+\dfrac{(n+k)\pi}{\fbox{f}}$ ,

$y=\dfrac{(-1)^n\pi}{\fbox{e}}+\dfrac{(n-k)\pi}{\fbox{f}}$ байна.

Бодлого №569

$\tg\Big(\alpha+\dfrac{\pi}{6}\Big)=2$ бол

$\dfrac{\sin\alpha-3\cos\alpha}{0.5\sin\alpha}$ илэрхийллийн утгыг ол.

Бодлого №574

$\ctg\Big(\dfrac{\pi}{4}-\dfrac{\alpha}{2}\Big)=3$ бол

$\sin\alpha$ илэрхийллийн утгыг ол.

Бодлого №587

$\tg(\alpha+\beta)=-1$ ба

$\tg\alpha=3$ бол

$\tg\beta$ илэрхийллийн утгыг ол.

Бодлого №676

$\tg\beta=a$ ,

$2\tg(\alpha-\beta)=\tg\beta-\tg\alpha$ бол

$\ctg(\alpha+\beta)$ - ол.

Бодлого №677

$\tg\beta=b$ ,

$1+\tg\alpha\tg\beta=4\ctg(\alpha-\beta)$ бол

$\tg(\alpha+\beta)$ -г ол.

Нийлбэр, ялгаврын тангес

$\tg\alpha=\dfrac 12$ ,

$\tg\beta=\dfrac 13$ үед

$\tg(\alpha-\beta)=\ebox$ , түүнчлэн

$\alpha$ ,

$\beta$ хурц өнцөг үед

$\alpha+\beta=\ebox$ .

Бодлого №10571

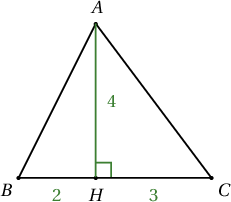
Эгц босоо хананд

$5$ м өндөртэй зураг өлгөв. Зурагны доод ирмэг газраас

$1$ м өндөрт байсан бол хананаас

$2$ м зайд байрлах, газар дээрх цэгээс энэ зурагны харагдах өнцгийг ол.

Бодлого №10578

$\sin\theta=s$ ,

$\cos\theta=c$ ,

$\tg\theta=t$ гэвэл

$\cos4\theta$ , $\cos5\theta$ -ийг $c$ -ээр илэрхийл.
$\sin 5\theta$ -ийг $s$ -ээр илэрхийл.
$\tg 3\theta$ , $\tg 4\theta$ -ийг $t$ -ээр илэрхийл.

Нийлбэр өнцгийн котангес

$0< \alpha< \dfrac{\pi}{2},$

$0< \beta< \dfrac{\pi}{2},$

$\ctg\alpha=4,$

$\ctg\beta=\dfrac 53$ бол

$\alpha+\beta=?$

A.

$\dfrac{\pi}{4}$ B.

$\dfrac{\pi}{3}$ C.

$\dfrac{\pi}{2}$ D.

$\dfrac{\pi}{6}$ E.

$\dfrac{\pi}{12}$

Нийлбэр өнцгийн тангес

$0< \alpha< \dfrac{\pi}{2}$ ,

$0< \beta< \dfrac{\pi}{2}$ ,

$\tg\alpha=\dfrac 12$ ,

$\tg\beta=\dfrac 13$ бол

$\alpha+\beta=?$

A.

$\dfrac{2\pi}{3}$ B.

$\dfrac{\pi}{4}$ C.

$\dfrac{\pi}{2}$ D.

$\dfrac{5\pi}{6}$ E.

$\dfrac{3\pi}{4}$

Нийлбэр өнцгийн тангес

бол

$\tg\measuredangle BAC=?$

A.

$\dfrac12$ B.

$1$ C.

$\dfrac32$ D.

$2$ E.

$\dfrac52$

Нийлбэр, ялгаврын тангес

$\tg\alpha=\dfrac 12$ ,

$\tg\beta=\dfrac 13$ үед

$\tg(\alpha-\beta)=\dfrac{\fbox{a}}{\fbox{b}}$ , түүнчлэн

$\alpha$ ,

$\beta$ хурц өнцөг үед

$\alpha+\beta=\fbox{cd}^\circ$ .

Бодлого №34

$\left(\dfrac13\right)^{-2}+\sin\dfrac{5\pi}{4}+(\sqrt2)^{-1}+\log_{\sqrt2}2$ илэрхийллийн утгыг ол.

Бодлого №171

$\left(\sqrt{\Big(\sqrt5-\dfrac52\Big)^2}-\sqrt[3]{\Big(\dfrac32-\sqrt5\Big)^3}\right)^{\frac12}-\sqrt2\sin\dfrac{7\pi}4$ илэрхийллийн утгыг ол.

Бодлого №172

$\left(\sqrt{\Big(\sqrt5-\dfrac32\Big)^2}+\sqrt[3]{(1-\sqrt5)^3}\right)^{2}+2^{-\frac32}\cos\dfrac{3\pi}4$ илэрхийллийн утгыг ол.

Бодлого №550

$\sin(-330^{\circ})$ илэрхийллийн утгыг ол.

Бодлого №689

$x=313,-313$ утгуудийн аль дээр

$f(x)=\sin x$ функц эерэг утга авах вэ?

Тригонометр функцийн

$\boldsymbol{36^{\circ}}$ -ийн утга

$\cos 36^{\circ}$ -ийн утгыг дараах хоёр аргаар ол.

$\theta=36^\circ$ гээд $\cos\theta$ -ийн хувьд тэгшитгэл зохиож бод.
Адил хажуут гурвалжны суурийн өнцгийн биссектрисийг ашиглан ол.

Дараах тригонометр функцийн утгыг ол.

$\sin 690^{\circ}$
$\cos(-120^{\circ})$
$\tg (-585^{\circ})$

Дараах утгуудыг ол.

$\sin 1020^{\circ}$
$\cos (-240^{\circ})$
$\tg 585^{\circ}$

Бодлого №10099

2 талтай

$ABCDE$ зөв таван өнцөгтийн

$AD$ ,

$CE$ диагоналиудын огтлолцлын цэгийг

$F$ гэе .

$DF$ -ийн уртыг ол.
$\sin 18^{\circ}$ -ийн утгыг ол.
$S_{ABCDE}$ -ийг ол.

Бодлого №10102

Нэгж тойрог дээрх

$P(\cos \theta,\sin \theta);$

$Q(\cos2\theta,\sin 2\theta);$

$R(\cos 4\theta,\sin 4\theta)$ цэгүүдийн хувьд

$PQ^2+QR^2$ -ийн утгын мужийг ол.

$0^{\circ}\le\theta< 360^{\circ}$

Дараах өнцгийн синус, косинус, тангесийн утгыг ол.

$210^{\circ}$
$-45^{\circ}$
$-315^{\circ}$
$720^{\circ}$
$-570^{\circ}$
$2220^{\circ}$

Бодлого №10551

Дараах утгыг ол.

$\sin(-210^{\circ})$
$\cos510^{\circ}$
$\tg(-330^{\circ})$

Бодлого №10583

$0^{\circ}\leq x\leq 180^{\circ}$ ,

$0^{\circ}\leq y\leq 180^{\circ}$ бол

$\sin(x+y)$ ба

$\sin{x}+\sin{y}$ -ийг жиш, тэнцэх нөхцлийг ол.

Бодлого №10598

$\sin 18^{\circ}$ -ийн утгыг ол.

Тригонометр функцийн тодорхойлолт

$\sin 30^\circ$ -ийн утгыг ол.

A.

$0$ B.

$-1$ C.

$0.5$ D.

$\dfrac{\sqrt{2}}2$ E.

$\dfrac{\sqrt{3}}2$

Бодлого №5667

$\sin45^\circ\cdot\cos30^\circ\cdot\sin60^\circ\cdot\ctg60^\circ\cdot\tg30^\circ\cdot\tg60^\circ=?$

A.

$\dfrac{2\sqrt3}{4}$ B.

$\dfrac{4\sqrt3}{7}$ C.

$16$ D.

$-16$ E.

$\dfrac{\sqrt3}{4\sqrt2}$

Тангесийн утга

$\tg 135^\circ=?$

A.

$\sqrt3$ B.

$1$ C.

$0$ D.

$-1$ E.

$-\sqrt{3}$

Дараах тоонуудын аль нь

$0\le\alpha\le\pi$ байх өнцгийн синус болж чадах вэ?

A.

$-0.5$ B.

$0.8$ C.

$\sqrt3$ D.

$-\sqrt3$ E.

$\dfrac{4}{3}$

Тригонометрийн хялбар утгууд

$\tg 60^\circ$ -ийн утга аль нь вэ?

A.

$-\sqrt3$ B.

$-\dfrac{\sqrt3}{3}$ C.

$1$ D.

$\dfrac{\sqrt3}{3}$ E.

$\sqrt3$

Тригонометрийн функцийн зааглагдах чанар

$y=\sin x+\cos x$ функцийн боломжит хамгийн их утга дараах тоонуудын аль нь вэ?

A.

$-2$ B.

$-\sqrt2$ C.

$0$ D.

$\sqrt2$ E.

$2$

Косинусын утга

Дараах тоонуудын аль нь III мужид байрлах

$\alpha$ өнцгийн косинусын утга болж чадах вэ?

A.

$0$ B.

$\dfrac12$ C.

$\dfrac{\sqrt3}{2}$ D.

$-\dfrac{\sqrt3}{2}$ E.

$-\sqrt3$

2018 №A.14

$5\sin\dfrac{\pi}{6}-\ctg\dfrac{\pi}{4}$ утгыг ол.

A.

$\dfrac{5\sqrt{3}}{2}-\dfrac{\sqrt2}{2}$ B.

$3.5$ C.

$\dfrac{5\sqrt{3}}{2}-1$ D.

$1.5$ E.

$2.5$

Бодлого №15523

$\cos45^\circ\cdot\sin30^\circ\cdot\cos60^\circ\cdot\tg60^\circ\cdot\ctg30^\circ\cdot\ctg60^\circ=?$

A.

$\dfrac{\sqrt6}{8}$ B.

$\dfrac{4\sqrt3}{9}$ C.

$3$ D.

$-3$ E.

$\dfrac{\sqrt3}{4}$

Сорилго №2, 2019-2020

$\sin 750^\circ$ -ийн утгыг ол.

A.

$0$ B.

$-1$ C.

$0.5$ D.

$\dfrac{\sqrt{2}}2$ E.

$\dfrac{\sqrt{3}}2$

Бодлого №6863

$3+\dfrac{\cos 15}{|\cos 15|}=\fbox{a}$ байна.

Бодлого №6864

$3+\dfrac{\sin 15}{|\sin 15|}=\fbox{a}$ байна.

Бодлого №492

$\sin^2\alpha+\cos^2\alpha=1$ адилтгалыг батал.

Бодлого №493

$\ctg\alpha-\tg\alpha=2\ctg2\alpha$ адилтгалыг батал.

Бодлого №494

$\dfrac{1}{\tg^2\alpha}-1=\dfrac{2\cos 2\alpha}{1+\sin\left(2\alpha+\dfrac{3\pi}{2}\right)}$ адилтгалыг батал.

Бодлого №495

$\tg\beta\left(1+\dfrac{1}{\cos 2\beta}\right)=\tg 2\beta$ адилтгалыг батал.

Бодлого №496

$\dfrac{\cos2\alpha}{1+\cos2\alpha}=\dfrac{\tg\alpha}{\tg2\alpha}$ адилтгалыг батал.

Бодлого №497

$\dfrac{\sin\alpha+\cos\alpha}{\cos\alpha-\sin\alpha}=\tg2\alpha+\sec2\alpha$ адилтгалыг батал.

Бодлого №498

$\ctg^2\alpha-\ctg^2\beta=\dfrac{\cos^2\alpha-\cos^2\beta}{\sin^2\alpha\sin^2\beta}$ адилтгалыг батал.

Бодлого №499

$\dfrac{2\sin\left(\dfrac{\pi}{4}+\beta\right)-\sqrt2\sin\beta}{2\cos\left(\dfrac{\pi}{6}+\beta\right)-\sqrt3\cos\beta}$ адилтгалыг батал.

Бодлого №500

$\tg^2\left(\dfrac{\pi}{4}-\alpha\right)=\dfrac{1-\sin2\alpha}{1+\sin2\alpha}$ адилтгалыг батал.

Бодлого №501

$\dfrac{2\sin2x+\sin4x}{2(\cos x+\cos3x)}=\tg2x\cdot\cos x$ адилтгалыг батал.

Бодлого №502

$\dfrac{\sin2x-2\sin x}{\sin2x+2\sin x}=-\tg^2\dfrac{x}{2}$ адилтгалыг батал.

Бодлого №503

$\dfrac{1+\sin\alpha-2\sin^2\left(45^{\circ}-\dfrac{\alpha}{2}\right)}{4\cos\dfrac{\alpha}{2}}=\sin\dfrac{\alpha}{2}$ адилтгалыг батал.

Бодлого №504

$\dfrac{1+\sin2\alpha+\cos2\alpha}{1+\sin2\alpha-\cos2\alpha}=\ctg\alpha$ адилтгалыг батал.

Бодлого №505

$\sin^2(30^{\circ}+\alpha)-\sin^{2}(30^{\circ}-\alpha)=\dfrac{\sqrt3\sin2\alpha}{2}$ адилтгалыг батал.

Бодлого №506

$\dfrac{2\tg\alpha}{\tg^2\alpha-1}=\dfrac{2\cos^2\alpha\cdot\tg\alpha}{\sin^2(-\alpha)-\cos^2\alpha}$ адилтгалыг батал.

Бодлого №507

$\dfrac{\sin^2\alpha}{\sin\alpha-\cos\alpha}+\dfrac{\sin\alpha+\cos\alpha}{1-\tg^2\alpha}-\sin\alpha=\cos\alpha$ адилтгалыг батал.

Бодлого №508

$\sin^4\alpha+\cos^4\alpha+\dfrac{1}{2}\sin^22\alpha=1$ адилтгалыг батал.

Бодлого №509

$\dfrac{\sin\alpha+\sin\dfrac{\alpha}{2}}{1+\cos\alpha+\cos\dfrac{\alpha}{2}}=\tg\dfrac{\alpha}{2}$ адилтгалыг батал.

Бодлого №510

$\tg\left(\dfrac{\pi}{4}+\alpha\right)=\dfrac{1+\sin2\alpha}{\cos2\alpha}$ адилтгалыг батал.

Бодлого №511

$(\tg\alpha+\ctg\alpha)^2-(\tg\alpha-\ctg\alpha)^2=4$ адилтгалыг батал.

Бодлого №512

$\sin^6\alpha+\cos^6\alpha+3\sin^2\alpha\cos^2\alpha=1$ адилтгалыг батал.

Бодлого №513

$\dfrac{\sin(\pi+x)\cos\Big(\dfrac{3\pi}{2}-x\Big)\tg\Big(x-\dfrac{\pi}{2}\Big)}{\cos\Big(\dfrac{\pi}{2}+x\Big)\cos\Big(\dfrac{3\pi}{2}+x\Big)\tg(\pi+x)}=\ctg^2x$ адилтгалыг батал.

Бодлого №514

$1+\dfrac{1-\cos^2\alpha+\tg^2\alpha\cos^2\alpha}{\sin^2\alpha}$ илэрхийллийг хялбарчил.

Бодлого №615

$\dfrac{\sin43^{\circ}+\sin17^{\circ}}{2\cos13^{\circ}+3\sin77^{\circ}}$ илэрхийллийн утгыг ол.

Бодлого №623

$\dfrac{\sin(\alpha+\pi)}{\sin(\alpha+\dfrac{3\pi}{2})}+\dfrac{\cos(3\pi-\alpha)}{\cos(\dfrac{\pi}{2}+\alpha)-1}=\dfrac{A}{\cos\alpha}$ адилтгал биелэж байхаар

$A$ -г ол.

Бодлого №624

$\dfrac{1+\cos x}{\sin x}=B\tg\dfrac{x}{2}$ адилтгал биелэж байхаар

$B$ -г ол.

Бодлого №625

$\sin^4\alpha+\dfrac14\sin^2(2\alpha+\pi)=(\sin\alpha)^k$ адилтгал биелэж байхаар

$k$ -г ол.

Бодлого №626

$2\sin4x(\cos^42x-\sin^42x)=\sin kx$ адилтгал биелэж байхаар

$k$ -г ол.

Бодлого №632

$\cos^2x+\cos^2(x+\alpha)-2\cos\alpha\cdot\cos x\cdot\cos(x+\alpha)$ илэрхийлэл

$x$ -ээс хамаарахгүй болохыг батал.

Бодлого №635

$f(x)=\sin^22x+0.5\cos4x+2\sin^2x+\cos2x$ нь

$x$ -ээс хамаарахгүй тогтмол утга авахыг харуулж тэр утгийг ол.

Бодлого №637

$\sin5\alpha\cos\Big(\dfrac{\pi}{2}-4\alpha\Big)+\sin(\pi-4\alpha)\sin3\alpha +\sin2\alpha\cos\Big(\dfrac{7\pi}{2}-\alpha\Big)=2\cos\alpha\sin3\alpha\sin5\alpha$ батал.

Бодлого №638

$\dfrac{-4\tg\alpha}{\tg^2\alpha-1}=\tg\Big(\alpha+\dfrac{\pi}{4}\Big) +\tg\Big(\alpha-\dfrac{\pi}{4}\Big)$ батал.

Бодлого №639

$\dfrac{\sin^2\alpha}{\sin\alpha-\cos\alpha}+\dfrac{\sin\alpha+\cos\alpha}{1-\tg^2\alpha}-\sin\alpha=\cos\alpha$ батал.

Бодлого №640

$\dfrac{1+\cos(2\alpha+630^{\circ})+\sin(2\alpha+810^{\circ})} {1-\cos(2\alpha-630^{\circ})+\sin(2\alpha+630^{\circ})}=\ctg\alpha$ батал.

Бодлого №641

$\cos(\arcsin x)=\sqrt{1-x^2}$ томьёог батлаж биелэх мужийг заа.

Бодлого №642

$\sin(\arccos x)=\sqrt{1-x^2}$ томьёог батлаж биелэх мужийг заа.

Бодлого №643

$\tg(\arcsin x)=\dfrac{x}{\sqrt{1-x^2}}$ ,

$\tg(\arccos x)=\dfrac{\sqrt{1-x^2}}{x}$ томьёог батлаж биелэх мужийг заа.

Бодлого №644

$\sin\Big(\dfrac12\arccos x\Big)=\sqrt{\dfrac{1-x}{2}}$ томьёог батлаж биелэх мужийг заа.

Бодлого №645

$\cos\Big(\dfrac12\arccos x\Big)=\sqrt{\dfrac{1+x}{2}}$ томьёог батлаж биелэх мужийг заа.

Бодлого №646

$\tg(\arcctg x)=\dfrac1x$ ,

$\ctg(\arcctg x)=\dfrac1x$ томьёог батлаж биелэх мужийг заа.

Бодлого №647

$\cos(\arcctg x)=\dfrac{1}{\sqrt{1+x^2}}$ ,

$\sin(\arcctg x)=\dfrac{1}{\sqrt{1+x^2}}$ томьёог батлаж биелэх мужийг заа.

Бодлого №648

$\sin(\arctg x)=\dfrac{x}{\sqrt{1+x^2}}$ томьёог батлаж биелэх мужийг заа.

Бодлого №649

$2(\sin^6\alpha+\cos^6\alpha)-3(\sin^4\alpha+\cos^4\alpha)+1=0$ томьёог батлаж биелэх мужийг заа.

Бодлого №650

$\pi< \alpha< 2\pi$ үед

$\dfrac{\sqrt{1+\cos\alpha}+\sqrt{1-\cos\alpha}}{\sqrt{1+\cos\alpha}-\sqrt{1-\cos\alpha}}=\ctg\Big(\dfrac{\alpha}{2}+\dfrac{\pi}{2}\Big)$ томьёог батлаж биелэх мужийг заа.

Бодлого №651

$\dfrac{\ctg\alpha+\ctg(270^{\circ}+\alpha)}{\ctg\alpha-\ctg(270^{\circ}+\alpha)}-2\cos(135^{\circ}+\alpha)\cos(315^{\circ}-\alpha)=2\cos2\alpha$ батал.

Адилтгал батлах, илэрхийллийн утга олох

$\sin(\alpha+\beta)\cdot \sin(\alpha-\beta)=\sin^2\alpha-\sin^2\beta$ адилтгалыг батал.
$\sin\alpha+\sin\beta=\dfrac 12$ , $\cos \alpha+\cos\beta=\dfrac 23$ бол $\cos(\alpha-\beta)$ -ийн утгыг ол.

Адилтгал батлах

$\triangle ABC$ -ийн өнцгүүд

$A$ ,

$B$ ,

$C$ бол дараах адилтгал биелэхийг батал.

$\sin A+\sin B+\sin C=4\cdot \cos \dfrac A2\cdot \cos\dfrac B2\cdot \cos \dfrac C2$

Илэрхийлэл хялбарчлах ба адилтгал батлах

$\dfrac{\sin \theta}{1+\cos\theta}+\dfrac 1{\tg\theta}=\dfrac 1{\sin \theta}$ адитгалыг батал.
$\sin \theta+\cos \theta=\dfrac 13$ бол $\sin^3 \theta+\cos^3 \theta$ -ийн утгыг ол.

Бодлого №10110

$\cos 5\theta=f(\cos \theta)$ нөхцлийг хангах $f(x)$ функцийг ол.
$\alpha=18^{\circ}$ бол $\cos \alpha\cos 3\alpha\cos7\alpha=\dfrac5{16}$ болохыг батал.

Универсал орлуулга

$90^{\circ}< \alpha< 180^{\circ}$ , $\sin\alpha=\dfrac 35$ бол $\cos2\alpha$ , $\sin2\alpha$ , $\tg\dfrac{\alpha}{2}$ -ийн утгыг ол.
$t=\tg\dfrac{\theta}{2}$ бол дараах адилтгалыг батал. $\sin\theta=\dfrac{2t}{1+t^2}, \cos\theta=\dfrac{1-t^2}{1+t^2}, \tg\theta=\dfrac{2t}{1-t^2}.$

Бодлого №10547

Дараах адилтгалыг батал.

$\sin^4 \theta-\cos^4 \theta=1-2\cos^2 \theta$
$\tg^2 \theta-\sin^2 \theta=\tg^2 \theta\cdot \sin^2 \theta$
$\dfrac{\cos \theta}{1+\sin \theta}+\tg\theta=\dfrac1{\cos \theta}$
$\dfrac{\cos \theta}{1+\sin \theta}+\dfrac{\cos \theta}{1-\sin \theta}=\dfrac2{\cos \theta}$

Бодлого №10567

Дараах адилтгалыг батал.

$\cos(\alpha-\beta)\cdot \cos(\alpha+\beta)=\cos^2\alpha-\sin^2\beta=\cos^2\beta-\sin^2\alpha.$
$\cos x\cdot \sin(y-z)+\cos y\cdot \sin(z-x)+\cos z\cdot \sin(x-y)=0.$

Бодлого №10582

Дараах адилтгал биелэхийг батал.

$A+B+C=360^{\circ}$ бол $\sin A+\sin B+\sin C=4\cdot \sin \dfrac A2\cdot \sin \dfrac B2\cdot \sin \dfrac C2.$
$\triangle ABC$ -ны дотоод өнцгүүдийн хувьд $\cos A+\cos B-\cos C=4\cos \dfrac A2\cdot \cos\dfrac B2\cdot \sin \dfrac C2-1 .$

Бодлого №10596

$\sin x+\sin 3x=a\sin x\cos^2 x$ адилтгал биелэгдэх тогтмол тоо

$a$ -г ол.

Эмхэтгэлийн томьёо

$\sin(\alpha-30^\circ)$ нь аль илэрхийлэлтэй тэнцүү вэ?

A.

$\sin(30^\circ-\alpha)$ B.

$\sin(120^\circ+\alpha)$ C.

$\sin(120^\circ-\alpha)$ D.

$\cos(120^\circ-\alpha)$ E.

$\cos(90^\circ-\alpha)$

Эмхэтгэлийн томьёо

$\sin(\alpha-30^\circ)$ нь аль илэрхийлэлтэй тэнцүү вэ?

A.

$\sin(30^\circ-\alpha)$ B.

$\sin(120^\circ+\alpha)$ C.

$\sin(120^\circ-\alpha)$ D.

$\cos(120^\circ-\alpha)$ E.

$\cos(90^\circ-\alpha)$

Бодлого №515

$(3\sin x+2\cos x)^2+(2\sin x-3\cos x)^2$ илэрхийллийг хялбарчил.

Бодлого №516

$\dfrac{\Big(\sin\dfrac{\alpha}{2}+\cos\dfrac{\alpha}{2}\Big)^2}{1+\sin\alpha}$ илэрхийллийг хялбарчил.

Бодлого №517

$\cos^2(\pi-\alpha)+\cos^2\Big(\dfrac{3\pi}{2}-\alpha\Big)$ илэрхийллийг хялбарчил.

Бодлого №518

$\tg^2(270^{\circ}+\alpha)\sin^2(180^{\circ}+\alpha)$ илэрхийллийг хялбарчил.

Бодлого №519

$\dfrac{1+\tg\alpha}{1-\tg\alpha}-\tg(45^{\circ}+\alpha)$ илэрхийллийг хялбарчил.

Бодлого №520

$1-\sin\alpha\cos\alpha\tg\alpha+\sin^2\alpha+3$ илэрхийллийг хялбарчил.

Бодлого №521

$\dfrac{\tg\alpha+\sin\alpha}{2\cos^2\dfrac{\alpha}{2}}$ илэрхийллийг хялбарчил.

Бодлого №522

$\dfrac{2\sin\alpha-\sin2\alpha}{2\sin\alpha+\sin2\alpha}$ илэрхийллийг хялбарчил.

Бодлого №523

$\dfrac{2(1+\sin2\alpha-\cos2\alpha)}{\sin\alpha(\sin\alpha+\cos\alpha)}$ илэрхийллийг хялбарчил.

Бодлого №524

$\alpha=\dfrac{\pi}{36}$ үед

$\dfrac{\sqrt3\cos3\alpha}{10(\cos9\alpha+\cos3\alpha)}$ илэрхийлэлийн утгийг ол.

Бодлого №525

$\alpha=\dfrac{\pi}{12}$ үед

$\dfrac{1-\sin^42\alpha-\cos^42\alpha}{2\sin^42\alpha}+1$ илэрхийлэлийн утгийг ол.

Бодлого №526

$\alpha=\dfrac{\pi}{3}$ үед

$\dfrac{1+\cos\alpha+\cos2\alpha+\cos3\alpha}{\cos\alpha+2\cos^2\alpha-1}$ илэрхийлэлийн утгийг ол.

Бодлого №527

$\cos2\alpha+\sin2\alpha\cdot\tg\alpha$ илэрхийллийг хялбарчил.

Бодлого №528

$\dfrac{1+\tg x\tg2x}{\tg x+\ctg2x}$ илэрхийллийг хялбарчил.

Бодлого №529

$\cos^42x+6\sin^22x\cos^22x+\sin^42x-2\sin^24x$ илэрхийллийг хялбарчил.

Бодлого №530

$\dfrac{\cos\Big(\dfrac{\pi}{2}-\alpha\Big)\cos\Big(\dfrac{\pi}{2}+\beta\Big)-\cos(\pi-\alpha)\cos(2\pi-\beta)}{\sin\Big(\dfrac{\pi}{2}+\alpha+\beta\Big)}$ илэрхийллийг хялбарчил.

Бодлого №531

$\sin^2\alpha+\sin(60^{\circ}+\alpha)\sin(60^{\circ}-\alpha)$ илэрхийллийг хялбарчил.

Бодлого №532

$\dfrac{(\sin\alpha+\cos\alpha)^2-1}{\tg\Big(\dfrac{\pi}{2}-\alpha\Big)-\sin\alpha\cos\alpha}-2\tg^2\alpha$ илэрхийллийг хялбарчил.

Бодлого №533

$\dfrac{2(\sin2\alpha+2\cos^2\alpha-1)}{\cos\alpha-\sin\alpha-\cos3\alpha+\sin3\alpha}$ илэрхийллийг хялбарчил.

Бодлого №534

$2\sin\alpha\cos\alpha-\dfrac{\sin\alpha-\sin(\pi+3\alpha)+\sin2\alpha}{2\cos\alpha+1}$ илэрхийллийг хялбарчил.

Бодлого №535

$\dfrac{2}{\sin\alpha}-\dfrac{2}{\sin3\alpha}-\dfrac{4\cos2\alpha}{\sin3\alpha}$ илэрхийллийг хялбарчил.

Бодлого №536

$\dfrac{1+\sin\Big(\dfrac{3\pi}{2}+2x\Big)-\sin^2x}{\sin2x\sin\Big(\dfrac{\pi}{2}+x\Big)+\sin x\cos(\pi-2x)}$ илэрхийллийг хялбарчил.

Бодлого №537

$\dfrac{\tg(180^{\circ}-\alpha)\cos(180^{\circ}-\alpha)\tg(90^{\circ}-\alpha)}{\sin(90^{\circ}+\alpha)\ctg(90^{\circ}-\alpha)\tg(90^{\circ}+\alpha)}$ илэрхийллийг хялбарчил.

Бодлого №538

$\dfrac{\sqrt2\cos\alpha-2\cos(45^{\circ}-\alpha)}{2\sin(30^{\circ}+\alpha)-\sqrt3\sin\alpha}+\sqrt2\tg\alpha$ илэрхийллийг хялбарчил.

Бодлого №589

$\dfrac{2\cos^2\alpha-1}{8\tg\Big(\dfrac{\pi}{4}-\alpha\Big)\cos^2\Big(\dfrac{\alpha-\pi}{4}\Big)}$ илэрхийллийн утгыг ол.

Бодлого №591

$\dfrac{2\sin^270^{\circ}-1}{2\ctg115^{\circ}\cdot\cos^2155^{\circ}}$ илэрхийллийн утгыг ол.

Бодлого №595

$\tg\alpha=0.1$ бол

$\dfrac{4\sin(30^{\circ}+\alpha)\sin(30^{\circ}-\alpha)}{\cos^2\alpha}$ илэрхийллийн утгыг ол.

Бодлого №596

$\cos45^{\circ}\cdot\sin3105^{\circ}+\dfrac12\ctg(-315^{\circ})-\cos270^{\circ}$ илэрхийллийн утгыг ол.

Бодлого №597

$\alpha=112^{\circ}30'$ бол

$\ctg\alpha$ илэрхийллийн утгыг ол.

Бодлого №598

$\cos\alpha=0.7$ бол

$\dfrac{\sin\alpha}{\sin\alpha-\cos\alpha\cdot\tg\dfrac{\alpha}{2}}$ илэрхийллийн утгыг ол.

Бодлого №599

$\ctg x=-\dfrac45$ бол

$\dfrac{\sin4x\cdot\cos2x }{(1+\cos2x)(1+\cos4x)}$ илэрхийллийн утгыг ол.

Бодлого №602

$\sin2x=3^{-\frac12}$ бол

$\dfrac{\sin^2(4x-540^{\circ})}{\cos^2(4x-540^{\circ})}$ илэрхийллийн утгыг ол.

Бодлого №604

$\tg\alpha=3$ бол

$\dfrac{\sin\alpha-2\sin2\alpha+3\sin3\alpha}{\cos\alpha-2\cos2\alpha+3\cos3\alpha}$ илэрхийллийн утгыг ол.

Бодлого №608

$\sin x=\dfrac13$ бол

$3\cdot\dfrac{\sin2x-\sin3x+\sin5x}{1+\cos x-2\sin^22x}$ илэрхийллийн утгыг ол.

Бодлого №609

$\dfrac{1}{2\sin10^{\circ}}-2\sin70^{\circ}$ илэрхийллийн утгыг ол.

Бодлого №610

$\sin16^{\circ}+\cos16^{\circ}\cdot\tg37^{\circ}$ илэрхийллийн утгыг ол.

Бодлого №611

$\cos67^{\circ}30'$ ба

$\cos75^{\circ}$ илэрхийллийн утгыг ол.

Бодлого №612

$\dfrac{\ctg15^{\circ}+1}{2\ctg15^{\circ}}$ илэрхийллийн утгыг ол.

Бодлого №614

$\dfrac{\cos\dfrac{4\pi}{9}}{\sin\dfrac{19\pi}{18}}+2\cos\pi$ илэрхийллийн утгыг ол.

Бодлого №616

$\Big(\dfrac{\sin80^{\circ}+\sin40^{\circ}}{\sin70^{\circ}}\Big)^2$ илэрхийллийн утгыг ол.

Бодлого №617

$\dfrac{16\sin251^{\circ}-10\cos161^{\circ}}{\cos19^{\circ}}$ илэрхийллийн утгыг ол.

Бодлого №618

$\Big(\tg\dfrac{5\pi}{16}+\tg\dfrac{3\pi}{16}\Big)\cdot\cos\dfrac{\pi}{8}$ илэрхийллийн утгыг ол.

Бодлого №619

$\left[\tg\Big(\dfrac{\pi}{4}-\dfrac{\alpha}{4}\Big)+\tg\Big(\dfrac{\pi}{4}+\dfrac{\alpha}{2}\Big)\right] \big(2\cos^2\dfrac{\alpha}{2}-1\big)$ илэрхийллийн утгыг ол.

Бодлого №621

$2\cos20^{\circ}\cos40^{\circ}-\cos20^{\circ}$ илэрхийллийн утгыг ол.

Бодлого №627

$\cos20^{\circ}+2\sin^255^{\circ}=1+\sqrt2\sin65^{\circ}$ тэнцэтгэлийг шалга.

Бодлого №652

$\sin^2(45^{\circ}+\alpha)-\sin^2(30^{\circ}-\alpha)-\sin15^{\circ}\cos(15^{\circ}+2\alpha).$

Бодлого №653

$\sin^6\alpha+\cos^6\alpha+3\sin^2\alpha\cos^2\alpha$ хялбарчил.

Бодлого №654

$2(\sin^6\alpha+\cos^6\alpha)-3(\sin^4\alpha+\cos^4\alpha)$ хялбарчил.

Бодлого №655

$\tg^3x+\tg^2x+\tg x+1-\dfrac{\sin x}{\cos^3x}$ хялбарчил.

Бодлого №656

$\dfrac{(\tg\alpha+\cos^{-1}\alpha)(\cos\alpha-\ctg\alpha)}{(\cos\alpha+\ctg\alpha)(\tg\alpha-\cos^{-1}\alpha)}$ хялбарчил.

Бодлого №660

$\sin(2\arcctg(\dfrac13))+\cos(\arcctg2\sqrt2)$ тооцоол.

Бодлого №663

$\cos2\alpha=0.4$ бол

$\cos^6\alpha-\sin^6\alpha$ -г ол.

Бодлого №664

$\cos\alpha+\sin\alpha=\dfrac{\sqrt2}{2}$ бол

$\cos^4\alpha+\sin^4\alpha$ -г ол.

Бодлого №665

$\dfrac{1}{\tg^2\alpha}+\dfrac{1}{\ctg^2\alpha}+\dfrac{1}{\sin^2\alpha}+\dfrac{1}{\cos^2\alpha}=8$ бол

$\sin^22\alpha$ -г ол.

Бодлого №666

$\sin\alpha-\cos\alpha=a$ бол

$\dfrac{\sin^2\alpha}{\cos\alpha}-\dfrac{\cos^2\alpha}{\sin\alpha}$ -г ол.

Бодлого №667

$\tg9^{\circ}-\tg63^{\circ}+\tg81^{\circ}-\tg27^{\circ}$ тооцоол.

Бодлого №668

$\sin70^{\circ}\cdot\sin50^{\circ}\cdot\sin10^{\circ}$ тооцоол.

Бодлого №669

$\cos70^{\circ}\cdot\cos50^{\circ}\cdot\cos10^{\circ}$ тооцоол.

Бодлого №670

$\dfrac{1-4\sin10^{\circ}\sin70^{\circ}}{2\sin10^{\circ}}$ тооцоол.

Бодлого №671

$4\sin20^{\circ}\cdot\sin40^{\circ}\cdot\sin60^{\circ}\cdot\sin80^{\circ}$ тооцоол.

Бодлого №672

$16\sin^220^{\circ}\cdot\sin^240^{\circ}\cdot\sin^260^{\circ}\cdot\sin^280^{\circ}$ тооцоол.

Бодлого №673

$\tg20^{\circ}\cdot\tg40^{\circ}\cdot\tg80^{\circ}$ тооцоол.

Бодлого №678

$\dfrac{96\sin80^{\circ}\cdot\sin65^{\circ}\cdot\sin35^{\circ}}{\sin20^{\circ}+\sin50^{\circ}+\sin110^{\circ}}$ тооцоол.

Бодлого №679

$\dfrac{\sin50^{\circ}\cdot\cos12^{\circ}-\sin40^{\circ}\cos78^{\circ}}{\cos68^{\circ}-\sqrt3\sin68^{\circ}}$ тооцоол.

Бодлого №693

$\cos\dfrac{\pi}{7}\cdot\cos\dfrac{4\pi}{7}\cdot\cos\dfrac{5\pi}{7}=\dfrac18$ байхыг батал.

Бодлого №694

$\sin\dfrac{2}{5\alpha}\cos\dfrac{\alpha}{2}-\sin3\alpha\cos\dfrac{\pi}{3}-\dfrac14$ -г үржвэр хэлбэрт хувирга.

Бодлого №695

$\sec\alpha-\cos\alpha+\sec60^{\circ}\cdot\cos2\alpha\sin3\alpha-\sin5\alpha$ -г үржвэр хэлбэрт хувирга.

Бодлого №696

$\tg2x=-\dfrac34$ ба

$\sin2x>0$ бол

$\log_{\tg\frac{\pi}{6}}\tg x$ илэрхийлэл тодорхойлогдохыг харуулж утгыг ол.

Бодлого №697

$\sin(\delta+\frac{\pi}{4})+\cos(\delta+\frac{\pi}{4})=-\sqrt{\dfrac45}$ бол

$\log_{\frac{14}{25}}|\cos\delta|+\log_{\frac{14}{25}}|\cos3\delta|$ -г тооцоол.

Бодлого №699

$\sin x+\cos x=a$ бол

$\dfrac{\sin^3x+\cos^3 x}{a(a^2-3)}$ -г ол.

Бодлого №700

$0< \alpha< 90^{\circ}$ бол

$\dfrac{\sqrt{1+\sin\alpha}-\sqrt{1-\sin\alpha}}{4\sin\dfrac{\alpha}{2}}$ -г хялбарчил.

Бодлого №701

$\sin5\alpha\cdot\sin4\alpha+\sin4\alpha\cdot\sin3\alpha-\sin2\alpha\cdot\sin\alpha-2\sin3\alpha\cdot\sin5\alpha\cdot\cos\alpha$ -г хялбарчил.

Бодлого №702

$\tg3\alpha-\tg(\dfrac{\pi}{3}-\alpha)\tg(\dfrac{\pi}{3+\alpha})\tg\alpha+1$ -г хялбарчил.

Бодлого №703

$(\sqrt5+1)\sin18^{\circ}$ -г тооцоол.

Бодлого №704

$\sin\alpha+\cos\alpha=1.4$ ба

$0< \alpha< \dfrac{\pi}{4}$ бол

$3\tg\dfrac{\alpha}{2}$ -г тооцоол.

$0^{\circ}< \theta< 90^{\circ}$ ба

$4\cos\theta\cdot \sin \theta\cdot \sin 3\theta=\cos3\theta$ нөхцлийг хангадаг бол

$\cos \theta$ ,

$\cos 2\theta$ ,

$\cos 4\theta$ -ийн утгыг ол.

Адилтгал батлах, илэрхийллийн утга олох

$\sin(\alpha+\beta)\cdot \sin(\alpha-\beta)=\sin^2\alpha-\sin^2\beta$ адилтгалыг батал.
$\sin\alpha+\sin\beta=\dfrac 12$ , $\cos \alpha+\cos\beta=\dfrac 23$ бол $\cos(\alpha-\beta)$ -ийн утгыг ол.

Илэрхийлэл хялбарчлах ба адилтгал батлах

$\dfrac{\sin \theta}{1+\cos\theta}+\dfrac 1{\tg\theta}=\dfrac 1{\sin \theta}$ адитгалыг батал.
$\sin \theta+\cos \theta=\dfrac 13$ бол $\sin^3 \theta+\cos^3 \theta$ -ийн утгыг ол.

Бодлого №10110

$\cos 5\theta=f(\cos \theta)$ нөхцлийг хангах $f(x)$ функцийг ол.
$\alpha=18^{\circ}$ бол $\cos \alpha\cos 3\alpha\cos7\alpha=\dfrac5{16}$ болохыг батал.

Бодлого №10112

$a=\sin^236^{\circ}$ ,

$b=\sin^272^{\circ}$ гэвэл

$a+b$ болон

$a\cdot b$ нь рациональ тоо болохыг батал.

Тригонометрийн илэрхийллийн утга

$\sin^2\theta=\cos\theta$ бол $\dfrac1{1+\cos\theta}+\dfrac1{1-\cos\theta}$ -ийн утгыг ол.
$\sin20^{\circ}+\cos160^{\circ}+\sin200^{\circ}+\cos(-20^{\circ})$ -ийн утгыг ол.

Бодлого №10548

Илэрхийлэл хялбарчил.

$(\sin\theta+2\cos\theta)^2+(2\sin\theta-\cos \theta)^2$
$\dfrac{\sin 4\theta+4\cos^2\theta-\cos^4 \theta+1}{3(1+\cos^2\theta)}$
$\dfrac{1+\sin \theta}{\cos\theta}+\dfrac{\cos \theta}{1+\sin \theta}$

Бодлого №10549

$\sin \theta+\cos\theta=\dfrac 12$ бол

$\sin \theta\cdot \cos \theta=\ebox$ ,

$\sin\theta-\cos\theta=\ebox.$

$\sin \theta\cdot\cos\theta=\dfrac 12$ бол

$\cos \theta+ \sin \theta=\ebox$ ,

$\sin^3\theta+\cos^3\theta=\ebox.$

Бодлого №10558

$\theta$ нь III мужийн өнцөг ба

$\tg\theta=\sqrt{2}$ бол дараах илэрхийллийн утгыг ол.

$\dfrac{\cos^2\theta}{1+2\sin\theta\cdot \cos\theta}$
$\dfrac{1-\sin\theta}{\cos\theta}+\dfrac{\cos\theta}{1-\sin\theta}$

Бодлого №10560

$-45^{\circ}\leq \theta\leq 60^{\circ}$ гэе.

$g(\theta)=2+\sin\theta-\cos^2\theta$ ,

$f(\theta)=\dfrac3{g(\theta)}$ бол

$g(\theta)$ ,

$f(\theta)$ -ийн хамгийн их, хамгийн бага утгыг ол.

Бодлого №10561

Илэрхийллийн утгыг ол.

$\sin(-\theta)+\sin(90^{\circ}-\theta)-\sin(90^{\circ}+\theta)+\sin(180^{\circ}-\theta);$
$\cos(-10^{\circ})+\cos 80^{\circ}+\cos100^{\circ}+\cos170^{\circ}+\cos260^{\circ}+\cos280^{\circ}.$

Бодлого №10562

$-90^{\circ}\leq \theta\leq 90^{\circ}$ үед

$2a\cos\theta+2-\sin^2\theta$ -илэрхийллийн хамгийн их, хамгийн бага утгыг ол.

Бодлого №10575

$\triangle ABC$ -ны дотоод өнцөг

$\alpha$ ,

$\beta$ ,

$\gamma$ -ийн хувьд

$\cos^2\alpha+\cos^2\beta+\cos^2\gamma+ 2\cos\alpha\cos\beta\cos \gamma$ илэрхийллийн утгыг ол.

Бодлого №10581

Дараах илэрхийллийг хялбарчил.

$\cos \theta\cdot \cos (\theta+120^{\circ})\cdot \cos (\theta-120^{\circ})$
$\sin (\theta-60^{\circ})+\sin \theta+ \sin (\theta+60^{\circ})$

Бодлого №10597

$-90^{\circ}< \theta< 90^{\circ}$ ба

$2\cos \theta+\sin 2\theta=1$ бол

$\tg \theta$ -ийн утгыг ол.

Утгыг ол

$\alpha=15^{\circ}$ бол

$\dfrac{\cos4\alpha+1}{\ctg\alpha-\tg\alpha}$ илэрхийллийн утгыг ол.

A.

$\dfrac12$ B.

$\dfrac{\sqrt3}4$ C.

$\dfrac14$ D.

$\dfrac{\sqrt3}2$ E.

$1$

Үржвэрийг нийлбэрт хувиргах томьёонууд

$\tg18^{\circ}\tg288^{\circ}+\sin32^{\circ}\sin148^{\circ}-\sin302^{\circ}\sin122^{\circ}$ илэрхийллийн утгыг ол.

A.

$0$ B.

$1$ C.

$2$ D.

$3$ E.

$4$

$\alpha=\dfrac{\pi}{36}$ үед

$\dfrac{\sqrt3\cos3\alpha}{10(\cos9\alpha+\cos3\alpha)}$ илэрхийллийн утгийг ол.

A.

$0$ B.

$1$ C.

$\dfrac12$ D.

$\dfrac1{10}$ E.

$-\dfrac12$

Илэрхийллийн утгыг олох

Хэрэв

$\tg\alpha=2$ бол

$\dfrac{\sin\alpha}{\sin^3\alpha+\cos^3\alpha}$ -г ол.

A.

$\dfrac{2}{9}$ B.

$\dfrac{5}{9}$ C.

$\dfrac{9}{2}$ D.

$\dfrac{10}{9}$ E. 2

Илэрхийлэл хялбарчлах

$\dfrac{\tg\alpha+\sin\alpha}{2\cos^2\frac{\alpha}{2}}$ илэрхийллийг хялбарчил.

A.

$1$ B.

$\tg\alpha$ C.

$\cos\alpha$ D.

$\sin\alpha$ E.

$\dfrac{\tg\alpha}{2}$

sin 75

$\sin 75^\circ=?$

A.

$\dfrac{\sqrt6+\sqrt2}{4}$ B.

$\dfrac{\sqrt6-\sqrt2}{4}$ C.

$\dfrac{\sqrt5+1}{4}$ D.

$\dfrac{\sqrt5-1}{4}$ E.

$\cos 105^\circ$

Үндсэн адилтгал ашиглаж зэрэг шилжүүлэх

Хэрэв

$\tg\alpha=3$ бол

$\dfrac{\sin\alpha}{\sin^3\alpha+\cos^3\alpha}=?$

A.

$\dfrac{15}{14}$ B.

$\dfrac{7}{9}$ C.

$1$ D.

$\dfrac{10}{9}$ E.

$\dfrac{35}{28}$

Синус ба косинусын хамаарал

$\sin(\theta+45^\circ)$ нь дараах илэрхийллүүдийн алинтай нь тэнцүү вэ?

A.

$\cos(45^\circ-\theta)$ B.

$\cos(45^\circ+\theta)$ C.

$\sin45^\circ$ D.

$\sin(225^\circ+\theta)$ E. алинтай нь ч тэнцүү биш

Бодлого №5668

$\sqrt{\dfrac{1+\sin\theta}{1-\sin\theta}}-\sqrt{\dfrac{1-\sin\theta}{1+\sin\theta}}$

A.

$\sec\theta-1$ B.

$2\csc\theta$ C.

$2\tg\theta$ D.

$\sec\theta\cdot\ctg\theta$ E.

$2\cdot\dfrac{\sin\theta}{|\cos\theta|}$

Синус ба косинусын хамаарал

$\dfrac{\sin35^\circ\cdot\cos35^\circ}{\sin55^\circ\cdot\cos55^\circ}$ илэрхийллийг хялбарчил.

A.

$0$ B.

$\dfrac13$ C.

$\dfrac12$ D.

$1$ E.

$-1$

Хялбарчил

$2\cos140^\circ\cdot\sin(-40^\circ)$

A.

$-\sin10^\circ$ B.

$-\cos10^\circ$ C.

$\cos10^\circ$ D.

$\sin40^\circ$ E.

$\cos20^\circ$

Үржвэрийг нийлбэрт хувиргах

$\sin70^{\circ}\cdot\sin50^{\circ}\cdot\sin10^{\circ}$ тооцоол.

A.

$\dfrac18$ B.

$\dfrac38$ C.

$\dfrac58$ D.

$-\dfrac38$ E.

$\dfrac78$

$\sin^210^{\circ}+\sin^2130^{\circ}+\sin^2110^{\circ}$ илэрхийллийн утгыг ол.

A.

$1.4$ B.

$1.2$ C.

$1.7$ D.

$1.8$ E.

$1.5$

$\dfrac1{2\sin10^{\circ}}-2\sin70^{\circ}$ илэрхийллийн утгыг ол.

A.

$1.5$ B.

$0.5$ C.

$1$ D.

$2$ E.

$-1$

Үржвэрийг нийлбэрт шилжүүлэх

$\dfrac{\tg60^{\circ}}{\sin40^{\circ}}+4\cos100^{\circ}$ илэрхийллийн утгыг ол.

A.

$3$ B.

$2$ C.

$1.5$ D.

$1$ E.

$0$

$\dfrac{\sqrt{2}\cos\alpha-2\cos\left(\frac{\pi}{4}-\alpha\right)}{2\sin\left(\frac{\pi}{6}+\alpha\right)-\sqrt{3}\sin\alpha}$ хялбарчил.

A.

$\sqrt{2}\cos \alpha$ B.

$-\sqrt{2}\tg\alpha$ C.

$\frac{\ctg\alpha}{\sqrt{2}}$ D.

$-\sqrt{2}\sin\alpha$ E.

$-\sqrt{2}\ctg\alpha$

Бодлого №6720

$\dfrac{\cos\alpha-2\cos (\frac{\pi}{3}+\alpha)}{2\sin (\alpha-\frac{\pi}{6})-\sqrt{3}\sin\alpha}$ хялбарчил.

A.

$-\sqrt{3}\tg\alpha$ B.

$\sqrt{3}\sin\alpha$ C.

$\dfrac{\ctg\alpha}{\sqrt{3}}$ D.

$-\sqrt{3}\cos\alpha$ E.

$\sqrt{3}\cos\alpha$

Хялбарчил

$\dfrac{\sin 2t -2\sin (\frac{\pi}{2}-t)}{\cos(\frac{\pi}{2}-t)-\sin^2t}$ -хялбарчил.

A.

$2\tg t$ B.

$2$ C.

$-2$ D.

$2\ctg t$ E.

$-2\ctg t$

Бодлого №6722

$\dfrac{1-\cos 2t+\sin 2t}{1+\cos 2t+\sin 2t}\cdot \tg \left(\dfrac{\pi}{2}-t\right)$ -хялбарчил.

A.

$2\tg t$ B.

$-1$ C.

$1$ D.

$\tg 2t$

Давхар өнцгийн томьёо

$\dfrac{1+\cos40^{\circ}+\cos80^{\circ}}{\sin 80^{\circ}+\sin 40^{\circ}}\cdot \tg 40^{\circ}$ -хялбарчил.

A.

$0$ B.

$1$ C.

$\dfrac 12$ D.

$\dfrac 32$ E.

$\dfrac 23$

Бодлого №6725

$\sqrt{4\cos^4\alpha-6\cos2\alpha+3}$ -хялбарчил.

A.

$2\cos^2\alpha+1$ B.

$1+2\sin^2\alpha$ C.

$2(\cos^2\alpha+1)$ D.

$2(1+\sin^2\alpha)$

Бодлого №6726

$\sqrt{\sin^4\alpha+\cos2\alpha}+\sqrt{\cos^4\alpha-\cos2\alpha}$ -хялбарчил.

A.

$2$ B.

$2|\cos\alpha|$ C.

$2|\sin\alpha|$ D.

$1$

Бодлого №6727

$\dfrac{(\sin\beta+\cos\beta)(1-\sin\beta\cdot \cos\beta)}{\sin\beta\cdot \tg\beta+\cos\beta\cdot \ctg\beta}$ -хялбарчил.

A.

$\tg\beta\cdot \sin\beta$ B.

$\frac 12\sin2\beta$ C.

$\ctg\beta\cdot \cos\beta$ D. 1

Бодлого №6728

$\dfrac{\cos\alpha\cdot \ctg\alpha-\sin\alpha\tg\alpha}{1+\sin\alpha\cdot \cos\alpha}$ -хялбарчил.

A.

$\tg\alpha-\ctg\alpha$ B.

$\tg\alpha+\frac1{\tg\alpha}$ C.

$\frac1{\sin\alpha}-\frac1{\cos\alpha}$ D.

$\sin\alpha-\cos\alpha$

Хялбарчил

$\sin^6\alpha+\cos^6\alpha+3\sin^2\alpha\cdot\cos^2\alpha$ -хялбарчил.

A.

$\dfrac43$ B.

$\dfrac32$ C.

$\dfrac23$ D.

$1$ E.

$\dfrac12$

Бодлого №6730

$\sin^2\alpha+\cos\left(\dfrac{\pi}{3}-\alpha\right)\cdot \cos\left(\dfrac{\pi}{3}+\alpha\right)$ -хялбарчил.

A.

$-\frac 14$ B.

$\frac 34$ C.

$\frac 12$ D.

$\frac 14$

Үндсэн адилтгал ашиглан илэрхийллийг хялбарчлах

$\sin 2x=\dfrac 45$ бол

$\sin^6x+\cos^6x=?$

A.

$\dfrac{12}{25}$ B.

$\dfrac{13}{25}$ C.

$\dfrac{24}{25}$ D.

$\dfrac{7}{25}$ E.

$\dfrac{8}{25}$

Хагас өнцгийн томьёо

$\cos 2x=-\dfrac 35$ бол

$\sin^8x-\cos^8x=?$

A.

$\dfrac{51}{125}$ B.

$\dfrac{57}{125}$ C.

$\dfrac{13}{25}$ D.

$-\dfrac{12}{25}$ E.

$-\dfrac{51}{125}$

Үндсэн адилтгал

$\sin t\cdot \cos t=-0.5$ бол

$\sin^4t+\cos^4t=?$

A.

$\dfrac14$ B.

$\dfrac18$ C.

$\dfrac12$ D.

$\dfrac1{16}$ E.

$\dfrac32$

Тооцоол

$\tg t-\ctg t=-\dfrac7{12}$ ба

$0< t< \dfrac{\pi}{2}$ бол

$\sin t+\cos t=?$

A.

$\dfrac 75$ B.

$\dfrac 76$ C.

$\dfrac 54$ D.

$\dfrac 43$ E.

$\dfrac 32$

Тангес, котангесийн үржвэр

$\tg\alpha+\ctg\alpha=m$ бол

$\tg^2\alpha+\ctg^2\alpha=?$

A.

$m^2-1$ B.

$m^2-m$ C.

$m^2-2$ D.

$m^2+1$ E.

$m^2+2$

Бодлого №6776

$\tg\alpha+\ctg\alpha=m$ бол

$\tg^3\alpha+\ctg^3\alpha=?$

A.

$m^3-m;$ B.

$m^3-3m;$ C.

$m^3-2m;$ D.

$m^3-m^2;$

Үндсэн адилтгал ашиглан зэрэг өөрчлөх

$\tg\alpha=-2$ бол

$\dfrac{\sin^3\alpha+\cos^3\alpha}{3\cos\alpha-\sin\alpha}=?$

A.

$-\frac75$ B.

$\frac7{25}$ C.

$-\frac7{25}$ D.

$\frac{21}{5}$ E.

$-\frac{21}{5}$

Үндсэн адилтгал ашиглан зэрэг өсгөх

$\ctg\alpha=2$ бол

$\dfrac{\cos\alpha+3\sin\alpha}{\cos^3\alpha-\sin^3\alpha}=?$

A.

$\dfrac 73$ B.

$\dfrac{25}{2}$ C.

$\dfrac{25}{4}$ D.

$\dfrac{25}{7}$ E.

$\dfrac{16}{7}$

Тригонометрийн адилтгал хувиргалт

$\sin2\alpha\cdot \ctg\alpha=?$

A.

$\sin^2\alpha$ B.

$2\sin^2\alpha$ C.

$\cos^2\alpha$ D.

$2\cos^2\alpha$ E.

$1$

Нийлбэрийн тангес

$\tg\Big(\alpha+\dfrac{\pi}{4}\Big)=?$

A.

$\dfrac{1-\tg\alpha}{1+\tg\alpha}$ B.

$\dfrac{1+\tg\alpha}{1-\tg\alpha}$ C.

$\dfrac{\tg\alpha-1}{1+\tg\alpha}$ D.

$\dfrac{1+\tg\alpha}{\tg\alpha-1}$ E.

$-1$

$\dfrac{\tg3\alpha+\tg\alpha}{\tg3\alpha-\tg\alpha}=?$

A.

$2$ B.

$\sin2\alpha$ C.

$2\cos2\alpha$ D.

$-\sin2\alpha$ E.

$2\sin2\alpha$

Тригонометрийн тооцоолох бодлого

$\dfrac{1+\cos250^\circ}{\sin35^\circ\cos55^\circ}$ илэрхийллийн утгыг ол.

A.

$0.5$ B.

$1$ C.

$1.5$ D.

$2$ E.

$4$

Тригонометрийн илэрхийлэлийн утгыг олох

$\sin(\alpha+\beta)=0.8$ ,

$\cos(\alpha-\beta)=0.3$ бол

$(\sin\alpha-\cos\alpha)(\sin\beta-\cos\beta)$ илэрхийллийн утгыг ол.

A.

$1.1$ B.

$0.5$ C.

$-0.5$ D.

$0.73$ E.

$0.24$

$4\sin18^\circ\cos36^\circ$

$4\sin18^\circ\cos36^\circ=?$

A.

$-1$ B.

$1$ C.

$\dfrac{\sqrt{6}-\sqrt{2}}{4}$ D.

$\dfrac{\sqrt{6}+\sqrt{2}}{4}$ E.

$-2$

Хагас өнцгийн томьёо

$2\cos^215^\circ-1=?$

A.

$\dfrac12$ B.

$\dfrac{\sqrt3}2$ C.

$-\dfrac12$ D.

$-\dfrac{\sqrt3}2$ E.

$1$

Нийлбэрийг үржвэрт хувиргах

$\dfrac{\cos50^\circ+\cos10^\circ}{\cos20^\circ}$

A.

$-\sqrt3$ B.

$\sqrt3$ C.

$-\dfrac{\sqrt3}2$ D.

$\dfrac{\sqrt3}2$ E.

$\dfrac12$

Нийлбэр өнцгийн синусын томьёо

$\sin50^\circ\cdot\cos10^\circ+2\sin10^\circ\cdot\sin20^\circ\cdot\cos20^\circ$

A.

$\sin50^\circ$ B.

$0.5$ C.

$\dfrac{\sqrt3}{2}$ D.

$\dfrac{\sqrt2}{2}$ E.

$\cos50^\circ$

Нийлбэрийн томьёонууд

$\dfrac{1}{\sin10^\circ}-\dfrac{\sqrt3}{\cos10^\circ}=?$

A.

$3$ B.

$2$ C.

$1$ D.

$\sqrt3$ E.

$4$

Тригонометр функцийн утгууд

$\cos^2\dfrac{\pi}{3}-\sqrt3\sin\dfrac{\pi}{6}\cdot\cos\dfrac{5\pi}{6}$ хялбарчил.

A.

$0$ B.

$\dfrac14+\dfrac{\sqrt3}{2}$ C.

$\dfrac{1-\sqrt3}{4}$ D.

$1$ E.

$-1$

Нийлбэр, ялгаврын томьёонууд

$\dfrac{\sin75^\circ}{\sin15^\circ}-\dfrac{\cos75^\circ}{\cos15^\circ}=?$

A.

$\sqrt3$ B.

$2\sqrt3$ C.

$3\sqrt3$ D.

$-\sqrt3$ E.

$-2\sqrt3$

Нийлбэрийг үржвэрт хувиргах

$\dfrac{\sin20^\circ-\sin30^\circ+\sin40^\circ}{\cos20^\circ-\cos30^\circ+\cos40^\circ}$

A.

$\dfrac12$ B.

$\dfrac{1}{\sqrt3}$ C.

$1$ D.

$\dfrac{\sqrt3}{2}$ E.

$\dfrac34$

Тригонометрийн илэрхийллийг хялбарчлах

Хэрэв

$\tg\alpha \cdot\ctg\alpha=2$ бол

$\dfrac{\sin(\alpha+\beta)}{\sin(\alpha-\beta)}=?$

A.

$1$ B.

$2$ C.

$\frac12$ D.

$3$ E.

$\frac23$

Үндсэн адилтгал

$\dfrac{\sin^4\alpha+\cos^4\alpha-1}{\sin^6\alpha+\cos^6\alpha-1}$

A.

$\dfrac23$ B.

$\dfrac13$ C.

$\dfrac12$ D.

$\dfrac32$ E.

$1$

Нийлбэр, ялгавар өнцгийн томьёо

Хэрэв

$\tg\alpha\cdot\ctg\beta=2$ бол

$\dfrac{\sin(\alpha+\beta)}{\sin(\alpha-\beta)}=?$

A.

$1$ B.

$2$ C.

$\dfrac12$ D.

$3$ E.

$\dfrac23$

Тригонометрийн илэрхийлэл хялбарчлах

$\sin^2\dfrac{\pi}{6}+\sin\dfrac{\pi}{3}\cdot\cos\dfrac{\pi}{6}$ хялбарчил.

A.

$0$ B.

$\dfrac14-\dfrac{\sqrt3}{2}$ C.

$\dfrac{1+\sqrt3}{4}$ D.

$-1$ E.

$1$

$\alpha=-\dfrac{\pi}{36}$ үед

$\dfrac{\sqrt3\cos3\alpha}{10(\cos9\alpha+\cos3\alpha)}$ илэрхийллийн утгийг ол.

A.

$0$ B.

$\dfrac1{10}$ C.

$\dfrac12$ D.

$1$ E.

$-\dfrac12$

Хялбарчил

$\cos115^{\circ}-\cos 35^{\circ}+\cos65^{\circ}+\cos 25^{\circ}$ илэрхийллийг хялбарчил.

A.

$\cos5^{\circ}$ B.

$\sin5^{\circ}$ C.

$\cos15^{\circ}$ D.

$\sin 35^{\circ}$ E.

$\sin105^\circ$

Нийлбэрийн тангес

$\tg\Big(\alpha+\dfrac{\pi}{4}\Big)=?$

A.

$\dfrac{1-\tg\alpha}{1+\tg\alpha}$ B.

$\dfrac{1+\tg\alpha}{1-\tg\alpha}$ C.

$\dfrac{\tg\alpha-1}{1+\tg\alpha}$ D.

$\dfrac{1+\tg\alpha}{\tg\alpha-1}$ E.

$-1$

$\alpha=\dfrac{\pi}{36}$ үед

$\dfrac{\sqrt3\cos3\alpha}{10(\cos9\alpha+\cos3\alpha)}$ илэрхийллийн утгийг ол.

A.

$0$ B.

$1$ C.

$\dfrac12$ D.

$\dfrac1{10}$ E.

$-\dfrac12$

Утгыг ол

$\alpha=15^{\circ}$ бол

$\dfrac{\cos4\alpha+1}{\ctg\alpha-\tg\alpha}$ илэрхийллийн утгыг ол.

A.

$\dfrac12$ B.

$\dfrac{\sqrt3}4$ C.

$\dfrac14$ D.

$\dfrac{\sqrt3}2$ E.

$1$

Бодлого №14664

$\dfrac{1-\cos 2t+\sin 2t}{1+\cos 2t+\sin 2t}\cdot \tg \left(\dfrac{\pi}{2}-t\right)$ -хялбарчил.

A.

$2\tg t$ B.

$-1$ C.

$1$ D.

$\tg 2t$

Синус ба косинусын хамаарал

$\dfrac{\sin65^\circ\cdot\cos65^\circ}{\sin25^\circ\cdot\cos25^\circ}$ илэрхийллийг хялбарчил.

A.

$1$ B.

$\dfrac16$ C.

$\dfrac12$ D.

$0$ E.

$-1$

2021 B №25

$OAB$ гурвалжны

$AB$ тал дээр

$AC$ :

$CB$ =3:1

$байх$ C

$цэг авав.$ \vec{\mathstrut OA}=\vec{\mathstrut a}

$,$ \vec{\mathstrut OB}= \vec{\mathstrut b}

$,$ \vec{\mathstrut OC}= \vec{\mathstrut c}

$- ийг$ \vec{\mathstrut a}

$,$ \vec{\mathstrut b}$ векторуудаар илэрхийл.

A.

$\frac{\vec{\mathstrut b}+\vec{\mathstrut 3a}}{4}$ B.

$\frac{\vec{\mathstrut 3b}-\vec{\mathstrut a}}{4}$ C.

$\frac{\vec{\mathstrut -b}+\vec{\mathstrut 5a}}{4}$ D.

$\frac{\vec{\mathstrut 3b}+\vec{\mathstrut a}}{4}$ E.

$\frac{\vec{\mathstrut b}-\vec{\mathstrut a}}{4}$

2019 A №25

Хэрэв

$\ctg= 0.2$ бол

$\dfrac{1+\cos2\alpha+\sin2\alpha}{1-\cos2\alpha+\sin2\alpha}$ илэрхийллийн утгыг олоорой.

A.

$0.2$ B.

$\dfrac12$ C.

$0.02$ D.

$\dfrac13$ E.

$0.4$

2019 A №25

Хэрэв

$\ctg= 0.4$ бол

$\dfrac{1-\cos2\alpha+\sin2\alpha}{1+\cos2\alpha-\sin2\alpha}$ илэрхийллийн утгыг олоорой.

A.

$0.04$ B.

$\dfrac14$ C.

$0.4$ D.

$\dfrac13$ E.

$0.2$

2019 B №25

Хэрэв

$\tg= 0.4$ бол

$\dfrac{1- \cos2\alpha+\sin2\alpha}{1+\cos2\alpha+\sin2\alpha}$ илэрхийллийн утгыг олоорой.

A.

$0.04$ B.

$\dfrac14$ C.

$0.4$ D.

$\dfrac13$ E.

$0.2$

Утгыг ол.

$\dfrac{\cos(-13)^{\circ}\sin 77^{\circ}+\cos(-77^{\circ})\sin 167^{\circ}}{0.1}+\dfrac{\tg^245^{\circ}}{0.002}=\fbox{abc}.$

Эмхтгэлийн томьёо

$\dfrac{\cos 93^{\circ}\tg 267^{\circ}+\sin 87^{\circ}}{0.1}+16\sin^415^{\circ}\cdot \cos^415^{\circ}=\dfrac{\fbox{c}}{\fbox{ab}}.$

Бодлого №6865

$\sin \dfrac x2-\cos\dfrac x2=\sqrt{0.1}$ бол

$\tg x=\pm \dfrac{\fbox{a}}{\sqrt{\fbox{bc}}}$ байна.

Бодлого №6866

$\sin \dfrac x2+\cos\dfrac x2=\sqrt{0,3}$ бол

$\ctg x=\pm \dfrac{\sqrt{\fbox{ab}}}{\fbox{c}}$ байна.

$\sin\alpha-\cos\alpha=1.2$ бол

$\cos^3\alpha-\sin^3\alpha=-\fbox{a.bcd}$ байна.

Утгыг ол

$\sin\alpha+\cos\alpha=0.8$ бол

$\sin^3\alpha+\cos^3\alpha=\fbox{a.bcd}$ байна.

$\dfrac{2\sin^220^{\circ}-1}{3\ctg 65^{\circ}\cdot \cos^2205^{\circ}}=-\dfrac{\cos \fbox{ab}^{\circ}}{3\tg \fbox{cd}^{\circ}\cdot \cos^2\fbox{ef}^{\circ}}=-\dfrac{\fbox{g}}{\fbox{h}}.$

Давхар өнцөг ба эмхтгэлийн томьёо

$\dfrac{2\sin^270^{\circ}-1}{\tg 115^{\circ}\cdot \cos^2 115^{\circ}}=\dfrac{\cos \fbox{abc}^{\circ}}{\tg \fbox{de}^{\circ}\cdot \cos^2\fbox{fg}^{\circ}}=-\fbox{h}.$

Бодлого №6871

$\dfrac{\sqrt{2}-\sin \alpha-\cos\alpha}{\sin \alpha-\cos\alpha}=\tg\left(\dfrac{\alpha}{\fbox{a}}-\dfrac{\pi}{\fbox{b}}\right).$

$\sin165^\circ$

$\sin 165^{\circ}=\dfrac{\sqrt{\fbox{a}}-\sqrt{\fbox{b}}}{\fbox{c}}.$

$\sin162^\circ$

$\sin 162^{\circ}=\dfrac{\sqrt{\fbox{a}}-\fbox{b}}{\fbox{c}}$ .

Бодлого №6875

$3\cos 2x+5\cos 2y-8\sin xcos x-24\sin y\cos y=18$ бол

$\sin 2x-\sin 2y=\dfrac{\fbox{c}}{\fbox{ab}},$

$\dfrac{\tg x+1}{\tg y+1}=\fbox{d,e}$ байна.

Бодлого №6876

$12\cos\varphi-10\sin \dfrac{\varphi}{2}\cos \dfrac{\varphi}{2}-a=\cos\psi+b\tg^2\psi$ гэж өгөгдөв.

1)

$a=14, b=1$ бол

$\sin\varphi\cdot \cos \psi =\dfrac{\fbox{c}}{\fbox{ab}}$ байна.

2)

$a=-14, b=-2$ бол

$\cos \varphi+\cos\psi=\dfrac{1}{\fbox{de}}$ байна.

Тригонометрийн утгууд

$\cos165^\circ=-\dfrac{\sqrt{\fbox{a}}}{\fbox{b}}(\sqrt{\fbox{c}}+1)$
$\cos162^\circ=-\dfrac{\sqrt{\fbox{de}+\fbox{f}\sqrt{5}}}{4}$

Өнцгүүдийн давхцал олох

$\alpha=90^{\circ}\cdot k$ ба

$\beta=30^{\circ}+60^{\circ}\cdot n$ ,

$k, n\in\mathbb{Z}$ хэлбэрийн томьёогоор илэрхийлэгдэх өнцгүүдийн давхцлыг ол.

A.

$\pm30^{\circ}+180^{\circ}p$ B.

$90^{\circ}+180^{\circ}p$ C.

$180^{\circ}p$ D.

$90^{\circ}+360^{\circ}p$ E.

$90^{\circ}$

Радиан ба градусан хэмжээ

$\dfrac{4\pi}{9}$ радиан өнцөг аль нь вэ?

A.

$20^\circ$ B.

$25^\circ$ C.

$50^\circ$ D.

$80^\circ$ E.

$100^\circ$

Радиан өнцөг

$\dfrac{\pi}{15}$ хэдэн градус өнцөг вэ?

A.

$6^\circ$ B.

$10^\circ$ C.

$12^\circ$ D.

$15^\circ$ E.

$18^\circ$

Радиан өнцөг

$27^\circ$ хэдэн радиан өнцөг вэ?

A.

$\dfrac{13\pi}{20}$ B.

$\dfrac{9\pi}{20}$ C.

$\dfrac{11\pi}{20}$ D.

$\dfrac{3\pi}{20}$ E.

$\dfrac{7\pi}{10}$

Зөв олон өнцөгтийн дотоод өнцөг

Зөв 17 өнцөгтийн оройн өнцгийн радиан хэмжээг ол.

A.

$\dfrac{18\pi}{17}$ B.

$\dfrac{13\pi}{17}$ C.

$\dfrac{15\pi}{17}$ D.

$\dfrac{15\pi}{34}$ E.

$\dfrac{16\pi}{17}$

Тригонометрийн функцийн тодорхойлолт

$\dfrac{35\pi}{6}$ өнцөгтэй ижил синус, косинустай өнцгийг ол.

A.

$\dfrac{5\pi}{8}$ B.

$\dfrac{11\pi}{6}$ C.

$\dfrac{\pi}{4}$ D.

$\dfrac{\pi}{2}$ E.

$\dfrac{\pi}{6}$

ЭЕШ 2015 D №3

$55^\circ$ градусыг радианаар илэрхийл.

A.

$\dfrac{\pi}{3}$ B.

$\dfrac{11\pi}{36}$ C.

$\dfrac{5\pi}{11}$ D.

$\dfrac{13\pi}{36}$ E.

$\dfrac{2\pi}{7}$

ЭЕШ 2015 A №3

$75^\circ$ градусыг радианаар илэрхийл

A.

$\dfrac{\pi}{2}$ B.

$\dfrac{7\pi}{12}$ C.

$\dfrac{5\pi}{6}$ D.

$\dfrac{5\pi}{12}$ E.

$\dfrac{3\pi}{4}$

ЭЕШ 2015 B №3

$25^\circ$ градусыг радианаар илэрхийл.

A.

$\dfrac{\pi}{6}$ B.

$\dfrac{7\pi}{36}$ C.

$\dfrac{2\pi}{7}$ D.

$\dfrac{5\pi}{36}$ E.

$\dfrac{3\pi}{5}$

ЭЕШ 2015 C №3

$35^\circ$ градусыг радианаар илэрхийл.

A.

$\dfrac{\pi}{6}$ B.

$\dfrac{7\pi}{12}$ C.

$\dfrac{5\pi}{21}$ D.

$\dfrac{7\pi}{36}$ E.

$\dfrac{3\pi}{19}$

Тригонометрийн функцийн тодорхойлолт

Зурагт үзүүлсэн

$\alpha$ өнцгийн хувьд дараах хариултуудын аль үнэн бэ?

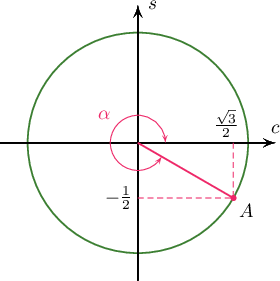
A.

$\sin\alpha=\dfrac{1}{2}$ ,

$\cos\alpha=\dfrac{\sqrt3}{2}$ B.

$\sin\alpha=\dfrac{\sqrt3}{2}$ ,

$\cos\alpha=-\dfrac{1}{2}$ C.

$\sin\alpha=-\dfrac{1}{2}$ ,

$\cos\alpha=\dfrac{\sqrt3}{2}$ D.

$\sin\alpha=-\dfrac{\sqrt3}{2}$ ,

$\cos\alpha=\dfrac{1}{2}$ E.

$\sin\alpha=\dfrac{1}{2}$ ,

$\cos\alpha=-\dfrac{\sqrt3}{2}$

Бодлого №553

$\arcctg\Big(-\sqrt3\Big)+\arccos\Big(-\dfrac{\sqrt3}{2}\Big)+\arcsin1-\arcctg0$ илэрхийллийн утгыг ол.

Бодлого №554

$\arcsin\Big(-\dfrac{1}{\sqrt2}\Big)-\arcctg\Big(-\dfrac{1}{\sqrt3}\Big)+\arccos\Big(-\dfrac{1}{2}\Big)+\arcctg1$ илэрхийллийн утгыг ол.

Бодлого №555

$\tg\left(\arcctg\Big(-\dfrac{1}{\sqrt3}\Big)+\dfrac{\pi}{6}\right)$ илэрхийллийн утгыг ол.

Бодлого №657

$\tg(2\arccos\dfrac{12}{13})$ тооцоол.

Бодлого №658

$\sin(2.5\pi+\arcctg(0.75))$ тооцоол.

Бодлого №660

$\sin(2\arcctg(\dfrac13))+\cos(\arcctg2\sqrt2)$ тооцоол.

Бодлого №680

$\sqrt3(\sin\arccos(-\dfrac{1}{2}))$ тооцоол.

Бодлого №681

$\cos^2(2\arcctg(-2))$ тооцоол.

Бодлого №698

$\arccos(\sin5.3)-\dfrac{5\pi}{2}$ -г тооцоол.

Бодлого №705

$\sqrt5\sin(\dfrac12\arcctg(-\dfrac43))$ -г тооцоол.

$\arctg$ -ийн утга

$\arctg(\tg130^{\circ})$ өнцгийг градусаар илэрхийл.

A.

$-130^\circ$ B.

$-50^\circ$ C.

$50^\circ$ D.

$130^\circ$ E.

$40^\circ$

ЭЕШ 2009 B1 №20

$\tg\left(\arcsin\left(-\frac2{\sqrt5}\right)\right)=a$ бол

$\lim\limits_{x\to a}\dfrac{x^2+8x+12}{x^2-4}$ хязгаарыг бод.

A.

$-5$ B.

$-1$ C.

$3$ D.

$-4$ E.

$7$

ЭЕШ 2010 A №18

$\cos\Big(\pi+\dfrac12\arcsin\dfrac{4}{\sqrt{17}}\Big)$ илэрхийллийн утгыг тооцоол.

A.

$\sqrt{\dfrac{17-\sqrt{17}}{34}}$ B.

$-\sqrt{\dfrac{17+\sqrt{17}}{34}}$ C.

$-\dfrac{1}{17}$ D.

$-\dfrac{2}{17}$ E.

$\sqrt{\dfrac{\sqrt{17}+1}{2}}$

ЭЕШ 2011 A №10

$\sin\Big(\dfrac12\arcsin\Big(-\dfrac{2\sqrt2}{3}\Big)\Big)$ утгыг ол.

A.

$-\dfrac{\sqrt3}{3}$ B.

$\dfrac{\sqrt6}{6}$ C.

$\dfrac{2\sqrt3}{3}$ D.

$\sqrt{\dfrac23}$ E.

$\sqrt6$

ЭЕШ 2012 A №10

$\arccos(\cos200^\circ)$ -ийг градусаар илэрхийл.

A.

$100^\circ$ B.

$110^\circ$ C.

$130^\circ$ D.

$160^\circ$ E.

$200^\circ$

$\sin 15^\circ$ -ийн утга

$\sin\left(\dfrac\pi4-\arccos\dfrac{\sqrt3}2\right)$ илэрхийллийн утгыг ол.

A.

$0$ B.

$1$ C.

$\frac{\sqrt6-\sqrt2}4$ D.

$\frac{\sqrt2-\sqrt6}4$ E.

$-\frac12$

Тригонометрийн илэрхийлэл бодох

$\sin(\arctg(-\sqrt{3}))$ илэрхийллийн утгыг ол.

A.

$0$ B.

$-\dfrac12$ C.

$\dfrac12$ D.

$-\dfrac{\sqrt3}{2}$ E.

$\dfrac{\sqrt3}{2}$

Тригонометрийн урвуу функцийн утга

$\sin(\arcctg(-\sqrt3))=?$ илэрхийллийн утгыг ол.

A.

$0$ B.

$-\dfrac{1}{2}$ C.

$\dfrac12$ D.

$\dfrac{\sqrt3}{2}$ E.

$-\dfrac{\sqrt3}{2}$

Арккосинусын утга

$\arccos(-0.5)=?$

A.

$-\dfrac{2\pi}{3}$ B.

$\dfrac{2\pi}{3}$ C.

$\dfrac{\pi}{3}$ D.

$-\dfrac{\pi}{3}$ E.

$0.5$

Бодлого №6731

$\sin\left(2\arctg\dfrac 13\right)+\cos\left(\arctg2\sqrt{2}\right)$ хялбарчил.

A.

$\dfrac 45$ B.

$\dfrac1{15}$ C.

$\dfrac 23$ D.

$\dfrac{14}{15}$ E.

$\dfrac 13$

Бодлого №6732

$\sin\left(2\arctg\dfrac 12\right)-\tg\left(\dfrac 12\arcsin\dfrac{15}{17}\right)$ -хялбарчил.

A.

$\dfrac{24}{25}$ B.

$-\dfrac15$ C.

$\dfrac 15$ D.

$-\dfrac{24}{25}$ E.

$\dfrac 45$

ЭЕШ 2012 B №10

$\arccos(\cos230^\circ)$ -ыг градусаар илэрхийл.

A.

$100^\circ$ B.

$110^\circ$ C.

$130^\circ$ D.

$160^\circ$ E.

$230^\circ$

ЭЕШ 2010 B №18

$\dfrac{1}{\pi}\Big(2\arctg\dfrac14+\arctg\dfrac{7}{23}\Big)$ илэрхийллийн утгыг тооцоол.

A.

$\dfrac13$ B.

$\dfrac34$ C.

$\dfrac{1}{6}$ D.

$\dfrac{1}{2}$ E.

$\dfrac{1}{4}$

Тригонометрийн илэрхийлэл бодох

$\cos(\arctg(-\sqrt{3}))$ илэрхийллийн утгыг ол.

A.

$0$ B.

$-\dfrac12$ C.

$\dfrac12$ D.

$-\dfrac{\sqrt3}{2}$ E.

$\dfrac{\sqrt3}{2}$

Тригонометрийн урвуу функц

2.9 Үйлдлийг гүйцэтгэ.

$\frac{4}{5}(1+9^{log_38})^{log_{65}{5}}$
$8^{2-2\log_{4}\sqrt3}+ \frac{1}{3}\cdot7^{log_{49}{4}}$

2.10.

$a$ - г

$b$ - ээр илэрхийл.

$\log_{30}{3}=a$ , $\log_{30}{5}=b$ , $\log_{30}{8}$ - г
$\log_{7}{12}=a$ , $\log_{12}{24}=b$ , $\log_{54}{168}$ - г

2.11 Дараах илэрхийллийг хялбарчил:

$\frac{\log_3{12}}{\log_{36}{3}} - \frac{\log_3{4}}{\log_{108}{3}}$

Тангесийн нийлбэр

$\tg\Big(\arcsin\dfrac45+\dfrac{3\pi}{2}\Big)=-\dfrac{\fbox{a}}{\fbox{b}}$ тооцоол.

Бодлого №766

$\cos3x+\sin3x=\sqrt2, \dfrac{7\pi}4\le x\le\dfrac{9\pi}4$ тэгшитгэлийг бод.

Бодлого №767

$\sin\dfrac x4+\cos\dfrac x4=1$ тэгшитгэлийг бод.

Бодлого №768

$\sin x+\cos x=\sqrt2$ тэгшитгэлийг

$[-\pi, \pi]$ завсарт бод.

Бодлого №769

$1+\cos2x+\sin2x=0$ тэгшитгэлийг бод.

Бодлого №770

$\sin x-\cos x=1$ тэгшитгэлийг

$[-3\pi, 4\pi]$ бод.

Бодлого №771

$\sin x+\cos x=\sqrt2\sin5x$ тэгшитгэлийг бод.

Бодлого №772

$\sin x+\cos x=\sin 2x+\cos 2x$ тэгшитгэлийг бод.

Бодлого №773

$\sqrt3\sin2x-\cos2x-2=0$ тэгшитгэлийг бод.

Бодлого №774

$\dfrac{\sqrt3}2\sin x+\dfrac12\cos x=\dfrac12$ тэгшитгэлийг бод.

Бодлого №775

$\sin x+\sqrt3\cos x=2$ тэгшитгэлийг бод.

Бодлого №776

$\sqrt3\cos x+\sin x+\sqrt2=0$ тэгшитгэлийг бод.

Бодлого №777

$\cos 7x-\sin 5x=\sqrt3(\cos5x-\sin 7x)$ +тэгшитгэлийн

$0^\circ< x< 30^\circ$ муж дахь хамгийн их шийдийг ол.

Бодлого №778

$\sqrt{3}(\cos x-\sin 3x)=\cos3x-\sin x, 0^\circ\le x\le 20^\circ$ тэгшитгэлийг бод.

Бодлого №779

$(\sin2x-\sqrt3\cos2x)^2-5=\cos\left(\dfrac\pi6-2x\right)$ тэгшитгэлийг бод.

Бодлого №780

$(\sin x+\sqrt{3}\cos x)^2-5=\cos\left(\dfrac\pi6-x\right)$ тэгшитгэлийг бод.

Бодлого №907

$5\cos x+2\sin x=3$ тэгшитгэлийг бод.

Бодлого №908

$\sin2x-4\cos2x=4$ тэгшитгэлийг бод.

Бодлого №910

$3\sin2x-4\cos2x=5$ тэгшитгэлийг бод.

Бодлого №911

$\cos 2x+3\sin 2x=2$ тэгшитгэлийг бод.

Бодлого №912

$\cos2x+3\sin2x=2$ тэгшитгэлийг бод.

Бодлого №913

$6\sqrt3\sin x+4\cos x=7$ тэгшитгэлийг бод.

Бодлого №914

$\dfrac{2}{\pi}\sin x+\cos(19\pi)=\cos x$ тэгшитгэлийг бод.

Тригонометрийн тэгшитгэл, тэнцэтгэл биш

$0^{\circ}\leq \theta< 360^{\circ}$ үед дараах тэгшитгэл, тэнцэтгэл бишийг бод.

$\cos \theta+\sqrt{3}\sin \theta+1=0$
$\cos 2\theta+\sqrt{3}\sin 2\theta+1>0$

$a\sin \theta+b\cos \theta$ -ийн хувиргалт

Дараах илэрхийллийг

$r\sin(\theta+\alpha)$ ,

$r>0$ ,

$-180^{\circ}< \alpha\leq 180^{\circ}$ хэлбэрт хувирга.

$\sqrt{3}\sin\theta-\cos \theta$
$\cos \theta-\sin(30^{\circ}-\theta)$

Бодлого №10601

Дараах илэрхийллүүдийг

$r\cdot\sin(\theta+\alpha)$ хэлбэрт хувирга.

$\sin \theta-\cos \theta$
$2\sin \theta+3\cos\theta$
$\sin(\theta+90^{\circ})+\sin \theta$
$\sin(\theta+30^{\circ})+\cos (\theta-60^{\circ})$
$\sin \theta+\sqrt{3}\cos (\theta+60^{\circ})$

Бодлого №10604

$0^{\circ}\leq \theta< 360^{\circ}$ үед дараах тэгшитгэл, тэнцэтгэл бишийг бод.

$\sin \theta+\sqrt{3}\cos\theta=\sqrt{2}$
$\sin\theta< \sqrt{3}\cos \theta$
$\sqrt{3}\sin 2\theta+\cos2\theta< 1$

ЭЕШ 2006 C №21

$5\cos^2x+\dfrac56\sin2x=1$ тэгшитгэл

$[\pi/2; 3\pi/2]$ завсарт хэдэн шийдтэй вэ?

A.

$6$ B.

$7$ C.

$2$ D.

$1$ E.

$3$

$a\sin x+b\cos x=c$ хэлбэрийн тэгшитгэл бодох

$\cos x+\sin x= \sqrt{2}$ тэгшитгэлийг бод.

A.

$\dfrac{\pi}{2}+\pi k , k\in \mathbb{Z}$ B.

$\dfrac{\pi}{4}+\pi k \cup -\dfrac{\pi}{4}+\pi k , k\in \mathbb{Z}$ C.

$\dfrac{\pi}{4}+2\pi k , k\in \mathbb{Z}$ D.

$\dfrac{\pi}{4}+\pi k , k\in \mathbb{Z}$ E.

$-\dfrac{\pi}{4}+\pi k , k\in \mathbb{Z}$

$a\sin x\pm b\cos x=\sqrt{a^2+b^2}\sin(x\pm\alpha)$ хувиргалт

$f(x)=7\sin x - 24 \cos x$ функцийн хамгийн их ба хамгийн бага утгуудын ялгаврыг ол.

A. 25 B. 24 C. 48 D. 49 E. 50

Бодлого №5065

$\displaystyle\sin x+\cos x=\frac{\sqrt 6}{2}$ бол

$\sin 2x$ хэдтэй тэнцүү вэ?

A.

$\displaystyle\frac{1}{4}$ B.

$\displaystyle\pm\frac{1}{2}$ C.

$\displaystyle\frac{1}{2}$ D.

$1$ E.

$0$

Туслах өнцөг оруулах арга

$2\sin 17x+\sqrt{3}\cos 5x+\sin 5x=0$ тэгшитгэлийг бод.

A.

$-\dfrac{\pi}{33}+\dfrac{\pi k}{22}, \dfrac{\pi}{9}+\dfrac{\pi k}{6};$ B.

$-\dfrac{\pi}{66}+\dfrac{\pi k}{11}, \dfrac{\pi}{9}+\dfrac{\pi k}{6};$ C.

$-\dfrac{\pi}{66}+\dfrac{\pi k}{33}, \dfrac{\pi}{6}+\dfrac{\pi k}{3};$ D.

$-\dfrac{\pi}{11}+\dfrac{\pi k}{3}, \dfrac{\pi}{3}+\dfrac{2\pi k}{3}$ E.

$\varnothing$

Бодлого №6782

$5\sin x-12\cos x+13\sin 3x=0$ тэгшитгэлийг бод.

A.

$\frac 13\arccos\frac{5}{12}+\frac{\pi k}{3}, \frac{\pi}{3}-\frac 12\arccos\frac{5}{13}+\pi k;$ B.

$\frac 13\arccos\frac{12}{13}+\frac{2\pi k}{3}, \frac{\pi}{2}-\frac 12\arccos\frac{12}{13}+\pi k;$ C.

$\frac 14\arccos\frac{5}{13}+\frac{\pi k}{2}, \frac{\pi}{2}-\frac 12\arccos\frac{5}{13}+\pi k;$ D.

$\frac 14\arccos\frac{12}{13}+\frac{\pi k}{4}, \frac{\pi}{3}-\frac 13\arccos\frac{12}{13}+\pi k; (k\in Z)$

Бодлого №6783

$(\sin x+\sqrt{3}\cos x)^2-5=\cos\left(\dfrac{\pi}{6}-x\right)$ тэгшитгэлийг бод.

A.

$\frac{7\pi}{6}+2\pi k;$ B.

$\frac{\pi}{6}+\pi k;$ C.

$\frac{5\pi}{6}+2\pi k;$ D.

$\frac{7\pi}{6}+\pi k; (k\in Z)$

Бодлого №6784

$(\sqrt{3}\sin x-\cos x)^2+1=4\cos\left(x+\dfrac{\pi}{3}\right)$ тэгшитгэлийг бод.

A.

$\pi n;\frac{\pi}{3}+\pi k;$ B.

$2\pi k;-\frac{2\pi}{3}+2\pi n;$ C.

$2\pi k,\pm\frac{\pi}{3}+2\pi n;$ D.

$\pi k,-\frac{2\pi}{3}+2\pi n; (k, n\in Z)$

Бодлого №6795

$\cos 7x-\sqrt{3}\sin 7x=-\sqrt{2}$ тэгшитгэлийн

$\dfrac{2}{5}\pi < x< \dfrac{6}{7}\pi$ нөхцөлийг хангах хамгийн их шийдийг, хамгийн бага шийдэд харьцуулсан харьцааг ол.

A.

$\frac{59}{35};$ B.

$\frac{84}{35};$ C.

$\frac{84}{59};$ D.

$\frac{33}{17};$

Бодлого №6796

$\sqrt{2}\cos 8x+\sqrt{2}\sin 8x=-1$ тэгшитгэлийн

$\dfrac{3\pi}{8}< x< \dfrac{7\pi}{10}$ нөхцөлийг хангах хамгийн бага шийдийг хамгийн их шийдэд харьцуулсан харьцааг ол.

A.

$\frac{43}{67};$ B.

$\frac{67}{96};$ C.

$\frac{37}{48};$ D.

$\frac{23}{43};$

Бодлого №6847

$3\cos 2x-8m\cdot \sin 2x=-5$ тэгшитгэл

$m$ -ийн ямар утганд шийдгүй байх вэ?

A.

$-\frac 12< m<\frac 13;$ B.

$0<m< \frac 12;$ C.

$-\frac 12< m<0;$ D.

$-\frac 12< m< \frac 12;$

Бодлого №6848

$12\sin x+4\sqrt{3}\cos x=m\sqrt{3}$ тэгшитгэл

$m$ -ийн ямар утганд шийдтэй байх вэ?

A.

$m\leq -8\vee m\geq 8;$ B.

$-8\leq m\leq 8;$ C.

$m\leq -8;$ D.

$8\leq m;$

Их шийд ба бага шийдийн харьцаа

$\sqrt{2}\cos 8x+\sqrt{2}\sin 8x=-1$ тэгшитгэлийн

$\dfrac{3\pi}{8}< x< \dfrac{7\pi}{10}$ нөхцөлийг хангах хамгийн бага шийдийг хамгийн их шийдэд харьцуулсан харьцааг ол.

A.

$\dfrac{43}{67}$ B.

$\dfrac{67}{97}$ C.

$\dfrac{34}{67}$ D.

$\dfrac{43}{97}$ E.

$\dfrac{50}{67}$

Бодлого №14875

$\displaystyle\sin x-\cos x=\frac{\sqrt 6}{2}$ бол

$\sin 2x$ хэдтэй тэнцүү вэ?

A.

$-\dfrac{1}{2}$ B.

$\displaystyle\pm\frac{1}{2}$ C.

$\dfrac{1}{4}$ D.

$1$ E.

$0$

Бодлого №6872

$\dfrac{\sqrt{2}}{2}(\cos \alpha+\sin\alpha) =\cos\left(\dfrac{\pi}{\fbox{a}}-\alpha\right).$

Бодлого №7303

$f(x)=5\sin x+3\cos x$ бол

$f'(x)=f'(0)$ тэгшитгэлийн шийдүүд нь

$x_1=\fbox{a}\cdot m\pi$ ;

$x_2=\fbox{b}\cdot m\pi-2\arctg \displaystyle\frac{\fbox{c}}{\fbox{d}}$ ;

$m\in Z$ болно.

Бодлого №7304

$f(x)=5\sin x+3\cos x$ бол

$f'(x)=f'(\pi)$ тэгшитгэлийн шийдүүд нь

$x_1=(\fbox{a}\cdot k+1)\pi,$

$x_2=2k\pi+\fbox{b}\cdot \arcctg \displaystyle\frac{\fbox{c}}{\fbox{d}}$ ;

$k\in Z$ болно.

ЭЕШ 2011 C №13

$x_0$ нь

$2-\cos 2x-2\sin 2x=0$ тэгшитгэлийн хамгийн бага эерэг язгуур бол

$\tg x_0$ хэд вэ?

A.

$1$ B.

$3$ C.

$\frac14$ D.

$4$ E.

$\frac13$

ЭЕШ 2017 D №12

$\tg\alpha=\dfrac{4}{5}$ бол

$\cos2\alpha=?$

A.

$\dfrac35$ B.

$-\dfrac{9}{41}$ C.

$\dfrac{15}{17}$ D.

$\dfrac{9}{41}$ E.

$-\dfrac{15}{17}$

ЭЕШ 2017 D №12

$\tg\alpha=\dfrac{3}{5}$ бол

$\sin2\alpha=?$

A.

$\dfrac35$ B.

$-\dfrac{9}{41}$ C.

$-\dfrac{15}{17}$ D.

$\dfrac{9}{41}$ E.

$\dfrac{15}{17}$

Бодлого №539

$\cos\alpha=0.8$ ба

$0^{\circ}< \alpha< 90^{\circ}$ бол

$\tg\alpha$ илэрхийллийн утгыг ол.

Бодлого №540

$\cos\alpha=-0.8$ ба

$\alpha\in\Big(\pi;\dfrac{3\pi}{2}\Big)$ бол

$\tg\alpha$ илэрхийллийн утгыг ол.

Бодлого №544

$\cos\alpha=\dfrac{\sqrt3}{2}$ ба

$\dfrac{3\pi}{2}< \alpha< 2\pi$ бол

$\sin\alpha$ илэрхийллийн утгыг ол.

Бодлого №545

$\tg\alpha=\sqrt{15}$ ба

$0^{\circ}< \alpha< 90^{\circ}$ бол

$\cos\alpha$ илэрхийллийн утгыг ол.

Бодлого №551

$\sin\alpha=-\dfrac{1}{3},\cos\beta=-\dfrac23$ ба

$\pi< \alpha,\beta< \dfrac{3\pi}{2}$ бол

$\sin(\alpha+\beta)$ -г ол.

Бодлого №559

$\sin\alpha=\dfrac{8}{17},\sin\beta=\dfrac{15}{17}$ ба

$\alpha$ ,

$\beta\in\big(\frac{\pi}{2};\pi\big)$ бол

$\sin(\alpha+\beta)$ илэрхийллийн утгыг ол.

Бодлого №561

$\tg\alpha=\dfrac{12}{5}$ ба

$\pi< \alpha< \dfrac{3\pi}{2}$ бол

$\sin\alpha$ илэрхийллийн утгыг ол.

Бодлого №563

$\tg\alpha=-4$ ба

$-90^{\circ}< \alpha< 90^{\circ}$ бол

$5\sqrt{17}\sin\alpha$ илэрхийллийн утгыг ол.

Бодлого №573

$\sin\alpha=\dfrac45$ ба

$\dfrac{\pi}{2}< \alpha< \pi$ бол

$\cos\Big(\dfrac{\pi}{3}+\alpha\Big)$ илэрхийллийн утгыг ол.

Бодлого №577

$\sin\alpha=a$ ба

$\alpha\in\Big[\dfrac{\pi}{2};\pi\Big]$ бол

$\cos\Big(\alpha+\dfrac{\pi}{4}\Big)$ илэрхийллийн утгыг ол.

Бодлого №578

$\cos\alpha=a$ ба

$\alpha\in\Big(0;\dfrac{\pi}{4}\Big)$ бол

$\sin2\alpha$ ,

$\cos\Big(2\alpha+\dfrac{\pi}{4}\Big)$ илэрхийллийн утгыг ол.

Бодлого №579

$\sin(\pi-x)=a$ ба

$x\in\Big[-\pi;-\dfrac{\pi}{2}\Big]$ бол

$\ctg\Big(\dfrac{\pi}{2}-x\Big)$ илэрхийллийн утгыг ол.

Бодлого №580

$\tg(\pi+x)=a$ ба

$x\in\Big[\pi;\dfrac{3\pi}{2}\Big]$ бол

$\cos\Big(\dfrac{\pi}{2}-x\Big)$ илэрхийллийн утгыг ол.

Бодлого №588

$\cos\alpha=\dfrac{1}{\sqrt3}$ бол

$\tg^{-2}\Big(\dfrac{7\pi}{2}+2\alpha\Big)$ илэрхийллийн утгыг ол.

Бодлого №605

$\sin\alpha=-\dfrac{5}{13}$ ба

$\pi< \alpha< \dfrac{3\pi}{2}$ бол

$\ctg\alpha-2\tg\dfrac{\alpha}{2}$ илэрхийллийн утгыг ол.

Бодлого №661

$\cos2\alpha=\sin\alpha$ ба

$\alpha\in\left(\dfrac{\pi}{2},\pi\right)$ бол

$\cos\alpha$ -г ол.

Тригонометрийн үндсэн адилтгал

$180^{\circ}\leq\theta\leq 360^{\circ}$ ба $\cos\theta=-\dfrac{24}{25}$ бол $\sin\theta$ , $\tg\theta$ -ийн утгыг ол.
$90^{\circ}\leq \theta\leq 270^{\circ}$ ба $\tg \theta=-3$ бол $\sin\theta$ , $\cos\theta$ -ийн утгыг ол.

Бодлого №10546

$\sin \theta$ ,

$\cos \theta$ ,

$\tg \theta$ -ийн нэг нь өгөгдсөн үед нөгөө хоёрыг ол.

$\sin \theta=-\dfrac 2{\sqrt{5}}, 270^{\circ}< \theta< 360^{\circ}$
$\cos \theta=\dfrac13$ , $180^{\circ}< \theta< 360^{\circ}.$
$\tg \theta=2+\sqrt{3}$

Бодлого №10558

$\theta$ нь III мужийн өнцөг ба

$\tg\theta=\sqrt{2}$ бол дараах илэрхийллийн утгыг ол.

$\dfrac{\cos^2\theta}{1+2\sin\theta\cdot \cos\theta}$
$\dfrac{1-\sin\theta}{\cos\theta}+\dfrac{\cos\theta}{1-\sin\theta}$

Бодлого №10566

$\alpha$ нь I мужийн өнцөг ба

$\sin\alpha=\dfrac5{13}$ ,

$\beta$ нь III мужийн өнцөг ба

$\cos\beta=-\dfrac 35$ гэе.

$\sin(\alpha-\beta)=\ebox$ ,

$\cos(\alpha+\beta)=\ebox$ ,

$\cos(\alpha-\beta)=\ebox.$

ЭЕШ 2007 A1 №12

$\ctg\beta=2$ бол

$\dfrac{7\cos\beta}{11\sin^3\beta+3\cos^3\beta}$ илэрхийллийн утгыг ол.

A.

$1$ B.

$2$ C.

$3$ D.

$4$ E.

$5$

Үндсэн адилтгал

$\sin\alpha=\dfrac34$ бол

$\tg^2\alpha=?$

A.

$\dfrac 43$ B.

$\dfrac 54$ C.

$\dfrac 79$ D.

$\dfrac 97$ E.

$1$

Хурц өнцгийн синус ба тангес

$\theta$ өнцөг нь хурц бөгөөд

$\cos\theta=\dfrac{x}{y}$ ,

$x>0$ ,

$y>0$ ба

$x\neq y$ бол

$\tg\theta=?$

A.

$\dfrac{y}{\sqrt{x^2+y^2}}$ B.

$\dfrac{\sqrt{y^2-x^2}}{\sqrt{x^2+y^2}}$ C.

$\dfrac{\sqrt{y^2-x^2}}{x}$ D.

$\dfrac{\sqrt{y^2-x^2}}{y}$ E.

$\dfrac{x^2+y^2}{xy}$

Синус ба косинусуудын нийлбэр ба үржвэрийн хамаарал

Хэрэв

$\sin\alpha+\cos\alpha=\dfrac13$ бол

$\sin\alpha\cdot\cos\alpha=?$

A.

$\dfrac{11}{18}$ B.

$-\dfrac49$ C.

$-\dfrac34$ D.

$\dfrac52$ E.

$\dfrac58$

Бодлого №5673

$\sin^440^\circ-\cos^440^\circ=?$

A.

$\cos80^\circ$ B.

$\sin80^\circ$ C.

$\cos100^\circ$ D.

$\sin100^\circ$ E.

$1$

Бодлого №5678

Хэрэв

$\alpha\in\big(0;\frac\pi2\big)$ ба

$\sin\alpha=\frac35$ бол

$\cos\alpha\cdot(\tg\alpha+\ctg\alpha)$ хэдтэй тэнцүү вэ?

A.

$\dfrac35$ B.

$\dfrac53$ C.

$-\dfrac35$ D.

$-\dfrac53$ E.

$\dfrac45$

Эмхэтгэлийн томьёо

$0< t< \dfrac{\pi}{2}$ ба

$\sin(4\pi+t)=\dfrac 35$ бол

$\tg (\pi-t)=?$

A.

$-\dfrac 54$ B.

$-\dfrac34$ C.

$-\dfrac 23$ D.

$-\dfrac 43$ E.

$-\dfrac 12$

$\dfrac{3\pi}{2}< t< 2\pi$ ба

$\cos (2\pi+t)=\dfrac{12}{13}$ бол

$\ctg (\pi-t)=?$

A.

$\dfrac{13}{5}$ B.

$-\dfrac{13}{12}$ C.

$-\dfrac{12}5$ D.

$\dfrac{12}{5}$ E.

$\dfrac{13}{12}$

Бодлого №6769

$\dfrac{\pi}{2}< \alpha< \pi,$

$\dfrac{\pi}{2}< \beta< \pi,$

$\sin\alpha=\dfrac 45,$

$\cos\beta=-\dfrac{15}{17}$ бол

$\sin(\alpha+\beta)=?$

A.

$-\frac{84}{85};$ B.

$-\frac{7}{17};$ C.

$-\frac{28}{85};$ D.

$-\frac{12}{17};$

Нийлбэрийн косинусын томьёо

$0< \alpha< \dfrac{\pi}{2}$ ,

$\dfrac{3\pi}{2}< \beta< 2\pi$ ,

$\sin\alpha=\dfrac{9}{41}$ ,

$\sin\beta=-\dfrac{40}{41}$ бол

$\cos(\alpha+\beta)=?$

A.

$\dfrac{1600}{1681}$ B.

$\dfrac{720}{1681}$ C.

$\dfrac{360}{1681}$ D.

$\dfrac{369}{1681}$ E.

$\dfrac{365}{1681}$

Ялгавар өнцгийн косинус

$\sin\alpha+\sin\beta=1,$

$\cos\alpha+\cos\beta=\sqrt{2}$ бол

$\cos(\alpha-\beta)=?$

A.

$\dfrac 13$ B.

$\dfrac 12$ C.

$\dfrac{1-\sqrt{2}}{2}$ D.

$\dfrac{\sqrt{2}}{4}$ E.

$-\dfrac12$

Үндсэн адилтгал

$\alpha$ нь III мужийн өнцөг ба

$\tg\alpha=3$ бол

$\cos\alpha$ хэд байх вэ?

A.

$-\dfrac13$ B.

$\dfrac3{10}$ C.

$-\dfrac3{10}$ D.

$-\dfrac{\sqrt{10}}{10}$ E.

$\dfrac{\sqrt{10}}{10}$

Үндсэн адилтгал

$\alpha$ нь II мужийн өнцөг ба

$\tg\alpha=-2$ бол

$\cos\alpha$ хэд байх вэ?

A.

$-\dfrac13$ B.

$\dfrac1{2}$ C.

$-\dfrac1{4}$ D.

$\dfrac{\sqrt{5}}{5}$ E.

$-\dfrac{\sqrt{5}}{5}$

$\sec$ функц

$\alpha$ ,

$\beta$ нь хурц өнцөг болно.

$\cos\alpha=\dfrac{15}{17}$ ба

$\cos\beta=\dfrac{3}{5}$ бол

$\sin(\alpha+\beta)=?$

A.

$\dfrac{84}{85}$ B.

$\dfrac{56}{57}$ C.

$\dfrac{7}{8}$ D.

$\dfrac{37}{38}$ E.

$\dfrac{99}{100}$

Давхар өнцгийн синус

$\sin\alpha+\cos\alpha=m$ бол

$\sin2\alpha=?$

A.

$m^2$ B.

$m^2-1$ C.

$\dfrac{m^2-1}{2}$ D.

$-\dfrac{m^2-1}{2}$ E.

$1-m^2$

Нийлбэрийн томьёо ба үндсэн адилтгалыг хэрэглэх

$x$ ба

$y$ нь II мужийн өнцгүүд ба

$\sin x=\dfrac{2}{\sqrt{5}}$ ,

$\sin y=\dfrac{3}{5}$ бол

$\sin(x-y)$ хэдтэй тэнцүү вэ?

A.

$-\dfrac{2\sqrt{5}}{25}$ B.

$-\dfrac{\sqrt{5}}{25}$ C.

$-\dfrac{2}{25}$ D.

$-\dfrac{\sqrt{5}}{5}$ E.

$-\dfrac{22}{25}$

Тангесийн утга олох

Хэрэв

$\tg\alpha=3$ бол

$\dfrac{\sin\alpha}{\sin^3\alpha+\cos^3\alpha}=?$

A.

$\dfrac{15}{14}$ B.

$\dfrac{7}{9}$ C.

$1$ D.

$\dfrac{10}{9}$ E.

$\dfrac{35}{28}$

tan utga oloh

$\dfrac{\pi}2\leq\theta\leq\pi$ байх

$\theta$ -ийн хувьд

$\sin^2\theta-\cos^2\theta=\dfrac13$ бол

$\tan\theta$ -г ол.

A.

$\sqrt2$ B.

$\frac1{\sqrt2}$ C.

$1$ D.

$-\frac1{\sqrt2}$ E.

$-\sqrt2$

2-р мөчийн өнцгийн синус

$\alpha$ нь 2-р мөчид байрлах ба

$\tg\alpha=-\dfrac{15}{8}$ бол

$\sin\alpha=?$

A.

$\dfrac{8}{17}$ B.

$\dfrac{15}{17}$ C.

$-\dfrac{17}{15}$ D.

$-\dfrac{8}{17}$ E.

$\dfrac{8}{15}$

ЭЕШ 2017 D №12

$\tg\alpha=\dfrac{5}{12}$ ба

$\pi<\alpha<\dfrac{3\pi}{2}$ бол

$\cos\alpha=?$

A.

$-\dfrac45$ B.

$\dfrac{12}{13}$ C.

$-\dfrac35$ D.

$-\dfrac{12}{13}$ E.

$-\dfrac{5}{13}$

ЭЕШ 2017 B №12

$\ctg\alpha=\dfrac{5}{12}$ ба

$\pi<\alpha<\dfrac{3\pi}{2}$ бол

$\cos\alpha=?$

A.

$-\dfrac45$ B.

$\dfrac{12}{13}$ C.

$-\dfrac35$ D.

$-\dfrac{5}{13}$ E.

$-\dfrac{12}{13}$

$\dfrac{3\pi}{2}< t< 2\pi$ ба

$\cos (2\pi+t)=\dfrac{12}{13}$ бол

$\ctg (\pi-t)=?$

A.

$\dfrac{13}{5}$ B.

$-\dfrac{13}{12}$ C.

$-\dfrac{12}5$ D.

$\dfrac{12}{5}$ E.

$\dfrac{13}{12}$

2018 №A.27

Хэрэв

$\tg\alpha=2$ бол

$\sqrt{2\ctg\alpha+\dfrac{1}{\sin^2\alpha}}$ илэрхийллийн утгыг ол.

A.

$3$ B.

$1.5$ C.

$1$ D.

$\dfrac23$ E.

$0$

$\sec$ функц

$\alpha$ ,

$\beta$ нь хурц өнцөг болно.

$\cos\alpha=\dfrac{15}{17}$ ба

$\cos\beta=\dfrac{3}{5}$ бол

$\cos(\alpha+\beta)=?$

A.

$-\dfrac{13}{85}$ B.

$-\dfrac{16}{57}$ C.

$-\dfrac{3}{8}$ D.

$-\dfrac{17}{38}$ E.

$-\dfrac{33}{100}$

Бодлого №15536

$\sin^480^\circ-\cos^480^\circ=?$

A.

$\cos20^\circ$ B.

$\sin20^\circ$ C.

$\cos80^\circ$ D.

$\sin80^\circ$ E.

$0$

Үндсэн адилтгал, ялгавар өнцгийн синус

$\sin\alpha=-\dfrac{12}{13}$ ,

$\cos\beta=\dfrac{24}{25}$ ба

$0<\beta<\dfrac{\pi}{2}$ ,

$\pi<\alpha<\dfrac{3\pi}{2}$ бол

$\sin(\alpha-\beta)=-0.\fbox{abc}\dots$ байна.

Нийлбэр ялгавар өнцгийн синусын томьёо

$\alpha$ нь I мужийн өнцөг ба

$\sin\alpha=\dfrac{5}{13}$ ,

$\beta$ нь III мужийн өнцөг ба

$\cos\beta=-\dfrac{3}{5}$ гэе.

$\sin(\alpha-\beta)=\dfrac{\fbox{ab}}{\fbox{cd}}$ ,

$\sin(\alpha+\beta)=-\dfrac{\fbox{ef}}{\fbox{gh}}$ .

Үндсэн адилтгал

$\cos x=\dfrac 14$ ;

$\sin x< \cos x$ бол

$\tg x=\fbox{a}\sqrt{\fbox{bc}}$ байна.

Бодлого №6854

$\sin x=\dfrac 35; \cos x< \sin x$ бол

$\tg x=\fbox{a}\dfrac{\fbox{c}}{\fbox{b}}$ байна.

Бодлого №6861

$\sin\alpha=-\dfrac 35 \Bigl(|\alpha|< \dfrac{\pi}{2}\Bigr), \cos\beta=\dfrac{5}{13} \Bigl(-\pi< \beta< 0\Bigr)$ бол

$\sin(\alpha-\beta)=\dfrac{\fbox{ab}}{\fbox{cd}}$ байна.

Бодлого №6862

$\sin\alpha=-\dfrac 45 \Bigl(|\alpha|< \dfrac{\pi}{2}\Bigr),$

$\sin \beta=-\dfrac{12}{13} \left(\dfrac{\pi}{2}< |\beta|< \pi\right)$ бол

$\cos(\alpha+\beta)=-\dfrac{\fbox{cd}}{\fbox{ab}}$ байна.

Бодлого №567

$8(\sqrt3-\sqrt2)\sin52^{\circ}30'\cdot\cos7^{\circ}30'$ илэрхийллийн утгыг ол.

Бодлого №826

$\sin3x\cos x=\sin5x\cos3x$ тэгшитгэлийг бод.

Бодлого №827

$\sin2x\cos5x-\sin3x\cos4x$ тэгшитгэлийг бод.

Бодлого №828

$\cos\pi x\sin7\pi x=\cos3\pi x\sin5\pi x$ тэгшитгэлийн

$[1, 2]$ муж дахь шийдийн тоог ол.

Бодлого №829

$2\sin3x\sin2x-\cos x+1=0, -250^\circ< x< -200^\circ$ тэгшитгэлийг бод.

Бодлого №830

$2\sin2x\cos3x+\sin x+\cos2x=0$ тэгшитгэлийг бод.

Бодлого №831

$\sin5x-1=2\sin x\cos 4x, -100^\circ< x< -10^\circ$ тэгшитгэлийг бод.

Бодлого №832

$2\cos5x\cos8x-\cos13x=0$ тэгшитгэлийн хамгийн бага эерэг шийдийг градусаар илэрхийл.

Бодлого №833

$2\sin x\sin8x=\cos7x, 150^\circ< x< 180^\circ$ тэгшитгэлийг бод.

Бодлого №834

$4\sin\left(x-\dfrac\pi3\right)\cos x=-\sqrt3, -1\le x\le 3$ тэгшитгэлийг бод.

Бодлого №835

$\cos(x+70^\circ)\cos(x+10^\circ)=\sin30^\circ$ тэгшитгэлийн

$[-10^\circ, 170 ^\circ]$ муж дахь шийдийн тоог ол.

Бодлого №836

$\sin\left(x+\dfrac\pi4\right)\sin\left(x-\dfrac\pi4\right)=\dfrac14$ тэгшитгэлийг бод.

Бодлого №837

$2\sin x\cos 2x=\sin3x-\dfrac{\sqrt3}2$ тэгшитгэлийг бод.

Бодлого №838

$\cos(70^\circ+x)\cos(20^\circ-x)=\dfrac12, 0^\circ< x< 180^\circ$ тэгшитгэлийг бод.

Бодлого №839

$2\cos3x\sin x+2\cos^2\left(\dfrac\pi4-x\right)=1$ тэгшитгэлийг бод.

Бодлого №840

$2(\sin6x-\sin4x\sin2x)=\cos6x+\cos2x$ тэгшитгэлийг бод.

Бодлого №841

$\sin x\sin3x=\dfrac12$ тэгшитгэлийг бод.

Бодлого №842

$\dfrac x2\cos{3x}2-\sin x\sin3x-\sin2x\sin3x$ тэгшитгэлийг бод.

Бодлого №843

$\sin3x=4\sin x\cos2x$ тэгшитгэлийг бод.

Нийлбэр, ялгавар, үржвэрийн томьёонууд

Дараах утгыг ол.

$\cos 15^{\circ}-\cos 75^{\circ}$
$\sin40^{\circ}\cdot\cos70^{\circ}\cdot \sin 80^{\circ}$

Бодлого №10579

Нийлбэр, үржвэрийн томъёог хэрэглэж, дараах утгыг ол.

$\sin 75^{\circ}\cdot \cos 15^{\circ}$
$\cos 45^{\circ}\cdot \sin 75^{\circ}$
$\sin 105^{\circ}\cdot \sin 45^{\circ}$
$\cos45^{\circ}\cdot \cos 75^{\circ}$
$\sin 75^{\circ}+\sin 15^{\circ}$
$\sin 75^{\circ}-\sin 15^{\circ}$
$\cos 105^{\circ}+\cos 15^{\circ}$
$\cos 105^{\circ}-\cos 15^{\circ}$

Бодлого №10580

Илэрхийллийг хялбарчил.

$\sin20^{\circ}\cdot \sin 40^{\circ}\cdot \sin80^{\circ}$
$\cos 10^{\circ}+\cos 110^{\circ}+\cos 230^{\circ}$

Үржвэрийг хялбарчил

$A=\sin\dfrac{\pi}{7}\cdot\sin\dfrac{2\pi}{7}\cdot\sin\dfrac{3\pi}{7}$ илэрхийллийн утгыг ол.

Бодлого №4796

$\dfrac{\cos3x}{\cos x}=\dfrac{\cos4x}{\cos2x}$ тэгшитгэлийн шийд аль нь вэ?

A.

$k\pi$ B.

$\dfrac{k\pi}{2}$ C.

$2k\pi$ D.

$-\dfrac{2\pi}{3}$ E.

$\dfrac{2\pi}{3}$

Хялбарчил

$2\cos140^\circ\cdot\sin(-40^\circ)$

A.

$-\sin10^\circ$ B.

$-\cos10^\circ$ C.

$\cos10^\circ$ D.

$\sin40^\circ$ E.

$\cos20^\circ$

Бодлого №6791

$\cos 11x-\cos 7x\cdot \sin \left(\dfrac{13\pi}{2}-4x\right)=0$ тэгшитгэлийг бод.

A.

$\frac{\pi k}{11}, \dfrac{\pi n}{7};$ B.

$\frac{\pi k}{7}, \frac{\pi n}{4};$ C.

$\frac{\pi}{8}+\frac{\pi k}{4}, \frac{\pi}{14}+\frac{\pi n}{7};$ D.

$\frac{\pi}{14}+\frac{\pi k}{7}; (k,n\in Z)$

Нийлбэрийг үржвэрт хувиргах, косинусуудын нийлбэр

$\cos 15^\circ+\cos 75^\circ$ илэрхийллийн утга аль нь вэ?

A.

$\sqrt2$ B.

$1$ C.

$2\sqrt2$ D.

$\dfrac{\sqrt6}{2}$ E.

$\dfrac{\sqrt3}{2}$

Үржвэрийг нийлбэрт хувиргах томьёо

$\sin 75^{\circ}\cdot \cos 15^{\circ}=?$

A.

$\dfrac{2-\sqrt3}{4}$ B.

$\dfrac{2+\sqrt3}{4}$ C.

$\dfrac{1}{2}$ D.

$\dfrac{\sqrt{2+\sqrt3}}{2}$ E.

$\dfrac{\sqrt{2-\sqrt3}}{2}$

Үржвэрийг нийлбэрт задлах

$\begin{align*} \sin 20^\circ\cdot\sin 40^\circ&\cdot\sin 80^\circ=\dfrac12(\cos\fbox{ab}^\circ-\cos\fbox{cd}^\circ)\cdot\sin80^\circ\\ &=\dfrac12\left(\dfrac12\cdot\dfrac{\sqrt3}{2}+\dfrac12\sin\fbox{efg}^\circ-\dfrac12\sin80^\circ\right)=\dfrac{\sqrt{\fbox{h}}}{\fbox{i}} \end{align*}$

Параметртэй тригонометр тэгшитгэл

$2\sin7x\cdot\sin 3x=\sqrt{p}-2+\cos 4x$ тэгшитгэл өгөгдөв.

Тэгшитгэлийг шийдтэй байлгах $p$ параметрийн утга нь $p\in[\fbox{a};\fbox{b}]$ байна.
$p=9$ үед тэгшитгэлийн шийд нь $x=\dfrac{\pi}{\fbox{cd}}+\dfrac{\pi k}{\fbox{e}}$ байна.

ЭЕШ 2016 C №38

$\sin7x\cdot\cos8x=\sin5x\cdot\cos6x$ тэгшитгэлийг бодоорой.

Бодолт. Үржвэр тус бүрийг нийлбэрт шилжүүлвэл:

$\dfrac{1}{\fbox{a}}(\sin\fbox{bc}x-\sin x)=\dfrac{1}{\fbox{a}}(\sin\fbox{de}x-\sin x)$ буюу

$\sin\fbox{bc}x-\sin\fbox{de}x=0$ болно. Энэ ялгаварыг үржвэрт шилжүүлвэл

$2\cdot\cos\fbox{fg}x\cdot\sin\fbox{h}x=0$ тул

$\left[\begin{array}{c}\cos\fbox{fg}x=0\\ \sin\fbox{h}x=0\end{array}\right.\Rightarrow\left[\begin{array}{c}x=\dfrac{\pi}{\fbox{fg}}(\frac12+n)\\ x=\dfrac{k\pi}{\fbox{h}}\end{array}\right. (k,n\in\mathbb Z)$

ЭЕШ 2016 D №38

$\sin9x\cdot\cos10x=\sin7x\cdot\cos8x$ тэгшитгэлийг бодоорой.

Бодолт. Үржвэр тус бүрийг нийлбэрт шилжүүлвэл:

$\dfrac{1}{\fbox{a}}(\sin\fbox{bc}x-\sin x)=\dfrac{1}{\fbox{a}}(\sin\fbox{de}x-\sin x)$ буюу

$\sin\fbox{bc}x-\sin\fbox{de}x=0$ болно. Энэ ялгаварыг үржвэрт шилжүүлвэл

$2\cdot\cos\fbox{fg}x\cdot\sin\fbox{h}x=0$ тул

$\left[\begin{array}{c}\cos\fbox{fg}x=0\\ \sin\fbox{h}x=0\end{array}\right.\Rightarrow\left[\begin{array}{c}x=\dfrac{\pi}{\fbox{fg}}(\frac12+n)\\ x=\dfrac{k\pi}{\fbox{h}}\end{array}\right. (k,n\in\mathbb Z)$

ЭЕШ 2016 B №38

$\cos7x\cdot\cos8x=\cos9x\cdot\cos10x$ тэгшитгэлийг бодоорой.

Бодолт. Үржвэр тус бүрийг нийлбэрт шилжүүлвэл:

$\dfrac{1}{\fbox{a}}(\cos\fbox{bc}+\cos x)=\dfrac{1}{\fbox{a}}(\cos\fbox{de}x+\sin x)$ буюу

$\cos\fbox{bc}x-\cos\fbox{de}x=0$ болно. Энэ ялгаварыг үржвэрт шилжүүлвэл

$2\cdot\sin\fbox{fg}x\cdot\sin\fbox{h}x=0$ тул

$\left[\begin{array}{c}\sin\fbox{fg}x=0\\ \sin\fbox{h}x=0\end{array}\right.\Rightarrow\left[\begin{array}{c}x=\dfrac{k\pi}{\fbox{fg}}\\ x=\dfrac{n\pi}{\fbox{h}}\end{array}\right. (k,n\in\mathbb Z)$

Үржвэрийг нийлбэрт шилжүүлэх

$\cos6x\cdot\cos7x=\cos8x\cdot\cos9x$ тэгшитгэлийг бодоорой.

Бодолт. Үржвэр тус бүрийг нийлбэрт шилжүүлвэл:

$\dfrac{1}{\fbox{a}}(\cos\fbox{bc}+\cos x)=\dfrac{1}{\fbox{a}}(\cos\fbox{de}x+\sin x)$ буюу

$\cos\fbox{bc}x-\cos\fbox{de}x=0$ болно. Энэ ялгаварыг үржвэрт шилжүүлвэл

$2\cdot\sin\fbox{fg}x\cdot\sin\fbox{h}x=0$ тул

$\left[\begin{array}{c}\sin\fbox{fg}x=0\\ \sin\fbox{h}x=0\end{array}\right.\Rightarrow\left[\begin{array}{c}x=\dfrac{k\pi}{\fbox{fg}}\\ x=\dfrac{n\pi}{\fbox{h}}\end{array}\right. (k,n\in\mathbb Z)$

Бодлого №542

$\sin\alpha=\sqrt{0.2}$ бол

$\cos(2\alpha-\pi)$ илэрхийллийн утгыг ол.

Бодлого №565

$\tg(\pi+\alpha)=-3$ бол

$\sin4\alpha$ илэрхийллийн утгыг ол.

Бодлого №570

$\cos2\alpha=\dfrac13$ бол

$\tg\alpha\cdot\ctg\Big(\dfrac{\pi}{2}-\alpha\Big)$ илэрхийллийн утгыг ол.

Бодлого №579

$\sin(\pi-x)=a$ ба

$x\in\Big[-\pi;-\dfrac{\pi}{2}\Big]$ бол

$\ctg\Big(\dfrac{\pi}{2}-x\Big)$ илэрхийллийн утгыг ол.

Бодлого №580

$\tg(\pi+x)=a$ ба

$x\in\Big[\pi;\dfrac{3\pi}{2}\Big]$ бол

$\cos\Big(\dfrac{\pi}{2}-x\Big)$ илэрхийллийн утгыг ол.

Бодлого №583

$\sin(\alpha-90^{\circ})=\dfrac{5}{13}$ ба

$\sin\alpha< 0$ бол

$\tg2\alpha$ илэрхийллийн утгыг ол.

Бодлого №586

$\tg\Big(\dfrac{\pi}{2}-\alpha\Big)=5$ бол

$A=\cos2\alpha+\sin2\alpha\tg\alpha+\ctg\alpha$ илэрхийллийн утгыг ол.

Бодлого №588

$\cos\alpha=\dfrac{1}{\sqrt3}$ бол

$\tg^{-2}\Big(\dfrac{7\pi}{2}+2\alpha\Big)$ илэрхийллийн утгыг ол.

Бодлого №592

$\cos x=0.5$ бол

$\ctg^2(630^{\circ}+2x)$ илэрхийллийн утгыг ол.

Бодлого №593

$\sin\Big(\dfrac{\pi}{2}+2\alpha\Big)=a$ ба

$\alpha\in\Big(\dfrac{3\pi}{2};2\pi\Big)$ бол

$\tg\alpha+\ctg\alpha$ илэрхийллийн утгыг ол.

Бодлого №601

$\sin2\alpha=-\dfrac{1}{\sqrt6}$ бол

$\tg^{-2}(\dfrac{\pi}{2}+4\alpha)$ илэрхийллийн утгыг ол.

Бодлого №602

$\sin2x=3^{-\frac12}$ бол

$\dfrac{\sin^2(4x-540^{\circ})}{\cos^2(4x-540^{\circ})}$ илэрхийллийн утгыг ол.

Дараах тригонометр функцийн утгыг ол.

$\sin 690^{\circ}$
$\cos(-120^{\circ})$
$\tg (-585^{\circ})$

Дараах утгуудыг ол.

$\sin 1020^{\circ}$
$\cos (-240^{\circ})$
$\tg 585^{\circ}$

Дараах өнцгийн синус, косинус, тангесийн утгыг ол.

$210^{\circ}$
$-45^{\circ}$
$-315^{\circ}$
$720^{\circ}$
$-570^{\circ}$
$2220^{\circ}$

Бодлого №10550

Дараах тригонометр функцийн утгыг, хурц өнцгийн тригонометр функцээр илэрхийл.

$\sin495^{\circ}$
$\cos827^{\circ}$
$\tg(-250^{\circ})$

Бодлого №10551

Дараах утгыг ол.

$\sin(-210^{\circ})$
$\cos510^{\circ}$
$\tg(-330^{\circ})$

Универсал орлуулга

$\tg\Big(\dfrac{3\pi}{2}+\alpha\Big)=\dfrac12$ бол

$\sin2\alpha$ илэрхийллийн утгыг ол.

A.

$\dfrac45$ B.

$\dfrac14$ C.

$-\dfrac45$ D.

$-\dfrac14$ E.

$\dfrac15$

ЭЕШ 2006 C №6

$32\cdot(\cos121^\circ\cdot\cos1^\circ+\sin59^\circ\cdot\cos89^\circ)$ илэрхийллийн утгыг ол.

A.

$32$ B.

$-16$ C.

$16$ D.

$8$ E.

$-8$

Эмхэтгэлийн томьёо

$\sin(\alpha-30^\circ)$ нь аль илэрхийлэлтэй тэнцүү вэ?

A.

$\sin(30^\circ-\alpha)$ B.

$\sin(120^\circ+\alpha)$ C.

$\sin(120^\circ-\alpha)$ D.

$\cos(120^\circ-\alpha)$ E.

$\cos(90^\circ-\alpha)$

Эмхэтгэлийн томьёо

$0< t< \dfrac{\pi}{2}$ ба

$\sin(4\pi+t)=\dfrac 35$ бол

$\tg (\pi-t)=?$

A.

$-\dfrac 54$ B.

$-\dfrac34$ C.

$-\dfrac 23$ D.

$-\dfrac 43$ E.

$-\dfrac 12$

$\dfrac{3\pi}{2}< t< 2\pi$ ба

$\cos (2\pi+t)=\dfrac{12}{13}$ бол

$\ctg (\pi-t)=?$

A.

$\dfrac{13}{5}$ B.

$-\dfrac{13}{12}$ C.

$-\dfrac{12}5$ D.

$\dfrac{12}{5}$ E.

$\dfrac{13}{12}$

ЭЕШ 2011 C №11

$\alpha+\beta=\dfrac{\pi}{2}$ бол

$\dfrac{\cos\alpha+\cos\beta}{\sin\alpha+\sin\beta}=?$

A.

$-1$ B.

$1$ C.

$\sqrt3$ D.

$-\sqrt3$ E.

$0$

Эмхэтгэлийн томьёо

$\cos 510^\circ=?$

A.

$0$ B.

$-\dfrac{1}{2}$ C.

$-\dfrac{\sqrt2}{2}$ D.

$-\dfrac{\sqrt3}{2}$ E.

$-1$

Эмхэтгэлийн томьёо

$\tg(-120^\circ)=?$

A.

$-\dfrac{\sqrt3}{3}$ B.

$-\sqrt3$ C.

$\dfrac{\sqrt3}{2}$ D.

$\dfrac{\sqrt3}{3}$ E.

$\sqrt3$

Эмхэтгэлийн томьёо

$\sin 690^\circ=?$

A.

$-\dfrac{\sqrt3}{2}$ B.

$-\dfrac12$ C.

$0$ D.

$\dfrac12$ E.

$\dfrac{\sqrt3}{2}$

Бодлого №13853

$\cos^2 39^\circ+\cos^251^\circ$ утгыг ол.

A.

$1$ B.

$2\cos^239$ C.

$2\cos^251$ D.

$90^\circ$ E.

$\dfrac{\sqrt{3}}{2}$

Эмхэтгэлийн томьёо

$\sin(\alpha-30^\circ)$ нь аль илэрхийлэлтэй тэнцүү вэ?

A.

$\sin(30^\circ-\alpha)$ B.

$\sin(120^\circ+\alpha)$ C.

$\sin(120^\circ-\alpha)$ D.

$\cos(120^\circ-\alpha)$ E.

$\cos(90^\circ-\alpha)$