Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Holy guacamole! www.integral.mn сайт 2026-01-01-ээс шинэчлэгдэж www.mathminds.club хуудас руу шилжинэ.
Комбинаторик
Давталттай сэлгэмэл
$1, 2,\ldots,9$ цифрүүдээр хэчнээн 5 оронтой тоо зохиож болох вэ?
6 өөр чихрийг 3 хүүхдэд хэчнээн янзаар хувааж өгч чадах вэ?
$\{a,b,c\}$ олонлогийн бүх дэд олонлогийг бич.
- Бүх 5 оронтой тооны тоог ол.
- 8-г агуулаагүй бүх 5 оронтой тооны тоог ол.
- 8-г агуулаасан бүх 5 оронтой тооны тоог ол.
- 0 ба 8-г агуулаагүй бүх 5 оронтой тооны тоог ол.
- 2, 3, 5, 7 цифрүүдээр бичиж болох бүх 5 оронтой тооны тоог ол.
- 2, 3, 5, 7 цифрүүдээр бичиж болох $10^6$-ээс бага бүх тооны тоог ол.
12 өөр эдлэлийг 3 өөр хайрцагт хэчнээн янзаар байрлуулж болох вэ?
16 цаасны 4 дээр нь А үсэг, 4 дээр нь Б үсэг, 4 дээр нь В үсэг, 4 дээр нь
Г үсэг бичжээ. Эдгээрээс 4 цаасыг сонгон аваад ямар нэг эрэмбээр байрлуулах
замаар хэчнээн ялгаатай үгийг бичиж чадах вэ?
Нэг гүрний хүмүүсийн шүдний бүтэц нь бүгд ялгаатай байв. Хүн 32 шүдтэй
гэвэл энэ гүрэн хамгийн олондоо хэдэн хүнтэй вэ?
10, 11, 12-р ангид харгалзан 80, 70, 60 хүүхэдтэй бол анги бүрээс дор хаяж
нэг хүүхэд орсон хэдэн хүүхдийг хэчнээн янзаар сонгож болох вэ?
1, 2, 3, 5, 10, 15, 20, 50-тын мөнгийг 2 халаасандаа хэчнээн янзаар хийж
чадах вэ?
Саяас бага бөгөөд 1, 2, 3, 4 цифрүүдийг нэгэн зэрэг агуулсан тоо хэд вэ?
Хоёр ижил цифрээр эхэлсэн зургаан оронтой тоо хэчнээн байх бэ?
A. $\dfrac{10!}{4!}$
B. $A_{10}^5$
C. $9A_9^5$
D. $10^5$
E. $9\cdot10^4$
Бүх 4 оронтой тоонуудын тоо $\fbox{abcd}$, үүнээс бүх цифрүүд нь ялгаатай нь $\fbox{efgh}$ ба ижил цифр орсон нь $\fbox{ijkl}$ байна.
Бүх 4 оронтой тоонуудын тоо $\fbox{abcd}$, үүнээс бүх цифрүүд нь ялгаатай нь $\fbox{efgh}$ ба ижил цифр орсон нь $\fbox{ijkl}$ байна.
Давталттай хэсэглэл
$k$ адил бөмбөгийг $m$ өөр хайрцагт хэчнээн янзаар байрлуулж
болох вэ?
Шуудан дээр 10 төрлийн захидал худалдаж байв. 12 ил захидлыг хэчнээн янзаар худалдаж авч чадах вэ? 8 өөр захидлыг хэчнээн янзаар худалдаж авах вэ?
Ирмэгүүдийн урт нь 1-ээс 10-ын хоорондох натурал тоонуудаар илэрхийлэгдэх
хэчнээн янзын шулуун параллелопипед орших вэ?
$x_1+\ldots+x_m=k$ тэгшитгэлийн натурал шийдийн тоог ол.
1-ээс 100 хүртэлх тоонуудаас нийлбэр нь 3-т хуваагдах гурван тоог хэчнээн
янзаар сонгож болох вэ?
Айл: 10 малтай байх боломжийг ол. 10 малтай айл:
- дан бодтой байх,
- яг 3 хоньтой байх,
- 5 бод, 5 богтой байх,
- хоньтой байх,
- бодтой ба богтой байх,
- 3-аас цөөнгүй бодтой байх
10 төрлийн чихрээс
- 1 найздаа 2 ялгаатай чихрийг
- 1 найздаа 3 ширхэгийг
- 5 найздаа тус бүр 2 ялгаатай чихрийг
- 5 найздаа тус бүр 3 ширхэгийг
50 самрыг 10 хүнд хүн бүр ядаж хоёрыг авсан байхаар хэчнээн янзаар хувааж болох вэ?
Цэцгийн дэлгүүрт сарнай, хонгорзул, балжингарав гэсэн 3 төрлийн цэцэг байв. 5 цэцэгтэй баглааг хэчнээн аргаар бэлтгэж болох вэ?
A. $C_{5}^3$
B. $A_5^3$
C. $C_7^5$
D. $C_8^3$
E. $A_7^5$
$8$ вагонтой галт тэргэнд 9 хүүхдийг хэдэн янзаар суулгаж болох вэ? Боломжууд зөвхөн хүүхдийн тоогоороо л ялгагдана.
A. $C_{16}^8$
B. $C_{16}^9$
C. $C_{17}^8$
D. $C_{17}^9$
E. $C_{9}^8$
Өөр хоорондоо ялгагдахгүй 2 бөмбөгийг өөр хоорондоо ялгаатай, хангалттай багтаамжтай $n+1$ ширхэг хайрцагт байрлуулах боломжийн тоог ол.
A. $\dfrac{n^2+3n+2}{2}$
B. $\dfrac{n(n+1)}{2}$
C. $n(n+2)$
D. $(n+1)(n+2)$
E. $\dfrac{n(n-1)}{2}$
20 ижил бөмбөгийг 3 ялгаатай хайрцагт хувааж хийх боломжийн тоог ол.
A. $C_{20}^3$
B. $C_{3}^{20}$
C. $A_{20}^3$
D. $C_{22}^{20}$
E. $20^3$
Цифрүүд нь үл буурах эрэмбээр байрлах 4 оронтой тоо хэдэн ширхэг байх вэ? Үл буурах тул цифр давтагдан орж болно.
A. $126$
B. $255$
C. $450$
D. $495$
E. $550$
$a+b+c=38$ байх сөрөг биш бүхэл тоон $(a;b;c)$ гурвал хэчнээн байх вэ?
A. $380$
B. $720$
C. $841$
D. $760$
E. $780$
$a+b+c\le 20$ байх $(a,b,c)$ гэсэн сөрөг биш бүхэл тоон хос хэчнээн байх вэ?
A. 8855
B. 2083
C. 1981
D. 1708
E. 1771
Талуудын урт нь 4, 5, 6, 7 см тоонуудын аль нэг байх хэчнээн гурвалжин орших вэ?
A. $10$
B. $12$
C. $15$
D. $20$
E. $25$
$8$ вагонтой галт тэргэнд 9 хүүхдийг хэдэн янзаар суулгаж болох вэ? Боломжууд зөвхөн хүүхдийн тоогоороо л ялгагдана.
A. $C_{16}^8$
B. $C_{16}^9$
C. $C_{17}^8$
D. $C_{17}^9$
E. $C_{9}^8$
$1, 2, 3, 4, 5$ дугаартай хайрцгуудад өөр хоорондоо ялгаагүй 7 ширхэг бөмбөгийг $\fbox{abc}$ янзаар байрлуулж болох ба дурын нэг байрлуулалт авч үзэхэд 5-р хайрцаг хоосон биш байх магадлал $\frac{\fbox{d}}{\fbox{ef}}$ болно.
10 малтай айл дан бодтой байх боломжийн тоо $\fbox{ab}$, ядаж нэг адуутай байх боломжийн тоо $\fbox{cde}$, яг гурван хоньтой байх боломжийн тоо $\fbox{fgh}$ байна.
Талууд нь $\{9,11,12,15,18\}$ олонлогоос утгаа авах
- Элдэв талт гурвалжин $\fbox{ab}$ ширхэг
- Зөв биш адил хажуут гурвалжин $\fbox{cd}$ ширхэг
- Талууд нь дээрх олонлогоос утгаа авах гурвалжнуудаас санамсаргүйгээр нэг гурвалжин сонгон авахад зөв гурвалжин байх магадлал $\dfrac{\fbox{e}}{\fbox{fg}}$ байна.
10 малтай айл дан богтой байх боломжийн тоо $\fbox{ab}$, ядаж нэг тэмээтэй байх боломжийн тоо $\fbox{cde}$, яг хоёр үхэртэй байх боломжийн тоо $\fbox{fgh}$ байна.
$1, 2, 3, 4, 5$ дугаартай хайрцгуудад өөр хоорондоо ялгаагүй 7 ширхэг бөмбөгийг $\fbox{abc}$ янзаар байрлуулж болох ба дурын нэг байрлуулалт авч үзэхэд 5-р хайрцаг хоосон биш байх магадлал $\frac{\fbox{d}}{\fbox{ef}}$ болно.
Комбинаторикийн элдэв бодлогууд
300-аас бага 3-т хуваагдах натурал тоонуудыг залгуулан бичиж нэг натурал тоо үүсгэв. Энэ тооны цифрүүдийн нийлбэрийг ол.
Цифрүүдийн нийлбэр нь 21 байх хэчнээн 4 оронтой тоо байгаа вэ?
$A=3\cdot 5\cdot 7$ тооны хуваагчдын тоог ол.
A. $7$
B. $8$
C. $4$
D. $12$
E. $9$
Аль ч 3 нь нэг цэгт огтлолцдоггүй, аль ч 2 нь параллель биш нэг хавтгай дээр орших 4 шулуун уг хавтгайг хэдэн хэсэгт хуваах вэ?
A. $16$
B. $7$
C. $10$
D. $11$
E. $12$
Хайрцагт $8$ хар, $9$ шар, $5$ ногоон бөмбөг байв. Тэгвэл таамгаар авсан бөмбөгөнд ижил өнгийн бөмбөг заавал орсон байхаар хамгийн багадаа хэдийг авах хэрэгтэй вэ?
A. $2$
B. $22$
C. $4$
D. $14$
E. $3$
$n$ натурал тоо бол $100^n-1$ тоог $99$-д хуваахад гарах тооны аравтын бичлэг хэдэн тэгтэй вэ?
A. $n-1$
B. $n$
C. $n+1$
D. $\dfrac{n}{2}$
E. $\left[\dfrac{n}{2}\right]$
Хоёр шоог зэрэг хаяхад туссан нүднүүдийн нийлбэр 8 байх эгэл үзэгдлийн тоо хэд вэ?
A. 9
B. 8
C. 7
D. 6
E. 5
Мөнгө орхиж, сүлдээрээ туссан тохиолдолд дахин 1 мөнгө орхисон, тоогоор туссан тохиолдолд шоо орхисон. Бүх боломжит эгэл үзэгдлийн тоог ол.
A. $12$
B. $10$
C. $8$
D. $6$
E. $5$
Гүдгэр 14 өнцөгт хэдэн диагоналтай вэ?
A. 91
B. 182
C. 14
D. 77
E. 168
Гүдгэр 10 өнцөгт хэчнээн диагоналтай вэ?
A. 70
B. 45
C. 35
D. 80
E. 90
Гурван оронтой бүх тэгш тооны цифрүүдийн нийлбэрийг ол.
A. 6060
B. 6065
C. 6070
D. 6075
E. 6080
500 хуудастай номыг дугаарлахад 1-ийн цифр хэдэн удаа ашиглах вэ?
A. 300
B. 250
C. 220
D. 200
E. 180
Гүдгэр 11 өнцөгт хэдэн диагоналтай вэ?
A. 120
B. 44
C. 55
D. 110
E. 99
Гүдгэр 12 өнцөгт хэдэн диагоналтай вэ?
A. 108
B. 132
C. 66
D. 86
E. 54
$A=3\cdot 7\cdot 11$ тооны хуваагчдын тоог ол.
A. 7
B. 8
C. 3
D. 6
E. 9
Зөвхөн 1, 2, 3, 4, 5 цифрүүдээр бичиж болох 4-д хуваагддаг 4 оронтой тоо хэдэн ширхэг байх вэ? (цифр давтагдаж орж болно)
A. $5^4$
B. $125$
C. $\dfrac{5^4-1}{4}$
D. $100$
E. $225$
1-200 хүртэлх тоонуудыг цувуулан бичихэд 1-ийн цифрийг хэдэн удаа ашиглах вэ?
A. 55
B. 110
C. 130
D. 140
E. 160
1000-аас эрс бага бүх натурал тоонуудыг багаас эхлэн залгуулж бичихэд гарах тооны цифрүүдийн нийлбэр хэдтэй тэнцүү байх вэ?
A. $9500$
B. $11000$
C. $12500$
D. $13000$
E. $13500$
$x^2+y^2=26$ тойрог дээр хоёр координат нь бүхэл байх хэдэн цэг байх вэ?
A. 0
B. 4
C. 8
D. 12
E. 16
$2017^{2016}$-ын натурал тоон хуваагчдын тоог ол.
A. $2016^2$
B. $2^{2016}$
C. $2016$
D. $2017$
E. $2018$
$M$ цэгээс зөвхөн $\uparrow$, $\rightarrow$ чиглэлээр $N$ цэгт хүрэх хэчнээн ялгаатай зам байгаа вэ? (будагдсан хэсэг рүү очихгүй)
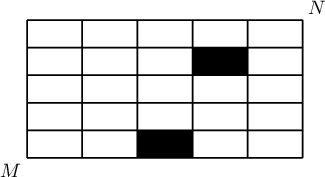

A. 12
B. 19
C. 21
D. 34
E. 53
$X=\{11,31,25,45,67,91,69,63,57,97,73\}$ олонлогийн дэд олонлогийн тоо хэд вэ?
A. 256
B. 512
C. 1024
D. 2048
E. 5096
$A$ цэгээс эхлэн эсвэл дээш 1 нэгж, эсвэл баруун тийш 1 нэгж явсаар $B$ цэгийг дайран $C$ цэгт очих бүх ялгаатай замын тоог ол.
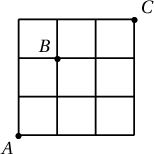

A. $9$
B. $8$
C. $10$
D. $11$
E. $12$
600 хуудастай номыг дугаарлахад 6-ийн цифр хэдэн удаа ашиглах вэ?
A. 101
B. 150
C. 121
D. 200
E. 100
Хоёр шоог зэрэг хаяхад туссан нүднүүдийн нийлбэр 6 байх эгэл үзэгдлийн тоо хэд вэ?
A. 9
B. 8
C. 7
D. 6
E. 5
Аль ч 3 нь нэг цэгт огтлолцдоггүй, аль ч 2 нь параллель биш нэг хавтгай дээр орших 4 шулуун уг хавтгайг хэдэн хэсэгт хуваах вэ?
A. $16$
B. $7$
C. $10$
D. $11$
E. $12$
Гурван оронтой бүх тэгш тооны цифрүүдийн нийлбэрийг ол.
A. 6060
B. 6065
C. 6070
D. 6075
E. 6080
500 хуудастай номыг дугаарлахад 1-ийн цифр хэдэн удаа ашиглах вэ?
A. 300
B. 250
C. 220
D. 200
E. 180
- Хавтгайд аль ч хоёр нь параллель биш, аль ч гурав нь нэг цэг дээр үл огтлолцох 10 шулуун байв. Эдгээр шулуунаар талаа хийсэн гурвалжин $\fbox{abc}$ ширхэг байна.
- Хавтгайд яг гурав нь параллель, аль ч гурав нь нэг цэг дээр үл огтлолцох 10 шулуун байв. Эдгээр шулуунуудаар талаа хийсэн гурвалжин $\fbox{de}$ ширхэг байна.
- Хавтгайд аль ч хоёр нь параллель биш, аль ч гурав нь нэг цэг дээр үл огтлолцох 8 шулуун байв. Тус бүр нь тэдгээр шулууны гурвыг нь шүргэсэн тойрог $\fbox{abc}$ ширхэг байна.
- Хавтгайд яг хоёр нь параллель, аль ч гурав нь нэг цэг дээр үл огтлолцох 8 шулуун байв. Эдгээр шулуунуудаар талаа хийсэн гурвалжин $\fbox{de}$ ширхэг байна.
Нийлбэрийн зарчим
Ангийн 42 сурагчийн 16 нь гүйлтээр, 24 нь хөл бөмбөгөөр, 15
нь шатраар, 11 нь гүйлт ба хөл бөмбөгөөр, 8 нь гүйлт ба шатраар, 12 нь хөл бөмбөг
ба шатраар, 6 нь дээрх 3 төрлөөр зэрэг хичээллэдэг ба үлдэх сурагчид нь зөвхөн
цанаар хичээллэдэг бол хэчнээн сурагч цанаар хичээллэдэг вэ?
Нэг ангийн сурагчдын $80\%$ нь шатарчин, $60\%$ нь сайн сурдаг бол
сурагчдын дор хаяж хэдэн хувь нь сайн сурдаг ба шатар тоглодог вэ?
Ангийн 35 сурагчийн 20 нь тооны, 11 нь физикийн дугуйланд явдаг ба 10 сурагч эдгээр дугуйлангийн алинд нь ч явдаггүй байв. Хэдэн сурагч 2 дугуйланд зэрэг явдаг ба хэдэн сурагч зөвхөн тооны дугуйланд явдаг вэ?
100 оюутны 28 нь англи хэл, 30 нь герман хэл, 42 нь франц хэл, 8 нь
англи ба герман хэл, 10 нь англи ба франц хэл, 5 нь герман ба франц хэл, 3 нь
энэ гурван хэлийг мэддэг байв. Энэ гурван хэлээс
- нэгийг нь ч мэддэггүй,
- ядаж хоёр хэл мэддэг,
- яг хоёр хэл мэддэг,
- зөвхөн англи хэл мэддэг,
- яг нэг хэл мэддэг хэдэн оюутан байв?
Институтийн нэг хэлтсийн ажилтан бүр ядаж нэг гадаад хэл мэддэг ба 6 хүн
англи, 7 хүн франц, 6 хүн герман, 4 нь англи ба герман, 3 нь герман ба франц,
2 нь англи ба франц, 1 нь бүх хэлийг мэддэг бол хэлтэс хэдэн ажилтантай байсан
бэ? Хэдэн хүн зөвхөн англи хэл мэддэг вэ? Хэдэн хүн зөвхөн нэг хэл мэддэг вэ?
Эхний 100 натурал тооны дотор 2, 3, 5-ын алинд ч хуваагдахгүй тоо хэд бий
вэ? 2, 3, 5-ын ядаж нэгд нь хуваагдахгүй тоо хэд бий вэ? 2, 3, 5, 7-гийн алинд ч
хуваагдахгүй тоо хэд бий вэ? 2, 3, 5, 7-гийн ядаж хоёрт нь хуваагддаг тоо хэд
бий вэ?
Салаа 30 цэрэг, 4 офицертэй байсан ба харуулд 6 цэрэг эсвэл 4 цэрэг 2 офицер эсвэл 3 цэрэг 1 офицер эсвэл 3 офицер гарахыг зөвшөөрдөг бол өдөр бүр ялгаатай хувилбараар хэдэн өдрийн манааг томилох боломжтой вэ?
A. $A_{30}^6+A_{30}^4+A_{30}^3+A_4^1+A_{4}^2+A_{4}^3$
B. $C_{30}^6+2\cdot C_{30}^4+C_{30}^3+3$
C. $C_{30}^6+C_{30}^4\cdot C_{4}^2+4\cdot C_{30}^3+C_{4}^3$
D. $C_{30}^6+C_{30}^4\cdot C_{30}^2+C_4^1+C_4^2+C_4^3$
E. $\frac{23}{30}$
$a+b+c=38$ байх сөрөг биш бүхэл тоон $(a;b;c)$ гурвал хэчнээн байх вэ?
A. 380
B. 820
C. 741
D. 760
E. 780
$a+b\le 30$ байх $(a;b)$ натурал тоонуудын хосын тоо хэд вэ?
A. 361
B. 384
C. 406
D. 435
E. 465
Ангийн 20 хүүхдийн 10 нь сагсан бөмбөг, 12 нь даам тоглодог бөгөөд 2 хүүхэд алийг нь ч тоглодоггүй бол даам ба сагсан бөмбөг тоглодог хүүхэд хэд вэ?
A. $12$
B. $10$
C. $18$
D. $8$
E. $4$
1000-аас бага 12-т хуваагддаг тоонуудын олонлогийг $A$, 18-д хуваагддаг тоонуудын олонлогийг $B$ гэе. $A\cup B$ олонлог хэчнээн элементтэй вэ?
A. 110
B. 210
C. 111
D. 138
E. 27
1-4 тоогоор дугаарлагдсан хайрцагт мөн 1-4 тоогоор дугаарлагдсан 4 бөмбөг хийжээ. Хайрцаг болон бөмбөгний дугаар ялгаатай байхаар хэдэн янзаар хийх вэ?
A. 18
B. 16
C. 12
D. 8
E. 9
100-аас хэтрэхгүй 2 юмуу 3-ийн яг нэгэнд нь хуваагддаг тоо хэд байх вэ?
A. 67
B. 51
C. 63
D. 48
E. 37
20-оос хэтрэхгүй, 3 ба 4-ийн ядаж нэгэнд нь хуваагддаг бүх натурал тоонуудаас тогтох олонлог хэдэн элементтэй вэ?
A. 10
B. 9
C. 1
D. 6
E. 5
Тойрог дээр өгөгдсөн $2015$ цэгийн $3$ нь улаан бусад нь хөх өнгөтэй байв. Эдгээр цэгүүд дээр оройтой, ядаж нэг орой нь улаан өнгөтэй гурвалжин хэчнээн байх вэ?
A. $C_{2012}^3$
B. $C_{2015}^3$
C. $C_{2015}^3-C_{2012}^3$
D. $C_{2013}^3$
E. $C_{2014}^3$
Аравтын бичлэгт нь 5 ба 6-ийн цифрийн ядаж нэг нь орсон 3 оронтой тоо хэчнээн байх вэ?
A. $448$
B. $452$
C. $252$
D. $400$
E. $300$
1-ээс 100 хүртэлх тоонууд дотор 2 ба 3-ын алинд нь ч хуваагдахгүй тоо хэд вэ?
A. 50
B. 67
C. 45
D. 25
E. 33
6-д эсвэл 7-д хуваагддаг 101-ээс бага тоо хэчнээн байх вэ?
A. 30
B. 29
C. 28
D. 27
E. 31
5-д эсвэл 6-д хуваагддаг 101-ээс бага тоо хэчнээн байх вэ?
A. 33
B. 34
C. 36
D. 37
E. 30
Ангийн хүүхдүүдийн 24 нь математикийн, 20 нь англи хэлний, 16 нь математик ба англи хэлний ЭЕШ өгнө. Энэ 2 шалгалтын алийг ч өгөхгүй сурагчид 4 байсан бол анги нийт хэдэн сурагчтай вэ?
A. $64$
B. $36$
C. $32$
D. $28$
E. $24$
$a+b+c=38$ байх сөрөг биш бүхэл тоон $(a;b;c)$ гурвал хэчнээн байх вэ?
A. $380$
B. $720$
C. $841$
D. $760$
E. $780$
Ангийн 32 хүүхдүүдийн 24 нь математикийн, 20 нь англи хэлний, 16 нь математик ба англи хэлний ЭЕШ өгнө. Энэ 2 шалгалтын алийг ч өгөхгүй сурагчид нийт хэд байгаа вэ?
A. $4$
B. $6$
C. $8$
D. $10$
E. $16$
1000–аас бага 12-т хуваагддаг тоонуудын олонлогийг $A$, 20-д хуваагддаг тоонуудын олонлогийг $B$ гэе. $A\cup B$ (нэгдэл) олонлогт хэчнээн тоо байх вэ?
A. 110
B. 210
C. 121
D. 116
E. 27
100-аас хэтрэхгүй 2 юмуу 3-ийн яг нэгэнд нь хуваагддаг тоо хэд байх вэ?
A. 67
B. 51
C. 63
D. 48
E. 37
Талуудын урт нь бүхэл тоо, периметр нь $23$-тай тэнцүү, өөр хоорондоо тэнцүү биш гурвалжин нийт хэчнээн ширхэг байх вэ?
A. 12
B. 13
C. 14
D. 22
E. 23
1-4 тоогоор дугаарлагдсан хайрцагт мөн 1-4 тоогоор дугаарлагдсан 4 бөмбөг хийжээ. Хайрцаг болон бөмбөгний дугаар ялгаатай байхаар хэдэн янзаар хийх вэ?
A. 18
B. 16
C. 12
D. 8
E. 9
6-д эсвэл 7-д хуваагддаг 101-ээс бага тоо хэчнээн байх вэ?
A. 30
B. 29
C. 28
D. 27
E. 31
$A$ нь 32, $B$ нь 64, $A\cup B$ нь 256 ширхэг дэд олонлогтой
бол $A$ олонлог $\fbox{a}$ ширхэг, $A\cup B$
олонлог $\fbox{b}$ ширхэг, $A\cap B$ олонлог $\fbox{c}$ ширхэг элементтэй байна.
I бригад 1 метр өргөн, 15 метр урт зам, II бригад 2 метр өргөн 20 метр урт зам зассан ба уг 2 зам хоорондоо $30^\circ$ өнцгөөр бүтэн огтлолцсон бол 2 бригад хамтарч $\fbox{a}\text{ м}^{2}$, нийлээд $\fbox{bc}\text{ м}^{2}$ талбайтай зам засжээ.
Цифрүүдийн нийлбэр нь 3-тай тэнцүү байх 10 оронтой тоо $\fbox{ab}$ ширхэг байна.
$\{0; 1; 2; 3\}$ цифрүүдээр зохиосон 9-д хуваагддаг, 4 оронтой тоо $\fbox{ab}$ ширхэг байна.
Өгөгдсөн бүтэц бүхий давталттай сэлгэмэл
$(a+b+c)^3$-г задалж бич.
Хайрцаг бүрд 7 эдлэл орсон байхаар 28 өөр эдлэлийг 4 хайрцагт
байрлуулах боломжийг:
- хайрцгууд ялгаатай байх,
- хайрцгууд ялгаагүй байх тохиолдолд тус тус бод.
"Хатанбаатар", "тэнцэтгэл" гэсэн үгүүдээс үсгүүдийн байрыг солих замаар хэчнээн үг гаргаж чадах вэ?
Ээжид 4 алим, 3 жүрж, 6 нимбэг байв. Ээж өдөр болгон хүүдээ нэг жимс
өгдөг бол хэчнээн янзаар өгч чадах вэ?
Алгебрын 3, анализын 4, геометрийн 8 номоор ангийн 30 сурагчийн талыг
шагнах болов. Хэчнээн янзаар шагнаж чадах вэ?
"Төөрөгдөл" гэсэн үгэнд үсгүүдийн байрыг солиход:
а) 4 "ө" үсэг, б) 3 "ө" үсэг, в) 2 "ө" үсэг зэрэгцэж ороогүй байх боломжийн тоог тус тус ол.
а) 4 "ө" үсэг, б) 3 "ө" үсэг, в) 2 "ө" үсэг зэрэгцэж ороогүй байх боломжийн тоог тус тус ол.
Шатрын хөлөг дээр
- 2 хар, 1 цагаан тэргийг
- 2 цагаан тэргийг
- 1 хар, 1 цагаан, 1 ногоон тэргийг
- 3 цагаан тэргийг
- 3 цагаан, 4 хар тэргийг
ANAGRAMMA гэдэг үгийн үсгүүдийн байрыг солин нийт хэчнээн янзын үг үүсгэх вэ?
Цифр бүр яг 2 удаа орсон 20 оронтой тоо хэдэн ширхэг байх вэ?
Яг 3 ялгаатай сондгой цифрээс бүрдэх ба цифр бүр яг 2 удаа орсон байх 6 оронтой тоо хэчнээн байх вэ?
БОТГО үгийн үсгүүдийн байрыг солих замаар хэчнээн ялгаатай үг (утгатай байх албагүй) зохиож болох вэ?
A. 15
B. 30
C. 45
D. 60
E. 120
"СЭЛГЭМЭЛ" үгийн үсгүүдийн байрыг сэлгээд хэчнээн ялгаатай үг зохиож болох вэ?
A. 3340
B. 3360
C. 3400
D. 3280
E. 3300
ДААЛГАВАР гэдэг үгийн үсгүүдийг бүх боломжоор нь сэлгэж
утгатай, утгагүй үг зохиох боломжийн тоо хэд вэ?
A. $9!$
B. $6!$
C. $\dfrac{9!}{4!}$
D. $4\cdot 5!$
E. $\dfrac{9!}{5!}$
"хамгаалуул" гэдэг үгийн үсгүүдийг бүх боломжоор нь сэлгэж
утгатай, утгагүй "үгс" зохиох боломжийн тоо хэд вэ?
A. $10!$
B. $6!$
C. $\frac{10!}{3!2!}$
D. $\frac{10!}{3!2!2!}$
"БОЛОЛЦОО" үгийн үсгүүдийн байрыг солих замаар хэчнээн үг үүсгэж болох вэ?
A. 420
B. 630
C. 800
D. 820
E. 840
"МАТЕМАТИК" үгийн үсгүүдийн байрыг солих замаар хэчнээн ялгаатай үг үүсгэх вэ? Үсгүүдийн дурын дарааллыг үг гэж үзнэ.
A. 12005
B. 45360
C. 45000
D. 64120
E. 10000
"СОЛОНГО" үгийн үсгүүдийн байрыг солиход гурван O үсэг зэрэгцэж ороогүй хэчнээн ялгаатай үг үүсэх вэ?
A. $120$
B. $380$
C. $600$
D. $720$
E. $840$
"ОРХОН" үгийн үсгүүдийг ашиглан хэчнээн ялгаатай үг зохиож болох вэ?
A. $5!$
B. $4!$
C. $\dfrac{5!}{2!}$
D. $\dfrac{4!}{2!}$
E. $2\cdot 4!$
ТЭМЭЭ үгийн үсгүүдийн байрыг солих замаар гурван Э үсэг зэрэгцэж ороогүй хэчнээн ялгаатай үг (утгатай байх албагүй) зохиож болох вэ?
A. 10
B. 14
C. 20
D. 60
E. 120
2 ширхэг "A", 2 ширхэг "У", 1 ширхэг "Р" ба 1 ширхэг "Л" үсэг бичигдсэн 6 картыг ашиглан 6 үсэгтэй үг хэдийг зохиож болох вэ?
A. $6!$
B. $\dfrac{6!}{4!}$
C. $\dfrac{6!}{2!\cdot 2!}$
D. $C_6^2\times C_4^2\times C_2^1\times C_1^1$
E. $A_6^2\times A_4^2\times A_2^2$
$1000044$ тооны цифрүүдийн байрыг сэлгэн хэчнээн ялгаатай тоо үүсгэж болох вэ?
A. 45
B. 90
C. 120
D. 720
E. 5040
Ээж нь хүүдээ өдөр бүр нэг ширхэг жимс өгч явуулдаг байв. 3 алим, 2 банана, 1 жүрж, 1 тоор, 1 чавга жимсийг хэчнээн ялгаатай аргаар өгөх вэ?
A. 3340
B. 3380
C. 3400
D. 3360
E. 3300
2 ширхэг "A", 2 ширхэг "У", 1 ширхэг "Р" ба 1 ширхэг "Л" үсэг бичигдсэн 6 картыг ашиглан 6 үсэгтэй үг хэдийг зохиож болох вэ?
A. $6!$
B. $\dfrac{6!}{4!}$
C. $\dfrac{6!}{2!\cdot 2!}$
D. $C_6^2\times C_4^2\times C_2^1\times C_1^1$
E. $A_6^2\times A_4^2\times A_2^2$
СЭЛГЭМЭЛ гэдэг үгийн үсгүүдийн байрыг сэлгэх замаар
$\fbox{abcd}$ ширхэг ялгаатай "үг" бичиж чадах ба эдгээрээс
$\fbox{ef}$ ширхэг нь 2; 5; 7-р байранд "Э" үсэгтэй үг байна.
$1, 1, 1, 2, 3, 4, 5$ цифрүүдийн байрыг сэлгэх замаар $\fbox{abc}$
ширхэг 7 оронтой тоо бичиж чадах ба эдгээрээс
$\fbox{def}$ ширхэг нь 3 ширхэг "1" цифр дараалж орсон тоо байна.
$1, 1, 1, 2, 3, 4, 5$ цифрүүдийн байрыг сэлгэх замаар $\fbox{abc}$
ширхэг 7 оронтой тоо бичиж чадах ба эдгээрээс
$\fbox{def}$ ширхэг нь 3 ширхэг "1" цифр дараалж орсон тоо байна.
Сэлгэмэл, гүйлгэмэл
Ангийн 40 сурагчаас ангийн дарга, сагсан бөмбөгийн багийн ахлагч, гар бөмбөгийн багийн ахлагч гурвыг хэчнээн янзаар сонгож болох вэ? (Нэг хүн хоёр сонгууль зэрэг хүлээхгүй гэж үз).
а) 5 өнгийн даавуугаар тууш 3 өнгөтэй дарцгийг хэчнээн янзаар хийж болох вэ?
б) Нэг үе нь заавал улаан байх тохиолдолд а)-г бод.
б) Нэг үе нь заавал улаан байх тохиолдолд а)-г бод.
Тасаг 8 ажилчинтай. Хүн бүр нэг нэг эдлэл хийхээр 3 янзын эдлэл хийх
даалгаврыг 3 ажилчинд нь хэчнээн янзаар өгч болох вэ? (нэг хүн нэг л эдлэл хийнэ.)
2, 4, 6-р байранд нь гийгүүлэгч байхаар "Логарифм" гэдэг үгэнд үсгүүдийн
байрыг хэчнээн янзаар сольж болох вэ?
0-ээс бусад цифрүүдээр бичиж болох цифрүүд нь ялгаатай байх бүх 5 оронтой
тоонуудын нийлбэрийг ол.
10 охиныг 7 хүү бүжигт урих ёстой байв. Нэр заасан 2 охин заавал бүжиглэх
ёстой байсан бол хэчнээн янзаар бүжигт урьж болох вэ?
1, 2, 3, 4, 5 элементийн хэчнээн сэлгэмэлд
- 1 нь 2-ын зүүн талд орох вэ?
- 2 нь 1-ийн яг ард орох вэ?
Ангийн 40 сурагчийн 24 нь эрэгтэй байв. Ангийн ахлагч, шатрын багийн ахлагч, сагсан бөмбөгийн багийн ахлагч тэдний орлогчид гэсэн 6 орон тоог сонгох ёстой байв.
- сонгох бүх боломжийг ол,
- эдний дотор эмэгтэй сурагчид байх,
- ангийн дарга эрэгтэй байх,
- жинхэнэ дарга нар нь эрэгтэй байх,
- дарга нарын талаас цөөнгүй нь эрэгтэй байх
$1234567$ тооны цифрүүдийн байрыг солиход гарах бүх $7!$ тооны нийлбэрийг ол.
Гүйлтийн тэмцээнд 25 хүн оролцов. Бүгд барианд орсон ба зэрэг ирсэн 2 хүн байгаагүй бол
- Эдгээр хүмүүс нийт хэчнээн ялгаатай янзаар барианд орж болох вэ?
- Эхний 3 байрыг хэчнээн ялгаатай янзаар эзэлж болох вэ?
8 оронтой тоо хэчнээн ширхэг тоо байх вэ? Үүнээс хэчнээн нь
- хөрш цифрүүд нь ялгаатай
- 7-ийн цифр агуулаагүй
- 7-ийн цифр агуулсан
$0, 1, \dots, 9$ цифрүүдийн хэдэн сэлгэмэлд 0, 1 цифрүүд зэрэгцэн орсон ба 1, 2 цифрүүд зэрэгцэн ороогүй байх вэ?
1-р ангийн 20 сурагч үдийн цайгаа уухаар нэг цуваанд жагсах болжээ. Болд Амарын урд явахыг хүсч байв. Тэд Болдын хүсэлд тохирохоор хэдэн янзаар жагсан явж болох вэ?
A. $20!$
B. $19!$
C. $18!$
D. $\dfrac{20!}{2}$
E. $20\cdot 19$
$1, 2, 3, 4, 5, 6$ цифрүүдийг ашиглан цифр давталгүй, 2 ба 4 цифр зэрэгцэн орсон байхаар 5 оронтой хэчнээн тоо үүсгэж болох вэ?
A. $8\cdot 4!$
B. $4\cdot 4!$
C. $2\cdot 4!$
D. $5!$
E. $2C_6^5$
4 хүнийг нэг эгнээнд хэчнээн янзаар жагсаах боломжтой вэ?
A. $4$
B. $12$
C. $16$
D. $24$
E. $10$
Ангийн дарга нь хамгийн урдаа зогсож байхаар ангийн 30 сурагчийг хэчнээн янзаар жагсааж болох вэ?
A. $30!$
B. $\dfrac{30!}{2}$
C. $\dfrac{29!}{2}$
D. $29!$
E. $C_{30}^{29}$
Улаан, цагаан, хөх өнгийн хөндлөн судалтай далбааг хэчнээн янзаар зохиож болох вэ?
A. $1$
B. $2$
C. $4$
D. $5$
E. $6$
Цифрүүд нь сондгой бөгөөд өөр хоорондоо ялгаатай байх 3 оронтой тоо хэчнээн байх вэ?
A. $125$
B. $100$
C. $90$
D. $60$
E. $50$
Квадратын оройг $A,B,C,D$ үсгээр тэмдэглэх нийт боломжийн тоо хэд вэ?
A. $36$
B. $28$
C. $24$
D. $16$
E. $8$
Аравтын тооллын системд бүх цифр нь ялгаатай гурван оронтой тоо хэчнээн байдаг вэ?
A. $3!C_{10}^3-2!C_9^2$
B. $3!C_{10}^3$
C. $3C_{10}^3$
D. $3!C_9^3$
E. $C_{10}^3$
Аравтын бичлэгт нь тэг цифр орсон, ялгаатай цифрүүд бүхий дөрвөн оронтой тоо хэчнээн байх вэ?
A. $3\cdot3!C_9^3$
B. $3!C_9^3$
C. $3C_9^3$
D. $3!C_{10}^3$
E. $A_{10}^4-A_9^4$
$1,2,3,\dots,9$ цифрүүдээр бичигдсэн бүх цифр нь ялгаатай 9 оронтой тооны дотор 1 ба 2-ын цифр зэрэгцэж орсон тоо хэд вэ?
A. $2\cdot8!$
B. $8!$
C. $\frac12\cdot9!$
D. $9!$
E. $\frac12\cdot8!$
$1,2,3,\dots,9$ цифрүүдээр бичигдсэн ба бүх цифр нь ялгаатай $9$ оронтой тооны дотор $1$ ба $3$-ын цифр зэрэгцэж ороогүй тоо хэд вэ?
A. $\dfrac{9!}2$
B. $7\cdot8!$
C. $2\cdot8!$
D. $8!$
E. $9!-8!$
$5$ сурагчийг $20$ суудалд хэчнээн аргаар суулгаж болох вэ?
A. $A_{20}^5=5!C_{20}^5$
B. $5!A_{20}^5$
C. $\frac1{5!}A_{20}^5$
D. $5C_{20}^5$
E. $5!A_{20}^5$
Аль ч хоёр нь ялгаатай $n$ бөмбөгийг тус бүр нь яг нэг бөмбөгний багтаамжтай $n+2$ хайрцагт байрлуулах боломжийн тоог ол.
A. $A_{n+2}^2$
B. $\dfrac{(n+1)!}{2}$
C. $A_{n+3}^2$
D. $\dfrac{(n+2)!}{2}$
E. $n^{n+2}$
Сургууль төгсөгчид бие биендээ зурагаа дурсгахад нийт 930 зураг солилцжээ. Төгсөгчид хэд байсан бэ?
A. 30
B. 31
C. 32
D. 33
E. 35
1, 2, 3, 5, 7, 8, 9 цифрүүдийг ашиглан цифр давталгүй, 7 ба 9 цифр зэрэгцэн орсон зургаан оронтой хэчнээн тоо үүсгэж болох вэ?
A. $6\cdot 5!$
B. $10\cdot 5!$
C. $5\cdot 5!$
D. $6!$
E. $2C_7^6$
5 өөр бөмбөгийг нэг эгнээнд хэчнээн янзаар байрлуулах боломжтой вэ?
A. $5$
B. $25$
C. $20$
D. $120$
E. $10$
0, 1, 2, 3 цифрүүдээр бичигдэх 3 оронтой тоо хэчнээн байх вэ?
A. $64$
B. $48$
C. $54$
D. $3^4$
E. $42$
Аравтын тооллын системд бүх цифр нь ялгаатай 5 оронтой тоо нийт хэдэн ширхэг байх вэ?
A. 24685
B. 25682
C. 26380
D. 27200
E. 27216
Лигийн тэмцээнд $n$ баг оролцов. Баг тус бүр бусад багтайгаа өөрийн болон өрсөлдөгчийн талбайд тоглодог бол лигийн тэмцээнд нийт хэдэн тоглолт гарах вэ?
A. $\dfrac{n(n+1)}{2}$
B. $2n!$
C. $A_{n}^2$
D. $C_{n+1}^2$
E. $C_{n-1}^2$
Охид нь голын 3 байранд жагсаж байхаар 4 хүү, 3 охиныг нэг эгнээнд хэчнээн янзаар жагсааж болох вэ?
A. 100
B. 121
C. 144
D. 150
E. 160
Шатрын тэмцээнд 10 сурагч оролцов. Хэрэв аль ч хоёр сурагч хоорондоо хар ба цагаанаар ээлжлэн 1, 1 удаа тоглосон бол нийт хэдэн өрөг гарсан бэ?
A. $10$
B. $20$
C. $45$
D. $90$
E. $100$
1-4 тоогоор дугаарлагдсан хайрцагт мөн 1-4 тоогоор дугаарлагдсан 4 бөмбөг хийжээ. Ядаж нэг хайрцаг болон бөмбөгний дугаар ижил байхаар хэдэн янзаар хийх вэ?
A. 18
B. 16
C. 12
D. 8
E. 9
11 сурагчийг нэг эгнээнд жагсаах боломжийн тоо аль нь вэ?
A. $C_{11}^{11}$
B. $P(11,11)$
C. $\dfrac{11!}{2}$
D. $\dfrac{1}{11!}$
E. $A_{11}^{11}$
10 сурагчийг нэг эгнээнд жагсаах боломжийн тоо аль нь вэ?
A. $C_{10}^{10}$
B. $A_{10}^{10}$
C. $\dfrac{10!}{2}$
D. $\dfrac{1}{10!}$
E. $P(10,10)$
1-р ангийн 24 сурагч үдийн цайгаа уухаар нэг цуваанд жагсах болжээ. Болд Цэцэгийн яг урд эсвэл ард нь явахыг хүсч байв. Тэд Болдын хүсэлд тохирохоор хэдэн янзаар жагсан явж болох вэ?
A. $24!$
B. $23!$
C. $\dfrac{24!}{2}$
D. $2\cdot23!$
E. $24\cdot 23$
Улаан, цагаан, хөх өнгийн хөндлөн судалтай далбааг хэчнээн янзаар зохиож болох вэ?
A. $1$
B. $2$
C. $4$
D. $5$
E. $6$
Ангийн дарга нь хамгийн урдаа зогсож байхаар ангийн 30 сурагчийг хэчнээн янзаар жагсааж болох вэ?
A. $30!$
B. $\dfrac{30!}{2}$
C. $\dfrac{29!}{2}$
D. $29!$
E. $C_{30}^{29}$
Аравтын бичлэгт нь тэг цифр орсон, ялгаатай цифрүүд бүхий таван оронтой тоо хэчнээн байх вэ?
A. $A_{10}^4-A_9^4$
B. $4!C_{9}^4$
C. $4C_{10}^4$
D. $4!C_{10}^4$
E. $4\cdot4!C_9^4$
$1,2,3,\dots,9$ цифрүүдээр бичигдсэн бүх цифр нь ялгаатай 9 оронтой тооны дотор 1 ба 2-ын цифр зэрэгцэж орсон тоо хэд вэ?
A. $2\cdot8!$
B. $8!$
C. $\frac12\cdot9!$
D. $9!$
E. $\frac12\cdot8!$
1, 2, 3, 5, 7, 8, 9 цифрүүдийг ашиглан цифр давталгүй, 7 ба 9 цифр зэрэгцэн орсон зургаан оронтой хэчнээн тоо үүсгэж болох вэ?
A. $6\cdot 5!$
B. $10\cdot 5!$
C. $5\cdot 5!$
D. $6!$
E. $2C_7^6$
Аль нь $u_n=4u_{n-1}-4u_{n-2}$ рекуррент харьцааны шийд болохгүй вэ?
A. $2^{n+4}$
B. $(n+1)2^n$
C. $c2^n$
D. $n2^n$
E. $2^{cn}$
6 сурагчаас 3-ийг сонгож жижүүр хийлгэх болжээ.
- Нэг нь шал цэвэрлэх, нөгөө нь цонх угаах, 3 дахь нь ширээ арчих боломжийн тоо $\fbox{abc}$,
- гурвуулаа хамтдаа ангиа цэвэрлэх боломжийн тоо $\fbox{de}$ байна.
11 гишүүнтэй хөл бөмбөгийн баг ахлагч, хаалгач 2-оо $\fbox{abc}$
янзаар, үүний дараа 2 довтлогчийг $\fbox{de}$
янзаар сонгож чадна.
$\{1, 2,\dots,9\}$ олонлогийн хувьд
- 2 тэгш, 3 сондгой тоонооос тогтсон дэд олонлог $\fbox{ab}$;
- 2 тэгш, 3 сондгой тоо буцаалтгүй сонгож 5 оронтой тоо бичих боломж $\fbox{cdef}$ ширхэг байна.
$\{\text{А, О, У, М, Н, Г, Л, Б, В, Р}\}$ олонлогийн хувьд
- 2 эгшиг, 2 гийгүүлэгчээс тогтох дэд олонлог $\fbox{ab}$ ширхэг,
- 2 эгшиг, 2 гийгүүлэгч буцаалтгүй сонгож 4 үсэгтэй үг бичих боломж $\fbox{cdef}$ ширхэг байна.
Бүх 4 оронтой тоонуудын тоо $\fbox{abcd}$, үүнээс бүх цифрүүд нь ялгаатай нь $\fbox{efgh}$ ба ижил цифр орсон нь $\fbox{ijkl}$ байна.
Бүх 4 оронтой тоонуудын тоо $\fbox{abcd}$, үүнээс бүх цифрүүд нь ялгаатай нь $\fbox{efgh}$ ба ижил цифр орсон нь $\fbox{ijkl}$ байна.
Үржвэрийн зарчим
32 үсэг ба 10 цифрийг ашиглан 2 үсэг ба түүний ард 3 цифр
орсон хэчнээн дугаарыг зохиож болох вэ?
Хос бүр дэх 2 үсэг нь ялгаатай байхаар 32 үсгээс хэчнээн хосыг
зохиож болох вэ?
$k$-тийн $i$-р координатыг $n_i$ янзаар сонгож болдог бол
нийт $k$-тийн тоо нь $n_1\ldots n_k$ байна.
Маркгүй 5 төрлийн дугтуй ба 4 төрлийн марк байв. Дугтуй ба маркийг хэчнээн
янзаар сонгон авч болох вэ?
"Ургамал" гэдэг үгээс эгшиг ба гийгүүлэгчийг хэчнээн янзаар сонгон авч болох вэ?
Шатрын нүднээс хар ба цагаан нүдийг хэчнээн янзаар зааж болох вэ? Шатрын
хөлгөөс 2 нүдийг хэчнээн янзаар зааж чадах вэ? Мөн 2 цагаан нүдийг хэчнээн янзаар
зааж чадах вэ?
Нэг хэвтээ юмуу босоо шугам дээр оршихгүй хар ба цагаан нүдийг шатрын
хөлгөн дээр хэчнээн янзаар зааж чадах вэ?
Гүдгэр $n$ өнцөгтөд хэчнээн диагонал татаж болох вэ?
Хоёр цифр нь хоёулаа тэгш байх хоёр оронтой тоо хэд вэ?
0, 1, 2, 3, 4, 5 цифрүүдээр хэчнээн 4 оронтой тоо бичиж чадах вэ? Тэдгээрийн нийлбэрийг ол.
0, 1, 2, 3, 4, 5 цифрүүдээр бичигдэх 3-т хуваагдах 3 оронтой тоо хэчнээн
байх вэ?
$n=p_1^{\alpha_1}\ldots p_s^{\alpha_s}$, $,p_i$ бүр нь анхны тоо бол
$n$-ийн бүх хуваагчдын тоог ол.
Зэрэгцээ цифрүүд нь ялгаатай 5 оронтой тоо хэд байх вэ?
Бичлэгт нь 0, 4, 6, 8 цифрүүдээс ороогүй 4-д хуваагдах 5 оронтой тоо хэд байх вэ?
2, 4-р цифрүүд нь сондгой ба бүх цифрүүд нь ялгаатай байх 6 оронтой тоо
хэд бий вэ?
10 хар, 20 цагаан, 30 улаан бөмбөг байв. Өнгө тус бүрээс ядаж хоёрыг
агуулсан хэдэн бөмбөгийг хэчнээн янзаар сонгож авч чадах вэ?
$10^6$ хүртэлх тоонуудын дотор бичлэгтээ 1-г агуулсан ба агуулаагүй тооны аль нь олон бэ?
0, 1, 2, 3, 4, 5 цифрүүдээр 5-д хуваагддаг, ижил цифр агуулаагүй, 6 оронтой тоо хэчнээнийг зохиож болох вэ? Хэрэв ижил цифр агуулж болох бол хэчнээн тоо зохиож болох вэ?
- 0, 1, 2, 3, 4, 5
- 0, 1, 2, 3, 4, 5, 6
- 1, 2, 3, 4, 5, 6
10 хос гутлаас нэг ч хос гутал сонгогдоогүй байхаар 6 гутлыг хэчнээн янзаар сонгож болох вэ?
Салаа 30 цэрэг, 4 офицертэй байсан ба харуулд 6 цэрэг эсвэл 4 цэрэг 2 офицер эсвэл 3 цэрэг 1 офицер эсвэл 3 офицер гарахыг зөвшөөрдөг бол өдөр бүр ялгаатай хувилбараар хэдэн өдрийн манааг томилох боломжтой вэ?
A. $A_{30}^6+A_{30}^4+A_{30}^3+A_4^1+A_{4}^2+A_{4}^3$
B. $C_{30}^6+2\cdot C_{30}^4+C_{30}^3+3$
C. $C_{30}^6+C_{30}^4\cdot C_{4}^2+4\cdot C_{30}^3+C_{4}^3$
D. $C_{30}^6+C_{30}^4\cdot C_{30}^2+C_4^1+C_4^2+C_4^3$
E. $\frac{23}{30}$
$A=3\cdot 5\cdot 7$ тооны хуваагчдын тоог ол.
A. $7$
B. $8$
C. $4$
D. $12$
E. $9$
Цэцэрлэгийн бага бүлэг 20 хүүхэдтэй, 2 багштай байв. Нэг багш нь ангийн хэсэг хүүхдийг авч салхинд гарч, нөгөө нь үлдэх хүүхдүүдийг харж үлдэхээр болов. Хэрвээ багш бүр дор хаяж нэг хүүхэдтэй үлдэнэ гэж тооцвол үүнийг хэчнээн ялгаатай аргаар хийж болох вэ?
A. $2^{21}-2$
B. $2^{20}-2$
C. $2^{21}$
D. $2^{21}-4$
E. $2^{20}-4$
Цифрүүдийнх нь нийлбэр сондгой байх 5 оронтой тоо хэчнээн байх вэ?
A. $5^5$
B. $5\cdot10^4$
C. $45\cdot 9^4$
D. $45\cdot 10^3$
E. $45\cdot 10^4$
4 өөр өнгийн 4 шагайг хаяхад 3 морь буух боломжийн тоо хэд вэ?
A. $10$
B. $11$
C. $12$
D. $13$
E. $14$
$1260$ тооны натурал тоон хуваагчдын тоог ол.
A. $48$
B. $36$
C. $32$
D. $28$
E. $18$
Гүдгэр 20 өнцөгт хэчнээн диагоналтай вэ? (Санамж: талыг диагоналд тооцохгүй)
A. $190$
B. $185$
C. $180$
D. $175$
E. $170$
Аравтын бичлэгт нь тэг цифр орсон, ялгаатай цифрүүд бүхий дөрвөн оронтой тоо хэчнээн байх вэ?
A. $3\cdot3!C_9^3$
B. $3!C_9^3$
C. $3C_9^3$
D. $3!C_{10}^3$
E. $A_{10}^4-A_9^4$
$20$ шагай орхиход яг $5$ морь тусах боломжийн тоог ол.
A. $C_{20}^5\cdot 3^{15}$
B. $C_{15}^3\cdot 4^{20}$
C. $C_{20}^5C_{15}^3$
D. $C_{20}^5\cdot 4^{15}$
E. $C_{20}^5\cdot 5!\cdot 3^{15}$
$5$ хүү $7$ охинтой бүжгийн дугуйлангаас нэг хосыг тэмцээнд оруулах ёстой бол хосыг сонгох нийт боломжийн тоо хэд вэ?
A. $12$
B. $35$
C. $7$
D. $5$
E. $24$
6 хүүхэд ба хэсэг морьдоос морьтой хүүхдийг 48 ялгаатай аргаар сонгож болдог бол хэдэн морь байсан бэ?
A. 6
B. 12
C. 48
D. 24
E. 8
$A=\{a_1,a_2,...,a_n\}, B=\{b_1,b_2,...,b_k\},$ $C=\{c_1,c_2,...,c_s\}$ олонлогуудын $A$ олонлогоос 1 элемент, $B$ олонлогоос 2 элемент, $C$-ээс 3 элемент оролцсон цуглуулга хийх боломжийн тоог ол.
A. $nA_k^2A_s^3$
B. $nC_k^2C_s^3$
C. $nk^2s^3$
D. $C_n^2C_s^3$
E. $C_{n+k+s}^6$
$A=\{a_1,a_2,...,a_n\},$ $B=\{b_1,b_2,...,b_k\}$ олонлогуудын $A$ олонлогоос $s$ элемент авч индексийн өсөх дарааллаар эрэбэлэн жагсааж түүний араас $B$ олонлогоос $m$ элемент авч дурын дарааллаар жагсаав. Хэдэн янзаар ингэж жагсааж болох вэ?
A. $A_n^s\cdot A^m_k$
B. $C_n^sA_k^m$
C. $A_n^SC_k^m$
D. $C_n^sC_k^m$
Гүдгэр $n$ өнцөгт хэдэн диагоналтай вэ?
A. $\dfrac{n(n-3)}{2}$
B. $\dfrac{n(n-1)}{2}$
C. $n(n-3)$
D. $n(n-1)$
E. $n$
3 ялгаатай ном, 5 өөр дэвтрээс 1 ном, 1 дэвтрийг хэчнээн ялгаатай аргаар сонгон авч болох вэ?
A. $A_5^3$
B. $5!\cdot 3!$
C. $C_5^3$
D. $15$
E. $\dfrac{1}{15}$
$A=3\cdot 7\cdot 11$ тооны хуваагчдын тоог ол.
A. 7
B. 8
C. 3
D. 6
E. 9
$2016$-ын натурал тоон хуваагчдын тоог ол.
A. $3$
B. $10$
C. $20$
D. $18$
E. $36$
600 тоо хэчнээн хуваагчтай вэ?
A. 12
B. 24
C. 20
D. 18
E. 30
$1,2,3,4,5,7,8,9$ тоонуудаас үржвэр нь тэгш тоо байхаар 2 ялгаатай тоог хэчнээн аргаар сонгож болох вэ?
A. 26
B. 18
C. 22
D. 17
E. 14
180 тоо хэчнээн хуваагчтай вэ?
A. 12
B. 15
C. 16
D. 18
E. 20
$1,2,3,4,5,6,7,8,9$ тоонуудаас үржвэр нь тэгш тоо байхаар 2 ялгаатай тоог хэчнээн аргаар сонгож болох вэ?
A. 26
B. 20
C. 32
D. 27
E. 24
Сумо бөхийн дээд зиндаанд нийт 40 бөх барилддаг. Нэг тэмцээнд бөх тус бүр 15 удаа барилддаг бол нэг тэмцээний туршид нийт хэчнээн барилдаан гарах вэ?
A. $C_{40}^2$
B. $C_{15}^2$
C. $600$
D. $300$
E. $C_{40}^{15}$
4 шагайг орхиход яг 2 морь буух боломжын тоо хэд вэ?
A. $C_4^2\times3\times3$
B. $1\times1\times3\times3$
C. $C_4^2\times1\times1$
D. $4^4-3^2$
E. $4^4-C_4^2\times3\times3$
$A$-аас $B$ хүртэл 3 өөр замтай, $B$-ээс $C$ хүртэл 4 өөр замтай бол $A$-аас $B$-г дайрч $C$ хүрээд буцаад $B$-г дайрч $A$-д ирэх замыг хэдэн янзаар явж болох вэ?
A. $12$
B. $24$
C. $144$
D. $72$
E. $36$
4 шагайг орхиход яг 1 морь, 1 тэмээ буух боломжын тоо хэд вэ?
A. $C_4^2\times3\times3$
B. $1\times1\times3\times3$
C. $C_4^2\times1\times1$
D. $4^4-3^2$
E. $4^4-C_4^2\times3\times3$
$200$ тооны хуваагчдын тоо аль нь вэ?
A. $10$
B. $12$
C. $15$
D. $30$
E. $60$
2, 3, 4, 5, 6, 7 цифрүүдээр бичигдэх 3-т хуваагдах 3 оронтой тоонуудын цифрүүдийн нийлбэр аль нь вэ?
A. $966$
B. $972$
C. $975$
D. $978$
E. $984$
Сагсан бөмбөгийн тэмцээнд нийт 20 баг оролцов. Хэрвээ баг бүр 10 өдрийн турш өдөр бүр 1, 1 тоглолт хийсэн бол нийт хэдэн тоглолт гарсан бэ?
A. $10$
B. $20$
C. $50$
D. $100$
E. $200$
3, 4, 5, 6, 7, 8 цифрүүдээр бичигдэх 3-т хуваагдах 3 оронтой тоонуудын цифрүүдийн нийлбэр аль нь вэ?
A. $1188$
B. $1185$
C. $1191$
D. $1194$
E. $1185$
A хотоос B хот хүртэл 3 өөр замаар, B хотоос C хот хүртэл 5 өөр замаар явдаг бол A хотоос гарч, B хотоор дайран C хотод хүрээд буцаж B хотоор дайран A хотод ирж болох бүх замын тоог ол.
A. $30$
B. $225$
C. $15$
D. $16$
E. $64$
A хотоос B хот хүртэл 4 өөр замаар, B хотоос C хот хүртэл 6 өөр замаар явдаг бол A хотоос гарч, B хотоор дайран C хотод хүрээд буцаж B хотоор дайран A хотод ирж болох бүх замын тоог ол.
A. $576$
B. $48$
C. $20$
D. $100$
E. $24$
A хотоос B хот хүртэл 4 өөр замаар, B хотоос C хот хүртэл 5 өөр замаар явдаг бол A хотоос гарч, B хотоор дайран C хотод хүрээд буцаж B хотоор дайран A хотод ирж болох бүх замын тоог ол.
A. $20$
B. $40$
C. $400$
D. $18$
E. $81$
Аль ч хөрш хоёр цифр нь ялгаатай зургаан оронтой тоо хэчнээн бэ?
A. $9^6$
B. $9\cdot 10^5$
C. $C_{10}^6-C_9^6$
D. $10\cdot 9^5$
E. $621000$
$0,4,6,8$ цифр агуулаагүй, дөрөвт хуваагддаг таван оронтой тоо хэд байх вэ?
A. $2800$
B. $2950$
C. $3000$
D. $4200$
E. $4500$
A хотоос B хот хүртэл 5 өөр замаар, B хотоос C хот хүртэл 6 өөр замаар явдаг бол A хотоос гарч, B хотоор дайран C хотод хүрээд буцаж B хотоор дайран A хотод ирж болох бүх замын тоог ол.
A. $60$
B. $900$
C. $22$
D. $121$
E. $30$
A хотоос B хот хүртэл 4 өөр замаар, B хотоос C хот хүртэл 5 өөр замаар явдаг бол A хотоос гарч, B хотоор дайран C хотод хүрээд буцаж B хотоор дайран A хотод ирж болох бүх замын тоог ол.
A. $20$
B. $40$
C. $400$
D. $18$
E. $81$
5 хүнээс дарга, туслах гэсэн 2 хүнийг хэчнээн янзаар сонгож болох вэ?
A. $10$
B. $5$
C. $8$
D. $3$
E. $20$
$270$ хэчнээн натурал тоон хуваагчтай вэ?
A. $12$
B. $15$
C. $16$
D. $18$
E. $20$
$240$ хэчнээн натурал тоон хуваагчтай вэ?
A. $20$
B. $18$
C. $16$
D. $15$
E. $12$
4 өөр өнгийн 4 шагайг хаяхад 3 морь буух боломжийн тоо хэд вэ?
A. $10$
B. $11$
C. $12$
D. $13$
E. $14$
420-ийн хуваагчдын тоог олоорой.
A. 8
B. 24
C. 6
D. 12
E. 20
$X=\{11,31,25,45,67,91,69,63,57,97,73\}$ олонлогийн дэд олонлогийн тоо хэд вэ?
A. 256
B. 512
C. 1024
D. 2048
E. 5096
8 цифрийг ядаж нэг удаа агуулсан 5 оронтой тоо хэд байгаа вэ?
A. 22800
B. 52488
C. 90000
D. 37512
E. 11400
7 цифрийг ядаж нэг удаа агуулсан 5 оронтой тоо хэд байгаа вэ?
A. 22800
B. 52488
C. 90000
D. 37512
E. 11400
Аравтын бичлэгт нь тэг цифр орсон, ялгаатай цифрүүд бүхий таван оронтой тоо хэчнээн байх вэ?
A. $A_{10}^4-A_9^4$
B. $4!C_{9}^4$
C. $4C_{10}^4$
D. $4!C_{10}^4$
E. $4\cdot4!C_9^4$
$20$ шагай орхиход яг $5$ морь тусах боломжийн тоог ол.
A. $C_{20}^5\cdot 3^{15}$
B. $C_{15}^3\cdot 4^{20}$
C. $C_{20}^5C_{15}^3$
D. $C_{20}^5\cdot 4^{15}$
E. $C_{20}^5\cdot 5!\cdot 3^{15}$
Сумо бөхийн дээд зиндаанд нийт 40 бөх барилддаг. Нэг тэмцээнд бөх тус бүр 15 удаа барилддаг бол нэг тэмцээний туршид нийт хэчнээн барилдаан гарах вэ?
A. $C_{40}^2$
B. $C_{15}^2$
C. $600$
D. $300$
E. $C_{40}^{15}$
2, 3, 4, 5, 6, 7 цифрүүдээр бичигдэх 3-т хуваагдах 3 оронтой тоонуудын цифрүүдийн нийлбэр аль нь вэ?
A. $966$
B. $972$
C. $975$
D. $978$
E. $984$
Шоог гурван удаа хаяхад
- Бүгд $5$-аас ихгүй байх боломжийн тоо $\fbox{abc}$ байна.
- Бүгд $4$-өөс ихгүй байх боломжийн тоо $\fbox{de}$ байна.
- Хамгийн их нь $5$ байх боломжийн тоо $\fbox{fg}$ байна.
Ерөнхий байршилтай (аль ч хоёр нь давхцахгүй, аль ч гурав нь нэг шулуун дээр үл орших) 10 цэгийн 5-ыг нь улаанаар, 2-ыг нь хөхөөр, 3-ыг нь ногооноор будаж хос хосоор нь хэрчмээр холбожээ.
- 2 ижил өнгийн төгсгөлтэй хэрчим $\fbox{ab}$ ширхэг.
- 3 өөр өнгийн оройтой гурвалжин $\fbox{cd}$ ширхэг.
- Санамсаргүйгээр нэг гурвалжин авахад бүх орой нь ижил өнгөтэй байх магадлал $\dfrac{\fbox{ef}}{120}$
$21168$ тоог анхны тоонуудын үржвэрт задалбал $21168={\fbox{a}}^{\fbox{b}}\cdot{\fbox{c}}^{\fbox{d}}\cdot{\fbox{e}}^{\fbox{f}},$ $(\fbox{a}< \fbox{c}< \fbox{e})$ байна. Иймд энэ тоо нь $\fbox{ghi}$ ширхэг хуваагчтай.
$ 14112$ тоог анхны тоонуудын үржвэрт задалбал $14112={\fbox{a}}^{\fbox{b}}\cdot{\fbox{c}}^{\fbox{d}}\cdot{\fbox{e}}^{\fbox{f}},$ $(\fbox{a}< \fbox{b}< \fbox{c})$ байна. Иймд энэ тоо нь $\fbox{gh}$ ширхэг хуваагчтай.
4 өнгийн шагайг орхиход:
- 4 морь буух боломжийн тоо $\fbox{a}$,
- яг нэг морь буух боломжийн тоо $\fbox{bcd}$ байна.
4 өнгийн шагайг орхиход:
- 4 бэрх буух боломжийн тоо $\fbox{ab}$,
- ядаж нэг морь буух боломжийн тоо $\fbox{cde}$ байна.
Зөвхөн сондгой цифрүүдээр 2 оронтой тоо $\fbox{ab}$ ширхэгийг зохиож чадах ба эдгээрээс $\fbox{c}$ ширхэг нь 5-д, $\fbox{d}$ ширхэг нь 11-д, $\fbox{e}$ ширхэг нь 3-д хуваагдана.
Зөвхөн тэгш цифрүүдээр 2 оронтой тоо $\fbox{ab}$ ширхэгийг зохиож чадах ба эдгээрээс $\fbox{c}$ ширхэг нь 10-д, $\fbox{d}$ ширхэг 11-д, $\fbox{e}$ ширхэг нь 3-д хуваагдана.
$\text{ХИЕХ}(X;Y)=7$, $\text{ХБЕХ}(X;Y)=420$ байх $(X,Y)$ хос тоо $\fbox{a}$ ширхэг байна.
$\text{ХИЕХ}(X;Y)=5$, $\text{ХБЕХ}(X;Y)=630$ байх $(X, Y)$ хос тоо $\fbox{a}$ ширхэг байна.
Хэсэглэлийн тоо
7 гүйгчээс 4 хүнтэй багийг хэчнээн янзаар сонгож болох вэ?
$k$ ширхэг $a$, $n$ ширхэг $x$-г агуулсан $k+n$-түүдийн тоог ол.
Ангийн 40 сурагчийн 24 нь эрэгтэй байв. Эднээс:
- 4 хүнтэй баг хэчнээн янзаар гаргах вэ?
- 1 ахлагч бүхий 4 хүнтэй багийг хэчнээн янзаар гаргах вэ?
- Баг эмэгтэй сурагчтай байх тохиолдолд 1-г бод.
- Баг эмэгтэй ба эрэгтэй сурагч байх тохиолдолд 1 ба 2-г бод.
- $C^k_n=C^{k-1}_{n-1}+C^k_{n-1}$,
- $C^k_n=C^{n-k}_n$,
- $C_n^k=\frac nk\cdot C_{n-1}^{k-1}$,
- $(x+a)^n=\sum^n_{k=0}C^k_na^kx^{n-k}$,
- $2^n=\sum^n_{k=0}C^k_n$,
- $\sum^n_{k=0}kC^k_n=n\cdot2^{n-1}$,
- $C^p_{n+m}=\sum^p_{k=0}C^k_mC^{p-k}_n$
Шуудан дээр 10 төрлийн захидал худалдаж байв. 12 ил захидлыг хэчнээн янзаар худалдаж авч чадах вэ? 8 өөр захидлыг хэчнээн янзаар худалдаж авах вэ?
12 хүүхдэд 4 хар, 8 сүүтэй шоколадыг хүүхэд бүрд нэг шоколад оногдож байхаар хэчнээн янзаар хувааж болох вэ?
100 гишүүнтэй клубийн удирдах зөвлөлийг 4 хүнтэйгээр хэчнээн янзаар сонгож болох вэ? Хэрэв нэгэн зэрэг удирдах зөвлөлд орж болдоггүй 2 хүн байдаг бол хэчнээн янзаар сонгож болох вэ?
100 ширхэг ялгаатай зүйлийг а) 1 улаан, 1 цэнхэр б) 2 ижил хайрцагт хайрцаг тус бүрд 50 зүйл орсон байхаар хэчнээн янзаар байрлуулж болох вэ?
Яг 3 ялгаатай сондгой цифрээс бүрдэх ба цифр бүр яг 2 удаа орсон байх 6 оронтой тоо хэчнээн байх вэ?
10 төрлийн чихрээс
- 1 найздаа 2 ялгаатай чихрийг
- 1 найздаа 3 ширхэгийг
- 5 найздаа тус бүр 2 ялгаатай чихрийг
- 5 найздаа тус бүр 3 ширхэгийг
Дараах адилтгалыг батал.
- $C_n^k=\dfrac{n}{k}C_{n-1}^{k-1}$
- $C_n^mC_m^k=C_n^kC_{n-k}^{m-k}$
- $C_k^k+C_{k+1}^k+C_{k+2}^k+\dots+C_n^k=C_{n+1}^{k+1}$
- $C_n^0-C_n^1+C_n^2-\dots\pm C_n^n=0$
- $C_n^0C_m^k+C_n^1C_m^{k-1}+\dots+C_n^kC_m^0=C_{n+m}^k$
- $1C_n^1+2C_n^2+\dots+nC_n^n=n2^{n-1}$
Ижил өнгийн бөмбөлгүүд нь ялгаагүй 9 цагаан, 8 хар бөмбөлгийг хар бөмбөлгүүд дараалан ороогүй байхаар нэг эгнээнд хэчнээн янзаар байрлуулж болох вэ?
A. $15$
B. $21$
C. $28$
D. $36$
E. $45$
Зурагт дүрслэгдсэн $\ell_1$ ба $\ell_2$ параллел шулуунууд дээр харгалзан 3 ба 2 цэг тэмдэглэв. Эдгээр цэгүүд дээр оройтой гурвалжны тоог ол.
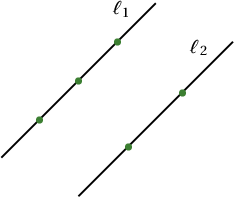

A. 6
B. 5
C. 10
D. 9
E. 3
Ангийн 30 сурагчийн 20 нь хүү байв. 4 хүү, 2 охиноос бүрдэх ангийн жижүүрийг хэдэн янзаар сонгож болох вэ?
A. $C_{30}^6$
B. $C_{20}^4C_{10}^2$
C. $A_{20}^4A_{10}^2$
D. $A_{30}^6$
E. $C_{(20)}^4C_{(10)}^2$
7 хүн уулзаад бүгд хоорондоо яг нэг удаа гар барив. Нийт хэдэн гар барилт явагдсан бэ?
A. $7!$
B. $\dfrac{7!}{2}$
C. $C_7^1$
D. $C_7^2$
E. $A_7^2$
Тойрог дээр 3 улаан, 4 хөх цэг тэмдэглэв. Эдгээр цэгүүд дээр оройтой, бүх орой нь ижил өнгөтэй биш гурвалжны тоог ол.
A. 10
B. 12
C. 18
D. 30
E. 35
Ангийн 15 хүү, 10 охиноос 2 хүү, 2 охиноос бүрдсэн ангийн жижүүрийг хэчнээн янзаар сонгож болох вэ?
A. $A_{15}^2A_{10}^2$
B. $15\cdot 10=150$
C. $P_{15}\cdot P_{10}$
D. $C_{15}^2C_{10}^2$
E. $\dfrac{15!\cdot 10!}{2}$
Тойрог дээр өгөгдсөн $2015$ цэгийн $3$ нь улаан бусад нь хөх өнгөтэй байв. Эдгээр цэгүүд дээр оройтой, ядаж нэг орой нь улаан өнгөтэй гурвалжин хэчнээн байх вэ?
A. $C_{2012}^3$
B. $C_{2015}^3$
C. $C_{2015}^3-C_{2012}^3$
D. $C_{2013}^3$
E. $C_{2014}^3$
Ангийн шатрын тэмцээнд 10 сурагч оролцож, тойргоор тоглохоор болжээ. Нийт хэдэн өрөг гарах вэ?
A. $90$
B. $100$
C. $50$
D. $36$
E. $45$
Дараагийн цифр нь өмнөхөөсөө бага байх 5 оронтой тоо хэд вэ?
A. $C_9^5$
B. $C_{10}^5$
C. $2C_9^5$
D. $\frac12C_{10}^5$
E. $A_9^5$
Дараагийн цифр нь өмнөхөөсөө бага бөгөөд 10-д хуваагдах 5 оронтой
тоо хэд вэ?
A. $C_{10}^5$
B. $2C_9^4$
C. $C_9^4$
D. $\frac12C_{10}^5$
E. $9000$
Сурагч конкурсын 3 шалгалтыг 9 өдөрт багтаан өгөх ёстой байжээ.
өдөрт нэгээс илүүгүй шалгалт өгөх бол түүний шалгалтаа өгөх боломж нь хэд вэ?
A. $A_9^3$
B. $3!A_9^3$
C. $C_9^3$
D. $\frac{9!}{3!}$
E. $\dfrac{A_9^3}{2}$
Тэмцээнд 20 шатарчин оролцсон. Нийт 6 өрөгт тэнцсэн бол хэн нэг нь хожсон өргийн тоог ол.
A. $C_{20}^2-6$
B. $A_{20}^2-6$
C. $32!-6$
D. $32!-6!$
E. $20!-6$
$A=\{a_1,a_2,...,a_n\}, B=\{b_1,b_2,...,b_k\},$ $C=\{c_1,c_2,...,c_s\}$ олонлогуудын $A$ олонлогоос 1 элемент, $B$ олонлогоос 2 элемент, $C$-ээс 3 элемент оролцсон цуглуулга хийх боломжийн тоог ол.
A. $nA_k^2A_s^3$
B. $nC_k^2C_s^3$
C. $nk^2s^3$
D. $C_n^2C_s^3$
E. $C_{n+k+s}^6$
Дөрвөн мөнгийг зэрэг орхиход хоёр нь сүлдээрээ, 2 нь тоогоороо буух эгэл үзэгдлийн тоо хэд вэ?
A. $8$
B. $7$
C. $6$
D. $5$
E. $4$
$36$ модтой хөзрөөс таамгаар гурвыг сугалахад гурвуулаа хүн (ноён, хатан боол) байх эгэл үзэгдлийн тоо хэд вэ?
A. $C_{12}^3$
B. $\dfrac16C_{36}^3$
C. $3!C_{12}^3$
D. $C_{24}^3$
E. $C_{36}^3$
$6$ адилхан мөнгийг зэрэг хаяхад 4 нь тоогоороо буух эгэл үзэгдлийн тоо хэд вэ?
A. $C_6^3$
B. $2!C_6^4$
C. $15$
D. $18$
E. $A_6^4$
Шигшээ тэмцээнд оролцон шатарчлан тоглосон даамчид нийт 120 өрөг тоглосон бол тэмцээнд хэдэн даамчин оролцсон бэ?
A. 12
B. 14
C. 16
D. 18
Ангийн 30 сурагчаас 4 сурагчаас бүрдсэн ангийн жижүүрийг хэчнээн янзаар сонгож болох вэ?
A. $C_{30}^4$
B. $A_{30}^4$
C. $P_4$
D. $C_{4}^{30}$
E. $\dfrac{4}{30}$
9 сурагчаас 5-аас цөөнгүй сурагчтай бүлэг хэчнээн янзаар зохиож болох вэ?
A. $64$
B. $96$
C. $128$
D. $200$
E. $256$
Зурагт дүрслэгдсэн $\ell_1$ ба $\ell_2$ параллель шулуунууд дээр харгалзан 4 ба 3 цэг тэмдэглэв. Эдгээр цэгүүд дээр оройтой гурвалжны тоог ол.


A. 12
B. 7
C. 30
D. 25
E. 32
Тойрог дээр 5 хар, 6 улаан цэг өгөгдөв. Тэгвэл эдгээр цэгүүд дээр оройтой таван өнцөгтүүдээс яг хоёр орой нь улаан байх таван өнцөгт хэд вэ?
A. 145
B. 150
C. 120
D. 136
E. 110
Ангийн 25 сурагчийн сурагчийн 15 нь хүү, 10 нь охин байв. Сондгой тооны хөвгүүнтэй хэсэг сурагчийг нийт хэчнээн янзаар сонгож болох вэ?
A. $2^{25}$
B. $15\cdot 10$
C. $2^{23}$
D. $C_{13}^1\cdot C_{17}^{k}$
E. $2^{24}$
Цифрүүд нь буурах эрэмбээр байрлах 4 оронтой тоо хэдэн ширхэг байх вэ?
A. $A_{10}^4$
B. $4!$
C. $A_{(10)}^4=\overline{A_{10}^4}$
D. $C_{10}^4$
E. $C_{(10)}^4=\overline{C_{10}^4}$
Ангийн 20 сурагчийн 10 нь эрэгтэй, 10 нь эмэгтэй байв. Эрэгтэй, эмэгтэй сурагчид тус бүр сондгой тоотой орсон байхаар хэсэг сурагчийг сонгох боломжийн тоо хэдтэй тэнцүү вэ?
A. $C_{10}^5\cdot C_{10}^5$
B. $2^{20}$
C. $2^{19}$
D. $2^{18}$
E. $A_{10}^5\cdot A_{10}^5$
Бага ангийн 8, дунд ангийн 5 сурагчаас анги бүрээс 2 сурагч орсон байхаар 4 сурагчтай бүлгийг хэдэн янзаар сонгох вэ?
A. 1600
B. 1120
C. 1680
D. 280
E. 1260
Ялгаатай 5 номноос 3 номыг хэчнээн ялгаатай аргаар сонгон авч болох вэ?
A. $P_5\cdot P_3$
B. $C_5^3$
C. $A_5^3$
D. $5\cdot 3$
E. $20$
Ангийн 7 хөвгүүнээс 5 хүнтэй баг хэчнээн аргаар бүрдүүлж болох вэ?
A. $42$
B. $1760$
C. $21$
D. $2520$
E. $35$
Ангийн 7 хөвгүүнээс 2 хүнтэй баг хэчнээн аргаар бүрдүүлж болох вэ?
A. $42$
B. $1760$
C. $35$
D. $630$
E. $21$
Найман хүнийг 2 ба 6 хүнтэй хоёр багт хуваах нийт боломжийн тоог ол.
A. $2!\cdot 6!$
B. $A_8^2\cdot A_6^6$
C. $8!$
D. $6!$
E. $C_8^2\cdot C_6^6$
Найман хүнийг 3 ба 5 хүнтэй хоёр багт хуваах нийт боломжийн тоог ол.
A. $A_8^3\cdot A_5^5$
B. $C_8^3\cdot C_5^5$
C. $8!$
D. $5!$
E. $3!\cdot 5!$
7 хүн уулзаад бүгд хоорондоо яг нэг удаа гар барив. Нийт хэдэн гар барилт явагдсан бэ?
A. $7!$
B. $\dfrac{7!}{2}$
C. $C_7^1$
D. $C_7^2$
E. $A_7^2$
Спортлото-ны картанд буй 36 тооноос 6-г нь дарахад яг 3 тоо зөв дарагдсан байх боломжийн тоог ол.
A. $C_6^3\cdot C_{30}^3$
B. $A_{36}^3$
C. $C_6^3$
D. $C_{36}^3$
E. $C_6^3\cdot C_{36}^3$
1-ээс 100 хүртэлх тоонуудаас нийлбэр нь 3-т хуваагдах гурван ялгаатай тоог хэчнээн янзаар сонгож авах вэ?
A. $53922$
B. $52928$
C. $47828$
D. $63021$
E. $53932$
Дараагийн цифр нь өмнөхөөсөө бага байх 5 оронтой тоо хэд вэ?
A. $C_9^5$
B. $C_{10}^5$
C. $2C_9^5$
D. $\frac12C_{10}^5$
E. $A_9^5$
9 сурагчаас 5-аас цөөнгүй сурагчтай бүлэг хэчнээн янзаар зохиож болох вэ?
A. $64$
B. $96$
C. $128$
D. $200$
E. $256$
Ангийн 25 сурагчийн сурагчийн 15 нь хүү, 10 нь охин байв. Сондгой тооны хөвгүүнтэй хэсэг сурагчийг нийт хэчнээн янзаар сонгож болох вэ?
A. $2^{25}$
B. $15\cdot 10$
C. $2^{23}$
D. $C_{13}^1\cdot C_{17}^{k}$
E. $2^{24}$
$4,5,6,7,8$ гэсэн дугаартай таван картыг хэрэглэн цифрүүд нь өсөх гурван оронтой тоо хэдийг зохиож болох вэ?
A. $9$
B. $15$
C. $6$
D. $10$
E. $8$
$1234567$ тооны цифрүүдээр цифрүүд нь өсөх эрэмбээр байрлах 5 оронтой тоо хэчнээнийг зохиож болох вэ?
A. $10$
B. $14$
C. $15$
D. $19$
E. $21$
$1,2,3,4,5$ гэсэн дугаартай таван картыг хэрэглэн цифрүүд нь өсөх гурван оронтой тоо хэдийг зохиож болох вэ?
A. $10$
B. $15$
C. $6$
D. $9$
E. $8$
Найман сурагчийг тус бүр 6 хүний багтаамжтай 2 машинд суулгав. Машин бүрт тэнцүү тооны сурагч суусан байх боломжийн тоо $\fbox{ab}$ байна. Машинуудад тэнцүү биш тооны зорчигч суусан байх боломжийн тоо $\fbox{cde}$
Ангийн 10 хүү, 10 охиноос 4 хүнтэй баг бүрдүүлэв.
- Нийт боломжийн тоо нь $\fbox{abcd}$.
- Баг дан эрэгтэй сурагчаас бүрдсэн байх боломжийн тоо $\fbox{efg}$.
- Багийн эрэгтэй ба эмэгтэй сурагчдын тоо тэнцүү байх магадлал $\dfrac{\fbox{hij}}{\fbox{klm}}$ байна.
Ангийн 10 хүү, 10 охиноос 6 хүнтэй баг бүрдүүлэв.
- Нийт боломжийн тоо тоо нь $\fbox{abcde}$.
- Баг дан эрэгтэй сурагчаас бүрдсэн байх боломжийн тоо $\fbox{fgh}$.
- Багийн эрэгтэй ба эмэгтэй сурагчдын тоо тэнцүү байх магадлал $\dfrac{\fbox{hij}}{\fbox{323}}$ байна.
6 сурагчаас 3-ийг сонгож жижүүр хийлгэх болжээ.
- Нэг нь шал цэвэрлэх, нөгөө нь цонх угаах, 3 дахь нь ширээ арчих боломжийн тоо $\fbox{abc}$,
- гурвуулаа хамтдаа ангиа цэвэрлэх боломжийн тоо $\fbox{de}$ байна.
11 гишүүнтэй хөл бөмбөгийн баг ахлагч, хаалгач 2-оо $\fbox{abc}$
янзаар, үүний дараа 2 довтлогчийг $\fbox{de}$
янзаар сонгож чадна.
9 сурагчийг I хэсэгт 3, II хэсэгт 3, III хэсэгт 3 сурагч байхаар $\fbox{abcd}$ янзаар, харин хэсгүүд ялгаагүй бол $\fbox{efg}$ янзаар 3 хэсэгт хувааж чадна.
7 сурагчийг I хэсэгт 3, II хэсэгт 2, III хэсэгт 2 сурагч байхаар
$\fbox{abc}$ янзаар, харин хэсгүүд
ялгаагүй бол $\fbox{def}$ янзаар 3 хэсэгт хувааж чадна.
$\{1, 2,\dots,9\}$ олонлогийн хувьд
- 2 тэгш, 3 сондгой тоонооос тогтсон дэд олонлог $\fbox{ab}$;
- 2 тэгш, 3 сондгой тоо буцаалтгүй сонгож 5 оронтой тоо бичих боломж $\fbox{cdef}$ ширхэг байна.
$\{\text{А, О, У, М, Н, Г, Л, Б, В, Р}\}$ олонлогийн хувьд
- 2 эгшиг, 2 гийгүүлэгчээс тогтох дэд олонлог $\fbox{ab}$ ширхэг,
- 2 эгшиг, 2 гийгүүлэгч буцаалтгүй сонгож 4 үсэгтэй үг бичих боломж $\fbox{cdef}$ ширхэг байна.
6 зорчигчийг тус бүртээ 4 хүний багтаамжтай суудлын 2 автомашинд хуваан суулгасан.
- Машин бүрт тэнцүү тооны зорчигч суусан байхаар $\fbox{ab}$ янзаар суулгаж болно.
- Машинуудад тэнцүү биш тооны зорчигч суусан байхаар $\fbox{cd}$ янзаар суулгаж болно.
- Хавтгайд аль ч хоёр нь параллель биш, аль ч гурав нь нэг цэг дээр үл огтлолцох 15 ширхэг шулуун өгөгдөв. Талууд нь өгөгдсөн шулуунууд дээр байрлах $\fbox{abc}$ ширхэг гурвалжин байна.
- Хавтгайд яг хоёр нь хоорондоо параллель, аль ч гурав нь нэг цэг дээр үл огтлолцох 15 ширхэг шулуун өгөгдөв. Талууд нь өгөгдсөн шулуунууд дээр байрлах $\fbox{def}$ ширхэг гурвалжин байна.
32 модтой хөзрөөс таамгаар 5 мод сонгон авахад
- Яг нэг ширхэг дөрвөлжин сонгогдсон байх боломжийн тоо $\fbox{abcde}$ байна.
- 3 улаан, 2 хар мод сонгогдсон байх магадлал $\dfrac{\fbox{fgh}}{\fbox{ijk}}$ байна.
Ангийн 10 хүү, 10 охиноос 6 хүнтэй баг бүрдүүлэв.
- Нийт боломжийн тоо тоо нь $\fbox{abcde}$.
- Баг дан эрэгтэй сурагчаас бүрдсэн байх боломжийн тоо $\fbox{fgh}$.
- Багийн эрэгтэй ба эмэгтэй сурагчдын тоо тэнцүү байх магадлал $\dfrac{\fbox{hij}}{\fbox{323}}$ байна.