Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Holy guacamole! www.integral.mn сайт 2026-01-01-ээс шинэчлэгдэж www.mathminds.club хуудас руу шилжинэ.
Интеграл
Интеграл ашиглан талбай бодох
$a>0$ байг. $y=x^3-(2a-1)x^2+a(a+1)x, y=x^2-ax$
муруйнуудын огтолцолд үүсэх 2 хэсэг дүрсийн талбай хоорондоо
тэнцүү байх $a$-ийн утгыг ол.
$y=x^3-3x, y=x^3-3ax^2+3a^2x, (a>0)$ муруйнуудын огтлолд үүсэх
дүрсийн талбайг $S$ гэе. $\dfrac{S}{a}$ хамгийн бага утгатай байх $a$ ба тэр үеийн $S$-ийг ол.
Дараах шугамуудаар хүрээлэгдсэн дүрсийн талбайг ол.
- $y=x^3-3x^2$, $x$ тэнхлэг
- $y=x^4-4x^2, y=x^2-4$
- $C: y=x^3-x$, $C$ муруйн $P$ цэг дээрх шүргэгч.
$y=x-1$ шулуун дээр орших $P$ цэгээс $y=x^2$ парабол руу татсан 2 шүргэгч ба параболоор хүрээлэгдсэн дүрсийн талбайн хамгийн бага утгыг ол.
$(1,2)$ цэгийг дайрсан өнцгийн коэффициент нь $2k$
байх шулуун $y=x^2$ параболыг $P$, $Q$ цэгүүдээр огтолно. $P$, $Q$
цэгүүдэд татсан шүргэгч шулуунуудыг $\ell_1$, $\ell_2$ гэе. $-2\leq k\leq
2$ үед $\ell_1$, $\ell_2$ ба параболоор хүрээлэгдсэн дүрсийн талбай $S$-ийн
хамгийн их, хамгийн бага утгуудыг ол.
$y=|x^2-4|$, $x$ тэнхлэг $x=t$, $x=t+1 (t\geq 0)$ шугамуудаар хүрээлэгдсэн талбайн хамгийн бага утгыг ол. Тэр үед
$t$-г ол.
Дараах муруй ба $x$ тэнхлэгээр хүрээлэгдсэн дүрсийн талбайг ол.
- $y=-x^2+8$ $(-2\leq x\leq 1)$
- $y=x^2-5x-5$ $(0\leq x\leq 5)$
Дараах муруй болон шулуунаар хүрээлэгдсэн дүрсийн талбайг ол.
- $y=-x^2+2x+3$, $x$ тэнхлэг
- $y=2x^2+3x-2$, $x$ тэнхлэг
- $y=x^2-x-1$, $x$ тэнхлэг
- $y=2x^2-3x+1$, $y=2x-1$
$y=x^2$ парабол, $y=2x+1$ шулуунаар хүрээлэгдсэн
дүрсийн талбайг $y=2x+a$ шулуун 2 тэнцүү хэсэгт хуваадаг бол $a$-г ол.
$y=x^2-2x-3$ парабол ба $y=ax$ шулууны огтолцолд үүсэх дүрсийн талбайг $S(a)$ гэвэл $S(a)$-ийн хамгийн бага утгыг
ол.
$C: y=x^2$ гэе. $C$ муруй ба $y=ax+b$ шулуунаар
хүрээлэгдсэн дүрсийн талбайг $S_1$, $C$ муруй ба $y=bx+a$ шулуунаар
хүрээлэгдсэн дүрсийн талбайг $S_2$ гэе. Хэрэв $S_1=S_2$ бол
$a, b$-г ол.
$C_1: y=x^3-3x, C_2:y=-x^2-x+5$ байг.
- $C_2$ муруйтай $(1, 0)$ цэгийн хувьд тэгш хэмтэй муруй $C_3$-ийг ол.
- $C_1$ ба $C_3$-ийн ерөнхий шүргэгч шулуун $C_4$-ийг ол.
- $C_2$ ба $C_4$-өөр хүрээлэгдсэн дүрсийн талбай $S$-ийг ол.
$y=x^2$ параболын
$A(a,a^2), B(b,b^2) (a< b)$ цэгүүдэд татсан шүргэгчүүд $S$ цэгт огтолцдог байг.
- $S$ цэгийн координатыг ол.
- $AS, SB$ хэрчмүүд, $y=x^2$ параболоор хүрээлэгдсэн дүрсийн талбай $\dfrac{1}{12}(b-a)^3$ байхыг батал.
- $y=x^2$ параболын $C(c, c^2) (a< c< b)$ цэг дээрх шүргэгч $AS$ хэрчимтэй $P$, $SB$ хэрчимтэй $Q$ цэгт огтолцдог бол $AP, PQ, QB$ хэрчмүүд ба $y=x^2$ параболоор хүрээлэгдсэн дүрсийн талбай хамгийн бага байх $C$ цэгийг ол.
$y=x^2+1$ парабол дээр $P$ цэгийг авав. $O$ оройн цэг бөгөөд $OP$ хэрчмийг $t^2:(1-t^2) (0< t< 1)$ харьцаанд хуваах дотоод $Q$ цэг авав.
- $P$ цэг парабол дээр хөдлөхөд $Q$ цэг $C$ муруй зурдаг бол $C$-ийн тэгшитгэлийг бич.
- $y=x^2+1$ ба $C$ муруйгаар хүрээлэгдсэн дүрсийн талбайн хамгийн их утгыг ол.
$(1, 2)$ цэгийг дайрсан өнцгийн коэффициент нь $k$ байх шулуун $C: y=x^2$ параболыг $P, Q$ цэгээр огтолно. $C$ муруйн $P, Q$ цэгүүд дээрх шүргэгчүүд ба $C$-ээр хүрээлэгдсэн талбай $S$ бол
- $S$-ийг $k$-аар илэрхийл.
- $-3\leq x\leq 3$ үед $S$-ийн хамгийн их ба хамгийн бага утгыг ол.
$y=x^2-2px$ параболын $(t, t^2-2pt)$ цэг дээрх шүргэгчийг $y$ тэнхлэгийн дагуу $b$ нэгжээр зөөхөд гарах шулууныг $l(t, b)$ гэе. $l(t, b)$ шулуун параболтой 2 цэгээр огтолцоход үүссэн дүрсийн талбайг ол. $x=u$ гэсэн шулуун уг дүрсийн талбайг 2 тэнцүү хэсэгт хуваадаг бoл $u$-г ол.
$y=x^2-5x+6$ парабол $y=kax-a^2-5a$ шулуун өгөгдөв.
- Дурын $a$-ийн хувьд парабол ба шулуун хоёр ялгаатай 2 цэгээр огтолцолдог байх $k$-ийн утгын мужийг ол.
- (1)-д олдсон $k$-ийн мужид парабол ба шулуунаар хүрээлэгдсэн талбай нь $a$-аас хамаарахгүй байх $k$-ийн утгыг ол.
$a$ бодит тоо
- $y=\dfrac{8}{27}x^3, y=(x+a)^2$ муруйнууд $x$ тэнхлэгээс ялгаатай 2 ерөнхий шүргэгч шулуунтай байх $a$-ийн утгын мужийг ол.
- (1)-д олдсон 2 шүргэгч ба параболоор хүрээлэгдсэн дүрсийн талбай $S$-ийг $a$-аар илэрхийл.
$y=x(x-1)^2, y=kx^2 (k>0)$ муруйнууд өгөгдөв.
- Дээрх 2 муруй ялгаатай 3 цэгээр огтолцохыг харуул.
- Дээрх 2 муруйгаар хүрээлэгдсэн 2 хэсгийн талбай тэнцүү бол $k$-г ол.
$y=|x^2-4|$, абсцисс тэнхлэг, $x=t$ ба $x=t+1 (t\geq 0)$ шугамуудаар хүрээлэгдсэн дүрсийн талбайн хамгийн бага утгыг ол. Ямар $t$-ийн хувьд энэ утгад хүрэх вэ?
$x$-ийн хувьсах мужид $y$ бa абсцисс тэнхлэгээр зааглагдсан хэсгийн талбайг ол.
- $y=x^2-2x+2, [-1, 2]$
- $y=x^2-x, [0, 2]$
$y=2x^2-5x, y=-x^2+x+12$ функцүүдын графикууд огтлолцоход үүсэх дүрсийн талбайг ол.
$(1, 2)$ цэгийг дайрсан
шулуун ба $y=x^2$ параболоор хүрээлэгдсэн дүрсийн талбайг $S$ гэе.
$S$-ийн хамгийн бага утгыг ол.
$l\colon y=m(x-2)+5, C\colon y=x^2$ байг. $l$ ба $C$-ээр хүрээлэгдсэн дүрсийн талбайг $S$, $(2, 5)$ цэгийг дайрсан $l$-д перпендикуляр шулууныг $l_1$ гэе. $l_1$ ба $C$-ээр хүрээлэгдсэн дүрсийн талбайг $S_2$ гэе. $S_1=S_2$ байх $m$-ийн бүх утгуудыг ол.
$y=|x^2-x|$ муруйг $y=mx$ шулуун 3 ялгаатай цэгээр огтолдог байв. Муруй ба шулууны огтлолд үүсэх 2 дүрсийн талбайн нийлбэр хамгийн бага байх $m$-ийг ол. Тэр үеийн талбайг ол.
$C\colon y=x^3-6x^2-9x$,
$P$ нь $C$ муруй дээр орших $x$ координат нь $p, (p< 2)$ байх цэг
байг. $C$ муруй ба $P$ цэг дээрх шүргэгч шулуун $l$-ээр
хүрээлэгдсэн талбай $S$-г $p$-ээр илэрхийл.
$C\colon y=x^3-6x^2+9x$, $\ell: y=mx$ байг. $C$ ба $\ell$
нь $x\geq 0$ байх ялгаатай 3 цэгүүдээр огтолцох ба
огтлолд үүсэх 2 хэсэг талбай тэнцүү бол $m$-г ол.
$x=a$, $x=2a$ ($0< a< 2,5$), $y=0$, $y=5-4x-x^2$ шугамуудаар хүрээлэгдсэн дүрс $a$-ийн ямар утганд хамгийн их талбайтай байх вэ?
A. $1$
B. $\dfrac{6+\sqrt{71}}{7}$
C. $\dfrac{-6+\sqrt{71}}{7}$
D. $2$
E. $\dfrac{-9+\sqrt{186}}{4}$
$x=a$, $x=2a$, $\left(0< a< 2\right)$, $y=0$, $y=8+2x-x^{2} $ шугамуудаар хүрээлэгдсэн дүрс $a$-ийн ямар утганд хамгийн их талбайтай байх вэ?
A. $1$
B. $\dfrac{-3+\sqrt{65} }{7} $
C. $\dfrac{9+\sqrt{753} }{14} $
D. $\dfrac{-9+\sqrt{753} }{14} $
E. $\dfrac{3+\sqrt{65} }{7} $
$y=x^2$, $y=x+2$ шугамуудаар хязгаарлагдсан дүрсийн талбайг ол.
A. $\dfrac72$
B. $\dfrac92$
C. $\dfrac{11}2$
D. $\dfrac2{11}$
E. $\dfrac29$
$y=x^2$, $x+y=2$ функцийн графикуудаар хязгаарлагдсан дүрсийн талбайг ол.
A. $5.5$
B. $6.5$
C. $6$
D. $4.5$
E. $5$
$y=x^3$, $y=\frac{1}{2} x^3$, $x=1$, $x=2$ шугамуудаар хашигдсан дүрсийн талбайг ол.
A. $\dfrac{15}{8}$
B. $2$
C. $\dfrac{17}{8}$
D. $\dfrac{9}{4}$
E. $\dfrac{19}{8}$
$y=0$ шулуун ба $y=2x^2-2x-1.5$ параболоор хүрээлэгдсэн дүрсийн талбайг ол.
A. $\dfrac83$
B. $\dfrac23$
C. $\dfrac86$
D. $\dfrac53$
E. $3$
$y=-x^2+2, y=x$ шугамуудаар зааглагдсан дүрсийн талбайг ол.
A. $\dfrac{16}{3}$
B. $9$
C. $4.5$
D. $\dfrac{26}{3}$
E. $\dfrac{29}{6}$
$y=x^2-9x+18$ парабол ба $OX$ тэнхлэгийн хооронд үүсэх дүрсийн талбайг ол.
A. $-\dfrac{9}{2}$
B. $4.5$
C. $6$
D. $\dfrac{13}{2}$
E. $9$
$y=x^2-1$ парабол ба $OX$ тэнхлэгийн хооронд үүсэх дүрсийн талбайг ол.
A. $\dfrac12$
B. $\dfrac13$
C. $\dfrac23$
D. $1$
E. $\dfrac43$
$\displaystyle\int_{0}^4\sqrt{16-x^2} \,\mathrm{d}x$ интегралыг бод.
A. $16\pi$
B. $10\pi$
C. $3\pi$
D. $4\pi$
E. $9\pi$
$y=x^2-4x+5$ ба $y=x+1$ шугамуудаар хүрээлэгдсэн дүрсийн талбайг ол.
A. $9$
B. $5$
C. $4,5$
D. $3,5$
$y=-x^2+10x-16$ ба $y=0$ шугамуудаар хүрээлэгдсэн дүрсийн талбайг ол.
A. $48$
B. $36$
C. $18$
D. $27$
$y=x^2$ ба $y=2x-x^2$ шугамуудаар хүрээлэгдсэн дүрсийн талбайг ол.
A. $2$
B. $\dfrac16$
C. $\dfrac 13$
D. $\dfrac 15$
E. $1$
$y=x^2+4x$ ба $y=-x^2$ шугамуудаар хүрээлэгдсэн дүрсийн талбайг ол.
A. $\displaystyle\frac 73$
B. $\displaystyle\frac53$
C. $\displaystyle\frac43$
D. $\displaystyle\frac 83$
Зураг дээрх зурааслагдсан дүрсийн талбай аль вэ? {Зураг}
A. $20\displaystyle\frac56$
B. $19\displaystyle\frac16$
C. $21\displaystyle\frac 56$
D. $18\displaystyle\frac 16$
Зураг дээрх зурааслагдсан дүрсийн талбай аль вэ? {Зураг}
A. $5\displaystyle\frac16$
B. $4\displaystyle\frac 16$
C. $4\displaystyle\frac 12$
D. $5\displaystyle\frac 12$
$y=x^2; y=ax$ шугамуудаар хүрээлэгдсэн дүрсийн талбай 36 бол $a$-гийн бүх утга нь аль вэ?
A. $a=6$
B. $a=-6$
C. $a=-6; a=6$
D. $\emptyset$
$y=-x^2; y=ax$ шугамуудаар хүрээлэгдсэн дүрсийн талбай 4 бол $a$-гийн бүх утга нь аль вэ?
A. $a=2\sqrt[3]3; a=-2\sqrt[3]3$
B. $a=-2\sqrt[3]3$
C. $a=2\sqrt[3]3$
D. $\varnothing$
$y=x^2$, $y=x+6$ шугамуудаар хязгаарлагдсан дүрсийн талбайг ол.
A. $\dfrac{120}{7}$
B. $\dfrac{127}{11}$
C. $\dfrac{11}{2}$
D. $\dfrac{125}{6}$
E. $\dfrac{131}{11}$
$y=x^2$, $y=2-x, x=0, x\ge 0$ функцийн графикуудаар хязгаарлагдсан дүрсийн талбайг ол.
A. $1.5$
B. $1\dfrac{1}{6}$
C. $2$
D. $2\dfrac56$
E. $\dfrac67$
$y=-x^2+5$, $y=x^2+1$, $x=0$, $x=1$ шугамуудаар зааглагдсан дүрсийн талбайг ол.
A. $\dfrac{11}{3}$
B. $\dfrac{14}{3}$
C. $4$
D. $\dfrac23$
E. $\dfrac{10}{3}$
$\displaystyle\int_{-1}^{1}2x^2\,\mathrm{d}x$ интегралаар бодогдох дүрсийн талбай аль нь вэ?
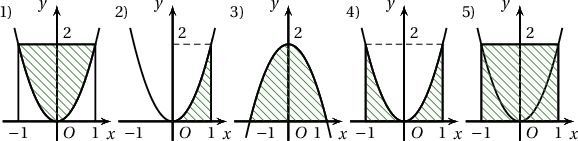
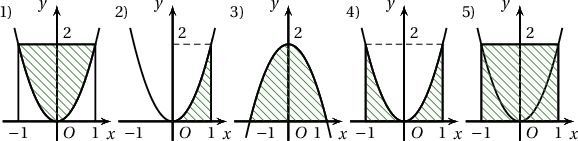
A. 1)
B. 2)
C. 3)
D. 4)
E. 5)
$y=\sin\dfrac{x}{3}$, $y=0$, $x=\pi$, $x=\dfrac{3\pi}{2}$ шугамуудаар зааглагдсан дүрсийн талбайг ол.
A. $2$
B. $1.5$
C. $0.5$
D. $\dfrac{3\sqrt3}{2}$
E. $\dfrac{\pi}{6}$
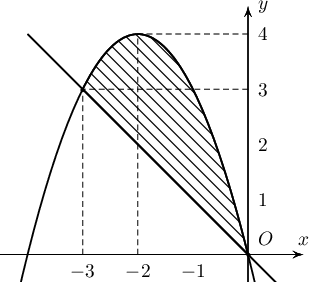
A. $5\dfrac16$
B. $4\dfrac16$
C. $4\dfrac12$
D. $5\dfrac12$
E. $5\dfrac34$
$x=a$, $x=2a\ (0< a<2.5)$, $y=0$, $y=5+4x-x^2$ шугамуудаар хүрээлэгдсэн дүрс $a$-ийн ямар утганд хамгийн их талбайтай байх вэ?
A. $\dfrac{-6+\sqrt{71}}{7}$
B. $\dfrac{-6-\sqrt{71}}{7}$
C. $\dfrac{9-\sqrt{186}}{7}$
D. $\dfrac{-9+\sqrt{186}}{7}$
E. $\dfrac{6+\sqrt{71}}{7}$
$y=x^2$, $y=-x^2+4x+6$ параболуудын огтлолцолд үүсэх дүрсийн талбайг ол.
A. $-10$
B. $21.3$
C. $20$
D. $\dfrac{61}{3}$
E. $\dfrac{64}{3}$
$y=x^2-3x+1$ парабол, $y=4-x$ шулуун ба $OY$ тэнхлэгээр хүрээлэгдсэн дүрсийн талбайг ол.
A. $12$
B. $11$
C. $10$
D. $9$
E. $8$
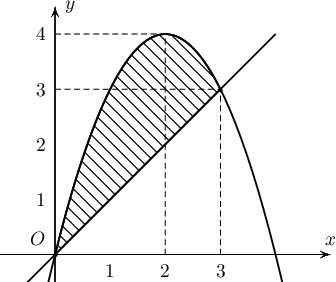
A. $5\dfrac16$
B. $4\dfrac16$
C. $4\dfrac12$
D. $5\dfrac12$
E. $5\dfrac34$
$y=x^2-4x+10$ парабол, $y=2x+1$ шулуун ба $OY$ тэнхлэгээр хүрээлэгдсэн дүрсийн талбайг ол.
A. $14$
B. $13$
C. $12$
D. $10$
E. $9$
$y=x^2+2x+5$ параболын $(-2;5)$ цэгт татсан шүргэгч шулуун, $x=0$ шулуун ба уг параболын хооронд үүсэх дүрсийн талбайг ол.
A. $\dfrac{10}{3}$
B. $3$
C. $\dfrac{8}{3}$
D. $\dfrac{5}{2}$
E. $8$
$y=0$ шулуун ба $y=2x^2-2$ муруйгаар хязгаарлагдсан дүрсийн талбайг олоорой!
A. $4$
B. $1$
C. $2$
D. $\dfrac{8}{3}$
E. $3$
$y=0$ шулуун ба $y=x^2-4$ муруйгаар хязгаарлагдсан дүрсийн талбайг олоорой!
A. $4$
B. $10\dfrac23$
C. $2$
D. $\dfrac{16}{3}$
E. $9\dfrac23$
$y=0$ шулуун ба $y=3x^2-3$ муруйгаар хязгаарлагдсан дүрсийн талбайг олоорой!
A. $4$
B. $1$
C. $2$
D. $2.5$
E. $6$
$y=0$ шулуун ба $y=6x^2-6$ муруйгаар хязгаарлагдсан дүрсийн талбайг олоорой!
A. $4$
B. $8$
C. $6$
D. $12$
E. $15$
$y=0$ шулуун ба $y=3x^2-3$ муруйгаар хязгаарлагдсан дүрсийн талбайг олоорой!
A. $4$
B. $1$
C. $2$
D. $2.5$
E. $6$
$y=x^2+4x$ ба $y=-x^2$ параболуудаар хүрээлэгдсэн дүрсийн талбайг ол.
A. $\dfrac73$
B. $\dfrac53$
C. $\dfrac43$
D. $\dfrac83$
E. $3$
$y=-2x^2+8x$ ба $y=2x^2$ параболуудаар хүрээлэгдсэн дүрсийн талбайг ол.
A. $\dfrac{16}{3}$
B. $\dfrac{10}{3}$
C. $\dfrac43$
D. $\dfrac83$
E. $3$
$y=x^3$, $y=\frac{1}{3} x^3$, $x=0$, $x=1$ шугамуудаар хашигдсан дүрсийн талбайг ол.
A. $\dfrac{1}{8}$
B. $2$
C. $\dfrac{1}{6}$
D. $\dfrac{1}{2}$
E. $\dfrac{1}{3}$
$y=2x^3$ ба $y=2x$ функцийн графикуудаар хязгаарлагдсан дүрсийн талбайг ол.
A. $1$
B. $\dfrac13$
C. $1\dfrac14$
D. $2$
E. $\dfrac12$
$y=6x^3$ ба $y=6x$ функцийн графикуудаар хязгаарлагдсан дүрсийн талбайг ол.
A. $3$
B. $2\dfrac23$
C. $1\dfrac12$
D. $4$
E. $\dfrac16$
$y=x^2-1$ парабол ба $OX$ тэнхлэгийн хооронд үүсэх дүрсийн талбайг ол.
A. $\dfrac12$
B. $\dfrac13$
C. $\dfrac23$
D. $1$
E. $\dfrac43$
$y=x^3$, $y=\frac{1}{2} x^3$, $x=1$, $x=2$ шугамуудаар хашигдсан дүрсийн талбайг ол.
A. $\dfrac{15}{8}$
B. $2$
C. $\dfrac{17}{8}$
D. $\dfrac{9}{4}$
E. $\dfrac{19}{8}$
$y=x^3$, $y=\frac{1}{2} x^3$, $x=-2$, $x=-1$ шугамуудаар хашигдсан дүрсийн талбайг ол.
A. $\dfrac{17}{8}$
B. $2$
C. $\dfrac{15}{8}$
D. $\dfrac{9}{4}$
E. $\dfrac{19}{8}$
Зурагт өгөгдсөн кубийн $ A_1B_1$ ба $D_1C_1$ ирмэгүүд дээр харгалзан $N$ ,$M$ цэгүүдийг, $A_1N : NB_1=2:3 $ , $ D_1M:МC_1=2:3 $ байхаар авчээ. Кубийг $MNBC$ хавтгайгаар огтлоход үүссэн $ BB_1NCC_1M$ ба $ABNA_1DCMD_1$ призмүүдийн эзлэхүүний харьцааг олоорой.
A. $ 3:7 $
B. $ 2:3 $
C. $ 3:10 $
D. $ 7:10$
E. $ 1:4 $
$y=x^6$ функцийн график дээр орших $P$ цэгийн $Ox$, $Oy$ тэнхлэгт буулгасан перпендикулярын суурь харгалзан $A$, $B$ бол $OAPB$ тэгш өнцөгтийн талбайг $y=x^6$ функцийн график ямар харьцаатай хуваах вэ?


A. $3:1$
B. $6:7$
C. $1:5$
D. $6:1$
E. $6:5$
$y=x^5$ функцийн график дээр орших $P$ цэгийн $Ox$, $Oy$ тэнхлэгт буулгасан перпендикулярын суурь харгалзан $A$, $B$ бол $OAPB$ тэгш өнцөгтийн талбайг $y=x^5$ функцийн график ямар харьцаатай хуваах вэ?


A. $3:1$
B. $6:7$
C. $1:5$
D. $6:1$
E. $6:5$
$A(-4, 0), B(-2, 8), C(2, 8), D(4, 0)$ цэгүүд дээр оройтой дөрвөн өнцөгтийн талбайг $y = x^2 +4$ тэгшитгэлтэй парабол ямар харьцаатай хэсгүүдэд хуваах вэ?
A. $ 4:13 $
B. $ 3:8 $
C. $ 3:11 $
D. $ 5:16$
E. $ 2:7 $
$A(-8, 0), B(-4, 32), C(4, 32), D(8, 0)$ цэгүүд дээр оройтой дөрвөн өнцөгтийн талбайг $y = x^2 +16$ тэгшитгэлтэй парабол ямар харьцаатай хэсгүүдэд хуваах вэ?
A. $ 2:7 $
B. $ 2:9 $
C. $ 2:5 $
D. $ 5:8$
E. $ 5:9 $
$A(-8, 0), B(-4, 32), C(4, 32), D(8, 0)$ цэгүүд дээр оройтой дөрвөн өнцөгтийн талбайг $y = x^2 +16 $ тэгшитгэлтэй парабол ямар харьцаатай хэсгүүдэд хуваах вэ?
A. $ 2:7 $
B. $ 2:9 $
C. $ 2:5 $
D. $ 5:8$
E. $ 5:9 $
$C\colon y=x^2-x+1$ параболын $A(1;1)$ цэгт татсан шүргэгч шулууны тэгшитгэл нь $y=\fbox{a}x+\fbox{b}$. Энэ шүргэгч шулуун, $x=0$ шулуун ба $C$ параболын дунд үүсэх дүрсийн талбай нь $$\displaystyle\int\limits_{\fbox{c}}^{\fbox{d}}(x-\fbox{e})^2 \,\mathrm{d}x=\frac{\fbox{f}}{\fbox{g}}$$ байна.
$k>0$ байг. $C\colon y=x^2$ параболын $(k,k^2)$ цэгт татсан шүргэгч шулууныг $\ell$ гэе.
- $\ell$ шулууны тэгшитгэл $y=\fbox{a}kx-k^2$ болно.
- $C$ парабол $\ell$ шулуун ба $y$ тэнхлэгээр хүрээлэгдсэн дүрсийн талбай $S=\dfrac{k^{\fbox{b}}}{\fbox{c}}$.
- $S=72$ бол $k=\fbox{d}$ байна.
$y=x^2$ параболыг $A(1;1)$ цэгт шүргэх шулууны тэгшитгэл $y=\fbox{a}x-\fbox{b}$, $B(3;9)$ цэгт шүргэх шулууны тэгшитгэл ${y=\fbox{c}x-\fbox{d}}$ байна. Эдгээр шүргэгч шулуунууд $C(\fbox{e};\fbox{f})$ цэгүүдэд огтлолцоно. Парабол болон түүний хоёр шүргэгчийн хооронд үүсэх дүрсийн талбай нь $\dfrac{\fbox{g}}{\fbox{h}}$ байна.
$y=x^2$ параболыг $A(1;1)$ цэгт шүргэх шулууны тэгшитгэл $y=\fbox{a}x-\fbox{b}$, $B(3;9)$ цэгт шүргэх шулууны тэгшитгэл ${y=\fbox{c}x-\fbox{d}}$ байна. Эдгээр шүргэгч шулуунууд $C(\fbox{e};\fbox{f})$ цэгүүдэд огтлолцоно. Парабол болон түүний хоёр шүргэгчийн хооронд үүсэх дүрсийн талбай нь $\dfrac{\fbox{g}}{\fbox{h}}$ байна.
$k>0$ байг. $C\colon y=x^2$ параболын $(k,k^2)$ цэгт татсан шүргэгч шулууныг $\ell$ гэе.
- $\ell$ шулууны тэгшитгэл $y=\fbox{a}kx-k^2$ болно.
- $C$ парабол $\ell$ шулуун ба $y$ тэнхлэгээр хүрээлэгдсэн дүрсийн талбай $S=\dfrac{k^{\fbox{b}}}{\fbox{c}}$.
- $S=72$ бол $k=\fbox{d}$ байна.
$f(x)=x^2$, $g(x)=2-x^2$ параболууд нь $x_1=\fbox{ab}$, $x_2=\fbox{c}$ абсцисстэй цэгүүдэд огтлолцох ба параболуудын огтлолцолд үүсэх дүрсийн талбай нь $\displaystyle\int_{x_1}^{x_2}\fbox{d}-\fbox{e}x^2 \,\mathrm{d}x=\dfrac{\fbox{f}}{\fbox{g}}$ байна.
$y=2x+3$ шулуун ба $y=x^2$ параболын нь $x_1=\fbox{ab}$, $x_2=\fbox{c}$ цэгүүдэд огтлолцох ба эдгээрийн огтлолцолд үүсэх дүрсийн талбай нь
$S=\displaystyle\int_{\fbox{ab}}^{\fbox{c}}(\fbox{d}x+\fbox{e}-x^2) \,\mathrm{d}x$ тул $S=\dfrac{\fbox{fg}}{3}$.
$f(x)=x^2-4x+5$ функц өгөгдөв.
- $x=0$ абсцисстэй цэгт татсан шүргэгч шулууны тэгшитгэл $y=\fbox{ab}x+\fbox{c}$ байна.
- $x=1$ шулуун $f(x)$ функцийн график болон дээрх шүргэгч шулууны хооронд үүсэх дүрсийн талбай нь $\dfrac{1}{\fbox{d}}$ байна.
- Шүргэгч шулуунд перпендикуляр $(0;5)$ цэгийг дайрсан шулуун тэгшитгэл нь $y=\dfrac{1}{\fbox{e}}{x}+\fbox{f}$ ба энэ шулууны $OX$ тэнхлэгийг огтлох цэг нь $x=\fbox{ghi}$
$x\in\big]-\frac\pi2;\frac\pi2\big[$ завсарт $f(x)=\sin 2x$, $g(x)=\cos x$ функцийн графикуудын хооронд үүсэх дүрсийн талбайг бодъё.
- $x\in\big]-\frac\pi2;\frac\pi2\big[$ завсарт $x=\dfrac{\pi}{\fbox{a}}$ абсцистай цэгт огтлолцоно.
- $x\in\big]-\frac\pi2;\frac\pi{\fbox{a}}\big[$ үед $g(x)>f(x)$ байх тул графикуудын хооронд үүсэх дүрсийн талбай нь $\displaystyle\int_{-\frac\pi2}^{\frac{\pi}{\fbox{a}}} g(x)-f(x) \,\mathrm{d}x=\dfrac{\fbox{b}}{\fbox{c}}$
- $x\in\big]\frac\pi{\fbox{a}};\frac\pi2\big[$ үед $g(x)< f(x)$ байх тул графикуудын хооронд үүсэх дүрсийн талбай нь $\displaystyle\int_{-\frac\pi2}^{\frac{\pi}{\fbox{a}}} f(x)-g(x) \,\mathrm{d}x=\dfrac{\fbox{1}}{\fbox{d}}$
- Иймд нийт талбай нь $\dfrac{\fbox{e}}{\fbox{f}}$ байна.
$k>0$ байг. $C\colon y=x^2$ параболын $(k, k^2)$ цэгт татсан шүргэгч шулууныг $\ell$ гэе.
- $\ell$ шулууны тэгшитгэл $y=\fbox{a}kx-k^2$ болно.
- $C$ парабол $\ell$ шулуун ба $y$ тэнхлэгээр хүрээлэгдсэн дүрсийн талбай $S=\dfrac{k^{\fbox{b}}}{\fbox{c}}$.
- $S=72$ бол $k=\fbox{d}$ байна.
$y=x^2$ парабол өгөгдөв.
- Уг параболын $x=2$ цэгт татсан шүргэгч шулууны тэгшитгэл нь $y=\fbox{a}x-\fbox{b}$
- Уг парабол, түүний $x=2$ цэгт татсан шүргэгч шулуун, $OY$ тэнхлэгээр үүсэх дүрсийн талбай нь $\dfrac{\fbox{c}}{\fbox{d}}$.
$y=x^3, y=\sqrt[3]{x}$ муруйнуудаар хүрээлэгдсэн дүрсийн талбай нь $S=\fbox{a}\cdot \displaystyle\int\limits_{\fbox{c}}^{\fbox{b}}(\sqrt[3]{x}-x^3)\,\mathrm{d}x=\fbox{d}$ болно.
$y=x^2, y=\sqrt{|\,x|}$ шугамуудаар хүрээлэгдсэн дүрсийн талбай нь $S=\fbox{a}\cdot \displaystyle\int\limits_{\fbox{c}}^{\fbox{b}}(\sqrt{|\,x|}-x^2)\,\mathrm{d}x=\displaystyle\frac{2}{\fbox{d}}$ болно.
$y=x^2-5x+7, y=-2x^2+10x-5$ муруйнуудаар хүрээлэгдсэн дүрсийн талбай нь $S=\displaystyle\int\limits_{\fbox{a}}^{\fbox{b}}(\fbox{cd}\cdot x^2+\fbox{ef}\,\,x-\fbox{fh})\,\mathrm{d}x=\fbox{i}\,3.5$ кв. нэгж. болно.
$y=x^2+3x+4, y=-2x^2+15x-5$ муруйнуудаар хүрээлэгдсэн дүрсийн талбай нь $S=\displaystyle\int\limits_{\fbox{a}}^{\fbox{b}}(\fbox{cd}\cdot x^2+\fbox{ef}\, x-\fbox{gh})\,\mathrm{d}x=\fbox{i}$ кв. нэгж. болно.
$yx=3, x+y=4$ муруйнуудаар хүрээлэгдсэн дүрсийн талбай нь $S=\displaystyle\int\limits_{\fbox{a}}^{\fbox{b}}(4-x-\displaystyle\frac{3}{x})\,\mathrm{d}x=\fbox{c}-\fbox{d}\cdot\ln \fbox{e}$ байна.
$yx=2, x+y=3$ муруйнуудаар хүрээлэгдсэн дүрсийн талбай нь $S=\displaystyle\int\limits_{\fbox{a}}^{\fbox{b}}(3-x-\displaystyle\frac{2}{x})\,\mathrm{d}x=\displaystyle\frac{\fbox{c}}{2}-\fbox{d}\cdot\ln \fbox{e}$ байна.
$x=a, x=2a (a>0), y=0, y=1+\displaystyle\frac{1}{x^2}$ муруйнуудаар хүрээлэгдсэн дүрсийн талбай нь $S(a)=\fbox{a}\cdot a+\displaystyle\frac{\fbox{b}}{\fbox{c}\cdot a}$ учраас
$a^*=\displaystyle\frac{1}{\sqrt{\fbox{d}}}$ утганд минимум $S_{\min}=\sqrt{\fbox{e}}$ утгаа авна.
$x=a, x=2a (a>0), y=0, y=\displaystyle\frac12+\displaystyle\frac{1}{x^2}$ муруйнуудаар хүрээлэгдсэн дүрсийн талбай нь $S(a)=\displaystyle\frac{a}{\fbox{a}}+\displaystyle\frac{\fbox{b}}{\fbox{c}\cdot a}$ учраас $a^*=\fbox{d}$ утганд минимум
$S_{\min}=\fbox{e}$ утгаа авна.
$y=\displaystyle\frac{1}{\sqrt{4x-3}}, y=0, x=a, x=3a (a>\displaystyle\frac 34)$ муруйнуудаар хүрээлэгдсэн дүрсийн талбай нь $S(a)=\displaystyle\frac{\sqrt{\fbox{a}\cdot(\fbox{b}\cdot a-1)}-\sqrt{\fbox{c}\cdot a-3}}{\fbox{d}}$ учраас
$a^*=\fbox{e}$ утганд $S(a)$ нь минимум $S_{\min}=\fbox{f}$ утгаа авна.
$y=\displaystyle\frac{1}{\sqrt{2x-1}}, y=0, x=a, x=2a (a>\displaystyle\frac 12)$ муруйнуудаар хүрээлэгдсэн дүрсийн талбай нь
$S(a)=\sqrt{\fbox{a}\cdot a-\fbox{b}}-\sqrt{\fbox{c}\cdot a-\fbox{d}}$ учраас $a^*=\displaystyle\frac{3}{\fbox{e}}$ утганд минимум $S_{\min}=\displaystyle\frac{1}{\sqrt{\fbox{f}}}$ утгаа авна.
$x=a, x=2a (0< a< \dfrac{\sqrt 7}{2}), y=0, y=7-x^2$ шугамуудаар хүрээлэгдсэн дүрсийн талбай $S(a)=\fbox{a}\cdot a\Bigl(\fbox{b}-\displaystyle\frac{a^2}{\fbox{c}}\Bigr)$ учраас $a^*=\fbox{d}$ утганд максимум $S_{\max}=\displaystyle\frac{1\fbox{e}}{\fbox{f}}$ утгаа авна.
$x=a, x=2a (0< a< \sqrt 7), y=0, y=28-x^2$
шугамуудаар хүрээлэгдсэн дүрсийн талбай $S(a)=\fbox{a}\cdot
a\Bigl(\fbox{b}-\displaystyle\frac{a^2}{\fbox{c}}\Bigr)$ учраас
$a^*=\fbox{d}$ утганд максимум $S_{\max}=\displaystyle\frac{\fbox{e}12}{\fbox{f}}$ утгаа авна.
$f(x)=\displaystyle\frac 12x+3, g(x)=-x^2+1, x=-2, x=1$ муруйнуудаар хашигдсан дүрсийн талбай
$S=\displaystyle\int\limits_{\fbox{ab}}^{\fbox{c}}[\fbox{d}x^2+\displaystyle\frac {\fbox{e}}{\fbox{f}}x+2]\,\mathrm{d}x=\displaystyle\frac {\fbox{gh}}{4}$
$f(x)=5-x^2, g(x)=2-2x$ муруйнуудаар хашигдсан дүрсийн талбай
$S=\displaystyle\int\limits_{\fbox{ab}}^{\fbox{c}}[\fbox{de}x^2+\fbox{f}x+3]\,\mathrm{d}x=\displaystyle\frac {\fbox{gh}}{\fbox{i}}$
$y=4x-x^2$ парабол ба ОХ тэнхлэгээр хязгаарлагдсан дүрсийн талбай $\displaystyle\frac{\fbox{ab}}{\fbox{c}}$ байна.
$y=2-x^2$ парабол $y=x$ шулуунаар хүрээлэгдсэн дүрсийн талбай $\displaystyle\frac{\fbox{c}}{\fbox{d}}$ байна.
$y=x^2$ парабол ба $(-1, 1)$, $(2, 4)$ цэгүүдийг дайрах шулуунуудаар хүрээлэгдсэн дүрсийг $D$ гэе. Параболын оройн цэгийг дайрсан $D$-г тэнцүү талбайтай 2 хэсэгт хуваах шулууны тэгшитгэл нь $y=\dfrac{\fbox{ab}}{\fbox{cd}}x$ байна.
$y=\dfrac{x-2}{x-1}$ функц өгөгдөв.
- $y=\dfrac{x-2}{x-1}$ функцийн $x_0=2$ цэгт татсан шүргэгч шулууны тэгшитгэлийг бичвэл $y=\fbox{a}x-\fbox{b}$;
- $y=\dfrac{x-2}{x-1}$, $x=2$, $x=5$ ба $y=0$ шугамуудаар хүрээлэгдсэн дүрсийн талбай $\fbox{c}-\ln\fbox{d}$;
- $y=5x+5$ шулуунд перпендикулар ба $(1;1)$ цэгийг дайрсан шулууны тэгшитгэл нь $\fbox{e}x+\fbox{f}y-6=0$;
- $y=\dfrac{x-2}{x-1}$ муруй ба $x-3y-2=0$ шулууны огтлолцлын цэгүүдийн хоорондох зай $\dfrac{2}{3}\sqrt{\fbox{gh}}$.
$y=\dfrac{x}{x-1}$ функц өгөгдөв.
- $y=\dfrac{x}{x-1}$ функцийн $x_0=2$ цэгт татсан шүргэгч шулууны тэгшитгэлийг бичвэл $y=-\fbox{a}x+\fbox{b}$
- $y=\dfrac{x}{x-1}$, $x=2$, $x=4$ ба $y=0$ шугамуудаар хүрээлэгдсэн дүрсийн талбай $\fbox{c}+\ln\fbox{d}$
- $y=2x+5$ шулуунд перпендикуляр ба $(1;1)$ цэгийг дайрсан шулууны тэгшитгэл нь $\fbox{e}x+\fbox{f}y-3=0$.
- $y=\dfrac{x}{x-1}$ функц ба $x+5y-12=0$ шулууны огтлолцлын цэгүүдийн хоорондох зай $\dfrac45\sqrt{\fbox{gh}}$
$y=\dfrac{x}{x-1}$ функц өгөгдөв.
- $y=\dfrac{x}{x-1}$ функцийн $x_0=0$ цэгт татсан шүргэгч шулууны тэгшитгэлийг бичвэл $y=-\fbox{a}x+\fbox{b}$;
- $y=\dfrac{x}{x-1}$, $x=2$, $x=5$ ба $y=0$ шугамуудаар хүрээлэгдсэн дүрсийн талбай $\fbox{c}+\ln\fbox{d}$;
- $y=3x+5$ шулуунд перпендикулар ба $(1;1)$ цэгийг дайрсан шулууны тэгшитгэл нь $\fbox{e}x+\fbox{f}y-4=0$;
- $y=\dfrac{x}{x-1}$ муруй ба $x+4y-10=0$ шулууны огтлолцлын цэгүүдийн хоорондох зай $\dfrac{3}{4}\sqrt{\fbox{gh}}$.
$y=\dfrac{x-2}{x-1}$ функц өгөгдөв.
- $y=\dfrac{x-2}{x-1}$ функцийн $x_0=0$ цэгт татсан шүргэгч шулууны тэгшитгэлийг бичвэл $y=\fbox{a}x+\fbox{b}$;
- $y=\dfrac{x-2}{x-1}$, $x=2$, $x=4$ ба $y=0$ шугамуудаар хүрээлэгдсэн дүрсийн талбай $\fbox{c}-\ln\fbox{d}$;
- $y=4x+5$ шулуунд перпендикулар ба $(1;1)$ цэгийг дайрсан шулууны тэгшитгэл нь $\fbox{e}x+\fbox{f}y-5=0$;
- $y=\dfrac{x-2}{x-1}$ муруй ба $x-3y+6=0$ шулууны огтлолцлын цэгүүдийн хоорондох зай $\dfrac23\sqrt{\fbox{gh}}$.
$f(x)=x^2-8x+17$ функц өгөгдөв.
- $f(x)$ функцийн $x_0=5$ абсцисстэй $M$ цэгт татсан шүргэгч шулууны тэгшитгэл $y=\fbox{a}x-\fbox{b}$ (2 оноо).
- $f(x)$ функцийн график, дээрх шүргэгч шулуун болон координатын тэнхлэгүүдээр хүрээлэгдсэн дүрсийн талбай $\dfrac{\fbox{cd}}{3}$ (2 оноо).
- $f(x)$ функцийн графикийг $M$ цэгт шүргэх, төв нь $OX$ (абсцисс) тэнхлэг дээр орших тойргийн тэгшитгэл $(x-\fbox{e})^2+y^2=\fbox{fg}$ (3 оноо).
$y=x^2$ парабол ба $y=kx-k$ шулуун нь $\fbox{a}< k<\fbox{b}$ үед ерөнхий цэггүй байна. $k_1=\fbox{a}$, $k_2=\fbox{b}$ ба $\ell_1\colon y=k_1x-k_1$, $\ell_2=k_2x-k_2$ гэе. Парабол ба $\ell_1$, $\ell_2$ шулуунуудаар хүрээлэгдсэн дүрсийн талбай нь $\dfrac{\fbox{c}}{\fbox{d}}$ байна.
$k>0$ байг. $C\colon y=-x^2$ параболын $(k,-k^2)$ цэгт татсан шүргэгч шулууныг $\ell$ гэе.
- $\ell$ шулууны тэгшитгэл $y=-\fbox{a}kx+k^2$ болно.
- $C$ парабол $\ell$ шулуун ба $y$ тэнхлэгээр хүрээлэгдсэн дүрсийн талбай $S=\dfrac{k^{\fbox{b}}}{\fbox{c}}$.
- $S=9$ бол $k=\fbox{d}$ байна.
$C\colon y=x^2+x+1$ параболын $A(-1;1)$ цэгт татсан шүргэгч шулууны тэгшитгэл нь $y=-\fbox{a}x+\fbox{b}$. Энэ шүргэгч шулуун, $x=0$ шулуун ба $C$ параболын дунд үүсэх дүрсийн талбай нь $$\displaystyle\int\limits_{-\fbox{c}}^{\fbox{d}}(x+\fbox{e})^2 \,\mathrm{d}x=\frac{\fbox{f}}{\fbox{g}}$$ байна.
$f(x)=x^3-3x^2+3x$ функцийн графикийг $C$ гэе. $y=f(x)$ функцийн $x_0=2$ цэг дээрх шүргэгч шулуун $\ell$ бол түүний тэгшитгэл $y=\fbox{a}x-\fbox{b}$ (2 оноо) байна. $C$ муруй ба $\ell$-ийн шүргэлтийн цэгээс өөр ерөнхий цэг $\left( \fbox{cd}, \fbox{ef}\right)$ (2 оноо) байна. Иймд $C$ ба $\ell$-ээр хүрээлэгдсэн талбай $A=\int\limits_{\fbox{cd}}^ 2\left(f(x)-\fbox{a}x+\fbox{b}\right) dx=\dfrac{\fbox{gh}}{4}$ (3 оноо) байна.
- $(2,-2)$ цэгт оройтой параболын тэгшитгэл $y=x^2-\fbox{a}x+\fbox{b}$ байна.
- $A(0,-6)$, $B(4,2)$ цэгүүдийг дайрсан шулууны тэгшитгэл $y=\fbox{c}x-\fbox{d}$ байна.
- Эдгээр функцийн графикаар хязгаарлагдсан дүрсийн талбай $\fbox{e}\dfrac{\fbox{f}}{\fbox{g}}$ байна.
$f(x)=\dfrac13x^3-3x$ функц өгөгдөв.
- $f'(2)=\fbox{a}$ байна.
- $f(x)$ функцийн $(2,f(2))$ цэгт татсан шүргэгч шулууны тэгшитгэл $$y=\fbox{a}x-\dfrac{\fbox{bc}}{3}$$ байна.
- $f(x)$ функцийн график, шүргэгч шулуунтай огтлолцох цэгийн абсцисс нь $x=\fbox{de}$
- $f(x)$ функцийн график ба шүргэгч шулуунаар хүрээлэгдсэн дүрсийн талбай $\fbox{fg}$ байна.
$f(x)=\dfrac13x^3-3x$ функц өгөгдөв.
- $f'(-2)=\fbox{a}$ байна.
- $f(x)$ функцийн $(-2,f(-2))$ цэгт татсан шүргэгч шулууны тэгшитгэл $$y=\fbox{a}x+\dfrac{\fbox{bc}}{3}$$ байна.
- $f(x)$ функцийн график, шүргэгч шулуунтай огтлолцох цэгийн абсцисс нь $x=\fbox{d}$
- $f(x)$ функцийн график ба шүргэгч шулуунаар хүрээлэгдсэн дүрсийн талбай $\fbox{ef}$ байна.
Модультай интеграл
$\displaystyle\int_{-2}^{6}|x-2|\,\mathrm{d}x$ интегралыг ол.
A. 12
B. 13
C. 14
D. 15
E. 16
$\int\limits_{-1}^2 |1-x^2|dx$ бод.
A. $\dfrac{5}{3}$
B. $\dfrac{7}{3}$
C. $2$
D. $-2$
E. $2\dfrac{2}{3}$
Ньютон-Лейбницийн томьёо
Дараах интегралуудыг бод.
- $\int(x^4-4x^3+6x^2-1)\,\textrm{d}x$
- $\mathop{\int\limits_{-2}^{2}}(x^4-2x^3 3x^2-3x+5)\,\textrm{d}x$
- $\mathop{\int\limits_{1}^{2}}|x(x-1)(x-2)|\,\textrm{d}x$
- $\mathop{\int\limits_{0}^{3}}|(x+1)^2(x-2)|\,\textrm{d}x$
- $\int (2x+3)^3\,\textrm{d}x$
- $\mathop{\int\limits_{1}^{2}}(x-1)^2(x-2)\,\textrm{d}x$
Дараах тодорхой интегралуудыг бод.
- $\mathop{\int\limits_{1}^{2}}(2x^2-3x+4)\,\mathrm{d}x$
- $\mathop{\int\limits_{2}^{5}}(x-2)^2\,\mathrm{d}x$
- $\mathop{\int\limits_{-2}^{2}}(5x^2-x-2)\,\mathrm{d}x$
- $\mathop{\int\limits_{-1}^{1}}(2t+1)(1-3t)\,\mathrm{d}t$
- $\mathop{\int\limits_{2}^{1}}(2x^2-2x+k)\,\mathrm{d}x$ ${(k\text{--тогтмол})}$
Дараах интегралуудлыг бод.
- $\mathop{\int\limits_{-1}^{2}}(x^2-3x-4)\,\mathrm{d}x$
- $\mathop{\int\limits_{-2}^{3}}(3t+1)(1-t)\,\mathrm{d}t$
- $\mathop{\int\limits_{-2}^{2}}(3x^2-4x+1)\,\mathrm{d}x$
$\displaystyle\int_0^{2\pi} \cos^2 x\,\,\mathrm{d}x= ?$
A. $\pi$
B. $2\pi$
C. $\dfrac{1}{2}\pi$
D. $\dfrac{1}{3}\pi$
E. $0$
$\displaystyle\int_0^{2\pi} \sin^2 x\,\,\mathrm{d}x= ?$
A. $\pi$
B. $2\pi$
C. $\frac{1}{2}\pi$
D. $\frac{1}{3}\pi$
E. $0$
$\displaystyle\int_{1}^2 (x^2-3x+2) \,\mathrm{d}x$ интегралыг бод.
A. $\dfrac{x^3}3-\dfrac{3x^2}2+2x+C$
B. $-\dfrac16$
C. $\dfrac16$
D. $-\dfrac{1}{12}$
E. $0$
$\displaystyle\int_3^{3e^4} \dfrac{\mathrm{d}x}{2x}$ интегралийг бод.
A. $1$
B. $2$
C. $3$
D. $4$
E. $5$
$\displaystyle\int_{-1}^2\,\,\mathrm{d}x$
A. 0
B. 1
C. 2
D. 3
E. 4
$\displaystyle\int_{1}^2 \frac{2x^3+1}{x^2}\,\,\mathrm{d}x$
A. 3
B. 3.5
C. 4
D. 4.5
E. 5
$\displaystyle\int_{e^{-1}}^{e^2} \frac{1}{x}\,\,\mathrm{d}x$
A. $1$
B. $e^{-2}e^{-1}$
C. $2$
D. $e$
E. $3$
$\displaystyle\int_0^\pi\cos^2x\,\mathrm{d}x$ бод.
A. $\dfrac {\pi}4$
B. $\dfrac{\pi}2$
C. $0$
D. $-\dfrac {\pi}2$
E. $\pi$
$\displaystyle\int_{-\pi}^{\frac\pi 2}\sin^22x\,\mathrm{d}x$ бод.
A. $\displaystyle\frac {3\pi}4$
B. $\pi$
C. $\displaystyle\frac32\pi$
D. $0$
$\displaystyle\int_{0}^{0.5}\Bigl(4x-\displaystyle\frac 1{2x+1}\Bigr)\,\mathrm{d}x$ бод.
A. $\ln\big(\frac {e}2\big)$
B. $0$
C. $\displaystyle\frac 12$
D. $0.5\ln\big(\frac e2\big)$
$\displaystyle\int_{0}^{\frac{2\pi}{3}}\sin \Bigl(\displaystyle\frac {\pi}3-3x\Bigr)\,\mathrm{d}x$ бод.
A. $0$
B. $\displaystyle\frac {\pi}2$
C. $\pi$
D. $\displaystyle\frac {2\pi}3$.
$\displaystyle\int_0^{0.5}\displaystyle\frac{\,\mathrm{d}x}{\sqrt{1-2x^2}}$ интегралыг бод.
A. $\displaystyle\frac{\pi}8$
B. $\displaystyle\frac{\pi\sqrt{3}}4$
C. $\displaystyle\frac{\pi\sqrt{2}}8$
D. $\displaystyle\frac {\sqrt{2}}{8}$
$\displaystyle\int_{0}^{1}\frac{x^2\,\mathrm{d}x}{1+x^2}$ интегралыг бод.
A. $\displaystyle\frac \pi 4$
B. $3-\displaystyle\frac\pi 4$
C. $1-\displaystyle\frac\pi 4$
D. $1+\displaystyle\frac\pi 4$
$\displaystyle\int_0^{\frac{\pi}{2}}\sin x\,\mathrm{d}x=?$
A. $\dfrac12$
B. $\dfrac{\sqrt3}2$
C. $\dfrac{\sqrt2}2$
D. $0$
E. $1$
$\displaystyle\int_0^{\frac{\pi}{2}}\sin x\mathrm{d}x=?$
A. $\dfrac12$
B. $\dfrac{\sqrt3}2$
C. $\dfrac{\sqrt2}2$
D. $0$
E. $1$
Орлуулгын аргаар интеграл бодох
$\displaystyle\int x\sqrt{1-x^2}dx$
$\displaystyle\int_1^{e^2}\dfrac{\ln x}{x}\,\mathrm{d}x$
A. $4$
B. $2$
C. $0.5(e^4-1)$
D. $e^2-1$
E. $1$
$\displaystyle\int_{0}^{\ln 3}\dfrac{e^{x}}{e^{x} +1} \,\mathrm{d}x$ интегралыг бод.
A. $e^{2} $
B. $\ln 2$
C. $\dfrac{1}{4} $
D. $e^{4}-e^{2}$
E. $\ln 8$
$\displaystyle\int_1^{e^4}\dfrac{\,\mathrm{d}x}{x(\ln x+1)}$ интеграл бод.
A. $e+\ln 5$
B. $\ln 5$
C. $e+1$
D. $\frac15\ln 5$
E. $e$
$\displaystyle\int_{0}^4\sqrt{16-x^2} \,\mathrm{d}x$ интегралыг бод.
A. $16\pi$
B. $10\pi$
C. $3\pi$
D. $4\pi$
E. $9\pi$
$\displaystyle\int\frac{x}{\sqrt{x+2}}\,\mathrm{d}x$
A. $\dfrac13(x+2)^{\frac 13}-4(x+2)^{\frac 12}+C$
B. $\dfrac23(x+2)^{\frac{3}{2}}-(x+2)^{\frac12}+C$
C. $\dfrac23(x+2)^{\frac 32}-4(x+2)^{\frac{1}{2}}+C$
D. $\dfrac23(x+2)^{\frac23}-4(x+2)^{\frac{1}{2}}+C$
E. $\dfrac23(x+2)^{\frac 32}+4(x+2)^{\frac{1}{2}}+C$
$\displaystyle\int x\sqrt{x+1}\,\mathrm{d}x$
A. $\displaystyle\frac{2(x+1)^{\frac 52}}{5}-\displaystyle\frac{2(x+1)^{\frac 32}}{3}+C$
B. $\displaystyle\frac{(x+1)^{\frac 52}}{5}-\displaystyle\frac23(x+1)^{\frac 32}+C$
C. $\displaystyle\frac{(x+1)^{\frac 52}}{5}+\displaystyle\frac23(x+1)^{\frac 23}+C$
D. $\displaystyle\frac25(x+1)^{\frac52}+\displaystyle\frac23(x+1)^{\frac 32}+C$
E. $(x+1)^{\frac52}+(x+1)^{\frac 32}+C$
$\int(4x+2)e^{x^2+x+1}\,\mathrm{d}x$
A. $3e^{x^2+2x+1}+C$
B. $2e^{x^2+x+1}+C$
C. $2e^{x^2+x+1}+x+C$
D. $2e^{x^2+2x+1}+C$
$\displaystyle\int(x^2+2x)e^{x^3+3x^2}\,\mathrm{d}x$
A. $\displaystyle\frac 13e^{x^3+3x^2}+C$
B. $\displaystyle\frac 13e^{x^3+6x}+C$
C. $\displaystyle\frac 13e^{x^3+x^2}+C$
D. $\displaystyle\frac 12e^{x^3+3x^2}+C$
E. $\displaystyle\frac 13e^{x^2+2x}+C$
$\displaystyle\int e^x\ln (1+e^x)\,\mathrm{d}x$
A. $(1+e^x)(\ln(1+e^x)+1)+C$
B. $(1+e^x)(\ln(1+e^x)-1)+C$
C. $[(1+e^x)\ln(1+e^x)-e^x]+C$
D. $[e^x\ln(1+e^x)+(1+e^x)]+C$
E. $\dfrac{e^x}{1+e^x}+e^x\ln(1+e^x)+C$
$\displaystyle\int\frac{\ln(1+\sqrt x)}{\sqrt x}\,\mathrm{d}x$
A. $[(1+\sqrt x)\ln(1+\sqrt x)+(1+\sqrt x)]+C$
B. $[(1+\sqrt x)\ln(1+e^x)-\sqrt x]+C$
C. $2[\sqrt x\ln(1+e^x)-(1+\sqrt x)]+C$
D. $2(1+\sqrt x)(\ln(1+\sqrt x)-1)+C$
$\displaystyle\int_{0}^{1}\displaystyle\frac {\,\mathrm{d}x}{\sqrt[3]{1+2x}}\,\mathrm{d}x$ бод.
A. $\displaystyle\frac 32$
B. $\displaystyle\frac 34(\sqrt[3]{9}-1);$
C. $2$
D. $\displaystyle\frac 34(\sqrt[3]{9}+1)$.
$\displaystyle\int_{0}^{\frac{\pi}{2}}\sin x\cos x\,\mathrm{d}x$ бод.
A. $\displaystyle\frac 14$
B. $\displaystyle\frac 12$
C. $0$
D. $1$.
$\displaystyle\int_{0}^{a}\displaystyle\frac{x\,\mathrm{d}x}{\sqrt {x^2+a^2}}$ бод.
A. $2a(\sqrt{2}-1)$
B. $a(\sqrt{2}-1)$
C. $a\sqrt 2-1$
D. $a\sqrt 2+1$.
$\displaystyle\int_{1}^{a^2}\displaystyle\frac{x\,\mathrm{d}x}{x^2+a}$ бод.
A. $\ln \sqrt{|a|}$
B. $\ln |a|$
C. $\ln \sqrt{2|a|}$
D. $0$
$\displaystyle\int_{\frac{\pi}6}^{\frac{\pi}4}\tg x\cdot \displaystyle\frac{\,\mathrm{d}x}{\cos^2x}$ интегралыг бод.
A. $\displaystyle\frac12$
B. $\displaystyle\frac13$
C. $\displaystyle\frac15$
D. $\displaystyle\frac14$
$\displaystyle\int_{\frac\pi 2}^{\pi}\displaystyle\frac{\sin x}{1-2\cos x}\,\mathrm{d}x$ интегралыг бод.
A. $\ln 3$
B. $\ln 2$
C. $\ln\sqrt{5}$
D. $\ln\sqrt{3}$
$\displaystyle\int \dfrac{x}{\sqrt{x+1}}\,\mathrm{d}x=?$
A. $\dfrac{2(x-1)\sqrt{x+1}}{3}+C$
B. $\dfrac{2(x-2)\sqrt{x+1}}{6}+C$
C. $\dfrac{2(x-1)\sqrt{x+1}}{6}+C$
D. $\dfrac{2(x-2)\sqrt{x+1}}{3}+C$
E. $\dfrac{2(x-1)\sqrt{x-1}}{6}+C$
$\displaystyle\int_{\frac{\pi}{2}}^{\pi}\cos^2x \sin x\mathrm{d}x$
A. $\frac13$
B. $-\frac1{12}$
C. $\frac1{12}$
D. $-\frac9{12}$
E. $\frac9{12}$
$\displaystyle\int_0^{\ln 3}\dfrac{5e^x}{3+5e^x}\mathrm{d}x$ интегралыг бод.
A. $2\ln 6$
B. $\ln 5$
C. $\ln\dfrac94$
D. $\dfrac{5}{24}$
E. $\ln36$
$F(x)$ нь $x\cdot e^{x^2}$ функцийн $F(1)=e$ байх эх функц бол түүнийг ол.
A. $e^{x^2}-e$
B. $xe^x-e^{\frac12}$
C. $\frac12e^{x^2}+C$
D. $\frac12e^{x^2}-\frac12e$
E. $\frac12e^{x^2}+\frac12e$
$\displaystyle\int_{-1}^1\displaystyle\frac{e^x}{e^{-x}+e^x}\,\mathrm{d}x=
\displaystyle\frac{1}{\fbox{a}}
\ln\displaystyle\frac{e^{\fbox{b}}+1}{e^{\fbox{cd}}+1}=1$
$\displaystyle\int_{7}^8\displaystyle\frac{\ln(t-5)}{t-5}dt=\displaystyle\frac{1}{\fbox{a}}\ln\displaystyle\frac{\fbox{b}}{2}\ln\fbox{c}$
- $\displaystyle\int\cos^3x\sin^2x\,\mathrm{d}x=\frac{\sin^{\scriptsize\fbox{a}} x}{\fbox{a}}-\frac{\sin^{\scriptsize\fbox{b}}x}{\fbox{b}}+C$ (4 оноо)
- $\displaystyle\int_0^\frac{\pi}{2}\cos^3x\sin^2x\,\mathrm{d}x=\dfrac{\fbox{c}}{\fbox{de}}$ (3 оноо) байна.
- $\displaystyle\int\sin^3x\cos^4x\,\mathrm{d}x=\frac{\cos^{\scriptsize\fbox{a}}x}{\fbox{a}} -\frac{\cos^{\scriptsize\fbox{b}}x}{\fbox{b}}+C$ (4 оноо)
- $\displaystyle\int_0^{\frac{\pi}{2}}\sin^3x\cos^4x\,\mathrm{d}x=\dfrac{\fbox{c}}{\fbox{de}}$ байна. (3 оноо)
Тодорхой биш интеграл бодох
$\displaystyle\int (2-3\sqrt{x})^2dx$
$\displaystyle\int_0^\pi \sin x\cos3x\,\mathrm{d}x$ интегралыг бод.
A. $-\frac12$
B. $\frac12$
C. $0$
D. $1$
E. $-1$
$\displaystyle\int\dfrac{2x + 3}{x^2 - 9} dx=?$
A. $\dfrac12\ln|x-3|+\dfrac32\ln|x+3|+C$
B. $\dfrac32\ln|x-3|+\dfrac12\ln|x+3|+C$
C. $3\ln|x-3|+\ln|x+3|+C$
D. $\ln|x-3|+3\ln|x+3|+C$
E. $\dfrac12\ln|x-3|-\dfrac32\ln|x+3|+C$
$\displaystyle\int\dfrac{x^2-2}{x+1} dx=?$
A. $\dfrac{x^2}{2}+x-\ln|x+1|+C$
B. $\dfrac{x^2}{2}-x+\ln|x+1|+C$
C. $-\dfrac{x^2}{2}-x+\ln|x+1|+C$
D. $\dfrac{x^2}{2}+x+\ln|x+1|+C$
E. $\dfrac{x^2}{2}-x-\ln|x+1|+C$
$\displaystyle\int\dfrac{dx}{x^2+4x+8}=?$
A. $\arctg\dfrac{x+2}{2}+C$
B. $2\arctg\dfrac{x+2}{2}+C$
C. $\dfrac12\arctg x+C$
D. $\dfrac12\arctg (x+2)+C$
E. $\dfrac12\arctg\dfrac{x+2}{2}+C$
$\displaystyle\int\dfrac{x^2dx}{(x-1)(x-2)(x-3)}=?$
A. $-\dfrac12\ln|x-1|+4\ln|x-2|+\dfrac92\ln|x-3|+C$
B. $-\dfrac12\ln|x-1|-4\ln|x-2|+\dfrac92\ln|x-3|+C$
C. $\dfrac12\ln|x-1|-4\ln|x-2|-\dfrac92\ln|x-3|+C$
D. $\dfrac12\ln|x-1|-4\ln|x-2|+\dfrac92\ln|x-3|+C$
E. $\dfrac12\ln|x-1|+4\ln|x-2|+\dfrac92\ln|x-3|+C$
$\displaystyle\int\dfrac{dx}{(x+1)(x^2+1)}=?$
A. $\dfrac12\ln\left|\dfrac{x+1}{x^2+1}\right|+\dfrac12\arctg x+C$
B. $\ln|x+1|+\arctg x +C$
C. $\ln|x+1|\cdot\arctg x +C$
D. $\dfrac14\ln\dfrac{(x+1)^2}{x^2+1}+\dfrac12\arctg x+C$
E. $\dfrac12\ln\dfrac{(x+1)^2}{x^2+1}+\dfrac12\arctg x+C$
$\displaystyle\int\dfrac{dx}{x^3+1}=?$
A. $\dfrac16\ln\dfrac{(x+1)^2}{x^2-x+1}+\dfrac{1}{\sqrt3}\arctg\dfrac{2x-1}{\sqrt3}+C$
B. $\ln|x^3+1|+C$
C. $x^2\ln|x^3+1|+C$
D. $\dfrac16\ln\dfrac{(x+1)^2}{x^2-x+1}-\dfrac{1}{\sqrt3}\arctg\dfrac{2x-1}{\sqrt3}+C$
E. $\ln\dfrac{x+1}{x^2-x+1}+\dfrac{1}{\sqrt3}\arctg\dfrac{2x-1}{\sqrt3}+C$
$\displaystyle\int\dfrac{dx}{x^4-1}=?$
A. $\ln\left|\dfrac{x-1}{x+1}\right|-\dfrac12\arctg x+C$
B. $\dfrac14\ln\left|\dfrac{x-1}{x+1}\right|-\dfrac12\arctg x+C$
C. $\ln\left|\dfrac{x-1}{x+1}\right|-\arctg x+C$
D. $\ln\left|\dfrac{x-1}{x+1}\right|+\arctg x+C$
E. $\dfrac14\ln\left|\dfrac{x+1}{x-1}\right|+\arctg x+C$
$\displaystyle\int\dfrac{5x}{(x-1)^3}dx=?$
A. $-\dfrac{5}{2(x-1)^2}-\dfrac{5}{x-1}+C$
B. $\dfrac{5}{3(x-1)^2}+C$
C. $\dfrac{5}{2(x-1)^2}-\dfrac{5}{x-1}+C$
D. $-\dfrac{5}{2(x-1)^2}+\dfrac{5}{x-1}+C$
E. $\dfrac{10x^2}{(x-1)^4}+C$
$\displaystyle\int \dfrac{3x+1}{x(x+1)(x-2)}dx$
A. $-\dfrac16\ln\left|\dfrac{(x-2)^7}{x^3(x+1)^4}\right|+C$
B. $\dfrac16\ln\left|\dfrac{(x-2)^7}{x^3(x+1)^4}\right|+C$
C. $\ln\left|\dfrac{(x-2)^7}{x^3(x+1)^4}\right|+C$
D. $-\ln\left|\dfrac{(x-2)^7}{x^3(x+1)^4}\right|+C$
E. $\dfrac13\ln\left|\dfrac{(x-2)^7}{x^4(x+1)^3}\right|+C$
$\displaystyle\int\dfrac{x^2-2}{x+1} dx=?$
A. $\dfrac{x^2}{2}+x-\ln|x+1|+C$
B. $\dfrac{x^2}{2}-x+\ln|x+1|+C$
C. $-\dfrac{x^2}{2}-x+\ln|x+1|+C$
D. $\dfrac{x^2}{2}+x+\ln|x+1|+C$
E. $\dfrac{x^2}{2}-x-\ln|x+1|+C$
$\displaystyle\int\dfrac{3x^2+2x+7}{x^2+1}dx=?$
A. $3x-\ln(x^2+1)+4\arctg x+C$
B. $3x+\ln(x^2+1)+\arctg x+C$
C. $3x+4\ln(x^2+1)+\arctg x+C$
D. $3x-4\ln(x^2+1)+\arctg x+C$
E. $3x+\ln(x^2+1)+4\arctg x+C$
$ P(x)=x^3+x^2-3x-5$ олон гишүүнтийг $ Q(x) =x+2$ олон гишүүнтэд хуваахад гарах үлдэгдлийг ол.
A. $ 5$
B. $ 1 $
C. $ -3 $
D. $ -7$
E. $-5 $
$\displaystyle\int (x-1)(x-2)x$ интегралыг бод.
A. $(x-1)^2(x-2)+C$
B. $\dfrac{x^3}{3}-\dfrac{3x^2}{2}+2x+C$
C. $x^3-\dfrac23x^2+3x+C$
D. $\dfrac{x^3}{3}+\dfrac{3x^2}{2}-2x+C$
E. $\dfrac{x^3}{4}-\dfrac{3x^2}{2}+2x+C$
$\displaystyle\int\dfrac{x+1}{\sqrt{x}}dx$ интегралыг бод.
A. $\dfrac23x\sqrt{x}+\dfrac12\sqrt{x}+C$
B. $\dfrac32x\sqrt{x}+2\sqrt{x}+C$
C. $\dfrac23x\sqrt{x}+2\sqrt{x}+C$
D. $\dfrac32x\sqrt{x}+\frac{1}{2}\sqrt{x}+C$
E. $\dfrac13x\sqrt{x}+\sqrt{x}+C$
$\displaystyle\int\dfrac{x-2}{\sqrt{x}}dx$ интегралыг бод.
A. $\dfrac23x\sqrt{x}-\dfrac14\sqrt{x}+C$
B. $\dfrac32x\sqrt{x}-4\sqrt{x}+C$
C. $\dfrac23x\sqrt{x}-4\sqrt{x}+C$
D. $\dfrac32x\sqrt{x}-\sqrt{x}+C$
E. $\dfrac13x\sqrt{x}+2\sqrt{x}+C$
$\displaystyle\int\dfrac{x-2}{\sqrt{x}}dx$ интегралыг бод.
A. $\dfrac23x\sqrt{x}-4\sqrt{x}+C$
B. $\dfrac32x\sqrt{x}-4\sqrt{x}+C$
C. $\dfrac23x\sqrt{x}-\frac14\sqrt{x}+C$
D. $\dfrac32x\sqrt{x}-\sqrt{x}+C$
E. $\dfrac13x\sqrt{x}-2\sqrt{x}+C$
$\displaystyle\int\dfrac{\sqrt[3]{x-8}}{x} dx=\fbox{a}\sqrt[3]{x-8}-\fbox{b}\ln|\sqrt[3]{x-8}+2|+\ln\big((\sqrt[3]{x-8})^3-\fbox{c}\sqrt[3]{x-8}+\fbox{d}\big)-\dfrac{\fbox{e}}{\sqrt3}\arctg\dfrac{\sqrt[3]{x-8}+1}{\sqrt3}+C$
Тодорхой интеграл
$f(x)=x^2+ax+b, g(x)$-дурын шугаман функц
$\mathop{\int\limits_{-1}^{1}}f(x)\cdot g(x)\,\textrm{d}x=0$ байдаг бол
$a, b$-г ол.
Квадрат функц $f(x)$-ийн хувьд
$\mathop{\int\limits_{-1}^{1}}f(x)\,\textrm{d}x=0$,
$\mathop{\int\limits_{-1}^{1}}xf(x)\,\textrm{d}x=\dfrac43$,
$\mathop{\int\limits_{1}^{x}}f(t)\,\textrm{d}t$ функцийн максимум утгa $0$
бол $\mathop{\int\limits_{-1}^{1}}f^2(x)\,\textrm{d}x$-ийн утгыг ол.
$f(x)=\left\{\begin{array}{ll} -2x^2+2x+4, & x< 3\\
4x^2-28x+40, & x\geq 3\end{array}\right.$ гэе.
$g(x)=\mathop{\int\limits_{0}^{x}}f(t)\,\mathrm{d}t$ функцийн $x\geq 0$ үеийн
экстремум утгуудыг ол.
$y=\int\limits_{1}^{x} (4t^2-8t+3)\, dt$ функцийн экстремумыг ол.
Дараах функцүүдийн экстремум утгуудыг ол.
- $f(x)=\int\limits_{-3}^{x}(t^2-x)\, dt$
- $f(x)=\int\limits_{x}^{x+1}(t^2-5t+7)\,dt$
$x$ нь $t$-ээс хамаарахгүй бол дараах функцүүдын график зур.
- $y=\int\limits_{-1}^{2}(3t^2-2xt)\,dt$
- $y=\int\limits_{0}^{x}(2t-3t^2)\,dt$
- $y=\int\limits_{0}^{x}|t-1|\,dt$
$0\leq a\leq 1$ үед
$\mathop{\int\limits_{-a}^{1-a}}|x(x-a)|\,\textrm{d}x$ функц хамгийн их ба
бага утгаа авах $a$-ийн утгыг ол.
$a$ тогтмол тоо, $f(x), g(x)$ нь $f(x)=-x^2+ax\mathop{\int}\limits_{-1}^{1}g(t)\,\textrm{d}t-\mathop{\int\limits_{-1}^{1}}t\cdot
g(t)\,\textrm{d}t$ ба
$g(x)=-\dfrac12\mathop{\int\limits_{x-1}^{x+1}}f(t)\,\textrm{d}t+ax\mathop{\int}\limits_{-1}^{1}g(t)\,\textrm{d}t$
нөхцлүүдийг хангах бол+$f(x), g(x)$-ийг ол. $-1\leq x\leq 1$ үед $f(x)$-ийн хамгийн их утгыг ол.
Дараах нөхцлийг хангах $a$ тоо ба $f(x)$-г ол.
- $\mathop{\int\limits_{a}^{x}}f(t)\,\mathrm{d}t=x^2+2x-3$
- $\mathop{\int\limits_{1}^{x}}tf(t)\,\mathrm{d}t=x^3+2x^2+a$
Дараах интегралуудыг бод.
- $\mathop{\int\limits_{1}^{1}}(-2x^2+5x-2)\,dx$
- $2\mathop{\int\limits_{1}^{3}}x^2\,dx+3\mathop{\int\limits_{1}^{3}}x^2\,dx$
- $\mathop{\int\limits_{-2}^{3}}(2x^2-1)\,dx-\mathop{\int\limits_{-2}^{3}}(x^2+x-5)\,dx$
- $\mathop{\int\limits_{1}^{4}}|x^2-2x-3|\,dx$
- $\mathop{\int\limits_{-3}^{2}}(x^2+3)\,dx+\mathop{\int\limits_{2}^{3}}(x^2+3)\,dx$
Дараах тодорхой интегралуудыг бод.
- $\mathop{\int\limits_{-1}^{3}}(x+1)(x-3)\,\mathrm{d}x$
- $\mathop{\int\limits_{0}^{2}}(x^2-2x)\,\mathrm{d}x$
- $\mathop{\int\limits_{-2-\sqrt{7}}^{-2+\sqrt{7}}}(2x^2+8x-6)$
- $\mathop{\int\limits_{0}^{2}}|x^2+2x-4|\,\mathrm{d}x$
$\mathop{\int\limits_{-1}^{0}}f(x)\,\mathrm{d}x=1, \mathop{\int\limits_{0}^{1}}f(x)\,\mathrm{d}x=0,
\mathop{\int\limits_{1}^{2}}f(x)\,\mathrm{d}x=2$ адитгалуудыг хангах квадрат
функцийг ол.
$f(x)$ нь 3-аас хэтрэхгүй зэргийн олон гишүүнт
бол $\mathop{\int\limits_{-1}^{1}}f(x)\,\mathrm{d}x$-утгыг
$f(-1), f(0), f(1)$-ээр илэрхийл.
Дараах адилтгалыг хангах $f(x)$-г ол.
- $f(x)=x+2\mathop{\int\limits_{0}^{1}}f(t)\,\mathrm{d}t$
- $f(x)=\mathop{\int\limits_{0}^{1}}(x^2-6xf(t))\,\mathrm{d}t+1$
Дараах функцүүдийн графикыг зур.
- $f(x)=\mathop{\int\limits_{0}^{1}}(t-x)\,\mathrm{d}t$
- $f(x)=\mathop{\int\limits_{0}^{1}}|t-x^2|\,\mathrm{d}t$
$F(a)=\mathop{\int\limits_{0}^{1}}|t^2-at|\,\mathrm{d}t$-ийн хамгийн
бага утгыг ол.
$y=ax+b$ шулуун $(1, 1)$ цэгийг дайрах бол $\mathop{\int\limits_{-1}^{1}}(ax+b)^2\,\mathrm{d}x$ хамгийн бага утгаа авах $a, b$-г ол.
$f^\prime(x)=x^n+\mathop{\int\limits_{-1}^{1}}f(t)\,\mathrm{d}t, f(0)=0$ нөхцлийг
хангах бүх $f(x)$-ийг ол.
$f_1(x)=2x^2+1, f_n(x)=2x^2+\mathop{\int\limits_{0}^{1}}f_{n-1}(t)\,\mathrm{d}t, (n\geq
2)$ нөхцөл хангах $f_n(x)$ функцэн дараалалыг $n, x$-ээр илэрхийл.
$p(x)$ шугаман функц бөгөөд $$\textstyle\mathop{\int\limits_{0}^{1}}p(x)\,\mathrm{d}x=0,
\mathop{\int\limits_{0}^{1}}(p(x))^2\,\mathrm{d}x=1, p(0)>0$$
бол
- $p(x)$-ийг ол.
- Дурын шугаман функц $f(x)$-ийг $f(x)=ap(x)+b$ хэлбэрээр бич.
- $f(x)=ap(x)+b$ бa $\mathop{\int\limits_{0}^{1}}(f(x))^2\,\mathrm{d}x=1$ бол $f(x)$-ийн боломжит утгуудын олонлогийг ол.
Дурын бодит тооны хувьд $f(x)=x^2-x+2\mathop{\int\limits_{0}^{2}}|t-1|f(t)\,\mathrm{d}t$ нөхцөл хангах $f(x)$ функцийг ол.
$0< a< 1, O(0, 0), P(1, a), Q(2, 4)$ байг. $OPQ$
тахир шугам график нь байх функцийг $y=f_a(x)$ гэе.
- $y=f_a(x)$ ба $y=x^2$-ийн огтлолын цэгүүдийн координатуудыг ол.
- $S(a)=\mathop{\int\limits_{0}^{2}}|x^2-f_a(x)|\,\mathrm{d}x$ функцийн хамгийн бага утгыг ол.
$\mathop{\int\limits_{0}^{x}}f(t)\,\mathrm{d}t=x\{af(x)+bf(x/2)+c\cdot
f(0)\}$ нөхцөл хангах $f(x)$ олон гишүүнтүүдийн олонлогийг $M$ гэе. $M$ олонлог нь 2-оос ихгүй зэргийн бүх олон гишүүнтийг агуулдаг бол $a, b, c$-г ол.
$0\leq a\leq 1$ үед $\mathop{\int\limits_{-a}^{1-a}}|x(x-a)|\,\mathrm{d}x$ функц хамгийн их ба бага утгаа авах $a$-ийн утгыг ол.
$y=(ax+b)^2 (0\leq x\leq 1)$ функцийн хамгийн их утгыг $M(a, b)$
гэе. $M(a, b)\leq m \mathop{\int\limits_{0}^{1}}(ax+b)^2\,\mathrm{d}x$ тэнцэтгэл биш дурын $a, b$ бодит тооны хувьд биелэх $m$-ийн хамгийн бага утгыг ол.
$a>0$ үед $g(x)=\mathop{\int\limits_{-2}^{2}}|x-t|(t^2-a^2)\,\mathrm{d}t$ функц хамгийн бага утгатай байх $a$-ийн утгын мужийг ол. Энэ үед $g(x)$-ийн хамгийн бага утгыг $a$-аар илэрхийл.
Дараах интегралуудыг бод.
- $\mathop{\int\limits_{2}^{2}}(5x^2-x+4)\,\mathrm{d}x$
- $\mathop{\int\limits_{0}^{1}}(-x^2+2)\,\mathrm{d}x-\mathop{\int\limits_{0}^{1}}x^2\,\mathrm{d}x$
- $\mathop{\int\limits_{0}^{1}}x^2\,\mathrm{d}x+\mathop{\int\limits_{1}^{3}}x^2\,\mathrm{d}x $
- $\mathop{\int\limits_{0}^{2}}|x^2+x-2|\,\mathrm{d}x$
$(1)$, $(2)$-ийг
батлаад түүнийгээ ашиглан $1\sim3$-ийг бод.
\begin{align*}
&\int_{\alpha}^{\beta}(x-\alpha)^2\,dx=\dfrac13(\beta-\alpha)^3 & (1)\\
&\int_{\alpha}^{\beta}(x-\alpha)(x-\beta)\,dx=-\dfrac{1}{6}(\beta-\alpha)^3 & (2)
\end{align*}
- $\displaystyle\int_{2}^{5}(x-2)^2\,dx$
- $\displaystyle\int_{1-\sqrt{2}}^{1+\sqrt{2}}(2x^2-4x-2)\,dx$
- $\displaystyle\int_{0}^{\frac{\sqrt{5}-1}{2}}(x^2+x-1)\,dx$
$\int\limits_{-1}^{1}f(x)\,dx=5$, $\int\limits_{-1}^{1}xf(x)\,dx=-4$
нөхцөлийг хангах $f(x)$ шугаман функцийг ол.
$(1) f(x)=\mathop{\int\limits_{-1}^{1}}(9xt^2+2x^2t-x^3)\,\mathrm{d}t$-г
$x$-ээр илэрхийл.
$(2) f(x)=x+\mathop{\int\limits_{0}^{1}}tf(t)\,\mathrm{d}t$ нөхцлийг хангах
$f(x)$-г ол.
$f(x)=\mathop{\int\limits_{0}^{1}}|t-x|\,\mathrm{d}t$ функцийн график зур.
$0\leq t\leq 1$ үед $F(t)=\mathop{\int\limits_{0}^{1}}|x^2-t^2|\,\mathrm{d}x$ функцийн хамгийн их ба хамгийн бага утгыг ол.
Дараах тэнцэтгэл бишийг батал.
$$\Big|\mathop{\int\limits_{0}^{1}}(ax+b)(px+q)\,\mathrm{d}x\Big|^2 \leq
\mathop{\int\limits_{0}^{1}}(ax+b)^2\,\mathrm{d}x
\mathop{\int\limits_{0}^{1}}(px+q)^2\,\mathrm{d}x$$
$f_n(x)=f_0(x)+\int_{0}^{c}f_{n-1}(t)\,\mathrm{d}t$, $f_0(x)=-2x+1, (n=1, 2, 3,\ldots, c\neq 1)$ гэж тодорхойлогдох $f_{n}(x)$-ийг ол.
Дурын $x$-ийн хувьд $\int\limits_{a}^{x}f(t)\,dt=x^2-1$ нөхцөлийг хангах $a$ тоо болон $f(x)$ функцийг ол.
$\displaystyle f(x)=\int_{-2}^{x}(t^2+t-2)\,dt$ функцийн эктремумыг ол.
$g(x)=\int\limits_{x}^{x+1}|t(t-3)|dt (0\leq x\leq 3)$
функцийн хамгийн их ба бага утгыг ол. Тэр үеийн $x$-ийг ол.
$f(x), g(x)$ нь дараах нөхцлүүдийг хангадаг бол $f(x), g(x)$-г ол.
\begin{gather*}\mathop{\textstyle\int\limits_{0}^{x}}(f(t)+g(t))\,\textrm{d}t=x^3+x^2-3x, f'(x)\cdot
g'(x)=8x^2+2x-3,\\
f'(0)=3, f(0)=-6, g(0)=3
\end{gather*}
$\mathop{\int\limits_{-1}^{1}}x^k\cdot
f(x)\,\textrm{d}x=0, k=0, 1, 2$ ба ахлах гишүүний коэффициент нь 1 байх бүх 3
зэргийн функцүүдийг ол.
$f(x)=x^3$ функцийн графикыг $(Ox)$ тэнхлэгийн дагуу $a$ зайд, $(Oy)$ тэнхлэгийн дагуу $b$ зайд шилжүүлэхэд $y=g(x)$ функц үүсэх ба $g(0)=0$ байв.
$$\int_a^{3a}g(x)\,\mathrm{d}x-\int_0^{2a}f(x)\,\mathrm{d}x=32$$ бол $a^4$-г ол.
A. $1$
B. $1/16$
C. $16$
D. $1/81$
E. $81$
$f(x)=x^3$ функцийн графикийг $(ox)$ тэнхлэгийн дагуу $a$ зайд, $(oy)$ тэнхлэгийн дагуу $b$ зайд шилжүүлэхэд $y=g(x)$ функц үүсгэх ба $g(0)=0$ байв.
$$\int_{a}^{3a}g(x)\,\mathrm{d}x-\dfrac12\int_{0}^{2a}f(x)\,\mathrm{d}x=162$$ бол $a^4=?$
A. $1$
B. $16$
C. $5$
D. $\dfrac{81}{2}$
E. $24$
$\displaystyle\int_0^3|1-x^2|\,\mathrm{d}x$ интегралыг бод.
A. $\dfrac{22}{3}$
B. $\dfrac{8}{3}$
C. $\dfrac{16}{3}$
D. $2$
E. $\dfrac{11}{3}$
$\displaystyle\int_{-2}^1|5x-3|\,\mathrm{d}x$ нь аль тоо вэ?
A. $17\frac{3}{10}$
B. $15\frac{3}{10}$
C. $18\frac{7}{10}$
D. $16\frac{7}{10}$
E. $18\frac{3}{10}$
$f(x)=\displaystyle\int_x^{x+2}|2t-4|\,\mathrm{d}t$ бол $f(x)$-ийн хамгийн бага утгыг ол.
A. 1
B. 2
C. 3
D. 4
E. 5
$\displaystyle\int_{-1}^2 2(t-1)x\,\mathrm{d}x = 2t$ бол $t=?$
A. $-2$
B. $-3$
C. $2$
D. $3$
E. $0$
$\displaystyle\int_{0}^4 |x-2|\,\,\mathrm{d}x$
A. 0
B. 2
C. 4
D. 6
E. 8
$\left(\displaystyle\int_0^x\sin 5tdt\right)'$ нь аль вэ?
A. $\cos 5x+1$
B. $\sin 5x+1$
C. $\sin 5x$
D. $\cos 5x$
$\Big(\displaystyle\int_0^x\cos 3t\,\mathrm{d}t\Big)^\prime$ нь аль вэ?
A. $\cos 3x+1$
B. $\cos 3x$
C. $\sin 3x+1$
D. $\sin 3x$
E. $3\cos 3x$
$\displaystyle\int_{0}^{2a}x|x^2-a^2|\,\mathrm{d}x$ бод.
A. $a^4$
B. $\displaystyle\frac {a^4}2$
C. $\displaystyle\frac 25a^4$
D. $\displaystyle\frac 52a^4$
E. $0$
$\displaystyle\int_{0}^{2a}|x-a|\,\mathrm{d}x$ бод.
A. $\displaystyle\frac 32a^2$
B. $a^2$
C. $\displaystyle\frac 12a^2$
D. $2a$
$\displaystyle\int_0^t\sin x\cdot \cos x\,\mathrm{d}x=\frac 14$ тэгшитгэлийн $[0;\pi]$ завсар дахь шийд аль вэ?
A. $\displaystyle\frac \pi 4$
B. $\displaystyle\frac\pi6$
C. $\displaystyle\frac \pi 3$
D. $\displaystyle\frac\pi 2$
$\displaystyle\int_0^t(1-2\cos^2 x)\,\mathrm{d}x=\frac 12$ тэгшитгэлийн $[0;\pi]$ завсар дахь шийд аль вэ?
A. $\displaystyle\frac {3\pi} 4$
B. $\displaystyle\frac\pi 4$
C. $\displaystyle\frac {2\pi} 3$
D. $\displaystyle\frac\pi 3$
$\displaystyle\int_{y-1}^y(x^2+1)\,\mathrm{d}x< \frac {10}3$ тэнцэтгэл бишийн бүх шийд аль олонлог вэ?
A. $]-\infty;-1[\cup]2;+\infty[$
B. $]-\infty;-1[$
C. $]2;+\infty[$
D. $]-1;2[$
E. $\varnothing$
$\displaystyle\int_{y}^{y+2}(x^2+x)\,\mathrm{d}x>\frac 23$ тэнцэтгэл бишийн бүх шийд аль олонлог вэ?
A. $]-\infty;-2[\cup]-1;+\infty[$
B. $]-\infty;-2[$
C. $]-1;+\infty[$
D. $]-2;-1[$
$\displaystyle\int_{-y}^y(3x^2+1)\,\mathrm{d}x\leq y^2$ тэнцэтгэл бишийн $[0;+\infty[$ завсар дахь шийд аль вэ?
A. $[0;+\infty;[$
B. $[0;7]$
C. ${0}$
D. $[7;+\infty[.$
$\displaystyle\int_{-3}^{2y}(x^2+6x)\,\mathrm{d}x\geq 4y^2-18$ тэнцэтгэл бишийн $[-2;+\infty[$ завсар дахь шийд аль вэ?
A. $[-2;+\infty[$
B. $]-2;4]$
C. $[4;+\infty[$
D. $\varnothing$
$\displaystyle\int_{-1}^3|7x+2|\,\mathrm{d}x$ нь аль тоо вэ?
A. $37\displaystyle\frac57$
B. $39\displaystyle\frac47$
C. $43\displaystyle\frac 67$
D. $45\displaystyle\frac 37$
E. $40$
$\displaystyle\int_{-2}^1|5x-3|\,\mathrm{d}x$ нь аль тоо вэ?
A. $17.3$
B. $15.3$
C. $18.7$
D. $16.7$
E. $17.5$
$\displaystyle\int_{-2}^3(x^2-7|x|+12)\,\mathrm{d}x$ нь аль тоо вэ?
A. $23\displaystyle\frac 16$
B. $27\displaystyle\frac 56$
C. $28\displaystyle\frac 23$
D. $26\displaystyle\frac 16$
$\displaystyle\int_{-2}^3(x^2-|7x-14|)\,\mathrm{d}x$ нь аль тоо вэ?
A. $-47\displaystyle\frac56$
B. $47\displaystyle\frac 56$
C. $48\displaystyle\frac 23$
D. $-48\displaystyle\frac 23$
$\displaystyle\int_{3}^5|x^2-7x+12|\,\mathrm{d}x$ нь аль тоо вэ?
A. $2\displaystyle\frac56$
B. $3\displaystyle\frac 16$
C. $1\displaystyle\frac 56$
D. $4\displaystyle\frac 16$
$\displaystyle\int_{0}^4|-x^2+5x-6|\,\mathrm{d}x$ нь аль тоо вэ?
A. $3\dfrac13$
B. $4\dfrac 23$
C. $1\dfrac 13$
D. $7\dfrac 23$
E. $5\dfrac 23$
$\displaystyle\int_3^6\dfrac{\,\mathrm{d}x}{2x-3}$ интералыг бод.
A. $\ln\sqrt[3]{3}$
B. $\ln\sqrt3$
C. $\ln\sqrt2$
D. $\ln\sqrt[3]2$
E. $\ln\sqrt[3]5$
$\displaystyle\int_{-2}^3|x-1|\,\mathrm{d}x=?$
A. $-\dfrac52$
B. $\dfrac32$
C. $\dfrac52$
D. $\dfrac{11}2$
E. $\dfrac{13}2$
$\displaystyle\int_{-1}^4|x-2|\,\mathrm{d}x=?$
A. $-\dfrac52$
B. $\dfrac32$
C. $\dfrac52$
D. $\dfrac{11}2$
E. $\dfrac{13}2$
$\displaystyle\int_{-2}^{5}|x^2-4x+3|\,\mathrm{d}x$
A. $22$
B. $23$
C. $24$
D. $25$
E. $26$
$\displaystyle\int_0^{\pi} \sin^2 x\,\,\mathrm{d}x= ?$
A. $\pi$
B. $2\pi$
C. $\dfrac{1}{2}\pi$
D. $\dfrac{1}{3}\pi$
E. $0$
$\displaystyle\int_{0}^4 |x-2|\,\,\mathrm{d}x$
A. 0
B. 2
C. 4
D. 6
E. 8
$\displaystyle\int_{\frac{b}{2}}^b\dfrac{1-2x}{3}dx=-\dfrac{4}{3}$ тэнцэтгэл $b$-ийн ямар утгад биелэх вэ?
A. $2;-\dfrac85$
B. $2;-\dfrac83$
C. $8;-6$
D. $-2;\dfrac83$
E. шийдгүй
Хэрэв $\displaystyle\int_0^3f(x)dx=4$ бол $\displaystyle\int_0^3\big(f(x)+4x+1\big)dx$-ийг олоорой.
A. $21$
B. $25$
C. $22$
D. $33$
E. $30$
$\displaystyle\int_0^3x(x-3)dx$ интегралыг бод.
A. $-4.5$
B. $-3$
C. $-\dfrac{27}{2}$
D. $3$
E. $\dfrac{9}{2}$
Хэрэв $\displaystyle\int_0^3f(x)dx=5$ бол $\displaystyle\int_0^3\big(f(x)+2x+3\big)dx$-ийг олоорой.
A. $24$
B. $17$
C. $14$
D. $33$
E. $23$
Хоёр дугуйчин нэгэн гараанаас нэг чиглэлд харгалзан $v_1(t)=\displaystyle\frac 38(\sqrt{t}+t)$, $v_2(t)=2(\sqrt[3]{t}+1)$ м/с хурдтайгаар зэрэг хөдөлжээ. Тэдний явсан зам нь
$S_1=\displaystyle\frac{1}{\fbox{a}}t^{\frac{3}{2}}+\displaystyle\frac{\fbox{b}}{16} t^2+\fbox{c}$,
$S_2=\displaystyle\frac{3}{\fbox{d}}t^{\frac{4}{3}}+\fbox{e} t+\fbox{f}$ тул 64 секундийн дараа бие биенээсээ $S_1(t)-S_2(t)=\fbox{g}84$ м зайтай байна.
$v(t)=\displaystyle\frac {\sin 2t}{2}$ м/с хурдтайгаар материаллаг цэг шулуун замаар хөдөлжээ. $t=\displaystyle\frac{\pi}{3}$ секундын хугацаанд $\displaystyle\frac{7}{18}$ м явсан гэвэл түүний явсан зам нь $S=\fbox{a}-\displaystyle\frac{\cos\fbox{b} t}{\fbox{c}}$, харин $t=\displaystyle\frac{\pi}{3}$ секундын дараа өмнөхөөсөө 2 дахин их хурдтай хөдөлсөн бол явсан зам нь $S=\displaystyle\frac{\fbox{d}}{\fbox{e}6}-\displaystyle\frac{\cos\fbox{f}\,t}{\fbox{g}}$ болно.
$\displaystyle\int_0^1x^2\sqrt[3]{(2-x^3)^2}\,\mathrm{d}x=\displaystyle\frac{\fbox{a}}{\fbox{b}}(\fbox{c}\cdot\sqrt[3]{\fbox{d}}-\fbox{e})$ болно.
$\displaystyle\int^{\sqrt 2}_{\frac{\sqrt{6}}{2}}x\sqrt{(2x^2-3)}\,\mathrm{d}x=\displaystyle\frac{\fbox{a}}{\fbox{b}}$ болно.
$\displaystyle\int_0^1\sqrt{1+x}\,\mathrm{d}x=\frac{\fbox{a}}{\fbox{b}}(\sqrt{\fbox{c}}-\fbox{d})$ болно.
$\displaystyle\int_{-2}^{-1}\frac{\,\mathrm{d}x}{(11+5x)^3}=\displaystyle\frac{\fbox{a}}{\fbox{bc}}$ болно.
$f(x)=Ax^2+Bx+C$ -ийн хувьд $f^\prime(1)=8\, , \, f(2)+f^{\prime\prime}(2)=33\, , \,\displaystyle\int_0^1f(x)\,dx=\frac73$ бол $A, B, C$-г олъё.
$$\left\{\begin{array}{l}
f^\prime(1)=\fbox{a}A+B=8\\
f(2)+f^{\prime\prime}(2)=\fbox{b}A+\fbox{c}B+\fbox{d}C=33\\
\displaystyle\int_0^1f(x)\,dx=\dfrac{A}{\fbox{e}}+\dfrac{B}{\fbox{f}}+C=\dfrac73
\end{array} \right.$$
Тэгшитгэлийн системийг бодвол $A=\fbox{g}\, , \, B=\fbox{hi}\, , \, C=\fbox{j}$ болно.
$f(x)=\left\{
\begin{array}{rl}
2x^2+1&x\leq 1\\
4-x&x>1
\end{array}
\right.$ функц өгөгдөв.
- $f(0)+f(1)+f(2)=\fbox{a}$ /1 оноо/
- $\int\limits_0^2f(x)\,dx=\dfrac{\fbox{bc}}{\fbox{d}}$ /2 оноо/
- $f(x)=0$ тэгшитгэлийн шийд $x=\fbox{e}$ байна. /1 оноо/
- $g(a)=\int\limits_0^af(x)\,dx$ гэвэл $g(a)$ функцийн максимум утга $a=\fbox{f}$ үед $g_{\max}=\dfrac{\fbox{gh}}{\fbox{i}}$ байна. /3 оноо/
Трапецийн дүрэм
Хувьсах хилтэй интеграл
$h$ функцийг бүх бодит тооны хувьд $h(x)=\displaystyle\int_0^{x^2}e^{x+t}\,\mathrm{d}t$ гэж тодорхойлъё. Тэгвэл $h^\prime(1)=?$
A. $e-1$
B. $e^2$
C. $e^2-e$
D. $2e^2$
E. $3e^2-e$
$f$ функцийг бүх бодит тооны хувьд $f(x)=\displaystyle\int_0^{x^2}e^{2x+t}\,\mathrm{d}t$ гэж тодорхойлъё. Тэгвэл $f^\prime(1)=?$
A. $4e^3-2e^2$
B. $e^2$
C. $e^3-e$
D. $2e^2$
E. $3e^2-e$
Хэсэгчлэн интегралчлах арга
$\displaystyle\int e^x\sin xdx$ бод.
$\displaystyle\int x e^{2x} \,\mathrm{d}x$ интегралыг бод.
A. $\dfrac12e^{2x}\cdot x-\dfrac14e^{2x}+C$
B. $\dfrac12e^{2x}\cdot x+\dfrac14e^{2x}+C$
C. $x^2e^{2x}+C$
D. $2xe^{2x}+e^{2x}$
E. $2xe^{2x}+e^{2x}+C$
$\int 9x\sin 3x \,\mathrm{d}x$ интегралыг бод.
A. $\sin3x-3x\cos 3x+C$
B. $\cos3x-x\sin 3x+C$
C. $\cos3x-3x\sin 3x+C$
D. $\cos3x+3x\sin 3x+C$
E. $\sin 3x-3x\sin 3x+C$
$\displaystyle\int x\cos{2x}\,\mathrm{d}x$ бод.
A. $x\sin{2x}+0.5\cos{2x}+C$
B. $x\sin{2x}-0.5\cos{2x}+C$
C. $0.5x\sin{2x}-0.25\cos{2x}+C$
D. $0.5x\sin{2x}+0.25\cos{2x}+C$
E. $x\sin{2x}+\cos{2x}+C$
$\displaystyle\int x^2e^{2x}\mathrm{d}x$ интегралыг бод.
A. $4xe^{2x}+C$
B. $(x^2-x+1)e^{2x}+C$
C. $(2x^2-2x+1)e^{2x}+C$
D. $(2x^2-2x+1)e^{x}+C$
E. $\frac14(2x^2-2x+1)e^{2x}+C$
$\displaystyle\int_0^{\pi}x\sin x\,\mathrm{d}x$ интегралыг бод.
A. $\pi$
B. $2\pi$
C. $\dfrac{\pi}{2}$
D. $0$
E. $1$
$\int\limits_0^{\frac{\pi}2}(x+1)\sin x\,dx$ интеграл бод.
A. $\pi$
B. $\pi-2$
C. $\frac{\pi}2$
D. $2$
E. $1$
$\displaystyle\int_0^{\frac{\pi}2}(x+1)\cos x\,\mathrm{d}x$ интеграл бод.
A. $\pi$
B. $\pi-2$
C. $\dfrac{\pi}{2}$
D. $2$
E. $1$
$\displaystyle\int x e^{3x} \,\mathrm{d}x$ интегралыг бод.
A. $\dfrac13e^{3x}\cdot x-\dfrac19e^{3x}+C$
B. $\dfrac13e^{3x}\cdot x+\dfrac19e^{2x}+C$
C. $x^2e^{3x}+C$
D. $3xe^{3x}+e^{3x}$
E. $3xe^{3x}+e^{3x}+C$
$f(x)=\left\{
\begin{array}{rl}
x^2+1&x\leq 1\\
3-x&x>1
\end{array}
\right.$ функц өгөгдөв.
- $f(0)+f(1)+f(2)=\fbox{a}$ /1 оноо /
- $\displaystyle\int_0^2f(x)\,dx=\dfrac{\fbox{bc}}{\fbox{d}}$ /2 оноо /
- $f(x)=0$ тэгшитгэлийн шийд $x=\fbox{e}$ байна. /1 оноо /
- $g(a)=\displaystyle\int_0^af(x)\,dx$ гэвэл $g(a)$ функцийн максимум утга $a=\fbox{f}$ үед $g_{\max}=\dfrac{\fbox{gh}}{\fbox{i}}$ байна. /3 оноо /
Хялбар өргөтгөсөн интеграл
Эргэлтийн биетийн эзлэхүүн
Интеграл ашиглан дараах биеийн эзлэхүүнийг ол.
- $r$ радиустай, $h$ өндөртэй конусын эзлэхүүн;
- $r$ радиустай бөмбөрцгийн эзлэхүүн.
$y=x^2, y=2a^2-x^2 (a>0)$
параболуудын огтлолд үүсэх дүрсийн хувьд
(1) $x$ тэнхлэгийг тойруулан эргүүлэхэд үүсэх биетийн эзлэхүүн $\upsilon_1$ ба $y$
тэнхлэгийг тойруулан эргүүлэхэд үүсэх биетийн эзлэхүүн $\upsilon_2$-ийг ол.
(2) $\upsilon_1=\upsilon_2$ бол $a$-г ол.
$y=\sqrt{x}$ функийн графикийн $0\le x\le1$ завсарт харгалзах хэсгийг $OX$ тэнхлэгийг тойруулан эргүүлэхэд үүсэх биетийн эзлэхүүнийг ол.
A. $\dfrac{\pi}6$
B. $\dfrac{\pi}4$
C. $\dfrac{\pi}3$
D. $\dfrac{\pi}2$
E. ${\pi}$
$y=x^3$, $y=8$, $x=0$ шугамуудаар хүрээлэгдсэн мужийг $y$-тэнхлэгийг тойруулан эргүүлэхэд үүсэх биеийн эзлэхүүнийг ол.
A. $\dfrac{32\pi}{3}$
B. $\dfrac{64\pi}{3}$
C. $\dfrac{64\pi}{5}$
D. $\dfrac{32\pi}{5}$
E. $\dfrac{96\pi}{5}$
$y=\dfrac{1}{\sqrt{1+x^2}}$ функцийн график, $x=0$, $x=\sqrt3$ шулуунууд ба абсцисс тэнхлэгээр хашигдсан дүрсийг $Ox$ тэнхлэг тойруулан эргүүлэхэд үүсэх биетийн эзлэхүүн $\dfrac{\pi^{\fbox{b}}}{\fbox{a}}$ байна. $x=1$ цэгийг дарсан $Ox$ тэнхлэгт перпендикуляр $\alpha$ хавтгай биетийн эзлэхүүнийг $\fbox{c}:\fbox{d}$ ($c>d$) харьцаагаар хуваана. Энэ биетийн эзлэхүүнийг таллан хуваадаг, $\alpha$-тай паралель хавтгай $x=\dfrac{\fbox{e}}{\sqrt{\fbox{f}}}$ цэгээр дайрна.
$\ell_1: y=x^2,$ $\ell_2: y=\sqrt{x}$ муруйнууд $O(0,0)$ ба $A(x,y)$ цэгүүдэд огтолцоно.
- $x=\fbox{a} , y=\fbox{b}$
- $\ell_1$ муруйн $OA$ нумыг $OX$ тэнхлэгийг тойруулан эргүүлэхэд үүсэх биетийн эзлэхүүн $V_1=\dfrac{\pi}{\fbox{c}}$
- $\ell_2$ муруйн $OA$ нумыг $OX$ тэнхлэгийг тойруулан эргүүлэхэд үүсэх биетийн эзлэхүүн $V_2=\dfrac{\pi}{\fbox{d}}$
- $\ell_1$ ба $\ell_2$ муруйнуудын огтлолд үүсэх хавтгайн хэсгийг $OX$ тэнхлэгийг тойруулан эргүүлэхэд үүсэх биетийн эзлэхүүн $V_3=\dfrac{\fbox{e}}{\fbox{fg}}\pi$ байна.
$y=\dfrac{1}{\sqrt{1+x^2}}$ функцийн график, $x=-\sqrt3$, $x=0$ шулуунууд ба абсцисс тэнхлэгээр хашигдсан дүрсийг $Ox$ тэнхлэг тойруулан эргүүлэхэд үүсэх биетийн эзлэхүүн $\dfrac{7\pi^2}{\fbox{ab}}$ байна. $x=0$ цэгийг дарсан $Ox$ тэнхлэгт перпендикуляр $\alpha$ хавтгай биетийн эзлэхүүнийг $\fbox{c}:\fbox{d}$ ($c>d$) харьцаагаар хуваана. Энэ биетийн эзлэхүүнийг $2:5$ харьцаатай хуваадаг, $\alpha$-тай параллель хавтгайн нэг нь $x=\dfrac{\fbox{e}}{\sqrt{\fbox{f}}}$ цэгээр дайрна.
Эх функц, тодорхой биш интеграл
$f(x)-g(x)=x^2, f^\prime(x)+g^\prime(x)=5x^2+x+1, f(0)=7$ бол
$f(x), g(x)$-ийг ол.
$f^\prime(x)=|3x^2-6x|, f(1)=0$ нөхцлүүдийг хангах $f(x)$-ийг ол. $y=f(x)$ функцийн графикыг зур.
Дараах интегралуудыг бод.
- $\int (x^2-3x+2) \,\mathrm{d}x$
- $\int (x-2)(1-3x)\,\mathrm{d}x$
- $\int (x-2)^2 \,\mathrm{d}x$
- $\int (2t+1)^2 \,\mathrm{d}t$
$f(x)=2x^2-3x-1$ бол
- $\dfrac{\mathrm{d}}{\,\mathrm{d}x}\left\{\int f(x)\,\mathrm{d}x\right\}$
- $\int\left\{\dfrac{\mathrm{d}}{\,\mathrm{d}x} f(x)\right\}\,\mathrm{d}x$ ол.
$f^\prime(x)=(x+1)(x-3), f(0)=-2$ байх $f(x)$-ийг ол.
Дараах интегралуудыг бод.
- $\int (2x^2-4x+1)\,\mathrm{d}x$
- $\int (t-1)(t+3)\,\mathrm{d}t$
- $\int(2x-3)^2\,\mathrm{d}x$
- $f^\prime(x)=2x^2-3x, f(0)=2$ нөхцөлүүдийг хангах $f(x)$ функцийг ол.
- $y=f(x)$ нь $(1, 0)$ цэгийг дайрдаг $(x, f(x))$ цэг дээрх шүргэгчийн өнцгийн коэффициент нь $x^2-1$ бол $f(x)$ функцийг ол.
$f(x)+g(x)=x^2, 2f^\prime(x)+g^\prime(x)=3x^2-2x, f(0)=-2$ нөхцөлийг хангах $f(x), g(x)$-ийг ол.
$\displaystyle\int (2-3\sqrt{x})^2dx$
$\displaystyle\int\dfrac{\sqrt[3]{x^2}-2}{\sqrt[3]{x}}\,\mathrm{d}x$ интеграл бод.
A. $\dfrac34\sqrt[3]{x^4}-3\sqrt[3]{x^2}+C$
B. $3\sqrt[3]{x^4}-\dfrac34\sqrt[3]{x^2}+C$
C. $3\sqrt[3]{x^4}+\dfrac34\sqrt[3]{x^2}+C$
D. $\dfrac34\sqrt[3]{x^4}+3\sqrt[3]{x^2}+C$
E. $\dfrac34\sqrt[3]{x^4}-\dfrac34\sqrt[3]{x^2}+C$
$\displaystyle\int(3x+1)^{20}\,\mathrm{d}x$ интеграл бод.
A. $\frac{(3x+1)^{21}}{21}+C$
B. $\frac{(3x+1)^{21}}{63}+C$
C. $-\frac{(3x+1)^{21}}{63}+C$
D. $\frac{(3x+1)^{20}}{63}+C$
E. $-\frac{(3x+1)^{20}}{63}+C$
$\displaystyle\int\cos3x \,\mathrm{d}x=?$
A. $\dfrac{\cos^23x}{2}+C$
B. $-\sin x+C$
C. $-\sin3x+C$
D. $\dfrac{\cos^23x}{6}+C$
E. $\dfrac{\sin 3x}{3}+C$
Интеграл бод.
$\displaystyle\int 6x^2+4x-\sqrt3-\sin 2x \,\,\mathrm{d}x$
A. $6x^3+4x^2-\sqrt3x+\frac12\cos x+C$
B. $2x^3+2x^2-\sqrt3x+\cos2x+C$
C. $12x+4-2\cos2x+C$
D. $2x^3+2x^2-\sqrt3x+\frac{\cos2x}{2}+C$
E. $x^3+x^2-\sqrt3x+\frac{\cos2x}{2}+C$
$\displaystyle\int(x-1)(x-2)\,\mathrm{d}x$ бод.
A. $(x-1)^2(x-2)+(x-1)(x-2)^2+C$
B. $\dfrac14(x-1)^2(x-2)^2+C$
C. $\dfrac{x^3}{3}+\dfrac{3x^2}{2}+2x+C$
D. $\dfrac{x^3}{3}-\dfrac{3x^2}{2}+2x+C$
E. $2x-3+C$
$\int\sin x\cos 3x \,\mathrm{d}x$ бод.
A. $-\frac13\cos x\sin 3x+C$
B. $-\frac18\cos4x+\frac14\cos2x+C$
C. $\frac18\cos4x-\frac14\cos2x+C$
D. $\cos x\cos 3x-3\sin x\sin 3x+C$
E. $\frac13\cos x\sin 3x+C$
$\int ax^2+bx+c \,\mathrm{d}x=?$
A. $3ax^3+2ax^2+cx+C$
B. $\frac{ax^3}{3}+\frac{bx^2}{2}+cx+C$
C. $ax^3+bx^2+cx+C$
D. $\frac{ax^2}{2}+\frac{bx}{2}+C$
E. $\frac{ax^3}{3}+\frac{ax^2}{2}+\ln x+C$
$\displaystyle\int\sin 2x \,\mathrm{d}x=?$
A. $-\cos2x+C$
B. $\cos2x+C$
C. $\cos^2x+C$
D. $\dfrac{\cos2x}{2}+C$
E. $\sin^2x+C$
$\int(x-1)(x-2)\,\mathrm{d}x$ интегралыг бод.
A. $\dfrac13x^3+\dfrac32x^2+2x+C$
B. $(x-1)^2(x-2)+(x-1)(x-2)^2+C$
C. $\dfrac13x^3-\dfrac32x^2+2x+C$
D. $2x-3+C$
E. $x^3-3x^2+2x+C$
$\displaystyle\int\sin ^2x \,\textrm{d}x=?$
A. $-\dfrac12\sin x\cos x+\dfrac{x}{2}+C$
B. $\cos^2x+C$
C. $-\sin2x+C$
D. $\sin 2x+\cos x+C$
E. $\cos 2x+C$
$\displaystyle\int\dfrac{\,\mathrm{d}x}{1+4x^2}$ интегралыг бод.
A. $\dfrac14\arctg 2x+C$
B. $\dfrac14\arctg 4x+C$
C. $\ln\dfrac{x}{1+4x^2}+C$
D. $\dfrac12\arctg 2x+C$
E. $\dfrac12\arctg 4x+C$
$f(x)=2x+1$ нь алиных нь нэг эх функц нь вэ?
A. $x^2+x+C$
B. $x^2+x$
C. $\dfrac{x^2}{2}+x+C$
D. $2$
E. $2x+C$
$f(x)=3x^2$-ийн бүх эх функцыг ол.
A. $6x$
B. $6x+1$
C. $x^3+C$
D. $\dfrac{x^3}{3}+C$
E. $\dfrac{x^2}{2}+C$
$f'(x)=8x^3-6x+1,$ $f(-1)=5$ бол $f(1)=?$
A. 3
B. 7
C. 8
D. 9
E. 11
$\displaystyle\int 5\,\,\mathrm{d}x$
A. $5x+C$
B. $6x+C$
C. $\dfrac{5x^2}{2}+C$
D. $5+C$
E. $4x+C$
$\displaystyle\int \frac{1}{x^2} \,\,\mathrm{d}x= ?$
A. $-\dfrac{1}{x}+C$
B. $\ln x^2+C$
C. $\dfrac{x^{-3}}{-3}+C$
D. $(\ln x)^2+C$
E. $\dfrac{1}{x}+C$
$\displaystyle\int \frac{2}{2x+1}\,\,\mathrm{d}x$
A. $\dfrac{2(2x+1)^0}{0}+C$
B. $2\ln(2x+1)+C$
C. $\dfrac{\ln(2x+1)}{2}+C$
D. $-\dfrac{4}{(2x+1)^2}+C$
E. $\ln(2x+1)+C$
$\displaystyle\int e^{-x}\,\,\mathrm{d}x$
A. $e^{-x}+C$
B. $-e^{-x}+C$
C. $e^{-\frac{x^2}{2}}+C$
D. $\ln e^x+C$
E. $-e^x+C$
$\displaystyle\int \ln2 \cdot 2^x\,\,\mathrm{d}x$
A. $2^x+C$
B. $\ln2 \cdot 2^x+C$
C. $(\ln2)^2 \cdot 2^x+C$
D. $\dfrac{2^x}{(\ln2)^2}+C$
E. $\dfrac{2^x}{\ln 2}+C$
$\displaystyle\int \cos{\pi}\,\,\mathrm{d}x$
A. $-x+C$
B. $\sin{\pi}+C$
C. $\sin{\pi}$
D. $\dfrac{\sin{\pi x}}{\pi}+C$
E. $x+C$
$\displaystyle\int \sin{2x}\,\,\mathrm{d}x$
A. $-\cos{2x}+C$
B. $\cos{2x}+C$
C. $\dfrac{\cos{2x}}{2}+C$
D. $-\dfrac{\cos^2 x }{2}+C$
E. $-\dfrac{\cos{2x}}{2}+C$
$\displaystyle\int \frac{1}{1+x^2}\,\,\mathrm{d}x$
A. $\arcsin{x}+C$
B. $\ln(x^2+1)+C$
C. $\arctg{x}+C$
D. $-\arctg{x}+C$
E. $\arccos{x}+C$
$\displaystyle\int \frac{1}{\cos^2 {2x}}\,\,\mathrm{d}x$
A. $\dfrac{\tg2x}{2}+C$
B. $-\dfrac{\ctg2x}{2}+C$
C. $\dfrac{(\cos2x)^{-1}}{-2}+C$
D. $\ln(\cos^2 {2x})+C$
E. $\ln(\sin^2 {2x})+C$
$\displaystyle\int \frac{3}{\sqrt{3x-2}} \,\,\mathrm{d}x$
A. $\ln(\sqrt{3x-2})+C$
B. $2\sqrt{3x-2}+C$
C. $6\sqrt{3x-2}+C$
D. $-2(3x-2)^{-\frac{1}{2}}+C$
E. $-2(3x-2)^{\frac{1}{2}}+C$
$\displaystyle\int \frac{2x}{x^2+1}\,\,\mathrm{d}x$
A. $x^2 \arctg x+C$
B. $2\ln(x^2+1)+C$
C. $\ln(x^2+1)+C$
D. $-2\arctg{x}+C$
E. $2\arctg{x}+C$
$\int \cos^2{x}\,\,\mathrm{d}x$
A. $0.25\sin{2x}+0.5x+C$
B. $0.5x-0.25\sin{2x}+C$
C. $0.5\sin{2x}+0.5x+C$
D. $0.5x-0.5\sin{2x}+C$
E. $\sin^2 x+C$
$F'(x)=3x^2+\sqrt x-\sin x; F(0)=7$ бол $F(x)$ нь аль вэ?
A. $x^3+\displaystyle\frac 23x\sqrt x+\sin x+7$
B. $x^3+\displaystyle\frac 23x\sqrt x+\cos x+6$
C. $3x^2+\displaystyle\frac23\sqrt x+\cos x+6$
D. $3x^3+\displaystyle\frac 23\sqrt x+\cos x+6$
$F'(x)=\cos x+\cos 2x; F(\displaystyle\frac\pi 2)=2$ бол $F(x)$ нь аль вэ?
A. $\displaystyle\frac 12\cos 2+\cos x+3$
B. $-\displaystyle\frac 12\sin 2x-\sin x+3$
C. $-\displaystyle\frac12\cos 2x-\cos x+\displaystyle\frac32$
D. $\displaystyle\frac 12\sin 2x +\sin x+1$
$\int(3x^2+2\sin2x)\,\mathrm{d}x=?$
A. $\frac13x^3-\cos 2x+C$
B. $x^3+\cos 2x+C$
C. $x^3-\sin 2x+C$
D. $\frac13x^3+2\sin 2x+C$
E. $x^3-\cos 2x+C$
$\displaystyle\int(x^2+\sin2x)\,\mathrm{d}x=?$
A. $\frac13x^3+\frac12\cos2x+C$
B. $\frac13x^3-\frac12\cos2x+C$
C. $\frac13x^3+\frac12\sin2x+C$
D. $2x+2\cos2x+C$
E. $\frac13x^3-\cos2x+C$
$\int(3x^2+\sin3x)\,\mathrm{d}x=?$
A. $x^3+\dfrac13\cos 3x+C$
B. $x^3-\dfrac13\cos 3x+C$
C. $x^3+3\cos 3x+C$
D. $x^3-3\cos 3x+C$
E. $3x^2-\dfrac13\cos x+C$
$\int(x^2+\sin3x)\,\mathrm{d}x=?$
A. $\dfrac13(x^2+\cos 3x)+C$
B. $2x+3\cos 3x+C$
C. $\dfrac13x^3-\dfrac13\cos 3x+C$
D. $x^3-\dfrac13\cos 3x+C$
E. $\dfrac13x^2+\cos 3x+C$
$\displaystyle2\int\cos5x \,\mathrm{d}x=?$
A. $\cos^25x+c$
B. $-2\sin x+c$
C. $-2\sin5x+c$
D. $\dfrac{2\sin 5x}{5}+c$
E. $\dfrac{\cos^2 5x}{5}+c$
$\displaystyle\int (\sqrt{x}+1)(\sqrt[3]{x}-1)\,\mathrm{d}x=?$
A. $(\sqrt{x^3}+1)(\sqrt[3]{x^4}-1)+C$
B. $x^{\frac{11}{6}}-x^{\frac32}+x^{\frac43}-x+C$
C. $\frac{6x^{\frac{11}{6}}}{11}-\frac{2x^{\frac32}}{3}+\frac{3x^{\frac43}}{4}-x+C$
D. $12(\sqrt[3]{x}+1)(\sqrt[4]{x}-1)+C$
E. $(\sqrt[3]{x}+1)(\sqrt[4]{x}-1)+C$
$y=x+\dfrac{1}{\cos^2x}$ функцийн эх функц аль нь вэ?
A. $x^2-\tg x+C$
B. $x^2+\tg x+C$
C. $\dfrac{x^2}{2}+\tg x+C$
D. $\dfrac{x^2}{2}+\ctg x+C$
E. $\dfrac{x^2}{2}-\ctg x+C$
$x^2+2x+1$ функцийн эх функцийг ол.
A. $2x+2$
B. $x^3+2x^2+x+C$
C. $\frac{x^3}3+x^2+x+C$
D. $\frac{x^3}3+2x+1+C$
E. $2x+2+C$
$x^2-4x+2$ функцийн эх функцийг ол.
A. $2x-4$
B. $x^3-2x^2+2x+C$
C. $2x-4+C$
D. $\frac{x^3}3-4x+2+C$
E. $\frac{x^3}3-2x^2+2x+C$
$\displaystyle\int\dfrac{dx}{\cos^2x\cdot\sin^2x}$ интеграл бод.
A. $\dfrac{1}{\cos^2x}+\dfrac{1}{\sin^2x}+C$
B. $\tg x-\ctg x+C$
C. $-\tg x+\ctg x+C$
D. $\dfrac{1}{\cos^2x}+\dfrac{1}{\sin^2x}+C$
E. $\tg x+\ctg x+C$
Уламжлал нь $\cos3x$ байх функц аль нь вэ?
A. $\dfrac{\cos^23x}{2}+C$
B. $-\sin x+C$
C. $-\sin3x+C$
D. $\dfrac{\cos^23x}{6}+C$
E. $\dfrac{\sin 3x}{3}+C$
Уламжлал нь $\sin2x$ байх функц аль нь вэ?
A. $-\dfrac{\cos2x}{2}+C$
B. $-\cos2x+C$
C. $\cos2x+C$
D. $\dfrac{\sin^22x}{2}+C$
E. $\dfrac{\sin^2 2x}{2}+C$
$\displaystyle\int2e^{2x}\,\mathrm{d}x$ интеграл бод.
A. $2e^{2x}+C$
B. $\dfrac{e^{2x}}{4}+C$
C. $4^{2x-1}+C$
D. $e^{2x}+C$
E. $\dfrac{e^{2x}}{2}+C$
$2e^{2x}$ нь доорх функцүүдийн алиных нь уламжлал болох вэ?
A. $y=2e^{2x}$
B. $y=\dfrac{e^{2x}}{4}$
C. $y=4^{2x-1}$
D. $y=e^{2x}$
E. $y=\dfrac{e^{2x}}{2}$
$e^{2x}$ нь доорх функцүүдийн алиных нь уламжлал болох вэ?
A. $y=2e^{2x}$
B. $y=\dfrac{e^{2x}}{4}$
C. $y=4^{2x-1}$
D. $y=e^{2x}$
E. $y=\dfrac{e^{2x}}{2}$
$\displaystyle\int2e^{6x}\,\mathrm{d}x$ интеграл бод.
A. $12e^{6x-1}+C$
B. $\dfrac{e^{6x}}{2}+C$
C. $\dfrac{e^{6x}}{3}+C$
D. $2e^{6x}+C$
E. $\dfrac{e^{6x}}{6}+C$
$\displaystyle\int \cos{\pi}\,\,\mathrm{d}x$
A. $-x+C$
B. $\sin{\pi}+C$
C. $\sin{\pi}$
D. $\dfrac{\sin{\pi x}}{\pi}+C$
E. $x+C$
$\displaystyle\int \frac{1}{x^2} \,\,\mathrm{d}x= ?$
A. $-\dfrac{1}{x}+C$
B. $\ln x^2+C$
C. $\dfrac{x^{-3}}{-3}+C$
D. $(\ln x)^2+C$
E. $\dfrac{1}{x}+C$
$\displaystyle\int \frac{3}{\sqrt{3x-2}} \,\,\mathrm{d}x$
A. $\ln(\sqrt{3x-2})+C$
B. $2\sqrt{3x-2}+C$
C. $6\sqrt{3x-2}+C$
D. $-2(3x-2)^{-\frac{1}{2}}+C$
E. $-2(3x-2)^{\frac{1}{2}}+C$
$\displaystyle\int\left(\dfrac{1}{2x}-e^{\frac{x}{2}}\right)dx$ интегралыг бод.
A. $\ln 2x-2e^{\frac{x}{2}}+C$
B. $\dfrac{\ln x}{2}-2e^{\frac{x}{2}}+C$
C. $\dfrac{\ln x}{2}-\dfrac{e^{\frac{x}{2}}}{2}+C$
D. $\dfrac{\ln 2x}{2}-e^{\frac{x}{2}}+C$
E. $\dfrac{e^{\frac{x}{2}}}{2x}+xe^x+C$
$f(x)=3x^2$-ийн бүх эх функцыг ол.
A. $6x$
B. $6x+1$
C. $x^3+C$
D. $\dfrac{x^3}{3}+C$
E. $\dfrac{x^2}{2}+C$
$f^\prime(x)=\dfrac{1}{x^2-5x+6}$, $f(4)=-\ln2$ бол $f(x)$ функцийг ол.
A. $f(x)=\ln\left|\dfrac{x+3}{x-2}\right|-2\ln 2$
B. $f(x)=\ln\left|\dfrac{x-3}{x-2}\right|+C$
C. $f(x)=\ln\left|\dfrac{x+3}{x+2}\right|$
D. $f(x)=\ln\left|\dfrac{x-3}{x-2}\right|$
E. $f(x)=\ln\left|\dfrac{x-3}{x-2}\right|+2\ln2$
$222^{555}$ тоог 7-д хуваахад гарах үлдэгдлийг ол.
A. 6
B. 5
C. 3
D. 1
E. 0
$f'(x)=4x^2+9x^{-2}$, $f(1)=\dfrac 43$ бол $f(x)=\dfrac{\fbox{a}}{\fbox{b}}x^3-\dfrac{\fbox{c}}{x}+\fbox{d}$ байна.
$f'(x)=\displaystyle\frac{x^3}{3}-4x+\displaystyle\frac 13, f(2)=1$ бол $f(x)=\displaystyle\frac{x^4}{\fbox{a}\,2}-\fbox{b}\,x^2+\displaystyle\frac{x}{\fbox{c}}+\fbox{d}$ байна.
$f(x)=x^4$ функцийн $M_0(-1;1)$ цэгийг дайрч гарсан эх функц нь $F(x)=\displaystyle\frac{x^{\fbox{a}}+\fbox{b}}{\fbox{c}}$ болно.
$f(x)=\sin 2x$ функцийн $M_0(0;1)$ цэгийг дайрч гарсан эх функц нь $F(x)=\displaystyle\frac{\fbox{a}-\cos \fbox{b}x}{\fbox{c}}$ болно.