Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Holy guacamole! www.integral.mn сайт 2026-01-01-ээс шинэчлэгдэж www.mathminds.club хуудас руу шилжинэ.
Огторгуйн геометр
Бөмбөлгийн гадаргуун талбай
Бөмбөрцгийн гадаргуугийн талбай ба түүнд багтсан кубийн гадаргуугийн талбайн харьцааг ол.
Хажуу ирмэгийн урт нь $a$-тай тэнцүү зөв гурвалжин пирамид бөмбөрцөгт багтсан байв. Пирамидын хажуу ирмэг суурийн хавтгайтаагаа $\alpha$ өнцөг үүсгэдэг гэвэл бөмбөрцөгийн гадаргуугийн талбай ба пирамидын эзлэхүүнийг ол.
Дөрвөн ижил бөмбөрцөгийн эзлэхүүнүүдийн нийлбэр тав дахь бөмбөрцөгийн эзлэхүүний хагастай тэнцүү бөгөөд гадаргуугийн талбайн нийлбэр нь тав дахь бөмбөлөгийн гадаргуугийн талбайн хагасаас $10$ м.кв-аар их байв. Тав дахь бөмбөрцөгийн радиусыг ол.
Нэг бөмбөрцөг гадаргуугийн талбай $43$. Үүнээс $27$ дахин их эзлэхүүнтэй бөмбөрцөг гадаргуугийн талбайг ол.
A. $361$
B. $429$
C. $208$
D. $387$
E. $109$
Бөмбөлөг ба хавтгайн харилцан байршил
Бөмбөлөг, бөмбөрцөг
Хайрцганд 13 улаан, 17 цагаан бөмбөлөг байна. Дараахи үйлдлүүдийг ямар ч дарааллаар, хэдэн ч удаа хийж болно. Үүнд: а/ улаан бөмбөлөгний тоог 2-оор нэмэхийн хажуугаар цагаан бөмбөлөгний \noindent тоог 1-ээр багасгах, б/ улаан бөмбөлөгний тоог 1-ээр нэмэхийн хажуугаар цагаан бөмбөлөгний тоог 2-оор нэмэх в/ улаан бөмбөлөгний тоог 2-оор багасгахын хажуугаар цагаан бөмбөлөгний тоог 1-ээр нэмэх+г/ улаан бөмбөлөгний тоог 1-ээр багасгахын хажуугаар цагаан бөмбөлөгний тоог 2-оор багасгах. Ийм үйлдлүүдийг хийснээрээ хайрцганд улаан бөмбөлөгнөөс 37, цагаанаас 43 байлгаж болох уу? Үндэслэлтэй хариу өгнө үү.
Бөмбөрцөгт хамгийн их эзлэхүүнтэй цилиндр багтжээ. Хэрвээ бөмбөрцөгийн радиус 5 см бол бөмбөрцөгийн эзлэхүүнийг цилиндрийн суурийн талбайд харьцуулсан харьцааг ол.
$R$ радиустай бөмбөрцөгт хамгийн их хажуу гадаргуутай цилиндр багтсан бол энэ цилиндрийн эзлэхүүнийг ол
Бөмбөрцгийг багтаасан зөв дөрвөн өнцөгт пирамидын өндөр бөмбөрцгийн диаметраас дөрөв дахин их бол пирамид ба бөмбөрцгийн эзлэхүүний харьцааг ол.
Бөмбөрцөгт багтсан пирамидын суурь нь 10 диагоналтай тэгш өнцөгт. Пирамидын хажуу ирмэг суурийн хавтгайтай $\beta$ өнцөг үүсгэдэг бол бөмбөрцгийн бүтэн гадаргуугийн талбай ба эзлэхүүнийг ол.
Зөв дөрвөн өнцөгт пирамидын хажуу ирмэг $\sqrt 6$, суурийг багтаасан тойргийн радиус $\sqrt2$ бол пирамидыг багтаасан бөмбөрцөгийн радиусыг ол.
$R$ радиустай бөмбөрцөгт зөв гурвалжин призм багтаасан бөгөөд призмын өндөр нь $H$ бол эзлэхүүнийг нь ол.
$ABC A_1B_1C_1$ зөв гурвалжин призмын хажуу ирмэгүүд $AA_1$, $BB_1$, $CC_1$ ба суурь нь адил талт $ABC$ гурвалжин болно. Түүнчлэн призмийн бүх ирмэгүүд ижилхэн $6$ урттай. $P$ ба $Q_1$ цэгүүд $BC$ ба $A_1C_1$ ирмэгүүдийг $BP:PC=A_1Q_1: Q_1C_1=1:2$ харьцаагаар хуваана. $ABB_1A_1$ ба $ACC_1A_1$ хавтгайг шүргэх, $PQ_1$ хэрчим дээр төвтэй бөмбөрцөгийн радиусыг ол.
$a=b=10$ см, $c=12$ см талууд бүхий гурвалжин 5 см радиустай бөмбөрцөгтөй шүргэлцжээ. Бөмбөрцгийн төвөөс гурвалжны хавтгай хүртлэх зайг ол.
Конуст багтсан бөмбөрцгийн гадаргуугийн талбай конусын суурийн талбайтай тэнцүү. Конусын тэнхлэг огтлолын оройн өнцгийн косинусыг ол.
Конусын тэнхлэг огтлол нь адил талт гурвалжин бол конусын эзлэхүүн ба түүнд багтсан бөмбөрцгийн эзлэхүүний харьцааг ол.
Диаметр нь $d=4$ см, өндөр $h=4$ см бүхий метал цилиндрийг хайлуулж бөмбөлөг хийв. Бөмбөлөгийн радиусыг ол.
Цилиндрт бөмбөрцөг багтав. Цилиндрийн эзлэхүүн $7.5$ бол түүнд багтсан бөмбөрцгийн эзлэхүүнийг ол.
Бөмбөрцгийн гадаргуугийн талбай ба түүнд багтсан кубийн гадаргуугийн талбайн харьцааг ол.
$2a$ урттай гипотенуз бүхий адил хажуут тэгш өнцөгт гурвалжны гипотенузыг нь тойруулан эргүүлэх үед үүссэн биетийн эзлэхүүнтэй ижил эзлэхүүн бүхий бөмбөрцөгийн радиусыг ол.
1 талтай кубэд конус багтсан бөгөөд түүний орой нь кубийн нэг оройтой давхцаж байв. Кубийн гурван тал конусын хажуу гадаргатай шүргэлцэнэ. Харин кубэд багтсан бөмбөрцөг конусын суурьтай шүргэлцэнэ. Конусын эзлэхүүнийг ол.
Бөмбөрцгийн нэг цэгээс татсан 3 хөвчийн урт $a$. Хөвчүүдийн хоорондын өнцөг $60^\circ$ бол бөмбөрцгийн радиусыг ол.
Ерөнхий суурьтай хоёр конусаас тогтсон биетэд бөмбөрцөг багтжээ. Хэрэв конусын суурийн радиус 1, өндөр нь 1 ба 2 бол бөмбөрцгийн эзлэхүүнийг ол.
Хажуу ирмэгийн урт нь $a$-тай тэнцүү зөв гурвалжин пирамид бөмбөрцөгт багтсан байв. Пирамидын хажуу ирмэг суурийн хавтгайтаагаа $\alpha$ өнцөг үүсгэдэг гэвэл бөмбөрцөгийн гадаргуугийн талбай ба пирамидын эзлэхүүнийг ол.
Дөрвөн ижил бөмбөрцөгийн эзлэхүүнүүдийн нийлбэр тав дахь бөмбөрцөгийн эзлэхүүний хагастай тэнцүү бөгөөд гадаргуугийн талбайн нийлбэр нь тав дахь бөмбөлөгийн гадаргуугийн талбайн хагасаас $10$ м.кв-аар их байв. Тав дахь бөмбөрцөгийн радиусыг ол.
Конусын байгуулагчийн урт $l$, суурьт налсан өнцөг $\alpha$ бол уг конуст багтсан бөмбөрцгийн эзлэхүүнийг ол.
Бөмбөрцгийн эзлэхүүн $4$ дм.куб. Уг бөмбөрцөгт багтсан цилиндрийн байгуулагч бөмбөрцгийн төвөөс $60^\circ$ өнцгөөр харагддаг бол цилиндрийн эзлэхүүнийг ол.
Конусын тэнхлэг огтлол нь адил талт гурвалжин бөгөөд конуст багтсан бөмбөрцөгийн радиус $r=2$ см бол конусын эзлэхүүнийг ол.
2 см суурийн радиустай конуст багтсан бөмбөрцгийн радиус 1 см бол конусын эзлэхүүнийг ол.
1 талтай кубийн оройнууд нь ижил радиустай бөмбөрцгүүдийн төв болно. Бөмбөрцгүүдийн гадна орших кубийн эзлэхүүн $1/2$ бол кубийн ирмэгийн ямар хэсэг бөмбөрцгийн дотор байрлах вэ?
$SABCD$ зөв дөрвөн өнцөгт пирамидын $SO$ өндөр нь $H$-тай тэнцүү. Харин $ASC$ ($AS$ ба $CS$ эсрэг байрлах хажуу ирмэгүүд) өнцөг $2\alpha$. $K$ цэг $SO$ шулуун дээр орших ба $SK:SO_1=1:3$ ($O_1$-пирамидын багтсан бөмбөрцгийн төв) гэсэн харьцаагаар байрлана. Пирамидын суурьтай параллель, $K$ цэгийг дайран гарах хавтгайгаар үүсэх огтлолын талбайг ол.
$ABCD A_1B_1C_1D_1$ кубийн ирмэг нь $a$-тай тэнцүү. $AA_1$, $BB_1$ ирмэгийн дундаж цэгүүд ба $A$, $C_1$ оройг дайран гарах бөмбөрцгийн радиусыг ол.
$ABCD A_1B_1C_1D_1$ кубийн $A$ орой, $AB$ ба $AD$ талуудын дундажыг дайрах бөмбөрцөг $A_1B_1C_1D_1$ талстай шүргэлцэнэ. Бөмбөрцгийн гадаргуугийн талбай ба кубийн бүтэн гадаргуугийн талбайн харьцааг ол.
$MABCD$ дөрвөн өнцөгт пирамидын суурь нь $AB=a$, $AD=b$ талуудтай $ABCD$ тэгш өнцөгт байв. $MAD$ ба $MAB$ талсууд суурийн хавтгайтай перпендикуляр, харин $MDC$ талс $45^\circ$-ийн өнцөгөөр налдаг бол пирамидыг багтаасан бөмбөрцгийн радиусыг ол.
$R$ радиустай гурван бөмбөрцөг бие биетэйгээ шүргэлцэж бөгөөд тус бүрдээ конусын хажуу гадаргууг шүргэнэ. Бөмбөрцгийн төвүүд конусын гадна орших бөгөөд конусын өндөр шарын төвүүд орших $\alpha$ хавтгайтай перпендикуляр. Конусын өндөр ба байгуулагчуудын хоорондох өнцөг $\varphi$ бол конусын оройгоос $\alpha$ хавтгай хүртлэх зайг ол.
Пирамидын суурь нь $a$ талтай зөв гурвалжин. Түүний нэг хажуу талс нь суурьтайгаа ижил гурвалжин бөгөөд түүнд перпендикуляр байв. Пирамидыг багтаасан бөмбөрцгийн эзлэхүүнийг ол.
$ABCDA_1B_1C_1D_1$ куб өгөгдөв. Хэрэв кубийн ирмэгийн урт 1 бол $AD$, $DD_1$, $CD$ ирмэгүүд болон $BC_1$ шулууныг шүргэх бөмбөрцгийн радиусыг ол.
Гурвалжин пирамидын $A$ ба $B$ оройг дайрсан, $AS$ ба $BS$ ирмэгүүдийг харгалзан $M$ ба $N$ цэгт огтлох бөмбөрцөг байгуулав. $B$ ба $N$ цэгүүдийг дайруулан $SC$ ирмэгийг $P$ ба $Q$ цэгт огтлох бөгөөд $PQ=\dfrac13SC$ байх өөр нэг бөмбөрцөг байгуулав. Хэрэв $M$ нь $SA$ ирмэгийн дундаж цэг бөгөөд $SC=\dfrac32SA$ бол $SC$ хэрчим $QC$ ($QC< PC$) хэрчмийн ямар хэсэгтэй тэнцэх вэ?
Пирамидын өндөр 5, суурийн талууд 7, 8, 9. Нэгэн бөмбөрцөг түүний бүх хажуу талсыг суурийн тал дээр орших цэгээр шүргэх бол бөмбөрцгийн радиусыг ол.
Гурван параллель шулуун $O$ төвтэй бөмбөрцгийг $A$, $B$, $C$ цэгүүдэд шүргэнэ. Хэрэв $OBC$ гурвалжны талбай 4, $ABC$ гурвалжны талбай 16-аас их бол $BAC$ өнцгийн хэмжээг ол.
$ABCD$ пирамидын $AC$, $BC$, $DC$ ирмэгүүд харилцан перпендикуляр бөгөөд $AC=BC=DC=4$ байв. $AB$ ирмэгийн дундаж цэг $N$, $AD$ ирмэг дээр $M$ цэг орших бөгөөд $AM:MD=3$. $CN$ шулуун дээр төвтэй бөмбөрцөг $AD$ ирмэгийг $M$ цэгт шүргэнэ. Бөмбөрцгийн радиусыг ол.
$PQ$ хэрчим $ABCD$ тэгш өнцөгтийн орших хавтгайд перпендикуляр ба $KL=1$, $PQ=3$ байв. $ABCD$ тэгш өнцөгтийн бүх талууд ба $KP$, $LP$, $NQ$, $MQ$, $PQ$ хэрчмүүд бүгд нэг бөмбөрцгийг шүргэж байсан бол энэ бөмбөрцгийн радиусыг ол.
$SABC$ пирамидын $SH$ өндрийн суурь $H$ цэг нь $ABC$ гурвалжны $CM$ медиан дээр орших бөгөөд $SH$ өндрийн дундаж цэг $O$ нь $S$ орой, $SA$ ирмэг дээрх $E$ цэг, $SB$ ирмэг дээрх $F$ цэгүүдээс нэгэн ижил зайд алслагдаж байв. Хэрэв $SH=8$, $AB=16\sqrt2$, $EF=8\sqrt{\dfrac25}$, $SMC$ өнцгийн хэмжээ $30^\circ$-ээс хэтрэхгүй, $AB$ ба $SC$ хэрчмүүдийн дундаж цэгүүд $4\sqrt{13}$ зайтай бол $SABC$ пирамидад багтсан бөмбөрцгийн радиусыг ол.
$KLMN$ гурвалжин пирамидад багтсан бөмбөрцгийн төв нь түүний нэг талсыг уг талсад багтсан гурвалжны төв цэгт шүргэнэ. Хэрэв $MK=\dfrac45$, $\angle NMK=\dfrac\pi2$, $\angle KML=3\arcctg\dfrac13$, $\angle NML=\dfrac\pi2-\arcctg\dfrac13$ бол пирамидын эзлэхүүнийг ол.
$SABCD$ дөрвөн өнцөгт пирамидын суурь нь $ABCD$ ромбо байв. Уг ромбын $A$ өнцөг хурц, өндөр нь 4 ба $S$ оройн суурь дээрх ортогнал проекц нь ромбын диагоналуудын огтлолцлын цэг болж байв. Хэрэв 2 радиустай бөмбөрцөг пирамидын бүх талсыг шүргэх бөгөөд уг бөмбөрцгийн төвөөс $AC$ шулуун хүртэлх зай нь $\dfrac{2\sqrt2}3AB$ бол пирамидын эзлэхүүнийг ол.
Призмийн суурь нь $\sqrt3$ талтай $ABC$ зөв гурвалжин. $AD$, $BE$, $CF$ хажуу ирмэгүүд нь суурьтаа перпендикуляр. $\dfrac72$ радиустай бөмбөрцөг $ABC$ хавтгай ба $AE$, $BF$, $CD$ хэрчмүүдийн үргэлжлэлүүдийг харгалзан $A$, $B$, $C$ цэгийн талд нь шүргэж байв. Призмийн хажуу ирмэгийн уртыг ол.
$SPQRT$ зөв дөрвөн өнцөгт пирамидын $SO$ өндрийн урт $h$, $SP$ хажуу ирмэг нь $PQRT$ хавтгайтай $\gamma$ өнцөг үүсгэнэ. Пирамидын суурийн хавтгайнууд болон бүх хажуу ирмэгийг шүргэсэн бөмбөрцөг ба пирамидын бүх оройгоос ижил зайд алслагдсан хавтгай хоёрын огтлолцолд үүсэх тойргийн радиусыг ол.
$\dfrac\pi3$ хэмжээтэй хоёр талст өнцөг дотор бие биеэ шүргэх хоёр бөмбөрцөг багтав. Нэг дэх бөмбөрцгийн нэг дэх талсыг шүргэх цэг нь $A$, хоёр дахь бөмбөрцгийн хоёр дахь талсыг шүргэх цэг нь $B$ байв. Хэрэв $AB$ хэрчмийн нэг ба хоёр дахь бөмбөрцгүүдийг огтлох цэгүүд нь харгалзан $K$ ба $L$ бол $AK:KL$ харьцааг ол.
Хавгай дээр нэг ерөнхий байгуулагчтай $r$ радиустай 2 цилиндр хэвтүүлж тавив. Эдгээр цилиндр дээр тэнхлэгүүд нь дээрх цилиндрүүдийн тэнхлэгүүдтэй перпендикуляр бөгөөд бие биеэ байгуулагчаараа шүргэх $R$ радиустай 2 цилиндрийг мөн хэвтүүлж тавив. Бүх дөрвөн цилиндрийг шүргэх бөмбөрцгийн радиусыг ол.
$SABC$ ($S$ нь оройн цэг) зөв гурвалжин пирамидад багтсан бөмбөрцөг нь $KL=LM=\sqrt{6}$ байх $KLMK_1L_1M_1$ шулуун, гурвалжин призмд багтах ба $KK_1$ ирмэг $AB$ шулуун дээр байрлаж байв. Хэрэв $SC$ ирмэг $LL_1M_1M$ хавтгайтай параллель бол бөмбөрцгийн радиусыг ол.
Хавтгай дээр бие бие шүргэх $r$ радиустай 2 бөмбөрцөг ба тэдгээрийг шүргэх $R$ ($R>r$) радиустай цилиндр байрлаж байв. Цилиндр нь хавтгайг өөрийн байгуулагчаар шүргэх бол хавтгай, цилиндр ба 2 бөмбөрцгийг шүргэх бөмбөрцгүүдээс бага радиустай бөмбөрцгийнх нь радиусыг ол.
Огторгуйд $P$, $Q$, $R$, $S$ цэгүүд өгөгдөв. $SQ$ ба $PR$ хэрчмүүдийн дундаж цэгүүд өгөгдсөн бөмбөрцөг дээр байрлах ба $PS$, $PQ$, $QR$ ба $SR$ хэрчмүүд тус бүрдээ бөмбөрцгөөр $1:2:1$ харьцаатай хэсгүүдэд хуваагдаж байв. Бөмбөрцгийн радиус $r$ бол $P$ цэгээс $QR$ шулуун хүртэлх зайг ол.
$ABCDA_1B_1C_1D_1$ кубийн ирмэг $9$. Харгалзан $BC$, $CD$, $CC_1$ хэрчмүүд дээр орших $M$, $N$, $K$ цэгүүдийг дайруулан хавтгай татав. $MCK$ гурвалжинд багтсан тойргийн радиус 1, $MNC$ гурвалжины талбай $\dfrac{21}2$, $CN$ ба $CK$ хэрчмүүдийн уртуудын ялгавар 3, $MNKC$ пирамидын эзлэхүүн 15-аас бага гэдэг нь мэдэгдэж байв. $MNK$ гурвалжны хавтгай ба $A_1$ оройг агуулсан гурван талсыг шүргэх бөмбөрцгийн радиусыг ол.
$ABCDA_1B_1C_1D_1$ кубийн ирмэг $1$. $DC$ болон $BC$ ирмэгүүдийн дундаж цэгүүд нь харгалзан $K$ ба $N$. $M$ цэг $CC_1$ ирмэг дээр $MC=\dfrac34$ байхаар байрлана. $M$, $N$, $K$ цэгүүдийг дайрч, $BB_1D_1D$ хавтгайг шүргэх бөмбөрцгийн радиусын боломжит хамгийн их утгыг ол.
4 ба 5 нэгж радиустай бөмбөрцөгийн төвүүдийн хоорондох зай 3 нэгж бол ерөнхий хэсгийн эзлэхүүнийг ол.
Нэгж радиустай бөмбөрцөгт багтсан хамгийн их хажуу гадаргуутай конусын суурийн
радиусыг ол.
Интеграл ашиглан дараах биеийн эзлэхүүнийг ол.
- $r$ радиустай, $h$ өндөртэй конусын эзлэхүүн;
- $r$ радиустай бөмбөрцгийн эзлэхүүн.
$2k-1$ талстад $k$ радиустай бөмбөрцөг багтаажээ ($\mathbb N\ni k\ge2$). Тэгвэл хоорондох зай нь $2k+1$-ээс их байх 2 цэг уг талст дээрээс олдоно гэж батал.
$A; B; C$ цэгүүд бөмбөрцөг дээр байрлах ба төвөөс $(ABC)$ хавтгай хүрэх зай $12$, $AB=6$, $BC=8$, $AC=10$ бол бөмбөрцөгийн гадаргуугийн талбайг ол.
A. $676\pi$
B. $484\pi$
C. $289\pi$
D. $784\pi$
E. $(6+8+10)\pi/12$
$A$, $B$, $C$ цэгүүд бөмбөрцөг дээр байрлах ба төвөөс $(ABC)$ хавтгай хүртэлх зай $24$, $AB=12$, $BC=16$, $AC=20$ бол бөмбөрцгийн гадаргуугийн талбайг ол.
A. $4072\pi$
B. $2704\pi$
C. $2074\pi$
D. $100\pi$
E. $(12+16+20)\pi/24$
3 радиустай бөмбөрцөгт багтсан зөв дөрвөн өнцөгт призмийн өндөр 4 бол бөмбөрцгийн эзлэхүүнийг призмийн эзлэхүүнд харьцуулсан харьцааг ол.
A. $\dfrac45\pi$
B. $\dfrac9{10}\pi$
C. $\dfrac{9}{20}\pi$
D. $\dfrac{6\pi}{5}$
E. $\dfrac{3\pi}{5}$
6 радиустай бөмбөрцөгт багтсан зөв дөрвөн өнцөгт призмийн өндөр 9 бол бөмбөрцгийн эзлэхүүнийг призмийн эзлэхүүнд харьцуулсан харьцааг ол.
A. $\dfrac{32}{63} \pi $
B. $\dfrac{64}{63} \pi $
C. $\dfrac{16}{21} \pi $
D. $\dfrac{8}{21} \pi $
E. $\dfrac{32}{21} \pi $
Бөмбөрцөгт багтсан зөв гурвалжин пирамидын суурь нь бөмбөрцгийн төвийг дайрч байв. Бөмбөрцгийн радиус $2\sqrt3$-тай тэнцүү. Пирамидын эзлэхүүнийг ол.
A. $4\sqrt3$
B. $16$
C. $20$
D. $19$
E. $18$
$6$ радиустай бөмбөрцөгт багтсан хамгийн их эзлэхүүнтэй конусын суурь бөмбөрцгийн төвөөс ямар зайд орших вэ?
A. 6 см
B. 5 см
C. 4 см
D. 3 см
E. 2 см
$R$ радиустай бөмбөрцөгт багтсан хамгийн их хажуу гадаргуутай цилиндрийн эзлэхүүнийг ол.
A. $\pi R^3$
B. $\dfrac{\pi R^3}{\sqrt2}$
C. $\dfrac{\pi R^3}{\sqrt3}$
D. $\dfrac{\pi R^3}{\sqrt4}$
E. $R^3$
3 см радиустай бөмбөрцөгийн эзлэхүүн $A$ см.куб, гадаргын талбай $B$ см.кв, 3 см суурийн радиустай 6 см өндөртэй конусын эзлэхүүн $C$ см.куб бол зөв өгүүлбэрийг сонго.
A. $B< A< C$
B. $C< B< A$
C. $C< A=B$
D. $A=B< C$
E. $C=A< B$
Цилиндрт багтсан бөмбөрцгийн эзлэхүүн нь 168 бол цилиндрийн эзлэхүүнийг ол.
A. 222
B. 162
C. 248
D. 252
E. 192
Зөв гурвалжин призмд бөмбөрцөг багтах бөгөөд призмийн бүтэн гадаргуугийн талбай $2\sqrt3$ бол багтсан бөмбөрцгийн радиусыг ол.
A. $\dfrac13$
B. $\dfrac12$
C. $1$
D. $\dfrac43$
E. $2$
Суурийн радиус нь 3, өндөр нь 4 байх конуст багтсан бөмбөрцгийн эзлэхүүнийг ол.
A. $\pi$
B. $4.5\pi$
C. $\dfrac{32\pi}{3}$
D. $\dfrac{\pi}{6}$
E. $\dfrac{2\pi}{3}$
Өндөр нь 4, суурийн радиус нь 3 байх конус өгөгдөв. Уг конусын эзлэхүүнийг түүнд багтсан бөмбөрцгийн эзлэхүүнд харьцуулсан харьцааг ол.
A. $7:4$
B. $2:1$
C. $3:1$
D. $8:3$
E. $11:4$
$C\colon x^2+y^2+z^2=6$ бөмбөрцөгт багтсан хамгийн их эзлэхүүнтэй цилиндрийн суурийн радиусыг ол.
A. $1$
B. $2$
C. $3$
D. $4$
E. $5$
$5$ радиустай бөмбөрцөгт $8$ өндөртэй конус багтжээ. Конусын эзлэхүүнийг бөмбөрцгийн эзлэхүүнд харьцуулсан харьцааг ол.
A. $\dfrac{16}{125}$
B. $\dfrac{32}{125}$
C. $\dfrac{96}{125}$
D. $\dfrac{32}{125}$
E. $\dfrac{8}{25}$
Цилиндрт багтсан бөмбөрцгийн эзлэхүүн нь $168$ бол цилиндрийн эзлэхүүнийг ол.
A. $222$
B. $162$
C. $248$
D. $252$
E. $192$
Их дугуйн талбай $144\pi$ байх бөмбөрцөгийн эзлэхүүнийг ол.
A. $288\pi$
B. $576\pi$
C. $1296\pi$
D. $2304\pi$
E. $2500\pi$
$A(-1;7;5\sqrt{2})$ цэгийг дайрсан шулуун $x^2+y^2+z^2=64$ бөмбөрцөгийг $B$ цэгт шүргэх бол $AB$ хэрчмийн уртыг ол.
A. $5$
B. $6$
C. $7$
D. $8$
E. $9$
Бөмбөрцөгийн төвөөс 4 см зайтай хавтгай татахад огтлолд нь 6 см диаметртэй дугуй үүсэв. Бөмбөрцөгийн радиусыг ол.
A. $5$
B. $6$
C. $\sqrt{20}$
D. $\sqrt{52}$
E. $8$
Гүйцэд гадаргуугийн талбай 24 см$^2$ байх кубэд багтсан бөмбөрцөгийн гадаргуугийн талбайг ол.
A. $4\pi$
B. $6\pi$
C. $8\pi$
D. $12\pi$
E. $16\pi$
Саванд 55 хүрэхгүй шар, хөх өнгийн бөмбөлөг байсан ба шар хөхийн харьцаа 3:2 байжээ. 6 бөмбөлөг авсны дараа энэ харьцаа 4:3 болсон бол анх бүгд хэдэн бөмбөлөг байсан бэ?
A. 20
B. 30
C. 40
D. 50
Бөмбөрцгийн ямар нэг радиусын төгсгөлийг дайрсан $\alpha$ хавтгайн
бөмбөрцгөөс огтолсон огтлолын талбай түүний тэнхлэг огтлолын талбайгаас 2 дахин
бага бол сонгосон радиус, $\alpha$ хавтгайтай үүсгэх өнцгийн хэмжээг ол.
A. $30^\circ$
B. $45^\circ$
C. $60^\circ$
D. $\arccos\frac13$
Бөмбөрцөг дээрх цэгийг дайруулан хийсэн хоёр огтлолын талбайн
нийлбэр нь бөмбөрцгийн тэнхлэг огтлолын талбайтай тэнцдэг бол огтлогч хоёр
хавтгайн хоорондох өнцгийн хэмжээг ол.
A. $30^\circ$
B. $45^\circ$
C. $60^\circ$
D. $90^\circ$
Конуст багтсан бөмбөрцөг конусын өндрийг оройгоос 1:4 харьцаагаар
хуваана. Конусын байгуулагч суурийн хавтгайтай үүсгэх өнцгийн хэмжээг ол.
A. $75^\circ$
B. $\arccos\dfrac35$
C. $45^\circ$
D. $60^\circ$
E. $\arccos\dfrac23$
Бөмбөрцөг багтаасан конусын байгуулагч суурийн хавтгайтай $\alpha=
\arccos\frac35$ хэмжээтэй өнцөг үүсгэдэг бол бөмбөрцөг конусын өндрийг оройгоос
нь ямар харьцаагаар хуваах вэ?
A. 1:4
B. 1:3
C. 2:3
D. 3:5
E. 3:4
Бөмбөрцгийн гадна байрлах $M$ цэгийг дайрсан хавтгайгаар бөмбөрцгийг
огтлоход үүсэх бүх огтлолын төвүүдийн геометр байрыг тодорхойл.
A. бөмбөрцөг
B. бөмбөрцгийн сегментийн хажуу гадаргуу
C. тойрог
D. конусын хажуу гадаргуу
Бөмбөрцгийн дотор (төвөөс ялгаатай) байрлах $M$ цэгийг дайрсан хавтгайгаар
бөмбөрцгийг огтлоход үүсэх огтлолын төвүүдийн геометр байрыг тодорхойл.
A. бөмбөрцөг
B. бөмбөрцгийн сегментийн гадаргуу
C. тойрог
D. конусын хажуу гадаргуу
$\alpha$ хавтгайгаас 1.5$a$ зайд байрлах $M$ цэгийг дайрч $\alpha$
хавтгайг шүргэсэн $a$ радиустай бөмбөрцгүүдийн төвийн геометр байрыг тодорхойл.
A. тойрог
B. бөмбөрцөг
C. 1 цэг
D. хавтгай
$\alpha$ хавтгайгаас $2a$ зайд байрлах $M$ цэгийг дайрч $\alpha$
хавтгайг шүргэсэн $1.5a$ радиустай бөмбөрцгүүдийн төвийн геометр байрыг ол.
A. 1 цэг
B. бөмбөрцөг
C. хавтгай
D. тойрог
Бөмбөрцгөөс радиустай нь тэнцүү зайд байгаа гэрэлтүүлэгч цэгээс бөмбөрцгийн
гадаргуугийн хэдэн хувьд гэрэл тусах вэ?
A. $50\%$
B. $30\%$
C. $25\%$
D. $20\%$
$26$ нэгж радиустай бөмбөрцгийн гадаргуу дээр 10 нэгж радиустай суурь
бүхий (суурь нь онгорхой) конус тавихад бөмбөрцгийн гадаргуугийн хэдэн кв.нэгж
талбай далдлагдах вэ?
A. $144\pi$ кв.н.
B. $104\pi$ кв.н.
C. $100\pi$ кв.н.
D. 16кв.н.
Зөв дөрвөн өнцөгт пирамидын өндөр 18 нэгж, түүнд багтсан бөмбөрцгийн радиус 5 нэгж бол пирамидын эзлэхүүнийг ол.
A. $1200$
B. $1350$
C. $2010$
D. $2100$
E. $2700$
Зөв гурвалжин пирамидын өндөр 18 нэгж, түүнд багтсан бөмбөрцгийн
радиус 5 нэгж бол пирамидын суурийн талыг ол.
A. 15
B. 32
C. $15\sqrt3$
D. $17\sqrt2$
Бөмбөрцөг багтаасан зөв зургаан өнцөгт призмийн өндөр 2 нэгж бол эзлэхүүн нь хэдэн куб нэгж вэ?
A. $2\sqrt{3};$
B. $3\sqrt{3};$
C. $4\sqrt{3};$
D. $5\sqrt{3}.$
$\sqrt{3}$ нэгж радиустай бөмбөрцөг багтаасан зөв зургаан өнцөгт призмийн эзлэхүүн хэдэн куб нэгж байх вэ?
A. $36$
B. $24$
C. $30$
D. $20$
E. $18$
Хоёр ижил бөмбөрцөг нэг нь нөгөөгийнхөө төвийг дайрч байралсан байв. Тэдгээрийн ерөнхий хэсгийн эзлэхүүн нэг бөмбөрцгийн эзлэхүүний хэдий хэсэг болох вэ?
A. $\dfrac{5}{16};$
B. $\dfrac{7}{16};$
C. $\dfrac{5}{12};$
D. $\dfrac{5}{14}.$
$R$ радиустай дугуйн $120^{\circ}$ төв өнцөгтэй сектор тэгш хэмийн тэнхлэгээ тойрон эргэхэд үүсэх биеийн эзлэхүүн аль вэ?
A. $\dfrac 25\pi R^3;$
B. $\dfrac 23\pi R^3;$
C. $\dfrac 13\pi R^3;$
D. $\dfrac 35\pi R^3.$
Бөмбөрцгийн секторт харилцан бие биеэ шүргэсэн 2дм, 6дм радиустай бөмбөрцгүүд багтжээ. Анхны бөмбөрцгийн радиус аль вэ?
A. 22дм
B. 24дм
C. 18дм
D. 20дм.
$R$ радиустай бөмбөрцгийн сегментэд багтсан бөмбөрцгийн гадаргуу нь сегментийн бүтэн гадаргуугаас 3 дахин бага бол сегментийн өндөр аль вэ?
A. $\dfrac 12R;$
B. $\dfrac 23R;$
C. $\dfrac
34R;$
D. $R.$
Бөмбөрцөгт багтсан зөв дөрвөн өнцөгт пирамидын суурь нь бөмбөрцгийн төвийг дайрсан байв. Пирамидын эзлэхүүн 18-тэй тэнцүү бол бөмбөрцгийн радиусыг ол.
A. $\sqrt3$
B. $3$
C. $4$
D. $2$
E. $\dfrac32$
$8$ радиустай бөмбөрцөгт багтсан хамгийн их эзлэхүүнтэй конусын суурь бөмбөрцгийн төвөөс ямар зайд орших вэ?
A. $2\dfrac13$ см
B. $2\dfrac23$ см
C. $8\dfrac37$ см
D. $\dfrac38$ см
E. $\dfrac37$ см
Кубийг багтаасан бөмбөрцгийн гадаргуугийн талбай $75\pi$ бол кубийн ирмэгийг ол.
A. $3$
B. $4$
C. $6$
D. $5$
E. $3\sqrt5$
$9$ радиустай бөмбөрцөгт багтсан зөв дөрвөн өнцөгт призмийн өндөр 12 бол бөмбөрцгийн эзлэхүүнийг призмийн эзлэхүүнд харьцуулсан харьцааг ол.
A. $\dfrac{27}{5}\pi$
B. $\dfrac{27}{20}\pi$
C. $\dfrac{19}{10}\pi$
D. $\dfrac{9}{10}\pi$
E. $\dfrac{3}{10}\pi$
Нэг бөмбөрцөг гадаргуугийн талбай $43$. Үүнээс $27$ дахин их эзлэхүүнтэй бөмбөрцөг гадаргуугийн талбайг ол.
A. $361$
B. $429$
C. $208$
D. $387$
E. $109$
$R=15$ радиустай бөмбөлөгт хамгийн их хажуу гадаргуугийн талбайтай шулуун дугуй конус багтаав. Энэ конусын өндрийг ол.
A. $30$
B. $5$
C. $10$
D. $15$
E. $20$
Бөмбөрцөг багтаасан цилиндрийн эзлэхүүн $255$ бол багтсан бөмбөрцгийн эзлэхүүнийг ол.
A. 222
B. 170
C. 248
D. 252
E. 192
Бөмбөрцөгт багтсан зөв дөрвөн өнцөгт пирамидын суурь нь бөмбөрцгийн төвийг дайрч байв. Пирамидын эзлэхүүн 18-тай тэнцүү бол бөмбөрцгийн радиусыг ол.
A. $\sqrt3$
B. $3$
C. $4$
D. $2$
E. $\dfrac32$
3 радиустай бөмбөрцөгт багтсан зөв дөрвөн өнцөгт призмийн өндөр 4 бол бөмбөрцгийн эзлэхүүнийг призмийн эзлэхүүнд харьцуулсан харьцааг ол.
A. $\dfrac45\pi$
B. $\dfrac9{10}\pi$
C. $\dfrac{9}{20}\pi$
D. $\dfrac{6\pi}{5}$
E. $\dfrac{3\pi}{5}$
Суурийн радиус нь 3, өндөр нь 4 байх конуст багтсан бөмбөрцгийн эзлэхүүнийг ол.
A. $\pi$
B. $4,5\pi$
C. $\dfrac{32\pi}{3}$
D. $\dfrac{\pi}{6}$
E. $\dfrac{2\pi}{3}$
2 см суурийн радиустай конуст багтсан бөмбөрцгийн радиус 1 см бол конусын эзлэхүүнийг ол.
A. $\dfrac{32}9\pi$ см.куб
B. $3\pi$ см.куб
C. $\dfrac{35}{9}\pi$ см.куб
D. $4\pi$ см.куб
E. $\dfrac{4}{3}\pi$ см.куб
Конуст бөмбөрцөг багтжээ. Байгуулагч нь бөмбөрцгийг шүргэсэн цэгээрээ оройгоос 8 нэгж, 12 нэгж урттай хэрчмүүдэд хуваагдсан байв.
- Конусын өндөр нь $H=\fbox{ab}$ байна.
- Бөмбөрцгийн радиус нь $R=\fbox{c}$ байна.
- Конус дотроос санамсаргүйгээр нэг цэг авахад тэр нь бөмбөрцөг дотроос авагдсан байх магадлал нь $P(A)=\dfrac{\fbox{d}}{\fbox{e}}$.
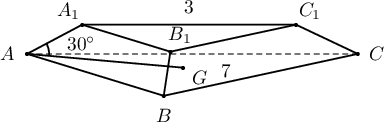
Гурвалжин пирамидын суурь нь $30^\circ$ хурц өнцөгтэй тэгш өнцөгт гурвалжин бөгөөд уг пирамидын хажуу ирмэгүүд нь тэнцүү 6 нэгж урттай ба суурийн хавтгайтай $45^\circ$ өнцөг үүсгэнэ.
- Пирамидын өндөр $\fbox{a}\sqrt{\fbox{b}}$ (2 оноо)
- Суурийн гурвалжны талбай $\fbox{c}\sqrt{\fbox{d}}$ (2 оноо)
- Пирамидын эзлэхүүн $\fbox{e}\sqrt{\fbox{f}}$ (1 оноо)
- Пирамидыг багтаасан бөмбөрцгийн радиус нь $\fbox{g}\sqrt{\fbox{h}}$ (2 оноо)
Суурь нь $\sqrt{2}$ талтай зөв гурвалжин , хажуу ирмэгүүд нь бүгд $1$ урттай байх гурвалжин пирамидын эзлэхүүн $\frac{\fbox{a}}{\fbox{b}}$ ба энэ пирамидыг багтаасан бөмбөрцгийн радиус $\frac{\sqrt{\fbox{c}}}{\fbox{d}}$ байна.
$ABCD$ тетраэдрийн ${AC=AB=AD=6,BC=BD=CD=6\sqrt{2}}$ байв.
- Тетраэдрийн бүтэн гадаргуугийн талбай $\fbox{ab}+\fbox{cd}\sqrt{3}$ байна.
- Тетраэдрийн эзлэхүүн $\fbox{ef}$ байна.
- Тетраэдрт багтсан бөмбөрцгийн радиус $\fbox{g}-\fbox{h}\sqrt3$ байна.
- $A$ цэгээс $(BCD)$ хавтгай хүртэлх зай $\fbox{i}\sqrt{\fbox{j}}$ байна.
$SABCD$ зөв дөрвөн өнцөгт пирамидын $ABCD$ суурийн тал 2-той,
хажуу ирмэг ба суурийн хавтгайн хоорондох өнцөг $\arccos
\dfrac1{\sqrt{5}}$-тай тэнцүү. $SA$, $SD$ ирмэгүүд дээр харгалзан
$E$, $F$ цэгүүдийг $AE=2\cdot ES$, $DF=8\cdot SF$ байхаар аваад, $E$ ба $F$ цэгүүдийг дайрсан $AB$-тэй параллель $\alpha$ хавтгайгаар пирамидыг огтлох огтлолыг байгуулав.
- Огтлолын талбай $S=\dfrac{\fbox{ab}\sqrt{\fbox{c}}}{\fbox{de}}$ байна.
- $A$ цэгт төвтэй $\alpha$ хавтгайг шүргэсэн бөмбөрцгийн радиус $R=\dfrac{\fbox{f}\cdot\sqrt{\fbox{g}}}{\fbox{h}}$ байна.
- $\alpha$ ба $(ABC)$ хавтгайн хоорондох өнцөг $\varphi=\arccos\dfrac{\fbox{k}}{\sqrt{\fbox{m}}}$.
Суурь нь $\sqrt{2}$ талтай зөв гурвалжин , хажуу ирмэгүүд нь бүгд $1$ урттай байх гурвалжин пирамидын эзлэхүүн $\frac{\fbox{a}}{\fbox{b}}$ ба энэ пирамидыг багтаасан бөмбөрцгийн радиус $\frac{\sqrt{\fbox{c}}}{\fbox{d}}$ байна.
Гурвалжин пирамидын суурь нь $45^\circ$ хурц өнцөгтэй тэгш өнцөгт гурвалжин бөгөөд уг пирамидын хажуу ирмэгүүд нь тэнцүү $4\sqrt3$ нэгж урттай ба суурийн хавтгайтай $60^\circ$ өнцөг үүсгэдэг бол:
- Пирамидын өндөр $\fbox{a}$
- Суурийн гурвалжны талбай $\fbox{bc}$
- Пирамидын эзлэхүүн $\fbox{de}$
- Пирамидыг багтаасан бөмбөрцгийн радиус нь $\fbox{f}$ байна.
$ABCDA_1B_1C_1D_1$ ($AA_1\parallel BB_1\parallel CC_1\parallel DD_1$) кубийн $A_1D_1$
ирмэгийн дундаж ба $B$, $C$, $C_1$ оройнуудыг дайрсан бөмбөрцөгийн
радиус $\sqrt{41}$-тэй тэнцүү бол кубийн гадаргуун талбай
$\fbox{abc}$ байна.
$R=5$ радиустай бөмбөлөгт хамгийн их хажуу гадаргуугийн талбайтай
шулуун дугуй конус багтаав. Энэ конусын өндөр нь
$H=\dfrac{\fbox{ab}}{\fbox{c}}$ байна.
$R=2$ радиустай бөмбөлөгт хамгийн их эзлэхүүнтэй шулуун дугуй
конус багтаав. Энэ конусын эзлэхүүн нь
$V=\dfrac{\fbox{abc}}{\fbox{de}}\cdot \pi$ байна.
Эзлэхүүн нь 8-тай тэнцүү параллелепипед $R=\sqrt{3}$ радиустай
бөмбөлөгт багтжээ. Параллелепипедийн бүтэн гадаргуугийн талбай
$\fbox{ab}$ байна.
Эзлэхүүн нь $\dfrac{8\sqrt{3}}{9}$-тай тэнцүү параллелепипед $R=1$ радиустай бөмбөлөгт багтжээ. Параллелепипедийн бүтэн гадаргуугийн талбай $\fbox{a}$ байна.
Харгалзан 1; 2; 5 нэгж радиустай гурван бөмбөрцөг хос хосоороо шүргэлцэх бөгөөд тус бүрдээ $\alpha, \beta$ хавтгайг шүргэж байхаар байрлажээ. I бөмбөрцгийн $\alpha, \beta$ хавтгайтай шүргэлцэх цэгүүдийн хоорондох зай $\dfrac{1}{\fbox{a}}\sqrt{\dfrac{\fbox{bc}}{\fbox{d}}}$ байна.
Харгалзан 1; 3; 4 нэгж радиустай гурван бөмбөрцөг хос хосоороо
шүргэж бөгөөд тус бүрдээ $\alpha, \beta$ хавтгайг шүргэлцэж
байхаар байрлажээ. I бөмбөрцгийн $\alpha, \beta$ хавтгайтай
шүргэлцэх цэгүүдийн хоорондох зай
$\dfrac{1}{\fbox{a}}\sqrt{\dfrac{\fbox{bc}}{\fbox{d}}}$ байна.
Зөв дөрвөн өнцөгт пирамидад оройнууд нь давхцдаг байхаар шулуун
дугуй конус багтжээ. Конусын суурийн радиус 6, конуст багтсан
бөмбөрцгийн радиус 2-той тэнцүү бол пирамид ба конусын эзлэхүүний
ялгавар $\fbox{ab}\cdot(\fbox{c}-\pi)$ байна.
Зөв дөрвөн өнцөгт пирамидад оройнууд нь давхцдаг байхаар шулуун
дугуй конус багтжээ. Тэдгээрийн өндөр (ерөнхий) $\dfrac 94$-тэй,
конуст багтсан бөмбөрцгийн радиус 1-тэй тэнцүү бол пирамид ба
конусын эзлэхүүнхий ялгавар $\fbox{ab}\cdot
\left(\fbox{c}-\dfrac{\pi}{4}\right)$ байна.
Зөв гурвалжин пирамид дотор хоёр бөмбөрцөг байрлажээ. Нэг нь $r=5$
радиустай бөгөөд пирамидын суурь ба хажуу талсуудыг шүргэдэг
байхаар, нөгөө нь I бөмбөрцгийг гадаад байдлаар болон пирамидын
хажуу талсуудыг шүргэдэг байхаар байрлажээ. Пирамид нь хамгийн
бага эзлэхүүнтэй гэж мэдэгдэж байгаа бол бөмбөрцгүүдийн эзлэхүүний
нийлбэр $\dfrac{\fbox{abc}}{\fbox{d}}\cdot \pi$ байна.
Зөв гурвалжин пирамид дотор хоёр бөмбөрцөг байрлажээ. Нэг нь $r=5$
радиустай бөгөөд пирамидын суурь ба хажуу талсуудыг шүргэдэг
байхаар, нөгөө нь I бөмбөрцгийг гадаад байдлаар болон пирамидын
хажуу талсуудыг шүргэдэг байхаар байрлажээ. Пирамид нь хамгийн
бага эзлэхүүнтэй гэж мэдэгдэж байгаа бол хоёр дахь бөмбөрцгийн
радиус $R=\dfrac{\fbox{a}}{\fbox{bc}}\cdot (\sqrt{\fbox{cd}}-1)$
байна.
$r$ радиустай гурван бөмбөрцөг хос хосоороо гадаад байдлаар
шүргэлцэх бөгөөд $R (R>r)$ радиустай бөмбөрцгийг гадаад байдлаар
шүргэнэ. Эдгээр дөрвөн бөмбөрцгийг шүргэсэн бөмбөрцгийн радиус
$$\dfrac{R\cdot
(R+r-\sqrt{R^2+\fbox{a}Rr-\dfrac{r^2}{\fbox{b}}})}{r+\sqrt{R^2+\fbox{c}\cdot
Rr-\dfrac{r^2}{\fbox{d}}-R}}$$-тай тэнцүү.
$r$ радиустай гурван бөмбөлөг хос хосоороо гадаад байдлаар
шүргэлцэх бөгөөд $R$ радиустай бөмбөлгийг дотоод байдлаар шүргэнэ.
$r$ радиустай гурван бөмбөлгийг гадаад байдлаар, харин $R$
радиустай бөмбөлгийг дотоод байдлаар шүргэсэн бөмбөлгийн радиус
$$\dfrac{R\left(R-r-\sqrt{R^2-\fbox{a}Rr-\dfrac{r^2}{\fbox{b}}}\right)}{r+R-\sqrt{R^2-\fbox{c}\cdot
Rr-\dfrac{r^2}{\fbox{d}}}}$$-тай тэнцүү.
$A(1;-6;0)$ цэгтэй, $B(3;2;-2)$ цэгийг дайрсан шулуунуудын
хувьд тэгшхэмтэй байрлах цэгүүдийн геометр байр нь
$(x-\fbox{a})^2+(y-\fbox{b})^2+(z+\fbox{c})^2=\fbox{de}$ тэгшитгэлтэй
бөмбөрцөг байна.
$A(-3;2;2)$ цэгтэй, $B(1;0;-2)$ цэгийг дайрсан хавтгайнуудын
хувьд тэгшхэмтэй байрлах цэгүүдийн геометр байр нь
$(x-\fbox{a})^2+(y-\fbox{b})^2+(z+\fbox{c})^2=\fbox{de}$ тэгшитгэлтэй
бөмбөрцөг гадаргуу үүсгэнэ.
$A(-1;0;2)$ цэгээс $B(3;-2;-2)$ цэгийг дайрсан шулуунуудад
буулгасан перпендикуляруудын суурийн геометр байр нь
$(x-\fbox{a})^2+(y+\fbox{b})^2+(z-\fbox{c})^2=\fbox{d}$ тэгшитгэлтэй
бөмбөрцөг гадаргуу байна.
$A(1;2;-3)$ цэгээс $B(5;4;1)$ цэгийг дайрсан хавтгайнуудад
буулгасан перпендикуляруудын суурийн геометр байр нь
$(x-\fbox{a})^2+(y-\fbox{b})^2+(z+\fbox{c})^2=\fbox{d}$ тэгшитгэлтэй
бөмбөрцөг гадаргуу үүсгэнэ.
Конуст бөмбөрцөг багтжээ. Байгуулагч нь бөмбөрцгийг шүргэсэн цэгээрээ оройгоос 8 нэгж, 12 нэгж урттай хэрчмүүдэд хуваагдсан байв.
- Конусын өндөр нь $H=\fbox{ab}$ байна. $\text{a}$ ба $\text{b}$ нь хэд вэ?
- Бөмбөрцгийн радиус нь $R=\fbox{c}$ болно. $\text{c}$ нь хэд вэ?
- Конусын дотроос санамсаргүйгээр нэг цэг авахад тэр нь бөмбөрцөг дотроос авагдсан байх магадлал нь $P(A)=\dfrac{\fbox{d}}{\fbox{e}}$ нь хэд вэ?
Гурвалжин пирамидын суурь нь $30^\circ$ хурц өнцөгтэй тэгш өнцөгт гурвалжин бөгөөд уг пирамидын хажуу ирмэгүүд тэнцүү 4 нэгж урттай ба суурийн хавтгайтай $60^\circ$ өнцөг үүсгэнэ.
- Пирамидын өндөр: $\fbox{a}\sqrt{\fbox{b}}$
- Суурийн гурвалжны талбай: $\fbox{c}\sqrt{\fbox{d}}$
- Пирамидын эзлэхүүн: $\fbox{e}$
- Пирамидыг багтаасан бөмбөрцгийн радиус нь $\dfrac{\fbox{f}}{\sqrt{\fbox{g}}}$ байна.
$ABCDEFS$ зөв зургаан өнцөгт пирамид дотор 4 см радиустай бөмбөрцөг багтжээ. Апофем нь суурийн хавтгайтай $60^\circ$ өнцөг үүсгэдэг бол пирамидын эзлэхүүнийг ол.
Бодолт:
$SOM$-аас $SO=8$ см. Иймд $SK=12$ см болох ба
Бодолт:

$SOM$-аас $SO=8$ см. Иймд $SK=12$ см болох ба
- $SGK$-аас $GK=\fbox{a}\sqrt{\fbox{b}}$ см тул (2 оноо)
- Суурийн талбай $S_c=\fbox{cd}\sqrt{\fbox{b}}$ см.кв болно. (3 оноо)
- Эндээс пирамидын эзлэхүүн $V=\fbox{efg}\sqrt{\fbox{b}}$ см.куб (3 оноо)
Улаан уутан доторх 4 бөмбөлөг 1, 2, 3, 4 гэсэн дугаартай, цагаан уутан доторх 5 бөмбөлөг 1, 2, 3, 4, 5 гэсэн дугаартай, шар уутан доторх 6 бөмбөлөг 1, 2, 3, 4, 5, 6 гэсэн дугаартай байв. Уут тус бүрээс нэг, нэг бөмбөлөг авахад бүгдээрээ тэгш дугаартай байх боломжийн тоо $\fbox{ab}$, бүгдээрээ сондгой дугаартай байх боломжийн тоо $\fbox{cd}$, дугааруудын нийлбэр 5-тай тэнцүү байх боломжийн тоо $\fbox{e}$, дугааруудын нийлбэр 10-тай тэнцүү байх боломжийн тоо $\fbox{fg}$, дугааруудын нийлбэр 15-тай тэнцүү байх боломжийн тоо $\fbox{h}$ байна.
Конуст бөмбөрцөг багтжээ. Байгуулагч нь бөмбөрцгийг шүргэсэн цэгээрээ оройгоос 8 нэгж, 12 нэгж урттай хэрчмүүдэд хуваагдсан байв.
- Конусын өндөр нь $H=\fbox{ab}$ байна.
- Бөмбөрцгийн радиус нь $R=\fbox{c}$ байна.
- Конус дотроос санамсаргүйгээр нэг цэг авахад тэр нь бөмбөрцөг дотроос авагдсан байх магадлал нь $P(A)=\dfrac{\fbox{d}}{\fbox{e}}$.
Бөмбөлөгт шүргэгч хавтгай
Геометр байр
Квадратаас ялгаатай ромбын оройнуудаас ижил зайд алсагдсан огторгуйн цэгүүдийн геометр байр аль вэ?
A. Шулуун
B. 1 цэг
C. $\emptyset$
D. $A, B, C$-д зөв хариу байхгүй.
Квадратаас ялгаатай тэгш өнцөгтийн талуудаас ижил зайд алслагдсан огторгуйн цэгүүдийн геометр байр аль вэ?
A. $\emptyset;$
B. 1 цэг
C. Шулуун
D. $A, B, C$-д зөв хариугүй.
$AB=5$ нэгж байх $A,B$ цэгүүд өгчээ. Нэгэн зэрэг $A$-аас 4 нэгж,
$B$-ээс 3 нэгж зайд байрлах огторгуйн цэгүүдийн геометр байрыг тодорхойл.
A. тийм цэг байхгүй
B. тойрог
C. 1 цэг
D. дугуй
$AB=10$ нэгж байх $A,B$ цэгүүд өгчээ. Нэгэн зэрэг $A$-аас 4 нэгж,
$B$-ээс 6 нэгж зайд орших огторгуйн цэгүүдийн геометр байрыг тодорхойл.
A. тийм цэг байхгүй
B. тойрог
C. 1 цэг
D. дугуй
Зөв олон талст
Конус
Конусын радиус 4дм, өнцөг нь 6дм бөгөөд түүнд хамгийн их эзлэхүүнтэй цилиндрийг багтаажээ. Цилинприйн өндрийг ол
Конуст багтсан бөмбөрцгийн гадаргуугийн талбай конусын суурийн талбайтай тэнцүү. Конусын тэнхлэг огтлолын оройн өнцгийн косинусыг ол.
Конусын байгуулагч $\ell$, суурийн өнцөг $60^\circ$ бол түүний эзлэхүүнийг ол.
Конусын тэнхлэг огтлол нь адил талт гурвалжин бол конусын эзлэхүүн ба түүнд багтсан бөмбөрцгийн эзлэхүүний харьцааг ол.
Конусын эзлэхүүн 384. Конусын суурийн тойргийн урт 15 бол түүний тэнхлэг огтлолын талбайг ол.
Конусын өндөртөй $30^\circ$-ийн өнцөг үүсгэн конусын оройг хэрчжээ. Конусын өндөр $3\sqrt3$ см, суурийн радиус $5$ см байсан бол огтлолын талбайг ол.
Зөв гурвалжин пирамидын өндөр 4, түүний суурийг багтаасан тойргийн урт $\sqrt3\pi$. Уг пирамидад багтсан ба түүнийг багтаасан конусуудын эзлэхүүний зөрөөг ол.
Конусын өндөр түүний суурийн диаметртэй тэнцүү. Конусын суурийн талбай ба хажуу гадаргуугийн талбайн харьцааны квадратыг ол.
1 талтай кубэд конус багтсан бөгөөд түүний орой нь кубийн нэг оройтой давхцаж байв. Кубийн гурван тал конусын хажуу гадаргатай шүргэлцэнэ. Харин кубэд багтсан бөмбөрцөг конусын суурьтай шүргэлцэнэ. Конусын эзлэхүүнийг ол.
Конусын харилцан перпендикуляр хоёр байгуулагч суурийн тойргоо $120^\circ$, $240^\circ$ нумуудад хуваадаг. Конусын өндөр $H$ бол түүний эзлэхүүнийг ол.
Бөмбөрцгийн нэг цэгээс татсан 3 хөвчийн урт $a$. Хөвчүүдийн хоорондын өнцөг $60^\circ$ бол бөмбөрцгийн радиусыг ол.
Ерөнхий суурьтай хоёр конусаас тогтсон биетэд бөмбөрцөг багтжээ. Хэрэв конусын суурийн радиус 1, өндөр нь 1 ба 2 бол бөмбөрцгийн эзлэхүүнийг ол.
Конусын хажуу гадаргуугийн дэлгээс $\dfrac{6\pi}5$ төв өнцөгтэй 5 радиустай дугуйн сектор болно. Конусын эзлэхүүнийг ол.
Конусын байгуулагчийн урт $l$, суурьт налсан өнцөг $\alpha$ бол уг конуст багтсан бөмбөрцгийн эзлэхүүнийг ол.
Конусын эзлэхүүн $V$. Түүний өндрийг 3 тэнцүү хэсэгт хувааж, хуваалтын цэгүүдийг дайруулан суурьтай нь параллель хавтгайнууд татав. Дунд хэсгийн эзлэхүүнийг ол.
Конусын тэнхлэг огтлол нь адил талт гурвалжин бөгөөд конуст багтсан бөмбөрцөгийн радиус $r=2$ см бол конусын эзлэхүүнийг ол.
2 см суурийн радиустай конуст багтсан бөмбөрцгийн радиус 1 см бол конусын эзлэхүүнийг ол.
$R$ радиустай гурван бөмбөрцөг бие биетэйгээ шүргэлцэж бөгөөд тус бүрдээ конусын хажуу гадаргууг шүргэнэ. Бөмбөрцгийн төвүүд конусын гадна орших бөгөөд конусын өндөр шарын төвүүд орших $\alpha$ хавтгайтай перпендикуляр. Конусын өндөр ба байгуулагчуудын хоорондох өнцөг $\varphi$ бол конусын оройгоос $\alpha$ хавтгай хүртлэх зайг ол.
$ABCD$ адил хажуут трапецын $BC$ суурь нь $MBCN$ ромбын тал болдог. $BC=a$, $AD=b$ ($a< b< 2a$). Трапецийн хурц өнцөг $30^\circ$, ромбын хурц өнцөг $60^\circ$ бол трапец ба ромбыг $BC$ шулуунийг тойруулан хамтад нь эргүүлэхэд үүсэх биетийн гадаргуугийн талбайг ол.
Зөв гурвалжин пирамидын хажуу ирмэгт үүсэх хоёр талст өнцөг $2\alpha$-тай тэнцүү. Пирамидын өндөр $H$. Пирамидыг багтаасан конусын эзлэхүүнийг ол.
$SABCD$ зөв дөрвөн өнцөгт пирамид ба суурийн төв цэг нь $SO$ шулуун дээр ($SO$ --- пирамидын өндөр) байрлах конус өгөгдөв. $E$ цэг $SD$ ирмэгийн дундаж ба $F$ цэг $AF=\dfrac32FD$ байхаар $AD$ ирмэг дээр байрлана. Конусын нэг тэхлэг огтлолын гурвалжины хоёр орой нь $CD$ шулуун дээр, гурав дахь орой нь $EF$ шулуун дээр байв. Хэрэв $AB=4$, $SO=3$ бол конусын эзлэхүүнийг ол.
Нэгж радиустай бөмбөрцөгт багтсан хамгийн их хажуу гадаргуутай конусын суурийн
радиусыг ол.
Интеграл ашиглан дараах биеийн эзлэхүүнийг ол.
- $r$ радиустай, $h$ өндөртэй конусын эзлэхүүн;
- $r$ радиустай бөмбөрцгийн эзлэхүүн.
Талуудын урт нь $\sqrt{17}+1$, $6$, $\sqrt{17}-1$ байх гурвалжин байв. Эдгээрээс аль богино хоёр талыг тойруулан эргүүлэхэд үүсэх 2 биетийн эзлэхүүнүүдийн харьцаа аль нь байж болох вэ?
A. $\dfrac{9-\sqrt{17}}{8}$
B. $\dfrac{9-\sqrt{17}}{16}$
C. $\dfrac{\sqrt{17}-9}{8}$
D. $\dfrac{18-2\sqrt{17}}{6}$
E. $\sqrt{17}+1$
$6$ радиустай бөмбөрцөгт багтсан хамгийн их эзлэхүүнтэй конусын суурь бөмбөрцгийн төвөөс ямар зайд орших вэ?
A. 6 см
B. 5 см
C. 4 см
D. 3 см
E. 2 см
3 см радиустай бөмбөрцөгийн эзлэхүүн $A$ см.куб, гадаргын талбай $B$ см.кв, 3 см суурийн радиустай 6 см өндөртэй конусын эзлэхүүн $C$ см.куб бол зөв өгүүлбэрийг сонго.
A. $B< A< C$
B. $C< B< A$
C. $C< A=B$
D. $A=B< C$
E. $C=A< B$
Суурийн радиус нь 3, өндөр нь 4 байх конуст багтсан бөмбөрцгийн эзлэхүүнийг ол.
A. $\pi$
B. $4.5\pi$
C. $\dfrac{32\pi}{3}$
D. $\dfrac{\pi}{6}$
E. $\dfrac{2\pi}{3}$
Өндөр нь 4, суурийн радиус нь 3 байх конус өгөгдөв. Уг конусын эзлэхүүнийг түүнд багтсан бөмбөрцгийн эзлэхүүнд харьцуулсан харьцааг ол.
A. $7:4$
B. $2:1$
C. $3:1$
D. $8:3$
E. $11:4$
$y=\frac12x+1$ функцийн графикийн $0\le x\le 2$ байх хэсгийг $OX$ тэнхлэгийг тойруулан эргүүлэхэд үүсэх биетийн эзлэхүүнийг ол.
A. $\dfrac{14}{3}\pi$
B. $\dfrac{12}{3}\pi$
C. $5\pi$
D. $4\pi$
E. $\dfrac{11}{3}\pi$
$5$ радиустай бөмбөрцөгт $8$ өндөртэй конус багтжээ. Конусын эзлэхүүнийг бөмбөрцгийн эзлэхүүнд харьцуулсан харьцааг ол.
A. $\dfrac{16}{125}$
B. $\dfrac{32}{125}$
C. $\dfrac{96}{125}$
D. $\dfrac{32}{125}$
E. $\dfrac{8}{25}$
Конусын байгуулагч нь өндөртэйгээ $60^\circ$ өнцөг үүсгэх бөгөөд байгуулагч өндөр хоёрын уртуудын нийлбэр нь 15 бол түүний эзлэхүүнийг ол.
A. $\dfrac{125\pi}{2}$
B. $\dfrac{125\pi}{4}$
C. $\dfrac{25\pi}{2}$
D. $\dfrac{25\pi}{4}$
E. $125\pi$
Конусын суурийн радиус 5, байгуулагч нь 10 бол хажуу гадагуугийн талбай хэдтэй тэнцүү вэ?
A. $25\pi$
B. $30\pi$
C. $50\pi$
D. $45\pi$
E. $15\pi$
Конусын суурийн радиус $4$, байгуулагч нь $5$ бол хажуу гадаргуугийн талбайг ол.
A. $12 \pi$
B. $20 \pi$
C. $15 \pi$
D. $40 \pi$
E. $30 \pi$
Хавтгайн гаднах $M$ цэгээс хавтгайд татсан $MA=5,$ $MB=8$
налуунуудын хавтгайтай үүсгэх өнцгүүд 2:1 харьцаатай бол $M$ цэгээс энэ
хавтгай хүртэлх зайг ол.
A. 4
B. 4.5
C. 4.8
D. 5
Хавтгайгаас 9.6 нэгж зайд орших $M$ цэгээс хавтгайд $AM< BM=16$
нэгж урттай хоёр налуу татав. Тэдгээрийн хавтгайтай үүсгэх өнцгүүд 2:1
харьцаатай бол $AM$ хэрчмийн уртыг ол.
A. 8
B. 9
C. 10
D. 12
Конуст багтсан бөмбөрцөг конусын өндрийг оройгоос 1:4 харьцаагаар
хуваана. Конусын байгуулагч суурийн хавтгайтай үүсгэх өнцгийн хэмжээг ол.
A. $75^\circ$
B. $\arccos\dfrac35$
C. $45^\circ$
D. $60^\circ$
E. $\arccos\dfrac23$
Бөмбөрцөг багтаасан конусын байгуулагч суурийн хавтгайтай $\alpha=
\arccos\frac35$ хэмжээтэй өнцөг үүсгэдэг бол бөмбөрцөг конусын өндрийг оройгоос
нь ямар харьцаагаар хуваах вэ?
A. 1:4
B. 1:3
C. 2:3
D. 3:5
E. 3:4
$26$ нэгж радиустай бөмбөрцгийн гадаргуу дээр 10 нэгж радиустай суурь
бүхий (суурь нь онгорхой) конус тавихад бөмбөрцгийн гадаргуугийн хэдэн кв.нэгж
талбай далдлагдах вэ?
A. $144\pi$ кв.н.
B. $104\pi$ кв.н.
C. $100\pi$ кв.н.
D. 16кв.н.
Суурийн радиус нь $R$ байх конусын гадаргуу дээр харилцан
перпендикуляр гурван байгуулагч татаж болдог байв. Конусын бүтэн гадаргуугийн
талбайг ол.
A. $(3+\sqrt2)\pi R^2$
B. $\frac{13}2\pi R^2$
C. $\Bigl(1+\sqrt{\frac32}\Bigr)\pi R^2$
D. $\Bigl(1+\sqrt3\Bigr)\pi R^2$
$H$ өндөртэй конусын гадаргуу дээр харилцан перпендикуляр гурван
байгуулагч татаж болдог байв. Конусын бүтэн гадаргуугийн талбайг ол.
A. $(3+\sqrt2)\pi H^2$
B. $(2+\sqrt3)\pi H^2$
C. $\Bigl(1+\sqrt{\frac32}\Bigr)\pi H^2$
D. $(2+\sqrt6)\pi H^2$
Конус, цилиндр хоёр тэнцүү суурь, өндөр, хажуу гадаргуугийн талбайтай бол конусын байгуулагчуудын хооронд үүсэх хамгийн их өнцөг аль вэ?
A. $30^{\circ};$
B. $60^{\circ};$
C. $120^{\circ};$
D. $45^{\circ}.$
Адил талт цилиндр, адил талт конус хоёулаа тэнцүү хажуу гадаргуугийн талбайтай бол бүтэн гадаргуугийн талбайнууд нь ямар харьцаатай байх вэ?
A. $1:2;$
B. $1:1;$
C. $2:3;$
D. $4:5.$
30 см байгуулагчтай конусын хажуу гадаргуугийн дэлгээс нь $120^{\circ}$ төв өнцөгтэй сектор үүсгэнэ. Конусын суурийн диаметрийг ол.
A. 18 см
B. 20 см
C. 24 см
D. 28 см
E. 30 см
8см өндөр, 6см радиустай конусын хажуу гадаргуугийн дэлгээс болж байгаа секторын төв өнцөг аль вэ?
A. $180^{\circ}$
B. $200^{\circ}$
C. $216^{\circ}$
D. $220^{\circ}$
E. $222^{\circ}$
Цилиндр, конус хоёр ерөнхий суурьтай ба суурийн хавтгайн нэг талд
байрлана. Хэрэв тэдгээр нь ижил эзлэхүүнтэй бол цилиндр дотор конусын эзлэхүүний
хэдий хэсэг харьяалагдах вэ?
A. $\dfrac13$
B. $\dfrac12$
C. $\dfrac{17}{20}$
D. $\dfrac{19}{27}$
E. $\dfrac{8}{27}$
Конусын өндрийн дунджийг дайрсан хавтгайгаар хуваагдсан конусын хэсгүүдийн эзлэхүүний ялгавар $V$ бол анхны конусын эзлэхүүнийг ол.
A. $3V$
B. $2V$
C. $\frac43V$
D. $\frac32V$
$R$ радиустай дугуйн $90^\circ$ төв өнцөгт харгалзах секторыг
хуйлж хийсэн хажуу гадаргуутай конусын эзлэхүүнийг ол.
A. $\frac{\sqrt{15}\pi}{192}R^3$
B. $\frac{\sqrt5\pi}{64}R^3$
C. $\frac{\sqrt{17}\pi}{201}R^3$
D. $\frac{\sqrt6\pi}{172}R^3$
$R$ радиустай дугуйн $120^\circ$ төв өнцөгт харгалзах секторыг хуйлж
хийсэн хажуу гадаргуутай конусын эзлэхүүнийг ол.
A. $\frac{\sqrt2\pi}{64}R^3$
B. $\frac{\sqrt8\pi}{81}R^3$
C. $\frac{\sqrt6\pi}{128}R^3$
D. $\frac{\sqrt3\pi}{92}R^3$
Зөв $n$ өнцөгт пирамидад багтсан ба түүнийг багтаасан конусуудын
эзлэхүүнүүдийн харьцаа $1:4$ бол $n$-г ол.
A. $n=3$
B. $n=4$
C. $n=5$
D. $n=6$
E. $n=8$
Зөв $n$ өнцөгт пирамидад багтсан ба түүнийг багтаасан конусуудын эзлэхүүний харьцаа $1:2$ бол $n$-г ол.
A. $n=3$
B. $n=4$
C. $n=5$
D. $n=6$
E. $n=8$
$R$ радиустай дугуйн $120^{\circ}$ төв өнцөгтэй сектор тэгш хэмийн тэнхлэгээ тойрон эргэхэд үүсэх биеийн эзлэхүүн аль вэ?
A. $\dfrac 25\pi R^3;$
B. $\dfrac 23\pi R^3;$
C. $\dfrac 13\pi R^3;$
D. $\dfrac 35\pi R^3.$
Суурийн радиус нь 9, өндөр нь 7 нэгж байх конусын оройг дайрсан
огтлолуудын талбайн хамгийн их утгыг ол.
A. 63
B. 65
C. $\frac{65\sqrt3}{2}$
D. $\frac{63}{\sqrt2}$
Суурийн радиус нь 8 нэгж байх конусын оройг дайрсан огтлолуудын
талбайн хамгийн их утга 50кв.н. бол конусын өндрийг ол (конусын өндөр суурийн
радиусаас богино).
A. 4
B. 5
C. 6
D. 7
E. 8
Конусын оройг дайрсан огтлолуудын талбайн хамгийн их утга нь
тэнхлэг огтлолын талбайгаас 2 дахин их бол конусын байгуулагч суурийн
хавтгайтай үүсгэх өнцөг ол.
A. $45^\circ$
B. $30^\circ$
C. $\frac{45^\circ }2$
D. $15^\circ$
Конусын өндөр, түүний оройг дайрсан огтлолуудын периметрийн хамгийн
их утгаас 4 дахин бага бол конусын байгуулагч суурийн хавтгайтай ямар өнцөг
үүсгэх вэ?
A. $\arccos\frac23$
B. $\arccos\frac35$
C. $30^\circ$
D. $45^\circ$
Талуудын урт нь $\sqrt{7}+1$, $4$, $\sqrt{7}-1$ байх гурвалжин байв. Эдгээрээс аль богино 2 талыг нь тойруулан эргүүлэхэд үүсэх 2 биетийн эзлэхүүнүүдийн харьцаа аль байж болох вэ?
A. $\dfrac{3}{4-\sqrt7}$
B. $\dfrac{4-\sqrt7}{3}$
C. $\dfrac{\sqrt7-2}{2}$
D. $\dfrac{18-\sqrt7}{6}$
E. $\sqrt{17}+1$
$8$ радиустай бөмбөрцөгт багтсан хамгийн их эзлэхүүнтэй конусын суурь бөмбөрцгийн төвөөс ямар зайд орших вэ?
A. $2\dfrac13$ см
B. $2\dfrac23$ см
C. $8\dfrac37$ см
D. $\dfrac38$ см
E. $\dfrac37$ см
6 см радиустай дугуйн хагасаар конус хэлбэрийн ёроолгүй биет хийв. Биетийн эзлэхүүнийг ол.
A. $3\sqrt3\pi$
B. $9\sqrt2\pi$
C. $6\pi$
D. $9\sqrt3\pi$
E. $\frac{9\sqrt3}2\pi$
9 см радиустай дугуйн $120^\circ$ сектороор конус хэлбэрийн ёроолгүй биет хийв. Биетийн эзлэхүүнийг ол.
A. $9\sqrt2\pi$
B. $18\sqrt2\pi$
C. $12\pi$
D. $9\sqrt3\pi$
E. $\frac{9\sqrt2}2\pi$
$R=15$ радиустай бөмбөлөгт хамгийн их хажуу гадаргуугийн талбайтай шулуун дугуй конус багтаав. Энэ конусын өндрийг ол.
A. $30$
B. $5$
C. $10$
D. $15$
E. $20$
Конусын байгуулагч нь 13см ба өндөр нь 12см бол түүний хажуу гадаргуугийн талбайг олоорой.
A. $60\pi$
B. $65\pi$
C. $165\pi$
D. $32\pi$
E. $56\pi$
Конусын байгуулагч нь 25см ба өндөр нь 24см бол түүний хажуу гадаргуугийн талбайг олоорой.
A. $160\pi$
B. $165\pi$
C. $135\pi$
D. $180\pi$
E. $175\pi$
Конусын байгуулагч нь 17 см ба өндөр нь 8 см бол түүний хажуу гадаргуугийн талбайг олоорой.
A. $226\pi$
B. $235\pi$
C. $256\pi$
D. $255\pi$
E. $275\pi$
Конусын байгуулагч нь 15 см ба өндөр нь 9 см бол түүний хажуу гадаргуугийн талбайг олоорой.
A. $170\pi$
B. $210\pi$
C. $160\pi$
D. $180\pi$
E. $150\pi$
Конусын байгуулагч нь 17 см ба өндөр нь 8 см бол түүний хажуу гадаргуугийн талбайг олоорой.
A. $226\pi$
B. $235\pi$
C. $256\pi$
D. $255\pi$
E. $275\pi$
Огтлогдсон конуст бөмбөрцөг багтах ба сууриуд нь 4 см, 8 см радиустай байв. Багтсан бөмбөрцгийн радиусыг ол.
A. $4\sqrt{3}$
B. $6$
C. $4\sqrt{2}$
D. $2\sqrt{2}$
E. $2\sqrt{3}$
Огтлогдсон конуст бөмбөрцөг багтах ба сууриуд нь 6 см, 8 см радиустай байв. Багтсан бөмбөрцгийн радиусыг ол.
A. $2\sqrt{3}$
B. $4$
C. $2\sqrt{2}$
D. $\sqrt{2}$
E. $4\sqrt{3}$
Суурийн радиус нь 3, өндөр нь 4 байх конуст багтсан бөмбөрцгийн эзлэхүүнийг ол.
A. $\pi$
B. $4,5\pi$
C. $\dfrac{32\pi}{3}$
D. $\dfrac{\pi}{6}$
E. $\dfrac{2\pi}{3}$
4 см өндөртэй, $\sqrt{2}$ суурийн радиустай конуст багтсан бөмбөрцгийн радиусыг ол.
A. $\dfrac{\sqrt{2}}{2}$
B. $1$
C. $\sqrt{2}$
D. $\sqrt{3}$
E. $2$
Конусын байгуулагч нь $ 8$ нэгж , суурийн радиус $ 6$ нэгж байв. Энэ конусын хажуу гадаргуугийн дэлгээс болох секторын өнцгийг ол.
A. $ 270^0$
B. $ 90^0 $
C. $ 480^0$
D. $ 240^0
E. $ \ arccos (-\frac{1}{8})$
2 см суурийн радиустай конуст багтсан бөмбөрцгийн радиус 1 см бол конусын эзлэхүүнийг ол.
A. $\dfrac{32}9\pi$ см.куб
B. $3\pi$ см.куб
C. $\dfrac{35}{9}\pi$ см.куб
D. $4\pi$ см.куб
E. $\dfrac{4}{3}\pi$ см.куб
Огтлогдсон конусын суурийн радиусууд 3м ба 9 м өндөр нь 8 м бол хажуу гадаргуугийн талбайг олоорой.
A. $120\pi$ м.кв
B. $216\pi$ м.кв
C. $96\pi$ м.кв
D. $100\pi$ м.кв
E. $48\pi$ м.кв
Огтлогдсон конусын суурийн радиусууд 2 м ба 7 м өндөр нь 12 м бол хажуу гадаргуугийн талбайг олоорой.
A. $108\pi$ м.кв
B. $91\pi$ м.кв
C. $10\pi$ м.кв
D. $117\pi$ м.кв
E. $168\pi$ м.кв
Огтлогдсон конусын суурийн радиусууд 2м ба 7 м өндөр нь 12 м бол хажуу гадаргуугийн талбайг олоорой.
A. $ 108\pi$ м.кв
B. $ 91\pi$ м.кв
C. $ 107\pi$ м.кв
D. $ 117\pi$ м.кв
E. $ 168\pi$ м.кв
Конуст бөмбөрцөг багтжээ. Байгуулагч нь бөмбөрцгийг шүргэсэн цэгээрээ оройгоос 8 нэгж, 12 нэгж урттай хэрчмүүдэд хуваагдсан байв.
- Конусын өндөр нь $H=\fbox{ab}$ байна.
- Бөмбөрцгийн радиус нь $R=\fbox{c}$ байна.
- Конус дотроос санамсаргүйгээр нэг цэг авахад тэр нь бөмбөрцөг дотроос авагдсан байх магадлал нь $P(A)=\dfrac{\fbox{d}}{\fbox{e}}$.
$R=5$ радиустай бөмбөлөгт хамгийн их хажуу гадаргуугийн талбайтай
шулуун дугуй конус багтаав. Энэ конусын өндөр нь
$H=\dfrac{\fbox{ab}}{\fbox{c}}$ байна.
$R=2$ радиустай бөмбөлөгт хамгийн их эзлэхүүнтэй шулуун дугуй
конус багтаав. Энэ конусын эзлэхүүн нь
$V=\dfrac{\fbox{abc}}{\fbox{de}}\cdot \pi$ байна.
Зөв дөрвөн өнцөгт пирамидад оройнууд нь давхцдаг байхаар шулуун
дугуй конус багтжээ. Конусын суурийн радиус 6, конуст багтсан
бөмбөрцгийн радиус 2-той тэнцүү бол пирамид ба конусын эзлэхүүний
ялгавар $\fbox{ab}\cdot(\fbox{c}-\pi)$ байна.
Зөв дөрвөн өнцөгт пирамидад оройнууд нь давхцдаг байхаар шулуун
дугуй конус багтжээ. Тэдгээрийн өндөр (ерөнхий) $\dfrac 94$-тэй,
конуст багтсан бөмбөрцгийн радиус 1-тэй тэнцүү бол пирамид ба
конусын эзлэхүүнхий ялгавар $\fbox{ab}\cdot
\left(\fbox{c}-\dfrac{\pi}{4}\right)$ байна.
$SABCD$ дөрвөн өнцөгт пирамидын эсрэг хоёр хажуу талс нь суурьт
перпендикуляр ба пирамидын өндөр $\sqrt{5}$-тай тэнцүү. Пирамидын
суурь $ABCD (AD=BC)$ нь тойрог багтаасан адил хажуут трапец бөгөөд
$AB=6, \angle BAD=\dfrac{\pi}{3}$ байв. $D$ цэгээс $(SAB)$ хавтгай
хүртэлх зай $\rho=\dfrac{\sqrt{\fbox{ab}}}{\fbox{c}}$ болно.
Пирамид дотор конус суурийн тойрог нь $SCD$ гурвалжинд багтсан
байхаар, харин орой нь $SAB$ талс дээр оршихоор байрлажээ.
Конусын эзлэхүүн $V=\dfrac{\pi\sqrt{\fbox{de}}}{\fbox{fg}}$ байна.
$SKLMN$ дөрвөн өнцөгт пирамидын эсрэг хоёр талс нь суурьт
перпендикуляр ба $SM=12.$ Пирамидын суурь $KLMN (MN>KL)$ нь
тойрог багтаасан адил хажуут трапец бөгөөд $KN=LM=4,$ $KN$ ба $LM$
шулуунуудын хоорондох өнцөг $\dfrac{\pi}{3}$-тай тэнцүү. $M$
цэгээс $(SKL)$ хавтгай хүртэлх зай
$\dfrac{\fbox{ab}\sqrt{\fbox{cde}}}{\fbox{fg}}$ байна. Пирамид
дотор конус суурийн тойрог нь $SMN$ гурвалжинд багтсан, харин орой
нь $SKL$ талс дээр оршихоор байрлажээ. Конусын өндөр
$H=\dfrac{\fbox{hk}\cdot\sqrt{\fbox{mn}}}{\fbox{pq}}$ байна.
Конуст бөмбөрцөг багтжээ. Байгуулагч нь бөмбөрцгийг шүргэсэн цэгээрээ оройгоос 8 нэгж, 12 нэгж урттай хэрчмүүдэд хуваагдсан байв.
- Конусын өндөр нь $H=\fbox{ab}$ байна. $\text{a}$ ба $\text{b}$ нь хэд вэ?
- Бөмбөрцгийн радиус нь $R=\fbox{c}$ болно. $\text{c}$ нь хэд вэ?
- Конусын дотроос санамсаргүйгээр нэг цэг авахад тэр нь бөмбөрцөг дотроос авагдсан байх магадлал нь $P(A)=\dfrac{\fbox{d}}{\fbox{e}}$ нь хэд вэ?
Конуст бөмбөрцөг багтжээ. Байгуулагч нь бөмбөрцгийг шүргэсэн цэгээрээ оройгоос 8 нэгж, 12 нэгж урттай хэрчмүүдэд хуваагдсан байв.
- Конусын өндөр нь $H=\fbox{ab}$ байна.
- Бөмбөрцгийн радиус нь $R=\fbox{c}$ байна.
- Конус дотроос санамсаргүйгээр нэг цэг авахад тэр нь бөмбөрцөг дотроос авагдсан байх магадлал нь $P(A)=\dfrac{\fbox{d}}{\fbox{e}}$.
Өндөр нь 2, суурийн диаметр нь 5 байх конус өгөгдөв.
- Конусын эзлэхүүн $V=\dfrac{2\fbox{a}}{\fbox{b}}$ байна.
- Уг конуст зөв гурвалжин призм багтааж, суурийн гурвалжны талыг $x$ гэвэл призмийн өндөр нь $\dfrac{2\fbox{c}-\fbox{d}\sqrt3x}{15}$ болно.
- Дээрх багтсан призмийн авч болох хамгийн их эзлэхүүн нь $V_{\textit{пр}}=\dfrac{2\fbox{e}\sqrt3}{\fbox{gh}}$ байна.
Конус, пирамидын эзлэхүүн
Өндөр нь 2, суурийн диаметр нь 5 байх конус өгөгдөв.
- Конусын эзлэхүүн $V=\dfrac{2\fbox{a}}{\fbox{b}}$ байна.
- Уг конуст зөв гурвалжин призм багтааж, суурийн гурвалжны талыг $x$ гэвэл призмийн өндөр нь $\dfrac{2\fbox{c}-\fbox{d}\sqrt3x}{15}$ болно.
- Дээрх багтсан призмийн авч болох хамгийн их эзлэхүүн нь $V_{\textit{пр}}=\dfrac{2\fbox{e}\sqrt3}{\fbox{gh}}$ байна.
Нийлмэл биетийн гадаргуун талбай, эзлэхүүн
Огтлогдсон пирамид
Зөв дөрвөн өнцөгт суурьтай огтлогдсон пирамидын суурийн талууд 3 см, 5 см. Огтлогдсон пирамидын ирмэг $\sqrt{17}$ см. Огтлогдсон пирамидын бүтэн гадаргуугийн талбайг ол.
Огтлогдсон зөв дөрвөн өнцөгт пирамидын хажуу гадаргуугийн талбай нь
тэгш хэмийн тэнхлэг огтлолуудынхаа талбайн нийлбэртэй тэнцүү бол пирамидын
их суурь дахь хоёр талст өнцгийн хэмжээг ол.
A. $30^\circ$
B. $45^\circ$
C. $\arcsin\sqrt{\frac23}$
D. $\arcsin2(\sqrt2-1)$
Огтлогдсон зөв дөрвөн өнцөгт пирамидын хажуу гадаргуугийн талбай нь
хоёр суурийнхаа талбайн нийлбэртэй тэнцүү ба сууриудын талбайн харьцаа 1:3
бол их суурь дахь хоёр талст өнцгийн хэмжээг ол.
A. $60^\circ$
B. $45^\circ$
C. $30^\circ$
D. $\arcsin\sqrt{\frac23}$
$a$ ирмэгтэй $ABCDA_1B_1C_1D_1$ кубийн $A,C$ оройнууд ба $A_1D_1$
ирмэгийн дунджийг дайрсан хавтгайгаар кубээс таслагдсан огтлогдсон пирамидын
эзлэхүүнийг ол.
A. $\frac7{24}a^3$
B. $\frac14a^3$
C. $\frac37a^3$
D. $\frac8{25}a^3$
Бүх ирмэг нь $a$ урттай зөв гурвалжин призм $ABCA_1B_1C_1$-ийн $B,C$
оройнууд ба $A_1C_1$ ирмэгийн дунджийг дайрсан хавтгайгаар призмээс таслагдсан
огтлогдсон пирамидын эзлэхүүнийг ол.
A. $\dfrac{9\sqrt3}{64}a^3$
B. $\dfrac{\sqrt3}{8}a^3$
C. $\dfrac16a^3$
D. $\dfrac{12\sqrt3}{77}a^3$
E. $\dfrac{7\sqrt3}{48}a^3$
3м өндөртэй огтлогдсон пирамидийн эзлэхүүн 95$\texttt{м}^{2}$ ба сууриудын периметр 2:3 харьцаатай бол сууриудын талбай хэдэн кв.метр байх вэ?
A. 12 ба 27
B. 20 ба 45
C. 16 ба 36
D. 24 ба 54.
Огтлогдсон зөв гурвалжин пирамидын дээд суурийн тал 4см, доод суурийн тал 6см урттай ба хажуу ирмэг суурийн хавтгайтай $30^\circ$ өнцөг үүсгэдэг бол уг огтлогдсон пирамидын эзлэхүүнийг олоорой.
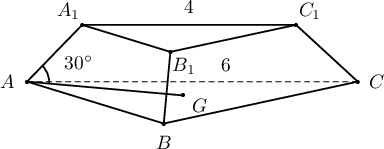

A. $\dfrac{38}{3\sqrt3}$
B. $\dfrac{37}{3\sqrt3}$
C. $37\sqrt3$
D. $10\sqrt3$
E. $12\sqrt3$
Огтлогдсон зөв гурвалжин пирамидын дээд суурийн тал 3см, доод суурийн тал 9см урттай ба хажуу ирмэг суурийн хавтгайтай $30^\circ$ өнцөг үүсгэдэг бол уг огтлогдсон пирамидын эзлэхүүнийг олоорой.
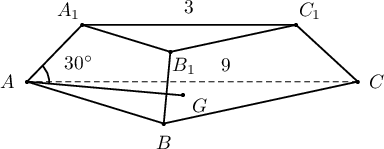

A. $\dfrac{26}{\sqrt3}$
B. $\dfrac{79}{2\sqrt3}$
C. $7\sqrt3$
D. $\dfrac{117}{2\sqrt3}$
E. $\dfrac{79}{3\sqrt3}$
Огтлогдсон зөв гурвалжин пирамидын дээд суурийн тал 3см, доод суурийн тал 7см урттай ба хажуу ирмэг суурийн хавтгайтай $60^\circ$ өнцөг үүсгэдэг бол уг огтлогдсон пирамидын эзлэхүүнийг олоорой.
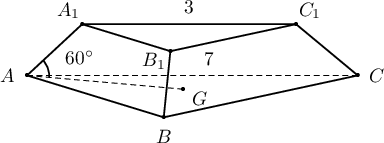

A. $\dfrac{79}{\sqrt3}$
B. $\dfrac{77}{\sqrt3}$
C. $27\sqrt3$
D. $9\sqrt3$
E. $18\sqrt3$
Огтлогдсон зөв гурвалжин пирамидын дээд суурийн тал 2см, доод суурийн тал 5см урттай ба хажуу ирмэг суурийн хавтгайтай $60^\circ$ өнцөг үүсгэдэг бол уг огтлогдсон пирамидын эзлэхүүнийг олоорой.
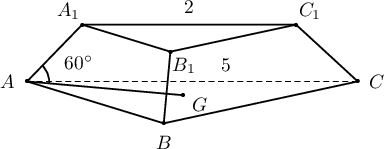

A. $\dfrac{26}{4}\sqrt3$
B. $\dfrac{39}{4\sqrt3}$
C. $\dfrac{39}{\sqrt3}$
D. $\dfrac{39}{4}\sqrt3$
E. $18\sqrt3$
Огтлогдсон зөв гурвалжин пирамидын дээд суурийн тал 3см, доод суурийн тал 7см урттай ба хажуу ирмэг суурийн хавтгайтай $30^\circ$ өнцөг үүсгэдэг бол уг огтлогдсон пирамидын эзлэхүүнийг олоорой.

A. $\dfrac{79}{\sqrt3}$
B. $\dfrac{77}{\sqrt3}$
C. $27\sqrt3$
D. $9\sqrt3$
E. $18\sqrt3$
Олон талст өнцөг
Адил талт гурвалжны нэг тал $p$ хавтгайтай $\alpha$ өнцөг үүсгэнэ. Өөр нэг тал нь мөн хавтгайтай $\beta$ өнцөг үүсгэнэ. Гурвалжны хавтгай ба $p$ хавтгайн хоорондох өнцгийг ол.
Гурван талст өнцгийн хавтгай өнцгүүдийн нэг нь тэгш, нөгөө хоёр нь ижил хэмжээтэй байв. өнцгийн ирмэгүүдээс ижил урттай хэрчим огтолсон хавтгай, тэгш хавтгай өнцөгтэй талст перпендикуляр бол нөгөө хоёр хавтгай өнцгийн хэмжээ аль вэ?
A. $\arcsin \dfrac 13;$
B. $60^{\circ};$
C. $45^{\circ};$
D. $30^{\circ}.$
Гурван талст өнцгийн хоёр хавтгай өнцөг нь ижил $60^{\circ}$ хэмжээтэй ба гурав дахь хавтгай өнцгийн эсрэг ирмэг дэх хоёр талст өнцөг тэгш байв. Гуравдахь хавтгай өнцгийн хэмжээ аль вэ?
A. $\arccos \dfrac 14;$
B. $45^{\circ};$
C. $\arccos \dfrac 13;$
D. $30^{\circ}.$
Олон талстын огтлол байгуулах
Олон талстын тэгш хэмийн хавтгай
Параллелепипед
$x^2+(a+2)x+3a+1=0$ тэгшитгэлийн шийдүүд нь бодит бөгөөд кубуудынх нь нийлбэр нь $5a-2$-оос бага байх $a$-ийн утгын мужийг ол.
Нэг бассейн 200 м.куб устай, нөгөө нь --- 112 м.куб устай байв. Цоргыг онгойлгож бассейнуудыг дүүргэв. Хэрвээ хоёр дахь бассейнд 1 цагт нэмэгдэх усны хэмжээ нэг дэхээс 22 м.куб-ээр их бол хоёр бассейн хэдэн цагийн дараа адил хэмжээний устай болох вэ?
54 м.куб эзлэхүүнтэй бассейныг хоёр хоолойгоор усаар дүүргэв. Үүний тулд I хоолойг 3 цаг, II хоолойг 2 цаг нээжээ. Хэрвээ I хоолой 1 м.куб ус шахахад II-аас 1 минут илүү зарцуулдаг бол эхний хоолойн чадлыг тодорхойл.
Тус бүр 3 см.куб гурван бодисыг холин 16 грамм бодис үүсгэжээ. Хоёр дахь бодисын 4 грамм нь 3 дахь бодисын 4 граммаас 1/2 см.куб-ээр илүү эзлэхүүнтэй. Хэрэв хоёр дахь бодисын жин нэг дэх бодисынхоос 2 граммаар илүү бол 3 дахь бодисын нягтыг ол.
1200 м.куб, 1400 м.куб, 1600 м.куб эзлэхүүнтэй бассейнуудын эхнийхийг нь нэгдүгээр хоолойгоор, 2 дахь бассейны 800 м.куб-ийг 1-р хоолойгоор, үлдсэн 600 м.куб-ийг нь 2-р хоолойгоор, 3 дахь бассейны 700 м.куб-ийг нь 1-р хоолойгоор, 900 м.куб-ийг нь 3-р хоолойгоор тус тус дүүргэж болно. Эхний хоолойн ажлын бүтээмж нь 2 дахь хоолойгоос 400 м.куб/цаг-аар бага. Хэрэв 2 дахь хоолойн ажлын бүтээмж 700 м.куб/цаг-аас багагүй, 1100 м.куб/цаг-аас хэтрэхгүй бол аль бассейн хурдан дүүрэх вэ?
Усан онгоцнууд өнөөгийн хөгжилд хүрээгүй байхад цагт зарцуулах түлшний хэмжээ нь түүний хурдын кубтай тэнцэнэ хэмээн үздэг байжээ. 15 км/цаг хурдтай үед цагт 1.5 т нүүрс зарцуулах бөгөөд нэг тонн нүүрсний үнэ нь 18 рубль. Бусад зардал нь цагт 16 рубль эзлэнэ. 2000 км замд шаардагдах хамгийн бага хэмжээний зарцуулалтын хэмжээг рублээр ол.
20 гэсэн тоог нэг нэмэгдэхүүн нь куб ба нөгөө нэмэгдэхүүний квадратых нь нийлбэр хамгийн бага байх 2 нэмэгдэхүүнд задал
Ямар нэгэн тооны квадратыг 3 дахин авсан нь түүний хамгийн их утгын кубээс их бол уг тоог ол
Квадрат суурьтай дөрвөн өнцөгт пирамид өгөгджээ. Түүний нэг хажуу ирмэг нь суурийн хавтгайд перпендикуляр. Уг пирамидад доод суурь нь пирамидын суурь дээр байрлах, дээд суурийн ирмэгүүд нь пирамидын талсууд дээр байрлаж байхаар куб багтав. Хэрэв пирамидын хажуу талс сууриа $\alpha$ өнцгөөр налсан, кубийн ирмэгийн урт $a$ бол пирамидын эзлэхүүнийг ол.
$a$ талтай кубийн нэг талсын төвийг түүний эсрэг орших талсын ирмэгүүдийн дундаж цэгүүдтэй хэрчмээр холбов. Түүнчлэн эдгээр хэрчмүүдийн төгсгөлүүдийг дараалуулан хэрчмээр холбов. Эдгээр хэрчмүүдээр үүсэх пирамидын бүтэн гадаргуугийн талбайг ол.
$ABCDA_1B_1C_1D_1$ куб өгөгджээ. $BCA_1$ ба $B_1C_1D$ хавтгайнууд перпендикуляр уу? Хариултай үндэслэ.
4 талтай кубийн нэг оройгоос гарсан гурван ирмэгийн дунджуудыг дайрсан огтлолын талбайн хэмжээг ол.
Тэгш өнцөгт параллелепипедийн суурийн квадратын диагнал $AC$ ба нөгөө суурийн нэг оройг дайран гарсан хавтгай $AB_1C$ гурвалжин үүсгэнэ. Гурвалжны $B_1$ оройн өнцөг нь параллелепипедийн суурь ба түүнийг огтлон гарсан хавтгайн хооронд үүсэх өнцгөөс хоёр дахин их бол $AB_1C$ өнцгийн хэмжээг ол.
Квадрат суурьтай тэгш өнцөгт параллелепипедыг огтлоход ромбо үүсчээ. Огтолсон хавтгай ба суурийн хавтгайн хоорондох хоёр талст өнцөг $30^\circ$ бол ромбын дотоод өнцгүүдийг ол.
$ABCDA_1B_1C_1D_1$ кубийн ирмэг $a$, $AB$ ирмэгийн дундаж цэг $K$, $DD_1$ ирмэгийн дундаж цэг $E$ байв. $A_1KE$ гурвалжны периметрийг ол. Энэ гурвалжныг агуулсан хавтгай кубийн эзлэхүүнийг ямар харьцаатай хэсгүүдэд хуваах вэ?
$ABCDA_1B_1C_1D_1$ тэгш өнцөгт параллелепипедын ирмэг $AB=a$, $BC=a$, $AA_1=b$ байв. $BD_1$ диагоналтай перпендикуляр, $A$ оройг дайран гарах огтлолын талбайг ол.
Зөв гурвалжин призмын суурийн тал ба түүний эсрэг орших ирмэгийн дундажыг агуулсан хавтгай суурийн хавтгайтай $60^\circ$-ийн өнцөг үүсгэнэ. Энэ хавтгайгаар үүсэх хөндлөн огтлолын талбай $S=8\sqrt3$. Призмын эзлэхүүн ба бүтэн гадаргуугийн талбайг ол.
Тэгш өнцөгт параллелепипедын диагонал 10 см ба суурийн хавтгайтай $45^\circ$-ийн өнцөг үүсгэнэ. Суурийн нэг тал нь нөгөөгөөсөө 2 см-ээр их бол параллелепипедын эзлэхүүнийг ол.
Шулуун параллелепипедын суурийн тал 13 см ба 14 см богино диагонал 17 см, талбай нь $168$ см.кв бол хажуу гадаргуугийн талбайг ол.
< p>< /p>Бодолтыг харах
$ABC A_1B_1C_1$ зөв гурвалжин призмын хажуу ирмэг $AA_1$, $BB_1$, $CC_1$, суурь нь 4 талтай адил талт $ABC$ гурвалжин болно. $AB$ ба $CA$ шулуунууд перпендикуляр бол призмын эзлэхүүнийг ол.
$ABC A_1B_1C_1$ зөв гурвалжин призмын хажуу ирмэгүүд $AA_1$, $BB_1$, $CC_1$ ба суурь нь адил талт $ABC$ гурвалжин болно. Түүнчлэн призмийн бүх ирмэгүүд ижилхэн $6$ урттай. $P$ ба $Q_1$ цэгүүд $BC$ ба $A_1C_1$ ирмэгүүдийг $BP:PC=A_1Q_1: Q_1C_1=1:2$ харьцаагаар хуваана. $ABB_1A_1$ ба $ACC_1A_1$ хавтгайг шүргэх, $PQ_1$ хэрчим дээр төвтэй бөмбөрцөгийн радиусыг ол.
Налуу параллелепипедийн суурь $a$ талтай, $\alpha$ хурц өнцөг бүхий $ABCD$ ромбо байв. $AA_1$ ирмэгийн урт $b$. $AB_1$, $AD$ ирмэгүүдийн хоорондох өнцөг $\varphi$ бол параллелепипедийн эзлэхүүнийг ол.
Квадрат суурьтай тэгш өнцөгт параллелепипедын диагонал $3,5$. Харин хажуу талcын диагонал $2,5$ бол параллелепипедын эзлэхүүнийг ол.
Тэгш өнцөгт параллелепипедын суурийн диагонал нь $d$ урттай бөгөөд суурийн талтайгаа $\varphi$ өнцөг үүсгэнэ. Харин энэ тал нь параллелепипедын диагоналтай $\beta$ өнцөг үүсгэнэ. Параллелепипедын хажуу гадаргуугийн талбайг ол.
Бөмбөрцгийн гадаргуугийн талбай ба түүнд багтсан кубийн гадаргуугийн талбайн харьцааг ол.
1 талтай кубэд конус багтсан бөгөөд түүний орой нь кубийн нэг оройтой давхцаж байв. Кубийн гурван тал конусын хажуу гадаргатай шүргэлцэнэ. Харин кубэд багтсан бөмбөрцөг конусын суурьтай шүргэлцэнэ. Конусын эзлэхүүнийг ол.
Бөмбөрцгийн эзлэхүүн $4$ дм.куб. Уг бөмбөрцөгт багтсан цилиндрийн байгуулагч бөмбөрцгийн төвөөс $60^\circ$ өнцгөөр харагддаг бол цилиндрийн эзлэхүүнийг ол.
$ABCD$ суурьтай $AA_1$, $BB_1$, $CC_1$, $DD_1$ хажуу ирмэгүүд бүхий куб өгөгдөв. Кубийн ирмэг 1. $AB$ ирмэгийг огтолсон, $A_1B$ ирмэгтэй $60^\circ$-ийн өнцөг үүсгэсэн, $B_1C$ талыг агуулсан хавтгай татав. Энэ хавтгай $AB$ ирмэгийг ямар харьцаагаар хуваах вэ?
$ABCD$ суурьтай $AA_1$, $BB_1$, $CC_1$, $DD_1$ хажуу ирмэгүүд бүхий куб өгөгдөв. Кубийн ирмэг 1-тэй тэнцүү бөгөөд $M$, $N$ цэгүүд харгалзан $CD_1$ ба $CC_1$ хэрчмүүдийн дундаж. $BM$, $AN$ шулуунуудын хоорондох зайг ол.
1 талтай кубийн оройнууд нь ижил радиустай бөмбөрцгүүдийн төв болно. Бөмбөрцгүүдийн гадна орших кубийн эзлэхүүн $1/2$ бол кубийн ирмэгийн ямар хэсэг бөмбөрцгийн дотор байрлах вэ?
$AB=6$, $AD=2$, $AA_1=1$ ирмэг бүхий $ABCDA_1B_1C_1D_1$ тэгш өнцөгт параллелепипедыг түүний $AC_1$ диагоналыг агуулсан хавтгайгаар огтлоход үүсэх дүрсийн талуудын квадратуудын нийлбэр хамгийн бага байв. Огтлолын талбай ба огтлогч хавтгайн $ABCD$ талстай үүсгэх өнцгийг ол.
$ABCD A_1B_1C_1D_1$ кубийн ирмэг нь $a$-тай тэнцүү. $AA_1$, $BB_1$ ирмэгийн дундаж цэгүүд ба $A$, $C_1$ оройг дайран гарах бөмбөрцгийн радиусыг ол.
$ABCD A_1B_1C_1D_1$ кубийн $A$ орой, $AB$ ба $AD$ талуудын дундажыг дайрах бөмбөрцөг $A_1B_1C_1D_1$ талстай шүргэлцэнэ. Бөмбөрцгийн гадаргуугийн талбай ба кубийн бүтэн гадаргуугийн талбайн харьцааг ол.
$ABCDA_1B_1C_1D_1$ куб өгөгджээ. $AD$ ба $CC_1$ ирмэгүүдийн дундаж ба $B$ оройг дайран гарсан хавтгай ба $ABCD$ талсын хооронд үүсэх өнцгийг ол.
$ABCDA_1B_1C_1D_1$ параллелепипедын $AB_1$ ба $BC_1$ диагоналууд дээр $M$ ба $N$ цэг оршино. $MN$ ба $A_1C$ хэрчмүүд параллель бол эдгээр хэрчмүүдийн харьцааг ол.
$ABCDA_1B_1C_1D_1$ куб өгөгдөв. Хэрэв кубийн ирмэгийн урт 1 бол $AD$, $DD_1$, $CD$ ирмэгүүд болон $BC_1$ шулууныг шүргэх бөмбөрцгийн радиусыг ол.
$ABCDA_1B_1C_1D_1$ куб өгөгдөв. Түүний $C$ оройгоос татсан диагоналын дундажыг дайрсан, уг диагоналд перпендикуляр огтлолын талбайг кубийн гадаргуугийн талбайд харьцуулсан харьцааг ол.
$ABCDA_1B_1C_1D_1$ кубийн ирмэг $9$. Харгалзан $BC$, $CD$, $CC_1$ хэрчмүүд дээр орших $M$, $N$, $K$ цэгүүдийг дайруулан хавтгай татав. $MCK$ гурвалжинд багтсан тойргийн радиус 1, $MNC$ гурвалжины талбай $\dfrac{21}2$, $CN$ ба $CK$ хэрчмүүдийн уртуудын ялгавар 3, $MNKC$ пирамидын эзлэхүүн 15-аас бага гэдэг нь мэдэгдэж байв. $MNK$ гурвалжны хавтгай ба $A_1$ оройг агуулсан гурван талсыг шүргэх бөмбөрцгийн радиусыг ол.
$ABCDA_1B_1C_1D_1$ кубийн ирмэг $1$. $DC$ болон $BC$ ирмэгүүдийн дундаж цэгүүд нь харгалзан $K$ ба $N$. $M$ цэг $CC_1$ ирмэг дээр $MC=\dfrac34$ байхаар байрлана. $M$, $N$, $K$ цэгүүдийг дайрч, $BB_1D_1D$ хавтгайг шүргэх бөмбөрцгийн радиусын боломжит хамгийн их утгыг ол.
$x^3+ax+b=0$ куб тэгшитгэлийг 2 шийдтэй (3 шийдгүй) байлгах
$a,b$ бодит тоо оршин байх зайлшгүй бөгөөд хүрэлцээтэй нөхцөл нь
$a\neq 0$ ба $\dfrac{b^2}{4}+\dfrac{a^3}{27}=0$ байхыг харуул.
Куб зэргийн функц $f(x)=ax^3+bx^2+cx+d$ нь $x=\alpha,\beta$
цэгүүдэд экстремум утгуудтай бол максимум утга ба минимум утгын
ялгаврыг $a$, $\alpha$, $\beta$-аар илэрхийл.
$x^3+2x^2+3x+4=0$ тэгшитгэлийн шийдүүд нь $\alpha$, $\beta$, $\gamma$ бол
$\alpha+\beta$, $\beta+\gamma$, $\gamma+\alpha$ тоонууд шийд нь болох куб тэгшитгэл зохио.
$f(x)$ нь куб функц бөгөөд ахлах гишүүний коэффициент нь $1$,
$f(1)=2$, $f(-1)=-2$, $f^\prime (-1)=0$ бол $f(x)$-г ол.
$f(x)$ нь ахлах гишүүний коэффициент нь 1-тэй тэнцүү куб олон
гишүүнт ба $f(3)=20$ байв. Хэрэв $f(x)$ нь $(x-1)^2$-д хуваагдах бол $f(x)$-ийг ол.
$f(x)$ куб функц байг. Хэрэв $y=f(x)$ функцийн $(-1, 9)$ цэг дээрх шүргэгч шулууны өнцгийн коэффициент $-12$ ба $f(x)$ функц нь $x=1$ үед минимум утга $-11$-ийг авдаг бол $f(x)$ функцийг ол.
Квадрат суурьтай гурван хэмжээсийн нийлбэр нь 1 байх тэгш өнцөгт
параллелепипедийн эзлэхүүн $V$, бүтэн гадаргуун талбай $S$ бол
$V-2S$-ийн хамгийн бага утгыг ол.
Тус бүр 3 см.куб гурван бодисыг холин 16 грамм бодис үүсгэжээ. Хоёр дахь бодисын 4 грамм нь 3 дахь бодисын 4 граммаас 1/2 см.куб-ээр илүү эзлэхүүнтэй. Хэрэв хоёр дахь бодисын жин нэг дэх бодисынхоос 2 граммаар илүү бол 3 дахь бодисын нягтыг ол.
Кубийн гол диагональ 10 нэгж бол эзлэхүүнийг нь ол.
A. $1000\sqrt3$
B. $\dfrac{\sqrt3}{9}\cdot1000$
C. $1000$
D. $\dfrac{1000}{3}$
E. $\dfrac{2000}{3}$
$ABCDA_1B_1C_1D_1$ кубийн $AA_1$ ирмэгийн дунджаас $C_1$ хүртэл $6$ нэгж бол эзлэхүүнийг ол.
A. $64$
B. $27$
C. $125$
D. $216$
E. $36$
Кубийн гол диагональ $\sqrt{12}$ бол түүний бүх ирмэгүүдийн уртын нийлбэрийг ол.
A. $13$
B. $34$
C. $24$
D. $47$
E. $12$
Кубийн ирмэг бүрийг 2 дахин урт болгоход гадаргуугийн талбай хэд дахин ихсэх вэ?
A. 4
B. 6
C. 8
D. 10
E. 16
3 см радиустай бөмбөрцөгийн эзлэхүүн $A$ см.куб, гадаргын талбай $B$ см.кв, 3 см суурийн радиустай 6 см өндөртэй конусын эзлэхүүн $C$ см.куб бол зөв өгүүлбэрийг сонго.
A. $B< A< C$
B. $C< B< A$
C. $C< A=B$
D. $A=B< C$
E. $C=A< B$
Ялаа $\sqrt5$ урттай ирмэгтэй $ABCDA_1B_1C_1D_1$ кубийн $D$ орой дээр сууж байв. $D$–ийн эсрэг орших $B_1$ оройд кубийн гадаргуугаар явж хүрэх хамгийн богино замын уртыг ол.
A. $2\sqrt5$
B. $15/2$
C. $5$
D. $\sqrt{15}$
E. $3\sqrt5$
Кубийн нэг талсын талбай нь 49 см.кв бол кубийн эзлэхүүнийг ол.
A. 49 см.куб
B. 64 см.куб
C. 125 см.куб
D. 144 см.куб
E. 343 см.куб
Тэгш өнцөгт параллелепепидийн урт, өргөн, өндрийг нь тус бүр 3 дахин ихэсгэв. Эхлэхүүн нь хэд дахин ихсэх вэ?
A. $3$
B. $6$
C. $9$
D. $18$
E. $27$
Тэгш өнцөгт параллелепипедийн $A$ оройгоос гарсан 3 ирмэгийн дундаж цэгүүд дээр суурьтай $A$ оройтой пирамидийн эзлэхүүнийг параллелепипедийн эзлэхүүнд харьцуулсан харьцааг ол.
A. $\dfrac{1}{12}$
B. $\dfrac{1}{6}$
C. $\dfrac{1}{24}$
D. $\dfrac{1}{48}$
E. $\dfrac{1}{16}$
Гүйцэд гадаргуугийн талбай 24 см$^2$ байх кубэд багтсан бөмбөрцөгийн гадаргуугийн талбайг ол.
A. $4\pi$
B. $6\pi$
C. $8\pi$
D. $12\pi$
E. $16\pi$
$3x^2-ax+2a-1=0$ тэгшитгэлийн шийдүүдийн кубийн нийлбэрийг
ол.
A. $\frac a{27}(a^2+18-9)$
B. $\frac{a^3+18a^2-9a}{18}$
C. $\frac{a(a^2-18a+9)}{27}$
D. $\frac{a^2-18a+9}9$
Кубийн ирмэгийг $10\%$ багасгахад бүтэн гадаргуу нь хэдэн хувиар багасах вэ?
A. $18\%$
B. $19\%$
C. $20\%$
D. $21\%$
E. $11\%$
$ABCDA_1B_1C_1D_1$ кубийн $BD_1$ диагональ, талсын $AC$ диагональтай
үүсгэх өнцгийг ол.
A. $45^\circ$
B. $60^\circ$
C. $90^\circ$
D. $120^\circ$
E. $150^\circ$
Тэгш өнцөгт параллелепипедийн диагонал хажуу ирмэгтэй $45^\circ$, суурийн ирмэгүүдтэй ижил өнцөг үүсгэдэг бол энэ өнцгийн хэмжээг ол.
A. $30^\circ$
B. $45^\circ$
C. $\arccos\frac23$
D. $60^\circ$
E. $75^\circ$
Тэгш өнцөгт параллелепипедийн диагональ суурийн хавтгайтай $45^\circ$,
хажуугийн хамар хоёр талстай ижил өнцөг үүсгэдэг бол энэ өнцгийн хэмжээг ол.
A. $30^\circ$
B. $45^\circ$
C. $\arccos\frac13$
D. $60^\circ$
Кубийн төвийг суурийн талсын оройнуудтай холбоход үүсэх пирамидын хажуу гадаргуугийн талбай кубийн диагональ огтлолын талбай $S$-ээр яаж илэрхийлэгдэх вэ? Кубийн диагональ огтлол гэдэг нь түүний аль нэг параллель хоёр талсын диагоналийг дайрсан огтлол юм.
A. $\dfrac14S$
B. $\dfrac12S$
C. $S$
D. $\dfrac32S$
E. $\dfrac23S$
Тэгш өнцөгт параллелепипедийн хажуу ирмэг 6 нэгж урттай, диагонал нь суурийн периметрээс 2 дахин богино бол суурийн талбайг ол.
A. 18 кв.нэгж
B. 24 кв.н.
C. 30 кв.н.
D. 36 кв.н.
Тэгш өнцөгт параллелепипедийн урт, өргөн, өндрийн нийлбэр 25 м, гүйцэд гадаргуугийн талбай 400 $\mbox{м}^2$ бол параллелепипедийн диагоналын уртыг ол.
A. 12 м
B. 15 м
C. 17 м
D. 12.5 м
Диагоналийн урт нь 2 нэгж байх бүх тэгш өнцөгт параллелепипедийн бүтэн гадаргуугийн талбайн хамгийн их утгыг ол.
A. 4кв.н.
B. 8кв.н.
C. 12кв.н.
D. 16кв.н.
Диагоналийн урт нь адилхан бүх тэгш өнцөгт параллелепипед дотроос хамгийн их
бүтэн гадаргуугийн талбайтай нь 18кв.нэгж талбайтай байвал эдгээр
параллелепипедийн диагоналийн уртыг ол.
A. $\sqrt3$ нэгж
B. $\sqrt6$ нэгж
C. $3$ нэгж
D. $\sqrt{10}$ нэгж
өгсөн тэгш өнцөгт параллелепипедийн бүтэн гадаргуугийн талбай
192кв.нэгж байснаа түүний урт, өргөн өндрийн хэмжээсийг 1 нэгжээр нэмэгдүүлэхэд
274кв.нэгж болж нэмэгдэв. Анхны параллелепипедийн диагоналийн уртыг ол.
A. 8 нэгж.
B. 10 н.
C. 13 н.
D. 15 н.
Диагональ нь 17 нэгж урттай, бүтэн гадаргуугийн талбай нь 552кв.нэгж
байсан тэгш өнцөгт параллелепипедийн урт, өргөн, өндрийн хэмжээг 1 нэгжээр
нэмэгдүүлэхэд бүтэн гадаргуугийн талбай нь хэд болох вэ?
A. 576кв.нэгж
B. 608кв.н.
C. 624кв.н.
D. 674кв.н.
Кубийн төвийг суурийн талсын оройнуудтай холбоход үүсэх пирамидын эзлэхүүнийг кубийн эзлэхүүн $V$-ээр илэрхийл.
A. $\dfrac14V$
B. $\dfrac16V$
C. $\dfrac38V$
D. $\dfrac12V$
E. $\dfrac58V$
Кубийн дээд суурийн төвийг доод суурийн оройнуудтай холбоход үүсэх
пирамидын эзлэхүүнийг кубийн эзлэхүүн $V$-ээр илэрхийл.
A. $\dfrac12V$
B. $\dfrac13V$
C. $\dfrac14V$
D. $\dfrac23V$
E. $\dfrac16V$
Тэгш өнцөгт параллелепипедийн диагонал нь гурван талсынхаа диагоналаас 1, 2, 10 нэгжээр урт бол параллелепипедийн эзлэхүүнийг ол.
A. $150\sqrt{61}$
B. $2001$
C. $100\sqrt{31}$
D. $160\sqrt{41}$
Тэгш өнцөгт параллелепипедийн гурван талсын диагонал 7, 8, 9 нэгж урттай бол параллелепипедийн эзлэхүүнийг ол.
A. $48\sqrt{11}$
B. $23\sqrt{23}$
C. $151$
D. $62\sqrt3$
Бөмбөрцөг багтаасан зөв зургаан өнцөгт призмийн өндөр 2 нэгж бол эзлэхүүн нь хэдэн куб нэгж вэ?
A. $2\sqrt{3};$
B. $3\sqrt{3};$
C. $4\sqrt{3};$
D. $5\sqrt{3}.$
$\sqrt{3}$ нэгж радиустай бөмбөрцөг багтаасан зөв зургаан өнцөгт призмийн эзлэхүүн хэдэн куб нэгж байх вэ?
A. $36$
B. $24$
C. $30$
D. $20$
E. $18$
Кубийн гол диагонал $\sqrt{12}$ бол түүний ирмэгийн уртын нийлбэрийг ол.
A. 13
B. 34
C. 24
D. 47
E. 12
Бүх талс нь будагтай кубийг 1000 тэнцүү кубд хуваав. Эдгээр кубээс таамгаар 1-ийг сонгоход ядаж 1 талс нь будагтай куб таарах магадлалыг ол.
A. $\dfrac{12}{125}$
B. $\dfrac{13}{125}$
C. $\dfrac{48}{125}$
D. $\dfrac{61}{125}$
E. $\dfrac{64}{125}$
Тэгш өнцөгт параллелепипедийн гурван ялгаатай талсын талбай 10, 25, 40 бол эзлэхүүнийг ол.
A. 50
B. 100
C. 125
D. 150
E. 200
Кубийн бүтэн гадаргуугийн талбай 3-тай тэнцүү бол талсын диагоналийн уртыг ол.
A. $2$
B. $3$
C. $1$
D. $\sqrt2$
E. $4$
Кубийг багтаасан бөмбөрцгийн гадаргуугийн талбай $75\pi$ бол кубийн ирмэгийг ол.
A. $3$
B. $4$
C. $6$
D. $5$
E. $3\sqrt5$
Кубийн гүйцэд гадаргуугийн талбай 72 бол гол диагоналын уртыг ол.
A. $4\sqrt3$
B. $8$
C. $6$
D. $8\sqrt2$
E. $12$
$ABCD$ суурьтай $ABCDA_1B_1C_1D_1$ кубийн $AD, D_1C_1$ ирмэгүүдийн дундаж цэгүүд, $B_1C_1$ ирмэгийг $1:3$ харьцаагаар хуваах цэгүүдийг дайрсан хавтгайгаар огтлоход огтлол дээр хэдэн өнцөгт үүсэх вэ?
A. $3$
B. $4$
C. $5$
D. $6$
E. $7$
Кубийн бүтэн гадаргуугийн талбай $3$-тай тэнцүү бол талсын диагоналийн урт хэдтэй тэнцүү вэ?
A. $2$
B. $3$
C. $4$
D. $\sqrt2$
E. $1$
$ABCD$ суурьтай $ABCDA_1B_1C_1D_1$ кубийн $AD, D_1C_1$ ирмэгүүдийн дундаж цэгүүд, $B_1C_1$ ирмэгийг $3:1$ харьцаагаар хуваах цэгүүдийг дайрсан хавтгайгаар огтлоход огтлол дээр хэдэн өнцөгт үүсэх вэ?
A. $7$
B. $6$
C. $5$
D. $4$
E. $3$
Ялаа $\sqrt3$ урттай ирмэгтэй $ABCDA_1B_1C_1D_1$ кубийн $D$ орой дээр сууж байв. $D$–ийн эсрэг орших $B_1$ оройд кубийн гадаргуугаар явж хүрэх хамгийн богино замын уртыг ол.
A. $2\sqrt5$
B. $15/2$
C. $5$
D. $\sqrt{15}$
E. $3\sqrt5$
Кубийн ирмэг бүрийг 4 дахин урт болгоход гадаргуугийн талбай хэд дахин ихсэх вэ?
A. 4
B. 6
C. 8
D. 10
E. 16
Нэгж эзлэхүүнтэй кубүүдийг өрөхөд үүссэн биетийн бүтэн гадаргуугийн талбайг ол.
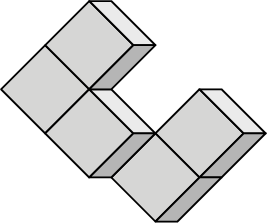

A. 30
B. 27
C. 24
D. 22
E. 20
Кубийн гол диагональ 10 нэгж бол эзлэхүүнийг нь ол.
A. $1000\sqrt3$
B. $\dfrac{\sqrt3}{9}\cdot1000$
C. $1000$
D. $\dfrac{1000}{3}$
E. $\dfrac{2000}{3}$
Тэгш өнцөгт параллелепипедийн хажуу ирмэг 6 нэгж урттай, диагонал нь суурийн периметрээс 2 дахин богино бол суурийн талбайг ол.
A. 18 кв.нэгж
B. 24 кв.н.
C. 30 кв.н.
D. 36 кв.н.
Куб хэдэн ирмэгтэй вэ?
A. $8$
B. $10$
C. $14$
D. $12$
E. $6$
Тэгш өнцөгт параллелепипед хэлбэртэй саванг хэрэглэсэний дараа урт, өргөн, өндөр нь тус бүр $20\%$-аар багассан бол гадаргуун талбай нь хэдэн хувиар багассан бэ?
A. $20\%$
B. $36\%$
C. $16\%$
D. $64\%$
E. $74.4\%$
Тэгш өнцөгт параллелепипедийн гурван ялгаатай талсын талбай 8, 15, 30 бол эзлэхүүнийг ол.
A. 40
B. 50
C. 60
D. 70
E. 90
Кубийн ирмэгийг $10\%$ ихэсгэхэд бүтэн гадаргуу нь хэдэн хувиар ихсэх вэ?
A. $18\%$
B. $19\%$
C. $20\%$
D. $21\%$
E. $11\%$
$ABCDA_1B_1C_1D_1$ кубийн ирмэгийн урт $a$, $M$ цэг $DD_1$ ирмэг дээр орших бөгөөд $D_1M=\dfrac14a$ бол
- $AB_1M$ гурвалжны периметр $$p=\dfrac{a}{2}(\fbox{a}+\fbox{b}\sqrt{2}+\sqrt{\fbox{cd}}),$$
- $B_1$ ба $M$ цэгийг дайрсан $C_1D$ шулуунуудтай параллель хавтгайн кубийг огтлох хэсгийн талбай $$S=\dfrac{\fbox{e}\sqrt{\fbox{fg}}}{32}a^2$$
Улаан, хар, шар гурван зөв шоог (куб хэлбэртэй, нэгэн төрлийн цул) тавцан дээр санамсаргүйгээр шидээд буусан нүхний тоог нь харгалзан $x; y; z$ гэж тэмдэглэв. (Жишээлбэл $x=1$ гэж улаан шоо нэг нүхтэй талаар буусныг илэрхийлнэ)
- $x$ тэгш байх магадлал $\dfrac{1}{\fbox{a}}$.
- $x< y$ байх магадлал $\dfrac{\fbox{b}}{\fbox{cd}}$.
- $x+y< z$ байх магадлал $\dfrac{\fbox{e}}{54}$ байна.
Улаан, хар, шар гурван зөв шоог (куб хэлбэртэй) тавцан дээр санамсаргүйгээр шидэхэд буусан нүхний тоог нь харгалзан $x;y;z$ гэж тэмдэглэв. (Жишээлбэл $x=1$ гэж улаан шоо нэг нүхтэй талаар буусныг илэрхийлнэ)
- $x$ анхны тоо байх магадлал $\dfrac{1}{\fbox{a}}$
- $x>y$ байх магадлал $\dfrac{\fbox{b}}{\fbox{cd}}$
- $x+y>z$ байх магадлал $\dfrac{\fbox{efg}}{216}$
4 нэгж талтай квадратын өнцгүүдээс нь нэг, нэг квадрат салган авч үлдсэн хэсгээр тэгш өнцөгт параллелепипед хэлбэрийн сав хийлээ. Савны эзлэхүүн хамгийн ихдээ хэд байх вэ?
Таслан авсан квадратын талыг $x$ гэвэл эзлэхүүн нь $$V=4x^3-\fbox{ab}x^2+\fbox{cd}x$$ болох ба түүний хамгийн их эзлэхүүн нь $V=\fbox{e}\dfrac{\fbox{fg}}{\fbox{hi}}$ байна.
$\dfrac1{x^2-2x}+\dfrac1{x^2-6x+8}=1$ тэгшитгэлийг
хувиргавал
$$x^3-\fbox{a}x^2+\fbox{b}x+\fbox{c}=0$$ куб тэгшитгэл гарах ба
$x^3-\fbox{a}x^2+\fbox{b}x+\fbox{c}=(x-2)(x^2-\fbox{d}x-\fbox{e})$
тул $x_1=2,$ $x_{2,3}=\fbox{f}\pm\sqrt{\fbox{g}}$ шийдтэй байна.
Тодорхойлогдох мужийг тооцвол анхны тэгшитгэлийн шийд $x_{2,3}$
болно.
А нь 8-аас цөөнгүй ялгаатай натурал тоонуудаас тогтох олонлог. Түүний бүх тоонуудын хамгийн бага ерөнхий хуваагдагч нь 462 ба аль ч 2 тооных нь хамгийн бага ерөнхий хуваагдагч 250-аас бага байв. А олонлогийн бүх элементүүдийн үржвэрийг 9 дахин нэмэгдүүлэхэд бүтэн куб болдог бол А олонлогийн хамгийн их тоо нь $\fbox{ab}$ ба хамгийн бага тоо нь $\fbox{c}$ байна.
$ABCDA_1B_1C_1D_1$ ($AA_1\parallel BB_1\parallel CC_1\parallel DD_1$) кубийн $A_1D_1$
ирмэгийн дундаж ба $B$, $C$, $C_1$ оройнуудыг дайрсан бөмбөрцөгийн
радиус $\sqrt{41}$-тэй тэнцүү бол кубийн гадаргуун талбай
$\fbox{abc}$ байна.
$ABCDA_1B_1C_1D_1$ ($AA_1\parallel BB_1\parallel CC_1\parallel DD_1$) кубийн $B_1C_1$
ирмэгийн дундаж ба $A, B, D$ оройнуудыг дайрсан бөмбөлгийн радиус
$\sqrt{82}$-тай тэнцүү бол кубийн талсын талбай $\fbox{abc}$ байна.
Эзлэхүүн нь 8-тай тэнцүү параллелепипед $R=\sqrt{3}$ радиустай
бөмбөлөгт багтжээ. Параллелепипедийн бүтэн гадаргуугийн талбай
$\fbox{ab}$ байна.
Эзлэхүүн нь $\dfrac{8\sqrt{3}}{9}$-тай тэнцүү параллелепипед $R=1$ радиустай бөмбөлөгт багтжээ. Параллелепипедийн бүтэн гадаргуугийн талбай $\fbox{a}$ байна.
$ABCDA_1B_1C_1D_1$ кубийн $AA_1, CC_1$ ирмэгүүд дээр харгалзан
$E, F$ цэгүүдийг $AE=2\cdot A_1E, CF=2\cdot C_1F$ байхаар авчээ.
$B, E, F$ цэгүүдийг дайрсан хавтгайгаар куб хоёр олон талстад
хуваагдав. $B_1$ цэгийг агуулсан олон талстын эзлэхүүнийг кубийн
эзлэхүүнд харьцуулсан харьцаа $\fbox{ab}:\fbox{cd}$ байна.
$ABCDA_1B_1C_1D_1$ кубийн $B_1C_1, AA_1$ ирмэгүүд дээр харгалзан $E,F$ цэгүүдийг $B_1E=EC_1, AF=2\cdot A_1F$ байхаар авчээ. $B, E, F$ цэгүүдийг дайрсан хавтгайгаар куб хоёр олон талстад хуваагдав. $B_1$ цэгийг агуулсан олон талстын эзлэхүүнийг кубийн эзлэхүүнд харьцуулсан харьцаа $\fbox{ab}:\fbox{cde}$ байна.
$ABCDA_1B_1C_1D_1$ кубийн ирмэг 6-тай тэнцүү. $A$ орой, $B_1C_1$
ирмэгийн дундаж $M$ цэг, $DD_1$ ирмэг дээр орших $K$ цэгийг
дайрсан хавтгай $A_1B_1C_1D_1$ талсыг талбайнууд нь 1:19
харьцаатай байхаар 2 хэсэгт хуваадаг байвал $AK=\fbox{a}\cdot
\sqrt{\fbox{bc}}$ байна.
$ABCDA_1B_1C_1D_1$ кубийн ирмэг 4-тэй тэнцүү. $D$ орой, $A_1B_1$
ирмэгийн дундаж $L$ цэг, $CC_1$ ирмэг дээр орших $M$ цэгийг
дайрсан хавтгай $A_1B_1C_1D_1$ талсыг талбайнууд нь 1:27
харьцаатай байхаар 2 хэсэгт хуваадаг байвал $D_1M=\fbox{a}$ байна.
Ирмэгийн урт нь 1-тэй тэнцүү $ABCDA_1B_1C_1D_1$ куб өгөгдөв.
- $BA, BB_1, BC$ ирмэгүүд ба $(A_1DC_1)$ хавтгайг шүргэсэн бөмбөлгийн радиус $$r=\dfrac{\fbox{a}\cdot \sqrt{\fbox{b}}-\fbox{c}\cdot \sqrt{\fbox{d}}}{\fbox{e}}$$ байна.
- $BA, BB_1, BC$ ирмэгүүд ба $DA_1$ шулууныг шүргэсэн бөмбөлгийн радиус $$R=\fbox{f}\cdot \sqrt{\fbox{g}}-\sqrt{\fbox{h}}$$ байна.
Ирмэгийн урт нь 1-тэй тэнцүү $ABCDA_1B_1C_1D_1$ куб өгөгдөв.
- $CB, CC_1, CD$ ирмэгүүд ба $(B_1AD_1)$ хавтгайг шүргэсэн бөмбөлгийн радиус $$r=\dfrac{\fbox{a}\cdot \sqrt{\fbox{b}}-\fbox{c}\cdot \sqrt{\fbox{d}}}{\fbox{e}}$$ байна.
- $CB, CC_1, CD$ ирмэгүүд ба $AD_1$ шулууныг шүргэсэн бөмбөлгийн радиус $$R=\fbox{f}\cdot \sqrt{\fbox{g}}-\sqrt{\fbox{h}}$$ байна.
$ABCDA_1B_1C_1D_1$ параллелепипедийн талсуудын $AC$, $DC_1$
диагоналиуд дээр харгалзан $M,N$ цэгүүдийг $MN\|BD_1$ байхаар
авав. $\overrightarrow{CD}=\vec a$, $\overrightarrow{CB}=\vec b$, $\overrightarrow{CC_1}=\vec c$
гэвэл $\overrightarrow{BD_1}=\vec a+\fbox{a}\vec b+\vec c$, $\overrightarrow{CA}=\vec
a+\vec b+\fbox{b}\vec c$ ба $MN:BD_1=\fbox{c}:\fbox{d}$ болно.
$a$ ирмэгтэй $ABCDA_1B_1C_1D_1$ кубийн $AA_1$, $BC$, $C_1D_1$
ирмэгүүд дээр харгалзан байрлах $P,Q,R$ цэгүүдийн хоорондох зайн
квадратуудын нийлбэрийн хамгийн бага утга нь
$\displaystyle\frac{\fbox{a}}{\fbox{b}}a^2$ байх ба энэ үед
$AP:PA_1=\fbox{c}:\fbox{d}$ юм.
Тэгш өнцөгт параллелепипед $ABCDA_1B_1C_1D_1$-ийн ирмэгүүд
$AA_1=a$, $BC=b$, $C_1D_1=c$ бол эдгээр ирмэгүүд дээр харгалзан
байрлах $P,Q,R$ цэгүүдийн хоорондох зайн квадратуудын нийлбэрийн
хамгийн бага утга нь
$\displaystyle\frac{\fbox{a}}{\fbox{b}}(a^2+b^2+c^2)$ байх ба энэ үед
$AP:PA_1=\fbox{c}:\fbox{d}$ болно.
$ABCDA_1B_1C_1D_1$ параллелепипедийн $BC$ ирмэгийн дундаж
цэг $M$-ийг дайрч $AC_1$, $DD_1$ шулуунуудыг харгалзан $N,P$
цэгүүдээр огтолсон шулуун оршин байх ба
$\overrightarrow{AN}=\dfrac2{\fbox{a}}\overrightarrow{AC_1}$,
$\overrightarrow{DP}=\fbox{b}\overrightarrow{DD_1}$, $MN:NP=\fbox{c}:\fbox{d}$ болно.
$ABCDA_1B_1C_1D_1$ параллелепипедийн $B,D,A_1$ оройнуудыг
дайрсан хавтгай түүний $AC_1$ диагоналийг $F$ цэгээр огтолдог ба
$\overrightarrow{AB}=\vec a$, $\overrightarrow{AD}=\vec b$, $\overrightarrow{AA_1}=\vec c$ гэвэл
$\overrightarrow{DF}=\displaystyle\frac13(\fbox{a}\vec a-\fbox{b}\vec b+\vec c)$,
$AF:FC_1=\fbox{c}:\fbox{d}$ болно.
$a$ урттай ирмэг бүхий кубийн зэргэлдээ хоёр талсын солбисон
диагоналиудын хоорондох зайг $\delta$ гэе. Эдгээр диагоналийн
ерөнхий перпендикуляр хэрчим диагоналийг $\fbox{a}:\fbox{b}$ $(a< b)$
харьцаагаар хуваах ба
$\delta=\displaystyle\frac{\sqrt{\fbox{c}}}3\,a$ байна.
$ABCDEFS$ зөв зургаан өнцөгт пирамид дотор 4 см радиустай бөмбөрцөг багтжээ. Апофем нь суурийн хавтгайтай $60^\circ$ өнцөг үүсгэдэг бол пирамидын эзлэхүүнийг ол.
Бодолт:
$SOM$-аас $SO=8$ см. Иймд $SK=12$ см болох ба
Бодолт:

$SOM$-аас $SO=8$ см. Иймд $SK=12$ см болох ба
- $SGK$-аас $GK=\fbox{a}\sqrt{\fbox{b}}$ см тул (2 оноо)
- Суурийн талбай $S_c=\fbox{cd}\sqrt{\fbox{b}}$ см.кв болно. (3 оноо)
- Эндээс пирамидын эзлэхүүн $V=\fbox{efg}\sqrt{\fbox{b}}$ см.куб (3 оноо)
Ирмэг нь 6 нэгж $ABCDA_1B_1C_1D_1$ кубийн $AA_1$, $CC_1$ ирмэгүүд дээр харгалзан $M, N$ цэгүүдийг
$|A_1M|=|C_1N|=2$ байхаар тэмдэглэв.


- $DN$ ба $D_1C_1$ шулуунуудын огтлолцлын цэг $K$, $DM$ ба $D_1A_1$ шулуунуудын огтлолцлын цэг $L$ бол $|C_1K|=|A_1L|=\fbox{a}$ (1 оноо).
- $KL$ шулуун $A_1B_1$ ба $B_1C_1$ ирмэгүүдийг харгалзан $E$ ба $F$ цэгүүдээр огтлох бол $|C_1F|=|A_1E|=\fbox{b}$ (1 оноо).
- $V_{A_1MLE}=V_{C_1KNF}=\fbox{c}$ (2 оноо).
- $V_{D_1DKL}=\fbox{de}$ (1 оноо).
- $D, M, N$ цэгүүдийг дайрсан хавтгайгаар куб 2 олон талстад хуваагдах бөгөөд $D_1$ цэгийг агуулсан олон талстын эзлэхүүн $\fbox{fg}$ (3 оноо).
Төгсгөлгүй буурах $b_{n}$ геометр прогрессийн бүх гишүүдийн нийлбэр нь $\sum\limits_{i=1}^{\infty} b_i=2$, квадратуудын нийлбэр нь $\sum\limits_{i=1}^{\infty} b_i^2=1$ бол $b_1=\dfrac{\fbox{a}}{\fbox{b}}$, $q=\dfrac{\fbox{c}}{\fbox{d}}$ болох тул кубуудын нийлбэр нь $\sum\limits_{i=1}^{\infty} b_i^3=\dfrac{\fbox{ef}}{\fbox{gh}}$ байна.
Параллель хавтгайнууд
Параллель шулуун ба хавтгай
18. Координатын эхийг дайрсан $ 5x-3y+2z-3=0 $ хавтгайтай параллель шулууны тэгшитгэлийг бич.
Параллель шулуунууд
Перпендикуляр хавтгайнууд
Пирамид
Хажуу ирмэгийн урт нь $1$ см байх зөв $4$ өнцөгт пирамидын эзлэхүүн хамгийн ихдээ хэд байх вэ?
Зөв дөрвөн өнцөгт пирамидын суурийн тэгш хэмийн төвөөс хажуу ирмэг хүртэлх зай $d$ бөгөөд хажуу ирмэг дэх хоёр талст өнцөг $\varphi$ бол пирамидын эзлэхүүнийг ол.
Зөв дөрвөн өнцөгт пирамидын эзлэхүүн нь $V$ болно. Хажуу ирмэгийн суурийн хавтгайд налсан өнцөг $\alpha$ бол пирамидын хажуу ирмэгийг ол.
Пирамидын суурь нь $\alpha$ хурц өнцөгтэй тэгш өнцөгт гурвалжин. Пирамидын өндөр нь $H$. Пирамидын хажуу ирмэгүүдийн суурийн хавтгайтай ижилхэн $\beta$-өнцөг үүсгэх бол пирамидийн эзлэхүүнийг ол.
$ABCF$ пирамидын $ABC$ суурийн $BK$ медиан ба $AF$ хажуу ирмэгийн дундаж $L$ цэгийг дайруулан хавтгай татав. $BCKLF$ олон талт ба $ABKL$ пирамидын эзлэхүүнүүдийн харьцааг ол.
Дөрвөн өнцөгт пирамидын суурь квадрат болно. Пирамидын нэг хажуу ирмэг суурийн хавтгайдаа перпендикуляр бөгөөд өөр хоёр ирмэг нь $60^\circ$ налсан байжээ. Хэрэв квадратын тал нь 4-тэй тэнцүү бол пирамидын бүтэн гадаргуугын талбайг ол.
Бөмбөрцгийг багтаасан зөв дөрвөн өнцөгт пирамидын өндөр бөмбөрцгийн диаметраас дөрөв дахин их бол пирамид ба бөмбөрцгийн эзлэхүүний харьцааг ол.
Зөв гурвалжин пирамидын суурийн талбай ба хажуу талын хоорондын өнцөг $45^\circ$. Пирамидын эзлэхүүн нь $\dfrac{1}{3}$ бол пирамидын суурийн талуудын уртыг ол.
Зөв зургаан өнцөгт пирамидын суурийн тал 2, хажуу ирмэг 4 бол пирамидын эзлэхүүнийг ол.
Зөв дөрвөн өнцөгт пирамидын хажуу ирмэг 3, суурийн тал 2 бол хажуу талын суурийн хавтгайтай үүсгэх өнцгийн косинусыг ол.
Зөв гурвалжин пирамидын өндөр $H$. Хажуу талсуудын үүсгэх хоёр талст өнцөг $2\alpha$ бол суурийн талуудын уртыг ол.
Бөмбөрцөгт багтсан пирамидын суурь нь 10 диагоналтай тэгш өнцөгт. Пирамидын хажуу ирмэг суурийн хавтгайтай $\beta$ өнцөг үүсгэдэг бол бөмбөрцгийн бүтэн гадаргуугийн талбай ба эзлэхүүнийг ол.
Зөв гурвалжин пирамидын хажуу талс суурьтайгаа $\alpha$ өнцөг үүсгэх бол хажуу талсуудын хооронд үүсэх хоёр талст өнцгийг ол.
$SABCD$ пирамидын суурь нь $ABCD$ тэгш өнцөгт бөгөөд түүний талууд нь $a\sqrt3$ ба $a$ байв. $SC$ хажуу ирмэг суурьтайгаа перпендикуляр, харин $SA$ хажуу ирмэг нь $\alpha$ өнцөг үүсгэнэ. Пирамидыг түүний $BD$ ирмэгийг дайрсан $SA$ ирмэгтэй параллель хавтгайгаар огтлоход үүсэх хөндлөн огтлолын талбайг ол.
Зөв гурвалжин пирамидын суурийн төвийг хажуу ирмэгийн дундажтай холбосон хэрчмийн урт суурийн талтай тэнцүү. Пирамидын хажуу талсуудын хоорондох өнцгийг ол.
Пирамидын суурь нь 3 ба 4 талтай тэгш өнцөгт. Тэгш өнцөгтийн богино талд налсан хажуу талс суурийн хавтайтай $45^\circ$-ийн өнцөг үүсгэх бол пирамидын эзлэхүүнийг ол.
Зөв дөрвөн өнцөгт пирамидын суурийн тал 8 ба хажуу ирмэгүүд нь суурьтайгаа $60^\circ$-ийн өнцөг үүсгэдэг. Суурийн оройг дайруулан түүнийг дайраагүй суурийн диагоналтай параллель хавтгай татахад пирамидын өндрийг сууриас тооцоход $1:2$ харьцаагаар хуваав. Хөдлөн огтлолын талбайг ол.
Зөв дөрвөн өнцөгт пирамидын суурийн талбай 8, хажуу ирмэгийн суурьтаа налсан өнцөг $60^\circ$. Пирамидыг түүний аль нэг суурийн оройг дайрсан, уг оройн эсрэг орших ирмэгтэй перпендикуляр хавтгайгаар огтлоход үүсэх хөндлөн огтлолын талбайг ол.
Зөв дөрвөн өнцөгт пирамидын хажуу ирмэг $\sqrt 6$, суурийг багтаасан тойргийн радиус $\sqrt2$ бол пирамидыг багтаасан бөмбөрцөгийн радиусыг ол.
Зөв дөрвөн өнцөгт пирамидын хажуу тал суурьтайгаа $\dfrac{\pi}{3}$ өнцөг үүсгэнэ. Суурьт багтсан тойргийн радиус $\sqrt3$ бол пирамидын эзлэхүүнийг ол.
Квадрат суурьтай дөрвөн өнцөгт пирамид өгөгджээ. Түүний нэг хажуу ирмэг нь суурийн хавтгайд перпендикуляр. Уг пирамидад доод суурь нь пирамидын суурь дээр байрлах, дээд суурийн ирмэгүүд нь пирамидын талсууд дээр байрлаж байхаар куб багтав. Хэрэв пирамидын хажуу талс сууриа $\alpha$ өнцгөөр налсан, кубийн ирмэгийн урт $a$ бол пирамидын эзлэхүүнийг ол.
Зөв дөрвөн өнцөгт пирамидын суурийн тал $a$, суурьт налсан хоёр талст өнцөг $2\alpha$ байв. Уг хоёр талст өнцгийг таллан хуваах хавтгай татав. Үүсэх хөндлөн огтлолын талбайг ол.
Гурвалжин пирамидын суурийн талууд 6 см, 5 см, 5 см ба хажуу талсууд нь суурьтайгаа үүсгэх 2 талст өнцөг $45^\circ$ бол пирамидын эзлэхүүнийг ол.
Зөв гурвалжин пирамидын өндөр 2, хажуу талс нь суурьтай $60^\circ$ үүсгэх бол пирамидын эзлэхүүнийг ол.
Пирамидыг суурьтай нь параллель хавтгайгаар огтлоход өндөр нь орой талаасаа $2:3$ харьцаагаар хуваагджээ. Хэрэв энэ хөндлөн огтлолын талбай нь суурийн талбайгаас $84$ см.кв-аар бага бол хөндлөн огтлолын талбайг ол.
Тэгш өнцөгт суурьтай пирамидын суурийн диагонал $l$ ба диагоналуудын хоорондох өнцөг $\alpha$. Пирамидын өндөр суурийн периметртэй тэнцүү бол пирамидын эзлэхүүнийг ол.
Зөв дөрвөн өнцөгт пирамидын апофем $m$, оройн өнцөг $\alpha$ бол түүний гадаргуугийн талбайг ол.
Адил хажуут гурвалжин суурьтай пирамидын суурийн хоёр тал 6 см, нөгөө тал нь 8 см. Хажуу ирмэгүүд өөр хоорондоо тэнцүү бүгд 9 см. Пирамидын эзлэхүүнийг ол.
Зөв зургаан өнцөгт пирамидын хажуу ирмэгийн суурьт налсан өнцөг $\alpha=45^\circ$. Суурийн приметр 24 бол пирамидын эзлэхүүнийг ол. Хариуг таслалаас хойш нэг орны нарийвчлалтайгаар ойролцоогоор тооцоол. $\sqrt3=1,73$ гэж ав.
Пирамидын суурь 6 талтай адил талт гурвалжин, өндөр нь 9 бол пирамидын эзлэхүүнийг ол. $\sqrt3=1,7$ гэж үз.
Тэгш өнцөгт гурвалжин суурьтай пирамидын суурийн катетууд 6 ба 8. Пирамидын хажуу талсууд суурьтай үүсгэх хоёр талст өнцгүүд бүгд тэнцүү $60^\circ$ бол пирамидын өндрийг ол. $\sqrt3=1,7$ гэж үз.
Зөв дөрвөн өнцөгт пирамидын диагонал огтлолын талбай суурьтайгаа хэм чацуу. Хажуу ирмэг 5 бол пирамидын суурийн талбайг ол.
Олон өнцөгт суурьтай зөв пирамидын суурийн дотоод өнцгүүдийн нийлбэр $540^\circ$. Пирамидын хажуу ирмэгийн урт нь $l$ ба суурьт налсан өнцөг нь $\beta$-бол пирамидын эзлэхүүнийг ол.
Зөв дөрвөн өнцөгт пирамидын хажуу ирмэг дэх хоёр талст өнцөг $120^\circ$. Пирамидын диагонал огтлолын талбай $q$ бол түүний хажуугийн гадаргуугийн талбайг ол.
$S$ оройтой $SABC$ зөв дөрвөн өнцөгт пирамидын $SC$ ирмэг дээрх $D$ цэг түүнийг $SD:DC=1:2$ гэж хуваана. Хэрэв $AB=a$, $\angle ASB=\alpha$ бол $ABD$ гурвалжны талбайг ол.
Зөв дөрвөн өнцөгт пирамидын хажуу ирмэг $18$, суурийн диагонал $16\sqrt2$ бол түүний өндөрийг ол.
Зөв зургаан өнцөгт пирамидын суурийн тал $a$. Түүний хажуу гадаргуугийн талбай суурийн талбайгаас 10 дахин их бол энэ пирамидын эзлэхүүнийг ол.
Зөв гурвалжин пирамидын суурийн тал $a$, хажуу ирмэг нь суурьтаа $\varphi$ өнцгөөр налдаг бол пирамидын эзлэхүүн, хажуу гадаргуугийн талбайг ол.
$a$ талтай кубийн нэг талсын төвийг түүний эсрэг орших талсын ирмэгүүдийн дундаж цэгүүдтэй хэрчмээр холбов. Түүнчлэн эдгээр хэрчмүүдийн төгсгөлүүдийг дараалуулан хэрчмээр холбов. Эдгээр хэрчмүүдээр үүсэх пирамидын бүтэн гадаргуугийн талбайг ол.
$ABCDA_1B_1C_1D_1$ шулуун призмийн суурь нь $ABCD$ параллельограмм. $K$, $L$, $M$, $N$ цэгүүд харгалзан $A_1B$, $B_1C$, $DA$ талууд дээр оршино. $KM$ шулуун $B_1C_1$ шулуунтай параллель, $A_2$ цэг $AA_1$ ирмэг дээр орших ба $AA_2:A_2A_1=3$ байв. $ABC$ хавтгайтай параллельиар $A_2$ цэгийг дайран гарах $\pi$ хавтгай $BK$, $BL$, $BM$, $BN$ хэрчмүүдийг харгалзан $E$, $F$, $G$, $H$ цэгүүдээр огтолно. Хэрэв $ABCD A_1B_1C_1D_1$ призмын эзлэхүүн $V$ бол $CEFGH$ дөрвөн өнцөгт пирамидын эзлэхүүнийг ол.
Зөв зургаан өнцөгт призмын хамгийн том диагонал огтлолын талбай 1 бол призмын хажуу гадаргуугийн талбайг ол.
Зөв гурвалжин пирамидын өндөр 4, түүний суурийг багтаасан тойргийн урт $\sqrt3\pi$. Уг пирамидад багтсан ба түүнийг багтаасан конусуудын эзлэхүүний зөрөөг ол.
Хажуу ирмэгийн урт нь $a$-тай тэнцүү зөв гурвалжин пирамид бөмбөрцөгт багтсан байв. Пирамидын хажуу ирмэг суурийн хавтгайтаагаа $\alpha$ өнцөг үүсгэдэг гэвэл бөмбөрцөгийн гадаргуугийн талбай ба пирамидын эзлэхүүнийг ол.
$SABCD$ дөрвөн өнцөгт пирамидын суурь нь $AB=4$, $BC=2$ талууд бүхий $ABCD$ тэгш өнцөгт. Бүх хажуу ирмэгүүдийн урт 3 бөгөөд $M$ цэг нь $SA$-ын дундаж. $BM$ шулууныг агуулсан $AC$ диагоналтай параллель хавтгай татав. $SAC$ өнцгийг ол.
< p>< /p>Бодолтыг харах!
Пирамидын суурь нь 2 см тал бүхий $ABC$ зөв гурвалжин байв. $ACD$ талс суурьтаа перпендикуляр бөгөөд $AD=CD=\sqrt{6}$ см. Пирамидын $BD$ ирмэгийн урт ба түүний бүх квадрат хэлбэртэй огтлолуудын талбайг ол.
$PQRS$ тетраэдрийн $PQ$ ирмэг дээрх $F$ цэгийг $RS$ ирмэг дээрх $G$ цэгтэй, $QS$ ирмэг дээрх $O$ цэгийг $PR$ ирмэг дээрх $N$ цэгтэй, $PS$ ба $QP$ ирмэгүүдийн дундаж $X$ ба $Y$ цэгүүдиийг тус тус хэрчмээр холбоход $FG$, $ON$, $XY$ хэрчмүүд нэг цэгт огтолцож байв. $PS=QR=PQ=5$, $PF=3$, $PS$ ба $QR$ шулуунуудын хоорондох өнцөг $60^\circ$-тай тэнцүү гэвэл $FOGN$ дөрвөн өнцөгтийн талбайг ол.
$SABCD$ зөв дөрвөн өнцөгт пирамидын $SO$ өндөр нь $H$-тай тэнцүү. Харин $ASC$ ($AS$ ба $CS$ эсрэг байрлах хажуу ирмэгүүд) өнцөг $2\alpha$. $K$ цэг $SO$ шулуун дээр орших ба $SK:SO_1=1:3$ ($O_1$-пирамидын багтсан бөмбөрцгийн төв) гэсэн харьцаагаар байрлана. Пирамидын суурьтай параллель, $K$ цэгийг дайран гарах хавтгайгаар үүсэх огтлолын талбайг ол.
$SABC$ пирамидын суурь нь $ABC$ тэгш өнцөгт гурвалжин. $B$ өнцөг тэгш, $A$ өнцөг $\alpha$-тай тэнцүү, пирамидын хажуу ирмэг бүр суурийн хавтгайтай $45^\circ$ өнцөг үүсгэдэг бол $SAC$, $SBC$ хавтгайнуудын хоорондох өнцгийг ол.
$MABCD$ дөрвөн өнцөгт пирамидын суурь нь $AB=a$, $AD=b$ талуудтай $ABCD$ тэгш өнцөгт байв. $MAD$ ба $MAB$ талсууд суурийн хавтгайтай перпендикуляр, харин $MDC$ талс $45^\circ$-ийн өнцөгөөр налдаг бол пирамидыг багтаасан бөмбөрцгийн радиусыг ол.
Пирамидын суурь адил хажуут трапец ба хажуу талын урт нь 5 байв. Мөн уг трапецад тойрог багтааж болох ба трапецийн дундаж шугам багтсан тойргийг талбайн харьцаа нь $3/7$ байх хоёр хэсэгт хуваана. Пирамидын өндөр суурийн периметртэй тэнцүү бол пирамидын эзлэхүүнийг ол.
Зөв гурвалжин пирамидын хажуу ирмэгт үүсэх хоёр талст өнцөг $2\alpha$-тай тэнцүү. Пирамидын өндөр $H$. Пирамидыг багтаасан конусын эзлэхүүнийг ол.
$SABC$ гурвалжин пирамидийн $S$ орой дахь хавтгай өнцгүүд бүгд тэгш байв. $SO$ нь пирамидын өндөр бөгөөд $AOB$ гурвалжны талбайг $BOC$ гурвалжны талбайд харьцуулсан харьцаа нь $k$ бол $ASB$ гурвалжны талбайг $BSC$ гурвалжны талбайд харьцуулсан харьцааг ол.
Пирамидын суурь нь $a$ талтай зөв гурвалжин. Түүний нэг хажуу талс нь суурьтайгаа ижил гурвалжин бөгөөд түүнд перпендикуляр байв. Пирамидыг багтаасан бөмбөрцгийн эзлэхүүнийг ол.
$SABC$ ($S$ --- оройн цэг) зөв гурвалжин пирамидын хажуу ирмэг болон суурийн хавтгайн хоорондох өнцөг $\alpha$, суурийн талын урт $a$ бөгөөд $SH$ нь пирамидын өндөр. $H$ цэгийг дайрсан $SA$ ба $BC$ ирмэгүүдтэй параллель огтлолын талбайг ол.
Гурвалжин пирамидын $A$ ба $B$ оройг дайрсан, $AS$ ба $BS$ ирмэгүүдийг харгалзан $M$ ба $N$ цэгт огтлох бөмбөрцөг байгуулав. $B$ ба $N$ цэгүүдийг дайруулан $SC$ ирмэгийг $P$ ба $Q$ цэгт огтлох бөгөөд $PQ=\dfrac13SC$ байх өөр нэг бөмбөрцөг байгуулав. Хэрэв $M$ нь $SA$ ирмэгийн дундаж цэг бөгөөд $SC=\dfrac32SA$ бол $SC$ хэрчим $QC$ ($QC< PC$) хэрчмийн ямар хэсэгтэй тэнцэх вэ?
Пирамидын өндөр 5, суурийн талууд 7, 8, 9. Нэгэн бөмбөрцөг түүний бүх хажуу талсыг суурийн тал дээр орших цэгээр шүргэх бол бөмбөрцгийн радиусыг ол.
$SABC$ ($S$ --- оройн цэг) зөв гурвалжин пирамидын $B$ ба $C$ оройг дайруулан $SA$ ирмэгийг $S$ оройгоос тооцоход $m:n$ харьцаагаар хуваах огтлогч хавтгай татав. Хэрэв $SABC$ пирамидын эзлэхүүн $V$, $ABC$ суурийн төвөөс огтлогч хавтгай хүртэлх зай $D$ бол огтлолын талбайг ол.
$ABCD$ пирамидын $AC$, $BC$, $DC$ ирмэгүүд харилцан перпендикуляр бөгөөд $AC=BC=DC=4$ байв. $AB$ ирмэгийн дундаж цэг $N$, $AD$ ирмэг дээр $M$ цэг орших бөгөөд $AM:MD=3$. $CN$ шулуун дээр төвтэй бөмбөрцөг $AD$ ирмэгийг $M$ цэгт шүргэнэ. Бөмбөрцгийн радиусыг ол.
$S$ оройтой $SABCD$ зөв дөрвөлжин пирамидын $BC$ ирмэг дээр $DM:DC=1:15$ байхаар $M$ цэг авав. $SAB$, $SCD$ хажуу талсуудыг шүргэх цилиндрийн нэг суурь нь $M$ цэгийг агуулдаг, нөгөө суурь нь $SC$ ирмэгтэй ерөнхий цэгтэй байв. Цилиндрийн хажуу гадаргуу пирамидын $SH$ өндөртэй $O$ цэгт огтлолцох ба $SO:SH=1:3$ байв. Цилиндр ба пирамидын ерөнхий цэгийг ол.
$SABC$ ($S$ нь оройн цэг) зөв гурвалжин пирамидын $BC$ ирмэг дээр $BD:DC=2:3$ байхаар $D$ цэг авав. $SAB$, $SBC$ хажуу талсуудыг шүргэх цилиндрийн нэг суурь нь $D$ цэгийг агуулдаг, нөгөө суурь нь $SC$ ирмэгтэй ерөнхий цэгтэй байв. Хэрэв цилиндрийн хажуу гадаргуу $AC$ талтай цор ганц ерөнхий цэгтэй гэвэл цилиндр ба пирамидын эзлэхүүний харьцааг ол.
$SABCD$ дөрвөн өнцөгт пирамидын суурь нь $ABCD$ параллелограмм ба $S$ оройн суурь дээрх ортогнал проекц нь параллелограммын диагоналиудын огтлолцлын цэг болж байв. $BS$ ба $BC$ ирмэгүүдэд дээр харгалзан $BE=\dfrac14BS$, $BF=\dfrac13BC$ байхаар $E$ ба $F$ цэгүүд авав. $P$ ба $Q$ цэгүүд нь харгалзан $AE$ ба $SF$ шулуунуудад харъяалагдах бөгөөд $PQ$ шулуун нь пирамидын суурийн хавтгайтай перпендикуляр байв. $ABCD$ параллелограммын талбай 3, $PQ=12$ бол пирамидын эзлэхүүнийг ол.
$SABCD$ дөрвөн өнцөгт пирамидын суурь нь $ABCD$ параллелограмм ба $S$ оройн суурь дээрх ортогнал проекц нь параллелограммын диагоналиудын огтлолцлын цэг болж байв. $DS$ ба $AD$ ирмэгүүдэд дээр харгалзан $DP=\dfrac15DS$, $DQ=\dfrac14AD$ байхаар $P$ ба $Q$ цэгүүд авав. $N$ ба $M$ цэгүүд нь харгалзан $CP$ ба $SQ$ шулуунуудад харъяалагдах бөгөөд $NM$ шулуун нь пирамидын суурийн хавтгайтай перпендикуляр байв. $ABCD$ параллелограммын талбай 6, $NM=8$ бол пирамидын эзлэхүүнийг ол.
$SABC$ пирамидын $SH$ өндрийн суурь $H$ цэг нь $ABC$ гурвалжны $CM$ медиан дээр орших бөгөөд $SH$ өндрийн дундаж цэг $O$ нь $S$ орой, $SA$ ирмэг дээрх $E$ цэг, $SB$ ирмэг дээрх $F$ цэгүүдээс нэгэн ижил зайд алслагдаж байв. Хэрэв $SH=8$, $AB=16\sqrt2$, $EF=8\sqrt{\dfrac25}$, $SMC$ өнцгийн хэмжээ $30^\circ$-ээс хэтрэхгүй, $AB$ ба $SC$ хэрчмүүдийн дундаж цэгүүд $4\sqrt{13}$ зайтай бол $SABC$ пирамидад багтсан бөмбөрцгийн радиусыг ол.
$PQRP_1Q_1R_1$ зөв гурвалжин призмийн доод суурийн $PQ$ ирмэгийг дайруулан $RR_1$ ирмэгийг огтлох огтлогч хавтгай татан түүнийг хоёр олон талст болгон хуваав. Эдгээрийн $PQR$ гурвалжин нэг талс нь болох олон талстын эзлэхүүнийг $QQ_1PP_1$ дөрвөн өнцөгт талс нь болох олон талстын эзлэхүүнд харьцуулсан харьцаа $q$. Хэрэв $PQ_1$ ба $RR_1$ шулуунуудын хоорондох өнцөг $\varphi$ бол огтлогч хавтгай ба пирамидын сууриудын хооронд үүсгэх өнцгийн хэмжээг ол.
$SKLM$ зөв гурвалжин пирамидын $ML$ тал ба $SK$ ирмэгтэй параллел $\pi$ хавтгайгаас $S$ ба $K$ цэгүүд хүртэлх зайнууд нь $ML$ шулуун хүртэлх зайнаас 2 дахин бага байв. $MSK$ хажуу талс дээр буулгасан $SP$ өндрийн урт $d$, $SL$ хажуу ирмэг ба пирамидын $SO$ өндрийн хоорондох өнцөг $\beta$ байв. $\pi$ хавтгайгаар үүсэх огтлолын талбайг ол.
$SABCD$ зөв дөрвөн өнцөгт пирамид ба суурийн төв цэг нь $SO$ шулуун дээр ($SO$ --- пирамидын өндөр) байрлах конус өгөгдөв. $E$ цэг $SD$ ирмэгийн дундаж ба $F$ цэг $AF=\dfrac32FD$ байхаар $AD$ ирмэг дээр байрлана. Конусын нэг тэхлэг огтлолын гурвалжины хоёр орой нь $CD$ шулуун дээр, гурав дахь орой нь $EF$ шулуун дээр байв. Хэрэв $AB=4$, $SO=3$ бол конусын эзлэхүүнийг ол.
$KLMN$ гурвалжин пирамидад багтсан бөмбөрцгийн төв нь түүний нэг талсыг уг талсад багтсан гурвалжны төв цэгт шүргэнэ. Хэрэв $MK=\dfrac45$, $\angle NMK=\dfrac\pi2$, $\angle KML=3\arcctg\dfrac13$, $\angle NML=\dfrac\pi2-\arcctg\dfrac13$ бол пирамидын эзлэхүүнийг ол.
$SABCD$ дөрвөн өнцөгт пирамидын суурь нь $ABCD$ ромбо байв. Уг ромбын $A$ өнцөг хурц, өндөр нь 4 ба $S$ оройн суурь дээрх ортогнал проекц нь ромбын диагоналуудын огтлолцлын цэг болж байв. Хэрэв 2 радиустай бөмбөрцөг пирамидын бүх талсыг шүргэх бөгөөд уг бөмбөрцгийн төвөөс $AC$ шулуун хүртэлх зай нь $\dfrac{2\sqrt2}3AB$ бол пирамидын эзлэхүүнийг ол.
$TABCD$ пирамидын суурь нь $BC\parallel AD, AD:BC=2$ байх $ABCD$ трапец байв. Пирамидын $T$ оройг дайруулан $BC$ шулуунтай параллел, $AB$ хэрчмийг $AM:MB=2$ байх $M$ цэгт огтлох хавтгай татахад үүсэх огтлолын талбай $S$, $BC$ ирмэгээс огтлогч хавтгай хүртэлх зай $D$ бол 1) Огтлогч хавтгай пирамидын эзлэхүүнийг ямар харьцаагаар хуваах вэ? 2) Пирамидын эзлэхүүнийг ол.
$SPQRT$ зөв дөрвөн өнцөгт пирамидын $SO$ өндрийн урт $h$, $SP$ хажуу ирмэг нь $PQRT$ хавтгайтай $\gamma$ өнцөг үүсгэнэ. Пирамидын суурийн хавтгайнууд болон бүх хажуу ирмэгийг шүргэсэн бөмбөрцөг ба пирамидын бүх оройгоос ижил зайд алслагдсан хавтгай хоёрын огтлолцолд үүсэх тойргийн радиусыг ол.
$SABC$ ($S$ нь оройн цэг) зөв гурвалжин пирамидад багтсан бөмбөрцөг нь $KL=LM=\sqrt{6}$ байх $KLMK_1L_1M_1$ шулуун, гурвалжин призмд багтах ба $KK_1$ ирмэг $AB$ шулуун дээр байрлаж байв. Хэрэв $SC$ ирмэг $LL_1M_1M$ хавтгайтай параллель бол бөмбөрцгийн радиусыг ол.
$KLMNK_1L_1M_1N_1$ призмийн суурь нь $K$ орой дахь өнцөг нь $60^\circ$-тэй тэнцүү $KLMN$ ромбо. $LL_1$ ба $LM$ ирмэгүүдийн дундаж цэгүү нь харгалзан $E$ ба $F$. $SABCD$ ($S$ оройтой) зөв дөрвөн өнцөгт пирамидын $SA$ ирмэг $LN$ шулуун дээр орших ба $B$, $D$ оройнууд нь харгалзан $MM_1$, $EF$ ирмэгүүд дээр оршино. Хэрэв $SA=2AB$ бол призм ба пирамидын эзлэхүүнүүдийн харьцааг ол.
$SABCD$ дөрвөн өнцөгт пирамидын суурь $ABCD$ ($BC\parallel AD$) трапец ба $BC=\dfrac45AD$, $\angle ASD=\angle CDS=\dfrac\pi2$ байв. Пирамидын бүх оройнууд $2$ өндөртэй, $\dfrac53$ суурийн радиустай цилиндрийн суурийн тойргууд дээр байрлах бол пирамидын эзлэхүүнийг ол.
Талсууд нь хурц өнцөгт гурвалжнууд байх $EFGH$ пирамидын өндрүүд өөр хоорондоо тэнцүү байв. Хэрэв $EF=17$, $HG=14$ ба $\angle EHG=60^\circ$ бол $HF$ ирмэгийн уртыг ол.
$SABCD$ пирамидын $AB$, $BC$, $AC$ ирмэгүүд дэх 2 талст өнцгүүд нь харгалзан $90^\circ$, $30^\circ$, $90^\circ$ байв. Өгөгдсөн хавтгай $SB$, $SC$, $AC$, $AB$ ирмэгүүдийг харгалзан $K$, $L$, $M$, $N$ цэгт огтлох ба $KLMN$ нь $KL$ суурь нь $MN$ сууриасаа 2 дахин богино байдаг трапец болно. Хэрэв трапецийн өндөр нь $13$ ба $AS=BC=13$ бол уг трапецийн талбайг ол.
$ABCDA_1B_1C_1D_1$ кубийн ирмэг $9$. Харгалзан $BC$, $CD$, $CC_1$ хэрчмүүд дээр орших $M$, $N$, $K$ цэгүүдийг дайруулан хавтгай татав. $MCK$ гурвалжинд багтсан тойргийн радиус 1, $MNC$ гурвалжины талбай $\dfrac{21}2$, $CN$ ба $CK$ хэрчмүүдийн уртуудын ялгавар 3, $MNKC$ пирамидын эзлэхүүн 15-аас бага гэдэг нь мэдэгдэж байв. $MNK$ гурвалжны хавтгай ба $A_1$ оройг агуулсан гурван талсыг шүргэх бөмбөрцгийн радиусыг ол.
Пирамидын суурь нь $30^\circ$-ын хурц өнцөг бүхий 6 талтай ромбо байв. Хажуу талсуудын суурьтай үүсгэх хоёр талст өнцгүүд тэнцүү бөгөөд пирамидын хажуу гадаргуугийн талбай 36 бол хажуу талсуудын суурьтай үүсгэх хоёр талст өнцгийг градусаар илэрхийл.
A. $15^\circ$
B. $30^\circ$
C. $45^\circ$
D. $60^\circ$
E. $75^\circ$
$ABCS$ пирамидын хажуу ирмэгүүд нь хоорондоо тэнцүү бөгөөд суурь нь $(\angle C=90^\circ)$ тэгш өнцөгт гурвалжин байв. Хэрэв $ACS$, $BCS$, $ABS$ хажуу талсуудын өндөр харгалзан $SD$, $SE$, $SO$ бол $\dfrac{V_{DEOS}}{V_{ABCS}}$-г ол.
A. $\dfrac{1}{2}$
B. $\dfrac{4}{5}$
C. $\dfrac{2}{3}$
D. $\dfrac{1}{4}$
E. $\dfrac{1}{6}$
Бөмбөрцөгт багтсан зөв гурвалжин пирамидын суурь нь бөмбөрцгийн төвийг дайрч байв. Бөмбөрцгийн радиус $2\sqrt3$-тай тэнцүү. Пирамидын эзлэхүүнийг ол.
A. $4\sqrt3$
B. $16$
C. $20$
D. $19$
E. $18$
Тэгш өнцөгт параллелепипедийн $A$ оройгоос гарсан 3 ирмэгийн дундаж цэгүүд дээр суурьтай $A$ оройтой пирамидийн эзлэхүүнийг параллелепипедийн эзлэхүүнд харьцуулсан харьцааг ол.
A. $\dfrac{1}{12}$
B. $\dfrac{1}{6}$
C. $\dfrac{1}{24}$
D. $\dfrac{1}{48}$
E. $\dfrac{1}{16}$
$ABCD$ зөв тетраэдрийн эсрэг ирмэг $AB$ ба $CD$-ийн хоорондох өнцгийг ол.
A. $45^\circ$
B. $60^\circ$
C. $90^\circ$
D. $120^\circ$
E. олох боломжгүй
Зөв гурвалжин пирамидийн суурийн талбайг хажуу гадаргуугийн талбайд харьцуулсан харьцаа $2:3$ бол түүний хажуу талс суурийн хавтгайтай үүсгэх өнцгийн хэмжээг ол.
A. $\arccos\dfrac4{\sqrt{21}}$
B. $\arccos\dfrac23$
C. $45^\circ$
D. $60^\circ$
E. $\dfrac23$
Зөв дөрвөлжин пирамидийн суурийн талбайг хажуу гадаргуугийн талбайд
харьцуулсан харьцаа $1:\sqrt3$ бол пирамидийн суурийн хоёр талст өнцгийн хэмжээг ол.
A. $\arctg\sqrt3$
B. $30^\circ$
C. $45^\circ$
D. $60^\circ$
E. $\arccos\dfrac1{\sqrt3}$
Бүх ирмэг нь $a$ урттай $ABCD$ тетраэдрийн $D$ орой, $BC$ ирмэгийн
дунджийг дайрч $AC$ ирмэгтэй параллел байрлах хавтгай $(ABC)$ талстай үүсгэх өнцгийн синусыг ол.
A. $\dfrac{3\sqrt{22}}{11}$
B. $\dfrac{7\sqrt{11}}{22}$
C. $\dfrac{4\sqrt{66}}{33}$
D. $\dfrac{3\sqrt{55}}{44}$
E. $\dfrac{4\sqrt{22}}{33}$
$a$ урттай ирмэг бүхий зөв тетраэдрийн суурийн нэг ирмэг ба эсрэг ирмэгийн дунджийг дайрсан хавтгай, тетраэдрийн суурийн талстай үүсгэх өнцгийн хэмжээг ол.
A. $30^\circ$
B. $45^\circ$
C. $\arcsin\frac{\sqrt2}3$
D. $\arcsin\frac{\sqrt3}3$
Гурвалжин пирамидын хажуу ирмэгүүд ижил урттай бол түүний суурь ямар
гурвалжин байхад пирамидын өндөр суурийн тал дээрээ буух вэ?
A. хурц өнцөгт
B. мохоо өнцөгт
C. тэгш өнцөгт
D. ямар ч
гурвалжны хувьд боломжгүй
Гурвалжин пирамидын хажуу ирмэгүүд ижил урттай бол түүний суурь
ямар гурвалжин байхад пирамидын өндөр суурийн талсынхаа гадна буух вэ?
A. хурц өнцөгт
B. мохоо өнцөгт
C. тэгш өнцөгт
D. ямар ч
гурвалжны хувьд боломжгүй
Зөв биш гурвалжин суурьтай пирамидын хажуу ирмэгүүд суурийн
хавтгайтай ижил өнцөг үүсгэдэг бол пирамидын өндөр суурийн гурвалжны хаана буух вэ?
A. медиануудын огтлолцлын цэг дээр
B. өндрүүдийн огтлолцлын цэг дээр
C. багтаасан тойргийн төв дээр
D. багтсан тойргийн төв дээр
E. аль нь ч биш
Зөв биш гурвалжин суурьтай пирамидын хажуу талсууд суурийн хавтгайтай
ижил өнцөг үүсгэдэг бол пирамидын өндөр суурийн гурвалжны
хаана буух вэ?
A. медиануудын огтлолцлын цэг дээр
B. өндрүүдийн огтлолцлын цэг дээр
C. багтаасан тойргийн төв дээр
D. багтсан тойргийн төв дээр
Кубийн төвийг суурийн талсын оройнуудтай холбоход үүсэх пирамидын хажуу гадаргуугийн талбай кубийн диагональ огтлолын талбай $S$-ээр яаж илэрхийлэгдэх вэ? Кубийн диагональ огтлол гэдэг нь түүний аль нэг параллель хоёр талсын диагоналийг дайрсан огтлол юм.
A. $\dfrac14S$
B. $\dfrac12S$
C. $S$
D. $\dfrac32S$
E. $\dfrac23S$
Пирамидын өндрийн дундаж цэгийг дайруулан суурьтай параллель
хавтгайгаар огтлоход үүсэх жижиг пирамидын хажуу гадаргуугийн талбай анхны
пирамидын хажуу гадаргуугийн талбай $S$-ээр яаж илэрхийлэгдэх вэ?
A. $\dfrac12S$
B. $\dfrac14S$
C. $\dfrac16S$
D. $\dfrac18S$
E. $\dfrac13S$
Гурвалжин пирамидын таван ирмэг ижил 2 нэгж урттай байхад бүтэн
гадаргуугийн талбайн хамгийн их утга хэд байх вэ?
A. $2(2+\sqrt3)$кв.н.
B. $2(\sqrt2+\sqrt3)$кв.н.
C. $4+\sqrt3$кв.н.
D. $2(1+\sqrt3)$кв.н.
Гурвалжин пирамидын таван ирмэг ижил 3 нэгж урттай бол бүтэн гадаргуугийн
талбайн хамгийн их утгыг ол.
A. $\frac92(1+\sqrt3)$кв.н.
B. $\frac92(\sqrt2+\sqrt3)$кв.н.
C. $\frac92(2+\sqrt3)$кв.н.
D. $9+\sqrt3$кв.н.
Гурвалжин пирамидын суурийн талууд 26, 28, 30 нэгж урттай ба хажуу
талсууд суурийн хавтгайтай нэг ижил $60^\circ$ өнцөг үүсгэнэ. Пирамидын бүтэн гадаргуугийн
талбайг ол.
A. 976 кв.н
B. 990 кв.н
C. 1008 кв.н
D. 1002 кв.н
E. 1000 кв.н
Гурвалжин пирамидын суурийн талууд 11, 25, 30 нэгж урттай ба хажуу
талсууд суурийн хавтгайтай ижил өнцөг үүсгэнэ. Пирамидын өндөр 12 нэгж бол
суурийн хоёр талст өнцгийн хэмжээг ол.
A. $30^\circ$
B. $60^\circ$
C. $\arctg4$
D. $\arctg3$
E. $75^\circ$
Кубийн төвийг суурийн талсын оройнуудтай холбоход үүсэх пирамидын эзлэхүүнийг кубийн эзлэхүүн $V$-ээр илэрхийл.
A. $\dfrac14V$
B. $\dfrac16V$
C. $\dfrac38V$
D. $\dfrac12V$
E. $\dfrac58V$
Кубийн дээд суурийн төвийг доод суурийн оройнуудтай холбоход үүсэх
пирамидын эзлэхүүнийг кубийн эзлэхүүн $V$-ээр илэрхийл.
A. $\dfrac12V$
B. $\dfrac13V$
C. $\dfrac14V$
D. $\dfrac23V$
E. $\dfrac16V$
$ABCD$ параллелограмм суурьтай $SABCD$ пирамидын эзлэхүүн $V$ ба
$SD,SC$ ирмэгүүдийн дундаж цэгүүд харгалзан $M,N$ бол $SMNB$ пирамидын эзлэхүүнийг ол.
A. $\frac18V$
B. $\frac16V$
C. $\frac38V$
D. $\frac14V$
$ABCD$ параллелограмм суурьтай пирамидын оpой $S$,
эзлэхүүн $V$ ба $SD$ ирмэгийн дундаж цэг $M$ бол $SABM$ пирамидын эзлэхүүнийг ол.
A. $\frac14V$
B. $\frac38V$
C. $\frac58V$
D. $\frac5{16}V$
Зөв $n$ өнцөгт пирамидад багтсан ба түүнийг багтаасан конусуудын
эзлэхүүнүүдийн харьцаа $1:4$ бол $n$-г ол.
A. $n=3$
B. $n=4$
C. $n=5$
D. $n=6$
E. $n=8$
Зөв $n$ өнцөгт пирамидад багтсан ба түүнийг багтаасан конусуудын эзлэхүүний харьцаа $1:2$ бол $n$-г ол.
A. $n=3$
B. $n=4$
C. $n=5$
D. $n=6$
E. $n=8$
Зөв дөрвөн өнцөгт пирамидын өндөр 18 нэгж, түүнд багтсан бөмбөрцгийн радиус 5 нэгж бол пирамидын эзлэхүүнийг ол.
A. $1200$
B. $1350$
C. $2010$
D. $2100$
E. $2700$
Зөв гурвалжин пирамидын өндөр 18 нэгж, түүнд багтсан бөмбөрцгийн
радиус 5 нэгж бол пирамидын суурийн талыг ол.
A. 15
B. 32
C. $15\sqrt3$
D. $17\sqrt2$
$1248$ м.кв эзлэхүүнтэй огтлогдсон зөв дөрвөн өнцөгт пирамидийн апофем ба сууриудын талууд $5:9:3$ харьцаатай бол бүтэн гадаргуугийн талбай хэдэн м.кв байх вэ?
A. $800$
B. $840$
C. $860$
D. $880$
E. $900$
Гурвалжин пирамидийн суурийн талууд 6, 8, 10 нэгж урттай байв. Суурийн нэг талыг дайрч эсрэг ирмэгт перпендикуляр байх огтлол суурийн хавтгайтай $60^{\circ}$ өнцөг үүсгэдэг бол талбай нь хэдэн кв.нэгж байх вэ?
A. $16$
B. $14$
C. $13$
D. $12$
E. $10$
Гурвалжин пирамидийн суурийн нэг талыг дайрч эсрэг ирмэгт перпендикуляр байрлах хавтгай суурийн хавтгайтай $45^{\circ}$ өнцөг үүсгэнэ. Энэ огтлолд 5, 6, 9 нэгж талуудтай гурвалжин үүссэн бол пирамидийн суурийн талбай хэдэн кв.нэгж байх вэ?
A. $18$
B. $20$
C. $24$
D. $25$
E. $28$
$SABCD$ пирамидын суурь $ABCD$ параллелограмм бол $A$ орой ба
$SB,SD$ ирмэгүүдийн дунджийг дайрсан хавтгай $SC$ ирмэгийг оройгоос ямар харьцаагаар
хуваах вэ?
A. 1:1
B. 1:2
C. 2:3
D. 1:3
$SABC$ зөв гурвалжин пирамидын $SA$ ирмэгийн дундаж цэг ба $BC$
ирмэгийг дайрсан хавтгай пирамидын өндрийг оройгоос нь ямар харьцаагаар
хуваах вэ?
A. 2:1
B. 3:2
C. 3:1
D. 1:1
Бөмбөрцөгт багтсан зөв дөрвөн өнцөгт пирамидын суурь нь бөмбөрцгийн төвийг дайрсан байв. Пирамидын эзлэхүүн 18-тэй тэнцүү бол бөмбөрцгийн радиусыг ол.
A. $\sqrt3$
B. $3$
C. $4$
D. $2$
E. $\dfrac32$
Хажуу ирмэгүүд нь 13 байх пирамидын суурь нь 6 ба 8 талтай тэгш өнцөгт байв. Эзлэхүүнийг ол.
A. 96
B. 188
C. 192
D. 196
E. 260
$ABCD$ суурьтай $ABCDA_1B_1C_1D_1$ кубийн $AD, D_1C_1$ ирмэгүүдийн дундаж цэгүүд, $B_1C_1$ ирмэгийг $1:3$ харьцаагаар хуваах цэгүүдийг дайрсан хавтгайгаар огтлоход огтлол дээр хэдэн өнцөгт үүсэх вэ?
A. $3$
B. $4$
C. $5$
D. $6$
E. $7$
$ABCD$ пирамидын $AB=2$, $BC=\sqrt7$, $CA=3$, $AD=BD=CD=4$ бол эзлэхүүнийг ол.
A. $6\sqrt3$
B. $\sqrt{41}$
C. $\dfrac{\sqrt{21}}{3}$
D. $\dfrac{\sqrt{42}}{3}$
E. $\dfrac{\sqrt{41}}{2}$
$ABCD$ пирамидын $AB=2, BC=\sqrt7, CA=3, AD=BD=CD=5$ бол эзлэхүүнийг ол.
A. $\sqrt{17}$
B. $\sqrt{41}$
C. $\frac{\sqrt{51}}{3}$
D. $\frac{\sqrt{42}}{3}$
E. $\frac{\sqrt{51}}{2}$
Зөв дөрвөн өнцөгтийн пирамидын эзлэхүүн $200$, хажуу ирмэгийн суурийн хавтгайд налсан өнцгийн косинус нь $\dfrac{5}{13}$ байв. Пирамидын хажуу ирмэгийн уртыг ол.
A. $12\sqrt2$
B. $13\sqrt2$
C. $13$
D. $26$
E. $20$
Зөв дөрвөн өнцөгтийн пирамидын эзлэхүүн $24$, хажуу ирмэгийн суурийн хавтгайд налсан өнцгийн косинус нь $\dfrac{3}{5}$ байв. Пирамидын хажуу ирмэгийн уртыг ол.
A. $4$
B. $4\sqrt3$
C. $6\sqrt3$
D. $7$
E. $5$
Бөмбөрцөгт багтсан зөв дөрвөн өнцөгт пирамидын суурь нь бөмбөрцгийн төвийг дайрч байв. Пирамидын эзлэхүүн 18-тай тэнцүү бол бөмбөрцгийн радиусыг ол.
A. $\sqrt3$
B. $3$
C. $4$
D. $2$
E. $\dfrac32$
$SABC$ зөв гурвалжин пирамидын $SA$ ирмэгийн дундаж цэг ба $BC$ ирмэгийг дайрсан хавтгай пирамидын өндрийг оройгоос ямар харьцаагаар хуваах вэ?
A. $1:3$
B. $3:2$
C. $3:1$
D. $1:2$
E. $1:1$
Хажуу ирмэгүүд нь 25 байх пирамидын суурь нь $7\sqrt2$ талтай квадрат байв. Эзлэхүүнийг ол.
A. 784
B. 688
C. 792
D. 800
E. 825
$ f(x)=x^2-4x+5 $ функцийг $ x=1 $ цэгт татсан нормал шулууны тэгшитгэл бич.
A. $ y=-2x+4$
B. $ y=\frac12+\frac32$
C. $ y=-\frac12x+\frac52 $
D. $ y=2x $
E. $ y=2x-4$
Зөв дөрвөн өнцөгт пирамидын хажуу талс суурьтай $60^\circ$ өнцөг үүсгэнэ. Суурийн тал нь 4 см бол хажуу ирмэгийн уртыг олоорой
A. $3\sqrt{5}$
B. $4\sqrt{5}$
C. $\sqrt{5}$
D. $2\sqrt{5}$
E. $\sqrt{3}$
Зөв дөрвөн өнцөгт пирамидын хажуу талс суурьтай $60^\circ$ өнцөг үүсгэнэ. Суурийн тал нь 6 см бол хажуу ирмэгийн уртыг олоорой
A. $\sqrt{5}$
B. $4\sqrt{5}$
C. $5\sqrt{5}$
D. $2\sqrt{5}$
E. $3\sqrt{5}$
Зөв дөрвөн өнцөгт пирамидын хажуу талс суурьтай $60^\circ$ өнцөг үүсгэнэ. Суурийн тал нь 6 см бол хажуу ирмэгийн уртыг олоорой
A. $ \sqrt{5}$
B. $ 4\sqrt{5}$
C. $ 5\sqrt{5}$
D. $ 2\sqrt{5}$
E. $ 3\sqrt{5}$
$ABCD$ пирамидын $ABD$, $BCD$, $CAD$ хажуу талсууд ижил талбайтай ба $AD$, $BD$, $CD$ ирмэгүүд дээр харгалзан $DA_1:DA=1:2$, $DB_1:DB=2:5$, $DC_1:DC=5:9$ байх $A_1, B_1, C_1$ цэгүүд авав. Тэгвэл $DA_1B_1C_1$ ба $DABC$ ($D$-орой) пирамидуудын хажуу гадаргуугийн талбайн харьцаа $\fbox{a}:\fbox{bc}$ (3 оноо), эзлэхүүний харьцаа $\fbox{d}:\fbox{e}$ байна. (4 оноо)
Гурвалжин пирамидын суурь нь $30^\circ$ хурц өнцөгтэй тэгш өнцөгт гурвалжин бөгөөд уг пирамидын хажуу ирмэгүүд нь тэнцүү 6 нэгж урттай ба суурийн хавтгайтай $45^\circ$ өнцөг үүсгэнэ.
- Пирамидын өндөр $\fbox{a}\sqrt{\fbox{b}}$ (2 оноо)
- Суурийн гурвалжны талбай $\fbox{c}\sqrt{\fbox{d}}$ (2 оноо)
- Пирамидын эзлэхүүн $\fbox{e}\sqrt{\fbox{f}}$ (1 оноо)
- Пирамидыг багтаасан бөмбөрцгийн радиус нь $\fbox{g}\sqrt{\fbox{h}}$ (2 оноо)
$ABCDEFS$ зөв зургаан өнцөгт пирамид дотор 3 см радиустай бөмбөрцөг багтжээ. Апофем нь суурийн хавтгайтай $60^\circ$ өнцөг үүсгэдэг бол пирамидын эзлэхүүнийг ол.
Бодолт:
$SOM$-аас $SO=6$ см. Иймд $SK=9$ см болох ба
Бодолт:

$SOM$-аас $SO=6$ см. Иймд $SK=9$ см болох ба
- $SGK$-аас $GK=\fbox{a}\sqrt{\fbox{a}}$ см тул (2 оноо)
- Суурийн талбай $S_c=\fbox{bc}\sqrt{\fbox{a}}$ см.кв болно. (3 оноо)
- Эндээс пирамидын эзлэхүүн $V=\fbox{def}\sqrt{\fbox{a}}$ см.куб (3 оноо)
Суурь нь $\sqrt{2}$ талтай зөв гурвалжин , хажуу ирмэгүүд нь бүгд $1$ урттай байх гурвалжин пирамидын эзлэхүүн $\frac{\fbox{a}}{\fbox{b}}$ ба энэ пирамидыг багтаасан бөмбөрцгийн радиус $\frac{\sqrt{\fbox{c}}}{\fbox{d}}$ байна.
$ABCD$ пирамидын $AB, CD$ ирмэгүүдийн дундаж цэгийг харгалзан $M, N$ гээд $DA$ ирмэг дээр $DP:PA=2:3$ байх $P$ цэг авахад $M, N, P$ цэгүүдийг дайрсан хавтгай $AC$ шулууныг $S$, $CB$ ирмэгийг $Q$ цэгээр огтолбол $\overrightarrow{SC}=\fbox{a}\overrightarrow{CA}$, $CQ:QB=\fbox{b}:\fbox{c}$ байна.
Зөв дөрвөн өнцөгт пирамидын хажуу талс суурьтайгаа $\dfrac{\pi}{3}$ өнцөг үүсгэнэ. Суурьт багтсан тойргийн радиус $\sqrt3$ бол хажуу ирмэгийн урт $\sqrt{\fbox{ab}}$, бүтэн гадаргуугийн талбай $\fbox{cd}$, эзлэхүүн нь $\fbox{ef}$ байна.
$ABCD$ тетраэдрийн ${AC=AB=AD=6,BC=BD=CD=6\sqrt{2}}$ байв.
- Тетраэдрийн бүтэн гадаргуугийн талбай $\fbox{ab}+\fbox{cd}\sqrt{3}$ байна.
- Тетраэдрийн эзлэхүүн $\fbox{ef}$ байна.
- Тетраэдрт багтсан бөмбөрцгийн радиус $\fbox{g}-\fbox{h}\sqrt3$ байна.
- $A$ цэгээс $(BCD)$ хавтгай хүртэлх зай $\fbox{i}\sqrt{\fbox{j}}$ байна.
$SABCD$ зөв дөрвөн өнцөгт пирамидын $ABCD$ суурийн тал 2-той,
хажуу ирмэг ба суурийн хавтгайн хоорондох өнцөг $\arccos
\dfrac1{\sqrt{5}}$-тай тэнцүү. $SA$, $SD$ ирмэгүүд дээр харгалзан
$E$, $F$ цэгүүдийг $AE=2\cdot ES$, $DF=8\cdot SF$ байхаар аваад, $E$ ба $F$ цэгүүдийг дайрсан $AB$-тэй параллель $\alpha$ хавтгайгаар пирамидыг огтлох огтлолыг байгуулав.
- Огтлолын талбай $S=\dfrac{\fbox{ab}\sqrt{\fbox{c}}}{\fbox{de}}$ байна.
- $A$ цэгт төвтэй $\alpha$ хавтгайг шүргэсэн бөмбөрцгийн радиус $R=\dfrac{\fbox{f}\cdot\sqrt{\fbox{g}}}{\fbox{h}}$ байна.
- $\alpha$ ба $(ABC)$ хавтгайн хоорондох өнцөг $\varphi=\arccos\dfrac{\fbox{k}}{\sqrt{\fbox{m}}}$.
Суурь нь $\sqrt{2}$ талтай зөв гурвалжин , хажуу ирмэгүүд нь бүгд $1$ урттай байх гурвалжин пирамидын эзлэхүүн $\frac{\fbox{a}}{\fbox{b}}$ ба энэ пирамидыг багтаасан бөмбөрцгийн радиус $\frac{\sqrt{\fbox{c}}}{\fbox{d}}$ байна.
Зөв гурвалжин пирамидын суурийн тал нь $4$ ба өндөр нь $\sqrt3$ байв. Cуурийн талбай нь $\fbox{a}\sqrt{\fbox{b}}$ ба эзлэхүүн нь $V=\fbox{c}$ байна.
Зөв 6 өнцөгт пирамидийн суурийг багтаасан тойргийн радиус $2\sqrt[4]3$, өндөр нь 5 бол суурийн талбай нь $S=\fbox{ab}$, эзлэхүүн нь $V=\fbox{cd}$ байна.
Гурвалжин пирамидын суурь нь $45^\circ$ хурц өнцөгтэй тэгш өнцөгт гурвалжин бөгөөд уг пирамидын хажуу ирмэгүүд нь тэнцүү $4\sqrt3$ нэгж урттай ба суурийн хавтгайтай $60^\circ$ өнцөг үүсгэдэг бол:
- Пирамидын өндөр $\fbox{a}$
- Суурийн гурвалжны талбай $\fbox{bc}$
- Пирамидын эзлэхүүн $\fbox{de}$
- Пирамидыг багтаасан бөмбөрцгийн радиус нь $\fbox{f}$ байна.
$ABCA_1B_1C_1$ шулуун призмийн $ABC$ суурийн талбай нь 8, өндөр 6 байв. $AA_1$, $BB_1$ ирмэгүүдийн дундаж цэгүүд нь харгалзан $M$ ба $N$ бол
- Призмийн эзлэхүүн $\fbox{ab}$;
- $CABNM$ пирамидын эзлэхүүн $\fbox{cd}$;
- Призм дотор санамсаргүйгээр цэг сонгоход тэр нь $CABMN$ пирамид дотор байх магадлал $\dfrac{1}{\fbox{e}}$ байна.
$SKLM$ зөв гурвалжин пирамидын $SK$ хажуу ирмэг ба $SO$ өндрийг
дайрсан огтлолын талбай пирамидын суурийн талбайгаас 2 дахин их ба
пирамидын хажуу ирмэгийн урт $\sqrt{13}$-тай тэнцүү бол пирамидын
хажуу талсын талбай
$\dfrac{\fbox{a}\sqrt{\fbox{b}}}{\fbox{c}}$-тай тэнцүү.
$SABCD$ зөв дөрвөн өнцөгт пирамидын $SB$ ба $SD$ хажуу ирмэгүүдийг дайран гарсан огтлолын талбай пирамидын суурийн талбайгаас 3 дахин их ба пирамидын хажуу ирмэгийн урт $\sqrt{37}$-той тэнцүү бол пирамидын хажуу талсын талбай $\dfrac{\sqrt{\fbox{ab}}}{\fbox{c}}$-тэй тэнцүү.
Зөв гурвалжин пирамидын өндөр $H=3$, эзлэхүүн нь $V=9\sqrt{3}$
байвал энэ пирамидыг багтаасан бөмбөлгийн радиус
$R=\dfrac{\fbox{a}}{\fbox{b}}$ байна.
Зөв гурвалжин пирамидын өндөр $H=4\sqrt{3}$, эзлэхүүн нь $V=48$
байвал энэ пирамидыг багтаасан бөмбөлгийн радиус
$R=2\sqrt{\dfrac{\fbox{ab}}{\fbox{c}}}$ байна.
Ирмэг бүрийн урт нь $2\sqrt{3}$-тай тэнцүү $SABCD$ зөв дөрвөн
өнцөгт пирамидыг $AD$ ирмэгийн дундаж цэгийг дайрсан, $AC$ ба $SD$
шулуунтай параллель хавтгайгаар огтлоход пирамидын огтлолд
$\fbox{a}$-өнцөгт үүсэв. Энэ олон өнцөгтийн периметр
$\sqrt{\fbox{b}}+2\sqrt{\fbox{c}}+\fbox{d}$ байна.
Ирмэг бүрийн урт нь 2-той тэнцүү $SABCD$ зөв дөрвөн өнцөгт
пирамидын $AB$ ирмэгийг огтолсон, $AC$ ба $SB$ шулуунтай параллель
хавтгайгаар огтлоход пирамидын огтлолд $\fbox{a}$-өнцөгт үүсэв.
Огтлолын пирамидын суурийн хавтгайтай огтолцоход үүсэх хэрчмийн
урт $\sqrt{2}$-той тэнцүү бол огтлолын олон өнцөгтийн периметр
$\fbox{b}+\sqrt{\fbox{c}}+\sqrt{\fbox{d}}$ байна.
$SABC$ зөв гурвалжин пирамидын хувьд $AB=BC=CA=1, \\
SA=SB=SC=2$ байв. $ABC$ гурвалжинд $BM$ медиан, $SAB$ гурвалжинд
$AD$ биссектрис татав. $DM=\dfrac{\sqrt{\fbox{ab}}}{\fbox{c}}$
байна.
$SABC$ зөв гурвалжин пирамидын хувьд $AB=BC=CA=3$, $SA=SB=SC=2\sqrt{3}$ байв. $ABC$ гурвалжинд $BM$ медиан, $ASB$ гурвалжинд $AR$ өндөр татав. $MR=\dfrac{\fbox{a}}{\fbox{b}}$ байна.
$SABC$ гурвалжин пирамидын хувьд $SC\perp AB, SC\perp AC,$
$AB=BC=2, AC=1,$ $SC=4$ байвал энэ пирамидыг багтаасан бөмбөлгийн радиус $R=\fbox{a}\cdot \sqrt{\dfrac{\fbox{bc}}{\fbox{de}}}$ байна.
$SKLM$ гурвалжин пирамидын хувьд $SK\perp LM$, $SK\perp KM$,
$KL=LM=3$, $KM=5$, $SK=2$ байвал энэ пирамидыг багтаасан
бөмбөлгийн радиус $R=\fbox{a}\cdot\sqrt{\dfrac{\fbox{bc}}{\fbox{de}}}$ байна.
$SABCD$ зөв дөрвөн өнцөгт пирамидын $SA$ хажуу ирмэг ба суурийн
хавтгай $(ABCD)$-ийн хоорондох өнцөг нь $SA$ хажуу ирмэг ба $SBC$
талсын хавтгайн хоорондох өнцөгтэй тэнцүү бол энэ өнцгийн хэмжээ
$\varphi=\arcsin\sqrt{\dfrac{\fbox{a}}{\fbox{b}}}$ байна.
$SABCD$ зөв дөрвөн өнцөгт пирамидын $SA$ хажуу ирмэг ба $BD$ диагональ нь $SBC$ хажуу талсын хавтгайтай тэнцүү өнцөг үүсгэнэ. Энэ өнцгийн хэмжээ $\varphi=\arcsin\sqrt{\dfrac{\fbox{a}}{\fbox{b}}}$ байна.
Ирмэгүүд нь 15; 9; 9; 12; 12; 3-тай тэнцүү гурвалжин пирамидыг багтаасан бөмбөлгийн радиус $R=\dfrac{\fbox{ab}}{\fbox{c}}$, пирамидын эзлэхүүн $V=\dfrac{\fbox{d}}{4}\sqrt{\fbox{efg}}$ байна.
Ирмэгүүд нь 2; 6; 6; 8; 8; 10-тай тэнцүү гурвалжин пирамидыг багтаасан бөмбөлгийн радиус $R=\fbox{a}$, пирамидын эзлэхүүн $V=\dfrac{\fbox{b}}{\fbox{c}}\sqrt{\fbox{def}}$ байна.
Зөв дөрвөн өнцөгт пирамидын суурь $ABCD$ ба орой нь $S$ байг.
$SA, SB, SC$ ирмэгүүд дээр харгалзан $M, N, K$ цэгүүдийг
$\dfrac{SM}{MA}=\dfrac 12, \dfrac{SN}{NB}=1, \dfrac{SK}{KC}=3$
байхаар авчээ. $M, N, K$ цэгүүдийг дайрсан хавтгай $SD$ ирмэгийг
огтлох цэгийг $L$ гэвэл
$\dfrac{SL}{LD}=\dfrac{\fbox{a}}{\fbox{b}}$ байна.
Зөв дөрвөн өнцөгт пирамидын суурь $ABCD$ ба орой нь $S$ байг. $SA, SB, SC$ ирмэгүүд дээр харгалзан $M, N, K$ цэгүүдийг $\dfrac{SM}{MA}=\dfrac 23, \dfrac{SN}{NB}=2, \dfrac{SK}{KC}=4$ байхаар авчээ. $M, N, K$ цэгүүдийг дайрсан хавтгай $SD$ ирмэгийг огтлох цэгийг $L$ гэвэл $\dfrac{SL}{LD}=\dfrac{\fbox{a}}{\fbox{b}}$ байна.
Зөв дөрвөн өнцөгт пирамидад оройнууд нь давхцдаг байхаар шулуун
дугуй конус багтжээ. Конусын суурийн радиус 6, конуст багтсан
бөмбөрцгийн радиус 2-той тэнцүү бол пирамид ба конусын эзлэхүүний
ялгавар $\fbox{ab}\cdot(\fbox{c}-\pi)$ байна.
Зөв дөрвөн өнцөгт пирамидад оройнууд нь давхцдаг байхаар шулуун
дугуй конус багтжээ. Тэдгээрийн өндөр (ерөнхий) $\dfrac 94$-тэй,
конуст багтсан бөмбөрцгийн радиус 1-тэй тэнцүү бол пирамид ба
конусын эзлэхүүнхий ялгавар $\fbox{ab}\cdot
\left(\fbox{c}-\dfrac{\pi}{4}\right)$ байна.
$DABC$ гурвалжин пирамидын $DAB, DAC, DBC$ талсууд тэнцүү
талбайтай. $DA$ ирмэг дээр $A_1$ цэгийг $DA_1:DA=2:5$ байхаар,
$DB$ ирмэг дээр $B_1$ цэгийг $DB_1:DB=5:6$ байхаар, $DC$ ирмэг
дээр $C_1$ цэгийг авав. $DA_1B_1C_1$ пирамидын хажуу гадаргуугийн
талбайг $DABC$ пирамидын хажуу гадаргуугийн талбайд харьцуулсан
харьцаа 47:90 байвал $DA_1B_1C_1$ пирамидын эзлэхүүнийг $DABC$
пирамидын эзлэхүүнд хаьцуулсан харьцаа $\fbox{a}:\fbox{b}$ байна.
$DABC$ гурвалжин пирамидын $DAB, DAC, DBC$ талсууд тэнцүү
талбайтай. $DA$ ирмэг дээр $A_1$ цэгийг $DA_1:DA=3:7$, $DB$ ирмэг
дээр $B_1$ цэгийг $DB_1:DB=7:9$ байхаар, $DC$ ирмэг дээр $C_1$
цэгийг авав. $DA_1B_1C_1$ пирамидын эзлэхүүнийг $DABC$ пирамидын
эзлэхүүнд харьцуулсан харьцаа 1:3 байвал $DA_1B_1C_1$ пирамидын
хажуу гадаргуугийн талбайг $DABC$ пирамидын хажуу гадаргуугийн
талбайд харьцуулсан харьцаа $\fbox{ab}:\fbox{cde}$ байна.
Зөв гурвалжин пирамид дотор хоёр бөмбөрцөг байрлажээ. Нэг нь $r=5$
радиустай бөгөөд пирамидын суурь ба хажуу талсуудыг шүргэдэг
байхаар, нөгөө нь I бөмбөрцгийг гадаад байдлаар болон пирамидын
хажуу талсуудыг шүргэдэг байхаар байрлажээ. Пирамид нь хамгийн
бага эзлэхүүнтэй гэж мэдэгдэж байгаа бол бөмбөрцгүүдийн эзлэхүүний
нийлбэр $\dfrac{\fbox{abc}}{\fbox{d}}\cdot \pi$ байна.
Зөв гурвалжин пирамид дотор хоёр бөмбөрцөг байрлажээ. Нэг нь $r=5$
радиустай бөгөөд пирамидын суурь ба хажуу талсуудыг шүргэдэг
байхаар, нөгөө нь I бөмбөрцгийг гадаад байдлаар болон пирамидын
хажуу талсуудыг шүргэдэг байхаар байрлажээ. Пирамид нь хамгийн
бага эзлэхүүнтэй гэж мэдэгдэж байгаа бол хоёр дахь бөмбөрцгийн
радиус $R=\dfrac{\fbox{a}}{\fbox{bc}}\cdot (\sqrt{\fbox{cd}}-1)$
байна.
$SABC$ гурвалжин пирамидын $SA$ хажуу ирмэг дээр $M$ цэгийг
$MA:MS=2:1$ байхаар авчээ. $M$ цэгийг дайрсан $AB$-тэй параллель
хавтгай $AC$ ирмэгийг $P$ цэгээр огтлох ба пирамидыг
эзлэхүүнүүдийнх нь харьцаа 5:4 байх хоёр олон талстад хуваана.
$PC:PA=\fbox{a}$ эсвэл
$PC:PA=(\fbox{b}+\sqrt{\fbox{cd}}):\fbox{e}$ байна.
$SABC$ гурвалжин пирамидын $SA$ хажуу ирмэг дээр $M$ цэгийг
$MA:MS=3:2$ байхаар авчээ. $M$ цэгийг дайрсан $AB$-тэй параллель
хавтгай $AC$ ирмэгийг $P$ цэгээр огтлох ба пирамидыг
эзлэхүүнүүдийнх нь харьцаа 13:12 байх хоёр олон талстад хуваана.
$PC:PA=\fbox{a}:\fbox{b}$ эсвэл
$PC:PA=(\fbox{c}+\sqrt{\fbox{def}}):\fbox{gh}$ байна.
$SABCD$ пирамидын суурь $ABCD$ нь $BC$ ба $AD$ суурьтай трапец
бөгөөд $BC:AD=2:3$ болно. Трапецийн диагоналиуд $E$ цэгт огтолцох
ба пирамидад багтсан бөмбөлгийн төв $O$ нь $SE$ хэрчим дээр орших
ба түүнийг $SO:OE=5:2$ харьцаанд хуваана. Хэрэв $SBC$ талсын
талбай 12-той тэнцүү байвал пирамидын бүтэн гадаргуугийн талбай
$\fbox{abc}$ байна.
$SABCD$ пирамидын суурь $ABCD$ нь $BC$ ба $AD$ суурьтай трапец
бөгөөд $BC:AD=2:5$ болно. Трапецийн диагоналиуд $E$ цэгт огтолцох
ба пирамидад багтсан бөмбөлгийн төв $O$ нь $SE$ хэрчим дээр орших
ба түүнийг $SO:OE=7:2$ харьцаанд хуваана. Хэрэв $SBC$ талсын
талбай 8-той тэнцүү байвал пирамидын бүтэн гадаргуугийн талбай
$\fbox{abc}$ байна.
$SABC$ гурвалжин пирамидын $SH$ өндрийн суурь $H$ нь $ABC$ талс
дээр оршино. $SH=\sqrt{\dfrac{5}{21}}, SA=1, SB=2,
\measuredangle ASB=120^{\circ}, \measuredangle ACB=60^{\circ}$
байвал $SABC$ пирамидыг багтаасан бөмбөлгийн радиус
$\dfrac{\sqrt{\fbox{ab}}}{\fbox{c}}$-тэй тэнцүү.
$SABC$ гурвалжин пирамидын $SH$ өндрийн суурь $H$ нь
$ABC$ талс дээр оршино. $SH=\dfrac{\sqrt{15}}{2}, SA=3, SB=2,
\measuredangle ASB=60^{\circ}, \measuredangle ACB=120^{\circ}$
байвал $SABC$ пирамидыг багтаасан бөмбөлгийн радиус
$\dfrac{\fbox{a}}{\fbox{b}}\sqrt{\dfrac{\fbox{c}}{\fbox{d}}}$-тэй
тэнцүү.
Зөв дөрвөн өнцөгт пирамидыг багтаасан бөмбөлгийн радиус 12-той тэнцүү ба энэ бөмбөлгийн төв $O$-оос хажуу ирмэг хүртэлх зай $4\sqrt{2}$-той тэнцүү.
- Пирамидын өндөр $H=\dfrac{\fbox{ab}}{\fbox{c}}$ байна.
- $O$ цэгээс пирамидын хажуу талс хүртэлх зай $\rho=\fbox{d}\cdot \sqrt{\fbox{e}}$ байна.
- Пирамидад багтсан бөмбөлгийн радиус $r=\dfrac{\fbox{f}}{\fbox{g}}(\fbox{h}\cdot \sqrt{\fbox{k}}-1)$ байна.
Зөв дөрвөн өнцөгт пирамидыг багтаасан бөмбөлгийн радиус $6\sqrt{2}$-той тэнцүү ба энэ бөмбөлгийн төв $O$-оос хажуу талс хүртэлх зай $3$-тай тэнцүү.
- Пирамидын өндөр
$H=\dfrac{\fbox{a}\sqrt{\fbox{b}}}{\fbox{c}}$ байна.
- $O$ цэгээс пирамидын хажуу ирмэг хүртэлх зай
$\rho=\fbox{d}$ байна.
- Пирамидад багтсан бөмбөлгийн радиус $r=\dfrac{\fbox{e}}{\fbox{f}}(\fbox{g}-\sqrt{\fbox{h}})$ байна.
$SABCD$ зөв дөрвөн өнцөгт пирамидын $ABCD$ суурийн тал нь 8-тай, $SO$ өндөр нь 3-тай тэнцүү. $M$, $K$ нь харгалзан $SB$, $BC$ ирмэгүүдийн дундаж цэгүүд бол
- $AMSK$ пирамидын эзлэхүүн $V=\fbox{a}$.
- $AM$ ба $SK$ шулуунуудын хоорондох өнцөг $\varphi=\arccos\dfrac{\fbox{b}}{\fbox{c}}$ байна.
- $AM$ ба $SK$ шулуунуудын хоорондох зай $\rho=\dfrac{\fbox{de}}{\fbox{fg}}$ байна.
$SABCD$ зөв дөрвөн өнцөгт пирамидын $ABCD$ суурйн тал нь
$4\sqrt{2}$-тoй, пирамидын хажуу ирмэг ба суурийн хавтгайн
хоорондох өнцөг $\arctg\dfrac 14$-тэй тэнцүү. $M, K$ нь харгалзан
$SD, AD$ ирмэгүүдийн дундаж цэгүүд бол
1) $CMSK$ пирамидын эзлэхүүн $V=\dfrac{\fbox{a}}{\fbox{b}}$ байна.
2) $CM$ ба $SK$ шулуунуудын хоорондох өнцөг $\varphi=\arccos\dfrac{\fbox{cd}}{\fbox{ef}}$ байна.
3) $CM$ ба $SK$ шулуунуудын хоорондох зай $\rho=\dfrac{\fbox{g}}{\fbox{h}\cdot\sqrt{\fbox{k}}}$ байна.
1) $CMSK$ пирамидын эзлэхүүн $V=\dfrac{\fbox{a}}{\fbox{b}}$ байна.
2) $CM$ ба $SK$ шулуунуудын хоорондох өнцөг $\varphi=\arccos\dfrac{\fbox{cd}}{\fbox{ef}}$ байна.
3) $CM$ ба $SK$ шулуунуудын хоорондох зай $\rho=\dfrac{\fbox{g}}{\fbox{h}\cdot\sqrt{\fbox{k}}}$ байна.
$ABCD$ гурвалжин пирамидын хувьд $AC\perp BD,$ $AB=BD=AD=6$ ба
$AC$ ирмэгийн дундаж цэг $(ABD)$ ба $(BCD)$ хавтгайнуудаас ижил
зайд орших бөгөөд $AC$ ирмэг болон $(CBD)$ хавтгайн хоорондох
өнцөг $\arcsin\dfrac 13$-тай тэнцүү байв.
1) $CD=\fbox{a}$ байна.
2) $\angle CAD=\dfrac{\pi}{\fbox{b}}$ байна.
3) $BD$ ирмэг ба $(ACD)$ хавтгайн хоорондох өнцөг $\varphi=\dfrac{\pi}{\fbox{c}}$-тэй тэнцүү.
1) $CD=\fbox{a}$ байна.
2) $\angle CAD=\dfrac{\pi}{\fbox{b}}$ байна.
3) $BD$ ирмэг ба $(ACD)$ хавтгайн хоорондох өнцөг $\varphi=\dfrac{\pi}{\fbox{c}}$-тэй тэнцүү.
$ABCD$ гурвалжин пирамидын хувьд $AB\perp DC$, $\angle ADB=\dfrac{\pi}{2}$, $\angle ABD=\dfrac{\pi}{6}$, $CD$ ирмэг ба $(ABD)$ хавтгайн
хоорондох өнцөг $\dfrac{\pi}{3}$-тай тэнцүү, $AD=5,$ $CD$ ирмэгийн
дундаж цэг $(ABD)$ ба $(ABC)$ хавтгайнуудаас ижил зайд оршино.
1) $BC=\fbox{a}\sqrt{\fbox{b}}$ байна.
2) $\angle CDB=\arccos\dfrac{\fbox{c}}{\fbox{d}}$ байна.
3) $AB$ ирмэг ба $(BCD)$ хавтгайн хоорондох өнцөг $\varphi=\arctg\dfrac{\fbox{e}}{\fbox{f}}$-тэй тэнцүү.
1) $BC=\fbox{a}\sqrt{\fbox{b}}$ байна.
2) $\angle CDB=\arccos\dfrac{\fbox{c}}{\fbox{d}}$ байна.
3) $AB$ ирмэг ба $(BCD)$ хавтгайн хоорондох өнцөг $\varphi=\arctg\dfrac{\fbox{e}}{\fbox{f}}$-тэй тэнцүү.
$SABCD$ дөрвөн өнцөгт пирамидын эсрэг хоёр хажуу талс нь суурьт
перпендикуляр ба пирамидын өндөр $\sqrt{5}$-тай тэнцүү. Пирамидын
суурь $ABCD (AD=BC)$ нь тойрог багтаасан адил хажуут трапец бөгөөд
$AB=6, \angle BAD=\dfrac{\pi}{3}$ байв. $D$ цэгээс $(SAB)$ хавтгай
хүртэлх зай $\rho=\dfrac{\sqrt{\fbox{ab}}}{\fbox{c}}$ болно.
Пирамид дотор конус суурийн тойрог нь $SCD$ гурвалжинд багтсан
байхаар, харин орой нь $SAB$ талс дээр оршихоор байрлажээ.
Конусын эзлэхүүн $V=\dfrac{\pi\sqrt{\fbox{de}}}{\fbox{fg}}$ байна.
$SKLMN$ дөрвөн өнцөгт пирамидын эсрэг хоёр талс нь суурьт
перпендикуляр ба $SM=12.$ Пирамидын суурь $KLMN (MN>KL)$ нь
тойрог багтаасан адил хажуут трапец бөгөөд $KN=LM=4,$ $KN$ ба $LM$
шулуунуудын хоорондох өнцөг $\dfrac{\pi}{3}$-тай тэнцүү. $M$
цэгээс $(SKL)$ хавтгай хүртэлх зай
$\dfrac{\fbox{ab}\sqrt{\fbox{cde}}}{\fbox{fg}}$ байна. Пирамид
дотор конус суурийн тойрог нь $SMN$ гурвалжинд багтсан, харин орой
нь $SKL$ талс дээр оршихоор байрлажээ. Конусын өндөр
$H=\dfrac{\fbox{hk}\cdot\sqrt{\fbox{mn}}}{\fbox{pq}}$ байна.
$ABCD$ зөв гурвалжин пирамидын $ABC$ суурийн тал 12,
$\angle ADB=2\arctg\dfrac 34.$ $ABD$ гурвалжинд $BA_1$ биссектрис, $BCD$ гурвалжинд $BC_1$ медиан, $CB_1$ өндөр татав.
1) $A_1B_1C_1D$ пирамидын эзлэхүүн $V=\dfrac{\fbox{ab}\cdot \sqrt{\fbox{cd}}}{\fbox{ef}}$
2) $A_1B_1C_1$ гурвалжны $ABC$ хавтгай дээрх проекцийн талбай $S=\dfrac{\fbox{ghkm}\cdot\sqrt{\fbox{n}}}{\fbox{pqr}}$ байна.
1) $A_1B_1C_1D$ пирамидын эзлэхүүн $V=\dfrac{\fbox{ab}\cdot \sqrt{\fbox{cd}}}{\fbox{ef}}$
2) $A_1B_1C_1$ гурвалжны $ABC$ хавтгай дээрх проекцийн талбай $S=\dfrac{\fbox{ghkm}\cdot\sqrt{\fbox{n}}}{\fbox{pqr}}$ байна.
$ABCD$ зөв гурвалжин пирамидын $ABC$ суурийн тал 6-тай, хажуу
талсуудын хоорондох өнцөг $\arccos\dfrac1{10}$-тэй тэнцүү.
$ABD$ гурвалжинд $BA_1$ биссектрис, $BCD$ гурвалжинд $BC_1$
медиан, $CB_1$ өндөр татав.
1) $A_1B_1C_1D$ пирамидын эзлэхүүн $V=\dfrac{\fbox{a}\cdot \sqrt{\fbox{bc}}}{\fbox{de}}$ байна.
2) $A_1B_1C_1$ гурвалжны $ABC$ хавтгай дээрх проекцийн талбай $S=\dfrac{\fbox{fg}\cdot\sqrt{\fbox{h}}}{\fbox{km}}$ байна.
1) $A_1B_1C_1D$ пирамидын эзлэхүүн $V=\dfrac{\fbox{a}\cdot \sqrt{\fbox{bc}}}{\fbox{de}}$ байна.
2) $A_1B_1C_1$ гурвалжны $ABC$ хавтгай дээрх проекцийн талбай $S=\dfrac{\fbox{fg}\cdot\sqrt{\fbox{h}}}{\fbox{km}}$ байна.
$SABCD$ зөв дөрвөн өнцөгт пирамидын $ABCD$ суурийн тал 2-той,
пирамидын өндөр $2\sqrt{2}$-той тэнцүү. $SA, SD$ ирмэгүүд дээр
харгалзан $E$ ба $F$ цэгүүдийг $AE=2\cdot ES, SF=5\cdot DF$
байхаар аваад, $E, F$ цэгүүдийг дайрсан $CD$-тэй параллель
$\alpha$ хавтгайгаар пирамидыг огтлох огтлолыг байгуулав.
1) Огтлолын талбай $S=\dfrac{\fbox{ab}}{\fbox{cd}}$ байна.
2) $A$ цэгт төвтэй $\alpha$ хавтгайг шүргэсэн бөмбөлгийн радиус $R=\dfrac{\fbox{ef}\cdot\sqrt{\fbox{g}}}{\fbox{hk}}$ байна.
3) $\alpha$ ба $(ABCD)$ хавтгайнуудын хоорондох өнцөг $\varphi=\arccos\dfrac{\fbox{m}}{\fbox{np}}$ байна.
1) Огтлолын талбай $S=\dfrac{\fbox{ab}}{\fbox{cd}}$ байна.
2) $A$ цэгт төвтэй $\alpha$ хавтгайг шүргэсэн бөмбөлгийн радиус $R=\dfrac{\fbox{ef}\cdot\sqrt{\fbox{g}}}{\fbox{hk}}$ байна.
3) $\alpha$ ба $(ABCD)$ хавтгайнуудын хоорондох өнцөг $\varphi=\arccos\dfrac{\fbox{m}}{\fbox{np}}$ байна.
$SABCD$ зөв дөрвөн өнцөгт пирамидын $ABCD$ суурийн тал 2-той,
хажуу ирмэг ба суурийн хавтгайн хоорондох өнцөг $\arccos
\dfrac1{\sqrt{5}}$-тай тэнцүү. $SA, SD$ ирмэгүүд дээр харгалзан
$E, F$ цэгүүдийг $AE=2\cdot ES, DF=8\cdot SF$ байхаар аваад, $E$
ба $F$ цэгүүдийг дайрсан $AB$-тэй параллель $\alpha$ хавтгайгаар
пирамидыг огтлох огтлолыг байгуулав.
1) Огтлолын талбай $S=\dfrac{\fbox{ab}\sqrt{\fbox{c}}}{\fbox{de}}$ байна.
2) $A$ цэгт төвтэй $\alpha$ хавтгайг шүргэсэн бөмбөлгийн радиус $R=\dfrac{\fbox{f}\cdot\sqrt{\fbox{g}}}{\fbox{h}}$ байна.
3) $\alpha$ ба $(ABC)$ хавтгайн хоорондох өнцөг $\varphi=\arccos\dfrac{\fbox{k}}{\sqrt{\fbox{m}}}$
1) Огтлолын талбай $S=\dfrac{\fbox{ab}\sqrt{\fbox{c}}}{\fbox{de}}$ байна.
2) $A$ цэгт төвтэй $\alpha$ хавтгайг шүргэсэн бөмбөлгийн радиус $R=\dfrac{\fbox{f}\cdot\sqrt{\fbox{g}}}{\fbox{h}}$ байна.
3) $\alpha$ ба $(ABC)$ хавтгайн хоорондох өнцөг $\varphi=\arccos\dfrac{\fbox{k}}{\sqrt{\fbox{m}}}$
$ABCD$ зөв тетраэдрийн ирмэг 5-тай тэнцүү. $AB,$ $CD$ ирмэгүүд дээр харгалзан $K, E$ цэгүүдийг $AK=KB,$ $EC:ED=1:2$ байхаар авав. $F$ нь $ABC$ талсын төв.
1) $BC$ ба $KE$ шулуунуудын хоорондох өнцөг $\varphi=\arccos\dfrac{\fbox{a}}{\fbox{b}\cdot \sqrt{\fbox{cd}}}$ байна.
2) $BC$ ба $KE$ шулуунуудын хоорондох зай $\rho=\dfrac{5\sqrt{\fbox{e}}}{\fbox{f}}$ байна.
3) $A, B, E, F$ цэгүүдийг дайрсан бөмбөлгийн радиус $R=5\cdot \sqrt{\dfrac{\fbox{gh}}{\fbox{k}}}$ байна.
1) $BC$ ба $KE$ шулуунуудын хоорондох өнцөг $\varphi=\arccos\dfrac{\fbox{a}}{\fbox{b}\cdot \sqrt{\fbox{cd}}}$ байна.
2) $BC$ ба $KE$ шулуунуудын хоорондох зай $\rho=\dfrac{5\sqrt{\fbox{e}}}{\fbox{f}}$ байна.
3) $A, B, E, F$ цэгүүдийг дайрсан бөмбөлгийн радиус $R=5\cdot \sqrt{\dfrac{\fbox{gh}}{\fbox{k}}}$ байна.
$ABCD$ зөв тетраэдрийн ирмэг 5-тай тэнцүү. $AB,$ $CD$ ирмэгүүд дээр харгалзан $K, E$ цэгүүдийг $AE=EB,$ $EC:ED=3:1$ байхаар авав. $F$ нь $ABC$ талсын төв.
1) $BC$ ба $KE$ шулуунуудын хоорондох өнцөг $\varphi=\fbox{ab}^{\circ}$ байна.
2) $BC$ ба $KE$ шулуунуудын хоорондох зай $\rho=\dfrac{\fbox{c}}{\sqrt{\fbox{d}}}$ байна.
3) $A, B, E, F$ цэгүүдийг дайрсан бөмбөлгийн радиус $R=\dfrac{5}{\fbox{e}}\cdot \sqrt{\dfrac{\fbox{fgh}}{\fbox{k}}}$ байна.
1) $BC$ ба $KE$ шулуунуудын хоорондох өнцөг $\varphi=\fbox{ab}^{\circ}$ байна.
2) $BC$ ба $KE$ шулуунуудын хоорондох зай $\rho=\dfrac{\fbox{c}}{\sqrt{\fbox{d}}}$ байна.
3) $A, B, E, F$ цэгүүдийг дайрсан бөмбөлгийн радиус $R=\dfrac{5}{\fbox{e}}\cdot \sqrt{\dfrac{\fbox{fgh}}{\fbox{k}}}$ байна.
$ABCD$ зөв гурвалжин пирамидын $ABC$ суурийн тал 2,
$\angle ADC=2\arcsin\dfrac1{6}$ байв. $K, M, N$ нь харгалзан
$AB, CD, AC$ ирмэгүүдийн дундаж цэгүүд, $KM$ хэрчим дээр $E$
цэгийг $3\cdot ME=KE$ байхаар авчээ. $E$ цэгийг дайрсан, $KM$
хэрчимд перпендикуляр $\alpha$ хавтгайгаар пирамидыг огтлох
огтлолыг байгуулав.
1) $\alpha\cap (AD)=A_1$ гэвэл $DA_1:DA=\fbox{a}:\fbox{bc}$.
2) Огтлолын талбай $S=\dfrac{\fbox{de}\cdot\sqrt{\fbox{fg}}}{\fbox{hkm}}$ байна.
3) $N$ цэгээс $\alpha$ хавтгай хүртэлх зай $\rho=\dfrac{\fbox{np}}{\fbox{q}\cdot\sqrt{\fbox{rs}}}$ байна.
1) $\alpha\cap (AD)=A_1$ гэвэл $DA_1:DA=\fbox{a}:\fbox{bc}$.
2) Огтлолын талбай $S=\dfrac{\fbox{de}\cdot\sqrt{\fbox{fg}}}{\fbox{hkm}}$ байна.
3) $N$ цэгээс $\alpha$ хавтгай хүртэлх зай $\rho=\dfrac{\fbox{np}}{\fbox{q}\cdot\sqrt{\fbox{rs}}}$ байна.
$ABCD$ зөв гурвалжин пирамидын хажуу ирмэгийн урт 12-той, суурийн
хавтгай $(ABC)$ ба хажуу талсын хоорондох өнцөг
$\arccos\dfrac1{\sqrt{105}}$-тай тэнцүү. $K, M, N$ нь харгалзан
$AB, CD, AC$ ирмэгүүдийн дундаж цэгүүд, $KM$ хэрчим дээр $E$
цэгийг $2\cdot ME=KE$ байхаар авчээ. $E$ цэгийг дайрсан, $KM$
хэрчимд перпендикуляр $\alpha$ хавтгайгаар пирамидыг огтлох
огтлолыг байгуулав.
1) $\alpha\cap (AD)=A_1$ гэвэл $DA_1:DA=\fbox{ab}:\fbox{cd}$.
2) Огтлолын талбай $S=\left(\dfrac{\fbox{ef}}{\fbox{gh}}\right)^2\cdot \sqrt{\fbox{km}}$ байна.
3) $N$ цэгээс $\alpha$ хавтгай хүртэлх зай $\rho=\dfrac{\fbox{np}}{\fbox{q}\cdot\sqrt{\fbox{rs}}}$ байна.
1) $\alpha\cap (AD)=A_1$ гэвэл $DA_1:DA=\fbox{ab}:\fbox{cd}$.
2) Огтлолын талбай $S=\left(\dfrac{\fbox{ef}}{\fbox{gh}}\right)^2\cdot \sqrt{\fbox{km}}$ байна.
3) $N$ цэгээс $\alpha$ хавтгай хүртэлх зай $\rho=\dfrac{\fbox{np}}{\fbox{q}\cdot\sqrt{\fbox{rs}}}$ байна.
$ABCD$ зөв гурвалжин пирамидын $ABC$ суурийн тал $4\sqrt{3}$ ба
$\angle DAB=\arctg\sqrt{\dfrac{37}{3}}$ байв. $A_1, B_1, C_1$ нь
харгалзан $AD, BD, CD$ ирмэгүүдийн дундаж цэгүүд.
1) $BA_1$ ба $AC_1$ шулуунуудын хоорондох өнцөг $\varphi=\arccos\dfrac{\fbox{ab}}{\fbox{cd}}$ байна.
2) $BA_1$ ба $AC_1$ шулуунуудын хоорондох зай $\rho=\dfrac{\fbox{ef}}{\sqrt{\fbox{ghk}}}$ байна.
3) $AC_1, BA_1, CB_1$ хэрчмүүд ба $(ABC)$ хавтгайг шүргэсэн бөмбөлгийн радиус $R=\fbox{m}$ байна.
1) $BA_1$ ба $AC_1$ шулуунуудын хоорондох өнцөг $\varphi=\arccos\dfrac{\fbox{ab}}{\fbox{cd}}$ байна.
2) $BA_1$ ба $AC_1$ шулуунуудын хоорондох зай $\rho=\dfrac{\fbox{ef}}{\sqrt{\fbox{ghk}}}$ байна.
3) $AC_1, BA_1, CB_1$ хэрчмүүд ба $(ABC)$ хавтгайг шүргэсэн бөмбөлгийн радиус $R=\fbox{m}$ байна.
$ABCD$ зөв гурвалжин пирамидын $ABC$ суурийн тал $8\sqrt{3}$ ба пирамидын өндөр $DO=6$ байв. $A_1, B_1, C_1$ нь харгалзан $AD, BD, CD$ ирмэгүүдийн дундаж цэгүүд.
1) $BA_1$ ба $AC_1$ шулуунуудын хоорондох өнцөг $\varphi=\arccos\dfrac{\fbox{ab}}{\fbox{cde}}$ байна.
2) $BA_1$ ба $AC_1$ шулуунуудын хоорондох зай $\rho=\dfrac{\fbox{fg}}{\sqrt{\fbox{hkm}}}$ байна.
3) $AC_1, BA_1, CB_1$ хэрчмүүд ба $(ABC)$ хавтгайг шүргэсэн бөмбөлгийн радиус \\ $R=\dfrac{\fbox{n}}{\fbox{p}}$ байна.
1) $BA_1$ ба $AC_1$ шулуунуудын хоорондох өнцөг $\varphi=\arccos\dfrac{\fbox{ab}}{\fbox{cde}}$ байна.
2) $BA_1$ ба $AC_1$ шулуунуудын хоорондох зай $\rho=\dfrac{\fbox{fg}}{\sqrt{\fbox{hkm}}}$ байна.
3) $AC_1, BA_1, CB_1$ хэрчмүүд ба $(ABC)$ хавтгайг шүргэсэн бөмбөлгийн радиус \\ $R=\dfrac{\fbox{n}}{\fbox{p}}$ байна.
$SABCD$ зөв дөрвөн өнцөгт пирамидын апофем 2-той, хажуу ирмэг нь
$ABCD$ суурьтай үүсэх өнцөг $\arctg\sqrt{\dfrac 32}$-тай тэнцүү.
$E, F, K$ цэгүүдийг харгалзан $AB, AD, SC$ ирмэгүүд дээр
$\dfrac{AE}{EB}=\dfrac{AF}{FD}=\dfrac{SK}{KC}=\dfrac 12$ байхаар
авав. $E, F, K$ цэгүүдийг дайрсан $\alpha$ хавтгайгар пирамидыг
огтлох огтлолыг байгуулав.
1) Огтлолын талбай $S=\dfrac{\fbox{ab}}{\fbox{c}}\cdot \sqrt{\dfrac{\fbox{d}}{\fbox{e}}}$ байна.
2) $D$ цэгээс $\alpha$ хавтгай хүртэлх зай $\rho=\dfrac{\fbox{f}}{\fbox{g}\cdot \sqrt{\fbox{h}}}$ байна.
3) $SD$ шулуун ба $\alpha$ хавтгайн хоорондох өнцөг $\varphi=\arcsin\dfrac{\fbox{k}}{\fbox{m}}$ байна.
1) Огтлолын талбай $S=\dfrac{\fbox{ab}}{\fbox{c}}\cdot \sqrt{\dfrac{\fbox{d}}{\fbox{e}}}$ байна.
2) $D$ цэгээс $\alpha$ хавтгай хүртэлх зай $\rho=\dfrac{\fbox{f}}{\fbox{g}\cdot \sqrt{\fbox{h}}}$ байна.
3) $SD$ шулуун ба $\alpha$ хавтгайн хоорондох өнцөг $\varphi=\arcsin\dfrac{\fbox{k}}{\fbox{m}}$ байна.
$SABCD$ зөв дөрвөн өнцөгт пирамидын $ABCD$ суурийн тал 2-той,
хажуу талс ба суурийн хавтгайн хоорондох өнцөг $\arctg 2$-той
тэнцүү. $E, F, K$ цэгүүдийг харгалзан $AB, AD, SC$ ирмэгүүд дээр
$\dfrac{AE}{EB}=\dfrac{AF}{FD}=\dfrac{CK}{KS}=2$ байхаар авав.
$E, F, K$ цэгүүдийг дайрсан $\alpha$ хавтгайгар пирамидыг огтлох
огтлолыг байгуулав.
1) Огтлолын талбай $S=\dfrac{\fbox{ab}\sqrt{\fbox{c}}}{\fbox{d}}$ байна.
2) $D$ цэгээс $\alpha$ хавтгай хүртэлх зай $\rho=\dfrac{\fbox{e}\sqrt{\fbox{fg}}}{\fbox{hk}}$ байна.
3) $SD$ шулуун ба $\alpha$ хавтгайн хоорондох өнцөг $\varphi=\arcsin\dfrac{\fbox{m}}{\fbox{n}}$ байна.
1) Огтлолын талбай $S=\dfrac{\fbox{ab}\sqrt{\fbox{c}}}{\fbox{d}}$ байна.
2) $D$ цэгээс $\alpha$ хавтгай хүртэлх зай $\rho=\dfrac{\fbox{e}\sqrt{\fbox{fg}}}{\fbox{hk}}$ байна.
3) $SD$ шулуун ба $\alpha$ хавтгайн хоорондох өнцөг $\varphi=\arcsin\dfrac{\fbox{m}}{\fbox{n}}$ байна.
$SABCD$ зөв дөрвөн өнцөгт пирамидын $ABCD$ суурийн тал 2-той
тэнцүү. Пирамидыг, $SC$ ба $AD$ шулуунуудтай пралллель $\alpha$
хавтгайгаар огтлоход тойргийг багтаасан дөрвөн өнцөгт үүсэх бөгөөд
түүний периметр $\dfrac{32}5$-тай тэнцүү.
1) $\alpha$ хавтгай пирамидын $DS$ ирмэгийг огтлох цэгийг $D_1$ гэвэл $SD_1:SD=\fbox{a}:\fbox{b}$
2) $\alpha$ хавтгай пирамидыг эзлэхүүнүүдийнх нь харьцаа $V_1:V_2=\fbox{cd}:\fbox{ef}$ байх хоёр олон талстад хуваана.
3) Пирамидыг багтаасан бөмбөлгийн төвөөс $\alpha$ хавтгай хүртэлх зай $\rho=\dfrac{\fbox{gh}\cdot \sqrt{\fbox{km}}}{\fbox{np}\cdot \sqrt{\fbox{qr}}}$ байна.
1) $\alpha$ хавтгай пирамидын $DS$ ирмэгийг огтлох цэгийг $D_1$ гэвэл $SD_1:SD=\fbox{a}:\fbox{b}$
2) $\alpha$ хавтгай пирамидыг эзлэхүүнүүдийнх нь харьцаа $V_1:V_2=\fbox{cd}:\fbox{ef}$ байх хоёр олон талстад хуваана.
3) Пирамидыг багтаасан бөмбөлгийн төвөөс $\alpha$ хавтгай хүртэлх зай $\rho=\dfrac{\fbox{gh}\cdot \sqrt{\fbox{km}}}{\fbox{np}\cdot \sqrt{\fbox{qr}}}$ байна.
$SABCD$ зөв дөрвөн өнцөгт пирамидын $ABCD$ суурийн тал 2-той
тэнцүү. Пирамидыг, $SB$ ба $AD$ шулуунуудтай паралллель $\alpha$
хавтгайгаар огтлоход тойргийг багтаасан дөрвөн өнцөгт үүсэх бөгөөд
түүний периметр $\dfrac{48}7$-тoй тэнцүү.
1) $\alpha$ хавтгай пирамидын $DS$ ирмэгийг огтлох цэгийг $D_1$ гэвэл $SD_1:SD=\fbox{a}:\fbox{b}$
2) $\alpha$ хавтгай пирамидыг эзлэхүүнүүдийнх нь харьцаа $V_1:V_2=\fbox{cd}:\fbox{efg}$ байх хоёр олон талстад хуваана.
3) Пирамидыг багтаасан бөмбөлгийн төвөөс $\alpha$ хавтгай хүртэлх зай $\rho=\dfrac{\fbox{hkm}\cdot \sqrt{\fbox{np}}}{\fbox{qrs}\cdot \sqrt{\fbox{tu}}}$ байна.
1) $\alpha$ хавтгай пирамидын $DS$ ирмэгийг огтлох цэгийг $D_1$ гэвэл $SD_1:SD=\fbox{a}:\fbox{b}$
2) $\alpha$ хавтгай пирамидыг эзлэхүүнүүдийнх нь харьцаа $V_1:V_2=\fbox{cd}:\fbox{efg}$ байх хоёр олон талстад хуваана.
3) Пирамидыг багтаасан бөмбөлгийн төвөөс $\alpha$ хавтгай хүртэлх зай $\rho=\dfrac{\fbox{hkm}\cdot \sqrt{\fbox{np}}}{\fbox{qrs}\cdot \sqrt{\fbox{tu}}}$ байна.
$ABCD$ гурвалжин пирамид ба цилиндр өгөгдөв. Цилиндрийн доод суурийн тойрог $ABC$ гурвалжинд багтсан тойрог болно. Цилиндрийн дээд суурийн тойрог $DA, DB, DC$ ирмэгүүдийг огтлох ба төв нь $ABD$ талс дээр оршино.
Цилиндрийн суурийн радиус 3, $ABCD$ пирамидын эзлэхүүн $27\sqrt{2},$ $AB=24$ байв.
1) $ABC$ ба $ABD$ талсуудын хоорондох хоёр талст өнцөг $\varphi=\arctg\dfrac{\sqrt{\fbox{a}}}{\fbox{b}}$ байна.
2) $ABCD$ пирамидыг багтаасан бөмбөлгийн радиус $R=\sqrt{\dfrac{\fbox{cde}}{\fbox{f}}}$ байна.
1) $ABC$ ба $ABD$ талсуудын хоорондох хоёр талст өнцөг $\varphi=\arctg\dfrac{\sqrt{\fbox{a}}}{\fbox{b}}$ байна.
2) $ABCD$ пирамидыг багтаасан бөмбөлгийн радиус $R=\sqrt{\dfrac{\fbox{cde}}{\fbox{f}}}$ байна.
$ABCD$ гурвалжин пирамид ба цилиндр өгөгдөв. Цилиндрийн доод
суурийн тойрог $ABC$ гурвалжинд багтсан тойрог болно. Цилиндрийн
дээд суурийн тойрог $DA, DB, DC$ ирмэгүүдийг огтлох ба төв нь
$ABD$ талс дээр оршино. Цилиндрийн суурийн радиус 4, $ABC$ ба
$ABD$ талсуудын хоорондох хоёр талст өнцөг
$\arctg\dfrac1{\sqrt{6}},$ $AB=24$ байв.
1) $ABCD$ пирамидын эзлэхүүн $V=\fbox{abc}\cdot \sqrt{\dfrac{\fbox{d}}{\fbox{e}}}$ байна.
2) $ABCD$ пирамидыг багтаасан бөмбөлгийн радиус $R=\fbox{fg}\cdot \sqrt{\dfrac{\fbox{h}}{\fbox{i}}}$ байна.
1) $ABCD$ пирамидын эзлэхүүн $V=\fbox{abc}\cdot \sqrt{\dfrac{\fbox{d}}{\fbox{e}}}$ байна.
2) $ABCD$ пирамидыг багтаасан бөмбөлгийн радиус $R=\fbox{fg}\cdot \sqrt{\dfrac{\fbox{h}}{\fbox{i}}}$ байна.
Гурвалжин пирамид $OABC$-ийн $OA$ ирмэгийн дундаж цэг $D$,
$OBC$ талсын медиануудын огтлолцлын цэг $E$ бол $\overrightarrow{OA}=\vec a$,
$\overrightarrow{OB}=\vec b$, $\overrightarrow{OC}=\vec c$ векторуудаар
$\overrightarrow{DE}=\displaystyle\frac1{\fbox{a}}(-\fbox{b}\vec a+\fbox{c}\vec
b+\fbox{d}\vec c)$ гэж задарна.
$OABC$ пирамидийн $OA$ ирмэгийн дундаж цэг $D$, $ABC$
талсын медиануудын огтлолцлын цэг $E$ бол $\overrightarrow{AO}=\vec a$,
$\vec{AB}=\vec b$, $\overrightarrow{AC}=\vec c$ векторуудаар
$\overrightarrow{DE}=-\displaystyle\frac1{\fbox{a}}\vec
a+\displaystyle\frac1{\fbox{b}}\vec
b+\displaystyle\frac1{\fbox{c}}\vec c$ гэж задрана.
$ABCD$ зөв тетраэдрийн $ABD$ талсын хүндийн төвийг $M$ гэвэл
$\overrightarrow{CA}=\vec p$, $\overrightarrow{CB}=\vec q$, $\overrightarrow{CD}=\vec r$
векторуудын хувьд $\overrightarrow{CM}=\dfrac{\fbox{a}}{\fbox{b}}(\vec p+\vec
q+\vec r)$ байх ба $\overrightarrow{CM}$, $\overrightarrow{BD}$ векторуудын хоорондох
өнцөг $\fbox{cd}^\circ$ байна.
Бүх ирмэг нь ижил урттай зөв дөрвөн өнцөгт пирамид $SABCD$-ийн $SC$ ирмэг дээр $SM:MC=3:1$ байх $M$ цэг авч $\overrightarrow{AD}=\vec p$, $\overrightarrow{AB}=\vec q$, $\overrightarrow{AS}=\vec r$ гэвэл $\overrightarrow{AM}=\dfrac14(\fbox{a}\vec p+3\vec q+\fbox{b}\vec r)$ байх ба
$\overrightarrow{AM}$, $\overrightarrow{BD}$ векторуудын хоорондох өнцөг $\fbox{cd}^\circ$ байна.
Гурвалжин пирамид $ABCD$-ийн $AB$, $CD$, $BC$ ирмэгүүд дээр
харгалзан $M,N,Q$ цэгүүдийг $AM=MB$, $CN=ND$, $CQ:QB=2:3$ байхаар
аваад $MQ$, $AC$ шулуунуудын огтлолцлын цэгийг $S$ гэвэл
$\overrightarrow{SC}=\fbox{a}\overrightarrow{CA}$ болох ба $M,N,Q$ цэгүүдийг дайрсан
хавтгай $AD$ ирмэгийг $AP:PD=\fbox{b}:\fbox{c}$ байх $P$ цэгээр
огтолно.
$ABCD$ пирамидын $AB$, $CD$ ирмэгүүдийн дундаж цэгийг
харгалзан $M,N$ гээд $DA$ ирмэг дээр $DP:PA=2:3$ байх $P$ цэг
авахад $M,N,P$ цэгүүдийг дайрсан хавтгай $AC$ шулууныг $S$, $CB$
ирмэгийг $Q$ цэгээр огтолбол $\overrightarrow{SC}=\fbox{a}\overrightarrow{CA}$,
$CQ:QB=\fbox{b}:\fbox{c}$ байна.
$ABCDS$ зөв дөрвөн өнцөгт пирамидын суурийн тал 6 нэгжтэй тэнцүү. $S$ оройгоос суурийн хавтгайд буулгасан өндрийн суурийг $O$ гэе. $D$ ба $B$ цэгүүдээс $SC$ ирмэгт харгалзан $DM$ ба $BM$ перпендикулярууд буулгасан ба $\angle OBM=30^\circ$ байв.
- $|OM|=\sqrt{\fbox{a}}$;
- $S$ оройгоос $BC$ талд буулгасан өндрийн суурь $K$ бол $SK=\fbox{b}\sqrt{\fbox{c}}$
- Пирамидын хажуу гадаргуугийн талбай $S=\fbox{de}\sqrt{\fbox{f}}$ юм.
Гурвалжин пирамидын суурь нь $30^\circ$ хурц өнцөгтэй тэгш өнцөгт гурвалжин бөгөөд уг пирамидын хажуу ирмэгүүд тэнцүү 4 нэгж урттай ба суурийн хавтгайтай $60^\circ$ өнцөг үүсгэнэ.
- Пирамидын өндөр: $\fbox{a}\sqrt{\fbox{b}}$
- Суурийн гурвалжны талбай: $\fbox{c}\sqrt{\fbox{d}}$
- Пирамидын эзлэхүүн: $\fbox{e}$
- Пирамидыг багтаасан бөмбөрцгийн радиус нь $\dfrac{\fbox{f}}{\sqrt{\fbox{g}}}$ байна.
$ABCDEFS$ зөв зургаан өнцөгт пирамид дотор 4 см радиустай бөмбөрцөг багтжээ. Апофем нь суурийн хавтгайтай $60^\circ$ өнцөг үүсгэдэг бол пирамидын эзлэхүүнийг ол.
Бодолт:
$SOM$-аас $SO=8$ см. Иймд $SK=12$ см болох ба
Бодолт:

$SOM$-аас $SO=8$ см. Иймд $SK=12$ см болох ба
- $SGK$-аас $GK=\fbox{a}\sqrt{\fbox{b}}$ см тул (2 оноо)
- Суурийн талбай $S_c=\fbox{cd}\sqrt{\fbox{b}}$ см.кв болно. (3 оноо)
- Эндээс пирамидын эзлэхүүн $V=\fbox{efg}\sqrt{\fbox{b}}$ см.куб (3 оноо)
Зөв дөрвөн өнцөгт пирамидын суурийн диагоналийн урт 8 нэгж, хажуу ирмэгийн урт 5 нэгж бол пирамидын суурийн талын урт нь $\fbox{a}\sqrt2$, суурийн талбай нь $\fbox{bc}$, өндөр нь $\fbox{e}$, эзлэхүүн нь $\fbox{fg}$ байна.
$\angle C=90^\circ$, $\angle A=45^\circ$, $AB=3$ байх $ABC$ гурвалжин суурьтай пирамидын хажуу ирмэгүүд суурийн хавтгайтай $60^\circ$ өнцөг үүсгэнэ.
- Суурийн талбай нь $S=\dfrac{\fbox{a}}{\fbox{b}}$;
- Пирамидын өндөр нь $H=\dfrac{\fbox{c}\sqrt{\fbox{d}}}{\fbox{e}}$
- Эзлэхүүн нь $V=\dfrac{\fbox{f}\sqrt{\fbox{g}}}{\fbox{h}}$
$a$ талтай $ABCD$ зөв тетраэдр (бүх ирмэгийн урт нь тэнцүү) өгөгдөв.
- $A$ оройгоос $BCD$ талд буулгасан $AH$ өндрийн урт $\dfrac{\sqrt{\fbox{a}}}{\fbox{b}}a$;
- $ABCD$ тетраэдрийн эзлэхүүн $\dfrac{\sqrt{\fbox{c}}}{\fbox{de}}a^3$
- Өндрийн суурь $H$ цэгээс $ABC$ талс хүртэлх зай $\dfrac{\sqrt{\fbox{f}}}{\fbox{g}}a$ байна.
Зөв гурвалжин пирамидын өндөр $H=6$, эзлэхүүн $V=36\sqrt{3}$ бол энэ пирамидыг багтаасан бөмбөлгийн радиус нь $R=\fbox{a}$ байна.
$ABC$ зөв гурвалжин суурьтай $SABC$ пирамидын суурийн талууд нь $8\sqrt2$см, $SC$ хажуу ирмэгийн урт нь $8$см бөгөөд суурийн хавтгайд перпендикуляр байв. $S$ орой ба $BC$ талын дундаж цэгийг дайрсан шулуун, $AB$ талын дундаж цэг ба $C$ оройг дайрсан шулуунуудын хоорондох өнцөг ба хоорондох зайг олоорой.
Бодолт. $AB$, $CB$ талын дундаж цэгүүдийг харгалзан $D$, $E$ гэе. $AB$ шулууныг агуулсан, $CD$ шулуунд перпендикуляр хавтгайд $SABC$ пирамидыг проекцлон $CD$ хэрчим $D^\prime$ цэгт, $E$ цэг $E^\prime$ цэгт, $S$ цэг $S^\prime$ цэгт тус тус буусан гэж үзвэл $S^\prime D^\prime\perp AB$ ба $S^\prime D^\prime=8$ болно. Бидний олох ёстой 2 шулууны хоорондох зай нь $S^\prime D^\prime E^\prime$ гурвалжны $S^\prime E^\prime$ гипотенуз дээр буусан $D^\prime H$ өндөр юм. $E^\prime D^\prime=2\sqrt{\fbox{a}}$; $S^\prime E^\prime=\fbox{b}\sqrt{\fbox{c}}$; $D^\prime H=\dfrac{\fbox{d}}{\fbox{e}}$. Олох ёстой өнцгөө $\alpha$ гэж тэмдэглэвэл $SE=\fbox{f}\sqrt6$ тул $\sin\alpha=\dfrac{\sqrt{\fbox{g}}}{2}\Rightarrow\alpha=\dfrac{\pi}{\fbox{h}}$ байна.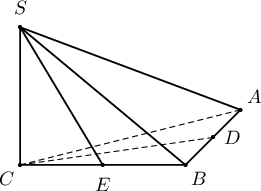
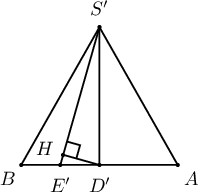
Бодолт. $AB$, $CB$ талын дундаж цэгүүдийг харгалзан $D$, $E$ гэе. $AB$ шулууныг агуулсан, $CD$ шулуунд перпендикуляр хавтгайд $SABC$ пирамидыг проекцлон $CD$ хэрчим $D^\prime$ цэгт, $E$ цэг $E^\prime$ цэгт, $S$ цэг $S^\prime$ цэгт тус тус буусан гэж үзвэл $S^\prime D^\prime\perp AB$ ба $S^\prime D^\prime=8$ болно. Бидний олох ёстой 2 шулууны хоорондох зай нь $S^\prime D^\prime E^\prime$ гурвалжны $S^\prime E^\prime$ гипотенуз дээр буусан $D^\prime H$ өндөр юм. $E^\prime D^\prime=2\sqrt{\fbox{a}}$; $S^\prime E^\prime=\fbox{b}\sqrt{\fbox{c}}$; $D^\prime H=\dfrac{\fbox{d}}{\fbox{e}}$. Олох ёстой өнцгөө $\alpha$ гэж тэмдэглэвэл $SE=\fbox{f}\sqrt6$ тул $\sin\alpha=\dfrac{\sqrt{\fbox{g}}}{2}\Rightarrow\alpha=\dfrac{\pi}{\fbox{h}}$ байна.


$ABC$ зөв гурвалжин суурьтай $SABC$ пирамидын суурийн талууд нь $8\sqrt2$см, $SC$ хажуу ирмэгийн урт нь $4$см бөгөөд суурийн хавтгайд перпендикуляр байв. $S$ орой ба $BC$ талын дундаж цэгийг дайрсан шулуун, $AB$ талын дундаж цэг ба $C$ оройг дайрсан шулуунуудын хоорондох өнцөг ба хоорондох зайг олоорой.
Бодолт. $AB$, $CB$ талын дундаж цэгүүдийг харгалзан $D$, $E$ гэе. $AB$ шулууныг агуулсан, $CD$ шулуунд перпендикуляр хавтгайд $SABC$ пирамидыг проекцлон $CD$ хэрчим $D^\prime$ цэгт, $E$ цэг $E^\prime$ цэгт, $S$ цэг $S^\prime$ цэгт тус тус буусан гэж үзвэл $S^\prime D^\prime\perp AB$ ба $S^\prime D^\prime=4$ болно. Бидний олох ёстой 2 шулууны хоорондох зай нь $S^\prime D^\prime E^\prime$ гурвалжны $S^\prime E^\prime$ гипотенуз дээр буусан $D^\prime H$ өндөр юм. $E^\prime D^\prime=2\sqrt{\fbox{a}}$; $S^\prime E^\prime=2\sqrt{\fbox{b}}$; $D^\prime H=\dfrac{\fbox{c}}{\sqrt{\fbox{d}}}$. Олох ёстой өнцгөө $\alpha$ гэж тэмдэглэвэл $SE=\fbox{e}\sqrt{\fbox{f}}$ тул $\sin\alpha=\dfrac{\sqrt{\fbox{g}}}{2}\Rightarrow\alpha=\dfrac{\pi}{\fbox{h}}$ байна.

Бодолт. $AB$, $CB$ талын дундаж цэгүүдийг харгалзан $D$, $E$ гэе. $AB$ шулууныг агуулсан, $CD$ шулуунд перпендикуляр хавтгайд $SABC$ пирамидыг проекцлон $CD$ хэрчим $D^\prime$ цэгт, $E$ цэг $E^\prime$ цэгт, $S$ цэг $S^\prime$ цэгт тус тус буусан гэж үзвэл $S^\prime D^\prime\perp AB$ ба $S^\prime D^\prime=4$ болно. Бидний олох ёстой 2 шулууны хоорондох зай нь $S^\prime D^\prime E^\prime$ гурвалжны $S^\prime E^\prime$ гипотенуз дээр буусан $D^\prime H$ өндөр юм. $E^\prime D^\prime=2\sqrt{\fbox{a}}$; $S^\prime E^\prime=2\sqrt{\fbox{b}}$; $D^\prime H=\dfrac{\fbox{c}}{\sqrt{\fbox{d}}}$. Олох ёстой өнцгөө $\alpha$ гэж тэмдэглэвэл $SE=\fbox{e}\sqrt{\fbox{f}}$ тул $\sin\alpha=\dfrac{\sqrt{\fbox{g}}}{2}\Rightarrow\alpha=\dfrac{\pi}{\fbox{h}}$ байна.


$ABC$ зөв гурвалжин суурьтай $SABC$ пирамидын суурийн талууд нь $4\sqrt2$см, $SC$ хажуу ирмэгийн урт нь $2$ см бөгөөд суурийн хавтгайд перпендикуляр байв. $S$ орой ба $BC$ талын дундаж цэгийг дайрсан шулуун, $AB$ талын дундаж цэг ба $C$ оройг дайрсан шулуунуудын хоорондох өнцөг ба хоорондох зайг олоорой.
Бодолт. $AB$, $CB$ талын дундаж цэгүүдийг харгалзан $D$, $E$ гэе. $AB$ шулууныг агуулсан, $CD$ шулуунд перпендикуляр хавтгайд $SABC$ пирамидыг проекцлон $CD$ хэрчим $D^\prime$ цэгт, $E$ цэг $E^\prime$ цэгт, $S$ цэг $S^\prime$ цэгт тус тус буусан гэж үзвэл $S^\prime D^\prime\perp AB$ ба $S^\prime D^\prime=2$ болно. Бидний олох ёстой 2 шулууны хоорондох зай нь $S^\prime D^\prime E^\prime$ гурвалжны $S^\prime E^\prime$ гипотенуз дээр буусан $D^\prime H$ өндөр юм. $E^\prime D^\prime=\sqrt{\fbox{a}}$; $S^\prime E^\prime=\sqrt{\fbox{b}}$; $D^\prime H=\dfrac{\fbox{c}}{\sqrt{\fbox{d}}}$. Олох ёстой өнцгөө $\alpha$ гэж тэмдэглэвэл $SE=\fbox{e}\sqrt{\fbox{f}}$ тул $\sin\alpha=\dfrac{\sqrt{\fbox{g}}}{2}\Rightarrow\alpha=\dfrac{\pi}{\fbox{h}}$ байна.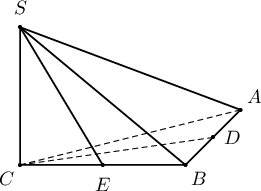
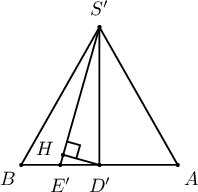
Бодолт. $AB$, $CB$ талын дундаж цэгүүдийг харгалзан $D$, $E$ гэе. $AB$ шулууныг агуулсан, $CD$ шулуунд перпендикуляр хавтгайд $SABC$ пирамидыг проекцлон $CD$ хэрчим $D^\prime$ цэгт, $E$ цэг $E^\prime$ цэгт, $S$ цэг $S^\prime$ цэгт тус тус буусан гэж үзвэл $S^\prime D^\prime\perp AB$ ба $S^\prime D^\prime=2$ болно. Бидний олох ёстой 2 шулууны хоорондох зай нь $S^\prime D^\prime E^\prime$ гурвалжны $S^\prime E^\prime$ гипотенуз дээр буусан $D^\prime H$ өндөр юм. $E^\prime D^\prime=\sqrt{\fbox{a}}$; $S^\prime E^\prime=\sqrt{\fbox{b}}$; $D^\prime H=\dfrac{\fbox{c}}{\sqrt{\fbox{d}}}$. Олох ёстой өнцгөө $\alpha$ гэж тэмдэглэвэл $SE=\fbox{e}\sqrt{\fbox{f}}$ тул $\sin\alpha=\dfrac{\sqrt{\fbox{g}}}{2}\Rightarrow\alpha=\dfrac{\pi}{\fbox{h}}$ байна.


$ABC$ зөв гурвалжин суурьтай $SABC$ пирамидын суурийн талууд нь $12\sqrt2$см, $SC$ хажуу ирмэгийн урт нь $6$см бөгөөд суурийн хавтгайд перпендикуляр байв. $S$ орой ба $BC$ талын дундаж цэгийг дайрсан шулуун, $AB$ талын дундаж цэг ба $C$ оройг дайрсан шулуунуудын хоорондох өнцөг ба хоорондох зайг олоорой.
Бодолт. $AB$, $CB$ талын дундаж цэгүүдийг харгалзан $D$, $E$ гэе. $AB$ шулууныг агуулсан, $CD$ шулуунд перпендикуляр хавтгайд $SABC$ пирамидыг проекцлон $CD$ хэрчим $D^\prime$ цэгт, $E$ цэг $E^\prime$ цэгт, $S$ цэг $S^\prime$ цэгт тус тус буусан гэж үзвэл $S^\prime D^\prime\perp AB$ ба $S^\prime D^\prime=6$ болно. Бидний олох ёстой 2 шулууны хоорондох зай нь $S^\prime D^\prime E^\prime$ гурвалжны $S^\prime E^\prime$ гипотенуз дээр буусан $D^\prime H$ өндөр юм. $E^\prime D^\prime=\fbox{a}\sqrt{2}$; $S^\prime E^\prime=\fbox{b}\sqrt{\fbox{c}}$; $D^\prime H=2\sqrt{\fbox{d}}$. Олох ёстой өнцгөө $\alpha$ гэж тэмдэглэвэл $SE=\fbox{e}\sqrt{\fbox{f}}$ тул $\sin\alpha=\dfrac{\sqrt{\fbox{g}}}{2}\Rightarrow\alpha=\dfrac{\pi}{\fbox{h}}$ байна.

Бодолт. $AB$, $CB$ талын дундаж цэгүүдийг харгалзан $D$, $E$ гэе. $AB$ шулууныг агуулсан, $CD$ шулуунд перпендикуляр хавтгайд $SABC$ пирамидыг проекцлон $CD$ хэрчим $D^\prime$ цэгт, $E$ цэг $E^\prime$ цэгт, $S$ цэг $S^\prime$ цэгт тус тус буусан гэж үзвэл $S^\prime D^\prime\perp AB$ ба $S^\prime D^\prime=6$ болно. Бидний олох ёстой 2 шулууны хоорондох зай нь $S^\prime D^\prime E^\prime$ гурвалжны $S^\prime E^\prime$ гипотенуз дээр буусан $D^\prime H$ өндөр юм. $E^\prime D^\prime=\fbox{a}\sqrt{2}$; $S^\prime E^\prime=\fbox{b}\sqrt{\fbox{c}}$; $D^\prime H=2\sqrt{\fbox{d}}$. Олох ёстой өнцгөө $\alpha$ гэж тэмдэглэвэл $SE=\fbox{e}\sqrt{\fbox{f}}$ тул $\sin\alpha=\dfrac{\sqrt{\fbox{g}}}{2}\Rightarrow\alpha=\dfrac{\pi}{\fbox{h}}$ байна.


$ABC$ зөв гурвалжин суурьтай $SABC$ пирамидын суурийн талууд нь $4\sqrt2$см, $SC$ хажуу ирмэгийн урт нь $2$см бөгөөд суурийн хавтгайд перпендикуляр байв. $S$ орой ба $BC$ талын дундаж цэгийг дайрсан шулуун, $AB$ талын дундаж цэг ба $C$ оройг дайрсан шулуунуудын хоорондох өнцөг ба хоорондох зайг олоорой.
Бодолт. $AB$, $CB$ талын дундаж цэгүүдийг харгалзан $D$, $E$ гэе. $AB$ шулууныг агуулсан, $CD$ шулуунд перпендикуляр хавтгайд $SABC$ пирамидыг проекцлон $CD$ хэрчим $D^\prime$ цэгт, $E$ цэг $E^\prime$ цэгт, $S$ цэг $S^\prime$ цэгт тус тус буусан гэж үзвэл $S^\prime D^\prime\perp AB$ ба $S^\prime D^\prime=2$ болно. Бидний олох ёстой 2 шулууны хоорондох зай нь $S^\prime D^\prime E^\prime$ гурвалжны $S^\prime E^\prime$ гипотенуз дээр буусан $D^\prime H$ өндөр юм. $E^\prime D^\prime=\sqrt{\fbox{a}}$; $S^\prime E^\prime=\sqrt{\fbox{b}}$; $D^\prime H=\dfrac{\fbox{c}}{\sqrt{\fbox{d}}}$. Олох ёстой өнцгөө $\alpha$ гэж тэмдэглэвэл $SE=\fbox{e}\sqrt{\fbox{f}}$ тул $\sin\alpha=\dfrac{\sqrt{\fbox{g}}}{2}\Rightarrow\alpha=\dfrac{\pi}{\fbox{h}}$ байна.

Бодолт. $AB$, $CB$ талын дундаж цэгүүдийг харгалзан $D$, $E$ гэе. $AB$ шулууныг агуулсан, $CD$ шулуунд перпендикуляр хавтгайд $SABC$ пирамидыг проекцлон $CD$ хэрчим $D^\prime$ цэгт, $E$ цэг $E^\prime$ цэгт, $S$ цэг $S^\prime$ цэгт тус тус буусан гэж үзвэл $S^\prime D^\prime\perp AB$ ба $S^\prime D^\prime=2$ болно. Бидний олох ёстой 2 шулууны хоорондох зай нь $S^\prime D^\prime E^\prime$ гурвалжны $S^\prime E^\prime$ гипотенуз дээр буусан $D^\prime H$ өндөр юм. $E^\prime D^\prime=\sqrt{\fbox{a}}$; $S^\prime E^\prime=\sqrt{\fbox{b}}$; $D^\prime H=\dfrac{\fbox{c}}{\sqrt{\fbox{d}}}$. Олох ёстой өнцгөө $\alpha$ гэж тэмдэглэвэл $SE=\fbox{e}\sqrt{\fbox{f}}$ тул $\sin\alpha=\dfrac{\sqrt{\fbox{g}}}{2}\Rightarrow\alpha=\dfrac{\pi}{\fbox{h}}$ байна.


Ирмэгүүд нь 3, 4, 5 урттай тэгш өнцөгт параллелепипедийн аль нэг орой болон түүнтэй холбогдсон оройнуудаар үүсэх пирамидын эзлэхүүн нь $\fbox{ab}$, уг пирамидыг багтаасан бөмбөрцгийн радиус нь $R=\dfrac{\fbox{c}\sqrt{\fbox{d}}}{2}$ байна.
Бүх ирмэг нь 4 урттай байх $ABCDE$ зөв дөрвөн өнцөгт пирамид өгөгджээ.
- Суурийн диагональ $AC=\fbox{a}\sqrt2$ байна.
- Диагональ огтлолын талбай $S_{ACE}=\fbox{b}$ байна.
- Пирамидын эзлэхүүн $V_{ABCDE}=\dfrac{32\sqrt2}{\fbox{c}}$ байна.
- Пирамидад багтсан бөмбөрцгийн радиус $r=\sqrt{\fbox{d}}-\sqrt2$ байна.
- Энэ пирамидад хамгийн их эзлэхүүнтэй, 4 орой нь хажуу ирмэг дээр, 4 орой нь суурь дээр орших тэгш өнцөгт параллелепипед багтаавал эзлэхүүн нь $V_{\text{пар}}=\dfrac{128\sqrt2}{\fbox{ef}}$ байна.
Бүх ирмэг нь 2 урттай байх $ABCDE$ зөв дөрвөн өнцөгт пирамид өгөгджээ.
- Суурийн диагональ $AC=2\sqrt{\fbox{a}}$ байна.
- Диагональ огтлолын талбай $S_{ACE}=\fbox{b}$ байна.
- Пирамидын эзлэхүүн $V_{ABCDE}=\dfrac{4\sqrt2}{\fbox{c}}$ байна.
- Пирамидад багтсан бөмбөрцгийн радиус $r=\dfrac{\sqrt{\fbox{d}}-\sqrt2}{2}$ байна.
- Энэ пирамидад хамгийн их эзлэхүүнтэй, 4 орой нь хажуу ирмэг дээр, 4 орой нь суурь дээр орших тэгш өнцөгт параллелепипед багтаавал эзлэхүүн нь $V_{\text{пар}}=\dfrac{16\sqrt2}{\fbox{ef}}$ байна.
Призмийн гадаргуугийн талбай
Бүх ирмэгүүдийн нийлбэр нь хамгийн бага байх зөв 6 өнцөгт призмийн эзлэхүүн нь $V$ бол бүтэн гадаргуугийн талбайг ол.
Зөв гурвалжин призмын хажуу талс нь квадрат болно. Призмын хажуу гадаргийн талбай 144 байв. Призмын талсуудын төвөөр оройгоо хийсэн олон талстын эзлэхүүнийг ол.
$R$ радиустай бөмбөрцөгт зөв гурвалжин призм багтаасан бөгөөд призмын өндөр нь $H$ бол эзлэхүүнийг нь ол.
Зөв гурвалжин призмын суурийн тал ба түүний эсрэг орших ирмэгийн дундажыг агуулсан хавтгай суурийн хавтгайтай $60^\circ$-ийн өнцөг үүсгэнэ. Энэ хавтгайгаар үүсэх хөндлөн огтлолын талбай $S=8\sqrt3$. Призмын эзлэхүүн ба бүтэн гадаргуугийн талбайг ол.
$ABC A_1B_1C_1$ зөв гурвалжин призмын хажуу ирмэг $AA_1$, $BB_1$, $CC_1$, суурь нь 4 талтай адил талт $ABC$ гурвалжин болно. $AB$ ба $CA$ шулуунууд перпендикуляр бол призмын эзлэхүүнийг ол.
$ABC A_1B_1C_1$ зөв гурвалжин призмын хажуу ирмэгүүд $AA_1$, $BB_1$, $CC_1$ ба суурь нь адил талт $ABC$ гурвалжин болно. Түүнчлэн призмийн бүх ирмэгүүд ижилхэн $6$ урттай. $P$ ба $Q_1$ цэгүүд $BC$ ба $A_1C_1$ ирмэгүүдийг $BP:PC=A_1Q_1: Q_1C_1=1:2$ харьцаагаар хуваана. $ABB_1A_1$ ба $ACC_1A_1$ хавтгайг шүргэх, $PQ_1$ хэрчим дээр төвтэй бөмбөрцөгийн радиусыг ол.
Нэгэн хавтгай зөв гурвалжин призмын хажуу ирмэгүүдийг доод сууриас нь дээш $1:2$, $3:4$ ба $1:5$ гэсэн харьцаагаар хуваажээ. Призмын эзлэхүүн ямар харьцаагаар хуваагдсан бэ?
Тэгш өнцөгт гурвалжин призмын суурь адил хажуут гурвалжин. Суурийн хажуу талын урт $a$, суурьт налсан өнцөг нь $\alpha$ болно. Гурвалжны суурийг дайран гарсан хавтгай түүнд $\beta$ өнцөгөөр налсан байв. Уг хавтгай призмыг огтлоход үүсэх гурвалжин огтлолын талбайг ол.
Тэгш өнцөгт гурвалжин призмын доод суурийн нэг талыг дайран гарсан хавтгай эсрэг талын хажуу ирмэгийг огтлож байсан бөгөөд суурийн хавтгайтай $45^\circ$-аар налж байв. Хэрэв призмын суурь $a$-талтай зөв гурвалжин байсан бол огтлолын талбайг ол.
$ABCDA_1B_1C_1D_1$ шулуун призмийн суурь нь $ABCD$ параллельограмм. $K$, $L$, $M$, $N$ цэгүүд харгалзан $A_1B$, $B_1C$, $DA$ талууд дээр оршино. $KM$ шулуун $B_1C_1$ шулуунтай параллель, $A_2$ цэг $AA_1$ ирмэг дээр орших ба $AA_2:A_2A_1=3$ байв. $ABC$ хавтгайтай параллельиар $A_2$ цэгийг дайран гарах $\pi$ хавтгай $BK$, $BL$, $BM$, $BN$ хэрчмүүдийг харгалзан $E$, $F$, $G$, $H$ цэгүүдээр огтолно. Хэрэв $ABCD A_1B_1C_1D_1$ призмын эзлэхүүн $V$ бол $CEFGH$ дөрвөн өнцөгт пирамидын эзлэхүүнийг ол.
Зөв зургаан өнцөгт призмын хамгийн том диагонал огтлолын талбай 1 бол призмын хажуу гадаргуугийн талбайг ол.
Зөв дөрвөн өнцөгт призмын өндөр $h$. Суурийн аль нэг оройгоос түүнийг агуулсан хоёр хажуу талд диагоналууд татахад тэдгээрийн хооронд $\alpha$ өнцөг үүсч байв. Призмын хажуу гадаргуугийн талбайг ол.
Шулуун призмын суурь нь нэг тал нь $a$-тай тэнцүү параллельограмм бөгөөд уг ирмэг ба түүний эсрэг орших, дээд суурийн ирмэгийг дайран гарах $Q$ талбай бүхий огтлол суурийн хавтгайтай $\beta$ өнцөг үүсгэнэ. Призмын эзлэхүүнийг ол.
$RST R_1S_1T_1$ шулуун призмийн дээд суурь нь $\dfrac{\sqrt3}{4}c^2$ талбайтай $R_1S_1T_1$ гэсэн зөв гурвалжин. $RS$ шулууныг агуулсан огтлогч хавтай $TT_1$ ирмэгтэй $\gamma$ өнцөг үүсгэнэ. Огтлолд үүсэх гурвалжныг багтаасан тойргийн радиусыг ол.
$ABCA_1B_1C_1$ шулуун призмийн суурийн талууд нь $AB=BC=1$, $AC=\sqrt3$. $AB_1C$ хавтгай уг призмд багтсан цилиндрийн эзлэхүүнийг ямар харьцаатай хэсгүүдэд хуваах вэ?
$ABCA_1B_1C_1$ зөв гурвалжин призмийн суурийн тал $a$, хажуу ирмэг нь $\dfrac54a$. $A_1C_1$ талын дундаж $D$, $M$ цэг $DB_1$ хэрчим дээр байрлах ба $DM=\dfrac16DB_1$. Өөр нэг призм нь $BM$ шулууны хувьд $ABCA_1B_1C_1$-тай симметр байв. Призмүүдийн ерөнхий хэсгийн эзлэхүүнийг ол.
$ABCA_1B_1C_1$ зөв гурвалжин призмийн суурийн тал $a$, хажуу ирмэг нь $\dfrac98a$. $AB$ талын дундаж $E$, $M$ цэг $EC$ хэрчим дээр байрлах ба $EM=\dfrac14EC$. Өөр нэг призм нь $MC_1$ шулууны хувьд $ABCA_1B_1C_1$-тай симметр байв. Призмүүдийн ерөнхий хэсгийн эзлэхүүнийг ол.
$PQRP_1Q_1R_1$ зөв гурвалжин призмийн доод суурийн $PQ$ ирмэгийг дайруулан $RR_1$ ирмэгийг огтлох огтлогч хавтгай татан түүнийг хоёр олон талст болгон хуваав. Эдгээрийн $PQR$ гурвалжин нэг талс нь болох олон талстын эзлэхүүнийг $QQ_1PP_1$ дөрвөн өнцөгт талс нь болох олон талстын эзлэхүүнд харьцуулсан харьцаа $q$. Хэрэв $PQ_1$ ба $RR_1$ шулуунуудын хоорондох өнцөг $\varphi$ бол огтлогч хавтгай ба пирамидын сууриудын хооронд үүсгэх өнцгийн хэмжээг ол.
Призмийн суурь нь $\sqrt3$ талтай $ABC$ зөв гурвалжин. $AD$, $BE$, $CF$ хажуу ирмэгүүд нь суурьтаа перпендикуляр. $\dfrac72$ радиустай бөмбөрцөг $ABC$ хавтгай ба $AE$, $BF$, $CD$ хэрчмүүдийн үргэлжлэлүүдийг харгалзан $A$, $B$, $C$ цэгийн талд нь шүргэж байв. Призмийн хажуу ирмэгийн уртыг ол.
$ABCA_1B_1C_1$ призмийн дээд суурь $A_1B_1C_1$ гурвалжин бөгөөд $A_1B_1=B_1C_1$ байв. Уг гурвалжны $B_1D$ медиан ба $A_1B_1$ талуудын хоорондох өнцөг $\varphi$ байв. $ABC$ гурвалжныг багтаасан тойргийн төв ба $A_1B_1C_1$ гурвалжны өндрүүдийн огтлолцлын цэгийг дайруулан $AC$ шулуунтай параллел хавтгай татав. Хэрэв $BB_1CC_1$ хажуу талсын $B_1C$ диагоналын урт $d$ ба $\angle BB_1A=\alpha$ бол уг хавгайгаар үүсэх огтлолын талбайг ол.
$SABC$ ($S$ нь оройн цэг) зөв гурвалжин пирамидад багтсан бөмбөрцөг нь $KL=LM=\sqrt{6}$ байх $KLMK_1L_1M_1$ шулуун, гурвалжин призмд багтах ба $KK_1$ ирмэг $AB$ шулуун дээр байрлаж байв. Хэрэв $SC$ ирмэг $LL_1M_1M$ хавтгайтай параллель бол бөмбөрцгийн радиусыг ол.
$ABCA_1B_1C_1$ шулуун призмийн суурь нь $AC=CB=2$, $\angle ACB=2\arcsin\dfrac45$ байх адил хажуут гурвалжин. $A_1B$ шулуунд перпендикуляр хавтгай $AB$ ба $A_1B_1$ ирмэгүүдийг харгалзан $AK=\dfrac{7}{16}AB$, $LB_1=\dfrac{7}{16}A_1B_1$ байх $K$ ба $L$ цэгт огтолно. Огтлолын талбайг ол.
$KLMNK_1L_1M_1N_1$ призмийн суурь нь $K$ орой дахь өнцөг нь $60^\circ$-тэй тэнцүү $KLMN$ ромбо. $LL_1$ ба $LM$ ирмэгүүдийн дундаж цэгүү нь харгалзан $E$ ба $F$. $SABCD$ ($S$ оройтой) зөв дөрвөн өнцөгт пирамидын $SA$ ирмэг $LN$ шулуун дээр орших ба $B$, $D$ оройнууд нь харгалзан $MM_1$, $EF$ ирмэгүүд дээр оршино. Хэрэв $SA=2AB$ бол призм ба пирамидын эзлэхүүнүүдийн харьцааг ол.
3 радиустай бөмбөрцөгт багтсан зөв дөрвөн өнцөгт призмийн өндөр 4 бол бөмбөрцгийн эзлэхүүнийг призмийн эзлэхүүнд харьцуулсан харьцааг ол.
A. $\dfrac45\pi$
B. $\dfrac9{10}\pi$
C. $\dfrac{9}{20}\pi$
D. $\dfrac{6\pi}{5}$
E. $\dfrac{3\pi}{5}$
6 радиустай бөмбөрцөгт багтсан зөв дөрвөн өнцөгт призмийн өндөр 9 бол бөмбөрцгийн эзлэхүүнийг призмийн эзлэхүүнд харьцуулсан харьцааг ол.
A. $\dfrac{32}{63} \pi $
B. $\dfrac{64}{63} \pi $
C. $\dfrac{16}{21} \pi $
D. $\dfrac{8}{21} \pi $
E. $\dfrac{32}{21} \pi $
Зөв гурвалжин суурьтай шулуун призмийн суурийн тал ба өндөр тэнцүү 3 нэгж байв. Суурийн 1 ирмэг ба призмийн суурийн төвүүдийг холбосон хэрчмийн дундаж цэгийг дайрсан огтлолын талбайг ол.
A. $3\sqrt3$
B. $4\sqrt2$
C. $3\sqrt2$
D. $4\sqrt3$
E. $8\sqrt3$
Зөв гурвалжин призмд бөмбөрцөг багтах бөгөөд призмийн бүтэн гадаргуугийн талбай $2\sqrt3$ бол багтсан бөмбөрцгийн радиусыг ол.
A. $\dfrac13$
B. $\dfrac12$
C. $1$
D. $\dfrac43$
E. $2$
Суурь нь $3$, $4$, $5$ талуудтай гурвалжин байх шулуун призмийн эзлэхүүн нь $30$ бол бүтэн гадаргуугийн талбайг ол.
A. $17$
B. $30$
C. $36$
D. $60$
E. $72$
$ABCA_1B_1C_1$ шулуун призмийн суурь $a$ талтай адил талт гурвалжин,
хажуу ирмэгийн урт $\sqrt2a$ бол призмийн талсуудын $A_1B,B_1C$ диагоналиудын
хоорондох хурц өнцгийг ол.
A. $45^\circ$
B. $60^\circ$
C. $\arccos\frac14$
D. $\arccos\sqrt{\frac23}$
E. $30^\circ$
$ABCA_1B_1C_1$ зөв гурвалжин призмийн бүх ирмэг $a$ урттай бол түүний
хажуу талсуудын $AB_1,BC_1$ диагоналиудын хоорондох хурц өнцгийг ол.
A. $45^\circ$
B. $60^\circ$
C. $\arccos\frac13$
D. $\arccos\frac14$
Налуу гурвалжин призмийн хажуу ирмэгүүд хоорондоо 3см, 4см, 5см зайтай ба урт нь 6см байв. Призмийн хажуу гадаргуугийн талбай аль вэ?
A. $48\texttt{см}^{2};$
B. $60\texttt{см}^{2};$
C. $64\texttt{см}^{2};$
D. $72\texttt{см}^{2}.$
Налуу дөрвөлжин призмйин хажуу ирмэг 3м урттай, хажуу гадаргуугийн талбай нь 66$\texttt{м}^{2}$ байв. Призмийн зэргэлдээ хажуу ирмэгүүдийн хоорондох зайнуудын харьцаа 1:2:3:5 бол хамгийн их зай нь хэдэн метр байсан бэ?
A. $10;$
B. $12;$
C. $14;$
D. $15.$
Зөв дөрвөн өнцөгт призмийн диагональ суурийн хавтгайтай $30^\circ$
өнцөг үүсгэх ба урт нь 2 нэгж бол призмийн бүтэн гадаргуугийн талбайг ол.
A. $3+4\sqrt3$кв.нэгж
B. $2+3\sqrt2$кв.н.
C. $2+3\sqrt3$кв.н.
D. $3+2\sqrt6$кв.н.
Зөв дөрвөн өнцөгт призмийн диагональ хажуу ирмэгтэй $30^\circ$ өнцөг
үүсгэх ба урт нь 2 нэгж бол призмийн бүтэн гадаргуугийн талбайг ол.
A. $1+4\sqrt3$кв.н.
B. $2+2\sqrt2$кв.н.
C. $1+2\sqrt6$кв.н.
D. $2+\sqrt6$кв.н.
Шулуун призмийн суурь параллель талууд ба диагональ нь харгалзан
21, 9, 17 нэгж урттай адил хажуут трапец бөгөөд бага хажуу талс нь квадрат байв.
Призмийн хажуу гадаргуугийн талбайг ол.
A. 450кв.нэгж.
B. 405кв.н.
C. 378кв.н.
D. 504кв.н.
Шулуун призмийн суурь трапецийн параллель талууд 9 ба 39 нэгж
урттай бөгөөд гурван хажуу талс нь квадрат байв. Призмийн гүйцэд
гадаргуугийн талбайг ол.
A. 6690кв.нэгж.
B. 6642кв.н.
C. 6774кв.н.
D. 6792кв.н.
Гурвалжин призмийн хажуу ирмэгт перпендикуляр огтлолын өнцгүүд
1:5:6 харьцаатай бөгөөд огтлолын их тал ба призмийн хажуу ирмэгийн урт $a$ бол
призмийн эзлэхүүнийг ол.
A. $\frac12a^3$
B. $\frac14a^3$
C. $\frac16a^3$
D. $\frac18a^3$
Гурвалжин призмийн бүх ирмэгийн урт $a$, нэг гурван талст өнцгийн хавтгай
өнцгүүд ижил хэмжээтэй бол призмийн эзлэхүүнийг ол.
A. $\sqrt2a^3$
B. $\frac{\sqrt2}2a^3$
C. $\frac{\sqrt2}4a^3$
D. $\frac{\sqrt2}6a^3$
Бөмбөрцөг багтаасан зөв зургаан өнцөгт призмийн өндөр 2 нэгж бол эзлэхүүн нь хэдэн куб нэгж вэ?
A. $2\sqrt{3};$
B. $3\sqrt{3};$
C. $4\sqrt{3};$
D. $5\sqrt{3}.$
$\sqrt{3}$ нэгж радиустай бөмбөрцөг багтаасан зөв зургаан өнцөгт призмийн эзлэхүүн хэдэн куб нэгж байх вэ?
A. $36$
B. $24$
C. $30$
D. $20$
E. $18$
Бүх ирмэг нь $a$ урттай зөв гурвалжин призмийн доод суурийн нэг
ирмэг дээд суурийн төвийг дайрсан огтлолын талбайг ол.
A. $\dfrac{3\sqrt{11}}{16}a^2$
B. $\dfrac{\sqrt{91}}6a^2$
C. $\dfrac5{24}a^2$
D. $\dfrac{25}{36}a^2$
E. $\dfrac{5\sqrt{39}}{36}a^2$
Бүх ирмэг нь $a$ урттай зөв гурвалжин призм $ABCA_1B_1C_1$-ийн $BC$
ирмэг ба $A_1C_1$ ирмэгийн $2A_1M=MC_1$ байх $M$ цэгийг дайрсан огтлолын талбайг ол.
A. $\dfrac{3\sqrt2}8a^2$
B. $\dfrac{2\sqrt6}9a^2$
C. $\dfrac{4\sqrt3}9a^2$
D. $\dfrac{\sqrt6}4a^2$
E. $\dfrac{2\sqrt3}9a^2$
$9$ радиустай бөмбөрцөгт багтсан зөв дөрвөн өнцөгт призмийн өндөр 12 бол бөмбөрцгийн эзлэхүүнийг призмийн эзлэхүүнд харьцуулсан харьцааг ол.
A. $\dfrac{27}{5}\pi$
B. $\dfrac{27}{20}\pi$
C. $\dfrac{19}{10}\pi$
D. $\dfrac{9}{10}\pi$
E. $\dfrac{3}{10}\pi$
3 радиустай бөмбөрцөгт багтсан зөв дөрвөн өнцөгт призмийн өндөр 4 бол бөмбөрцгийн эзлэхүүнийг призмийн эзлэхүүнд харьцуулсан харьцааг ол.
A. $\dfrac45\pi$
B. $\dfrac9{10}\pi$
C. $\dfrac{9}{20}\pi$
D. $\dfrac{6\pi}{5}$
E. $\dfrac{3\pi}{5}$
Өндөр нь 5см байх $ABCDA_1B_1C_1D_1$ зөв дөрвөн өнцөгт призмийн $ABCD$ суурийн тал 10см. $M$ цэг нь $AB$ тал дээр оршино.
- $\left(\dfrac{|A_1M|}{|MC_1|}\right)^2=\dfrac{1}{\fbox{a}}$ бол $|AM|=|MB|$ байна.
- Энэ тохиолдолд $(A_1MC_1)$ хавтгай нь $BC$ талыг $N$ цэгээр огтлох ба $S_{A_1MNC_1}=\fbox{bc}\cdot\dfrac{\sqrt3}{2}$ байна.
Өндөр нь 9 см байх $ABCDA_1B_1C_1D_1$ зөв дөрвөн өнцөгт призмын $ABCD$ суурийн тал 18 см. $M$ цэг нь $AB$ тал дээр оршино.
- $\Big(\dfrac{|A_1M|}{|MC_1|}\Big)^2=\dfrac{1}{\fbox{a}}$ бол $|AM|=|MB|$ байна.
- Энэ тохиолдолд $(A_1MC_1)$ хавтгай нь $BC$ талыг $N$ цэгээр огтлох ба $S_{A_1MNC_1}=\dfrac{\fbox{bcd}\sqrt{\fbox{3}}}{2}$ байна.
$ABCA_1B_1C_1$ шулуун призмийн $ABC$ суурийн талбай нь 8, өндөр 6 байв. $AA_1$, $BB_1$ ирмэгүүдийн дундаж цэгүүд нь харгалзан $M$ ба $N$ бол
- Призмийн эзлэхүүн $\fbox{ab}$;
- $CABNM$ пирамидын эзлэхүүн $\fbox{cd}$;
- Призм дотор санамсаргүйгээр цэг сонгоход тэр нь $CABMN$ пирамид дотор байх магадлал $\dfrac{1}{\fbox{e}}$ байна.
$ABCA_1B_1C_1$ зөв гурвалжин призмийн суурийн тал 12, призмийн өндөр $\dfrac{6\sqrt{6}}{\sqrt{7}}$ байв. $AC, A_1C_1, AB$ ирмэгүүд дээр харгалзан $P, F, E$ цэгүүдийг $AP=2, A_1F=6, AE=6$ байхаар авав. $P, F, E$ цэгүүдийг дайрсан хавтгайгаар призмийг огтлох огтлолыг байгуулав.
1) Огтлолын хавтгай ба $(ABC)$ хавтгайн хоорондох өнцөг $\varphi=\arccos \dfrac{\fbox{a}}{\sqrt{\fbox{b}}}$ байна.
2) Огтлолын талбай $S=\dfrac{\fbox{cde}}{\fbox{f}}$ байна.
1) Огтлолын хавтгай ба $(ABC)$ хавтгайн хоорондох өнцөг $\varphi=\arccos \dfrac{\fbox{a}}{\sqrt{\fbox{b}}}$ байна.
2) Огтлолын талбай $S=\dfrac{\fbox{cde}}{\fbox{f}}$ байна.
$ABCA_1B_1C_1$ шулуун призмийн суурь $ABC$-ийн хувьд
$AB=BC=5, AC=6$ ба призмийн өндөр нь $\sqrt{6}$-тай тэнцүү. $AC,
BC, A_1C_1$ талууд дээр харгалзан $D, E, D_1$ цэгүүдийг
$DC=\dfrac 14AC, BE=EC,$ $A_1D_1=\dfrac 13A_1C_1$ байхаар аваад
$\alpha=(DED_1)$ хавтгайгаар призмийг огтлох огтлолыг байгуулав.
1) Огтлолын талбай $S=\dfrac{\fbox{abc}}{\fbox{de}}$ байна.
2) $\alpha$ хавтгай ба $(ABC)$ хавтгайн хоорондох өнцөг $\varphi=\arccos\dfrac{\fbox{f}}{\fbox{g}}$ байна.
3) $C_1$ ба $C$ цэгүүдээс $\alpha$ хавтгай хүртэлх зай $\rho_1=\dfrac{\fbox{h}\cdot\sqrt{\fbox{k}}}{\fbox{m}},$ $\rho=\dfrac{\fbox{n}\cdot \sqrt{\fbox{p}}}{\fbox{q}}$ байна.
1) Огтлолын талбай $S=\dfrac{\fbox{abc}}{\fbox{de}}$ байна.
2) $\alpha$ хавтгай ба $(ABC)$ хавтгайн хоорондох өнцөг $\varphi=\arccos\dfrac{\fbox{f}}{\fbox{g}}$ байна.
3) $C_1$ ба $C$ цэгүүдээс $\alpha$ хавтгай хүртэлх зай $\rho_1=\dfrac{\fbox{h}\cdot\sqrt{\fbox{k}}}{\fbox{m}},$ $\rho=\dfrac{\fbox{n}\cdot \sqrt{\fbox{p}}}{\fbox{q}}$ байна.
$ABCA_1B_1C_1$ шулуун призмийн суурь $ABC$-ийн хувьд
$AB=BC=5, AC=6$ ба призмийн өндөр нь $\sqrt{6}$-тай тэнцүү.
$A_1C_1, B_1C_1, AC$ талууд дээр харгалзан $D_1, E_1, D$
цэгүүдийг $C_1D=\dfrac 14A_1C_1, B_1E_1=C_1E_1,$ $AD=\dfrac 13AC$
байхаар аваад $\alpha=(D_1E_1D)$ хавтгайгаар призмийг огтлох
огтлолыг байгуулав.
1) Огтлолын талбай $S=\dfrac{\fbox{abc}}{\fbox{de}}$ байна.
2) $\alpha$ хавтгай ба $(ABC)$ хавтгайн хоорондох өнцөг $\varphi=\arccos\dfrac{\fbox{f}}{\fbox{g}}$ байна.
3) $C$ ба $C_1$ цэгүүдээс $\alpha$ хавтгай хүртэлх зай харгалзан $\rho=\dfrac{\fbox{h}\cdot\sqrt{\fbox{k}}}{\fbox{m}},$ $\rho_1=\dfrac{\fbox{n}\cdot \sqrt{\fbox{p}}}{\fbox{q}}$ байна.
1) Огтлолын талбай $S=\dfrac{\fbox{abc}}{\fbox{de}}$ байна.
2) $\alpha$ хавтгай ба $(ABC)$ хавтгайн хоорондох өнцөг $\varphi=\arccos\dfrac{\fbox{f}}{\fbox{g}}$ байна.
3) $C$ ба $C_1$ цэгүүдээс $\alpha$ хавтгай хүртэлх зай харгалзан $\rho=\dfrac{\fbox{h}\cdot\sqrt{\fbox{k}}}{\fbox{m}},$ $\rho_1=\dfrac{\fbox{n}\cdot \sqrt{\fbox{p}}}{\fbox{q}}$ байна.
$ABCA_1B_1C_1$ призмийн талсуудын $AB_1$, $CA_1$ диагоналиуд
дээр харгалзан байрлах $E,F$ цэгүүдийн хувьд $EF\|BC_1$ нөхцөл
биелнэ. $\overrightarrow{CA}=\vec a$, $\overrightarrow{CB}=\vec b$, $\overrightarrow{CC_1}=\vec c$
гэвэл $\overrightarrow{AB_1}=\fbox{a}\vec a+\vec b+\fbox{b}\vec c$,
$\overrightarrow{CA_1}=\vec a+\fbox{c}\vec b+\vec c$, $\overrightarrow{BC_1}=-\vec
b+\fbox{d}\vec c$ ба $EF:BC_1=\fbox{e}:\fbox{f}$ байна.
Бүх ирмэг нь $a$ урттай зөв гурвалжин призмийн зэргэлдээ
хоёр хажуу талсын солбисон диагоналиудын хоорондох зайг $\delta$
гэе. Эдгээр диагоналийн ерөнхий перпендикуляр хэрчим диагоналийг
$\fbox{a}:\fbox{b}$ $(a< b)$ харьцаагаар хуваах ба
$\delta=\displaystyle\frac{\sqrt{\fbox{c}}}5\,a$ байна.
Призмийн эзлэхүүн
Төсөөтэй биетүүдийн гадаргуун талбай болон эзлэхүүний харьцаа
Харилцан перпендикуляр шулуунууд
Хялбар олон талст
Цилиндр
$M(-3, 3\sqrt {2} )$ цэгээс координатын эх хүртэлх зайг ол.
A. $\sqrt {17} $
B. $3\sqrt {3} $
C. $5\sqrt {3} $
D. $2\sqrt {5} $
E. $\sqrt {15} $
Цилиндрийн суурийн радуис $2$ дм , өндөр нь $4$ дм бол тэнхлэг огтлолын талбай нь хэдэн дм.кв вэ?
A. $32$дм.кв
B. $ 8 $дм.кв
C. $ 6 $дм.кв
D. $ 64$дм.кв
E. $ 16 $ дм.кв
$M(-3, 3\sqrt {2} )$ цэгээс координатын эх хүртэлх зайг ол.
A. $\sqrt {17} $
B. $3\sqrt {3} $
C. $5\sqrt {3} $
D. $2\sqrt {5} $
E. $\sqrt {15} $
Цилиндрийн суурийн радуис $3$ дм , өндөр нь $5$ дм бол тэнхлэг огтлолын талбай нь хэдэн дм.кв вэ?
A. $ 45$дм.кв
B. $ 8 $дм.кв
C. $ 15 $дм.кв
D. $ 30$дм.кв
E. $ 75 $ дм.кв
Цилиндрийн гадаргуугийн талбай
Бөмбөрцөгт хамгийн их эзлэхүүнтэй цилиндр багтжээ. Хэрвээ бөмбөрцөгийн радиус 5 см бол бөмбөрцөгийн эзлэхүүнийг цилиндрийн суурийн талбайд харьцуулсан харьцааг ол.
Конусын радиус 4дм, өнцөг нь 6дм бөгөөд түүнд хамгийн их эзлэхүүнтэй цилиндрийг багтаажээ. Цилинприйн өндрийг ол
$R$ радиустай бөмбөрцөгт хамгийн их хажуу гадаргуутай цилиндр багтсан бол энэ цилиндрийн эзлэхүүнийг ол
Диаметр нь $d=4$ см, өндөр $h=4$ см бүхий метал цилиндрийг хайлуулж бөмбөлөг хийв. Бөмбөлөгийн радиусыг ол.
Цилиндрт бөмбөрцөг багтав. Цилиндрийн эзлэхүүн $7.5$ бол түүнд багтсан бөмбөрцгийн эзлэхүүнийг ол.
Бөмбөрцгийн эзлэхүүн $4$ дм.куб. Уг бөмбөрцөгт багтсан цилиндрийн байгуулагч бөмбөрцгийн төвөөс $60^\circ$ өнцгөөр харагддаг бол цилиндрийн эзлэхүүнийг ол.
Цилиндрийн хажуу гадаргууг дэлгэхэд $4\sqrt[3]{\pi}$ талтай квадрат үүснэ. Цилиндрийн эзлэхүүнийг ол.
Тэнхлэг огтлол нь квадрат бөгөөд хажуу гадаргуугийн талбай нь $80$-тай тэнцүү цилиндрийн бүтэн гадаргуугийн талбайг ол.
$ABCD$ адил хажуут трапецын $BC$ суурь нь $MBCN$ ромбын тал болдог. $BC=a$, $AD=b$ ($a< b< 2a$). Трапецийн хурц өнцөг $30^\circ$, ромбын хурц өнцөг $60^\circ$ бол трапец ба ромбыг $BC$ шулуунийг тойруулан хамтад нь эргүүлэхэд үүсэх биетийн гадаргуугийн талбайг ол.
$ABCA_1B_1C_1$ шулуун призмийн суурийн талууд нь $AB=BC=1$, $AC=\sqrt3$. $AB_1C$ хавтгай уг призмд багтсан цилиндрийн эзлэхүүнийг ямар харьцаатай хэсгүүдэд хуваах вэ?
$S$ оройтой $SABCD$ зөв дөрвөлжин пирамидын $BC$ ирмэг дээр $DM:DC=1:15$ байхаар $M$ цэг авав. $SAB$, $SCD$ хажуу талсуудыг шүргэх цилиндрийн нэг суурь нь $M$ цэгийг агуулдаг, нөгөө суурь нь $SC$ ирмэгтэй ерөнхий цэгтэй байв. Цилиндрийн хажуу гадаргуу пирамидын $SH$ өндөртэй $O$ цэгт огтлолцох ба $SO:SH=1:3$ байв. Цилиндр ба пирамидын ерөнхий цэгийг ол.
$SABC$ ($S$ нь оройн цэг) зөв гурвалжин пирамидын $BC$ ирмэг дээр $BD:DC=2:3$ байхаар $D$ цэг авав. $SAB$, $SBC$ хажуу талсуудыг шүргэх цилиндрийн нэг суурь нь $D$ цэгийг агуулдаг, нөгөө суурь нь $SC$ ирмэгтэй ерөнхий цэгтэй байв. Хэрэв цилиндрийн хажуу гадаргуу $AC$ талтай цор ганц ерөнхий цэгтэй гэвэл цилиндр ба пирамидын эзлэхүүний харьцааг ол.
Хавгай дээр нэг ерөнхий байгуулагчтай $r$ радиустай 2 цилиндр хэвтүүлж тавив. Эдгээр цилиндр дээр тэнхлэгүүд нь дээрх цилиндрүүдийн тэнхлэгүүдтэй перпендикуляр бөгөөд бие биеэ байгуулагчаараа шүргэх $R$ радиустай 2 цилиндрийг мөн хэвтүүлж тавив. Бүх дөрвөн цилиндрийг шүргэх бөмбөрцгийн радиусыг ол.
Хавтгай дээр бие бие шүргэх $r$ радиустай 2 бөмбөрцөг ба тэдгээрийг шүргэх $R$ ($R>r$) радиустай цилиндр байрлаж байв. Цилиндр нь хавтгайг өөрийн байгуулагчаар шүргэх бол хавтгай, цилиндр ба 2 бөмбөрцгийг шүргэх бөмбөрцгүүдээс бага радиустай бөмбөрцгийнх нь радиусыг ол.
$SABCD$ дөрвөн өнцөгт пирамидын суурь $ABCD$ ($BC\parallel AD$) трапец ба $BC=\dfrac45AD$, $\angle ASD=\angle CDS=\dfrac\pi2$ байв. Пирамидын бүх оройнууд $2$ өндөртэй, $\dfrac53$ суурийн радиустай цилиндрийн суурийн тойргууд дээр байрлах бол пирамидын эзлэхүүнийг ол.
Суурийн радиус нь $a$, өндөр нь $2a$ байх цилиндрийн
суурийн диаметрийг дайрсан суурьт $60^\circ$ өнцгөөр налах хавтгай цилиндрийг ямар эзлэхүүнтэй хэсгүүдэд хуваах вэ?
Шулуун дугуй цилиндрийн дээд суурийн $M$ цэгээс доод суурийн $N$ цэг дээр буулгасан $MN$ перпендикулярыг бэхлэв. Дээд суурийн тойргийн дурын цэгийг доод суурийн тойргийн цэгтэй холбогч хэрчмүүдийн дотроос $MN$ хэрчмийг огтлогч бүх хэрчмүүдийн дундаж цэгүүдийн геометр байрыг ол.
5 см ба 15 см талтай тэгш өнцөгтийг талыг нь тойруулан эргүүлэхэд үүсэх хоёр цилиндрийн аль нь хэд дахин их эзлэхүүнтэй байх вэ?
A. $9$
B. тэнцүү
C. $5$
D. $3$
E. 6
$R$ радиустай бөмбөрцөгт багтсан хамгийн их хажуу гадаргуутай цилиндрийн эзлэхүүнийг ол.
A. $\pi R^3$
B. $\dfrac{\pi R^3}{\sqrt2}$
C. $\dfrac{\pi R^3}{\sqrt3}$
D. $\dfrac{\pi R^3}{\sqrt4}$
E. $R^3$
Цилиндрт багтсан бөмбөрцгийн эзлэхүүн нь 168 бол цилиндрийн эзлэхүүнийг ол.
A. 222
B. 162
C. 248
D. 252
E. 192
$C\colon x^2+y^2+z^2=6$ бөмбөрцөгт багтсан хамгийн их эзлэхүүнтэй цилиндрийн суурийн радиусыг ол.
A. $1$
B. $2$
C. $3$
D. $4$
E. $5$
Цилиндрт багтсан бөмбөрцгийн эзлэхүүн нь $168$ бол цилиндрийн эзлэхүүнийг ол.
A. $222$
B. $162$
C. $248$
D. $252$
E. $192$
Цилиндрийн эзлэхүүн нь $63 \pi$ см.куб ба тэнхлэг огтлолын талбай нь $18$ см.кв бол суурийн радиусыг ол.
A. 8
B. 7
C. 6
D. 9
E. 10
Цилиндрийн хажуу гадаргын дэлгээс нь $48\pi$ талбайтай квадрат байв. Суурийн талбайг ол.
A. $12$
B. $4 \pi$
C. $16$
D. $9 \pi$
E. $12\pi$
Адил талт цилиндрийн суурийн радиус $2$ бол эзлэхүүнийг ол.
A. $16 \pi$
B. $8 \pi$
C. $12 \pi$
D. $18 \pi$
E. $9\pi$
Конус, цилиндр хоёр тэнцүү суурь, өндөр, хажуу гадаргуугийн талбайтай бол конусын байгуулагчуудын хооронд үүсэх хамгийн их өнцөг аль вэ?
A. $30^{\circ};$
B. $60^{\circ};$
C. $120^{\circ};$
D. $45^{\circ}.$
Адил талт цилиндр, адил талт конус хоёулаа тэнцүү хажуу гадаргуугийн талбайтай бол бүтэн гадаргуугийн талбайнууд нь ямар харьцаатай байх вэ?
A. $1:2;$
B. $1:1;$
C. $2:3;$
D. $4:5.$
Цилиндр, конус хоёр ерөнхий суурьтай ба суурийн хавтгайн нэг талд
байрлана. Хэрэв тэдгээр нь ижил эзлэхүүнтэй бол цилиндр дотор конусын эзлэхүүний
хэдий хэсэг харьяалагдах вэ?
A. $\dfrac13$
B. $\dfrac12$
C. $\dfrac{17}{20}$
D. $\dfrac{19}{27}$
E. $\dfrac{8}{27}$
Адил талт цилиндрийн эзлэхүүн ба бүтэн гадаргуугийн талбай ижил тоогоор илэрхийлэгдэж байв. Энэ тоо аль вэ?
A. $32\pi;$
B. $48\pi;$
C. $54\pi;$
D. $66\pi.$
Адил талт цилиндрийн эзлэхүүн ба хажуу гадаргуугийн талбай ижил тоогоор илэрхийлэгдэнэ. Түүний бүтэн гадаргуугийн талбай аль вэ?
A. $24\pi;$
B. $32\pi;$
C. $48\pi;$
D. $52\pi.$
Цилиндрийн радиус 37, өндөр 24 нэгж урттай бол түүний квадрат
хэлбэртэй огтлол тэнхлэгээсээ ямар зайд хийгдэх вэ?
A. 25
B. 30
C. 35
D. $17\sqrt5$
Радиус нь 5, өндөр нь 15 нэгж урттай цилиндрийн суурийн тойргууд
дээр төгсгөлтэй 17 нэгж урттай хэрчим цилиндрийн тэнхлэгээс ямар зайд байрлах вэ?
A. 3
B. 2
C. $\sqrt{15}$
D. $3\sqrt2$
Тэнхлэг огтлолын периметр нь нэг ижил цилиндрүүд дотроос
хамгийн их хажуу гадаргуугийн талбайтай цилиндрийн тэнхлэг огтлолын
диагоналиудын хоорондох өнцгийн хэмжээг ол.
A. $45^\circ$
B. $60^\circ$
C. $\arccos\frac23$
D. $90^\circ$
Тэнхлэг огтлолын периметр нь $p$ байх цилиндрүүдийн хажуу гадаргуугийн
талбайн хамгийн их утгыг ол.
A. $\frac{\pi}{2}p^2$
B. $\frac{\pi}4p^2$
C. $\frac{\pi}8p^2$
D. $\frac{\pi}{16}p^2$
Цилиндрийн радиус 13 см ба түүний өндөр 24 см бол түүний квадрат хэлбэртэй огтлол тэнхлэгээс ямар зайд хийгдэх вэ?
A. 12 см
B. 13 см
C. 10 см
D. 8 см
E. 5 см
Цилиндрийн радиус 5 см ба түүний өндөр 8 см бол түүний квадрат хэлбэртэй огтлол тэнхлэгээс ямар зайд хийгдэх вэ?
A. 1 см
B. 2 см
C. 4 см
D. 3 см
E. 5 см
Цилиндрийн радиус 5 см ба түүний өндөр 6 см бол түүний квадрат хэлбэртэй огтлол тэнхлэгээс ямар зайд хийгдэх вэ?
A. 1 см
B. 2 см
C. 4 см
D. 3 см
E. 5 см
Цилиндрийн радиус 13 см ба түүний өндөр 10 см бол түүний квадрат хэлбэртэй огтлол тэнхлэгээс ямар зайд хийгдэх вэ?
A. 12 см
B. 13 см
C. 10 см
D. 8 см
E. 5 см
Шулуун цилиндрийн суурийн радиус 5см байв. Оройнууд нь цилиндрийн дээд доод суурь дээр байрлах тэгш өнцөгтийн суурь дээрх талын урт 6см, энэ хавтгай цилиндрийн суурьтай $60^\circ$ үүсгэх бол тэгш өнцөгтийн талбайг ол.
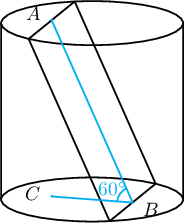

A. 96 см.кв
B. 60 см.кв
C. 72 см.кв
D. 80 см.кв
E. 48 см.кв
Цилиндрийн эзлэхүүн $V=65\pi$ ба тэнхлэг огтлолын талбай $26$ байв. Цилиндрийн суурийн радиусыг ол.
A. $4$
B. $6$
C. $7$
D. $5$
E. $9$
Цилиндрийн эзлэхүүн $V=63\pi$ ба тэнхлэг огтлолын талбай $18$ байв. Цилиндрийн суурийн радиусыг ол.
A. $3$
B. $6$
C. $7$
D. $8$
E. $9$
Цилиндрийн эзлэхүүн $V=65\pi$ ба тэнхлэг огтлолын талбай $26$ байв. Цилиндрийн суурийн радиусыг ол.
A. $5$
B. $6$
C. $7$
D. $8$
E. $9$
Суурийн радиус нь 4 см байх шулуун дугуй цилиндрийн нэг үзүүрээс зурагт үзүүлснээр хавтгайгаар огтлоход хамгийн урт байгуулагч нь 14 см, хамгийн богино байгуулагч нь 10 см болсон бол үүссэн биетийн эзлэхүүнийг ол.

A. $192\pi$
B. $182\pi$
C. $196\pi$
D. $160\pi$
E. $224\pi$
Суурийн радиус нь 4 см байх шулуун дугуй цилиндрийн нэг үзүүрээс зурагт үзүүлснээр хавтгайгаар огтлоход хамгийн урт байгуулагч нь 15 см, хамгийн богино байгуулагч нь 9 см болсон бол үүссэн биетийн эзлэхүүнийг ол.


A. $160\pi$
B. $240\pi$
C. $80\pi$
D. $192\pi$
E. $144\pi$
Суурийн радиус нь 5 см, өндөр нь 6 см цилиндрээс зурагт үзүүлснээр 2 см куб ухаж авчээ. Ухагдсан цилиндрийн бүтэн гадагуугийн талбайг олоорой.
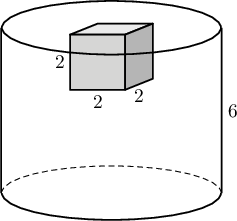

A. $110\pi+24$
B. $106\pi+24$
C. $106\pi+16$
D. $80\pi+16$
E. $110\pi+16$
Цилиндрийн тэнхлэг огтлол нь $5\sqrt2$ диагоналтай квадрат бол түүний хажуу гадаргуугийн талбайг ол.
A. $25\pi^2$
B. $25$
C. $25\pi$
D. $10\pi$
E. $10$
$ABCD$ гурвалжин пирамид ба цилиндр өгөгдөв. Цилиндрийн доод суурийн тойрог $ABC$ гурвалжинд багтсан тойрог болно. Цилиндрийн дээд суурийн тойрог $DA, DB, DC$ ирмэгүүдийг огтлох ба төв нь $ABD$ талс дээр оршино.
Цилиндрийн суурийн радиус 3, $ABCD$ пирамидын эзлэхүүн $27\sqrt{2},$ $AB=24$ байв.
1) $ABC$ ба $ABD$ талсуудын хоорондох хоёр талст өнцөг $\varphi=\arctg\dfrac{\sqrt{\fbox{a}}}{\fbox{b}}$ байна.
2) $ABCD$ пирамидыг багтаасан бөмбөлгийн радиус $R=\sqrt{\dfrac{\fbox{cde}}{\fbox{f}}}$ байна.
1) $ABC$ ба $ABD$ талсуудын хоорондох хоёр талст өнцөг $\varphi=\arctg\dfrac{\sqrt{\fbox{a}}}{\fbox{b}}$ байна.
2) $ABCD$ пирамидыг багтаасан бөмбөлгийн радиус $R=\sqrt{\dfrac{\fbox{cde}}{\fbox{f}}}$ байна.
$ABCD$ гурвалжин пирамид ба цилиндр өгөгдөв. Цилиндрийн доод
суурийн тойрог $ABC$ гурвалжинд багтсан тойрог болно. Цилиндрийн
дээд суурийн тойрог $DA, DB, DC$ ирмэгүүдийг огтлох ба төв нь
$ABD$ талс дээр оршино. Цилиндрийн суурийн радиус 4, $ABC$ ба
$ABD$ талсуудын хоорондох хоёр талст өнцөг
$\arctg\dfrac1{\sqrt{6}},$ $AB=24$ байв.
1) $ABCD$ пирамидын эзлэхүүн $V=\fbox{abc}\cdot \sqrt{\dfrac{\fbox{d}}{\fbox{e}}}$ байна.
2) $ABCD$ пирамидыг багтаасан бөмбөлгийн радиус $R=\fbox{fg}\cdot \sqrt{\dfrac{\fbox{h}}{\fbox{i}}}$ байна.
1) $ABCD$ пирамидын эзлэхүүн $V=\fbox{abc}\cdot \sqrt{\dfrac{\fbox{d}}{\fbox{e}}}$ байна.
2) $ABCD$ пирамидыг багтаасан бөмбөлгийн радиус $R=\fbox{fg}\cdot \sqrt{\dfrac{\fbox{h}}{\fbox{i}}}$ байна.
Цилиндрийн эзлэхүүн
Шулуун ба хавтгайн харилцан байршил
$A$ ба $B$ цэг $60^\circ$ өнцөг үүсгэх хоёр талст өнцгийн ирмэгүүд дээр орших ба $AC$ ба $BD$ нь нөгөө талс дээр орших ирмэгт буулгасан перпендикулярууд байв. Хэрэв $AB=3$ см, $AC=2$ см, $BD=3$ см бол $CD$-г ол.
Тэгш өнцөгт гурвалжны катет 7 см ба 24 см. Гурвалжны хавтгайд $30^\circ$-аар налсан, гипотенузыг нь агуулсан хавтгай тэгш өнцөгийн оройгоос ямар зайд байрлах вэ?
Хавтгайтайгаас $5\sqrt2$ зайд орших цэгээс хавтгайд $45^\circ$-ийн өнцөг үүсгэх хоёр налуу татахад тэдгээрийн хооронд $60^\circ$-ийн өнцөг үүссэн байв. Хоёр налуугийн төгсгөлийн цэгүүдийн хоорондох зайг ол.
$AB$ хэрчим $PMNQ$ хоёр талст тэгш өнцгийн талсуудыг тулдаг. Хэрчмийн төгсгөлийн цэгүүд нь хоёр талст өнцгийн $MN$ ирмэгээс ижил зайд байрладаг. Хэрчмийн талсуудад налсан өнцгүүдийн харьцааг ол.
< p>< /p>Бодолтыг харах!
Тэгш өнцөгт адил хажуут гурвалжны нэг катет $\alpha$ хавтгайд оршдог. Нөгөө катет нь уг хавтгайтай $45^\circ$-ийн өнцөг үүсгэдэг бол гипотенузын $\alpha$ хавтгайтай үүсгэх өнцгийг ол.
$ABC$ гурвалжны $C$ өнцөг $90^\circ$ ба түүний $AC$ катет нь уг гурвалжны хавтгай ба түүнтэй $30^\circ$ өнцөг үүсгэх $\alpha$ хавтгай хоёрын огтлолцол дээр байрлана. Хэрэв $AC=8$, $AB=3BC$ бол $B$ оройгоос $\alpha$ хавтгай хүртэлх зайг ол.
5. Дараах шулуунуудын хоорондох өнцгийг ол.
a. $\left\{\begin{array}{c} x=3t - 2\\ y=0 \\ z=-t + 3 \end{array}\right.$ ба $ \vec{\mathstrut r}= (1, 0, 3) + t(2, 0, 1) $
б. $ \frac{x-3}{1} = \frac{y+2}{-1} = \frac {z}{\sqrt{2}}$ ба $ \frac{x+2}{1}=\frac {y-3}{1}={z+5}{\sqrt{2}} $
в. $ \vec{\mathstrut r}= (1, 0, -1) +t(2, -2, 1) $ ба $ \vec{\mathstrut r} = (\frac{1}{7} , \frac{5}{14}, 0) + t(-6, -3, 2) $
a. $\left\{\begin{array}{c} x=3t - 2\\ y=0 \\ z=-t + 3 \end{array}\right.$ ба $ \vec{\mathstrut r}= (1, 0, 3) + t(2, 0, 1) $
б. $ \frac{x-3}{1} = \frac{y+2}{-1} = \frac {z}{\sqrt{2}}$ ба $ \frac{x+2}{1}=\frac {y-3}{1}={z+5}{\sqrt{2}} $
в. $ \vec{\mathstrut r}= (1, 0, -1) +t(2, -2, 1) $ ба $ \vec{\mathstrut r} = (\frac{1}{7} , \frac{5}{14}, 0) + t(-6, -3, 2) $