Монгол Бодлогын Сан
Эх хэлээрээ суралцаж, эх хэлээрээ мэдлэгээ түгээе.
Holy guacamole! www.integral.mn сайт 2026-01-01-ээс шинэчлэгдэж www.mathminds.club хуудас руу шилжинэ.
Магадлал
Байесийн томьёо
Гаалийн хэсэг гурван шалган нэвтрүүлэх цэгтэй ба нийт ачааны 50$\%$ нь I, $30\%$ нь II, $20\%$ нь III цэгээр шалгагддаг. Шалгах цэгүүд зөрчил илрүүлэх магадлал харгалзан $\dfrac 23; \dfrac 12; \dfrac 23$ байв. Шалгалтын эцэст 1 ачаа зөрчилтэй гарсан бол II шалгах цэг илрүүлсэн байх магадлалыг ол.
A. $\dfrac{9}{37}$
B. $\dfrac{37}{60}$
C. $\dfrac{3}{60}$
D. $\dfrac{3}{37}$
E. $\dfrac13$
Сурагчдын $10\%$ нь $A$, $20\%$ нь $B$, $30\%$ нь $C$, $30\%$ нь $D$, $10\%$ нь $F$ сурдаг байв. Сурагчид спортоор хичээллэдэг байх магадлал $A$ сурдаг бол $\dfrac1{10}$, $B$ сурдаг бол $\dfrac 18$, $C$ сурдаг бол $\dfrac 14$, $D$ сурдаг бол $\dfrac 12$, $F$ сурдаг бол $\dfrac 12$ байв. Санамсаргүйгээр сонгосон 1 сурагч спортоор хичээллэдэг бол $B$ сурдаг сурагч байх магадлалыг ол.
A. $\dfrac{31}{100}$
B. $\dfrac{1}{40}$
C. $\dfrac{5}{62}$
D. $\dfrac{57}{62}$
E. $\dfrac{69}{100}$
Гурван харваачийн байг нэг удаа харваад онох магадлалууд нь харгалзан $0.3$, $0.5$, $0.8$ байв. Нэг харваач санамсаргүйгээр сонгоод хоёр удаа харвуулахад байг оноогүй бол тэр нь нэгдүгээр харваач байх магадлалыг ол.
A. $\dfrac{31}{54}$
B. $\dfrac{25}{78}$
C. $\dfrac{4}{7}$
D. $\dfrac{1}{2}$
E. $\dfrac{49}{78}$
Үйлдвэр 3 машинаар бүтээгдэхүүн үйлдвэрлэдэг ба нийт бүтээгдэхүүний $50\%$-г I машин, $30\%$-г II машин , $20\%$-г III машин үйлдвэрлэдэг. Машин тус бүрийн гологдол гаргах магадлал I машин 0.1, II машин 0.2, III машин 0.05 бол үйлдвэрээс гологдол бүтээгдэхүүн гарах магадлалыг ол.
A. $0.05$
B. $0.1$
C. $0.12$
D. $0.15$
E. $0.2$
Бернуллийн томьёо
Шоог 10 удаа орхиход "3" тоо яг 2 удаа буух магадлалыг ол.\\
0.1 хүртэл нарийвчлалтай $p\approx\frac mn$ ойролцоо тэнцэл 0.9
магадлалтайгаар биелж байхын тулд туршилтыг хэчнээн хийвэл зохих вэ?
Шоог 10 хаяхад "1" оноо 3-аас илүүгүй буух магадлалыг ол.
Шоог 10 хаяхад 3-т хуваагдах оноо 2-оос их, 5-аас цөөн тусах магадлалыг ол.
Тэнцүү 2 өрсөлдөгчийн хувьд:\\
а) 4 өргөөс 3-ыг нь хожих, эсвэл 8 өргөөс 5-ыг нь хожих,\\
б) 4 өргөөс 3-аас доошгүйг эсвэл 8 өргөөс 5-аас цөөнгүйг хожихын аль нь илүү
магадлалтай вэ? (тоглолтонд хайнцаа гардаггүй гэж үзнэ).
$p(A)=0.3$ ба туршилтыг 5 удаа давтав. $A$ үзэгдэл 2-оос багагүй явагдах
магадлалыг ол.
0.01 хүртэл нарийвчлалтайгаар $p\approx\frac mn$ тэнцлийг 0.95
магадлалтайгаар олохын тулд хэчнээн туршилт хийвэл зохих вэ?
0.1 хүртэл нарийвчлалтай $p\approx\frac mn$ тэнцлийн магадлал 100
туршилтад хэдтэй тэнцүү вэ?
$p\approx\frac mn$ тэнцлийг 40 туршилтад 0.9 магадлалтайгаар олов. Түүний нарийвчлалыг ойролцоогоор үнэл.
Хуучин CD зардаг дэлгүүрийн 5 CD тутмын 1 нь гэмтэлтэй байв.
- Санамсаргүйгээр 15 CD авахад хамгийн ихдээ 2 нь гэмтэлтэй байх магадлалыг ол.
- Хэрвээ гэмтэлтэй байх магадлал нь хамгийн багадаа $0.85$ байхад хамгийн цөөндөө 1 гэмтэлтэй CD гарах хамгийн цөөн туршилтын тоог ол.
Хүү төрөх магадлал $p=0.51$ бол 4 хүүхэдтэй өрх 2-оос цөөнгүй хөвгүүдтэй байх магадлалыг ол.
A. $0.21$
B. $0.817$
C. $0.53$
D. $0.721$
E. $0.702$
$100$ бүтээгдэхүүнтэй хэсгээс $5$ бүтээгдэхүүн шалгаж ядаж нэг гологдол илэрвэл энэ хэсгийг буцаадаг. Энэ хэсгийн бүтээгдэхүүний $5\%$ нь гологдол байсан бол уг хэсгийг буцаах магадлалыг ол.
A. $1-\dfrac{C_{95}^5}{A_{100}^5}$
B. $\dfrac{A_{100}^1}{A_{100}^5}$
C. $1-\dfrac{C_{95}^5}{C_{100}^5}$
D. $\dfrac{C_{100}^1}{C_{100}^5}$
E. $\dfrac{C_{95}^4}{C_{100}^5}$
Анчин $0.9$ магадлалтайгаар байг онодог байв. Энэ анчин байг $3$ удаа буудахад ядаж нэг удаа алдах магадлал хэд вэ?
A. $0.36$
B. $0.27$
C. $0.729$
D. $0.271$
E. $0.261$
Зөв хэлбэртэй шоог 3 удаа хаяхад 1-ээс олонгүй удаа 6 буух үзэгдлийн магадлал хэдтэй тэнцүү вэ?
A. $\dfrac12$
B. $\dfrac13$
C. $\dfrac23$
D. $\dfrac{25}{27}$
E. $1$
Хэрэв хүү төрөх магадлал $\dfrac12$ бол 4 хүүхэдтэй айл 3 хүүтэй байх магадлал $\dfrac{1}{\fbox{a}}$; 2 хүү, 2 охинтой байх магадлал $\dfrac{\fbox{b}}{\fbox{c}}$; нэг ч хүүгүй байх магадлал $\dfrac{1}{\fbox{de}}$ байна.
Нэгэн шагайг орхиход морь буух магадлал $\dfrac{1}{10}$ байв. Уг шагайг 3 удаа орхиход
- Ядаж нэг удаа морь буух магадлал $1-\Big(\dfrac{\fbox{a}}{10}\Big)^{\fbox{b}}$;
- Яг нэг удаа морь буух магадал $0.\fbox{cde}$;
- Яг хоёр удаа морь буух магадлал $0.0\fbox{fg}$ байна.
Бүтэн магадлалын томьёо
Хайрцагт 2 бөмбөг байв. (бөмбөг бүр хар юмуу цагаан өнгөтэй байх ёстой).
Дээр нь 1 цагаан бөмбөг нэмж хийгээд 1 бөмбөг таамгаар авахад тэр нь цагаан
байх магадлалыг ол.
I уутанд 6 улаан, 4 цагаан, II уутанд 2 улаан, 3 цагаан бөмбөг байжээ. Таамгаар сонгосон нэг уутнаас нэгэн зэрэг хоёр бөмбөгийг таамгаар гаргаж ирэхэд хоёулаа цагаан байх магадлалыг ол.
A. $\dfrac{9}{65}$
B. $\dfrac{19}{60}$
C. $\dfrac{5}{12}$
D. $\dfrac{3}{20}$
E. $\dfrac{13}{60}$
Цагаан уутанд 4 улаан, 3 хөх, улаан уутанд 2 улаан, 4 хөх бөмбөг байжээ. Цагаан уутнаас таамгаар нэг бөмбөг авч, өнгийг нь харалгүйгээр улаан уутанд хийгээд, дараа нь улаан уутнаас таамгаар авсан бөмбөг улаан өнгөтэй байх магадлалыг ол.
A. $\dfrac{21}{64}$
B. $\dfrac{18}{49}$
C. $\dfrac{15}{36}$
D. $\dfrac{15}{64}$
E. $\dfrac{15}{49}$
Анчин гахайг 3 буудав. Түүний эхний сум онох магадлал $0.4$, II сум онох магадлал $0.5$, III сум онох магадлал $0.7$ байв. Гахайг нэг сум оноход үхэх магадлал $0.2$, хоёр сум оноход үхэх магадлал $0.6$, гурван сум оноход үхэх магадлал $1$ байг. Тэгвэл гахай үхэх магадлалыг ол.
A. $0.621$
B. $0.32$
C. $0.512$
D. $0.563$
E. $0.458$
Компьютерийн жижиг эдлэл хийдэг гурван машины 1-р машин бүх бүтээгдэхүүний $30\%$-ийг, 2-р машин $25\%$-ийг, 3-р машин $45\%$-ийг үйлдвэрлэдэг. Эдгээр машины гологдол гаргах хувь нь харгалзан $2\%$, $1\%$, $3\%$ болно. Таамгаар сонгон авсан эдлэл гологдол байх магадлалыг ол.
A. $0.011$
B. $0.025$
C. $0.027$
D. $0.022$
E. $0.03$
I уутанд 6 улаан, 4 цагаан, II уутанд 2 улаан, 3 цагаан бөмбөг байжээ. Таамгаар сонгосон нэг уутнаас нэгэн зэрэг хоёр бөмбөгийг таамгаар гаргаж ирэхэд хоёулаа улаан байх магадлалыг ол.
A. $\dfrac{9}{65}$
B. $\dfrac{19}{60}$
C. $\dfrac{5}{12}$
D. $\dfrac{3}{20}$
E. $\dfrac{13}{60}$
$A$ уутанд 3 улаан, 2 хөх; $B$ уутанд 7 улаан, 3 хөх; $C$ уутанд 4 улаан, 6 хөх бөмбөг байжээ. Бат $A$, $B$ уутны аль нэгийг санамсаргүйгээр сонгоод дотроос нь нэг бөмбөг гаргаж ирэв. Харин Дорж $C$ уутнаас санамсаргүйгээр нэг бөмбөг гаргаж иржээ. Бат, Дорж хоёрын сонгосон бөмбөгүүд ижил өнгөтэй байх магадлалыг ол.
A. $0.5$
B. $0.75$
C. $0.36$
D. $0.47$
E. $0.27$
Геометр магадлал
Хавтгайд зэрэгцээ хоёрын хоорондхи зай нь
$\ell$ байх параллель шулуунуудын бүл өгчээ. $\ell$ урттай хэрчмийг хаяхад тэр нь бүлийн
аль нэг шулуунтай огтлолцох магадлалыг ол.
Шулууны дагуу бие биеэс 15 метрийн зайтайгаар минүүд булжээ. Энэ шулуунд
перпендикуляраар 3 м өргөнтэй танк орж ирээд дэлбэрэх магадлалыг ол.
$R$ радиустай тойрог дээр $A$ цэгийг бэхлэжээ. Тойрог дээр санамсаргүй
хаяж буй $B$ цэгийн хувьд $|AB|\ge R$ байх магадлалыг ол.
Тойрогт санамсаргүйгээр гурвалжин багтааж зурж байна. Тэр нь хурц өнцөгт
гурвалжин байх магадлалыг ол.
Тойрогт квадрат багтжээ. Энэ тойргоор хүрээлэгдсэн дугуйд цэг хаяж байна.
Тэр нь квадратад унах магадлалыг ол.
5-р бодлогыг а) тэгш өнцөгт, б) адил хажуут гурвалжин,
в) мохоо өнцөгт гурвалжин байх тохиолдолд бод.
$x^2+px+q$ квадрат гурван гишүүнтийн коэффициент $p,q$-г $[-1,1]$ хэрчмээс
дураараа сонгон авч байна. Тэгвэл тэр нь бодит язгууруудтай байх магадлалыг ол.
$1,2,\ldots,n$ дараалалд $k$ тоог тэмдэглэжээ. Энэ дарааллаас таамгаар
авсан хоёр тооны нэг нь $k$-аас бага нөгөө нь $k$-аас их байх магадлалыг ол.
"6" оноо а) 0.5-аас их, б) 0.8-аас их, в) 0.9-өөс их магадлалтайгаар
туссан байхын тулд шоог хэдэн удаа орхивол зохих вэ?
$p(A)=p$ байв. $A$ үзэгдлийн ядаж нэг явагдах магадлал нь $r$-ээс бага
магадлалтай гэж баталж хэлэхийн тулд туршилтыг хэдэн удаа давтан хийвэл зохих вэ?
Аль нэг хоёрын нь төрсөн өдөр 0.5-аас багагүй магадлалтайгаар давхцаж
байхын тулд хамгийн цөөндөө хэдэн хүн байвал зохих вэ?
Хайрцагт $M$ цагаан, $N-M$ хар бөмбөг байв. Хайрцагнаас хоёр хүн нэг нэг
бөмбөг ээлжлэн аваад байхад (буцаалтгүйгээр) эхэлсэн хүн нь түрүүлж цагаан бөмбөг
авах магадлалыг:
а) $N=3$, $M=1$, б) $N=4$, $M=1$, в) $N=6$, $M=2$ тохиолдлуудад бод.
Замаар секунд тутамд $p$ магадлалтайгаар машин өнгөрнө. Явган зорчигч 3
секундэд зам хөндлөн гардаг. Зам хөндлөн гарах боломжийг а) 3 сек, б) 4 сек,
в) 5 сек хүлээх магадлалуудыг ол.
0.2 магадлалтай онодог хүн бай буудаж байна. Байгаа оновол л буудахаа
болино. Яг 6 буудах магадлалыг ол.
Алин дээр нь ч "1" оноо буугаагүй байх үзэгдлийн магадлал 0.3-аас бага
байхын тулд хэчнээн шоо орхивол зохих вэ?
I хайрцагт 2 хар, 8 цагаан, II хайрцагт 16 хар, 4 цагаан бөмбөг байв.
Хайрцаг бүрээс нэг нэг бөмбөг авч дараа нь тэр хоёрынхоо нэгийг авахад тэр нь
цагаан байх магадлалыг ол.
Бат ажилдаа дугуйгаар явбал 0.5, автобусаар явбал 0.25 магадлалтайгаар
хожимдож очно. Хэрэв Бат өнөөдөр хожимдоогүй бол маргааш нь тэр унаагаараа явах
ба хожимдсон бол унаагаа заавал солино. Бат ажилдаа 1000 дахь удаагаа явахдаа
ямар магадлалтайгаар хожимдож очих вэ?
$A,B$ хоёр дараахь нөхцөлтэйгөөр шатар тоглож байна:\\
а) хожсон нь 1 оноо авна (хайнцаа гарахгүй бол хожил урьд өргүүдээс
хамаарахгүй гэж үзнэ),\\
б) $A$ нь $\alpha$ магадлалтайгаар , $B$ нь $\beta$ магадлалтайгаар хождог ба
$\alpha+\beta=1$, $\beta<\alpha$,\\
в) өрсөлдөгчөөсөө 2 оноогоор тасарсан нь тэмцээнд ялна. $A$ ба $B$-ийн тус
бүрийн ялах магадлалыг ол.
Тус бүрийн урт нь $a$-аас хэтрэхгүй 3 хэрчим авав. Тэдгээрээр гурвалжин
байгуулж болох магадлалыг ол.
50 мм талтай квадратыг 5 мм өргөнтэй шугамаар татаж торлосон ширээн дээр
25 мм диаметртэй мөнгө хаяж байна. Мөнгө торын шугамыг огтлохгүй унах магадлалыг ол.
Дугуйн хөвчийн урт түүний радиусаас их байх магадлалыг ол.
Мөнгө босоогоороо унах магадлал $\frac13$ байхын тулд түүний өргөн ямар
байвал зохих вэ?
$L$ өргөнтэй сувгийн дагуу тогтмол $v_1$ хурдтай завь яаж байна. Хоёр
дахь завь мөн $v_2$ тогтмол хурдтайгаар сувгаар хөндлөн зогсолтгүй явж дохио
дуугаргаж байна. Энэ дохио $d
Хоёр хайрцагт хар, цагаан нийт 25 бөмбөг байв. Хайрцаг бүрээс нэг
бөмбөг авахад хоёул цагаан байх магадлал 0.54 бол хоёул хар байх магадлалыг ол.
Зөв $n$ өнцөгтийн $(n\ge6)$ ялгаатай цэгүүдийн 2 гуравтыг сонгож авахад
энэхүү сонгосон гуравтууд орой нь болох хоёр гурвалжин огтлолцохгүй байх магадлалыг ол.
Цэг $ABCDA'B'C'D'$ кубийн ирмэгээр явж байна. Аль ч оройгоос түүн дээр
ирдэг 3-н ирмэгийн алинаар нь ч адилхан $\frac13$ магадлалтай явж чадна. Харин
цэг $B'$ юмуу $C'$ орой дээр ирвэл цааш явахгүй. $A$ оройгоос хөдөлсөн цэг ямар
магадлалтайгаар:\\ а) $B'$, б) $C'$ оройд ирэх, в) $B'$ ба $C'$-ийн алинд нь ч
ирэхгүй вэ?
Таамгаар сонгож авсан хоёр натурал тоо харилцан анхны байх магадлалыг ол.
$p,q,r>0$ ба $\D p+q+r=1$ бол $\D1+r^3<(1-p^3)^3+(1-q^3)^3$ тэнцэтгэл
бишийг батал.
$m,n\in N$, $x_1,\ldots,x_n$, $y_1,\ldots,y_n\in[0,1]$ ба $x_i+y_i=1$,
$i=\overline{1,n}$ бол $\D(1-x_1\ldots x_n)^m+(1-y_1^m)\ldots(1-y_n^m)\ge1$
тэнцэтгэл бишийг батал. Тухайн тохиолдолд $x\in[0,1]$ бол $\D(1-x^n)^m+(1-(1-x
)^m)^n\ge1$ гэж гарна. Эндээс $(3^m-1)^n+(3^n-2^n)^m>3^{mn}$ гэж гарна.
$0\le x,y,z\le1$ бол $x(1-y)+y(1-z)+z(1-x)\le1$-г батал.
Тамхины фирм янжууртай хайрцаг бүрт хөзрийн 1 мод хийж худалддаг байв.
Худалдан авагч 52 мод бүхий 1 багц хөзөртэй болохын тулд дунджаар хамгийн
цөөндөө хэдэн хайрцаг янжуур худалдаж авбал зохих вэ?
$A,B$ хоёр "сүлд,тоо" гэсэн тоглоом тоглож байна. Орхисон мөнгө сүлдээрээ
буувал $B$ нь $A$-даа 1 мөнгө, тоогоороо буувал $A$ нь $B$-дээ 1 мөнгө өгнө.
Тоглолт эхлэхэд $A$ нь $n$, $B$ нь $m$ мөнгөтэй байсан бол хэн нэг нь бүх
мөнгийг авахын тулд дунджаар хэдэн удаа мөнгө орхивол зохих вэ?
Квадратын дотор санамсаргүй шидсэн цэг зураг дээр будагдсан хэсэгт унасан байх үзэгдлийн магадлалыг ол.


A. $\dfrac12$
B. $\dfrac14$
C. $\dfrac34$
D. $\dfrac25$
E. $1$
$a$ талтай квадрат нүдтэй тор уруу $r$ радиустай $(2r< a)$ бөмбөг шидэхэд торыг цохилгүйгээр нэвтрэх магадлалыг ол.
A. $\dfrac{a-2r}{a}$
B. $\dfrac{(a-2r)^2}{a^2}$
C. $\dfrac{r}{a}$
D. $\dfrac{\pi r^2}{a^2}$
E. $\dfrac{4r^2}{a^2}$
$a$ талтай зөв гурвалжин нүдтэй тор зурсан хавтгай дээр $r$ радиустай мөнгийг орхисон. Мөнгө торын зураастай огтлолцож унах магадлалыг ол.
A. $1-\frac{(a-2\sqrt{3}r)^2}{a^2}$
B. $\frac{(a-2\sqrt{3}r)^2}{a^2}$
C. $1-\frac{(a-2\sqrt{3})^2}{a^2}$
D. $\frac{a-2\sqrt{3}}{a^2}$
Замын уулзварын дохионы улаан гэрэл 2 минут, шар гэрэл 1 минут, ногоон гэрэл 3 минут асдаг бол замын уулзварт ирсэн машин дохион дээр сааталгүй нэвтрэх магадлалыг ол.
A. $\frac{1}{2}$
B. $\frac{3}{7}$
C. $\frac{3}{5}$
D. $\frac{2}{3}$
Фронтын шугаман дээр өөр хоорондоо 5 м зайтайгаар мина булсан. 3 м өргөнтэй танк фронтын шугамыг дэлбэрэлгүйгээр нэвтрэх магадлалыг ол.
A. $\dfrac{1}{3}$
B. $\dfrac{2}{5}$
C. $\dfrac{3}{5}$
D. $\dfrac{5}{8}$
E. $\dfrac{1}{2}$
Нэгж радиустай тойргийг 12 тэнцүү секторт хувааж улаан, хөх, ногоон 3 өнгөөp алаглуулан будав. Тойрог уруу санамсаргүйгээр 2 цэг шидэхэд ижил өнгийн секторт унасан байх магадлалыг ол.
A. $\frac{1}{3}$
B. $\frac{1}{9}$
C. $\frac{1}{12}$
D. $\frac{1}{6}$
Нэгж радиустай тойргийг 12 тэнцүү секторт хувааж улаан, хөх, ногоон 3 өнгөөp алаглуулан будав. Тойрог уруу санамсаргүйгээр 2 цэг шидэхэд өөр өнгийн секторуудад унасан байх магадлалыг ол.
A. $\dfrac{1}{12}$
B. $\dfrac{1}{9}$
C. $\dfrac{1}{3}$
D. $\dfrac{1}{6}$
E. $\dfrac{2}{3}$
Нэгж радиустай дугуй дотроос таамгаар нэг цэг авахад дугуйн төвөөс $\dfrac16$-ээс бага зайд байх магадлалыг ол.
A. $\dfrac{35}{36}$
B. $\dfrac12$
C. $\dfrac{1}{36}$
D. $\dfrac{5}{6}$
E. $\dfrac{1}{6}$
Нэгж радиустай дугуй дотроос таамгаар нэг цэг авахад дугуйн төвөөс $\dfrac13$-ээс бага зайд байх магадлалыг ол.
A. $\dfrac{8}{9}$
B. $\dfrac{1}{2}$
C. $\dfrac{1}{3}$
D. $\dfrac{2}{3}$
E. $\dfrac{1}{9}$
Нэгж радиустай дугуй дотроос таамгаар нэг цэг авахад дугуйн төвөөс $\dfrac14$-ээс бага зайд байх магадлалыг ол.
A. $\dfrac{15}{16}$
B. $\dfrac12$
C. $\dfrac{1}{16}$
D. $\dfrac{3}{4}$
E. $\dfrac{1}{4}$
Нэгж радиустай дугуй дотроос таамгаар нэг цэг авахад дугуйн төвөөс $\dfrac15$-ээс бага зайд байх магадлалыг ол.
A. $\dfrac{1}{5}$
B. $\dfrac12$
C. $\dfrac{24}{25}$
D. $\dfrac{4}{5}$
E. $\dfrac{1}{25}$
Нэгж тойрог дээр орших $A\left(\frac{\sqrt2}{2};\frac{\sqrt2}{2}\right)$; $B\left(\frac{\sqrt2}{2};-\frac{\sqrt2}{2}\right)$ цэгүүд өгөгдөв. Тойрог дээр санамсаргүй $C$ цэг авахад $ABC$ хурц өнцөгт гурвалжин болох магадлалыг ол.
A. $\dfrac18$
B. $\dfrac12$
C. $\dfrac34$
D. $\dfrac16$
E. $\dfrac14$
Нэгж тойрог дээр орших $A\left(\frac{\sqrt2}{2};\frac{\sqrt2}{2}\right)$; $B\left(-\frac{\sqrt2}{2};\frac{\sqrt2}{2}\right)$ цэгүүд өгөгдөв. Тойрог дээр санамсаргүй $C$ цэг авахад $ABC$ хурц өнцөгт гурвалжин болох магадлалыг ол.
A. $\dfrac16$
B. $\dfrac34$
C. $\dfrac12$
D. $\dfrac14$
E. $\dfrac18$
Квадратын дотор санамсаргүй шидсэн цэг зураг дээр будагдсан хэсэгт унасан байх үзэгдлийн магадлалыг ол.


A. $\frac12$
B. $\frac14$
C. $\frac34$
D. $\frac25$
E. $1$
Дурын гурвалжин сонгон авахад уг гурвалжин хурц өнцөгт гурвалжин байх магадлал аль нь вэ?
A. $\dfrac16$
B. $\dfrac13$
C. $\dfrac12$
D. $\dfrac14$
E. $\dfrac34$
1 урттай хэрчим дээр 2 цэг хаяхад түүнийг 3 хэсэгт хуваав. Үүссэн хэрчмүүд гурвалжин үүсгэх магадлалыг ол.
A. $\dfrac12$
B. $\dfrac13$
C. $\dfrac23$
D. $\dfrac14$
E. $\dfrac34$
Хоёр нөхөр уулзахаар болзохдоо 13-аас 14 цагийн хооронд бие биеэсээ
хамааралгүйгээр заасан газарт ирж хэрэв нөгөө хүнээ ирээгүй байвал 30 минутаас
илүүгүй хүлээгээд явна гэж тохиролцов. Тэдний уулзалдах магадлалыг ол.
A. $\dfrac14$
B. $\dfrac34$
C. $\dfrac12$
D. $\dfrac56$
E. $\dfrac16$
$x^2+3x-4<0$ тэнцэтгэл бишийн шийд, $x^2-x-12<0$ тэнцэтгэл бишийн шийд болох магадлал $\dfrac{\fbox{a}}{\fbox{b}}$, хоёр тэнцэтгэл бишийн ядаж нэгнийх нь шийд 2-оос бага байх магадлал $\dfrac{\fbox{c}}{\fbox{d}}$, тэдгээрийн зөвхөн нэгнийх нь шийд болдог тоо $(-1)$-ээс их байх магадлал $\dfrac{\fbox{e}}{\fbox{f}}$ байна.
$x^2-6x+5<0$ тэнцэтгэл бишийн шийд, $x^2-11x+24< 0$ тэнцэтгэл бишийн шийд болох магадлал $\dfrac{\fbox{a}}{\fbox{b}}$ (1 оноо), хоёр тэнцэтгэл бишийн ядаж нэгнийх нь шийд 6-аас бага байх магадлал $\dfrac{\fbox{c}}{\fbox{d}}$ (2 оноо), тэдгээрийн зөвхөн нэгнийх нь шийд болдог тоо $2$-оос их байх магадлал $\dfrac{\fbox{e}}{\fbox{f}}$ байна. (2 оноо)
$[0,1]$ хэрчмээс санамсаргүйгээр $a$ ба $b$ хоёр тоог сонгоход $x^{2}+ax+b=0$ тэгшитгэл бодит шийдтэй байх магадлал $\dfrac{\fbox{a}}{\fbox{bc}}$ байна.
$[-1,1]$ хэрчмээс санамсаргүйгээр $a$ ба $b$ хоёр тоог сонгоход $x^{2}+ax+b=0$ тэгшитгэл бодит шийдгүй байх магадлал $\dfrac{\fbox{ab}}{\fbox{cd}}$ байна.
Зурагт өгөгдсөн дартсын самбар уруу 1 удаа сум шидэхэд дотор талын
секторт оновол секторын дугаарыг 2-оор үржүүлж, цагирагт оновол
секторын дугаартай ижил оноо авна. 1 удаа сум шидэхэд 2 оноо авах
магадлал $\dfrac{\fbox{a}}{\fbox{b}},$ 2-оос ихгүй оноо авах
магадлал $\dfrac{\fbox{c}}{\fbox{de}}$ байна.
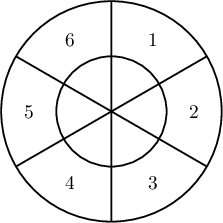

Зурагт өгөгдсөн дартсын самбар уруу 1 удаа сум шидэхэд дотор талын секторт оновол секторын дугаарыг 2-оор үржүүлж, цагирагт оновол секторын дугаартай ижил оноо авна. 1 удаа сум шидэхэд 6 оноо авах магадлал $\dfrac{\fbox{a}}{\fbox{b}}$, 5-аас бага оноо авах магадлал $\dfrac{\fbox{c}}{\fbox{de}}$ байна.


Өвлийн өвгөн жаалхүүгийнд шөнийн 1-2 цагийн хооронд ирж бэлэг тараадаг. Үүний дараа цай ууж суух, сүлд мод үзэх зэрэгт 20 минут зарцуулдаг байв (2 цаг болсон тохиолдолд шууд дараагийн айл руу явна). Жаалхүү шөнийн 1-2 цагийн хооронд санамсаргүйгээр сэрээд сүлд модоо эргэжээ.

- Энэ үед өвлийн өвгөн аль хэдийн бэлгээ тараасан байх магадлал $\dfrac{1}{\fbox{a}}$;
- Жаалхүү өвлийн өвгөнтэй тааралдах магадлал $\dfrac{\fbox{b}}{\fbox{cd}}$

$[0,1]$ хэрчмээс санамсаргүйгээр $a$ ба $b$ хоёр тоог сонгоход $ax^2+bx+1=0$ тэгшитгэл бодит шийдтэй байх магадлал $\dfrac{\fbox{a}}{\fbox{bc}}$ байна.
Суурийн радиус нь $5$ байх конусын байгуулагч $13$ байв. Конусын дотроос санамсаргүйгээр нэг цэг сонгоход тэр нь конуст багтсан бөмбөлөг дотор байхыг магадлалыг олъё. Конусын өндөр нь $h=\fbox{ab}$ байна. Иймд конусын эзлэхүүн $\fbox{cde}\pi$ ба багтсан бөмбөлгийн радиус нь $\dfrac{10}{\fbox{f}}$ тул бидний олох магадлал $\dfrac{\fbox{gh}}{81}$ байна.
Суурийн радиус нь $10$ байх конусын байгуулагч $26$ байв. Конусын дотроос санамсаргүйгээр нэг цэг сонгоход тэр нь конуст багтсан бөмбөлөг дотор байхыг магадлалыг олъё. Конусын өндөр нь $h=\fbox{ab}$ байна. Иймд конусын эзлэхүүн $\fbox{cde}\pi$ ба багтсан бөмбөлгийн радиус нь $\dfrac{20}{\fbox{f}}$ тул бидний олох магадлал $\dfrac{\fbox{gh}}{81}$ байна.
Магадлалын сонгодог тодорхойлолт
Гэр бүлийн 10 хос хооллож байв. Эндээс 5 хүнийг сугалж аваад ширээ
бүтээлгэхэд тэдний дотор нэг гэр бүлийнхэн ороогүй байх магадлалыг ол.
3 эмэгтэй 5 эрэгтэй оюутан театрын кассанд санамсаргүй байдлаар дугаарлан зогсов.
- Оюутнууд хэдэн янзаар дугаарлан зогсож болох вэ?
- Эхний 2 байранд эрэгтэй түүнээс хойш эрэгтэй эмэгтэйгээрээ ээлжлэн дугаарлах үзэгдлийн магадлалыг ол.
- 4 дэх байрлалд эрэгтэй оюутан байх үзэгдлийн магадлалыг ол.
- Дорж Бат хоёр нэг дор дарааллан зогсох үзэгдлийн магадлалыг ол.
Номын тавиур дээр магадлалын онолын 4 өөр ном, эдийн засгийн онолын 3 өөр номыг санамсаргүйгээр байрлуулахад ижил мэргэжлийн номнууд нэг дор байрласан байх үзэгдлийн магадлалыг ол.
Талууд нь $\{9,11,12,15,18\}$ олонлогоос утгаа авах
- Элдэв талт гурвалжны тоог ол.
- Зөв биш адил хажуут гурвалжны тоог ширхэг
- Талууд нь дээрх олонлогоос утгаа авах гурвалжнуудаас санамсаргүйгээр нэг гурвалжин сонгон авахад зөв гурвалжин байх магадлалыг ол.
$A=\{1,2,3,\dots,20\}$ олонлогоос нэг тоо сонгоход $4$-т эсвэл $6$-д хуваагдах магадлалыг ол.
Нэгээс мянга хүртэлх тоонуудаас таамгаар нэгийг авахад тэр нь 13-т хуваагдах тэгш тоо байх магадлалыг ол.
A. $0.037$
B. $0.038$
C. $0.039$
D. $0.04$
E. $0.041$
Хэлбэр хэмжээгээрээ ижил 13 улаан, 13 цэнхэр бөмбөгийг тэнцүү тоотой 2 хэсэгт санамсаргүйгээр хуваахад аль нэг хэсэгт нь 8 улаан, 5 цэнхэр байх магадлалыг ол.
A. $\dfrac17$
B. $\dfrac{C_{13}^8\cdot C_{13}^5}{C_{26}^{13}}$
C. $\dfrac{2(C_{13}^5)^2}{C_{26}^{13}}$
D. $\dfrac1{13}$
E. $\dfrac{A_{13}^5\cdot A_{13}^8}{A_{26}^{13}}$
Хэлбэр хэмжээгээрээ ижил 13 улаан, 13 цэнхэр бөмбөгийг тэнцүү тоотой 2 хэсэгт санамсаргүйгээр хуваахад аль нэг хэсэгт нь 13 улаан бөмбөг байх магадлалыг ол.
A. $\dfrac{1}{13}$
B. $\dfrac{1}{7}$
C. $\dfrac{1}{C_{26}^{13} }$
D. $\dfrac{2}{C_{26}^{13} }$
E. $\dfrac{1}{A_{26}^{13} }$
Уутанд 2 хөх, 4 улаан, 2 шар алчуур байв. Уутнаас таамгаар 2 алчуур авахад ижил өнгийн алчуур таарах магадлалыг ол.
A. $\dfrac37$
B. $\dfrac25$
C. $\dfrac27$
D. $\dfrac12$
E. $\dfrac35$
Хайрцагт 12 өнгийн будаг байв. Санамсаргүйгээр 3 өнгийн будаг авч тус бүрээр нь нэг нэг дугуй зурсан ба тэдгээрийгээ буцааж хийгээд дахин санамсаргүйгээр 3-ыг сонгон авч тус бүрээр нь нэг нэг дөрвөлжин зурав. Цаасан дээр хэдэн ялгаатай дүрслэл үүсэх боломжтой вэ? (Дүрс нь хэлбэр, эсвэл өнгөөрөө ялгаатай бол ялгаатайд тооцно)
A. $C_{12}^3$
B. $(C_{12}^3)^2$
C. $C_{12}^3\cdot C_9^3$
D. $A_{12}^3\cdot A_9^3$
E. $(A_{12}^3)^2$
Хайрцагт байгаа 1-р төрлийн 5 ширхэг, 2-р төрлийн 7 ширхэг алимнаас таамгаар 2 ширхэгийг сонгон авахад тэдгээр нь өөр өөр төрлийн алим байх үзэгдлийн магадлалыг ол.
A. $\frac{2}{33}$
B. $\frac{1}{33}$
C. $\frac{35}{66}$
D. $\frac{1}{66}$
E. $\frac{7}{5}$
Бүх талс нь будагтай кубийг 1000 ширхэг тэнцүү кубэд хуваав. Эдгээр кубүүдээс таамгаар 1-г сонгоход ядаж 2 талс нь будагтай куб таарах магадлалыг ол.
A. $\dfrac{12}{125}$
B. $\dfrac{13}{125}$
C. $\dfrac{26}{125}$
D. $\dfrac{64}{125}$
E. $\dfrac{96}{125}$
Гар утасны дугаарын эхний 4 оронгийн цифрүүдийн нийлбэр сүүлчийн 4 оронгийн цифрүүдийн нийлбэртэй тэнцүү байвал азтай дугаар гэе. 9499**59 хэлбэрийн дугаартай хэрэглэгч азтай дугаар барих магадлалыг ол.
A. $0.05$
B. $0.02$
C. $0.04$
D. $0.2$
E. $0.01$
Бүтэн хөзрийн 52 модноос таамгаар эхлээд 2 мод авахад 2 дөрвөлжин, дараа нь 3 мод авахад 2 дөрвөлжин, 1 цэцэг байв. Дахиад таамгаар 2 мод авахад ядаж 1 дөрвөлжин гарах магадлалыг ол.
A. $\dfrac{38}{47}$
B. $\dfrac{C_{47}^2-C_{38}^2}{C_{47}^2}$
C. $\dfrac{C_{9}^1\cdot C_{46}^1}{C_{47}^2}$
D. $\dfrac{C_9^1\cdot C_{38}^1}{C_{47}^2}$
E. $\dfrac{38\cdot47}{46\cdot 39}$
Шоог 3 удаа хаяхад гарах 3 тооны нийлбэр 17 байх магадлалыг ол.
A. $3$
B. $\dfrac{1}{17}$
C. $\dfrac{3}{17}$
D. $\dfrac{1}{316}$
E. $\dfrac{1}{72}$
Уутанд 2 цагаан, 3 хар, 4 улаан, 5 ногоон бөмбөг байв. Таамгаар авсан 2 бөмбөгийн нэг нь цагаан, нөгөө нь хар өнгөтэй байх магадлалыг ол.
A. $\dfrac{1}{7}$
B. $\dfrac{3}{7}$
C. $\dfrac{3}{14}$
D. $\dfrac{6}{91}$
E. $\dfrac{2}{13}$
Тус бүр 5 сонгох хариутай 10 асуултанд таамгаар хариулахад 9-д нь зөв хариулсан байх магадлал аль нь вэ?
A. $\dfrac{2}{5^9}$
B. $\dfrac{10}{C_{10}^9}$
C. $\dfrac{1}{5^{10}}$
D. $\dfrac{8}{5^{9}}$
E. $\dfrac{9}{10}$
Зөв хэлбэртэй 2 шоог зэрэг хаяхад гарах тоонуудын нийлбэрийг $n$ гэе. $n$-ийн дараах утгуудаас аль нь илүү магадлалтай вэ?
A. $2$
B. $3$
C. $7$
D. $8$
E. Бүгд ижил магадлалтай
1-ээс 10 хүртэлх тоонуудаас таамгаар 2 (ялгаатай) тоо авахад тэдгээр нь дараалсан тоонууд байх магадлал хэдтэй тэнцүү вэ?
A. $0.1$
B. $0.11$
C. $0.09$
D. $0.2$
E. $\dfrac{1}{9}$
1-ээс 10 хүртэлх тоонуудаас таамгаар 2 тоо авахад ялгавар нь 2-той тэнцүү байх магадлалыг ол.
A. $\dfrac{7}{90}$
B. $0.1$
C. $\dfrac{4}{45}$
D. $0.11$
E. $\dfrac{8}{45}$
Гурван шоог зэрэг хаяхад тэдгээрийн нийлбэр нь $4$ байх магадлалыг ол.
A. $\dfrac{1}{36}$
B. $\dfrac{1}{18}$
C. $\dfrac{1}{54}$
D. $\dfrac{1}{216}$
E. $\dfrac{1}{72}$
Шоог хаяхад 3-аас хэтрэхгүй сондгой тоо гарах үзэгдлийн магадлал аль нь вэ?
A. $\dfrac{5}{6}$
B. $\dfrac{3}{4}$
C. $\dfrac{1}{2}$
D. $\dfrac{1}{3}$
E. $\dfrac{2}{3}$
$10$ хүнийг дугуй ширээ тойруулан санамсаргүйгээр суулгахад тусгайлан сонгож авсан 3 хүн зэрэгцэж суух магадлалыг ол.
A. $\dfrac{C_{10}^3}{10!}$
B. $\dfrac{3!}{9!}$
C. $\dfrac{10}{C_{10}^3}$
D. $\dfrac{10}{A_{10}^3}$
E. $\dfrac{3!\cdot7!}{9!}$
$5$ улаан, $3$ ногоон, $8$ цагаан бөмбөгүүдийг нэг шулууны дагуу байрлуулжээ. Ижил өнгийн бөмбөгүүд бүгд нэг доор байрласан байх магадлалыг ол.
A. $\dfrac{5!\cdot 3!\cdot 8!}{16!}$
B. $\dfrac{C_3^1\cdot 5!\cdot 3!\cdot 8!}{16!}$
C. $\dfrac{3!\cdot5!\cdot 8!}{15!}$
D. $\dfrac{C_{16}^5\cdot C_{11}^3\cdot C_8^8}{16}$
E. $\dfrac{(3!)^2\cdot5!\cdot 8!}{16!}$
$4$ нь гологдол байх $18$ бүтээгдэхүүнээс таамгаар $4$-ийг сонгон авахад $2$ нь гологдол бүтээгдэхүүн байх магадлал аль вэ?
A. $\dfrac{C_4^2C_{14}^2}{C_{18}^4}$
B. $\dfrac{28}{C_{18}^4}$
C. $\dfrac{C_{14}^2}{C_{18}^4}$
D. $\dfrac{C_4^2}{C_{18}^4}$
E. $\dfrac{2C_4^2C_{14}^2}{C_{18}^4}$
$3$ нь гологдол байх $12$ бүтээгдэхүүнээс таамгаар $3$-ыг авахад яг $1$ нь гологдол байх магадлал аль вэ?
A. $\dfrac{C_{9}^2}{C_{12}^3}$
B. $\dfrac{3C_{9}^2}{C_{12}^3}$
C. $\dfrac{3!C_9^2}{C_{12}^3}$
D. $\dfrac{3\cdot9}{C_{12}^4}$
E. $\dfrac{12C_{9}^2}{C_{12}^3}$
I төрлийн бүтээгдэхүүн 200, II төрлийн бүтээгдэхүүн 150, III төрлийнх 215 байх бүтээгдэхүүнээс таамгаар авсан нэг бүтээгдэхүүн I эсвэл II төрлийн бүтээгдэхүүн байх магадлал аль вэ?
A. $\dfrac{40}{113}$
B. $\dfrac{30}{113}$
C. $\dfrac{50}{113}$
D. $\dfrac{10}{113}$
E. $\dfrac{70}{113}$
$1$-ээс $100$ хүртэл тоогоор дугаарласан $100$ билетээс нэгийг таамгаар сугалахад түүний дугаарт $5$-ын цифр орсон байх магадлалыг ол.
A. $\dfrac12$
B. $\dfrac{9}{50}$
C. $\dfrac{1}{5}$
D. $\dfrac{17}{100}$
E. $\dfrac{19}{100}$
$15$ эрэгтэй, $15$ эмэгтэй сурагчтай ангийн сурагчдыг санамсаргүйгээр хоёр тэнцүү хэсэгт хуваасан. Нэг хэсэг нь дан эрэгтэй хүүхдээс бүрдсэн байх магадлалыг ол.
A. $\dfrac{2}{C_{30}^{15}}$
B. $\dfrac{1}{C_{30}^{15}}$
C. $\dfrac{2}{A_{30}^{15}}$
D. $\dfrac{1}{A_{30}^{15}}$
E. $\dfrac{1}{2}$
Гар бөмбөгийн тэмцээнд оролцож байгаа 18 баг дотор 5 нь дээд зэрэглэлийн баг байсан. Багуудыг 9 багаас бүрдсэн 2 бүс болгон хуваахад нэг бүсд нь дээд зэрэглэлийн 2 баг орсон байх магадлалыг ол.
A. $\dfrac{2C_5^2C_{12}^7}{C_{18}^9}$
B. $\dfrac{C_5^2C_{12}^7}{C_{18}^9}$
C. $\dfrac{C_5^1C_{12}^1}{C_{18}^2}$
D. $\dfrac{C_5^3C_{12}^6}{C_{18}^9}$
E. $\dfrac{2C_{5}^3\cdot C_{13}^7}{C_{18}^9}$
$1,2,\dots,100$ тоонуудаас санамсаргүйгээр хоёрыг сонгосон. Сонгосон тоонуудын ялгаварын модул нь 20-с их байх магадлалыг ол.
A. $\dfrac{316}{495}$
B. $\dfrac{318}{495}$
C. $\dfrac{322}{495}$
D. $\dfrac{324}{495}$
E. $\dfrac{179}{495}$
$1,2,\dots,50$ тоонуудаас санамсаргүйгээр хоёрыг сонгосон. Сонгосон тоонуудын нийлбэр нь тэгш байх магадлалыг ол.
A. $\dfrac{1}{2}$
B. $\dfrac{A_{25}^2}{A_{50}^2}$
C. $\dfrac{C_{25}^2}{C_{50}^2}$
D. $\dfrac{C_{25}^2}{A_{50}^2}$
E. $\dfrac{A_{25}^2}{C_{50}^2}$
Шоог дахин дахин орхиж орхилтуудад өмнөх туссан нүднүүдийн нийлбэр дээр сүүлийн нүдний тоог нэмж оноо тооцов. 3-р хаялтанд онооны нийлбэр 16-аас их байх магадлалыг ол.
A. $\frac{1}{24}$
B. $\frac{1}{36}$
C. $\frac{1}{54}$
D. 0
Теннисний 9 шинэ бөмбөг байсан. Нэг тэмцээн явуулахад эдгээрээс 3 бөмбөг хэрэглэж буцааж хийдэг. 3 тэмцээн явуулсаны дараа шинэ бөмбөг үлдээгүй байх магадлалыг ол.
A. $\frac{1}{C_6^3\cdot C_3^1}$
B. $\frac{C_6^3}{(C_9^3)^2}$
C. $\frac{C_6^3}{C_9^3}$
D. $\frac{C_9^3}{(C_9^3)^2}$
Ижил пальтотой 4 сурагч өлгүүрт өлгөсөн пальтогоо санамсаргүйгээр сонгон өмссөн бол ядаж 1 сурагч өөрийнхөө пальтог өмссөн байх магадлалыг ол.
A. $\dfrac{5}{12}$
B. $\dfrac12$
C. $\dfrac{1}{4}$
D. $\dfrac{2}{3}$
E. $\dfrac{7}{12}$
Хэсэг сэтгүүлч орос, англи хэлний ядаж нэгийг мэддэг бөгөөд англи хэл мэддэг 6, орос хэл мэддэг 12, хоёр хэлийг хоёуланг нь мэддэг 3 сэтгүүлч байсан бол санамсаргүйгээр нэг сэтгүүлч сонгоход тэр нь зөвхөн орос хэл мэддэг байх магадлалыг ол.
A. $\frac{8}{15}$
B. $\frac{3}{5}$
C. $\frac{2}{3}$
D. $\frac{7}{15}$
Хайрцагт 5 улаан, 4 хөх бөмбөг байв. Хайрцагнаас таамгаар 2 бөмбөг буцааж хийхгүйгээр дараалан нэг нэгээр нь авахад эхэлж авсан бөмбөг нь улаан, дараа нь авсан бөмбөг нь хөх байх магадлалыг ол.
A. $\dfrac{5}{18}$
B. $\dfrac{15}{64}$
C. $\dfrac{1}{15}$
D. $\dfrac{15}{56}$
E. $\dfrac{25}{64}$
Дөрвөн хүүхэдтэй айл хоёр хүү, хоёр охинтой байх магадлалыг ол.
A. $\dfrac18$
B. $\dfrac14$
C. $\dfrac38$
D. $\dfrac12$
E. $\dfrac58$
Гурван оронтой тоо санамсаргүйгээр бичихэд цифрүүдийн нийлбэр нь 27 байх магадлалыг ол.
A. $\dfrac1{900}$
B. $\dfrac1{450}$
C. $\dfrac1{999}$
D. $\dfrac1{990}$
E. $\dfrac1{1000}$
Хоёр оронтой тоо санамсаргүйгээр бичихэд уг тоонд 1-ийн цифр оролцсон байх магадлалыг ол.
A. $0.1$
B. $0.2$
C. $0.3$
D. $0.4$
E. $0.5$
Хайрцагт 5 улаан, 3 хөх бөмбөг байв. Хайрцагнаас таамгаар 2 бөмбөг буцааж хийхгүйгээр дараалан нэг нэгээр нь авахад эхэлж авсан бөмбөг нь улаан, дараа нь авсан бөмбөг нь хөх байх магадлалыг ол.
A. $\dfrac{15}{28}$
B. $\dfrac{15}{64}$
C. $\dfrac1{15}$
D. $\dfrac{15}{56}$
E. $\dfrac{25}{64}$
Хайрцагт 10 улаан, 5 хөх бөмбөг байв. Санамсаргүйгээр хоёр бөмбөг гаргаж ирэхэд хоёулаа улаан байх магадлалыг ол.
A. $\dfrac{1}{5}$
B. $\dfrac13$
C. $\dfrac12$
D. $\dfrac37$
E. $\dfrac47$
Нэгээс мянга хүртэлх тоонуудаас таамгаар нэгийг авахад тэр нь 11-д хуваагдах тоо байх магадлалыг ол.
A. $0.08$
B. $0.09$
C. $0.1$
D. $0.11$
E. $0.12$
Хайрцагт 6 улаан, 3 хөх бөмбөг байв. Хайрцагнаас таамгаар 2 бөмбөг буцааж хийхгүйгээр дараалан нэг нэгээр нь авахад эхэлж авсан бөмбөг нь улаан, дараа нь авсан бөмбөг нь хөх байх магадлалыг ол.
A. $\dfrac{1}{15}$
B. $\dfrac{2}{9}$
C. $\dfrac{1}{4}$
D. $\dfrac{15}{56}$
E. $\dfrac{1}{2}$
Хайрцагт 6 улаан, 4 хөх бөмбөг байв. Хайрцагнаас таамгаар 2 бөмбөг буцааж хийхгүйгээр дараалан нэг нэгээр нь авахад эхэлж авсан бөмбөг нь улаан, дараа нь авсан бөмбөг нь хөх байх магадлалыг ол.
A. $\dfrac{15}{28}$
B. $\dfrac{15}{64}$
C. $\dfrac{4}{15}$
D. $\dfrac{5}{16}$
E. $\dfrac{25}{64}$
Бүх талс нь будагтай кубийг 1000 тэнцүү кубд хуваав. Эдгээр кубээс таамгаар 1-ийг сонгоход ядаж 1 талс нь будагтай куб таарах магадлалыг ол.
A. $\dfrac{12}{125}$
B. $\dfrac{13}{125}$
C. $\dfrac{48}{125}$
D. $\dfrac{61}{125}$
E. $\dfrac{64}{125}$
Гар утасны дугаарын эхний 4 оронгийн цифрүүдийн нийлбэр сүүлчийн 4 оронгийн цифрүүдийн нийлбэртэй тэнцүү байвал "аз"-тай дугаар гэе. 99945**9 хэлбэрийн дугаартай хэрэглэгч "аз"-тай дугаар барих магадлалыг ол.
A. $0.05$
B. $0.2$
C. $0.04$
D. $0.02$
E. $0.01$
Уутанд 5 улаан, 3 хөх бөмбөг байв. Санамсаргүйгээр гаргаж ирсэн 2 хоёр бөмбөг ижил өнгөтэй байх магадлалыг ол.
A. $\dfrac{1}{2}$
B. $\dfrac{15}{28}$
C. $\dfrac{17}{28}$
D. $\dfrac{1}{3}$
E. $\dfrac{13}{28}$
ШАЛГАЛТ үгэнд орсон үсгүүдийг нэг, нэг хуудас цаасан дээр бичээд сайтар хольсоны дараа нэг эгнээнд дахин байрлуулав. Шинээр үүсэх үг нь мөн л ШАЛГАЛТ гэсэн үг байх магадлал хэд вэ? Хуудас цааснуудын бүх сэлгэмэл ижил боломжтой гэж үз.
A. $\dfrac{1}{7!}$
B. $\dfrac{4}{7!}$
C. $\dfrac{4!}{7!}$
D. $\dfrac{1}{120}$
E. $\dfrac{1}{720}$
Уутанд 4 цагаан, 6 хар, 3 улаан, 8 ногоон бөмбөг байв. Таамгаар нэг бөмбөг авахад цагаан юмуу ногоон өнгөтэй байх магадлалыг ол.
A. $\dfrac{8}{21}$
B. $\dfrac{4}{7}$
C. $\dfrac{1}{2}$
D. $\dfrac{1}{3}$
E. $\dfrac{4}{21}$
1-10 тоонуудаас хоёрыг нь давталтгүйгээр сонгон авахад сонгогдсон тоонуудын ялгавар 3 байх магадлалыг ол.
A. $\dfrac15$
B. $\dfrac{2}{15}$
C. $\dfrac{8}{45}$
D. $\dfrac{7}{45}$
E. $\dfrac{3}{10}$
1-100 тоонуудаас санамсаргүйгээр сонгон авсан 2 тооны үржвэр тэгш байх магадлал аль нь вэ?
A. $\dfrac14$
B. $\dfrac29$
C. $\dfrac{49}{198}$
D. $\dfrac{149}{198}$
E. $0.5$
Хэлбэр хэмжээгээрээ ижил 13 улаан, 13 цэнхэр бөмбөгийг тэнцүү тоотой 2 хэсэгт санамсаргүйгээр хуваахад аль нэг хэсэг нь 12 улаан, 1 цэнхэр бөмбөг байх магадлалыг ол.
A. $\dfrac17$
B. $\dfrac1{13}$
C. $\dfrac{C_{13}^1\cdot C_{13}^{12}}{C_{26}^{13}}$
D. $\dfrac{2C_{13}^1\cdot C_{13}^{12}}{C_{26}^{13}}$
E. $\dfrac{A_{13}^1\cdot A_{13}^{12}}{A_{26}^{13}}$
3 оронтой 5-д хуваагддаг 1 тоог авахад тэр нь тэгш байх магадлалыг ол.
A. $\dfrac15$
B. $\dfrac1{18}$
C. $\dfrac12$
D. $\dfrac5{20}$
E. $\dfrac13$
Үйлчлэгчид 5 өрөөний түлхүүр байв. Үйлчлэгч эхний 2 өрөөг 3 удаагийн оролдлогоор онгойлгох магадлалыг ол.
A. $\dfrac7{60}$
B. $\dfrac3{20}$
C. $\dfrac1{15}$
D. $\dfrac25$
E. $\dfrac{13}{60}$
Нэгээс мянга хүртэлх тоонуудаас таамгаар нэгийг авахад тэр нь 13-т хуваагдах тэгш тоо байх магадлалыг ол.
A. $0.038$
B. $0.039$
C. $0.040$
D. $0.041$
E. $0.042$
Хавтгай дээр ерөнхий байршилтай 9 шулуун өгөгдөв. Тэдгээрийн 5-ийг нь улаан, 4-ийг нь хөхөөр будав. Эдгээр шулуунаар үүсгэгдсэн гурвалжнуудаас санамсаргүйгээр 1-ийг сонгоход ижил өнгийн талуудтай байх магадлалыг ол.
A. $\dfrac13$
B. $\dfrac16$
C. $\dfrac17$
D. $\dfrac25$
E. $\dfrac27$
3 оронтой 5-д хуваагддаг 1 тоог авахад тэр нь сондгой байх магадлалыг ол.
A. $\dfrac12$
B. $\dfrac15$
C. $\dfrac1{18}$
D. $\dfrac5{20}$
E. $\dfrac13$
Үйлчлэгчид 6 өрөөний түлхүүр байв. Үйлчлэгч эхний 2 өрөөг 3 удаагийн оролдлогоор онгойлгох магадлалыг ол.
A. $\dfrac7{40}$
B. $\dfrac3{40}$
C. $\dfrac1{10}$
D. $\dfrac25$
E. $\dfrac{13}{60}$
Зөв хэлбэртэй шоог 3-аас бага тоо буутал нь хаяв. Шоог 3-аас олонгүй удаа хаях магадлалыг ол.
A. $\dfrac{19}{27}$
B. $\dfrac{19}{36}$
C. $\dfrac{26}{27}$
D. $\dfrac{1}{3}$
E. $\dfrac{2}{9}$
Зөв хэлбэртэй шоог 5-аас бага тоо буутал нь хаяв. Шоог 3-аас олонгүй удаа хаях магадлалыг ол.
A. $\dfrac{1}{3}$
B. $\dfrac{29}{36}$
C. $\dfrac{26}{27}$
D. $\dfrac{19}{27}$
E. $\dfrac{2}{9}$
Түрийвчинд 20000-тын дэвсгэрт 7ш, 10000-тын дэвсгэрт 5ш, 5000-тын дэвсгэрт 8ш байв. Таамгаар 1-дэвсгэрт сугалахад 20000-тын дэвсгэрт байх магадлалыг олоорой!
A. $\dfrac13$
B. $\dfrac4{15}$
C. $\dfrac7{194}$
D. $\dfrac6{15}$
E. $\dfrac7{20}$
СУРГАЛТ гэдэг үгнээс 2 үсэг дарахад хоёулаа гийгүүлэгч үсэг байх магадлалыг олоорой.
A. $\dfrac13$
B. $\dfrac57$
C. $\dfrac79$
D. $\dfrac{10}{21}$
E. $\dfrac45$
Түрийвчинд 20000-тын дэвсгэрт 8ш, 10000-тын дэвсгэрт 9ш, 5000-тын дэвсгэрт 7ш байв. Таамгаар 1-дэвсгэрт сугалахад 10000-тын дэвсгэрт байх магадлалыг олоорой!
A. $\dfrac12$
B. $\dfrac45$
C. $\dfrac9{7\cdot8\cdot9}$
D. $\dfrac38$
E. $\dfrac7{24}$
СОНГОЛТ гэдэг үгнээс 2 үсэг дарахад хоёулаа гийгүүлэгч үсэг байх магадлалыг олоорой.
A. $\dfrac13$
B. $\dfrac57$
C. $\dfrac79$
D. $\dfrac45$
E. $\dfrac{10}{21}$
Түрийвчинд 20000-тын дэвсгэрт 8 ш, 10000-тын дэвсгэрт 7 ш, 5000-тын дэвсгэрт 6 ш байв. Таамгаар 1-дэвсгэрт сугалахад 10000-тын дэвсгэрт байх магадлалыг олоорой!
A. $\dfrac13$
B. $\dfrac7{20}$
C. $\dfrac7{8\cdot 7\cdot 6}$
D. $\dfrac8{21}$
E. $\dfrac6{21}$
ШАЛГАЛТ гэдэг үгнээс 2 үсэг дарахад хоёулаа гийгүүлэгч үсэг байх магадлалыг олоорой.
A. $\dfrac13$
B. $\dfrac57$
C. $\dfrac{10}{21}$
D. $\dfrac{7}{9}$
E. $\dfrac45$
Түрийвчинд 20000-тын дэвсгэрт 5 ш, 10000-тын дэвсгэрт 6 ш, 5000-тын дэвсгэрт 4 ш байв. Таамгаар 1-дэвсгэрт сугалахад 5000-тын дэвсгэрт байх магадлалыг олоорой!
A. $\dfrac13$
B. $\dfrac4{15}$
C. $\dfrac4{5\cdot 4\cdot 6}$
D. $\dfrac6{15}$
E. $\dfrac{11}{15}$
ТӨГСӨЛТ гэдэг үгнээс 2 үсэг дарахад хоёулаа гийгүүлэгч үсэг байх магадлалыг олоорой.
A. $\dfrac13$
B. $\dfrac57$
C. $\dfrac45$
D. $\dfrac{7}{9}$
E. $\dfrac{10}{21}$
Хайрцагт 8 ш улаан бөмбөг, 7 ш ногоон бөмбөг, 6 ш шар бөмбөг байв. Таамгаар 1 бөмбөг гаргаж ирэхэд шар өнгөтэй байх магадлалыг олоорой!
A. $\dfrac13$
B. $\dfrac7{20}$
C. $\dfrac7{8\cdot 7\cdot 6}$
D. $\dfrac8{21}$
E. $\dfrac27$
ШАЛГАЛТ гэдэг үгнээс 2 үсэг дарахад хоёулаа гийгүүлэгч үсэг байх магадлалыг олоорой.
A. $\dfrac13$
B. $\dfrac57$
C. $\dfrac{10}{21}$
D. $\dfrac{7}{9}$
E. $\dfrac45$
$1$-ээс $40$ хүртэл тоогоор дугаарласан $40$ билетээс нэгийг таамгаар сугалахад түүний дугаарт $3$-ын цифр орсон байх магадлалыг ол.
A. $\dfrac{11}{20}$
B. $\dfrac{13}{40}$
C. $\dfrac{1}{3}$
D. $\dfrac{17}{30}$
E. $\dfrac{19}{30}$
$1,2,\dots,40$ тоонуудаас санамсаргүйгээр хоёрыг сонгов. Сонгосон тоонуудын нийлбэр нь тэгш байх магадлалыг ол.
A. $\dfrac{A_{20}^2}{C_{40}^2}$
B. $\dfrac{A_{20}^2}{A_{40}^2}$
C. $\dfrac{C_{20}^2}{C_{40}^2}$
D. $\dfrac{C_{20}^2}{A_{40}^2}$
E. $\dfrac{1}{2}$
$1$-ээс $40$ хүртэл тоогоор дугаарласан $40$ билетээс нэгийг таамгаар сугалахад түүний дугаарт $4$-ын цифр орсон байх магадлалыг ол.
A. $\dfrac{1}{10}$
B. $\dfrac{1}{8}$
C. $\dfrac{1}{4}$
D. $\dfrac{1}{5}$
E. $\dfrac{11}{40}$
$1,2,\dots,41$ тоонуудаас санамсаргүйгээр хоёрыг сонгов. Сонгосон тоонуудын нийлбэр нь сондгой байх магадлалыг ол.
A. $\dfrac{A_{21}^2}{C_{41}^2}$
B. $\dfrac{A_{21}^2}{A_{41}^2}$
C. $\dfrac{C_{20}^2}{C_{41}^2}$
D. $\dfrac{C_{20}^2}{A_{41}^2}$
E. $\dfrac{1}{2}$
$1,2,\dots,500$ тоонуудаас таамгаар нэгийг авахад тэр нь 21-д хуваагдах тоо байх магадлалыг ол.
A. $0.008$
B. $0.019$
C. $0.021$
D. $0.046$
E. $0.049$
$1,2,\dots,500$ тоонуудаас таамгаар нэгийг авахад тэр нь 14-д хуваагдах тоо байх магадлалыг ол.
A. $0.070$
B. $0.035$
C. $0.021$
D. $0.046$
E. $0.049$
Ангийн нийт сурагчдын $80\%$ нь эмэгтэй сурагч байдаг. Ангиас санамсаргүйгээр нэг сурагч сонгоход эрэгтэй сурагч сонгогдох магадлалыг ол.
A. $\dfrac45$
B. $\dfrac15$
C. $0.02$
D. $\dfrac35$
E. $1$
Ангийн 30 сурагчийн 5 нь шатар, 15 нь даам тоглодог. Хэрвээ шатар, даам аль алийг нь тоглодог сурагч байхгүй бол дурын нэг сурагчийг сонгон авахад тэр нь шатар, даамны алийг нь ч тоглодоггүй сурагч байх магадлалыг ол.
A. $\dfrac{1}{2}$
B. $\dfrac{1}{3}$
C. $\dfrac{1}{4}$
D. $\dfrac{2}{3}$
E. $\dfrac{3}{4}$
$1,2,3,\dots,10$ тоонууд бичигдсэн 10 ширхэг картнаас санамсаргүйгээр 2-ийг нь сонгож аваад дээр нь бичигдсэн тоонуудыг нэмэхэд нийлбэр нь 6-аас бага байх магадлалыг ол.
A. $\dfrac{1}{8}$
B. $\dfrac{1}{5}$
C. $\dfrac{4}{45}$
D. $\dfrac{2}{45}$
E. $\dfrac19$
Ангийн 30 сурагчийн 10 нь шатар, 8 нь даам тоглодог. Хэрвээ шатар, даам аль алийг нь тоглодог сурагч байхгүй бол дурын нэг сурагчийг сонгон авахад тэр нь шатар, даамны алийг нь ч тоглодоггүй сурагч байх магадлалыг ол.
A. $\dfrac{1}{2}$
B. $\dfrac{1}{3}$
C. $\dfrac{1}{4}$
D. $\dfrac{2}{5}$
E. $\dfrac{3}{4}$
$1,2,3,\dots,10$ тоонууд бичигдсэн 10 ширхэг картнаас санамсаргүйгээр 2-ийг нь сонгож аваад дээр нь бичигдсэн тоонуудыг нэмэхэд нийлбэр нь 5-аас бага байх магадлалыг ол.
A. $\dfrac{1}{8}$
B. $\dfrac{1}{5}$
C. $\dfrac{4}{45}$
D. $\dfrac{2}{45}$
E. $\dfrac19$
Уутанд 3 хөх, 6 улаан, 4 шар бөмбөг байв. Уутнаас таамгаар 2 бөмбөг авахад ижил өнгийн бөмбөг таарах магадлалыг ол.
A. $\dfrac{4}{13}$
B. $\dfrac{3}{13}$
C. $\dfrac37$
D. $\dfrac12$
E. $\dfrac35$
Ангийн нийт сурагчдын $40\%$ нь эмэгтэй сурагч байдаг. Ангиас санамсаргүйгээр нэг сурагч сонгоход эрэгтэй сурагч сонгогдох магадлалыг ол.
A. $\dfrac35$
B. $\dfrac25$
C. $0.06$
D. $\dfrac15$
E. $1$
Нэгээс мянга хүртэлх тоонуудаас таамгаар нэгийг авахад тэр нь 13-т хуваагдах тэгш тоо байх магадлалыг ол.
A. $0.037$
B. $0.038$
C. $0.039$
D. $0.04$
E. $0.041$
1-10 тоонуудаас санамсаргүйгээр 1 тоо сонгон авахад 3-т хуваагддаг тоо сонгогдох магадлалыг ол.
A. $3$
B. $0.3$
C. $\dfrac{1}{3}$
D. $\dfrac{10}{3}$
E. $0.4$
Зөв 2018 өнцөгтийн оройн цэгүүдээс санамсаргүйгээр хоёр ширхэг гуравт сонгоход сонгогдсон гуравтууд дээр оройтой 2 гурвалжин огтлолцохгүй байх магадлалыг ол.
A. $0.3$
B. $0.6$
C. $0.1$
D. $0.03$
E. $0.67$
Улаан, цагаан өнгийн 2 шоог зэрэг хаяхад буусан нүднүүдийн нийлбэр 4-өөс их байх үзэгдлийн магадлалыг ол.
A. $\dfrac{11}{36}$
B. $\dfrac{1}{4}$
C. $\dfrac{10}{36}$
D. $\dfrac{5}{6}$
E. $\dfrac{2}{3}$
5 хүүхдийг жагсаан зогсооход Ану, Баяр 2 зэрэгцэж зогссон байх үзэгдлийн магадлалыг ол.
A. $\dfrac{3}{10}$
B. $\dfrac{5}{24}$
C. $\dfrac{1}{25}$
D. $\dfrac{4}{5}$
E. $\dfrac{2}{5}$
1-ээс 10 хүртэлх тоонуудаас таамгаар 2 тоо авахад ялгавар нь 2-той тэнцүү байх магадлалыг ол.
A. $\dfrac{7}{90}$
B. $0.1$
C. $\dfrac{4}{45}$
D. $0.11$
E. $\dfrac{8}{45}$
$\{1,2,3,\ldots,15,16\}$ олонлогоос ганц тоог санамсаргүйгээр сонгоход нэг оронтой тоо сонгогдох магадлалыг ол.
A. $\dfrac{5}{16}$
B. $\dfrac{7}{16}$
C. $\dfrac{9}{16}$
D. $\dfrac{1}{16}$
E. $\dfrac12$
Зөв хэлбэртэй шоог $n$ удаа хаяхад $X$ удаа $6$ буусан гэе. $X$ санамсаргүй хувьсагчийн дисперс аль нь вэ?
A. $\dfrac{\sqrt{2n}}{6}$
B. $\dfrac{n}{36}$
C. $\dfrac{5n}{6}$
D. $\dfrac{5n}{36}$
E. $\dfrac{\sqrt{5n}}{6}$
Дөрвөн хүүхэдтэй айл гурван хүү, нэг охинтой байх магадлалыг ол.
A. $\dfrac18$
B. $\dfrac14$
C. $\dfrac38$
D. $\dfrac12$
E. $\dfrac58$
1-100 тоонуудаас таамгаар нэгийг авахад тэр нь 7-д хуваагдах тоо байх магадлалыг ол.
A. $0.08$
B. $0.09$
C. $0.11$
D. $0.12$
E. $0.14$
1-100 тоонуудаас таамгаар нэгийг авахад тэр нь 8-д хуваагдах тоо байх магадлалыг ол.
A. $0.08$
B. $0.09$
C. $0.11$
D. $0.12$
E. $0.14$
ИНТЕГРАЛ үгэнд орсон үсгүүдээс санамсаргүйгээр нэг үсэг сонгоход эгшиг үсэг байх магадлал аль нь вэ?
A. $\dfrac12$
B. $\dfrac38$
C. $\dfrac34$
D. $\dfrac58$
E. $\dfrac14$
ИНТЕГРАЛ үгэнд орсон үсгүүдээс санамсаргүйгээр нэг үсэг сонгоход гийгүүлэгч үсэг байх магадлал аль нь вэ?
A. $\dfrac12$
B. $\dfrac38$
C. $\dfrac34$
D. $\dfrac58$
E. $\dfrac14$
Талууд нь $\{16, 13, 11, 9, 8\}$ олонлогоос утгаа авах
- элдэв талт гурвалжин $\fbox{ab}$ ширхэг,
- зөв биш адил хажуут гурвалжин $\fbox{cd}$ ширхэг,
- гурвалжнуудаас санамсаргүйгээр нэг гурвалжин авахад зөв гурвалжин байх магадлал $\dfrac{\fbox{e}}{\fbox{fg}}$ байна.
Талууд нь $\left\{6, 7, 8, 10, 12\right\}$ олонлогоос утгаа авах
- Элдэв талт гурвалжин $\fbox{ab}$ ширхэг
- Зөв биш адил хажуут гурвалжин $\fbox{cd}$ ширхэг
- Талууд нь дээрх олонлогоос утгаа авах гурвалжнуудаас санамсаргүйгээр нэг гурвалжин сонгон авахад зөв гурвалжин байх магадлал нь $\dfrac{\fbox{e}}{\fbox{fg}} $ байна.
72350 тоог 7 удаа залгаж бичвэл 72350723507235072350723507235072350 гэсэн 35 оронтой тоо үүснэ. Санамсаргүйгээр 2 цифрийг нь арилгахад үүсэх 33 оронтой тоо 15-д хуваагддаг байх магадлалыг ол.
Бодолт:
Бодолт:
- Санамсаргүйгээр 2 цифрийг нь арилгах бүх боломжийн тоо $\fbox{abc}$ болно. (3 оноо)
- Сүүлчийн 2 цифрээс бусад аливаа 2 цифрийг арилгах нь зөвхөн 3-д хуваагддаг чанарыг ашиглах боломж олгоно. Иймд 7-г 1-ээр, 3-г 0-ээр, 5-г 2-оор соливол чанар өөрчлөгдөхгүй тул дээрх тоог 12020120201202012020120201202012020 тоогоор төлөөлүүлж болно. Энэ тооны цифрүүдийн нийлбэр $\fbox{de}$ болно. (2 оноо)
- Сүүлчийн 2 цифрээс бусад цифрүүдээс 2-г нь арилгах боломжийн тоо (3-д хуваагдах тул)
- Эсвэл хоёр 1 цифрийг
- Эсвэл нэг 2 цифр ба нэг 0 цифрийг арилгах шаардлагатай. Ийм боломжийн тоо $\fbox{fgh}$ тул олох магадлал $P=\dfrac{\fbox{fgh}}{\fbox{abc}}$ юм. (3 оноо)
Шоог гурван удаа хаяхад
- Бүгд $5$-аас ихгүй байх боломжийн тоо $\fbox{abc}$ байна.
- Бүгд $4$-өөс ихгүй байх боломжийн тоо $\fbox{de}$ байна.
- Хамгийн их нь $5$ байх боломжийн тоо $\fbox{fg}$ байна.
Ерөнхий байршилтай (аль ч хоёр нь давхцахгүй, аль ч гурав нь нэг шулуун дээр үл орших) 10 цэгийн 5-ыг нь улаанаар, 2-ыг нь хөхөөр, 3-ыг нь ногооноор будаж хос хосоор нь хэрчмээр холбожээ.
- 2 ижил өнгийн төгсгөлтэй хэрчим $\fbox{ab}$ ширхэг.
- 3 өөр өнгийн оройтой гурвалжин $\fbox{cd}$ ширхэг.
- Санамсаргүйгээр нэг гурвалжин авахад бүх орой нь ижил өнгөтэй байх магадлал $\dfrac{\fbox{ef}}{120}$
Тус бүрдээ 1-10 тоогоор дугаарлагдсан 10 улаан, 10 ногоон, 10 хөх, 10 шар өнгийн нийт 40 карт байв. Эдгээрээс нэгэн зэрэг 2-ийг нь авахад
- Ижил тоотой байх магадлал $\dfrac{1}{\fbox{ab}}$ байна.
- Өнгө ба тоогоороо ялгаатай байх магадлал $\dfrac{\fbox{c}}{\fbox{de}}$
- Яг нэг нь улаан байх магадлал $\dfrac{5}{\fbox{fg}}$
- Гарч ирсэн улаан картнууд дээр бичигдсэн тоонуудын нийлбэрийн математик дундаж нь $\dfrac{\fbox{hi}}{\fbox{j}}$. (хэрэв улаан карт гарч ирэхгүй бол нийлбэр нь 0, яг нэг улаан карт гарч ирсэн бол нийлбэр нь улаан картны дугаар байна.)
Бүтэн хөзрийн 52 модноос хоёр хүнд 2, 2 мод тараав.
- I хүний мод нь хос байх магадлал $\dfrac{1}{\fbox{ab}}$ (2 оноо);
- I хүний мод хос гэдэг нь мэдэгдэж байх үед II хүний мод хос байх магадлал $\dfrac{\fbox{cd}}{C_{50}^2}$ (2 оноо);
- I ба II хүмүүсийн мод хоёулаа нэгэн зэрэг хос байх магадлал $\dfrac{\fbox{73}}{\fbox{efghi}}$ байна (3 оноо).
5 улаан, 3 хөх өнгийн харандаанаас таамгаар 2-ийг авахад
- Хоёулаа улаан байх магадлал $\dfrac{\fbox{a}}{14}$,
- Хоёулаа хөх байх магадлал $\dfrac{\fbox{b}}{\fbox{cd}}$,
- Ялгаатай өнгийн байх магадлал $\dfrac{\fbox{ef}}{\fbox{gh}}$ байна.
$1$, $2$, $3$, $4$, $5$ дугаартай хайрцгуудад өөр хоорондоо ялгаагүй 7 ширхэг бөмбөгийг $\fbox{abc}$ янзаар байрлуулж болох ба дурын нэг байрлуулалт авч үзэхэд 5-р хайрцаг хоосон биш байх магадлал $\dfrac{\fbox{d}}{\fbox{ef}}$ болно.
Ангийн 10 хүү, 10 охиноос 4 хүнтэй баг бүрдүүлэв.
- Нийт боломжийн тоо нь $\fbox{abcd}$.
- Баг дан эрэгтэй сурагчаас бүрдсэн байх боломжийн тоо $\fbox{efg}$.
- Багийн эрэгтэй ба эмэгтэй сурагчдын тоо тэнцүү байх магадлал $\dfrac{\fbox{hij}}{\fbox{klm}}$ байна.
Ангийн 10 хүү, 10 охиноос 6 хүнтэй баг бүрдүүлэв.
- Нийт боломжийн тоо тоо нь $\fbox{abcde}$.
- Баг дан эрэгтэй сурагчаас бүрдсэн байх боломжийн тоо $\fbox{fgh}$.
- Багийн эрэгтэй ба эмэгтэй сурагчдын тоо тэнцүү байх магадлал $\dfrac{\fbox{hij}}{\fbox{323}}$ байна.
Ангийн 30 сурагчийн 20 нь эрэгтэй байв.
- Ангийн дарга нь эрэгтэй байх магадлал нь $\dfrac{\fbox{a}}{\fbox{b}}$ (үл хураагдах).
- Ангийн дарга ба түүний орлогч нь хоёулаа эрэгтэй байх магадлал нь $\dfrac{\fbox{cd}}{\fbox{ef}}$.
- Ангийн дарга нь эрэгтэй түүний орлогч нь эмэгтэй байх магадлал нь $\dfrac{\fbox{gh}}{\fbox{ij}}$.
Ангийн 30 сурагчийн 20 нь эрэгтэй байв.
- Ангийн дарга нь эрэгтэй байх магадлал нь $\dfrac{\fbox{a}}{\fbox{b}}$ (үл хураагдах).
- Ангийн дарга ба түүний орлогч нь хоёулаа эрэгтэй байх магадлал нь $\dfrac{\fbox{cd}}{\fbox{ef}}$.
- Ангийн дарга нь эрэгтэй түүний орлогч нь эмэгтэй байх магадлал нь $\dfrac{\fbox{gh}}{\fbox{ij}}$.
Талууд нь $\{4; 5; 6; 8\}$ олонлогоос утгаа авах
- зөв гурвалжин $\fbox{a}$ ширхэг,
- зөв биш адил хажуут гурвалжин $\fbox{bc}$ ширхэг,
- санамсаргүйгээр дээрх нөхцлийг хангасан гурвалжин сонгож авахад зөв гурвалжин байх магадлал $\dfrac{4}{\fbox{de}}$ байна.
Талууд нь $\{3; 4; 5; 7\}$ олонлогоос утгаа авах
\par а) зөв гурвалжин $\fbox{a}$ ширхэг,
\par б) адил хажуут гурвалжин $\fbox{bc}$ ширхэг,
\par в) санамсаргүйгээр дээрх нөхцлийг хангасан гурвалжин сонгож авахад адил хажуут гурвалжин биш
байх магадлал $\dfrac{7}{\fbox{de}}$ байна.
Батын халаасанд 10-тын мөнгө 4 ширхэг, 50-тын мөнгө 1 ширхэг, 100-тын мөнгө 3 ширхэг байжээ. Халааснаасаа хэдэн мөнгө гаргаж ирэхэд нийт 2 төгрөг 60 мөнгө болох магадлал $\dfrac{\fbox{a}}{\fbox{bc}}$ байна.
Батын халаасанд 10-тын мөнгө 4 ширхэг, 50-тын мөнгө 5 ширхэг, 100-тын мөнгө 3 ширхэг байжээ. Халааснаасаа хэдэн мөнгө гаргаж ирэхэд нийт 2 төгрөг 60 мөнгө болох магадлал $\dfrac{\fbox{ab}}{\fbox{cde}}$ байна.
Сагсан бөмбөгийн тэмцээнд орох 8 багийг тус бүр 4 багтай А ба Б гэсэн 2 хэсэгт хуваах болжээ. Хамгийн хүчтэй 2 баг 2 өөр хэсэгт орох магадлал $\dfrac{\fbox{a}}{\fbox{b}}$ байна.
Сагсан бөмбөгийн тэмцээнд орох 8 багийг тус бүр 4 багтай А ба Б гэсэн 2 хэсэгт хуваах болжээ. Хамгийн хүчтэй 2 баг нэг хэсэгт орох магадлал $\dfrac{\fbox{a}}{\fbox{b}}$ байна.
Санамсаргүйгээр 2 оронтой тоо сонгож авахад тэр нь
- 3 ба 5-д хуваагддаг тоо байх магадлал $\dfrac{1}{\fbox{ab}}$,
- 3-д хуваагддаггүй тоо байх магадлал $\dfrac{\fbox{c}}{\fbox{d}}$,
- 5-д хуваагддаг боловч 3-д хуваагддаггүй байх магадлал $\dfrac{\fbox{e}}{15}$,
- 3-д эсвэл 5-д хуваагддаг тоо байх магадлал $\dfrac{\fbox{f}}{15}$ байна.
Санамсаргүйгээр 2 оронтой тоо сонгож авахад тэр нь
- 3 ба 7-д хуваагддаг байх магадлал $\dfrac{2}{\fbox{ab}};$
- 7-д хуваагддаггүй байх магадлал $\dfrac{\fbox{cd}}{90};$
- 7-д хуваагддаг боловч 3-т хуваагддаггүй байх магадлал $\dfrac{\fbox{e}}{10};$
- 7-д ч 3-д ч хуваагддаггүй байх магадлал $\dfrac{\fbox{fg}}{30}$ байна.
Аль ч 3 нь нэг шулуун дээр үл орших 10 цэгийн 5-ыг нь ягаанаар, 2-ыг нь хөхөөр, 3-ыг нь ногооноор будаж, хос хосоор
нь хэрчмээр холбожээ.
- 2 өөр өнгийн төгсгөлтэй хэрчим $\fbox{ab}$ ширхэг,
- 3 өөр өнгийн оройтой гурвалжин $\fbox{cd}$ ширхэг,
- санамсаргүйгээр нэг гурвалжин авахад бүх орой нь ижил өнгөтэй байх магадлал $\dfrac{\fbox{ef}}{120}$ байна.
Аль ч 3 нь нэг шулуун дээр үл орших 8 цэгийн 2 нь ягаан, 2 нь хөх, 2 нь ногоон, 2 нь улаан өнгөтэй байв. Тэдгээрийг хос хосоор нь хэрчмээр холбоход
- 2 өөр өнгийн төгсгөлтэй хэрчим $\fbox{ab}$ ширхэг,
- 3 өөр өнгийн оройтой гурвалжин $\fbox{cd}$ ширхэг,
- санамсаргүйгээр нэг дөрвөн өнцөгт авахад бүх орой нь өөр өнгөтэй байх магадлал $\dfrac{8}{\fbox{ef}}$ байна.
$1,\ldots,10$ дугаартай 10 ширхэг цааснаас гурвыг нэгэн зэрэг сугалахад
- 1 гэсэн дугаартай цаас сугалсан байх магадлал $\dfrac{\fbox{a}}{\fbox{bc}}$,
- 1 ба 2 гэсэн дугаартай цаас сугалсан байх магадлал $\dfrac{\fbox{d}}{\fbox{ef}}$,
- бүгд тэгш дугаартай байх магадлал $\dfrac{\fbox{g}}{\fbox{hi}}$ байна.
Тус бүрд нь 1, 2, 3, 4 дугаартай хөзөр нэг нэг ширхэг орсон 4 ширхэг хайрцаг байв. Хайрцаг тус бүрээс нэг ширхэг хөзөр гаргахад
- бүгд адил дугаартай байх магадлал $\dfrac{\fbox{a}}{\fbox{bc}}$,
- 1 эсвэл 2 гэсэн дугаартай хөзөр гарсан байх магадлал $\dfrac{\fbox{de}}{\fbox{fg}}$,
- 1 гэсэн дугаартай хөзөр яг 2 ширхэг гарсан байх магадлал $\dfrac{\fbox{hi}}{128}$ байна.
Шоог эхний удаа орхиход буусан тоог $x, 2$ дахь удаа орхиход буусан тоог $y$ гэвэл
- $x$ ба $y$ ялгаатай байх магадлал $\dfrac{\fbox{a}}{6};$
- $2x=y$ байх магадлал $\dfrac{1}{\fbox{bc}};$
- $x+y=6$ байх магадлал $\dfrac{\fbox{d}}{36};$
- $x+y=6$ гэж мэдэгдэж байгаа нөхцөлд $2x=y$ байх магадлал $\dfrac{1}{\fbox{e}}$ байна.
Шоог эхний удаа орхиход буусан тоог $x, 2$ дахь удаа орхиход буусан тоог $y$ гэвэл
- $x$ ба $y$ сондгой байх магадлал $\dfrac{1}{\fbox{a}};$
- $x^2=y$ байх магадлал $\dfrac{1}{\fbox{bc}};$
- $x-y=1$ байх магадлал $\dfrac{\fbox{d}}{36};$
- $x$ ба $y$ сондгой тоо гэж мэдэгдэж байгаа нөхцөлд $x^2=y$ байх магадлал $\dfrac{1}{\fbox{e}}$ байна.
1, $\ldots$ , 9 дугаартай 9 бөмбөгтэй хайрцгаас таамгаар 7 бөмбөг авахад 8 гэсэн дугаартай бөмбөг гарч ирсэн байх магадлал $\dfrac{\fbox{a}}{\fbox{b}}$, харин гарч ирсэн бөмбөгнүүдийн хамгийн их дугаар нь 8 байх магадлал $\dfrac{\fbox{c}}{\fbox{de}}$ байна.
1, $\ldots$ , 9 дугаартай 9 бөмбөгтэй хайрцгаас таамгаар 7 бөмбөг авахад 2 гэсэн дугаартай бөмбөг гарч ирсэн байх магадлал $\dfrac{\fbox{a}}{\fbox{b}}$, харин гарч ирсэн бөмбөгнүүдийн хамгийн бага дугаар нь 2 байх магадлал $\dfrac{\fbox{c}}{\fbox{de}}$ байна.
Хяналтын ажилд бэлтгэж 3 сэдэв бүрд 10 бодлого бодуулахаар гэрийн
даалгаварт өгчээ. Гэрэл сэдэв бүрээс 8 бодлого бодож чадсан байв.
Хяналтын ажилд сэдэв бүрээс 1 бодлого, нийт 3 бодлого ирсэн бол
Гэрэл
- 3 бодлогыг бүгдийг бодох магадлал $\dfrac{\fbox{ab}}{125};$
- нэг ч бодлого бодож чадахгүй байх магадлал $\dfrac{\fbox{c}}{125};$
- яг нэг бодлого бодох магадлал $\dfrac{\fbox{de}}{125};$
- ядаж 2 бодлого бодох магадлал $\dfrac{\fbox{fgh}}{125}$ байна.
Асуулт бүр нь 4 хариултын хувилбар бүхий 5 асуулттай тестыг
тааж бөглөхөд
- бүгдийг нь зөв бөглөх магадлал $\dfrac{\fbox{a}}{1024}$;
- бүгдийг нь буруу бөглөх магадлал $\dfrac{\fbox{bcd}}{1024}$;
- яг нэг асуултыг зөв бөглөх магадлал $\dfrac{\fbox{efg}}{1024}$;
- ядаж 4 асуултыг зөв бөглөх магадлал $\dfrac{\fbox{h}}{64}$ байна.
Улаан, шар, ногоон, цагаан 4 өнгийн карт тус бүр 5 ширхэг (1-5 тоогоор дугаарласан) нийт 20 карт байжээ. 3 картыг зэрэг сонгон авахад
- бүгд ижил дугаартай байх магадлал $\dfrac{\fbox{a}}{\fbox{bc}}$,
- 3 картны өнгө ба дугаар нь бүгд ялгаатай байх магадлал $\dfrac{\fbox{d}}{\fbox{ef}}$,
- яг нэг ширхэг улаан карт гарч ирэх магадлал $\dfrac{\fbox{gh}}{\fbox{ij}}$,
- гарч ирсэн улаан картны тооны математик дундаж нь $\dfrac{\fbox{k}}{\fbox{l}}$ байна.
3 улаан, 2 хөх, 1 шар өнгийн нийт 6 бөмбөгтэй уутнаас нэг бөмбөг авч өнгийг нь хараад буцааж хийх үйлдлийг дээд тал нь 3 удаа давтах ба улаан бөмбөг гарч ирвэл зогсоно.
- Нэг, эсвэл 2 удаа үйлдлийг давтах магадлал $\dfrac{\fbox{a}}{\fbox{b}}$,
- Нэг удаагийн үйлдэл бүр нь 100 төгрөгийн шагналтай бол шагналын математик дундаж нь $\fbox{cde}$,
- Шар бөмбөг ядаж нэг удаа гарч ирэх магадлал $\dfrac{\fbox{fg}}{\fbox{hi}}$ байна.
2 оронтой тоонуудаас таамгаар нэг тоо сонгоход сонгогдсон тоо:
- 4-ийн цифр агуулсан байх магадлал $\dfrac{\fbox{a}}{\fbox{b}}$;
- 4 ба 5 цифрүүдийн дор хаяж нэгийг нь агуулсан байх магадлал $\dfrac{\fbox{cd}}{45}$;
- 3-д хуваагддаг байх магадлал $\dfrac{\fbox{e}}{\fbox{f}}$;
- 4-ийн цифр агуулсан ба $3$-д хуваагддаг байх магадлал $\dfrac{\fbox{g}}{15}$.
Санамсаргүйгээр 2 оронтой тоо сонгон авахад тэр тоо
- 4 ба 5-д хуваагддаг байх магадлал $\dfrac{2}{\fbox{ab}}$
- 5-д хуваагддаггүй байх магадлал $\dfrac{\fbox{c}}{\fbox{d}}$.
Шоог гурван удаа хаяхад
- Бүгд $5$-аас ихгүй байх боломжийн тоо $\fbox{abc}$ байна.
- Бүгд $4$-өөс ихгүй байх боломжийн тоо $\fbox{de}$ байна.
- Хамгийн их нь $5$ байх боломжийн тоо $\fbox{fg}$ байна.
2 оронтой тоонуудаас таамгаар нэг тоо сонгоход, сонгогдсон тоо
- 1-ийн цифр агуулсан байх магадлал $\dfrac{\fbox{a}}{\fbox{b}}$.
- 1 ба 2 цифрийн дор хаяж нэгийг нь агуулсан байх магадлал $\dfrac{\fbox{cd}}{45}$.
- $3$-д хуваагддаг байх магадлал $\dfrac{\fbox{e}}{\fbox{f}}$.
- 1-ийн цифр агуулсан ба 3-д хуваагддаг байх магадлал $\dfrac{\fbox{g}}{15}$.
2 оронтой тоонуудаас таамгаар нэг тоо сонгоход сонгогдсон тоо:
- 2-ийн цифр агуулсан байх магадлал $\dfrac{\fbox{a}}{\fbox{b}}$;
- 2 ба 3 цифрүүдийн дор хаяж нэгийг нь агуулсан байх магадлал $\dfrac{\fbox{cd}}{45}$;
- 3-д хуваагддаг байх магадлал $\dfrac{\fbox{e}}{\fbox{f}}$;
- 2-ийн цифр агуулсан ба $3$-д хуваагддаг байх магадлал $\dfrac{\fbox{g}}{15}$.
2 оронтой тоонуудаас таамгаар нэг тоо сонгоход сонгогдсон тоо:
- 3-ийн цифр агуулсан байх магадлал $\dfrac{\fbox{a}}{\fbox{b}}$;
- 3 ба 4 цифрүүдийн дор хаяж нэгийг нь агуулсан байх магадлал $\dfrac{\fbox{cd}}{45}$;
- 3-д хуваагддаг байх магадлал $\dfrac{\fbox{e}}{\fbox{f}}$;
- 3-ийн цифр агуулсан ба $3$-д хуваагддаг байх магадлал $\dfrac{\fbox{g}}{15}$.
42650 тоог 7 удаа залгаж бичвэл 42650426504265042650426504265042650 гэсэн 35 оронтой тоо үүснэ. Санамсаргүйгээр 2 цифрийг нь арилгахад үүсэх 33 оронтой тоо 15-д хуваагддаг байх магадлалыг ол.
Бодолт:
Бодолт:
- Санамсаргүйгээр 2 цифрийг нь арилгах бүх боломжийн тоо $\fbox{abc}$ болно. (3 оноо)
- Сүүлчийн 2 цифрээс бусад аливаа 2 цифрийг арилгах нь зөвхөн 3-д хуваагддаг чанарыг ашиглах боломж олгоно. Иймд 4-г 1-ээр, 6-г 0-ээр, 5-г 2-оор соливол чанар өөрчлөгдөхгүй тул дээрх тоог 12020120201202012020120201202012020 тоогоор төлөөлүүлж болно. Энэ тооны цифрүүдийн нийлбэр $\fbox{de}$ болно. (2 оноо)
- Сүүлчийн 2 цифрээс бусад цифрүүдээс 2-г нь арилгах боломжийн тоо (3-д хуваагдах тул)
- Эсвэл хоёр 1 цифрийг
- Эсвэл нэг 2 цифр ба нэг 0 цифрийг арилгах шаардлагатай. Ийм боломжийн тоо $\fbox{fgh}$ тул олох магадлал $P=\dfrac{\fbox{fgh}}{\fbox{abc}}$ юм. (3 оноо)
Гурван оронтой тоо 3-т хуваагдах магадлал $\dfrac{1}{\fbox{a}}$, 4-т хуваагдах магадлал $\dfrac{1}{\fbox{b}}$, 3 ба 4-т зэрэг хуваагддаг байх магадлал $\dfrac{1}{\fbox{cd}}$ байна. Харин 3-т хуваагддаг боловч 4-т хуваагдаггүй байх магадлал $\dfrac{1}{\fbox{e}}$, 4-т хуваагддаг боловч 3-т хуваагдахгүй байх магадлал $\dfrac{1}{\fbox{f}}$ байна.
Хайрцаганд улаан, цагаан, хөх өнгийн бөмбөг тус бүр 9 ширхэг байсан ба нэг өнгийн бөмбөг бүрийг 1-9 тоогоор дугаарласан байв. Санамсаргүйгээр хайрцгаас 3 бөмбөг гаргав.
- Гаргаж ирсэн бөмбөгүүд дээрх тоонуудын нийлбэр 7 байх магадлал $\dfrac{\fbox{a}}{\fbox{bcd}}$;
- Гаргаж ирсэн бөмбөгүүд дээрх тоонуудын үржвэр 108 байх магадлал $\dfrac{\fbox{e}}{\fbox{fgh}}$.
Талууд нь $A=\{3;4;5;7\}$ олонлогоос утгаа авах
- Зөв гурвалжин $\fbox{a}$ ширхэг байна.
- Адил хажуут гурвалжин $\fbox{bc}$ ширхэг байна.
- Нийт гурвалжны тоо $\fbox{de}$ ширхэг байна.
- $A$ олонлогийн элементүүдээр талаа хийсэн гурвалжнуудаас санамсаргүйгээр сонгон авсан гурвалжин зөв гурвалжин байх магадлал $\dfrac{\fbox{f}}{\fbox{g}}$ байна.
- $A$ олонлогийн элементүүдээр талаа хийсэн гурвалжнуудаас Санамсаргүйгээр сонгон авсан гурвалжин адил хажуут гурвалжин байх магадлал $\dfrac{\fbox{h}}{\fbox{i}}$ байна.
- $A$ олонлогийн элементүүдээр талаа хийсэн гурвалжнуудаас санамсаргүйгээр сонгон авсан гурвалжин адил хажуут гурвалжин байсан бол тэр нь зөв гурвалжин байх магадал $\dfrac{4}{\fbox{jk}}$ байна.
Уутанд 0 дугаартай нэг цагаан, 1-5 дугаартай таван улаан, 6-9 дугаартай дөрвөн хөх өнгийн бөмбөг байв. Уутнаас санамсаргүйгээр 2 бөмбөг авчээ.
- 2 бөмбөг өөр өнгөтэй байх магадлал $\dfrac{\fbox{ab}}{\fbox{cd}}$;
- 2 бөмбөг сондгой дугаартай ба өөр өнгөтэй байх магадлал $\dfrac{\fbox{e}}{\fbox{fg}}$;
- Авсан 2 бөмбөгт байх улаан өнгийн бөмбөгний тооны математик дундаж нь $\fbox{h}$ байна.
Ангийн 20 сурагчийн 10 нь эрэгтэй, 10 нь эмэгтэй байв. 4 хүүхэдтэй ангийн жижүүр томилоход
- Бүгдээр эрэгтэй сурагч байх магадлал $\dfrac{\fbox{ab}}{323}$
- Нэг эрэгтэй сурагч, 3 эмэгтэй сурагч байх магадлал $\dfrac{\fbox{cd}}{323}$
- Эрэгтэй эмэгтэй сурагчийн тоо тэнцүү байх магадлал $\dfrac{\fbox{efg}}{323}$ байна.
1-10 дугаартай бөмбөгүүд бүхий хайрцагаас таамгаар 7 бөмбөг авахад 3 дугаартай бөмбөг гарч ирсэн байх магадлал $\dfrac{\fbox{a}}{\fbox{bc}}$; гарч ирсэн бөмбөгүүдийн хамгийн бага дугаартай нь $3$ байх магадлал $\dfrac{\fbox{d}}{\fbox{efg}}$ байна.
Талууд нь $\{9,11,12,15,18\}$ олонлогоос утгаа авах
- Элдэв талт гурвалжин $\fbox{ab}$ ширхэг
- Зөв биш адил хажуут гурвалжин $\fbox{cd}$ ширхэг
- Талууд нь дээрх олонлогоос утгаа авах гурвалжнуудаас санамсаргүйгээр нэг гурвалжин сонгон авахад зөв гурвалжин байх магадлал $\dfrac{\fbox{e}}{\fbox{fg}}$ байна.
Уутанд 0 дугаартай нэг цагаан, 1-5 дугаартай таван улаан, 6-9 дугаартай дөрвөн хөх өнгийн бөмбөг байв. Уутнаас санамсаргүйгээр 2 бөмбөг авчээ.
- 2 бөмбөг ижил өнгөтэй байх магадлал $\dfrac{\fbox{ab}}{\fbox{cd}}$;
- 2 бөмбөг тэгш дугаартай ба өөр өнгөтэй байх магадлал $\dfrac{\fbox{e}}{\fbox{fg}}$;
- Авсан 2 бөмбөгт байх хөх өнгийн бөмбөгний тооны математик дундаж нь $\dfrac{\fbox{h}}{\fbox{i}}$ байна.
32 модтой хөзрөөс таамгаар 5 мод сонгон авахад
- Яг нэг ширхэг дөрвөлжин сонгогдсон байх боломжийн тоо $\fbox{abcde}$ байна.
- 3 улаан, 2 хар мод сонгогдсон байх магадлал $\dfrac{\fbox{fgh}}{\fbox{ijk}}$ байна.
1-9 дугаартай 9 картнаас санамсаргүйгээр 7 карт сугалан авч тэдгээрийн хамгийн их дугаарыг $X$ гэе.
- $P(X=8)=\dfrac{\fbox{a}}{\fbox{bc}}$
- $X$ санамсаргүй хувьсагчийн математик дундаж $E(X)=\dfrac{\fbox{de}}{\fbox{f}}$ байна.
Зөв хэлбэртэй хоёр шоог зэрэг хаяхад гарах тоонуудын нийлбэр болох санамсаргүй хувьсагчийг $\xi$ гэе.
- $P(\xi=8)=\dfrac{\fbox{a}}{\fbox{bc}}$;
- $\xi$ санамсаргүй хувьсагчийн математик дундаж нь $\fbox{d}$ байна.
$1,2,\dots,13$ дугаартай 13 ширхэг картаас 2-ийг нь санамсаргүйгээр нэгэн зэрэг авахад
- Эдгээр дунд $1$ дугаартай карт орсон байх магадлал $\dfrac{\fbox{a}}{\fbox{bc}}$;
- 1 дугаартай карт ба тэгш дугаартай карт байх магадалал $\dfrac{\fbox{d}}{\fbox{bc}}$;
- Бүгд тэгш байх магадлал $\dfrac{\fbox{e}}{\fbox{fg}}$ байна. (хариуг үл хураагдах бутархай хэлбэрээр бичнэ).
Дорж, Дулам нар 2 ижил шоог орхиж тоглов. Хэрэв шооны унасан нүхний нийлбэр тэгш бол Дорж үгүй бол Дулам хожино.
- 2 шоог хаяхад гарч болох үр дүн $\fbox{ab}$ байна. /2 оноо/
- Дорж хожих магадлал $\dfrac{\fbox{c}}{\fbox{d}}$ /2 оноо/
- Дулам хожсон бол шооны нүхний нийлбэр 7 байх магадлал $\dfrac{\fbox{e}}{\fbox{f}}$ /3 оноо/
Шоог эхний удаа орхиход гарсан тоог $x$, хоёр дахь удаа орхиход гарсан тоог $y$ гэвэл
- $x-y=2$ байх магадлал $\dfrac{1}{\fbox{a}}$;
- $y=x^2$ байх магадлал $\dfrac{1}{\fbox{bc}}$;
- $y>x^2$ байх магадлал $\dfrac{\fbox{d}}{\fbox{ef}}$;
- $x$ тэгш гэж мэдэгдэж байгаа нөхцөлд $y>x^2$ байх магадлал $\dfrac{1}{\fbox{g}}$ байна.
Асуулт бүр нь 5 хувилбар бүхий 5 асуулттай тестийг тааж бөглөхөд
- бүгдийг нь зөв бөглөх магадлал $\dfrac{1}{\fbox{abcd}}$;
- ядаж 4 асуултыг зөв бөглөх магадлал $\dfrac{\fbox{ef}}{\fbox{abcd}}$;
- яг нэг удаа зөв бөглөх магадлал $\dfrac{\fbox{ghi}}{625}$;
- бүгдийг нь буруу бөглөх магадлал $\dfrac{\fbox{jklm}}{\fbox{abcd}}$ байна.
Хөх бэхтэй 5, улаан бэхтэй 3 үзэгнээс таамгаар 2-ыг авахад хоёулаа хөх байх магадлал $\dfrac{\fbox{a}}{\fbox{bc}}$, хоёулаа улаан байх магадлал $\dfrac{\fbox{d}}{\fbox{ef}}$, хөх улаан хоёр байх магадлал $\dfrac{\fbox{gh}}{\fbox{ef}}$, ижил өнгөтэй байх магадлал $\dfrac{\fbox{ij}}{\fbox{ef}}$ байна.
Дорж, Дулам нар 2ижил шоог орхиж тоглов. Хэрэв шооны унасан нүхний нийлбэр тэгш бол Дорж үгүй бол Дулам хожино.
- 2 шоог хаяхад гарч болох үр дүн $\fbox{ab}$ байна. /2 оноо/
- Дулам хожих магадлал $\dfrac{\fbox{c}}{\fbox{d}}$ /2 оноо/
- Дорж хожсон бол шооны нүхний нийлбэр 8 байх магадлал $\dfrac{\fbox{e}}{\fbox{f}}$ /3 оноо/
Таамгаар 3 оронтой тоо сонгон авахад цифр давтагдаж орсон байх магадлалыг олъё. Нийт 3 оронтой тоонуудын тоо $\fbox{a}\cdot 10^{\fbox{b}}$. Цифр огт давтагдаж ороогүй нь $\fbox{cde}$ тул цифр давхацсан $\fbox{fgh}$ ширхэг тоо байна. Иймд магадлал нь $\dfrac{\fbox{i}}{\fbox{jk}}$ байна.
$x^2+5x-14\le 0$ тэнцэтгэл бишийн дурын бүхэл шийдийг сонгов. Энэ тоо
- $x^2\le 1$ тэнцэтгэл бишийн шийд байх магадлал $\dfrac{\fbox{a}}{\fbox{bc}}$;
- $x^2\ge 4$ тэнцэтгэл бишийн шийд байх магадлал $\dfrac{\fbox{d}}{\fbox{ef}}$;
- $x^2+5x\ge 0$ тэнцэтгэл бишийн шийд байх магадлал $\dfrac{\fbox{g}}{\fbox{h}}$ байна.
$1, 2, 3, 4, 5$ дугаартай хайрцгуудад өөр хоорондоо ялгаагүй 7 ширхэг бөмбөгийг $\fbox{abc}$ янзаар байрлуулж болох ба дурын нэг байрлуулалт авч үзэхэд 4 ба 5-р хайрцаг хоёулаа хоосон байх магадлал $\frac{\fbox{d}}{\fbox{ef}}$ болно.
Шоог гурван удаа хаяхад
- Бүгд $4$-аас ихгүй байх боломжийн тоо $\fbox{ab}$ байна.
- Бүгд $3$-өөс ихгүй байх боломжийн тоо $\fbox{cd}$ байна.
- Хамгийн их нь $4$ байх боломжийн тоо $\fbox{ef}$ байна.
1-10 дугаартай бөмбөгүүд бүхий хайрцагаас таамгаар 7 бөмбөг авахад 4 дугаартай бөмбөг гарч ирсэн байх магадлал $\dfrac{\fbox{a}}{\fbox{bc}}$ (3 оноо); гарч ирсэн бөмбөгүүдийн хамгийн бага дугаартай нь $4$ байх магадлал $\dfrac{\fbox{d}}{\fbox{efg}}$ (4 оноо) байна.
1-10 дугаартай бөмбөгүүд бүхий хайрцагаас таамгаар 7 бөмбөг авахад 2 дугаартай бөмбөг гарч ирсэн байх магадлал $\dfrac{\fbox{a}}{\fbox{bc}}$ (3 оноо); гарч ирсэн бөмбөгүүдийн хамгийн бага дугаартай нь $2$ байх магадлал $\dfrac{\fbox{d}}{\fbox{ef}}$ (4 оноо) байна.
Хайрцагт байгаа 1-ээс 8 хүртэл дугаартай 8-н хөзрөөс санамсаргүйгээр 3-н хөзөр зэрэг сугалав.
- Сугалсан 3-н хөзөр бүгд сондгой дугаартай байх магадлал $\dfrac{1}{\fbox{ab}}$
- Сугалсан 3-н хөзрийн хамгийн их тоотой нь 5 байх магадлал $\dfrac{\fbox{c}}{\fbox{de}}$ байна.
- Сугалсан 3-н хөзрийн дугааруудын үржвэр нь тэгш байх магадлал $\dfrac{\fbox{fg}}{14}$ байна.
Хайрцагт байгаа 1-ээс 8 хүртэл дугаартай 8-н хөзрөөс санамсаргүйгээр 4 хөзөр зэрэг сугалав.
- Сугалсан 4 хөзөр нь бүгд сондгой дугаартай байх магадлал $\dfrac{1}{\fbox{ab}}$
- Сугалсан 4 хөзрийн хамгийн их тоотой нь 5 байх магадлал $\dfrac{\fbox{c}}{\fbox{de}}$ байна.
- Сугалсан 4 хөзрийн дугааруудын үржвэр нь тэгш байх магадлал $\dfrac{\fbox{fg}}{70}$ байна.
"Тамга" тоглоом нь дараах дүрэмтэй: 3 тамга, 2 ноён, 1 хатан бүхий 6 хөзрөөс 1 хөзөр сугалан хараад буцааж хийх үйлдлийг 3 хүртэл удаа хийнэ. Хэрэв тамга сугалвал хожих ба тоглоом дуусна.
a) 2-оос олонгүй удаа үйлдэл хийгээд хожих магадлал $\dfrac{\fbox{a}}{\fbox{b}}$ (2 оноо)
b) Хэрэв хожвол 200 төгрөгийн шагнал авах бол шагналын математик дундаж $\fbox{cde}$ (3 оноо) байна.
c) Тоглогч ядаж 1 удаа хатан сугалах магадал $\dfrac{\fbox{fg}}{\fbox{hi}}$ (2 оноо) байна.
a) 2-оос олонгүй удаа үйлдэл хийгээд хожих магадлал $\dfrac{\fbox{a}}{\fbox{b}}$ (2 оноо)
b) Хэрэв хожвол 200 төгрөгийн шагнал авах бол шагналын математик дундаж $\fbox{cde}$ (3 оноо) байна.
c) Тоглогч ядаж 1 удаа хатан сугалах магадал $\dfrac{\fbox{fg}}{\fbox{hi}}$ (2 оноо) байна.
1-50 хүртэлх тоо өгөгдөв.
- 4-д хуваагдах тоо $\fbox{ab}$ ширхэг
- 5-д хуваагдах тоо $\fbox{cd}$ ширхэг
- хоёуланд нь зэрэг хуваагдах тоо $\fbox{e}$ ширхэг
- өгсөн тоонуудаас 1 тоог санамсаргүйгээр сонгон авахад 4 эсвэл 5-д хуваагдах тоо байх үзэгдлийн магадлал $\dfrac{\fbox{f}}{\fbox{g}}$ байна.
Ангийн 30 сурагчийн 20 нь эрэгтэй байв.
- Ангийн дарга нь эрэгтэй байх магадлал нь $\dfrac{\fbox{a}}{\fbox{b}}$ (үл хураагдах).
- Ангийн дарга ба түүний орлогч нь хоёулаа эрэгтэй байх магадлал нь $\dfrac{\fbox{cd}}{\fbox{ef}}$.
- Ангийн дарга нь эрэгтэй түүний орлогч нь эмэгтэй байх магадлал нь $\dfrac{\fbox{gh}}{\fbox{ij}}$.
Оюутан англи, орос, франц хэлний шалгалт өгөв. Шалгалтын асуултууд хэл тус бүрээр 3 дугтуйд савлагдсан байв. Хэрэв эдгээр шалгалтын асуултуудын англи хэлний $60\%$, орос хэлний $45\%$, франц хэлний $80\%$ нь оюутны мэддэг асуулт байсан бол тэр таамгаар нэг дугтуй авч дотроос нь 1 асуулт харалгүйгээр сугалбал
- франц хэлний дугтуй авах магадлал $\dfrac{1}{\fbox{a}}$,
- франц хэлний дугтуйнаас мэддэг асуултаа сугалах магадлал $\dfrac{\fbox{b}}{4}$,
- мэддэг асуултаа сугалах магадлал $\dfrac{\fbox{c}}{6\fbox{d}}$,
- мэддэг асуулт франц хэлнийх байх магадлал $\dfrac{1\fbox{e}}{\fbox{gh}}$
$1,2,\ldots,12$ тоонуудыг таамгаар 2 тэнцүү хэсэгт хуваахад:
- Бүх тэгш тоонууд тоонууд 1-р хэсэгт орсон байх магадлал $\dfrac{1}{\fbox{abc}}$;
- 3-д хуваагдах бүх тоонууд хоёр хэсэгт тэнцүү хуваагдан орсон байх магадлал $\dfrac{5}{\fbox{de}}$;
- Хэсэг тус бүрд тэгш ба сондгой тоонууд тэнцүү тоотой орсон байх магадлал $\dfrac{\fbox{fgh}}{231}$
Хоёр сурагч Англи хэлний түвшин тогтоох шалгалт өгчээ. Шалгалтад I сурагч тэнцэх магадлал 0.9, II сурагч тэнцэх магадлал 0.85 бол
- хоёулаа тэнцэх магадлал $\dfrac{1\fbox{ab}}{200}$
- Яг нэг сурагч тэнцэх магадлал $\dfrac{\fbox{cd}}{50}$
- Ядаж нэг сурагч тэнцэх магадлал $\dfrac{\fbox{efg}}{200}$
Ангийн 10 хүү, 10 охиноос 6 хүнтэй баг бүрдүүлэв.
- Нийт боломжийн тоо тоо нь $\fbox{abcde}$.
- Баг дан эрэгтэй сурагчаас бүрдсэн байх боломжийн тоо $\fbox{fgh}$.
- Багийн эрэгтэй ба эмэгтэй сурагчдын тоо тэнцүү байх магадлал $\dfrac{\fbox{hij}}{\fbox{323}}$ байна.
Хоёр сурагч Англи хэлний түвшин тогтоох шалгалт өгчээ. Шалгалтад I сурагч тэнцэх магадлал 0.9, II сурагч тэнцэх магадлал 0.85 бол
- хоёулаа тэнцэх магадлал $\dfrac{1\fbox{ab}}{200}$
- Яг нэг сурагч тэнцэх магадлал $\dfrac{\fbox{cd}}{50}$
- Ядаж нэг сурагч тэнцэх магадлал $\dfrac{\fbox{efg}}{200}$
Хоёр сурагч Англи хэлний түвшин тогтоох шалгалт өгчээ. Шалгалтад I сурагч тэнцэх магадлал 0.9, II сурагч тэнцэх магадлал 0.85 бол
- хоёулаа тэнцэх магадлал $\dfrac{1\fbox{ab}}{200}$
- Яг нэг сурагч тэнцэх магадлал $\dfrac{\fbox{cd}}{50}$
- Ядаж нэг сурагч тэнцэх магадлал $\dfrac{\fbox{efg}}{200}$
Хоёр сурагч Англи хэлний түвшин тогтоох шалгалт өгчээ. Шалгалтад I сурагч тэнцэх магадлал 0.95, II сурагч тэнцэх магадлал 0.8 бол
- хоёулаа тэнцэх магадлал $\dfrac{1\fbox{ab}}{25}$
- Яг нэг сурагч тэнцэх магадлал $\dfrac{\fbox{cd}}{100}$
- Ядаж нэг сурагч тэнцэх магадлал $\dfrac{\fbox{efg}}{1g 0}$
Нийлмэл үзэгдлийн магадлал
Цех хэдэн машинтай. Ээлжинд яг нэг суурь машинд тохируулга
хийх магадлал 0.2 ба яг хоёр суурь машины хувьд уг магадлал 0.13, харин хоёроос
олон суурь машинд тохируулга хийх магадлал 0.07 бол ээлжинд суурь машинд
тохируулга хийх магадлалыг ол.
Нийцгүй үзэгдлүүд, магадлалуудыг нэмэх дүрэм
Дөрвөн харваач бие биенээсээ хамааралгүйгээр нэг байг зэрэг
харваж байна. Харваач бүрийн бай онох магадлал $\dfrac23$ бол бай оногдсон байх
магадлалыг ол.
Хоёр харваач бие биеэсээ хамаарахгүйгээр бай харваж байна. I
харваачийн бай онох магадлал 0.8, II харваачийн бай онох магадлал 0.75 бол бай
оногдсон байх магадлалыг ол.
Харваач 10-г 0.05, 9-г 0.2, 8-г 0.6 магадлалтайгаар онодог байв. Нэг
харвахад:
а) 8-аас багагүй оноо авах,
б) 8-аас олон оноо авах үзэгдлүүдийн магадлалыг ол.
а) 8-аас багагүй оноо авах,
б) 8-аас олон оноо авах үзэгдлүүдийн магадлалыг ол.
Хайрцагт 8 цагаан, 12 улаан бөмбөг байв. Таамгаар авсан
а) 3 бөмбөгний ядаж нэг нь цагаан байх,
б) 6 бөмбөгний нэгээс ихгүй нь цагаан байх,
в) 5 бөмбөгний хоёроос цөөнгүй нь цагаан байх,
г) 2 бөмбөг адил өнгөтэй байх магадлалуудыг ол.
а) 3 бөмбөгний ядаж нэг нь цагаан байх,
б) 6 бөмбөгний нэгээс ихгүй нь цагаан байх,
в) 5 бөмбөгний хоёроос цөөнгүй нь цагаан байх,
г) 2 бөмбөг адил өнгөтэй байх магадлалуудыг ол.
Хайрцагт 8 улаан, 10 ногоон, 12 цэнхэр бөмбөг байв. Таамгаар авсан 3
бөмбөгний ядаж 2 нь адил өнгөтэй байх магадлалыг ол.
Тасаг 3 суурь машинтай ба ээлжинд I суурь машинд тохируулга хийх
магадлал 0.15, II-т 0.1, III-т 0.12 байв. Гурвуул бие биеэс хамааралгүйгээр
тохируулга шаарддаг байсан бол ээлжинд ядаж нэг машинд тохируулга хийх
магадлалыг ол. (Уг үзэгдлээ нийцтэй ба нийцгүй үзэгдлүүдийн нийлбэрт хоёр янзаар тавьж бод)
Өөр хоорондоо харилцан нийцгүй 4 үзэгдлүүд явагдах магадлал нь харгалзан $0.1$, $0.2$, $0.3$, $0.25$ бол эдгээр үзэгдлүүдийн ядаж нэг нь явагдах магадлалыг ол.
A. $0.6$
B. $0.75$
C. $0.85$
D. $0.9$
E. $0.95$
Өөр хоорондоо харилцан нийцгүй 4 үзэгдэл илрэх магадлал нь харгалзан $0.1$, $0.2$, $0.3$, $0.3$ бол эдгээр үзэгдлүүдийн ядаж нэг нь илрэх магадлалыг ол.
A. $0.6$
B. $0.7$
C. $0.8$
D. $0.9$
E. $1$
Ангийн 20 сурагчийн 10 нь математикийн, 8 нь англи хэлний, 5-нь математик ба англи хэлний дугуйланд, үлдсэн нь аль ч дугуйланд явдаггүй бол санамсаргүйгээр сонгосон нэг сурагч ямар нэг дугуйланд явдаггүй байх магадлалыг ол.
A. $\dfrac{13}{20}$
B. $\dfrac{9}{10}$
C. $\dfrac{3}{4}$
D. $\dfrac{7}{20}$
E. $\dfrac{1}{3}$
$A$, $B$ үзэгдлүүд харилцан нийцгүй үзэгдлүүд ба $P(A)=0.34$, $P(A\cup B)=0.46$ бол $P(B)=?$
A. $0.12$
B. $0.10$
C. $0.39$
D. $0.65$
E. $0.78$
Хоёр хүн ээлжлэн мөнгө орхиж тоглож байна. Түрүүлэн сүлд буулгаж чадсан нь хожно. Тоглоомыг эхэлсэн хүн хожих магадлалыг ол.
A. $\dfrac12$
B. $\dfrac23$
C. $\dfrac34$
D. $\dfrac45$
E. $\dfrac{1}{3}$
Өөр хоорондоо харилцан нийцгүй 3 үзэгдэл илрэх магадлал нь харгалзан $0.1$, $0.2$, $0.3$ бол эдгээр үзэгдлүүдийн ядаж нэг нь илрэх магадлалыг ол.
A. $0.6$
B. $0.7$
C. $0.8$
D. $0.9$
E. $1$
Нөхцөлт магадлал
$a$ ширхэг цагаан, $b$ ширхэг хар уут байна. Цагаан уут бүрд
$x$ улаан, $y$ ногоон бөмбөг, харин хар уут бүрд $z$ улаан, $t$ ногоон бөмбөг
байв. Эхлээд нэг уут аваад дараа нь түүнээс нэг бөмбөг авья. Тэгвэл
$p(ц)$, $p(х)$, $p(ц\cap у)$, $p(у|ц)$, $p(у|х)$-үүдийг ол.
Энд $ц$="цагаан уут авах", $у|ц$="цагаан
уутнаас улаан бөмбөг гаргах", $ц\cap у$="авсан уут маань цагаан байсан ба түүнээс
авсан бөмбөг улаан өнгөтэй байна" гэсэн үзэгдлүүд болно. \\
0.7 магадлалтайгаар онодог 2 хүн бие биеэс хамааралгүйгээр
байг нэг нэг буудаад яг адил үр дүн үзүүлэв. Хоёул оносон байх магадлалыг ол.\\
Хүлээн авагчид 3 автоматаас бүтээгдэхүүн ирнэ. I, II, III автоматын
гологдол бүтээгдэхүүний хувь нь $0.3\%$, $0.2\%$, $0.4\%$ ба хүлээн авагчид
харгалзан 1000, 2000, 2500 бүтээгдэхүүн өгсөн бол хүлээн авагчид ирж буй
бүтээгдэхүүн гологдол байх магадлалыг ол.
Онгоц уруу 3 удаа буудна. I, II, III буудалтуудаар онох магадлал нь 0.5,
0.6, 0.8 ба онгоцны унах магадлал 1 онолтод 0.3, 2 онолтод 0.6 ба 3 онолтод
1 бол онгоц унах магадлалыг ол.
Нөхцөлт магадлалын дараахь үндсэн чанаруудыг батал.\\
а) $0\le p(A|B)\le1$,\\
б) $A\cap B=\O$ бол $p(A\cup B|C)=p(A|C)+p(B|C)$,\\
б$'$) $p(A+B|C)=p(A|C)+p(B|C)-p(AB|C)$,\\
в) $p(A|B)>p(A)$ бол $p(B|A)>p(B)$ байна,\\
г) $p(ABC)=p(A)p(B|A)p(C|AB)$.
Үржвэрийн томъёо (2)-ыг 2-оос олон үзэгдлийн хувьд бич.
Цагаан хайрцагт 12 улаан, 6 цэнхэр бөмбөг, шар хайрцагт 15 улаан, 10
цэнхэр бөмбөг байв. Хэрэв орхисон шоон дээр туссан оноо нь гуравт хуваагдаж
байвал цагаан хайрцагнаас, эсрэг тохиодолд шар хайрцагнаас бөмбөг гаргана.
Улаан бөмбөг гарах магадлалыг ол.
10 эдлэлийн 4-ийг буджээ. Эдлэл хэвийн хэмжээнээс хүнд байх магадлал
будагдсан эдлэлийн хувьд 0.3, будагдаагүй эдлэлийн хувьд 0.1 байв. Таамгаар
авсан эдлэл хэвийн хэмжээнээс хүнд байв. Тэгвэл тэр нь будагдсан эдлэл байх
магадлалыг ол.
Спартакиадад I, II, III курсээс 4, 6, 5 оюутан оролцов. Оюутан сургуулийн
шигшээ багт орох магадлал I курс бол 0.9, II курс бол 0.7, III курс бол 0.8 байв.
Таамгаар сонгож авсан оюутан сургуулийн шигшээ багт орж байв. Аль курсийн оюутны
хувьд энэ магадлал их вэ?
Бензин түгээгүүрийн хажуугаар ачааны ба хөнгөн тэрэг өнгөрдөг. Түүний
$60\%$ ачааны машин байдаг. Бензин авах магадлал нь ачааны машины хувьд 0.1,
хөнгөн тэрэгний хувьд 0.2 байдаг. Бензин авахаар ирсэн машин ачааных байх магадлалыг ол.
3 хүн зэрэг буудахад байнд 2 сум туссан байв. I, II, III хүний бай онох
магадлал нь 0.6, 0.5, 0.4 бол III хүн бай оносон байх магадлалыг ол.
Шалгалт өгөх 10 сурагчийн 3 нь онц, 4 нь сайн, 2 нь дунд, 1 нь муу
бэлджээ. Шалгалтын билет 20 асуулттай ба онц бэлдсэн сурагч бүх 20 асуултанд,
сайн нь 16-д, дунд нь 10-т, муу нь 5 асуултанд л хариулж чадна. Таамгаар авсан
сурагч 3 асуултанд хариулав. Тэгвэл энэ сурагч: а) онц, б) муу бэлдсэн сурагч
байх магадлалыг ол.
Хайрцагт 2 бөмбөг байв. (бөмбөг бүр хар юмуу цагаан өнгөтэй байх ёстой).
Дээр нь 1 цагаан бөмбөг нэмж хийгээд 1 бөмбөг таамгаар авахад тэр нь цагаан
байх магадлалыг ол.
I уутанд 6 улаан, 4 цагаан, II уутанд 2 улаан, 3 цагаан бөмбөг байжээ. Таамгаар сонгосон нэг уутнаас нэгэн зэрэг хоёр бөмбөгийг таамгаар гаргаж ирэхэд хоёулаа цагаан байх магадлалыг ол.
A. $\dfrac{9}{65}$
B. $\dfrac{19}{60}$
C. $\dfrac{5}{12}$
D. $\dfrac{3}{20}$
E. $\dfrac{13}{60}$
Улаан уутанд 6 улаан, 4 цагаан, хөх уутанд 2 улаан, 3 цагаан бөмбөг байжээ. Таамгаар сонгосон нэг уутнаас нэгэн зэрэг хоёр бөмбөгийг таамгаар гаргаж ирэхэд хоёулаа цагаан байх магадлалыг ол.
A. $\dfrac{13}{60}$
B. $\dfrac{5}{12}$
C. $\dfrac{3}{20}$
D. $\dfrac{19}{60}$
E. $\dfrac{19}{30}$
Сурагчдын $10\%$ нь $A$, $20\%$ нь $B$, $30\%$ нь $C$, $30\%$ нь $D$, $10\%$ нь $F$ сурдаг байв. Сурагчид спортоор хичээллэдэг байх магадлал $A$ сурдаг бол $\dfrac1{10}$, $B$ сурдаг бол $\dfrac 18$, $C$ сурдаг бол $\dfrac 14$, $D$ сурдаг бол $\dfrac 12$, $F$ сурдаг бол $\dfrac 12$ байв. Санамсаргүйгээр сонгосон 1 сурагч спортоор хичээллэдэг бол $B$ сурдаг сурагч байх магадлалыг ол.
A. $\dfrac{31}{100}$
B. $\dfrac{1}{40}$
C. $\dfrac{5}{62}$
D. $\dfrac{57}{62}$
E. $\dfrac{69}{100}$
Хайрцагт 5 улаан, 4 хөх бөмбөг байв. Хайрцагнаас таамгаар 2 бөмбөг буцааж хийхгүйгээр дараалан нэг нэгээр нь авахад эхэлж авсан бөмбөг нь улаан, дараа нь авсан бөмбөг нь хөх байх магадлалыг ол.
A. $\dfrac{5}{18}$
B. $\dfrac{15}{64}$
C. $\dfrac{1}{15}$
D. $\dfrac{15}{56}$
E. $\dfrac{25}{64}$
Хайрцагт 5 улаан, 3 хөх бөмбөг байв. Хайрцагнаас таамгаар 2 бөмбөг буцааж хийхгүйгээр дараалан нэг нэгээр нь авахад эхэлж авсан бөмбөг нь улаан, дараа нь авсан бөмбөг нь хөх байх магадлалыг ол.
A. $\dfrac{15}{28}$
B. $\dfrac{15}{64}$
C. $\dfrac1{15}$
D. $\dfrac{15}{56}$
E. $\dfrac{25}{64}$
Хайрцагт 6 улаан, 4 хөх бөмбөг байв. Хайрцагнаас таамгаар 2 бөмбөг буцааж хийхгүйгээр дараалан нэг нэгээр нь авахад эхэлж авсан бөмбөг нь улаан, дараа нь авсан бөмбөг нь хөх байх магадлалыг ол.
A. $\dfrac{15}{28}$
B. $\dfrac{15}{64}$
C. $\dfrac{4}{15}$
D. $\dfrac{5}{16}$
E. $\dfrac{25}{64}$
Анчин гахайг 3 буудав. Түүний эхний сум онох магадлал $0.4$, II сум онох магадлал $0.5$, III сум онох магадлал $0.7$ байв. Гахайг нэг сум оноход үхэх магадлал $0.2$, хоёр сум оноход үхэх магадлал $0.6$, гурван сум оноход үхэх магадлал $1$ байг. Тэгвэл гахай үхэх магадлалыг ол.
A. $0.621$
B. $0.32$
C. $0.512$
D. $0.563$
E. $0.458$
Улаан уутанд 6 улаан, 4 цагаан, хөх уутанд 3 улаан, 4 цагаан бөмбөг байжээ. Таамгаар сонгосон нэг уутнаас нэгэн зэрэг хоёр бөмбөгийг таамгаар гаргаж ирэхэд хоёулаа цагаан байх магадлалыг ол.
A. $\dfrac{22}{105}$
B. $\dfrac{1}{5}$
C. $\dfrac{3}{20}$
D. $\dfrac{19}{60}$
E. $\dfrac{17}{30}$
Улаан уутанд 5 улаан, 3 цагаан, хөх уутанд 3 улаан, 4 цагаан бөмбөг байжээ. Таамгаар сонгосон нэг уутнаас нэгэн зэрэг хоёр бөмбөгийг таамгаар гаргаж ирэхэд хоёулаа улаан байх магадлалыг ол.
A. $\dfrac{1}{4}$
B. $\dfrac{1}{5}$
C. $\dfrac{22}{105}$
D. $\dfrac{19}{60}$
E. $\dfrac{17}{30}$
Улаан, шар 2 шоог зэрэг орхиход туссан нүхнүүдийн нийлбэр тэгш байсан бол нийлбэр 2 байх магадлалыг ол.
A. $\dfrac{1}{36}$
B. $\dfrac{1}{18}$
C. $\dfrac{1}{12}$
D. $\dfrac{1}{9}$
E. $\dfrac{1}{6}$
Улаан уутанд 6 улаан, 4 цагаан, хөх уутанд 2 улаан, 3 цагаан бөмбөг байжээ. Таамгаар сонгосон нэг уутнаас нэгэн зэрэг хоёр бөмбөгийг таамгаар гаргаж ирэхэд хоёулаа цагаан байх магадлалыг ол.
A. $\dfrac{13}{60}$
B. $\dfrac{5}{12}$
C. $\dfrac{3}{20}$
D. $\dfrac{19}{60}$
E. $\dfrac{19}{30}$
Бүтээгдэхүүний $20\%$, $30\%$, $50\%$-г I, II, III тасгууд гаргадаг. Гологдол бүтээгдэхүүн гаргах магадлал эдний хувьд харгалзан $0.01$,
$0.005$, $0.006$ байв. Авсан бүтээгдэхүүн гологдол байх магадлалыг ол.
A. $0.0035$
B. $0.0050$
C. $0.0070$
D. $0.0055$
E. $0.0065$
$A$ уутанд 3 улаан, 2 хөх; $B$ уутанд 7 улаан, 3 хөх; $C$ уутанд 4 улаан, 6 хөх бөмбөг байжээ. Бат $A$, $B$ уутны аль нэгийг санамсаргүйгээр сонгоод дотроос нь нэг бөмбөг гаргаж ирэв. Харин Дорж $C$ уутнаас санамсаргүйгээр нэг бөмбөг гаргаж иржээ. Бат, Дорж хоёрын сонгосон бөмбөгүүд ижил өнгөтэй байх магадлалыг ол.
A. $0.5$
B. $0.75$
C. $0.36$
D. $0.47$
E. $0.27$
А хүнд 1, 3, 5, 7, 9 дугаартай 5 ширхэг бөмбөгтэй уут, Б хүнд 2, 4, 6, 8 дугаартай 4 бөмбөгтэй уут өгч дараах дүрмээр тоглуулжээ.
- Хүн тус бүр уутнаасаа нэг нэг бөмбөг гаргахад аль их тоотой бөмбөг гаргасан нь хожих бол А хүн хожих магадлал $\dfrac{\fbox{a}}{\fbox{b}}$,
- Хожсон хүн өөрийн гаргасан тоог оноо болгож авах ба хожигдсон хүн 0 оноо авах бол А хүний онооны математик дундаж нь $\dfrac{\fbox{c}}{\fbox{d}}$ байна.
А хүнд 1, 3, 5, 7, 9 дугаартай 5 ширхэг бөмбөгтэй уут, Б хүнд 2, 4, 6, 8 дугаартай 4 ширхэг бөмбөгтэй уут өгч дараах дүрмээр тоглуулжээ.
- Хүн тус бүр уутнаасаа нэг нэг бөмбөг гаргахад аль их тоотой бөмбөг гаргасан нь хожих бол Б хүн хожих магадлал $\dfrac{\fbox{a}}{\fbox{b}}$,
- Хожсон хүн өөрийн гаргасан тоог оноо болгож авах ба хожигдсон хүн 0 оноо авах бол Б хүний онооны математик дундаж нь $\fbox{c}$ байна.
3 мөнгөний 1 нь 2 талдаа сүлдтэй, 2 нь ердийн мөнгө байв.
Санамсаргүйгээр 1 мөнгө авч шидэхэд сүлд буух магадлал
$\dfrac{\fbox{a}}{\fbox{b}}$ байна. Энэ мөнгө сүлдээрээ буусан бол
2 талдаа сүлдтэй мөнгө байх
магадлал $\dfrac{\fbox{c}}{\fbox{d}}$ байна.
Үйлдвэрийн нийт бүтээгдэхүүний $40\%$-ийг $A$ цех, $60\%$-ийг $B$
цехэд хийдэг. $A$ цехээс гологдол гарах магадлал $0.02;$ $B$
цехээс гологдол гарах магадлал $0.01$ бол үйлдвэрээс гологдол гарах
магадлал $\dfrac{\fbox{a}}{\fbox{bcd}}$ байна. Нэг
бүтээгдэхүүн гологдол болсон бол түүнийг $A$ цехэд хийсэн байх магадлал $\dfrac{\fbox{e}}{\fbox{f}}$ байна.
9 ширхэг том, 12 ширхэг жижиг хайрцаг байв. Том хайрцаг бүрт 8 улаан, 6 хөх; жижиг хайрцаг бүрт 10 улаан, 6 хөх бөмбөг байв. Таамгаар нэг хайрцаг авч, түүнээс нэг бөмбөг авъя.
- Авсан хайрцаг том байх магадлал $\dfrac{\fbox{a}}{\fbox{b}}$ (1 оноо).
- Авсан бөмбөг том хайрцагны улаан байх магадлал $\dfrac{\fbox{c}}{\fbox{d}}$ (1 оноо).
- Хайрцаг том бөгөөд бөмбөг улаан байх магадлал $\dfrac{12}{\fbox{ef}}$ (2 оноо).
- Бөмбөг улаан байх магадлал $\dfrac{\fbox{gh}}{98}$ (2 оноо).
Оюутан англи, орос, франц хэлний шалгалт өгөв. Шалгалтын асуултууд хэл тус бүрээр 3 дугтуйд савлагдсан байв. Хэрэв эдгээр шалгалтын асуултуудын англи хэлний $60\%$, орос хэлний $45\%$, франц хэлний $80\%$ нь оюутны мэддэг асуулт байсан бол тэр таамгаар нэг дугтуй авч дотроос нь 1 асуулт харалгүйгээр сугалбал
- франц хэлний дугтуй авах магадлал $\dfrac{1}{\fbox{a}}$,
- франц хэлний дугтуйнаас мэддэг асуултаа сугалах магадлал $\dfrac{\fbox{b}}{4}$,
- мэддэг асуултаа сугалах магадлал $\dfrac{\fbox{c}}{6\fbox{d}}$,
- мэддэг асуулт франц хэлнийх байх магадлал $\dfrac{1\fbox{e}}{\fbox{gh}}$
Хайрцагт 12 улаан, 8 ногоон, 10 цэнхэр бөмбөг байв. 2 бөмбөг таамгаар
авахад тэр нь цэнхэр биш гэдэг нь мэдэгдэж байсан бол:
- хоёул ногоон байх магадлал $\dfrac{\fbox{ab}}{\fbox{cd}}$
- улаан ба ногоон өнгөтэй байх магадлал $\dfrac{\fbox{ef}}{\fbox{cd}}$
Хайрцагт 12 улаан, 8 ногоон, 10 цэнхэр бөмбөг байв. 2 бөмбөг таамгаар авахад тэр нь улаан биш гэдэг нь мэдэгдэж байсан бол:
- хоёул цэнхэр байх магадлал $\dfrac{\fbox{a}}{\fbox{bc}}$
- ногоон ба цэнхэр өнгөтэй байх магадлал $\dfrac{\fbox{de}}{\fbox{fgh}}$
Хоёр сурагч Англи хэлний түвшин тогтоох шалгалт өгчээ. Шалгалтад I сурагч тэнцэх магадлал 0.9, II сурагч тэнцэх магадлал 0.85 бол
- хоёулаа тэнцэх магадлал $\dfrac{1\fbox{ab}}{200}$
- Яг нэг сурагч тэнцэх магадлал $\dfrac{\fbox{cd}}{50}$
- Ядаж нэг сурагч тэнцэх магадлал $\dfrac{\fbox{efg}}{200}$
Хоёр сурагч Англи хэлний түвшин тогтоох шалгалт өгчээ. Шалгалтад I сурагч тэнцэх магадлал 0.9, II сурагч тэнцэх магадлал 0.85 бол
- хоёулаа тэнцэх магадлал $\dfrac{1\fbox{ab}}{200}$
- Яг нэг сурагч тэнцэх магадлал $\dfrac{\fbox{cd}}{50}$
- Ядаж нэг сурагч тэнцэх магадлал $\dfrac{\fbox{efg}}{200}$
Хоёр сурагч Англи хэлний түвшин тогтоох шалгалт өгчээ. Шалгалтад I сурагч тэнцэх магадлал 0.9, II сурагч тэнцэх магадлал 0.85 бол
- хоёулаа тэнцэх магадлал $\dfrac{1\fbox{ab}}{200}$
- Яг нэг сурагч тэнцэх магадлал $\dfrac{\fbox{cd}}{50}$
- Ядаж нэг сурагч тэнцэх магадлал $\dfrac{\fbox{efg}}{200}$
Хоёр сурагч Англи хэлний түвшин тогтоох шалгалт өгчээ. Шалгалтад I сурагч тэнцэх магадлал 0.95, II сурагч тэнцэх магадлал 0.8 бол
- хоёулаа тэнцэх магадлал $\dfrac{1\fbox{ab}}{25}$
- Яг нэг сурагч тэнцэх магадлал $\dfrac{\fbox{cd}}{100}$
- Ядаж нэг сурагч тэнцэх магадлал $\dfrac{\fbox{efg}}{1g 0}$
Санамсаргүй үзэгдэл, түүний магадлал
$0,1,\ldots,9$ гэсэн цифр бичсэн 10 ширхэг цаасыг уутанд
хийсэн байв. Сугалж авсан 3-н цаасан дээрх тоонуудыг авсан дарааллаар нь
байрлуулахад 541 гэсэн тоо гарах магадлалыг:
- авсан цаасаа буцааж хийхгүй тохиолдолд, ө.х буцаалтгүй түүврийн үед,
- авсан цаасаа буцааж хийх тохиолдолд буюу буцаалттай түүврийн үед тус тус бод.
Уутанд 12 хар, 10 цагаан бөмбөг байв. Таамгаар авсан 8 бөмбөгөн дотор:
а) 2 хар, 6 цагаан,
б) хар,
в) хар ба цагаан,
г) 3-аас илүүгүй хар,
д) ядаж 3 хар,
е) ядаж 2 хар ба 2 цагаан бөмбөг байх магадлалуудыг тус тус ол.
а) 2 хар, 6 цагаан,
б) хар,
в) хар ба цагаан,
г) 3-аас илүүгүй хар,
д) ядаж 3 хар,
е) ядаж 2 хар ба 2 цагаан бөмбөг байх магадлалуудыг тус тус ол.
35 үсгийг нэг нэгээр нь бичсэн 35 цаасыг уутанд хийсэн байв. Буцаалттай
түүврийн үед авсан 13 цаасан дээрх үсгүүд нь:
а) авсан дарааллаараа, б) дарааллыг анхаараагүй үед "Мөнхбат аварга" гэдэг үгийг
үүсгэж байх магадлалыг ол.
"Дашдондог" гэдэг үгийг үсгүүдийг нэг нэгээр нь жижиг цаасан дээр бичсэн
байв. Цаасуудыг байрлуулахад:
а) "о" үсгүүд зэрэгцэж орсон байх,
б) бүх "д" үсгүүд зэрэгцэж орсон байх,
в) зэрэгцэж орсон адил үсэг байх,
г) бүх "о"-ууд ба бүх "д"-үүд зэрэгцсэн байх,
д) адил үсгүүд нь зэрэгцэж ороогүй байх магадлалуудыг тус тус ол.
а) "о" үсгүүд зэрэгцэж орсон байх,
б) бүх "д" үсгүүд зэрэгцэж орсон байх,
в) зэрэгцэж орсон адил үсэг байх,
г) бүх "о"-ууд ба бүх "д"-үүд зэрэгцсэн байх,
д) адил үсгүүд нь зэрэгцэж ороогүй байх магадлалуудыг тус тус ол.
$A,B$ хоёр бие биеэс нууж 1-9 хүртэлх тоонуудаас нэг нэгийг цаасан дээр
яг зэрэг бичиж тоглож байна. Хэрэв бичсэн хоёр тооны нийлбэр тэгш бол $A$,
сондгой бол $B$ хожно. $A$ хожих магадлалыг ол.
Хайрцагт 10 эдлэл байв. Эдлэл тус бүрийг авах магадлал адил бол таамгаар
авсан хэдэн эдлэлийн тоо тэгш байх магадлалыг ол.
Микроскопоор 4 эсийг ажиглаж байв. Ажиглалтын явцад тэдгээрийн аль нь ч
хуваагдаж ч болно, хуваагдахгүй ч байж болох байв.
$A=$"яг нэг эс хуваагдав",
$B=$"ядаж нэг эс хуваагдав",
$C=$"хоёроос цөөнгүй эс хуваагдав",
$D=$"яг хоёр эс хуваагдав",
$M=$"яг гурван эс хуваагдав",
$F=$"бүх дөрвөн эс хуваагдав" гэсэн үзэгдлүүд бол:\\ а) $\overline F$, б) $A\cup B$, в) $A\cap B$, г) $B\cup C$, д) $B\cap C$, е) $(D\cup M)\cup F$,\\ ё) $B\cap F$ үзэгдлүүдийг үгээр бичиж, \hfill ж) $B\cap F=C\cap F$,\\ з) $B\cap C=D$ тэнцлүүд үнэн эсэхэд хариул.
$A=$"яг нэг эс хуваагдав",
$B=$"ядаж нэг эс хуваагдав",
$C=$"хоёроос цөөнгүй эс хуваагдав",
$D=$"яг хоёр эс хуваагдав",
$M=$"яг гурван эс хуваагдав",
$F=$"бүх дөрвөн эс хуваагдав" гэсэн үзэгдлүүд бол:\\ а) $\overline F$, б) $A\cup B$, в) $A\cap B$, г) $B\cup C$, д) $B\cap C$, е) $(D\cup M)\cup F$,\\ ё) $B\cap F$ үзэгдлүүдийг үгээр бичиж, \hfill ж) $B\cap F=C\cap F$,\\ з) $B\cap C=D$ тэнцлүүд үнэн эсэхэд хариул.
Дараахь үзэгдлүүдийн эсрэг үзэгдлүүдийг нэрлэ.\\
а) Туршилт: 2 мөнгө хаях. $A=$"2 сүлд буув",\\
б) Туршилт: байг 5 буудав. $A=$"2-оос илүүгүй онов",\\
в) Туршилт: шатар тоглов. $A=$"Бат хожив".
$A,B$ үзэгдлүүд явагдсан ба $C$ үзэгдэл явагдаагүй бол дараахь үзэгдлүүд
явагдсан уу:\\ $A\cup(B\cap C)$, $(A\cup B)\cap C$, $(A\cap B)\cup C$, $A\cap B\cap C$.
Дараах үзэгдлүүд эсрэг үзэгдлүүд мөн үү?
а) $A={}$"2 оронтой тоо нь тэгш цифрүүдээр бичигдсэн", $B={}$"2 оронтой тоо нь сондгой цифрүүдээр бичигдсэн",
б) $A={}$"Манай ангийн бүх сурагчид биеийн тамир сонирхдог", $B={}$"Манай ангийн бүх сурагчид биеийн тамир сонирхдоггүй". Энд буй $A$, $B$ үзэгдэл тус бүрийн эсрэгийг нь үгээр томъёол.
а) $A={}$"2 оронтой тоо нь тэгш цифрүүдээр бичигдсэн", $B={}$"2 оронтой тоо нь сондгой цифрүүдээр бичигдсэн",
б) $A={}$"Манай ангийн бүх сурагчид биеийн тамир сонирхдог", $B={}$"Манай ангийн бүх сурагчид биеийн тамир сонирхдоггүй". Энд буй $A$, $B$ үзэгдэл тус бүрийн эсрэгийг нь үгээр томъёол.
$5$ шагай, $3$ зоосыг зэрэг орхих туршилт явуулжээ. Бүх боломжит эгэл үзэгдлийн тоог ол.
A. $C_5^4C_3^2$
B. $4^5\cdot2^3$
C. $5^4\cdot 2^3$
D. $5^4\cdot3^2$
E. $2^8$
Дараах үзэгдлүүдийн аль нь гарцаагүй үзэгдэл вэ?
A. Шоо орхиход тэгш тоо буух
B. 2 мөнгө орхиход ижил талаар тусах
C. Шидсэн чулуу эргэж унах
D. Анх таарсан хүн эрэгтэй байх
E. Нар баруунаас гарах
Дараах үзэгдлүүдийн аль нь боломжгүй үзэгдэл вэ?
A. Зоос хаяхад тоогоор буух
B. Шоо орхиход сүлд буух
C. Бороо орох
D. Сар хиртэх
E. Нар баруунаас гарах
Хоёр шоон дээр туссан тоонуудын нийлбэр 1, 7, 8, 10, 11 байх үзэгдлийн аль нь илүү магадлалтай вэ?
A. 1
B. 7
C. 8
D. 10
E. 11
Хайрцагт 12 цагаан, 8 хар бөмбөг байв. Таамгаар авсан хоёр бөмбөг хоёул цагаан байх, хоёулаа өөр өнгөтэй байх магадлалууд аль нь вэ?
A. $\dfrac{C_{12}^2}{C_{20}^2}$ ба $\dfrac{C_{12}^1\cdot C_{8}^1}{C_{20}^2}$
B. $\dfrac{C_{12}^2}{C_{20}^2}$ ба $\dfrac{C_{8}^2}{C_{20}^2}$
C. $\dfrac{12}{20}$ ба $\dfrac{8}{20}$
D. $\dfrac{A_{12}^2}{A_{20}^2}$ ба $\dfrac{A_{8}^2}{A_{20}^2}$
E. $\dfrac{A_{12}^2}{A_{20}^2}$ ба $\dfrac{A_{12}^1\cdot A_{8}^1}{A_{20}^2}$
ДАШДОНДОГ гэдэг үгийн үсгүүдийг нэг нэгээр нь жижиг цаасан дээр бичсэн байв. Цааснуудыг нэг эгнээнд байрлуулахад бүх Д үсгүүд нэг дор дараалж орсон байх магадлалыг ол.
A. $\dfrac{1}{12}$
B. $\dfrac{1}{9}$
C. $\dfrac{2}{9}$
D. $\dfrac{1}{10}$
E. $\dfrac{1}{51}$
Хоёр шоог зэрэг орхих туршилтын туссан нүднүүдийн нийлбэр ба давтамжаар дараах хүснэгтийг үүсгэе.
$P(x)$-ээр $x$ үзэгдлийн магадлалыг тэмдэглэвэл:
I. $P(4)=\dfrac{1}{\fbox{de}}$
II. $P(3\le x\le 8)=\dfrac{\fbox{fg}}{36}$
III. $P(x\le 4)=\dfrac{1}{\fbox{h}}$
| Туссан нүдний тоо (x) | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Давтамж | 1 | 2 | 3 | 4 | $\fbox{a}$ | $\fbox{b}$ | 5 | $\fbox{c}$ | 3 | 2 | 1 |
$P(x)$-ээр $x$ үзэгдлийн магадлалыг тэмдэглэвэл:
I. $P(4)=\dfrac{1}{\fbox{de}}$
II. $P(3\le x\le 8)=\dfrac{\fbox{fg}}{36}$
III. $P(x\le 4)=\dfrac{1}{\fbox{h}}$
Хоёр шоог зэрэг орхих туршилтын туссан нүднүүдийн нийлбэр ба давтамжаар дараах хүснэгтийг үүсгэе.
$P(x)$-ээр $x$ үзэгдлийн магадлалыг тэмдэглэвэл:
I. $P(7)=\dfrac{1}{\fbox{d}}$
II. $P(3\le x\le 7)=\dfrac{\fbox{e}}{\fbox{f}}$
III. $P(x\le 6)=\dfrac{\fbox{g}}{\fbox{1h}}$
|
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Давтамж | 1 | 2 | 3 | 4 | $\fbox{a}$ | $\fbox{b}$ | 5 | $\fbox{c}$ | 3 | 2 | 1 |
I. $P(7)=\dfrac{1}{\fbox{d}}$
II. $P(3\le x\le 7)=\dfrac{\fbox{e}}{\fbox{f}}$
III. $P(x\le 6)=\dfrac{\fbox{g}}{\fbox{1h}}$
Хоёр шоог зэрэг орхих туршилтын туссан нүднүүдийн нийлбэр ба давтамжаар дараах хүснэгтийг үүсгэе.
$P(x)$-ээр $x$ үзэгдлийн магадлалыг тэмдэглэвэл:
I. $P(5)=\dfrac{1}{\fbox{d}}$
II. $P(2\le x\le 4)=\dfrac{\fbox{e}}{\fbox{f}}$
III. $P(x\ge 9)=\dfrac{\fbox{g}}{\fbox{1h}}$
| Туссан нүдний тоо (x) | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Давтамж | 1 | 2 | $\fbox{a}$ | 4 | 5 | $\fbox{b}$ | 5 | $\fbox{c}$ | 3 | 2 | 1 |
$P(x)$-ээр $x$ үзэгдлийн магадлалыг тэмдэглэвэл:
I. $P(5)=\dfrac{1}{\fbox{d}}$
II. $P(2\le x\le 4)=\dfrac{\fbox{e}}{\fbox{f}}$
III. $P(x\ge 9)=\dfrac{\fbox{g}}{\fbox{1h}}$
Хоёр шоог зэрэг орхих туршилтын туссан нүднүүдийн нийлбэр ба давтамжаар дараах хүснэгтийг үүсгэе.
$P(x)$-ээр $x$ үзэгдлийн магадлалыг тэмдэглэвэл:
I. $P(5)=\dfrac{1}{\fbox{d}}$
II. $P(4\le x\le 6)=\dfrac{\fbox{e}}{\fbox{f}}$
III. $P(x\ge 9)=\dfrac{\fbox{g}}{\fbox{1h}}$
| Туссан нүдний тоо (x) | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Давтамж | 1 | 2 | $\fbox{a}$ | 4 | $\fbox{b}$ | 6 | 5 | 4 | $\fbox{c}$ | 2 | 1 |
$P(x)$-ээр $x$ үзэгдлийн магадлалыг тэмдэглэвэл:
I. $P(5)=\dfrac{1}{\fbox{d}}$
II. $P(4\le x\le 6)=\dfrac{\fbox{e}}{\fbox{f}}$
III. $P(x\ge 9)=\dfrac{\fbox{g}}{\fbox{1h}}$
Хоёр шоог зэрэг орхих туршилтын туссан нүднүүдийн нийлбэр ба давтамжаар дараах хүснэгтийг үүсгэе.
$P(x)$-ээр $x$ үзэгдлийн магадлалыг тэмдэглэвэл:
I. $P(7)=\dfrac{1}{\fbox{d}}$
II. $P(9\le x\le 11)=\dfrac{\fbox{e}}{\fbox{f}}$
III. $P(x\ge 10)=\dfrac{\fbox{g}}{\fbox{h}}$
| Туссан нүдний тоо (x) | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Давтамж | 1 | 2 | 3 | 4 | $\fbox{a}$ | $\fbox{b}$ | 5 | $\fbox{c}$ | 3 | 2 | 1 |
$P(x)$-ээр $x$ үзэгдлийн магадлалыг тэмдэглэвэл:
I. $P(7)=\dfrac{1}{\fbox{d}}$
II. $P(9\le x\le 11)=\dfrac{\fbox{e}}{\fbox{f}}$
III. $P(x\ge 10)=\dfrac{\fbox{g}}{\fbox{h}}$
Хоёр шоог зэрэг орхих туршилтын туссан нүднүүдийн нийлбэр ба давтамжаар дараах хүснэгтийг үүсгэе.
$P(x)$-ээр $x$ үзэгдлийн магадлалыг тэмдэглэвэл:
I. $P(5)=\dfrac{1}{\fbox{d}}$
II. $P(4\le x\le 6)=\dfrac{\fbox{e}}{\fbox{f}}$
III. $P(x\ge 9)=\dfrac{\fbox{g}}{\fbox{1h}}$
| Туссан нүдний тоо (x) | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Давтамж | 1 | 2 | $\fbox{a}$ | 4 | $\fbox{b}$ | 6 | 5 | 4 | $\fbox{c}$ | 2 | 1 |
$P(x)$-ээр $x$ үзэгдлийн магадлалыг тэмдэглэвэл:
I. $P(5)=\dfrac{1}{\fbox{d}}$
II. $P(4\le x\le 6)=\dfrac{\fbox{e}}{\fbox{f}}$
III. $P(x\ge 9)=\dfrac{\fbox{g}}{\fbox{1h}}$
Үзэгдлийн магадлал тооцоолохдоо сэлгэмэл, хэсэглэлийн томьёо хэрэглэх
Гэр бүлийн 10 хос хооллож байв. Эндээс 5 хүнийг сугалж аваад ширээ
бүтээлгэхэд тэдний дотор нэг гэр бүлийнхэн ороогүй байх магадлалыг ол.
Үл хамаарах үзэгдлүүд, магадлалын үржвэр
Мөнгө шоо орхих туршилтанд мөнгө сүлдээрээ, шоо 3-т хуваагдах
тоогоор тусах үзэгдлүүд нь үл хамаарах үзэгдлүүд мөн үү?
Мөнгө, шоог орхиход мөнгө сүлдээрээ, шоо тэгш тоогоор тусах үзэгдлүүд нь
үл хамаарах үзэгдлүүд болохыг батал.
Эдлэлийг $k$ ажилчин дараалан боловсруулалт хийж гаргадаг. Ажилчин бүрийн
гологдол гаргах магадлал нь $p$ ба ажилчид бие биеэсээ хамааралгүйгээр
боловсруулалт хийдэг гэвэл гологдолгүй бүтээгдэхүүн гаргах магадлалыг ол.
$A,B$ нь нийцгүй үзэгдлүүд бол үл хамаарах үзэгдлүүд байх нь алба уу?
Нэгэн төрлийн материалаар хийсэн зөв гурвалжин пирамидын гурван талсыг
улаан, ногоон, хар өнгөөр, дөрөв дэх талсыг дээрх гурван өнгөөр алаглуулан
буджээ. Пирамидыг ширээн дээр орхиход ямар өнгөтэй талсаараа унахыг нь сонирхож
байна. $Y=$"улаан өнгөтөй талсаараа унав" гэсэн үзэгдэл гэх мэт бол $Y,H,X$-ууд
хос хосоороо үл хамаарах үзэгдлүүд боловч нийтдээ үл хамаарах үзэгдэл биш гэдгийг батал.
$0.8$ магадлалтай бууддаг 2 хүн зэрэг буудахад ядаж нэг нь байг онохгүй байх магадлалыг ол.
A. $0.64$
B. $0.36$
C. $0.04$
D. $0.96$
E. $0.16$
Автобусны буудал дээр тодорхой чиглэлийн автобусыг 5-аас ихгүй минут хүлээх магадлал $0.82$ бол 4 удаа автобусанд суухад ядаж нэгд нь 5-аас илүү минут хүлээх магадлалыг ол.
A. $0.98$
B. $0.21$
C. $0.55$
D. $0.81$
E. $0.33$
Шагай орхиход морь тусах магадал $0.1$. Нэг шагайг морь тустал нь орхиход 3-аас олонгүй орхилтонд морь тусах магадлалыг ол.
A. $0.271$
B. $0.15$
C. $0.9$
D. $0.4987$
E. $0.5$
Хоёр тамирчин нэг буудалтаар бай онох магадлал харгалзан $0.5$ ба $0.6$ бол тус бүр байг 2 удаа буудахад ядаж нэг нь байг 2 удаа онох магадлалыг ол.
A. $0.376$
B. $0.52$
C. $0.47$
D. $0.584$
E. $0.2$
Шагай орхиход мориор тусах магадлал $0.1$. $2$ шагай ба $2$ шоог нэгэн зэрэг орхиход ядаж нэг морь ба ядаж нэг 6 нүд тусах магадлалыг ол.
A. $\dfrac{203}{3600}$
B. $\dfrac{207}{3600}$
C. $\dfrac{209}{3600}$
D. $\dfrac{211}{3600}$
E. $\dfrac{217}{3600}$
Анчин $0.9$ магадлалтайгаар байг онодог байв. Энэ анчин байг $3$ удаа буудахад ядаж нэг удаа алдах магадлал хэд вэ?
A. $0.36$
B. $0.27$
C. $0.729$
D. $0.271$
E. $0.261$
$0.6$ магадлалтай бууддаг 2 хүн зэрэг буудахад ядаж нэг нь байг онохгүй байх магадлалыг ол.
A. $0.64$
B. $0.36$
C. $0.04$
D. $0.96$
E. $0.86$
Хоёр хүн байг буудаад онох магадлал харгалзан $0.4$, $0.5$ байв. Тэд бие биеэсээ хамаарахгүй нэг, нэг бууджээ. Хоёулаа байг оноогүй байх магадлалыг ол.
A. $0.9$
B. $0.7$
C. $0.3$
D. $0.2$
E. $0.8$
Хоёр довтлогч хаалга уруу өшиглөөд гоол оруулах магадлал нь харгалзан $0.2$ ба $0.3$ байв. Тоглолтын туршид I довтлогч 2 удаа, II довтлогч 1 удаа хаалга уруу өшиглөсөн бол аль нь ч гоол оруулаагүй байх магадлал аль нь вэ?
A. $0.024$
B. $0.048$
C. $0.448$
D. $0.824$
E. $0.700$
Хоёр довтлогч хаалга уруу өшиглөөд гоол оруулах магадлал нь харгалзан $0.2$ ба $0.3$ байв. Тоглолтын туршид I довтлогч 1 удаа, II довтлогч 2 удаа хаалга уруу өшиглөсөн бол аль нь ч гоол оруулаагүй байх магадлал аль нь вэ?
A. $0.032$
B. $0.392$
C. $0.500$
D. $0.724$
E. $0.618$
Хоёр хүн байг буудаад онох магадлал харгалзан $0.5$, $0.6$ байв. Тэд бие биеэсээ хамаарахгүй нэг, нэг бууджээ. Хоёулаа байг оноогүй байх магадлалыг ол.
A. $0.1$
B. $0.8$
C. $1.1$
D. $0.2$
E. $0.3$
Элсэлтийн шалгалтын эсээ нь 250-300 үгтэй байх ёстой. Нийт эсээний $3\%$ нь 250-аас цөөн үгтэй, $5\%$ нь 300-аас олон үгтэй байжээ. Санамсаргүйгээр сонгосон 2 эсээ хоёулаа шаардлага хангасан байх магадлалыг ол. Нийт эсээний тоог хангалттай олон гэж үз.
A. $0.80$
B. $0.64$
C. $0.92$
D. $0.85$
E. $0.76$
$A$, $B$ үзэгдлүүд үл хамаарах бөгөөд $P(A)=0.4$, $P(A\cap B)=0.36$ бол $P(B)=?$
A. $0.32$
B. $0.45$
C. $0.64$
D. $0.80$
E. $0.9$
Хоёр анчин бие биеэсээ хамааралгүйгээр туулайг зэрэг буудав. Хэрэв хоёул оновол туулай алагдана. Тэдний онох магадлал нь 0.8, 0.75 бол
туулай алагдах магадлалыг ол.
A. $\dfrac12$
B. $\dfrac14$
C. $\dfrac25$
D. $\dfrac35$
E. $\dfrac13$
Хоёр тамирчин нэг буудалтаар бай онох магадлал харгалзан $0.4$ ба $0.5$ бол тус бүр байг 2 удаа буудахад ядаж нэг нь байг 2 удаа онох магадлалыг ол.
A. $0.37$
B. $0.52$
C. $0.47$
D. $0.58$
E. $0.25$
Нэгэн шагайг орхиход морь буух магадлал $\dfrac{1}{10}$ байв. Уг шагайг 3 удаа орхиход
- Ядаж нэг удаа морь буух магадлал $1-\Big(\dfrac{\fbox{a}}{10}\Big)^{\fbox{b}}$;
- Яг нэг удаа морь буух магадал $0.\fbox{cde}$;
- Яг хоёр удаа морь буух магадлал $0.0\fbox{fg}$ байна.
Эсрэг үзэгдэл, түүний магадлал
52 ширхэг хөзрөөс 3 ширхэгийг авав. Эдгээр 3 хөзөр дунд 7 эсвэл 8 хөзрийн (дөрвөлжин, бундан, гил, цэцгийн 7 эсвэл 8) ядаж нэг нь байх магадлалыг ол.
A. $1-\dfrac{C_{50}^3}{C_{52}^3}$
B. $\dfrac{C_{50}^3}{C_{52}^3}$
C. $\dfrac{C_{44}^2}{C_{52}^3}$
D. $1-\dfrac{C_{44}^3}{C_{52}^3}$
E. аль нь ч биш.
Хоёр шоог зэрэг хаяхад ядаж нэг нь 3-аас их тоогоор буух магадлалыг ол.
A. $\dfrac14$
B. $\dfrac12$
C. $\dfrac13$
D. $\dfrac34$
E. $\dfrac23$
Дараах үзэгдлүүдийн аль нь эсрэг үзэгдлүүд болж чадах вэ?
A. $A$ дүн авах ба $C$ дүн авах
B. $B$-ээс их дүн авах ба $C$-ээс их дүн авах
C. Сүлд буух ба тоо буух
D. Гурвалжин мохоо байх ба хурц байх
E. Натурал тоо анхны тоо байх ба зохиомол тоо байх
$100$ бүтээгдэхүүнтэй хэсгээс $5$ бүтээгдэхүүн шалгаж ядаж нэг гологдол илэрвэл энэ хэсгийг буцаадаг. Энэ хэсгийн бүтээгдэхүүний $5\%$ нь гологдол байсан бол уг хэсгийг буцаах магадлалыг ол.
A. $1-\dfrac{C_{95}^5}{A_{100}^5}$
B. $\dfrac{A_{100}^1}{A_{100}^5}$
C. $1-\dfrac{C_{95}^5}{C_{100}^5}$
D. $\dfrac{C_{100}^1}{C_{100}^5}$
E. $\dfrac{C_{95}^4}{C_{100}^5}$
$1, 2, 3, 4, 5$ дугаартай хайрцгуудад өөр хоорондоо ялгаагүй 7 ширхэг бөмбөгийг $\fbox{abc}$ янзаар байрлуулж болох ба дурын нэг байрлуулалт авч үзэхэд 5-р хайрцаг хоосон биш байх магадлал $\frac{\fbox{d}}{\fbox{ef}}$ болно.
Хайрцагт 3 цагаан, 4 хар, 5 улаан бөмбөг байв. Таамгаар нэг бөмбөг сугалахад
- Цагаан биш байх магадлал $\dfrac{\fbox{a}}{4}$,
- Хар биш байх магадлал $\dfrac{\fbox{b}}{3}$,
- Улаан биш байх магадлал $\dfrac{\fbox{c}}{\fbox{de}}$
$1, 2, 3, 4, 5$ дугаартай хайрцгуудад өөр хоорондоо ялгаагүй 7 ширхэг бөмбөгийг $\fbox{abc}$ янзаар байрлуулж болох ба дурын нэг байрлуулалт авч үзэхэд 5-р хайрцаг хоосон биш байх магадлал $\frac{\fbox{d}}{\fbox{ef}}$ болно.