Монгол Бодлогын Сан

Тэгш өнцөгт гурвалжны периметр 6 ба нэг өнцгийн тангенс нь

$2.4$ бол энэ гурвалжныг багтаасан болон энэ гурвалжинд багтсан тойргийн радиусуудын нийлбэрийг ол.

A.

$1.5$ B.

$1.6$ C.

$1.7$ D.

$1.8$ E.

$1.9$

$ABC$ гурвалжныг багтаасан тойргийн радиус

$2\sqrt{3}$ ба өндрүүдийн сууриар үүсгэгдэх гурвалжны периметр 9 бол

$ABC$ гурвалжны талбайг ол.

A.

$18\sqrt{3}$ B.

$9\sqrt{3}$ C.

$36\sqrt{3}$ D.

$18$ E.

$36$

Зөв гурвалжныг багтаасан тойргийн радиус

$2\sqrt3$ бол талын уртыг ол.

A.

$3$ B.

$4$ C.

$5$ D.

$6$ E.

$7$

Синусын теорем

$ABC$ гурвалжныг багтаасан тойргийн радиус

$2$ ба

$\sin\alpha=\dfrac14$ бол

$BC$ талын уртыг ол.

A. 1 B. 2 C. 4 D. 8 E.

$\dfrac14$

Синусын теорем

$ABC$ гурвалжны

$AB=3$ ,

$\sin\measuredangle ACB=30^\circ$ бол

$ABC$ гурвалжныг багтаасан тойргоор үүсэх дугуйн талбай хэдтэй тэнцүү вэ?

A.

$4\pi$ B.

$5\pi$ C.

$8\pi$ D.

$9\pi$ E.

$16\pi$

Гурвалжны өндрүүдийн урвуугийн нийлбэр

Гурвалжны гурван өндрийн урвуу хэмжигдэхүүний нийлбэр ямар байх вэ?

$r$ ,

$R$ нь харгалзан багтсан ба багтаасан тойргийн радиус

A.

$\dfrac1r$ B.

$\dfrac1R$ C.

$\dfrac{R}{r^2}$ D.

$\dfrac{r^2}{R}$ E. Аль нь ч биш

Орто төв хүртэлх зай нь багтаасан тойргийн радиус болох гурвалжин

$ABC$ гурвалжны өндрүүдийн огтлолцол (ортотөв)

$H$ , багтаасан тойргийн радиус

$R$ ,

$CH=R$ байсан бол

$\measuredangle BCA$ ямар хэмжээтэй байх вэ?

A.

$30^\circ$ B.

$75^\circ$ C.

$45^\circ$ D.

$60^\circ$ E.

$90^\circ$

Бодлого №7706

$ABC$ гурвалжны

$A,B$ хоёр оройгоос ортотөв хүртэлх зай

$R$ ,

$\sqrt2R$ бөгөөд

$R$ нь багтаасан тойргийн радиус бол

$\measuredangle BCA$ аль нь вэ?

A.

$30^\circ$ B.

$60^\circ$ C.

$75^\circ$ D.

$120^\circ$

Бодлого №7716

$ABC$ гурвалжинд багтсан тойрог

$BC$ ,

$CA$ ,

$AB$ талыг харгалзан

$A_1$ ,

$B_1$ ,

$C_1$ цэгт шүргэжээ. Хэрэв

$A$ оройгоос өндрүүдийн огтлолцол хүртэлх зай багтаасан тойргийн радиустай тэнцүү бол

$\begin{array}{c} [-7mm]\smile [-2mm] C_1A_1B_1\end{array}$ ямар байх вэ?

A.

$220^\circ$ B.

$240^\circ$ C.

$230^\circ$ D.

$210^\circ$

Бодлого №7724

$ABC$ гурвалжны

$AH_1$ ,

$BH_2$ өндрүүд

$H$ цэгт огтлолцжээ. Хэрэв дотоод өнцгүүд нь

$\alpha,\beta,\gamma$ , багтаасан тойргийн радиус

$R$ бол

$AH\cdot HH_1$ аль нь вэ?

A.

$4R^2\cos\alpha\cos\beta\cos\gamma$ B.

$3R^2\sin\alpha\cos\beta\cos\gamma$ C.

$2R^2\cos\alpha\sin\beta\sin\gamma$ D.

$R^2\sin\alpha\sin\beta\sin\gamma$

Бодлого №7725

$ABC$ гурвалжныг багтаасан тойргийн төв

$O$ , радиус

$R$ ,

$A$ оройн дотоод өнцөг

$60^\circ$ бол

$O$ цэгээс

$BC$ тал хүртэлх зай аль нь вэ?

A.

$\frac R5$ B.

$\frac R4$ C.

$\frac R3$ D.

$\frac R2$

Бодлого №7726

$R$ радиустай тойрогт багтсан

$ABC$ гурвалжны

$AH_1$ өндрийн үргэлжлэл багтаасан тойрогтой

$D$ цэгт огтлолцжээ. Хэрэв орто төв нь

$H$ ,

$\measuredangle ABC=\beta$ ,

$\measuredangle BCA=\gamma$ бол

$HD$ -ийн урт аль вэ?

A.

$4R\cos\beta\cos\gamma$ B.

$4R\sin\beta\sin\gamma$ C.

$3R\sin\beta\sin\gamma$ D.

$3R\cos\beta\cos\gamma$

Бодлого №7735

$ABC$ гурвалжны

$A$ оройн дотоод өнцгийн биссектрисийн үргэлжлэл багтаасан тойрогтой

$D$ цэгт огтлолцжээ. Багтсан тойргийн төвөөс

$D$ хүртэлх зай багтаасан тойргийн радиустай тэнцүү бол

$A$ орой дахь дотоод өнцөг хэдэн градус вэ?

A.

$120^\circ$ B.

$30^\circ$ C.

$150^\circ$ D.

$60^\circ$

Бодлого №7736

$R$ радиустай тойрогт багтсан гурвалжны

$A$ оройн дотоод өнцгийн биссектрис багтаасан тойрогтой

$D$ цэгт огтлолцжээ. Хэрэв

$BC$ тал багтсан тойргийн төв

$P$ цэгээс

$150^\circ$ өнцгөөр харагдах бол

$PD$ хэрчмийн урт аль нь вэ?

A.

$\dfrac{R}{3}$ B.

$\sqrt3R$ C.

$\dfrac23R$ D.

$\sqrt2R$ E.

$\dfrac32R$

Бодлого №7738

$ABC$ гурвалжны

$BC$ талын медианы үргэлжлэл багтаасан тойрогтой

$D$ цэгт огтлолцсон. Хэрэв медиануудын огтлолцол

$M$ ,

$S_{ABC}:S_{DBC}=3:5$ бол

$MBC$ ,

$DBC$ хоёр гурвалжны

$M,D$ оройгоос татсан өндрүүдийн харьцаа ямар байх вэ?

A.

$3:8$ B.

$1:5$ C.

$2:5$ D.

$1:3$

Тэгш өнцөгт гурвалжныг багтсан ба багтаасн тойргийн радиус

Тэгш өнцөгт гурвалжинд багтсан тойргийн радиус 4, гипотенузэд буусан өндөр 9 бол багтаасан тойргийн радиус хэд вэ?

A.

$12$ B.

$14$ C.

$16$ D.

$18$ E.

$20$

ЭЕШ 2011 C №17

Тэгш өнцөгт гурвалжны катетууд

$2:3$ харьцаатай ба талбай нь

$156$ кв.нэгж бол түүнийг багтаасан дугуйн талбай хэдэн кв.нэгж вэ?

A.

$196\pi$ B.

$169\pi$ C.

$225\pi$ D.

$289\pi$ E.

$121\pi$

Гурвалжны орто төв

$ABC$ гурвалжны хувьд

$\measuredangle BAC=\alpha$ ба багтаасан тойргийн радиус нь

$R$ бол

$A$ оройгоос гурвалжны ортоцентр

$H$ хүртэлх зай аль нь вэ?

A.

$R\cos\alpha$ B.

$R\sin\alpha$ C.

$R\sin2\alpha$ D.

$2R\sin\alpha$ E.

$2R\cos\alpha$

Биссектрис

$ABC$ гурвалжныг багтаасан тойргийн радиус

$6$ ,

$\angle A=70^\circ$ ,

$\angle B=30^\circ$ бол

$\angle C$ -ийн биссектрисийн урт аль нь вэ?

A.

$3$ B.

$6$ C.

$8$ D.

$9$ E.

$10$

$ABC$ гурвалжныг багтаасан тойргийн радиус

$5$ ,

$\sin\angle BAC=\dfrac35$ бол

$ABC$ гурвалжны талбай хамгийн ихдээ хэдтэй тэнцүү байх вэ?

A.

$6$ B.

$20$ C.

$27$ D.

$50$ E.

$100$

$ABC$ гурвалжныг багтаасан тойргийн радиус

$10$ ,

$\sin\angle BAC=\dfrac45$ бол

$ABC$ гурвалжны талбай хамгийн ихдээ хэдтэй тэнцүү байх вэ?

A.

$48$ B.

$64$ C.

$100$ D.

$128$ E.

$256$

Зөв гурвалжны оройгоос шулуун хүртэлх зайн квадратуудын нийлбэр

Зөв

$ABC$ гурвалжин багтаасан 2 см радиустай тойргийн төвийг дайрсан шулуун

$AB$ ,

$AC$ хоёр талыг

$P$ ,

$Q$ цэгт огтолжээ. Хэрэв гурвалжны оройнуудаас

$PQ$ шулуун хүртэлх зайн квадратуудын нийлбэр

$PQ$ шулуунаас хамаардаггүй бол тэр нийлбэрийг ол.

A. 6 B. 9 C. 12 D. 8 E. 10

Синусын теорем

$ABC$ гурвалжныг багтаасан тойргийн радиус

$2$ ба

$\sin\alpha=\dfrac14$ бол

$BC$ талын уртыг ол.

A. 1 B. 2 C. 4 D. 8 E.

$\dfrac14$

Зөв гурвалжныг багтаасан тойргийн радиус

$2\sqrt3$ бол талын уртыг ол.

A.

$3$ B.

$4$ C.

$5$ D.

$6$ E.

$7$

Тэгш өнцөгт гурвалжныг багтсан ба багтаасн тойргийн радиус

Тэгш өнцөгт гурвалжинд багтсан тойргийн радиус 8, гипотенузэд буусан өндөр 18 бол багтаасан тойргийн радиус хэд вэ?

A.

$24$ B.

$28$ C.

$32$ D.

$36$ E.

$40$

ЭЕШ 2020, B23

$AD$ ,

$BC$ суурьтай

$ABCD$ трапецийн

$A$ ба

$B$ оройн биссектрисүүдийн огтлолцлын цэг

$K$ байв.

$ABK$ гурвалжныг багтаасан тойргийн радиус

$R=5$ бол

$AB$ талын уртыг ол.

A.

$10$ B.

$2\sqrt{5}$ C.

$5$ D.

$25$ E.

$20$

ЭЕШ сорилго №1А, Бодлого №23

$AD$ ,

$BC$ суурьтай

$ABCD$ трапецийн

$A$ ба

$B$ оройн биссектрисүүдийн огтлолцлын цэг

$K$ байв.

$AB$ талын урт

$20$ бол

$ABK$ гурвалжныг багтаасан тойргийн радиусыг ол.

A.

$10$ B.

$2\sqrt{5}$ C.

$5$ D.

$25$ E.

$20$

ЭЕШ 2020, A23

$AD$ ,

$BC$ суурьтай

$ABCD$ трапецийн

$A$ ба

$B$ оройн биссектрисүүдийн огтлолцлын цэг

$K$ байв.

$ABK$ гурвалжныг багтаасан тойргийн радиус

$R=3$ бол

$AB$ талын уртыг ол.

A.

$3$ B.

$2\sqrt{3}$ C.

$6$ D.

$9$ E.

$12$

$ABC$ гурвалжны талууд

$AB=2$ ,

$AC=3$ ,

$BC=4$ ба

$AM_1$ медианы үргэлжлэл уг гурвалжныг багтаасан тойргийг

$A_1$ цэгт огтолдог гэе.

$M_1A_1=\dfrac{\sqrt{2}\fbox{a}}{\sqrt{\fbox{b}}}$ ба

$A_1BC$ гурвалжны периметр нь

$\fbox{c}+2\sqrt{\fbox{de}}$ байна. Мөн

$A_1BC$ гурвалжны талбай

$\dfrac{\fbox{f}\sqrt{\fbox{gh}}}{\fbox{i}}$ болно.

$ABC$ гурвалжны талууд

$AB=4$ ,

$AC=5$ ,

$BC=6$ ба

$AM$ медианы үргэлжлэл уг гурвалжныг багтаасан тойргийг

$A_1$ цэгт огтолдог гэе.

$MA_1=\dfrac{\fbox{a}}{\fbox{bc}}\sqrt{46}$ ба

$A_1C$ талын урт

$\dfrac{\fbox{de}}{\fbox{fg}}\sqrt{\fbox{46}}$ байна. Мөн

$A_1BC$ гурвалжны талбай

$\dfrac{\fbox{hij}}{46}\sqrt{7}$ болно.

Бодлого №7903

$ABC$ гурвалжны талууд

$AB=5$ ,

$BC=7$ ба

$\cos \alpha=-\dfrac{1}{5}$ бол

$AC=\fbox{a}$ ,

$S_{ABC}=4\sqrt{\fbox{b}}$ болно. Мөн уг гурвалжинд багтсан тойргийн радиус

$\sqrt{\fbox{c}}/\fbox{d}$ , багтсан ба багтаасан тойргийн радиусуудын харьцаа

$\displaystyle\dfrac{12}{\fbox{ef}}$ ,

$AL$ биссектриссийн урт

$\displaystyle \sqrt{10}\dfrac{\fbox{g}}{\fbox{h}}$ байна.

Бодлого №7904

$ABC$ гурвалжны талууд

$AC=7$ ,

$BC=9$ ба

$\cos \beta =\dfrac{2}{3}$ ,

$AB< AC$ бол

$AB=\fbox{a}$ ,

$ABC$ гурвалжныг багтаасан тойргийн радиус

$\dfrac{\fbox{bc}\sqrt{5}}{10}$ ,

$\sin \alpha =\dfrac{\fbox{d}\sqrt{5}}{\fbox{e}}$ ба багтсан тойргийн радиус

$\fbox{f}\sqrt{5}/5$ болно. Энэхүү тойрог дээр

$A$ ,

$D$ цэгүүд

$BC$ талын

$2$ талд байхаар авахад

$BD=CD$ бол

$BD=\fbox{g}\sqrt{70}/\fbox{hi}$ байна.

Бодлого №7975

$ABC$ гурвалжныг багтаасан тойргийн төвийг

$O$ гэе.

$\measuredangle ABC=30^\circ$ ,

$\measuredangle ACB =20^\circ$ үед

$\measuredangle OBC=\fbox{ab}^\circ$ ,

$\measuredangle BOC=\fbox{cde}^\circ$ байна.

$ABC$ гурвалжинд багтсан тойргийн төвийг

$I$ гээд

$\measuredangle ABC=70^\circ$ ,

$\measuredangle ACB=60^\circ$ гэе.

$AI$ шулуун

$BC$ талыг

$D$ цэгээр огтолдог бол

$\measuredangle ADB =\fbox{fg} ^\circ$ ,

$\measuredangle CID=\fbox{hi}^\circ$ байна.

Бодлого №7976

$ABC$ гурвалжныг багтаасан тойргийн төвийг $O$ гэе. $\measuredangle ACB=40^\circ$ , $\measuredangle OAC =30^\circ$ үед $\measuredangle OAB= \fbox{ab}^\circ$ , $\measuredangle OBC= \fbox{cd}^\circ$ байна.
$ABC$ гурвалжинд багтсан тойргийн төвийг $I$ гээд $\measuredangle ABC=30^\circ$ , $\measuredangle ACB=100^\circ$ гэе. $IC$ шулуун $AB$ талыг $D$ цэгээр огтолдог бол $\measuredangle BID =\fbox{ef} ^\circ$ , $\measuredangle AIC=\fbox{ghi}^\circ$ байна.

Тойрогт багтсан зөв гурвалжин

Тойрогт

$5$ талтай

$ABC$ зөв гурвалжин багтжээ. Уг тойргийн

$\measuredangle BAC$ өнцөгт тулсан нум дээр

$P$ цэг авчээ.

$\measuredangle ACP =\theta$ бол

$PA+PB=\fbox{ab}\sin \Big(\theta-\dfrac{\pi}{\fbox{c}}\Big)$ болох ба

$S_{PAC}=\dfrac{\fbox{de}}{\sqrt{\fbox{f}}}\sin \Big(\dfrac{\fbox{g}}{\fbox{h}}\pi -\theta\Big)\sin \theta$ байна.

ЭЕШ 2020, B40

$R=6$ радиустай тойрогт багтсан

$ABCDE$ таван өнцөгтийн

$AB=6\sqrt{2}$ ,

$\measuredangle ABE=45^\circ$ ,

$\measuredangle EBD=30^\circ$ ба

$BC=CD$ бол таван өнцөгтийн талбайг ол.

Бодолт. Синусын теоремоор

$AE=2R\sin45^\circ$ гэдгээс

$AE=6\sqrt{\fbox{a}}$ . Иймд

$ABE$ гурвалжны талбай

$S_1=3\fbox{b}$ . Цаашилбал

$\measuredangle BDE=\fbox{c}0^\circ$ гэдгээс

$BD=6\sqrt{\fbox{d}}$ ,

$DE=\fbox{e}$ . Иймээс

$BDE$ гурвалжны талбай

$S_2=18\sqrt{\fbox{d}}$ . Харин

$BCDE$ дөрвөн өнцөгт тойрогт багтсан гэдгээс

$C$ оройн өнцгийг тооцоолж болно. Иймд

$BCD$ гурвалжны өндөр

$CF=\fbox{f}$ ба түүний талбай

$S_3=9\sqrt{\fbox{g}}$ . Эдгээрээс таван өнцөгтийн талбай

$S=S_1+S_2+S_3$ болно.

ЭЕШ 2020, A40

$R=4$ радиустай тойрогт багтсан

$ABCDE$ таван өнцөгтийн

$AB=4\sqrt{2}$ ,

$\measuredangle ABE=45^\circ$ ,

$\measuredangle EBD=30^\circ$ ба

$BC=CD$ бол таван өнцөгтийн талбайг ол.

Бодолт. Синусын теоремоор

$AE=2R\sin45^\circ$ гэдгээс

$AE=4\sqrt{\fbox{a}}$ . Иймд

$ABE$ гурвалжны талбай

$S_1=1\fbox{b}$ . Цаашилбал

$\measuredangle BDE=\fbox{c}0^\circ$ гэдгээс

$BD=4\sqrt{\fbox{d}}$ ,

$DE=\fbox{e}$ . Иймээс

$BDE$ гурвалжны талбай

$S_2=8\sqrt{\fbox{d}}$ . Харин

$BCDE$ дөрвөн өнцөгт тойрогт багтсан гэдгээс

$C$ оройн өнцгийг тооцоолж болно. Иймд

$BCD$ гурвалжны өндөр

$CF=\fbox{f}$ ба түүний талбай

$S_3=4\sqrt{\fbox{g}}$ . Эдгээрээс таван өнцөгтийн талбай

$S=S_1+S_2+S_3$ болно.

Бодлого №2319

$ABC$ гурвалжинд багтсан тойрог

$AB$ талыг

$D$ цэгээр,

$BC$ талыг

$E$ цэгээр шүргэнэ. Хэрэв

$BD:AD=1:2$ ,

$BE:CE=1:3$ бол гурвалжны өнцгүүдийг ол.

Бодлого №2323

$18$ см периметртэй гурвалжны багтсан тойрогт суурьтай нь параллель шүргэгч шулуун татав. Энэ шулууны хоёр хажуу талын хооронд үүсэх хэрчмийн урт

$2$ см бол гурвалжны суурийн уртыг ол.

Бодлого №2337

Гуралжинд

$4$ радиустай тойрог багтав. Хэрэв нэг тал нь шүргэлцлийн цэгээр

$6$ ,

$8$ -урттай хэсгүүдэд хуваагдсан бол гурвалжны талуудын уртыг ол.

Бодлого №2359

$ABC$ гурвалжинд

$BE$ биссектрис татсан ба багтсан тойргийн төв

$O$ нь түүнийг

$BO:OE=2$ харьцаанд хуваана. Хэрэв

$AC=7$ ,

$BC=8$ бол

$AB$ -г ол.

Бодлого №2361

$AB=8$ ,

$BC=6$ ,

$AC=4$ талуудтай гурвалжинд тойрог багтав. Тойрог

$AB$ болон

$AC$ талуудыг харгалзан

$D, E$ цэгүүдээр шүргэдэг бол

$DE$ хэрчмийн уртыг ол.

Бодлого №2365

$AB$ диаметртэй тойргийн гадна орших

$M$ цэг нь

$AB$ цэгтэй холбогджээ.

$MA$ ба

$MB$ хэрчмүүд нь тойргийг харгалзан

$C$ ба

$D$ цэгүүдээр огтлоно.

$AMB$ гурвалжинд багтсан тойргийн талбай нь

$CMD$ гурвалжинд багтсан тойргийн талбайгаас 4 дахин их. Хэрэв нэг өнцөг нь нөгөөгөөс 2 дахин их гэж үзвэл

$AMB$ гурвалжны өнцгүүдийг ол.

Бодлого №2381

$AB=12$ см,

$BC=15$ см,

$AC=9$ см талуудтай

$ABC$ гурвалжинд

$BB_{1}$ биссектрис татав. Багтсан тойрог

$AB$ талтай шүргэлцэх цэг нь

$C_1$ .

$BB_{1}$ ,

$CC_{1}$ хэрчмүүд

$P$ цэгт огтлолцох ба

$AP$ -ийн үргэлжлэл

$BC$ -тэй

$A_{1}$ цэгт огтлолцох бол

$AP:PA_1$ -г ол.

Бодлого №2385

$2a$ суурьтай,

$h$ өндөртэй адил хажуут гурвалжин өгөгдөв. Багтсан тойргийг шүргүүлэн суурьтай нь параллель шулуун татжээ. Тойргийн радиус ба шүргэгч шулууны талуудын хооронд үүсэх хэрчмийн уртыг ол.

Бодлого №2389

Адил хажуут гурвалжны суурийн өнцөг нь

$\alpha$ . Суурьт буулгасан өндрийн хэмжээ нь багтсан тойргийн радиусаас

$m$ -ээр их бол багтаасан тойргийн радиусыг ол.

Бодлого №2390

Адил хажуут

$KLM$ (

$KL=LM$ ) гурвалжны

$KLM$ өнцөг нь

$\varphi$ .

$KLM$ гурвалжны багтсан ба багтаасан тойргуудын радиусын харьцааг ол.

Бодлого №2391

$a$ суурьтай адил хажуут гурвалжинд

$R$ радиустай тойрог багтав. Гурвалжны периметрийг ол.

Бодлого №2395

$a$ суурьтай,

$b$ хажуутай адил хажуут гурвалжинд квадрат багтсан ба түүний 2 өнцөг нь суурин дээр, 2 өнцөг нь хоёр хажуу талууд дээр орших бол квадратын талыг ол.

Бодлого №2398

Өндөр нь

$8$ , суурийг хажуу талд харьцуулсан харьцаа нь

$6:5$ байх адил хажуут гурвалжин өгөгдөв. Багтсан тойргийн радиусыг ол.

Бодлого №2400

Адил талт

$ABC$ гурвалжинд багтсан тойргийг шүргүүлэн

$AB$ талтай параллельиар

$MN$ хэрчим татав (

$M, N$ цэгүүд

$AC, BC$ талууд дээр оршино). Хэрэв

$AB=18$ бол

$AMNB$ трапецийн периметрийг ол.

Бодлого №2407

Адил хажуут гурвалжинд

$r$ радиустай тойрог багтав. Багтсан тойрог нь суурьт буулгасан өндрийг оройг талаас

$1:2$ харьцаатай хэсгүүдэд хуваана. Гурвалжны талбайг ол.

Бодлого №2412

Адил хажуут гурвалжны суурь нь

$12$ , багтсан тойргийн радиус нь

$3$ бол талбайг ол.

Бодлого №2432

Адил хажуут гурвалжны суурийн урт

$12$ , хажуу талуудын урт

$10$ . Багтсан тойргийн хоёр хажууг шүргэх цэгүүдийн хоорондох зайг ол.

Бодлого №2434

Адил хажуут гурвалжны суурийн урт

$6$ см, хажуу талууд нь

$5$ см. Уг гурвалжинд багтсан тойргийн радиусыг ол.

Бодлого №2435

$CE$ нь адил хажуут

$ABC$ (

$AC=CB$ ) гурвалжны өндөр.

$ABC$ гурвалжинд багтсан тойргийн төв

$O$ нь

$CE$ хэрчмийг

$CO=13$ ,

$OE=5$ байх хэрчмүүдэд хуваах бол гурвалжны талуудыг ол.

Бодлого №2439

$2\sqrt3$ см радиустай тойргийн төвийг дайруулан түүнд багтсан зөв гурвалжны талтай параллель шулуун татав. Уг шулууны гурвалжны талуудын хооронд үүсэх хэрчмийн уртыг ол.

Бодлого №2442

Тэгш өнцөгт гурвалжны катетуудын ба гипотенуз дээрх проекцүүд нь

$m=9$ см ба

$n=16$ см бол гурвалжинд багтсан тойргийн талбайг ол.

Бодлого №2443

Тэгш өнцөгт гурвалжинд багтсан тойргийн аль нэг катетыг шүргэх цэг нь уг катетаа

$m, n$ урттай хэрчимүүдэд хуваасан бол гурвалжны талуудыг ол.

Бодлого №2444

Тэгш өнцөгт гурвалжны багтсан тойргийн шүргэлтийн цэг гипотенузыг

$m=2$ см,

$n=3$ см урттай хоёр хэрчимд хуваав. Гурвалжинд багтсан тойргийн радиусыг ол.

Бодлого №2446

Тэгш өнцөгт гурвалжны нэг катет нь

$15$ см. Нөгөө катетын гипотенуз дээрх проекц нь

$16$ см бол гурвалжинд багтсан тойргийн радиусыг ол.

Бодлого №2448

Тэгш өнцөгт гурвалжны катетуудын нийлбэр

$14$ см, түүнийг багтаасан тойргийн радиус

$5$ см бол өгсөн гурвалжинд багтсан тойргийн талбайг ол.

Бодлого №2464

Тэгш өнцөгт гурвалжны катетууд нь

$a$ ба

$b$ байв. Уг гурвалжинтай ерөнхий тэгш өнцөг бүхий түүнд багтсан квадратын периметрийг ол.

Бодлого №2466

$ABC$ гурвалжны

$C$ өнцөг нь тэгш. Хэрэв

$\angle B=30^\circ$ ,

$BC=6$ см бол багтсан тойргийн радиусыг ол.

Бодлого №2467

Тэгш өнцөгт гурвалжны катетууд нь

$6$ см,

$8$ см бол багтсан тойргийн радиусыг ол.

Бодлого №2470

Тэгш өнцөгт гурвалжны гипотенуз нь

$5$ см, харин түүнд татсан өндөр

$2$ см бол багтсан ба багтаасан тойргийн радиусийг ол.

Бодлого №2473

Хэрэв тэгш өнцөгт гурвалжныг багтаасан тойргийн радиус, багтсан тойргийн радиусаас

$2,5$ дахин их бол их хурц өнцгийн синусыг ол.

Бодлого №2480

Тэгш өнцөгт гурвалжны тэгш өнцгийн оройгоос буулгасан өндөр нь гипотенузыг

$9$ ба

$16$ урттай хэсгүүдэд хуваасан бол уг гурвалжинд багтсан тойргийн радиусыг ол.

Бодлого №2481

Тэгш өнцөгт гурвалжны катетууд нь

$15$ ба

$20$ . Багтсан тойргийн төвөөс тэгш өнцгөөс татсан өндөр хүртэлх зайг ол.

Бодлого №2484

Тэгш өнцөгт гурвалжины багтсан тойрог ба багтаасан тойргийн радиусуудын харьцаа

$2/5$ . Гурвалжны хурц өнцгүүдийг ол.

Бодлого №2487

Тэгш өнцөгт гурвалжны периметр

$36$ . Багтсан тойрог нь гипотенузыг

$2:3$ харьцаатай хэрчмүүдэд хуваах бол гипотенузыг ол.

Бодлого №2494

Тэгш өнцөгт гурвалжны гипотенуз

$20$ см, багтсан тойргийн радиус

$4$ см катетуудын уртын нийлбэрийг ол.

Бодлого №2495

Тэгш өнцөгт гурвалжны тэгш өнцгийн оройгоос татсан өндөр гипотенузыг

$25,6$ ба

$14,4$ урттай хэсгүүдэд хуваах бол уг гурвалжинд багтсан тойргийн радиусыг ол.

Бодлого №2674

Тэгш өнцөгт гурвалжины багтсан тойргийн гипотенузыг шүргэж байгаа цэгээр гипотенузыг хуваахад үүсэх хэрчмүүдийн уртуудын үржвэр гурвалжны талбайтай тэнцүү болохыг батал.

Бодлого №2676

$AC$ суурьтай, адил хажуут

$ABC$ гурвалжин өгчээ. Багтсан тойргийн төв

$O$ нь

$BC$ талыг

$P$ цэгт шүргэх бөгөөд

$B$ өнцгийн биссектрисийг

$Q$ цэгт огтолж байв.

$QP$ ба

$OC$ шулуунууд параллель гэдгийг батал.

Бодлого №2684

$ABC$ гурвалжинд багтсан тойрог

$AC$ ба

$BC$ талыг харгалзан

$M$ ба

$N$ цэгт шүргэх ба

$BD$ биссектрисийг

$P$ ба

$Q$ цэгт огтолжээ. Хэрэв

$\angle A=\pi/4$ ,

$\angle B=\pi/3$ бол

$PQM$ ба

$PQN$ гурвалжнуудын талбайн харьцааг ол.

Бодлого №2685

$ABC$ гурвалжинд багтсан тойргийн радиус

$\dfrac{10}3$ ,

$C$ өнцгийн косинус нь

$\dfrac{5}{13}$ ба талбай нь

$60$ бол гурвалжны талуудыг ол.

Бодлого №2693

$ABC$ гурвалжин ба

$BDEF$ ромбо өгөгджээ. Ромбын бүх оройнууд

$ABC$ гурвалжны талууд дээр орших бөгөөд

$E$ оройн өнцөг нь мохоо. Хэрэв

$AE=3$ ,

$CE=7$ ба ромбод багтсан тойргийн радиус

$1$ бол

$ABC$ гурвалжны талбайг ол.

Бодлого №2697

$ABC$ гурвалжны

$h_a, h_b, h_c$ өндрүүд мэдэгдэж байв.

$ABC$ гурвалжинд багтсан тойргийн радиусийг ол.

Бодлого №2698

$ABC$ гурвалжны

$A$ өнцөг нь

$60^\circ$ , багтсан тойргийн төв нь

$AK$ биссекрисийг

$A$ оройгоос

$(\sqrt3+1):2$ харьцаанд хуваадаг.

$B$ ба

$C$ өнцгүүдийг ол.

Бодлого №2707

Гурвалжны талуудын урт

$a=6$ ,

$b=8$ ба талбай нь

$S=3\sqrt 5$ байв. Гурав дахь талын урт нь уг талд буулгасан медианаас 2 дахин богино бол багтсан тойргийн радиусыг ол.

Бодлого №2710

Гурвалжинд багтсан тойргийн радиус

$1$ ба түүний өндрүүд бүхэл тоо бол түүний өнцгүүдийг ол.

Бодлого №2711

Гурвалжны талуудын урт нь

$13, 14, 15$ . Гурвалжинд багтсан тойрогтой ижил төвтэй 5 радиустай шинэ тойрог татав. Гурвалжны талуудыг огтлоход үүсэх шинэ тойргийн хөвчүүдийн уртыг ол.

Бодлого №2712

Адил хажуут гурвалжныг багтаасан тойргийн радиус

$25$ см, харин түүнд багтсан тойргийн радиус

$12$ см. Гурвалжны талуудын уртыг ол.

Бодлого №2716

Адил хажуут

$ABC$ (

$AB=BC$ ) гурвалжинд багтсан тойргийн төв нь

$O$ .

$AO$ шулуун нь

$BC$ хэрчимтэй

$M$ цэгт огтлолцдог.

$AO=3$ ,

$OM=27/11$ бол

$ABC$ гурвалжны талбайг ол.

Бодлого №2717

Адил хажуут гурвалжны медиануудын огтолцлын цэг ба биссектрисүүдийн огтлолцлын цэг нь хоорондоо

$2$ зайтай байв. Хэрэв уг гурвалжинд багтсан тойргийн урт

$20\pi$ бол гурвалжны периметрийг ол.

Бодлого №2718

Адил хажуут

$ABC$ (

$AB=BC$ ) гурвалжинд багтсан тойргийн

$AB$ талтай параллель шүргэгч шулуун

$AC$ талтай

$M$ цэгт огтлолцох ба

$MC=\dfrac25AC$ байв.

$ABC$ гурвалжны периметр 20 бол багтсан тойргийн радиусыг ол.

Бодлого №2724

Тэгш өнцөг

$ABC$ гурвалжны гипотенуз нь

$AB$ , талбай нь

$30$ , багтсан тойргийн төв нь

$O$ байв.

$AOB$ гурвалжны талбай

$13$ бол

$ABC$ гурвалжны талуудыг ол.

Бодлого №2726

Тэгш өнцөгт гурвалжны периметр нь

$36$ . Уг гурвалжинд багтсан тойргийн шүргэлтийн цэг нь гипотенузыг

$2:3$ харьцаагаар хуваана. Гипотенузын уртыг ол.

Бодлого №2790

$ABC$ гурвалжинд багтсан тойрог

$BM$ медианыг 3 тэнцүү хэсэгт хуваадаг.

$BC:CA:AB$ харьцааг ол.

Бодлого №10107

$\triangle ABC$ -д багтсан тойргийн радиус 1 ба багтаасан тойргийн төв нь гурвалжны дотор талд оршино.

$\measuredangle A=2\alpha$ ,

$\measuredangle B=2\beta$ ,

$\measuredangle C=2\gamma$ гэвэл

$BC$ талын уртыг $\beta$ , $\gamma$ -аар илэрхийл.
Багтаасан тойргийн радиус $R$ -ыг $\beta$ , $\gamma$ -аар илэрхийл.
Багтсан тойргийн төвийг $I$ гэвэл $R$ -г $IA$ , $IB$ , $IC$ -ээр илэрхийл.

ЭЕШ 2008 E1 №6

Тэгш өнцөгт гурвалжны катетууд 9 ба 40 бол багтсан тойргийн радиус хэд вэ?

A.

$4$ B.

$8$ C.

$6$ D.

$2$ E.

$5$

ЭЕШ 2008 E №10

Тэгш өнцөгт гурвалжны катетууд 27 ба 36 бол багтсан тойргийн радиус хэд вэ?

A.

$6$ B.

$18$ C.

$3$ D.

$9$ E.

$\dfrac{9}{2}$

ЭЕШ 2009 B1 №19

Талуудын урт нь

$6; 25; 29$ нэгж байх гурвалжныг багтаасан ба түүнд багтсан тойргуудын радиусын үржвэр хэдэн нэгж вэ?

A.

$21.25$ B.

$28.25$ C.

$36.25$ D.

$84$ E.

$92.5$

ЭЕШ 2011 B №5

$ABC$ гурвалжны

$AC$ талын урт

$9$ м ба

$B$ өнцөг

$60^\circ$ болно.

$O$ нь энэ гурвалжинд багтсан тойргийн төв бол

$O$ ,

$A$ ,

$C$ цэгийг дайрсан тойргийн радиусыг ол.

A.

$3\sqrt2$ B.

$3\sqrt3$ C.

$\dfrac92$ D.

$9$ E.

$\dfrac{2}{\sin 150^\circ}$

Тэгш өнцөгт гурвалжны периметр 6 ба нэг өнцгийн тангенс нь

$2.4$ бол энэ гурвалжныг багтаасан болон энэ гурвалжинд багтсан тойргийн радиусуудын нийлбэрийг ол.

A.

$1.5$ B.

$1.6$ C.

$1.7$ D.

$1.8$ E.

$1.9$

Багтсан тойргийн радиус

Талуудын урт нь

$5, 12, 13$ байх гурвалжинд багтсан тойргийн радиусыг ол.

A.

$1$ B.

$2$ C.

$3$ D.

$4$ E.

$5$

Багтсан тойрог

6 см, 1 дм, 12 см талтай гурвалжинд багтсан тойргийн, гурвалжны нэг талтай параллел шүргэгчээр 16 см периметртэй гурвалжин таслагдсан бол энэ шүргэгчийн гурвалжин дотор орших хэсгийн урт хэдэн см байх вэ?

A.

$7$ B.

$\dfrac{40}7$ C.

$\dfrac{48}7$ D.

$\dfrac{24}7$ E.

$\dfrac{20}7$

Тэгш өнцөгт гурвалжинд багтсан тойргийн радиус

Талуудын урт нь 5, 12, 13 байх гурвалжинд багтсан тойргийн радиусыг ол.

A.

$1$ B.

$2$ C.

$3$ D.

$4$ E.

$5$

Багтсан тойргийн төвийн өнцөг

$12$ ,

$15$ нэгж талтай гурвалжны гурав дахь тал багтсан тойргийн төвөөс

$\arccos\dfrac{-1}{\sqrt{10}}$ өнцгөөр харагддаг бол энэ өнцгийн эсрэг орших тал хэдэн нэгж вэ?

A.

$6$ B.

$9$ C.

$12$ D.

$10$ E.

$15$

Гурвалжны өндрүүдийн урвуугийн нийлбэр

Гурвалжны гурван өндрийн урвуу хэмжигдэхүүний нийлбэр ямар байх вэ?

$r$ ,

$R$ нь харгалзан багтсан ба багтаасан тойргийн радиус

A.

$\dfrac1r$ B.

$\dfrac1R$ C.

$\dfrac{R}{r^2}$ D.

$\dfrac{r^2}{R}$ E. Аль нь ч биш

Гипотенуз нь 5, түүнд буусан өндөр 2.4 нэгж бол тэгш өнцөгт гурвалжинд багтсан тойргийн радиус аль нь вэ?

A.

$\dfrac52$ B.

$2$ C.

$\dfrac32$ D.

$1$ E.

$\dfrac12$

Бодлого №7716

$ABC$ гурвалжинд багтсан тойрог

$BC$ ,

$CA$ ,

$AB$ талыг харгалзан

$A_1$ ,

$B_1$ ,

$C_1$ цэгт шүргэжээ. Хэрэв

$A$ оройгоос өндрүүдийн огтлолцол хүртэлх зай багтаасан тойргийн радиустай тэнцүү бол

$\begin{array}{c} [-7mm]\smile [-2mm] C_1A_1B_1\end{array}$ ямар байх вэ?

A.

$220^\circ$ B.

$240^\circ$ C.

$230^\circ$ D.

$210^\circ$

Бодлого №7726

$R$ радиустай тойрогт багтсан

$ABC$ гурвалжны

$AH_1$ өндрийн үргэлжлэл багтаасан тойрогтой

$D$ цэгт огтлолцжээ. Хэрэв орто төв нь

$H$ ,

$\measuredangle ABC=\beta$ ,

$\measuredangle BCA=\gamma$ бол

$HD$ -ийн урт аль вэ?

A.

$4R\cos\beta\cos\gamma$ B.

$4R\sin\beta\sin\gamma$ C.

$3R\sin\beta\sin\gamma$ D.

$3R\cos\beta\cos\gamma$

Бодлого №7735

$ABC$ гурвалжны

$A$ оройн дотоод өнцгийн биссектрисийн үргэлжлэл багтаасан тойрогтой

$D$ цэгт огтлолцжээ. Багтсан тойргийн төвөөс

$D$ хүртэлх зай багтаасан тойргийн радиустай тэнцүү бол

$A$ орой дахь дотоод өнцөг хэдэн градус вэ?

A.

$120^\circ$ B.

$30^\circ$ C.

$150^\circ$ D.

$60^\circ$

Бодлого №7781

6 см, 1 дм, 12 см талтай гурвалжинд багтсан тойргийн, гурвалжны нэг талтай параллел шүргэгчээр 16 см периметртэй гурвалжин таслагдсан бол энэ шүргэгчийн гурвалжин дотор орших хэсгийн урт хэдэн см байх вэ?

A.

$7$ B.

$\dfrac{40}7$ C.

$\dfrac{48}7$ D.

$\dfrac{20}7$ E.

$\dfrac{24}7$

Тэгш өнцөгт гурвалжныг багтсан ба багтаасн тойргийн радиус

Тэгш өнцөгт гурвалжинд багтсан тойргийн радиус 4, гипотенузэд буусан өндөр 9 бол багтаасан тойргийн радиус хэд вэ?

A.

$12$ B.

$14$ C.

$16$ D.

$18$ E.

$20$

Багтсан тойргийн радиус

Тэгш өнцөгт гурвалжны катетууд нь

$a$ ,

$b$ ; гипотенуз нь

$c$ бол уг гурвалжинд багтсан тойргийн радиус аль нь вэ?

A.

$\dfrac{c}{2}$ B.

$\dfrac{a+b}{2}$ C.

$\dfrac{a+b-c}{2}$ D.

$\dfrac{c+a-b}{2}$ E.

$\dfrac{c+b-a}{2}$

Бага катетийн урт

Тэгш өнцөгт

$\triangle ABC$ -ийн хувьд

$\angle A=90^\circ$ ,

$BC=10$ ба багтсан тойргийн радиус нь

$2$ бол катетуудын аль богинынх нь уртыг ол.

A.

$2$ B.

$4$ C.

$6$ D.

$8$ E.

$10$

ЭЕШ 2008 A №78

Тэгш өнцөгт гурвалжны катетууд 15 ба 8 бол багтсан тойргийн радиус хэд вэ?

A.

$6$ B.

$5$ C.

$3$ D.

$4$ E.

$\dfrac32$

Тэгш өнцөгт гурвалжны периметр 12 ба нэг өнцгийн тангенс нь

$\dfrac{5}{12}$ бол энэ гурвалжныг багтаасан болон энэ гурвалжинд багтсан тойргийн радиусуудын нийлбэрийг ол.

A.

$3$ B.

$3.2$ C.

$3.3$ D.

$3.4$ E.

$4$

Тэгш өнцөгт гурвалжны периметр 12 ба нэг өнцгийн тангенс нь

$\dfrac{5}{12}$ бол энэ гурвалжныг багтаасан болон энэ гурвалжинд багтсан тойргийн радиусуудын нийлбэрийг ол.

A.

$3$ B.

$3.2$ C.

$3.3$ D.

$3.4$ E.

$4$

Зөв гурвалжинд багтсан тойргийн радиус

$3$ талтай зөв гурвалжинд багтсан тойргийн радиус аль нь вэ?

A.

$1$ B.

$2$ C.

$\dfrac{\sqrt3}{2}$ D.

$\dfrac{1}{\sqrt3}$ E.

$\dfrac{1}{3}$

Тэгш өнцөгт гурвалжныг багтсан ба багтаасн тойргийн радиус

Тэгш өнцөгт гурвалжинд багтсан тойргийн радиус 8, гипотенузэд буусан өндөр 18 бол багтаасан тойргийн радиус хэд вэ?

A.

$24$ B.

$28$ C.

$32$ D.

$36$ E.

$40$

Бодлого №7869

$ABC$ гурвалжинд

$AC_1A_1B_1$ ромбо багтсан бөгөөд

$A_1$ ,

$B_1$ ,

$C_1$ цэгүүд харгалзан

$BC$ ,

$AC$ ,

$AB$ талууд дээр оршино.

$\dfrac{AC_1}{C_1B}=2$ ,

$B_1C=12$ байдаг бол

$AC_1=\fbox{a}$ ,

$C_1B=\fbox{b}$ байна.

$S_{AC_1B_1}=s$ гэвэл

$S_{ABC}=\dfrac{\fbox{c}}{\fbox{d}}s$ болох ба

$s=2\sqrt{11}$ үед

$BC=3\cdot \sqrt{\fbox{ef}-4\cdot \sqrt{\fbox{gh}}}$ байна.

Бодлого №7870

$ABC$ гурвалжинд

$AC_1A_1B_1$ ромбо багтсан бөгөөд

$A_1$ ,

$B_1$ ,

$C_1$ цэгүүд харгалзан

$BC$ ,

$AC$ ,

$AB$ талууд дээр оршино.

$\dfrac{AC_1}{C_1B}=3$ ,

$B_1C=9$ байсан бол

$AC_1=\fbox{a}$ ,

$C_1B=\fbox{b}$ байна.

$S_{AC_1B_1}=s$ гэвэл

$S_{ABC}=\dfrac{\fbox{cd}}{\fbox{e}}s$ ,

$s=3\sqrt{2}$ үед

$BC=\fbox{f}\sqrt{\fbox{g}}$ байна.

Бодлого №7885

Тэгш өнцөгт

$ABC$ гурвалжны

$BC$ гипотенуз ба

$AB$ катетад буулгасан медианы суурийг харгалзан

$A_1$ ,

$C_1$ , тэдгээрийн огтлолыг

$O$ гэе.

$BC=3\sqrt{6}$ ,

$AC=3\sqrt{2}$ бол

$\cos\widehat{C_1CA}=\sqrt{\fbox{a}}/{\fbox{b}}$ ,

$S_{OC_1A}+S_{OA_1C}={\fbox{c}\sqrt{\fbox{d}}}$ ,

$OAC$ гурвалжинд багтсан тойргийн радиус

$\fbox{e}\sqrt{2}/s$ байна. Энд

$s=3\sqrt{2}+2\sqrt{3}+\sqrt{6}$ юм.

Бодлого №7886

$ABC$ тэгш өнцөгт гурвалжны

$BC$ гипотенуз ба

$AB$ катетад буулгасан медианы суурийг харгалзан

$A_1$ ,

$C_1$ , тэдгээрийн огтлолыг

$O$ гэе.

$AB=8$ ,

$BC=4\sqrt{6}$ бол

$\cos\widehat{CC_1B}=-\sqrt{\fbox{a}}/{\fbox{b}}$ ,

$S_{OA_1C_1}+S_{OAC}=\fbox{cd}\sqrt{2}/3$ ,

$OA_1C_1$ гурвалжинд багтсан тойргийн радиус

$\fbox{e}\sqrt{2}/s$ байна. Энд

$s=3\sqrt{2}+2\sqrt{3}+\sqrt{6}$ юм.

Бодлого №7903

$ABC$ гурвалжны талууд

$AB=5$ ,

$BC=7$ ба

$\cos \alpha=-\dfrac{1}{5}$ бол

$AC=\fbox{a}$ ,

$S_{ABC}=4\sqrt{\fbox{b}}$ болно. Мөн уг гурвалжинд багтсан тойргийн радиус

$\sqrt{\fbox{c}}/\fbox{d}$ , багтсан ба багтаасан тойргийн радиусуудын харьцаа

$\displaystyle\dfrac{12}{\fbox{ef}}$ ,

$AL$ биссектриссийн урт

$\displaystyle \sqrt{10}\dfrac{\fbox{g}}{\fbox{h}}$ байна.

Бодлого №7904

$ABC$ гурвалжны талууд

$AC=7$ ,

$BC=9$ ба

$\cos \beta =\dfrac{2}{3}$ ,

$AB< AC$ бол

$AB=\fbox{a}$ ,

$ABC$ гурвалжныг багтаасан тойргийн радиус

$\dfrac{\fbox{bc}\sqrt{5}}{10}$ ,

$\sin \alpha =\dfrac{\fbox{d}\sqrt{5}}{\fbox{e}}$ ба багтсан тойргийн радиус

$\fbox{f}\sqrt{5}/5$ болно. Энэхүү тойрог дээр

$A$ ,

$D$ цэгүүд

$BC$ талын

$2$ талд байхаар авахад

$BD=CD$ бол

$BD=\fbox{g}\sqrt{70}/\fbox{hi}$ байна.

Бодлого №7911

Адил хажуут

$ABC$ (AC=BC) гурвалжны

$C$ өнцөгт

$\dfrac{12}{5}$ радиустай тойрог багтсан бөгөөд уг тойрог

$AC$ ,

$BC$ талуудыг харгалзан

$N$ ,

$M$ цэгт шүргэж

$AB$ талыг

$D$ ,

$E$ цэгүүдэд огтолж байв.

$BM=16/5$ ,

$\tg \beta ={3}/{4}$ ба уг тойргийн төв

$O$ бол

${MN}\colon{AB}={\fbox{a}}\colon{\fbox{bc}}$ , гурвалжны талууд

$\fbox{d}$ ,

$\fbox{e}$ болно. Мөн

$ONCM$ дөрвөн өнцөгтийн талбай

${\fbox{fgh}}{ }/{ }{\fbox{ij}}$ байна.

Бодлого №7912

Адил хажуут

$ABC$ (AB=BC) гурвалжны

$B$ өнцөгт

$6$ радиустай тойрог багтсан бөгөөд уг тойрог

$AB$ ,

$BC$ талуудыг харгалзан

$M$ ,

$N$ цэгүүдэд шүргэж

$AC$ талыг

$D$ ,

$E$ цэгүүдээр огтолж байв.

$AM=9$ ,

$\tg \alpha ={2}/{3}$ ба уг тойргийн төв

$O$ бол

${MN}\colon{AC}={\fbox{a}}\colon{\fbox{bc}}$ , гурвалжны талууд

$\fbox{de}$ ,

$\fbox{f}\sqrt{\fbox{gh}}$ болно. Мөн

$OMBN$ дөрвөн өнцөгтийн талбай

$\fbox{ij}$ байна.

Тэгш өнцөгт гурвалжинд багтсан тойргууд

$AB=1$ ,

$AC=2$ катетууд бүхий тэгш өнцөгт гурвалжинд багтсан тойргийн радиусыг

$r$ ,

$AC$ талыг шүргэн гадуур багтсан тойргийн радиусыг

$R_{b}$ гэвэл

$r=\dfrac{\fbox{a}-\sqrt{\fbox{b}}}{2}$ ,

$R_{b}=\dfrac{\sqrt{\fbox{c}}+1}{\fbox{d}}$ байна. Энэ хоёр тойргийн

$BC$ талыг шүргэх цэгүүдийг

$E_1$ ,

$E_2$ гэвэл

$E_1E_2=\sqrt{\fbox{e}}-\fbox{f}$ болно.

Бодлого №7975

$ABC$ гурвалжныг багтаасан тойргийн төвийг

$O$ гэе.

$\measuredangle ABC=30^\circ$ ,

$\measuredangle ACB =20^\circ$ үед

$\measuredangle OBC=\fbox{ab}^\circ$ ,

$\measuredangle BOC=\fbox{cde}^\circ$ байна.

$ABC$ гурвалжинд багтсан тойргийн төвийг

$I$ гээд

$\measuredangle ABC=70^\circ$ ,

$\measuredangle ACB=60^\circ$ гэе.

$AI$ шулуун

$BC$ талыг

$D$ цэгээр огтолдог бол

$\measuredangle ADB =\fbox{fg} ^\circ$ ,

$\measuredangle CID=\fbox{hi}^\circ$ байна.

Бодлого №7976

$ABC$ гурвалжныг багтаасан тойргийн төвийг $O$ гэе. $\measuredangle ACB=40^\circ$ , $\measuredangle OAC =30^\circ$ үед $\measuredangle OAB= \fbox{ab}^\circ$ , $\measuredangle OBC= \fbox{cd}^\circ$ байна.
$ABC$ гурвалжинд багтсан тойргийн төвийг $I$ гээд $\measuredangle ABC=30^\circ$ , $\measuredangle ACB=100^\circ$ гэе. $IC$ шулуун $AB$ талыг $D$ цэгээр огтолдог бол $\measuredangle BID =\fbox{ef} ^\circ$ , $\measuredangle AIC=\fbox{ghi}^\circ$ байна.

Катетуудыг шүргэсэн тойрог

$ABC$ тэгш өнцөгт гурвалжны

$AB$ гипотенуз дээр төв нь орших тойрог

$AC$ ба

$BC$ талуудыг харгалзан

$E$ ,

$D$ цэгүүдээр шүргэв. Хэрэв

$AE=1$ ,

$BD=3$ бол

$\measuredangle BAC=\fbox{ab}^\circ$ ,

$\triangle ABC$ -ийн периметр нь

$\fbox{c}+\fbox{d}\sqrt3$ , багтсан тойргийн радиус

$\fbox{e}$ байна.

Тэгш өнцөгт гурвалжны гипотенуз дээрх катетуудын проекц 25, 144 бол тэгш өнцгийн оройгоос татсан өндөр

$\fbox{ab}$ болно. Богино катет нь

$\fbox{cd}$ , урт катет нь

$\fbox{efg}$ болох бөгөөд уг гурвалжинд багтсан тойргийн радиус

$r=\fbox{hi}$ байна.

Гурвалжинд багтсан ромбо

$ABC$ гурвалжинд

$AC_1A_1B_1$ ромбо багтсан бөгөөд

$C_1$ ,

$A_1$ ,

$B_1$ цэгүүд нь харгалзан

$AB$ ,

$BC$ ,

$CA$ талууд дээр байрлах ба

$\dfrac{AC_1}{C_1B}=4$ ,

$B_1C=16$ бол

$AC_1=\fbox{a}$ ,

$C_1B=\fbox{b}$ байна.

$B_1C_1=4$ үед

$ABC$ гурвалжны талбай

$\fbox{cd}\sqrt{\fbox{e}}$

Героны томьёо

Талуудынх нь урт 5, 6, 7 нэгж байх гурвалжны талбай аль нь вэ?

A.

$6$ B.

$8\sqrt{2}$ C.

$3\sqrt{6}$ D.

$4\sqrt{3}$ E.

$6\sqrt6$

Героны томьёо

Талуудынх нь урт 10, 12, 14 нэгж байх гурвалжны талбай аль нь вэ?

A.

$24$ B.

$32\sqrt{2}$ C.

$12\sqrt{6}$ D.

$16\sqrt{3}$ E.

$24\sqrt6$

Бодлого №2316

$ABC$ гурвалжны

$AC$ талын урт

$b$ ,

$AB$ талын урт

$c$ байв.

$A$ цэгээс

$BC$ тал руу татсан биссектрис шулуун нь

$BC$ -г

$D$ цэгт огтлоно.

$DA=DB$ бол

$BC$ талын уртыг ол.

Бодлого №2317

Гурвалжны хоёр тал

$35$ см,

$14$ см урттай ба тэдгээрийн хоорондох өнцгийн биссектрисийн урт

$12$ см бол уг гурвалжны талбайг ол.

Бодлого №2336

$ABC$ гурвалжны

$B$ оройгоос

$BD$ өндөр,

$BL$ биссектрис татав. Хэрэв

$ABC$ гурвалжны

$AB=6.5$ ,

$BC=7.5$ ,

$AC=7$ бол

$BLD$ гурвалжны талбайг ол.

Бодлого №2350

$\angle B=30^\circ$ ,

$AB=4$ ,

$BC=6$ байх

$ABC$ гурвалжин өгөгдөв.

$B$ өнцгийн биссектрис нь

$AC$ талыг

$D$ цэгт огтлох бол

$ABD$ гурвалжны талбайг ол.

Бодлого №2351

$AC=5$ ,

$AB=6$ ,

$BC=7$ байх

$ABC$ гурвалжин өгөгдөв.

$C$ өнцгийн биссектрис нь

$AB$ талыг

$D$ цэгт огтлох бол

$ADC$ гурвалжны талбайг ол.

Бодлого №2359

$ABC$ гурвалжинд

$BE$ биссектрис татсан ба багтсан тойргийн төв

$O$ нь түүнийг

$BO:OE=2$ харьцаанд хуваана. Хэрэв

$AC=7$ ,

$BC=8$ бол

$AB$ -г ол.

Бодлого №2370

$ABC$ гурвалжны

$AD$ медиан болон

$BE$ биссектрисүүд харилцан перпедикуляр ба

$F$ цэгт огтлолцоно.

$DEF$ гурвалжны талбай нь

$5$ бол

$ABC$ гурвалжны талбайг ол.

Бодлого №2371

$4, 8, 9$ талуудтай гурвалжин өгөгдөв. Их тал руу буулгасан биссектрисийн уртыг ол.

Бодлого №2381

$AB=12$ см,

$BC=15$ см,

$AC=9$ см талуудтай

$ABC$ гурвалжинд

$BB_{1}$ биссектрис татав. Багтсан тойрог

$AB$ талтай шүргэлцэх цэг нь

$C_1$ .

$BB_{1}$ ,

$CC_{1}$ хэрчмүүд

$P$ цэгт огтлолцох ба

$AP$ -ийн үргэлжлэл

$BC$ -тэй

$A_{1}$ цэгт огтлолцох бол

$AP:PA_1$ -г ол.

Бодлого №2384

Адил хажуут

$ABC$ гурвалжны

$AD$ биссектрис нь түүнийг

$ABD$ ,

$ACD$ гурвалжнуудад хуваах ба талбай нь харгалзан

$4$ см.кв,

$2$ см.кв. Хэрэв

$AC$ нь суурь нь бол гурвалжны талуудыг ол.

Бодлого №2386

Адил хажуут

$ABC$ (

$AB=BC$ ) гурвалжинд

$AD$ биссектрис татав.

$ABD$ болон

$ADC$ гурвалжнуудын талбай харгалзан

$S_1, S_2$ . Суурийн уртыг ол.

Бодлого №2388

$a$ суурьтай адил хажуут гурвалжны хажуу тал нь

$b$ . Хажуу тал руу буулгасан биссектрисийн уртыг ол.

Бодлого №2404

Хэрэв адил хажуут гурвалжны суурийг суурьт харгалзах өнцгийн биссектрист

$5:6$ байдаг бол уг гурвалжны өнцгүүдийг ол.

Бодлого №2409

Адил хажуут гурвалжны суурийн эсрэг орших өнцгийн биссектрис ба суурийн нэг өнцгийн биссектрисийг татав. Хэрэв суурийн өнцгийн косинус нь

$p=\frac{\sqrt{975}}{32}$ бол уг 2 биссектрисийн хооронд үүсэх мохоо өнцгийн косинусыг ол.

Бодлого №2414

Адил хажуут

$ABC$ гурвалжны

$AD$ биссектрисийн

$AC$ суурьтай үүсгэх өнцгийн тангенс нь

$0,5$ .

$\angle ABC$ -ийн косинусыг ол.

Бодлого №2419

$AB=4$ ,

$BC=AC=12$ байх

$ABC$ гурвалжин өгөгдөв.

$AD$ нь биссектрис бол

$\angle ADC$ -г ол.

Бодлого №2421

Адил хажуут

$ABC$ (AB=BC) гурвалжинд

$AD$ биссектрис татав.

$BC:DC=k$ бол

$DC$ хэрчмийн уртыг

$ABC$ гурвалжныг багтаасан тойргийн радиуст харьцуулсан харьцааг ол.

Бодлого №2469

Тэгш өнцөгт гурвалжны

$1$ катет нь

$24$ см, гипотенуз нь

$25$ см бол гурвалжны бага өнцгийн оройгоос татсан биссектрисийг ол.

Бодлого №2479

Тэгш өнцөгт гурвалжны

$\angle B=90^\circ$ ба

$A$ оройгоос татсан биссектрис нь

$BC$ талыг

$D$ цэгт огтолно.

$BD=4$ ,

$DC=6$ бол

$ADC$ гурвалжны талбайг ол.

Бодлого №2486

$ABC$ гурвалжны

$ACB$ тэгш өнцгөөс

$CD$ биссектрис,

$DM$ ,

$DN$ нь харгалзан

$ADC$ ба

$BDC$ гурвалжнуудын өндрүүд байв. Хэрэв

$AM=4$ ,

$BN=9$ бол

$AC$ -г ол.

Бодлого №2489

Тэгш өнцөгт гурвалжны тэгш өнцгийн биссектрис гипотенузыг

$3$ см,

$4$ см урттай хэрчмүүдэд хуваав. Гурвалжны талбайг ол.

Бодлого №2493

$ABC$ тэгш өнцөгт гурвалжны

$BC$ гипотенузын урт

$20$ ,

$AB$ катетын урт

$16$ .

$A$ оройгоос

$C$ өнцгийн биссектрис хүртэлх зайн квадратыг ол.

Бодлого №2669

$ABC$ гурвалжинд

$AD$ биссектрис татав. Хэрэв

$AB+BD=AC+CD$ гэвэл

$ABC$ гурвалжин адил хажуут болохыг батал.

Бодлого №2676

$AC$ суурьтай, адил хажуут

$ABC$ гурвалжин өгчээ. Багтсан тойргийн төв

$O$ нь

$BC$ талыг

$P$ цэгт шүргэх бөгөөд

$B$ өнцгийн биссектрисийг

$Q$ цэгт огтолж байв.

$QP$ ба

$OC$ шулуунууд параллель гэдгийг батал.

Бодлого №2679

$ABC$ гурвалжны

$B$ оройгоос үлдэх оройнуудаас татсан биссектрисүүдэд

$BK$ ба

$BL$ перпендикуляруудыг буулгав.

$KL$ хэрчмийн урт нь

$ABC$ гурвалжны периметрийн хагастай тэнцүү болохыг батал.

Бодлого №2680

$KLM$ гурвалжины

$KN$ ба

$LP$ биссектрисүүд

$Q$ цэгт огтлолцдог.

$PN$ хэрчмийн урт нь

$1$ см ба

$M$ орой нь

$N, P, Q$ цэгүүдийг дайрах тойрог дээр оршино.

$PNQ$ гурвалжны талууд ба өнцгүүдийг ол.

Бодлого №2682

$ABC$ гурвалжны

$BAC$ өнцгийн биссектрис

$a$ -тай тэнцүү. Энэ биссектрисээр диаметрээ хийсэн тойрог

$AB$ ба

$BC$ талыг харгалзан

$2:1$ ба

$1:1$ харьцаагаар хуваах бол

$ABC$ гурвалжны талбайг ол.

Бодлого №2683

$ABC$ гурвалжны

$AD$ биссектрис нь

$BC$ талыг

$BD:CD=2:1$ харьцаагаар хуваах бол

$CE$ медиан нь биссектрисийг ямар харьцаатай хуваах вэ?

Бодлого №2684

$ABC$ гурвалжинд багтсан тойрог

$AC$ ба

$BC$ талыг харгалзан

$M$ ба

$N$ цэгт шүргэх ба

$BD$ биссектрисийг

$P$ ба

$Q$ цэгт огтолжээ. Хэрэв

$\angle A=\pi/4$ ,

$\angle B=\pi/3$ бол

$PQM$ ба

$PQN$ гурвалжнуудын талбайн харьцааг ол.

Бодлого №2687

$ABC$ гурвалжны талбай

$90$ см.кв,

$AD$ биссектрис нь

$BC$ талыг

$BD:CD=2:3$ харьцаагаар хуваадаг.

$BL$ хэрчим

$AD$ биссектристэй

$E$ цэгт огтлолцох ба

$L$ цэг

$AC$ хэрчмийг

$AL:CL=1:2$ байхаар хуваана.

$EDCL$ дөрвөн өнцөгтийн талбайг ол.

Бодлого №2688

$ABC$ гурвалжны талбай

$40$ см.кв,

$AD$ биссектрис

$BC$ талыг

$BD:DC=3:2$ байхаар хуваана.

$AD$ биссектрис

$BK$ медианыг

$E$ цэгт огтолно.

$EDCK$ дөрвөн өнцөгтийн талбайг ол.

Бодлого №2689

$ABC$ гурвалжны талбай

$70$ см.кв ба

$AD$ биссектрис нь

$BC$ талыг

$BD:DC=3:2$ байхаар хуваана.

$AD$ биссектрис

$BK$ хэрчмийг

$BE:EK=5:2$ харьцаагаар хувааж байхаар

$AC$ тал дээр

$K$ цэг авав.

$EDCK$ дөрвөн өнцөгтийн талбайг ол.

Бодлого №2690

$ABC$ гурвалжны

$AD$ ба

$BE$ биссектрисүүд

$O$ цэгт огтлолцоно. Хэрэв

$AC:AB:BC=4:3:2$ бол

$DOEC$ дөрвөн өнцөгтийн талбайг

$ABC$ гурвалжны талбайд харьцуулсан харьцааг ол.

Бодлого №2691

$ABC$ гурвалжинд

$AP$ биссектрис татахад

$BP=16$ ба

$PC=20$ байв.

$ABP$ гурвалжныг багтаасан тойргийн төв нь

$AC$ хэрчим дээр орших бол

$AB$ талын уртыг ол.

Бодлого №2692

$CQ$ нь

$ABC$ гурвалжны биссектрис.

$BCQ$ гурвалжныг багтаасан тойргийн радиус

$1/3$ ба төв нь

$AC$ хэрчим дээр оршиж байв. Хэрэв

$AQ:AB=2:3$ гэвэл

$ABC$ гурвалжны талбайг ол.

Бодлого №2695

$ABC$ гурвалжны

$AH$ биссектрис

$BE$ медианыг

$BK:KE=2$ харьцаагаар хуваах ба

$ABC$ өнцөг

$45^\circ$ байв.

$BCE$ гурвалжны талбайг энэ гурвалжныг багтаасан дугуйн талбайд харьцуулсан харьцааг ол.

Бодлого №2705

$BMC$ ба

$ANC$ өнцгүүд тэгш байхаар хурц өнцөгт

$ABC$ гурвалжны

$AD$ өндөр дээр

$M$ цэг,

$BP$ өндөр дээр

$N$ цэг тус тус авав.

$M$ ба

$N$ цэгүүдийн хоорондох зай

$4+2\sqrt3$ ба

$\angle MCN=30^\circ$ байв.

$CMN$ гурвалжны

$CL$ биссектрисийн уртыг ол.

Бодлого №2706

$KLM$ гурвалжны

$KL$ талын урт нь

$27$ ,

$KN$ биссектрисийн урт

$24$ ба

$MN$ хэрчмийн урт

$8$ байв.

$KMN$ гурвалжны периметрийг ол.

Бодлого №2717

Адил хажуут гурвалжны медиануудын огтолцлын цэг ба биссектрисүүдийн огтлолцлын цэг нь хоорондоо

$2$ зайтай байв. Хэрэв уг гурвалжинд багтсан тойргийн урт

$20\pi$ бол гурвалжны периметрийг ол.

Бодлого №2720

Тэгш өнцөгт гурвалжны гипотенузын урт

$a$ . Нэг хурц өнцгийнх нь биссектрис

$\dfrac{a}{\sqrt{3}}$ бол катетуудыг ол.

Бодлого №2721

$AD$ нь тэгш өнцөгт

$ABC$ (

$\angle C=90^\circ$ ) гурвалжны биссектрис.

$\sqrt{15}$ радиустай тойрог

$A, C, D$ цэгүүдийг дайрах бөгөөд уг тойрог

$AB$ талыг

$E$ цэгт

$AE:AB=3:5$ байхаар огтолно.

$ABC$ гурвалжны талбайг ол.

Бодлого №2722

Тэгш өнцөгт гурвалжны тэгш өнцгийн оройгоос буулгасан өндөр ба биссектрисийн уртууд харгалзан

$3$ ба

$4$ . Гурвалжны талбайг ол.

Бодлого №2725

Тэгш өнцөгт

$ABC$ (

$\angle B=90^\circ$ ) гурвалжны

$AM$ медиан ба

$CD$ биссектрис

$O$ цэгт огтлолцов. Хэрэв

$CO=9$ ,

$OD=5$ гэвэл

$ABC$ гурвалжны талбайг ол.

Бодлого №2781

2 тойрог дотоод байдлаар

$N$ цэгт шүргэлдэнэ.

$MN$ хэрчим том тойргийн диаметр болох ба том тойргийн

$MK$ хөвч бага тойргийг

$C$ цэгт шүргэнэ.

$MNK$ өнцгийн биссектрис

$NC$ гэж батал.

Бодлого №2787

Хурц өнцөгт

$ABC$ гурвалжны

$AD$ өндөр,

$BE$ медиан,

$CF$ биссектрис гурав

$O$ цэгт огтлолцоно. Хэрэв

$OE=2OC$ бол

$C$ өнцгийг ол.

Бодлого №2792

$ABC$ гурвалжны

$C$ оройгоос татсан медиан, биссектрис ба өндөр нь харгалзан 6, 5 ба 2 гэсэн урттай.

$AB$ талын уртыг ол.

ЭЕШ 2006 A №14

$ABC$ гурвалжны

$AN$ нь биссектрисс,

$AB=8$ ,

$AC=5$ ,

$BN=x+2$ ,

$NC=x$ бол

$x$ -г ол.

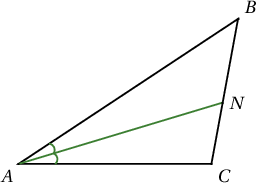
A.

$2$ B.

$3$ C.

$4$ D.

$\dfrac{10}{3}$ E.

$\dfrac{3}{10}$

ЭЕШ 2006 C №14

$ABC$ гурвалжны

$AM$ нь биссектрисс,

$AB=13$ ,

$AC=5$ ,

$BM=x$ ,

$MC=x-5\dfrac13$ бол

$x$ -г ол.

A.

$12$ B.

$14$ C.

$15$ D.

$26/3$ E.

$9$

ЭЕШ 2007 A1 №25

$AC=9$ ,

$AB=7$ нэгж урттай

$ABC$ гурвалжны

$A$ оройн дотоод өнцгийн биссектрис нь

$AD=DB$ байхаар

$BC$ талтай

$D$ цэгт огтлолцсон бол

$BC$ талын уртыг ол.

A.

$10$ B.

$11$ C.

$12$ D.

$13$ E.

$14$

Биссектрисийн чанар

$ABC$ гурвалжны

$AB=6$ ,

$AC=12$ ,

$BC=9$ байв.

$D$ цэг нь

$A$ оройгоос татсан дотоод өнцгийн биссектриссийн суурь бол

$BD$ -г ол.

A. 1 B. 2 C. 3 D. 4 E. 5

Биссектрисийн чанар

$ABC$ гурвалжны периметр 28 см.

$AD$ биссектрис суурийг

$BD=4$ см,

$DC=3$ см урттай хэсгүүдэд хуваах бол

$AC$ талын урт хэдтэй тэнцүү вэ?

A. 7 B. 9 C. 10 D. 12 E. 14

Ижил өндөртэй гурвалжнуудын талбайн харьцаа

$\triangle ABC$ -ийн

$AB=5$ ,

$AC=12$ ,

$BC=13$ байв. Хэрэв

$D$ нь

$A$ оройн биссектрисийн суурь бол

$ABD$ гурвалжны талбайг ол.

A.

$\dfrac{150}{17}$ B.

$8$ C.

$7$ D.

$10$ E.

$\dfrac{25}{3}$

Биссектрисийн чанар

Гурвалжны хоёр талын урт нь 12 ба 8 нэгж, тэдгээрийн хоорондох өнцгийн биссектрисийн сууриар гурав дахь талын хуваагдсан хоёр хэсгийн нэг нь 6 нэгж урт бол нөгөө хэсгийн урт хэд байж болох вэ?

A.

$9$ B.

$4$ C.

$4, 6$ D.

$4, 9$ E.

$6$

Биссектрисийн чанар

Гурвалжны нэг тал 14 нэгж бөгөөд түүнд налсан нэг өнцгийн биссектрис эсрэг орших талаа 7,9 нэгж урттай хэсгүүдэд хуваасан бол гурав дахь талын урт хэд байх вэ?

A.

$\dfrac{98}9, \dfrac{76}9$ B.

$16, 18$ C.

$18, \dfrac{98}9$ D.

$\dfrac{76}9, 16$ E.

$\dfrac{76}{9}, 18$

Гурвалжны биссектрис

Гурвалжны хоёр тал, тэдгээрийн хоорондох өнцгийн биссектрисийн урт харгалзан

$12$ ,

$24$ ,

$8\sqrt3$ нэгж бол энэ өнцөг хэдэн градус байх вэ?

A.

$60^\circ$ B.

$75^\circ$ C.

$30^\circ$ D.

$120^\circ$ E.

$45^\circ$

Биссектрисийн чанар

$ABC$ гурвалжны

$C$ өнцгийн биссектрисийн

$L_3$ суурийг дайрсан

$AC$ талтай параллель шулуун

$BC$ талыг

$E$ цэгт огтолжээ. Хэрэв

$BC=a$ ,

$AC=b$ бол

$L_3E$ хэрчмийн урт ямар байх вэ?

A.

$\dfrac{2ab}{a+b}$ B.

$\sqrt{ab}$ C.

$\dfrac12\sqrt{ab}$ D.

$2\sqrt{ab}$ E.

$\dfrac{ab}{a+b}$

Тэгш өнцөгт гурвалжны биссектрис

Тэгш өнцөгт гурвалжны хурц өнцгийн биссектрис хөндий орших катетыг

$m$ ,

$n$

$(m>n)$ урттай хэсгүүдэд хуваасан бол гипотенузийн урт ямар байх вэ?

A.

$n\sqrt{\dfrac{m-n}{m+n}}$ B.

$m\sqrt{\dfrac{m-n}{m+n}}$ C.

$n\sqrt{\dfrac{m+n}{m-n}}$ D.

$\dfrac{m+n}{2}\sqrt{\dfrac{m+n}{m-n}}$ E.

$m\sqrt{\dfrac{m+n}{m-n}}$

Бодлого №7702

Тэгш өнцөгт гурвалжны хурц өнцгийн биссектрис хөндий орших катетыг

$m$ ,

$n$

$(m>n)$ урттай хэсгүүдэд хуваасан бол нөгөө катетийн урт аль нь бэ?

A.

$m\sqrt{\frac{2n}{m-n}}$ B.

$n\sqrt{\frac{m+n}{m-n}}$ C.

$\sqrt{mn}$ D.

$m\sqrt{\frac{3n}{m-n}}$

Бодлого №7718

$ABC$ гурвалжинд

$AL_1$ биссектрис татахад

$L_{1}AC$ гурвалжин өгсөн гурвалжинтай төсөөтэй байсан бол өнцгүүдийн хамааралыг ол (

$\measuredangle BAC=\alpha$ ,

$\measuredangle CBA=\beta$ ,

$\measuredangle ACB=\gamma$ ).

A.

$\alpha-3\beta=0$ B.

$\alpha-2\beta=0$ C.

$3\alpha-4\beta=0$ D.

$2\alpha-3\beta=0$

Бодлого №7719

$ABC$ гурвалжны

$AL_1$ биссектрисийн уртыг

$\ell_1$ ,

$BC=a$ ,

$CA=b$ ,

$AB=c$ гэв.

$ac=(b+c)\ell_1$ байсан бол

$\measuredangle BAC=\alpha$ ,

$\measuredangle BCA=\gamma$ өнцгүүд ямар хамааралтай вэ?

A.

$3\alpha+2\gamma=2\pi$ B.

$2\alpha+3\gamma=\pi$ C.

$3\alpha+4\gamma=2\pi$ D.

$\alpha+3\gamma=\frac{2\pi}3$

Бодлого №7720

$ABC$ гурвалжны

$AL_1$ биссектрис,

$BC=a$ ,

$CA=b$ ,

$a C\,L_1=b^2$ бол

$\measuredangle BAC=\alpha$ ,

$\measuredangle CBA=\beta$ хоёр өнцөг ямар хамааралтай вэ?

A.

$\alpha=2\beta$ B.

$\beta+3\alpha=\pi$ C.

$3\beta+\alpha=\pi$ D.

$5\alpha+\beta=2\pi$

Бодлого №7721

$ABC$ гурвалжны

$AL_1$ биссектрис,

$CM_3$ медиантай

$P$ цэгт огтлолцжээ. Хэрэв

$AC=4$ см,

$AB=6$ см бол

$CP:PM_3$ аль вэ?

A. 3:2 B. 4:3 C. 2:3 D. 1:2

Бодлого №7722

$AB=12$ см,

$AC=9$ см гурвалжинд

$AL_1$ биссектрис,

$CM_3$ медиантай

$P$ цэгт огтлолцжээ.

$AP:PL_1$ аль вэ?

A. 7:4 B. 4:3 C. 7:3 D. 1:7

Бодлого №7727

$AB=12$ ,

$BC=18$ гурвалжны

$B$ оройн дотоод өнцгийн биссектрисийн суурь

$L$ -ийг дайрсан

$AB$ талтай параллель шулуун

$BC$ талтай

$D$ цэгт огтлолцсон бол

$S_{LBD}:S_{ABC}$ аль нь вэ?

A. 3:2 B. 2:3 C. 6:25 D. 12:25

Биссектрисийн чанар, талбайн харьцаа

$AB=12$ ,

$BC=18$ гурвалжны

$BL_2$ дотоод өнцгийн биссектрисийн

$L_2$ суурийг дайрсан

$AB$ талтай параллель шулуун

$BC$ талыг

$D$ цэгт огтолсон бол

$S_{L_2CD}:S_{L_2AB}$ аль нь вэ?

A.

$3:2$ B.

$9:10$ C.

$3:4$ D.

$4:5$ E.

$8:9$

Бодлого №7735

$ABC$ гурвалжны

$A$ оройн дотоод өнцгийн биссектрисийн үргэлжлэл багтаасан тойрогтой

$D$ цэгт огтлолцжээ. Багтсан тойргийн төвөөс

$D$ хүртэлх зай багтаасан тойргийн радиустай тэнцүү бол

$A$ орой дахь дотоод өнцөг хэдэн градус вэ?

A.

$120^\circ$ B.

$30^\circ$ C.

$150^\circ$ D.

$60^\circ$

Бодлого №7736

$R$ радиустай тойрогт багтсан гурвалжны

$A$ оройн дотоод өнцгийн биссектрис багтаасан тойрогтой

$D$ цэгт огтлолцжээ. Хэрэв

$BC$ тал багтсан тойргийн төв

$P$ цэгээс

$150^\circ$ өнцгөөр харагдах бол

$PD$ хэрчмийн урт аль нь вэ?

A.

$\dfrac{R}{3}$ B.

$\sqrt3R$ C.

$\dfrac23R$ D.

$\sqrt2R$ E.

$\dfrac32R$

ЭЕШ 2015 D №19

$ABC$ гурвалжны

$\measuredangle B$ өнцгийн биссектрис

$BK$ ,

$AB=4$ ,

$BC=6$ ба

$KC=3$ бол

$AK$ хэрчмийн уртыг ол.

A.

$\dfrac43$ B.

$3$ C.

$2$ D.

$8$ E.

$4$

ЭЕШ 2015 A №19

$ABC$ гурвалжны

$\measuredangle B$ өнцгийн биссектрисс

$BK$ .

$AB=4$ ,

$BC=6$ ба

$AK=2$ бол

$KC$ хэрчмийн уртыг ол.

A.

$\frac43$ B.

$3$ C.

$2\sqrt{13}-2$ D.

$\frac13$ E.

$4$

Биссектрис

Талуудын урт нь 6, 7, 8 нэгж байх гурвалжны 7 урттай тал дээр буусан биссектрисийн суурь уг талаа ямар урттай хэсгүүдэд хуваах вэ?

A. 1 ба 6 B. 2 ба 5 C. 3 ба 4 D.

$\sqrt 5$ ба

$7-\sqrt5$ E. тэнцүү

ЭЕШ 2015 B №19

$ABC$ гурвалжны

$\measuredangle B$ өнцгийн биссектрис

$BK$ ,

$AB=8$ ,

$BC=12$ ба

$AK=4$ бол

$KC$ хэрчмийн уртыг ол.

A.

$\dfrac83$ B.

$6$ C.

$4\sqrt{13}-4$ D.

$4$ E.

$8$

ЭЕШ 2015 C №19

$ABC$ гурвалжны

$\measuredangle B$ өнцгийн биссектрис

$BK$ ,

$AB=8$ ,

$BC=12$ ба

$KC=6$ бол

$AK$ хэрчмийн уртыг ол.

A.

$\dfrac43$ B.

$6$ C.

$\dfrac{8}{3}$ D.

$2$ E.

$4$

ЭЕШ 2014 B №35

Тэгш өнцөгт гурвалжны катетууд

$5\sqrt2$ см,

$4\sqrt2$ см урттай бол тэгш өнцгийн оройгоос татсан биссектрисийн уртыг ол.

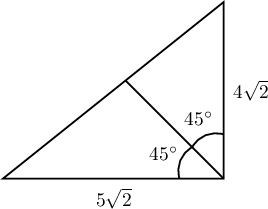
A.

$4\dfrac{4}{9}$ см B.

$4.6$ см C.

$\dfrac{9}{40}$ см D.

$4\sqrt{6}$ см E.

$2.4$ см

Тэгш өнцөгт гурвалжны хурц өнцгийн биссектрий

Тэгш өнцөгт гурвалжны нэг катет нь

$5$ , гипотенуз нь 13 байв. Их хурц өнцгийн оройгоос татсан биссектрисийн уртыг ол.

A.

$\dfrac{3\sqrt{13}}{5}$ B.

$12.5$ C.

$\dfrac{5\sqrt{13}}{3}$ D.

$\dfrac{7\sqrt{13}}{3}$ E.

$\dfrac{8\sqrt{13}}{5}$

Биссектрис

$ABC$ гурвалжныг багтаасан тойргийн радиус

$6$ ,

$\angle A=70^\circ$ ,

$\angle B=30^\circ$ бол

$\angle C$ -ийн биссектрисийн урт аль нь вэ?

A.

$3$ B.

$6$ C.

$8$ D.

$9$ E.

$10$

Тэгш өнцөгт гурвалжны хурц өнцгийн биссектрий

Тэгш өнцөгт гурвалжны нэг катет нь

$5$ , гипотенуз нь 13 байв. Бага өнцгийн оройгоос татсан биссектрисийн уртыг ол.

A.

$\dfrac{12\sqrt{26}}{5}$ B.

$12.5$ C.

$\dfrac{13\sqrt{26}}{3}$ D.

$\dfrac{7\sqrt{26}}{3}$ E.

$\dfrac{13\sqrt{26}}{5}$

Биссектрисийн урт

$ABC$ гурвалжны хувьд

$AB=10\sqrt{3}$ ,

$AC=15\sqrt{3}$ ,

$\measuredangle BAC=60^\circ$ байв.

$A$ оройгоос татсан биссектрисийн уртыг ол.

A.

$10$ B.

$14$ C.

$16$ D.

$18$ E.

$20$

Биссектрисийн урт

$ABC$ гурвалжны хувьд

$AB=7$ ,

$AC=8$ ,

$\measuredangle BAC=120^\circ$ байв.

$A$ оройгоос татсан биссектрисийн уртыг ол.

A.

$\dfrac{56}{15}$ B.

$4$ C.

$3\dfrac{3}{4}$ D.

$5$ E.

$6$

ЭЕШ 2006 A №14

$ABC$ гурвалжны

$AN$ нь биссектрисс,

$AB=8$ ,

$AC=5$ ,

$BN=x+2$ ,

$NC=x$ бол

$x$ -г ол.

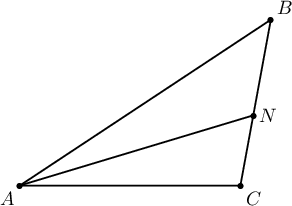
A.

$2$ B.

$3$ C.

$4$ D.

$\dfrac{10}{3}$ E.

$\dfrac{3}{10}$

Биссектрисийн чанар

$ABC$ гурвалжны

$AB=6$ ,

$AC=12$ ,

$BC=9$ байв.

$D$ цэг нь

$A$ оройгоос татсан дотоод өнцгийн биссектриссийн суурь бол

$CD$ -г ол.

A. 2 B. 3 C. 4 D. 5 E. 6

ЭЕШ 2020, B23

$AD$ ,

$BC$ суурьтай

$ABCD$ трапецийн

$A$ ба

$B$ оройн биссектрисүүдийн огтлолцлын цэг

$K$ байв.

$ABK$ гурвалжныг багтаасан тойргийн радиус

$R=5$ бол

$AB$ талын уртыг ол.

A.

$10$ B.

$2\sqrt{5}$ C.

$5$ D.

$25$ E.

$20$

ЭЕШ 2020, A23

$AD$ ,

$BC$ суурьтай

$ABCD$ трапецийн

$A$ ба

$B$ оройн биссектрисүүдийн огтлолцлын цэг

$K$ байв.

$ABK$ гурвалжныг багтаасан тойргийн радиус

$R=3$ бол

$AB$ талын уртыг ол.

A.

$3$ B.

$2\sqrt{3}$ C.

$6$ D.

$9$ E.

$12$

Бодлого №7866

$ABC$ гурвалжны

$AA_1$ биссектрисс,

$CC_1$ медиантай

$O$ цэгт огтлолцож,

$AC=8$ ,

$AB=10$ бол

$\dfrac{C_1O}{CC_1}=\dfrac{\fbox{a}}{\fbox{bc}}$ байна. Мөн

$BO$ шулууны

$AC$ талтай огтлолцох цэгийг

$B_1$ гэвэл

$\dfrac{B_1O}{OB}=\dfrac{\fbox{d}}{\fbox{e}}$ болох бөгөөд

$BA_1={5}$ үед

$AA_1={\fbox{е}}\sqrt{15}$ байна.

Бодлого №7873

$ABC$ гурвалжны талууд

$AB=2$ ,

$AC=3$ бөгөөд

$AL_1$ нь

$\measuredangle BAC=\alpha$ өнцгийн биссектрисс байв.

$L_1$ -ийг дайрсан

$AC$ талтай параллель шулуун

$AB$ талыг

$D$ цэгт огтолдог бол

$DL_1=\dfrac{\fbox{a}}{\fbox{b}}$ байна. Хэрвээ

$BL_1=1$ бол

$AL_1=\fbox{c}\sqrt{2}/2$ ,

$\cos \alpha =\dfrac{\fbox{d}}{\fbox{ef}}$ болно. Мөн энэ үед

$S_{ADL_1C}=\dfrac{\fbox{gh}}{\fbox{ij}}\sqrt{7}$ байна.

Бодлого №7874

$ABC$ гурвалжны талууд

$AB=4$ ,

$AC=3$ бөгөөд

$AL_1$ нь

$\measuredangle BAC=\alpha$ өнцгийн биссектрисс байв.

$L_1$ -ийг дайрсан

$AC$ талтай параллель шулуун

$AB$ талыг

$D$ цэгт огтолдог бол

$DL_1=\dfrac{\fbox{ab}}{7}$ байна. Хэрвээ

$BL_1=4/\sqrt{7}$ бол

$AL_1=\fbox{c}\sqrt{14}/7$ ,

$\cos \alpha =\dfrac{\fbox{d}}{\fbox{e}}$ болно. Мөн энэ үед

$S_{ADL_1C}=\dfrac{\fbox{fg}}{\fbox{hi}}\sqrt{7}$ байна.

Бодлого №7903

$ABC$ гурвалжны талууд

$AB=5$ ,

$BC=7$ ба

$\cos \alpha=-\dfrac{1}{5}$ бол

$AC=\fbox{a}$ ,

$S_{ABC}=4\sqrt{\fbox{b}}$ болно. Мөн уг гурвалжинд багтсан тойргийн радиус

$\sqrt{\fbox{c}}/\fbox{d}$ , багтсан ба багтаасан тойргийн радиусуудын харьцаа

$\displaystyle\dfrac{12}{\fbox{ef}}$ ,

$AL$ биссектриссийн урт

$\displaystyle \sqrt{10}\dfrac{\fbox{g}}{\fbox{h}}$ байна.

Бодлого №7917

$AB=3$ ,

$BC=4$ ,

$AC=5$ талтай гурвалжны биссектриссүүд нь

$AA_1$ ,

$BB_1$ ,

$CC_1$ бол

$\dfrac{A_1B_1}{A_1C_1}=\dfrac{\fbox{ab}\sqrt{87}}{\fbox{cde}}$ ба

$BB_1=\dfrac{12\sqrt{\fbox{f}}}{\fbox{g}}$ болно. Мөн

$\dfrac{S_{AC_1B_1}}{S_{CA_1B_1}}=\dfrac{\fbox{h}}{\fbox{i}}$ байна.

Бодлого №7918

$AB=5$ ,

$BC=4$ ,

$AC=6$ талтай гурвалжны биссектриссүүд нь

$AA_1$ ,

$BB_1$ ,

$CC_1$ бол

$\dfrac{A_1B_1}{A_1C_1}=\dfrac{\fbox{ab}\sqrt{\fbox{cd}}\sqrt{43}}{9}$ ба

$BB_1=\dfrac{\fbox{ef}}{\fbox{g}}$ болно. Мөн

$\left(\dfrac{S_{AC_1B_1}}{S_{CA_1B_1}}\right)^{-1}=\dfrac{\fbox{h}}{\fbox{ij}}$ байна.

Бодлого №7965

$ABC$ гурвалжин өгчээ.

$|AB|=10$ ,

$|BC|=10$ ,

$|AC|=18$ бол

$B$ оройгоос татсан биссектриссийн урт

$\fbox{ab}$ байна.

Бодлого №7966

$ABC$ гурвалжин өгчээ.

$|AB|=15$ ,

$|BC|=12$ ,

$|AC|=18$ бол

$B$ оройгоос татсан биссектриссийн урт

$\fbox{ab}$ байна.

Бодлого №7973

$ABC$ гурвалжны

$AB$ ,

$BC$ ,

$AC$ талуудыг харгалзан

$x$ ,

$y$ ,

$z$ гээд

$AB>AC$ гэж үзье.

$A$ өнцгийн дотоод болон гадаад өнцгийн биссектриссүүдийн

$BC$ талыг огтлох цэгүүд харгалзан

$D$ ,

$E$ бол

$DE=\dfrac{\fbox{a} xyz}{z^{\fbox{b}}-y^{\fbox{c}}}$ болох ба

$x=6$ ,

$y=5$ ,

$z=7$ үед

$DE=\dfrac{\fbox{de}}{\fbox{f}}$ байна.

Бодлого №7974

$ABC$ гурвалжны

$AB$ ,

$BC$ ,

$AC$ талуудыг харгалзан

$x$ ,

$y$ ,

$z$ гээд

$AB>AC$ гэж үзье.

$A$ өнцгийн дотоод болон гадаад өнцгийн биссектриссүүдийн

$BC$ талыг огтлох цэгүүд харгалзан

$D$ ,

$E$ бол

$DE=\dfrac{\fbox{a} xyz}{y^{\fbox{b}}-z^{\fbox{c}}}$ болох ба

$x=4$ ,

$y=8$ ,

$z=6$ үед

$DE=\dfrac{\fbox{de}}{\fbox{f}}$ байна.

Бодлого №2311

Гурвалжны

$2$ тал нь харгалзан

$6$ см ба

$8$ см байв. Уг

$2$ талд татсан медианууд нь хоорондоо перпендикуляр бол гурвалжны талбайг ол.

Бодлого №2312

Гурвалжны суурийн урт

$26$ см, хажуу талуудад буулгасан медианууд нь харгалзан

$30$ ба

$39$ см бол гурвалжны талбайг ол.

Бодлого №2313

Гурвалжны медианууд нь

$3$ см,

$4$ см,

$5$ см урттай. Гурвалжны талбайг ол.

Бодлого №2314

Гурвалжны суурь нь

$14$ см. Хажуу талууд руу нь буулгасан медиануудын урт нь харгалзан

$3\sqrt {7}, 6\sqrt {7}$ см. Гурвалжны хажуу талуудыг ол.

Бодлого №2325

$ABC$ гурвалжны

$AM$ медиан нь

$BN$ медиантай перпендикуляр. Хэрэв

$AM=3$ ,

$BN=4$ бол гурвалжны талбайг ол.

Бодлого №2327

$ABC$ гурвалжны

$B$ ,

$C$ өнцгүүд өгөгдөв (

$\angle B\neq\angle C$ ).

$A$ оройгоос татсан медианы

$BC$ талтай үүсгэх хурц өнцөг

$x$ -ийн котангенсийг ол.

Бодлого №2328

Хурц өнцөгт

$ABC$ гурвалжны

$BM$ ,

$CN$ медианууд ба

$AH$ өндрийн урт нь харгалзан

$4$ ,

$5$ ,

$6$ . Гурвалжны талбайг ол.

Бодлого №2330

Гурвалжны

$2$ талын урт нь

$1$ ба

$\sqrt {13}$ . Гурав дахь талын медиан нь

$2$ бол гурвалжны талбайг ол.

Бодлого №2331

$ABC$ гурвалжны

$AD$ болон

$BE$ медианууд нь перпендикуляр ба

$AC=3$ ,

$BC=4$ бол

$AB$ талыг ол.

Бодлого №2335

Гурвалжны

$2$ тал нь

$1$ см ба

$\sqrt{15}$ см. Гурав дахь талын медиан нь

$2$ см бол гурвалжны талбайг ол.

Бодлого №2339

Гурвалжны

$2$ талын урт

$a, b$ . Хэрэв гурав дахь тал нь түүнд буулгасан медианы урттай тэнцүү гэвэл түүний уртыг ол.

Бодлого №2342

Гурвалжны

$2$ тал нь

$27$ ,

$29$ . Гурав дахь талд буулгасан медианы урт

$26$ .

$27$ урттай талд буулгасан өндрийн уртыг ол.

Бодлого №2357

$ABC$ гурвалжны

$AD$ ,

$CE$ медианууд перпендикуляр ба

$AB=c$ ,

$BC=a$ бол

$AC$ -г ол.

Бодлого №2370

$ABC$ гурвалжны

$AD$ медиан болон

$BE$ биссектрисүүд харилцан перпедикуляр ба

$F$ цэгт огтлолцоно.

$DEF$ гурвалжны талбай нь

$5$ бол

$ABC$ гурвалжны талбайг ол.

Бодлого №2377

$ABC$ гурвалжны талбай нь

$12$ .

$B$ оройгоос

$BD$ медианы урт

$3$ . Хэрэв

$\angle ABD=90^\circ$ бол

$AC$ талыг ол.

Бодлого №2387

Адил хажуут

$ABC$ (

$AB=BC$ ) гурвалжинд

$AD$ медиан татав.

$\angle B=\alpha$ бол

$\angle BAD$ өнцгийг ол.

Бодлого №2396

Оройн өнцөг нь

$\alpha$ байх адил хажуут гурвалжин өгөгдөв. Суурь ба хажуу тал руу буулгасан медиан хоёрын хоорондох өнцгийг ол.

Бодлого №2397

Суурь нь

$\sqrt {32}$ , хажуу тал руу буулгасан медиан нь

$5$ байх адил хажуут гурвалжин өгөгдөв. Хажуу талыг ол.

Бодлого №2411

Адил хажуут гурвалжны суурь нь

$10$ ба талбай нь

$60$ . Хажуу талд буулгасан медианы уртыг ол.

Бодлого №2413

Адил хажуут гурвалжны хажуу тал нь

$4\sqrt {10}$ , хажуу талд татсан медиан нь

$3\sqrt{10}$ . Гурвалжны суурийн уртыг ол.

Бодлого №2422

Адил хажуут

$ABC$ гурвалжны суурь нь

$AC$ .

$D$ цэг

$BC$ талыг

$M$ -ээс

$2:1$ харьцаанд хуваах ба

$E$ цэг

$AB$ талын дундаж.

$CED$ гурвалжны

$CQ$ медиан нь

$\sqrt{23}/2$ ,

$DE=\sqrt{23}/2$ .

$ABC$ гурвалжныг багтаасан тойргийн радиусыг ол.

Бодлого №2433

Адил хажуут гурвалжны хажуу тал

$6$ см, хажууд буулгасан медиан

$5$ см бол суурийн уртыг ол.

Бодлого №2436

Адил хажуут гурвалжны суурь

$\sqrt{84}$ , суурийн эсрэг өнцөг

$30^\circ$ бол хажуу талд буулгасан медианы уртыг ол.

Бодлого №2438

Адил хажуут гурвалжны хажуу талд буулгасан медиан периметрийг

$15$ ,

$6$ гэсэн урттай 2 хэсэгт хуваана. Хажуу талын уртыг ол.

Бодлого №2454

$ABC$ гурвалжны

$\angle C=30^\circ$ байв.

$B$ тэгш өнцгийн оройгоос татсан медиан нь

$BK$ ба

$AB$ катетын урт нь

$4$ см бол

$BCK$ гурвалжны талбайг ол.

Бодлого №2458

Тэгш өнцөгт гурвалжны гипотенузд буусан медиан уг гурвалжныг

$p_1$ ,

$p_2$ периметртэй 2 гурвалжинд хуваасан бол гурвалжны талуудыг ол.

Бодлого №2459

Тэгш өнцөгт гурвалжны медиануудын огтлолцлын цэгээс катетууд хүртэлх зайнууд нь

$3$ ба

$4$ . Энэ цэгээс гипотенуз хүртэлх зайг ол.

Бодлого №2471

Тэгш өнцөгт гурвалжны тэгш өнцгийн оройгоос татсан өндрийг медианд нь харьцуулсан харьцаа

$2:3$ . Гурвалжны хурц өнгүүдийг ол.

Бодлого №2472

Тэгш өнцөгт гурвалжны катетуудын харьцаа

$1/2$ . Хурц өнцгүүдээс татсан медиануудын хоорондох хурц өнцгийн тангенсийг ол.

Бодлого №2474

Тэгш өнцөгт гурвалжны

$AC$ ,

$BC$ катетуудын урт харгалзан

$12$ ба

$8$ .

$K$ нь

$BD$ медианы дундаж цэг бол

$CK$ -г ол.

Бодлого №2476

Тэгш өнцөгт гурвалжны хурц өнцгүүдээс татсан медианууд

$89$ ба

$156$ . Гипотенузын уртыг ол.

Бодлого №2483

$ABC$ тэгш өнцөгт гурвалжны гадна талд түүний

$AC, BC$ катетууд дээр

$ACDE$ ,

$BCFG$ квадратууд байгуулав.

$ABC$ гурвалжны

$CM$ медианы үргэлжлэл

$DF$ шулууныг

$N$ цэгт огтолно. Хэрэв катетуудын урт нь

$1$ ба

$4$ бол

$CN$ -г ол.

Бодлого №2488

Тэгш өнцөгт гурвалжны тэгш өнцгийн оройгоос өндөр ба медиан татав. Хэрэв өндрийг медианд харьцуулсан харьцаа

$12/13$ бол гурвалжны их катетыг бага катетад харьцуулсан харьцааг ол.

Бодлого №2681

Гурвалжны нэг оройгоос татсан медиан ба өндөр нь оройн өнцөгөө

$3$ тэнцүү хэсэгт хуваах ба медиан нь 10 см урттай бол гурвалжны талуудыг ол.

Бодлого №2683

$ABC$ гурвалжны

$AD$ биссектрис нь

$BC$ талыг

$BD:CD=2:1$ харьцаагаар хуваах бол

$CE$ медиан нь биссектрисийг ямар харьцаатай хуваах вэ?

Бодлого №2686

$ABC$ гурвалжны

$BD$ медиан дээр

$BE=3ED$ байх

$E$ цэг авав.

$AE$ шулуун

$BC$ талыг

$M$ цэгт огтолно.

$AMC$ ба

$ABC$ гурвалжны талбайн харьцааг ол.

Бодлого №2688

$ABC$ гурвалжны талбай

$40$ см.кв,

$AD$ биссектрис

$BC$ талыг

$BD:DC=3:2$ байхаар хуваана.

$AD$ биссектрис

$BK$ медианыг

$E$ цэгт огтолно.

$EDCK$ дөрвөн өнцөгтийн талбайг ол.

Бодлого №2695

$ABC$ гурвалжны

$AH$ биссектрис

$BE$ медианыг

$BK:KE=2$ харьцаагаар хуваах ба

$ABC$ өнцөг

$45^\circ$ байв.

$BCE$ гурвалжны талбайг энэ гурвалжныг багтаасан дугуйн талбайд харьцуулсан харьцааг ол.

Бодлого №2699

$ABC$ гурвалжны

$AM$ ба

$BK$ медиануудын үргэлжилэл багтаасан тойргийг харгалзан

$E$ ба

$F$ цэгээр огтлох ба

$AE:AM=2:1$ ,

$BF:BK =3:2$ байв.

$ABC$ гурвалжны өнцөгүүдийг ол.

Бодлого №2700

$ABC$ гурвалжны

$AM, BK$ медиануудын үргэлжлэлүүд уг гурвалжныг багтаасан тойргийг харгалзан

$E$ ба

$F$ цэгт огтолох ба

$AE:AM=2:1$ ,

$BF:BK=3:2$ байв.

$ABC$ гурвалжны өнцгүүдийг ол.

Бодлого №2703

$ABC$ гурвалжны

$BE$ биссекрис ба

$AD$ медиан нь перпендикуляр бөгөөд ижилхэн

$4$ урттай.

$ABC$ гурвалжны талуудыг ол.

Бодлого №2707

Гурвалжны талуудын урт

$a=6$ ,

$b=8$ ба талбай нь

$S=3\sqrt 5$ байв. Гурав дахь талын урт нь уг талд буулгасан медианаас 2 дахин богино бол багтсан тойргийн радиусыг ол.

Бодлого №2708

$PQR$ гурвалжны

$Q$ оройноос татсан медианы урт

$\dfrac{3\sqrt{21}}{4}$ .

$P$ ба

$R$ орой дээр төвтэй

$5$ ба

$1$ радиустай тойргууд бие биеэ шүргэх ба

$Q$ орой нь эдгээр тойргуудын ерөнхий шүргэгч дээр байв. Хэрэв

$S< 7$ бол

$PQR$ гурвалжны талбай

$S$ -г ол.

Бодлого №2717

Адил хажуут гурвалжны медиануудын огтолцлын цэг ба биссектрисүүдийн огтлолцлын цэг нь хоорондоо

$2$ зайтай байв. Хэрэв уг гурвалжинд багтсан тойргийн урт

$20\pi$ бол гурвалжны периметрийг ол.

Бодлого №2725

Тэгш өнцөгт

$ABC$ (

$\angle B=90^\circ$ ) гурвалжны

$AM$ медиан ба

$CD$ биссектрис

$O$ цэгт огтлолцов. Хэрэв

$CO=9$ ,

$OD=5$ гэвэл

$ABC$ гурвалжны талбайг ол.

Бодлого №2778

$AOB$ гурвалжныг

$O$ цэгийг тойруулан

$90^{\circ}$ эргүүлэхэд

$A$ цэг

$A_1$ цэгт,

$B$ цэг

$B_1$ цэгт буув.

$OAB_1$ гурвалжны

$AB_1$ талд буулгасан медиан

$OA_1B$ гурвалжны

$A_1B$ талд буулгасан медиантай перпендикуляр болохыг батал.

Бодлого №2787

Хурц өнцөгт

$ABC$ гурвалжны

$AD$ өндөр,

$BE$ медиан,

$CF$ биссектрис гурав

$O$ цэгт огтлолцоно. Хэрэв

$OE=2OC$ бол

$C$ өнцгийг ол.

Бодлого №2790

$ABC$ гурвалжинд багтсан тойрог

$BM$ медианыг 3 тэнцүү хэсэгт хуваадаг.

$BC:CA:AB$ харьцааг ол.

Бодлого №2792

$ABC$ гурвалжны

$C$ оройгоос татсан медиан, биссектрис ба өндөр нь харгалзан 6, 5 ба 2 гэсэн урттай.

$AB$ талын уртыг ол.

Гурвалжны өнцгүүд

Тэгш өнцөгт гурвалжны хурц өнцгөөс татсан медиануудын уртын харьцаа

$2\sqrt{2}:\sqrt{17}$ бол гурвалжны хурц өнцгүүдийг ол.

A.

$\arctg3$ ,

$\dfrac\pi2-\arctg3$ B.

$\dfrac{\pi}{5}$ ,

$\dfrac{3\pi}{10}$ C.

$\dfrac{\pi}{4}$ ,

$\dfrac{\pi}{4}$ D.

$\dfrac{\pi}{6}$ ,

$\dfrac{\pi}{3}$ E.

$\arctg2$ ,

$\dfrac\pi2-\arctg2$

Медиануудаар үүсэх гурвалжин

Гурвалжны медиануудуудын урт нь 3, 4, 5 байв. Гурвалжны талбайг ол.

A.

$1$ B.

$4$ C.

$6$ D.

$8$ E.

$10$

Медианы урт

Гурвалжны хоёр талын урт 22, 46 нэгж, гурав дахь талын медиан 20 нэгж бол тэр талын урт нь аль нь вэ?

A. 60 B. 72 C. 48 D. 50 E. 55

Перпендикуляр медианууд

Гурвалжны 9, 12 урттай медианууд перпендикуляр байв. Талбайг ол.

A. 108 B. 96 C. 84 D. 72 E. 60

Медианы урт

$ABC$ гурвалжны

$AB=3$ ,

$AC=4$ ,

$BC=5$ бол

$AD$ медианы урт аль нь вэ?

A.

$2$ B.

$2.5$ C.

$3$ D.

$3.5$ E.

$4$

Медианы урт

$ABC$ гурвалжны талууд нь

$5, 7, 8$ бол хамгийн урт медианы уртыг ол.

A.

$\sqrt{21}$ B.

$\sqrt{201}/2$ C.

$\sqrt{129}/2$ D.

$\sqrt{65}/2$ E.

$5\sqrt{20}$

Медиануудаар байгуулсан гурвалжин

Талууд нь

$a,b,c$ урттай гурвалжны медиануудаар байгуулсан гурвалжны медиануудын урт аль вэ?

A.

$\dfrac45a, \dfrac45b, \dfrac45c$ B.

$\dfrac35a, \dfrac35b, \dfrac35c$ C.

$\dfrac34a, \dfrac34b, \dfrac34c$ D.

$\dfrac23a, \dfrac23b, \dfrac23c$ E.

$\dfrac32a, \dfrac32b, \dfrac32c$

Бодлого №7684

$a,b$ талтай

$ABCD$ параллелограммын

$DA,DC$ талын дундажууд болон

$B$ оройг холбоход үүссэн гурвалжны медианы урт өгсөн хоёр тал болон

$BD=d$ диагоналиар илэрхийлбэл аль нь вэ?

A.

$\frac45a, \frac45b, \frac45d$ B.

$\frac35a, \frac35b, \frac35d$ C.

$\frac34a, \frac34b, \frac34d$ D.

$\frac23a, \frac23b, \frac23d$

Адил хажуут гурвалжны медиан

Адил хажуут гурвалжны нэг хажуу талын медиан периметрийг 15 см, 6 см урт хэсгүүдэд хуваасан бол гурвалжны талуудын урт хэд хэд вэ?

A. 3, 9, 9 B. 5, 8, 8 C. 13, 4, 4 D. 1, 10, 10 E. 2, 9, 9

Адил хажуут гурвалжны медиан

27 см периметртэй адил хажуут гурвалжны нэг хажуу талын медиан периметрийг 1:2 харьцаатай хэсгүүдэд хуваасан бол талууд нь ямар ямар байх вэ?

A. 10, 10, 7 B. 15, 6, 6 C. 11, 8, 8 D. 12, 12, 3 E. 13, 7, 7

Медианы урт

Гурвалжны хоёр талын урт 11, 23 нэгж, гурав дахь талын медиан 10 нэгж бол тэр талын урт аль нь вэ?

A.

$25$ B.

$30$ C.

$36$ D.

$24$ E.

$26$

Гурвалжны медиан

Гурвалжны нэг тал 10 см, нөгөө хоёр талын медиан 9 см, 12 см бол талбай нь аль вэ?

A.

$36$ см.кв B.

$72$ см.кв C.

$108$ см.кв D.

$144$ см.кв E.

$150$ см.кв

Медиануудын огтлолцол

Адил хажуут гурвалжны талбай

$4.8$ , хоёр медианы урт

$3$ нэгж бол медиануудын огтлолцлоос суурийн харагдах өнцөг аль вэ?

A.

$\arcsin\frac35$ B.

$\arccos\frac35$ C.

$75^\circ$ D.

$60^\circ$ E.

$\arccos\frac35$ ,

$\pi-\arccos\frac35$

Бодлого №7721

$ABC$ гурвалжны

$AL_1$ биссектрис,

$CM_3$ медиантай

$P$ цэгт огтлолцжээ. Хэрэв

$AC=4$ см,

$AB=6$ см бол

$CP:PM_3$ аль вэ?

A. 3:2 B. 4:3 C. 2:3 D. 1:2

Бодлого №7722

$AB=12$ см,

$AC=9$ см гурвалжинд

$AL_1$ биссектрис,

$CM_3$ медиантай

$P$ цэгт огтлолцжээ.

$AP:PL_1$ аль вэ?

A. 7:4 B. 4:3 C. 7:3 D. 1:7

Медиануудаар үүсэх жижиг гурвалжны талбай

Хэрэв

$m,n$ урттай перпендикуляр хоёр медиантай гурвалжны нэг тал

$a$ урттай бол энэ талын өндрийн урт аль нь вэ?

A.

$\dfrac{mn}{2a}$ B.

$\dfrac{4mn}{3a}$ C.

$\dfrac{3mn}{4a}$ D.

$\dfrac{m^2+n^2}{2a}$ E.

$\dfrac{m^2+n^2}{4a}$

Бодлого №7732

$ABC$ гурвалжны

$B$ ,

$C$ хоёр оройгоос татсан медианы урт

$6$ ба

$4.5$ ,

$BC=5$ бол энэ талд буусан өндрийн урт аль нь вэ?

A.

$5$ B.

$4.5$ C.

$7.2$ D.

$6$ E.

$6.5$

Бодлого №7733

$AB=15$ ,

$BC=6$ ба

$AC$ талын медианы урт

$3\sqrt{11}$ бол

$\measuredangle ABC$ хэдэн градус вэ?

A.

$60^\circ$ B.

$\arccos\frac34$ C.

$\arcsin0.4$ D.

$\arccos0.3$

Гурвалжны медиан

$24$ см.кв талбайтай гурвалжны хоёр медиан 6 см, 8 см урт бол тэдгээрийн хоорондох өнцөг аль нь вэ?

A.

$60^\circ$ B.

$\arcsin\dfrac23$ C.

$\arcsin\dfrac34$ D.

$30^\circ$ E.

$\arccos\dfrac23$

Бодлого №7738

$ABC$ гурвалжны

$BC$ талын медианы үргэлжлэл багтаасан тойрогтой

$D$ цэгт огтлолцсон. Хэрэв медиануудын огтлолцол

$M$ ,

$S_{ABC}:S_{DBC}=3:5$ бол

$MBC$ ,

$DBC$ хоёр гурвалжны

$M,D$ оройгоос татсан өндрүүдийн харьцаа ямар байх вэ?

A.

$3:8$ B.

$1:5$ C.

$2:5$ D.

$1:3$

Перпендикуляр медианууд

Гурвалжны 6, 27 урттай медианууд перпендикуляр байв. Талбайг ол.

A. 108 B. 96 C. 86 D. 78 E. 72

Медиануудаар үүсэх гурвалжин

Гурвалжны медиануудуудын урт нь 5, 12, 13 байв. Гурвалжны талбайг ол.

A.

$5$ B.

$20$ C.

$30$ D.

$40$ E.

$50$

Бодлого №7866

$ABC$ гурвалжны

$AA_1$ биссектрисс,

$CC_1$ медиантай

$O$ цэгт огтлолцож,

$AC=8$ ,

$AB=10$ бол

$\dfrac{C_1O}{CC_1}=\dfrac{\fbox{a}}{\fbox{bc}}$ байна. Мөн

$BO$ шулууны

$AC$ талтай огтлолцох цэгийг

$B_1$ гэвэл

$\dfrac{B_1O}{OB}=\dfrac{\fbox{d}}{\fbox{e}}$ болох бөгөөд

$BA_1={5}$ үед

$AA_1={\fbox{е}}\sqrt{15}$ байна.

$ABC$ гурвалжны талууд

$AB=2$ ,

$AC=3$ ,

$BC=4$ ба

$AM_1$ медианы үргэлжлэл уг гурвалжныг багтаасан тойргийг

$A_1$ цэгт огтолдог гэе.

$M_1A_1=\dfrac{\sqrt{2}\fbox{a}}{\sqrt{\fbox{b}}}$ ба

$A_1BC$ гурвалжны периметр нь

$\fbox{c}+2\sqrt{\fbox{de}}$ байна. Мөн

$A_1BC$ гурвалжны талбай

$\dfrac{\fbox{f}\sqrt{\fbox{gh}}}{\fbox{i}}$ болно.

$ABC$ гурвалжны талууд

$AB=4$ ,

$AC=5$ ,

$BC=6$ ба

$AM$ медианы үргэлжлэл уг гурвалжныг багтаасан тойргийг

$A_1$ цэгт огтолдог гэе.

$MA_1=\dfrac{\fbox{a}}{\fbox{bc}}\sqrt{46}$ ба

$A_1C$ талын урт

$\dfrac{\fbox{de}}{\fbox{fg}}\sqrt{\fbox{46}}$ байна. Мөн

$A_1BC$ гурвалжны талбай

$\dfrac{\fbox{hij}}{46}\sqrt{7}$ болно.

Бодлого №7885

Тэгш өнцөгт

$ABC$ гурвалжны

$BC$ гипотенуз ба

$AB$ катетад буулгасан медианы суурийг харгалзан

$A_1$ ,

$C_1$ , тэдгээрийн огтлолыг

$O$ гэе.

$BC=3\sqrt{6}$ ,

$AC=3\sqrt{2}$ бол

$\cos\widehat{C_1CA}=\sqrt{\fbox{a}}/{\fbox{b}}$ ,

$S_{OC_1A}+S_{OA_1C}={\fbox{c}\sqrt{\fbox{d}}}$ ,

$OAC$ гурвалжинд багтсан тойргийн радиус

$\fbox{e}\sqrt{2}/s$ байна. Энд

$s=3\sqrt{2}+2\sqrt{3}+\sqrt{6}$ юм.

Бодлого №7886

$ABC$ тэгш өнцөгт гурвалжны

$BC$ гипотенуз ба

$AB$ катетад буулгасан медианы суурийг харгалзан

$A_1$ ,

$C_1$ , тэдгээрийн огтлолыг

$O$ гэе.

$AB=8$ ,

$BC=4\sqrt{6}$ бол

$\cos\widehat{CC_1B}=-\sqrt{\fbox{a}}/{\fbox{b}}$ ,

$S_{OA_1C_1}+S_{OAC}=\fbox{cd}\sqrt{2}/3$ ,

$OA_1C_1$ гурвалжинд багтсан тойргийн радиус

$\fbox{e}\sqrt{2}/s$ байна. Энд

$s=3\sqrt{2}+2\sqrt{3}+\sqrt{6}$ юм.

Бодлого №7909

$ABC$ гурвалжины

$CC_1$ ,

$AA_1$ медианууд харилцан перепендикуляр бөгөөд урт нь харгалзан

$3$ ,

$4$ байв.

$AC$ талын урт

$\dfrac{\fbox{ab}}{\fbox{c}}$ ба

$BH$ өндөр нь

$\dfrac{\fbox{de}}{5}$ болно.

$ABC$ гурвалжны медиануудын огтлолцлын цэг

$M$ бол

$S_{A_1C_1M}=\fbox{f}$ байна.

Бодлого №7910

$ABC$ гурвалжны

$AA_1$ ,

$CC_1$ медианууд харилцан перепендикуляр бөгөөд урт нь харгалзан

$9$ ,

$12$ байв.

$AC$ талын урт

${\fbox{ab}}$ ба

$BH$ өндөр нь

$\dfrac{\fbox{cd}}{\fbox{e}}$ ,

$S_{BA_1C_1}=\fbox{fg}$ байна.

Бодлого №7915

$ABC$ гурвалжны хувьд

$\sin^2 \alpha +\sin^2 \beta =\sin^2 \gamma$ нөхцөл биелдэг бол

$\gamma =\dfrac{\pi}{\fbox{a}}$ байна.

$AB=2\sqrt{3}$ үед

$CM$ медианы урт

$\sqrt{\fbox{b}}$ болно.

$AB=2\sqrt{3}$ талтай, эсрэг оройн өнцөг нь тогтмол

$\dfrac{\pi}{\fbox{a}}$ байх бүх гурвалжнууд дотроос хамгийн их талбайтай гурвалжны периметр

$(\fbox{c}\sqrt{\fbox{d}}+2\sqrt{3})$ байна.

Бодлого №2321

Гурвалжны өндөр нь

$12$ см, суурь нь

$14$ см, хоёр хажуу талын нийлбэр нь

$28$ см бол хоёр хажуу талыг нь ол.

Бодлого №2326

$ABC$ гурвалжныг багтаасан тойргийн

$B$ оройг дайрсан шүргэгч шулуунаас

$A, C$ цэгүүд хүртэлх зайнууд харгалзан

$4$ см ба

$9$ см.

$B$ оройгоос татсан өндрийн уртыг ол.

Бодлого №2328

Хурц өнцөгт

$ABC$ гурвалжны

$BM$ ,

$CN$ медианууд ба

$AH$ өндрийн урт нь харгалзан

$4$ ,

$5$ ,

$6$ . Гурвалжны талбайг ол.

Бодлого №2329

Гурвалжны суурь нь

$6$ . Хажуу талууд руу буулгасан өндрүүд нь харгалзан

$2$ ба

$2\sqrt{3}$ . Гурвалжны хажуу талуудыг ол.

Бодлого №2334

$BD$ нь

$ABC$ гурвалжны өндөр,

$E$ нь

$BC$ талын дундаж байг. Хэрэв

$AB=30$ см,

$BC=26$ см,

$AC=28$ см бол

$BDE$ гурвалжныг багтаасан тойргийн радиусыг ол.

Бодлого №2336

$ABC$ гурвалжны

$B$ оройгоос

$BD$ өндөр,

$BL$ биссектрис татав. Хэрэв

$ABC$ гурвалжны

$AB=6.5$ ,

$BC=7.5$ ,

$AC=7$ бол

$BLD$ гурвалжны талбайг ол.

Бодлого №2341

$ABC$ гурвалжны

$BC$ ,

$AC$ ,

$AB$ талуудын урт нь харгалзан

$41$ ,

$51$ ,

$58$ . Гурвалжны талбайг ба

$B$ оройгоос буулгасан өндрийг ол.

Бодлого №2342

Гурвалжны

$2$ тал нь

$27$ ,

$29$ . Гурав дахь талд буулгасан медианы урт

$26$ .

$27$ урттай талд буулгасан өндрийн уртыг ол.

Бодлого №2343

$ABC$ гурвалжны

$AD$ өндөр

$BC$ талаас

$4$ см-ээр бага,

$AC$ талын урт

$5$ см. Хэрвээ гурвалжны талбай нь

$16$ см.кв бол түүний периметрийг ол.

Бодлого №2358

$ABC$ гурвалжинд

$AE, CD$ өндрүүд татав. Хэрэв

$BD=18$ ,

$BC=30$ ,

$AE=20$ бол

$AB$ -г ол.

Бодлого №2362

Хурц өнцөгт

$ABC$ гурвалжинд

$CC_1, AA_1$ өндрүүд татав. Хэрэв

$AC=1$ ,

$\angle C_1CA_1=\alpha$ .

$C_1BA_1$ гурвалжныг багтаасан тойргийн талбайг ол.

Бодлого №2363

Хурц өнцөгт

$ABC$ гурвалжинд

$CH, AH_{1}$ өндрүүд татав.

$AC=2$ ба

$HBH_{1}$ гурвалжныг багтаасан тойргийн талбай нь

$\pi/3$ .

$CH$ өндөр ба

$BC$ талуудын хоорондох өнцгийг ол.

Бодлого №2369

$ABC$ гурвалжныг багтаасан тойргийн төвийг дайруулан

$AC$ ,

$BC$ талуудад перпендикуляр шулуун татав. Уг шулуунууд нь

$CH$ өндрийг эсвэл үргэлжлэлийг

$P$ ба

$Q$ цэгүүдээр огтолно.

$CP=p$ ,

$CQ=q$ бол

$ABC$ гурвалжныг багтаасан тойргийн радиусыг ол.

Бодлого №2372

$ABC$ гурвалжны мохоо өнцөгтэй

$A$ оройгоос

$AD$ өндөр татав.

$D$ цэгт төвтэй

$AD$ радиустай тойрог нь

$AB$ болон

$AC$ талуудыг харгалзан

$M$ ,

$N$ цэгүүдээр огтолсон ба

$AB=c$ ,

$AM=n$ ,

$AN=m$ бол

$AC$ талын уртыг ол.

Бодлого №2373

$ABC$ гурвалжны

$C$ өнцөг нь мохоо ба

$D$ цэг нь

$B$ -г дайрсан

$AB$ -д пердиндикуляр шулуун ба

$C$ -г дайрсан

$AC$ -д перпендикуляр шулуунуудын огтлолцол,

$ADC$ гурвалжны

$C$ оройгоос

$AB$ тал руу буулгасан өндрийн суурь

$M$ байв. Хэрэв

$AM=a$ ,

$MB=b$ бол

$AC$ -г ол.

Бодлого №2375

$ABC$ гурвалжны талууд

$AB=4\sqrt{7}, AC=5\sqrt {7}, BC=6\sqrt {7}$ .

$B$ оройгоос

$ABC$ гурвалжны ортоцентр хүртэлх зайг ол.

Бодлого №2383

Адил хажуут

$ABC$ гурвалжны

$BC$ хажуу руу буулгасан

$AD$ өндөр нь

$ABC$ -г

$ABD$ ,

$ADC$ гурвалжнуудад хуваах ба талбайнууд нь харгалзан

$4\text{ см}^2$ ,

$2\text{ см}^2$ ба

$AC$ нь суурь бол гурвалжны талуудын уртыг ол.

Бодлого №2385

$2a$ суурьтай,

$h$ өндөртэй адил хажуут гурвалжин өгөгдөв. Багтсан тойргийг шүргүүлэн суурьтай нь параллель шулуун татжээ. Тойргийн радиус ба шүргэгч шулууны талуудын хооронд үүсэх хэрчмийн уртыг ол.

Бодлого №2389

Адил хажуут гурвалжны суурийн өнцөг нь

$\alpha$ . Суурьт буулгасан өндрийн хэмжээ нь багтсан тойргийн радиусаас

$m$ -ээр их бол багтаасан тойргийн радиусыг ол.

Бодлого №2393

Суурь нь

$30$ см, суурьт буулгасан өндөр нь

$20$ см-тай тэнцүү байх адил хажуут гурвалжин өгөгдөв. Хажуу тал руу буулгасан өндрийн уртыг ол.

Бодлого №2398

Өндөр нь

$8$ , суурийг хажуу талд харьцуулсан харьцаа нь

$6:5$ байх адил хажуут гурвалжин өгөгдөв. Багтсан тойргийн радиусыг ол.

Бодлого №2399

Адил хажуут

$ABC$ гурвалжны суурийн

$B$ ,

$C$ оройнууд ба

$A$ оройгоос буулгасан өндрийн дундаж

$M$ -ийг дайруулан 2 шулуун татав. Уг шулуунууд нь

$AC$ ,

$AB$ талуудыг харгалзан

$D, E$ цэгүүдээр огтолно. Хэрэв

$ABC$ гурвалжны талбай

$93$ бол

$AEMD$ дөрвөн өнцөгтийн талбайг ол.

Бодлого №2402

Өндрүүдийн огтлолцлын цэг нь нь суурьт буулгасан өндрийг таллан хуваах адил хажуут гурвалжны өнцгүүдийг ол.

Бодлого №2406

Суурь нь

$a$ , хажуу тал нь

$b$ байх адил хажуут гурвалжин өгөгдөв. Хажуу тал руу буулгасан өндрийн уртыг ол.

Бодлого №2407

Адил хажуут гурвалжинд

$r$ радиустай тойрог багтав. Багтсан тойрог нь суурьт буулгасан өндрийг оройг талаас

$1:2$ харьцаатай хэсгүүдэд хуваана. Гурвалжны талбайг ол.

Бодлого №2408

$ABC$ адил хажуут гурвалжин өгөгдсөн ба

$AB=BC=10$ ,

$AC=\sqrt {80}$ .

$B, C$ оройнуудыг дайрсан

$CD$ өндөр дээр төвтэй тойргийн радиусыг ол.

Бодлого №2410

Адил хажуут

$ABC$ гурвалжны

$AD$ өндрийн суурь

$D$ нь

$BC$ талыг

$BD:DC=\sqrt {2}:(2-\sqrt {2})$ харьцаанд хуваана. Гурвалжны өнцгүүдийг ол.

Бодлого №2415

Суурь нь

$30$ , хажуу талд буулгасан өндөр нь

$24$ байх адил хажуут гурвалжин өгөгдөв. Хажуу талын уртыг ол.

Бодлого №2417

Адил хажуут гурвалжны суурьт буулгасан өндөр нь

$5$ , хажуу талд буулгасан өндөр нь

$6$ бол гурвалжны талбайг ол.

Бодлого №2418

Хэрэв суурьт буулгасан өндөр нь

$10$ , хажуу талд буулгасан өндөр нь

$12$ бол адил хажуут гурвалжны талбайг ол.

Бодлого №2420

Адил хажуут гурвалжны суурьд буулгасан өндөр, хажуу талд буулгасан өндрүүд харгалзан

$m, n$ . Гурвалжны талуудыг ол.

Бодлого №2425

Адил хажуут

$ABC$ гурвалжны

$AC$ суурийн урт

$6$ см, суурьт буулгасан өндөр

$4$ см.

$CD$ нь уг гурвалжны өндөр бол

$CDB$ гурвалжны периметрийг ол.

Бодлого №2427

Адил хажуут гурвалжны суурийн

$B, C$ оройнуудыг

$A$ оройгоос

$BC$ талд буулгасан өндрийн дундаж цэг

$M$ -тэй хэрчмээр холбов.

$BM, CM$ хэрчмийн үргэлжлэлүүд

$AC, AB$ талуудыг харгалзан

$D, E$ цэгүүдээр огтлов. Хэрэв

$AEMD$ дөрвөн өнцөгтийн талбай

$16$ бол

$BMA$ гурвалжны талбайг ол.

Бодлого №2428

Адил хажуут гурвалжны суурьт буулгасан өндөр

$10$ см, хажуу талуудад буулгасан өндөр

$12$ см бол талбайг ол.

Бодлого №2430

Адил хажуут гурвалжны талбай

$S$ , суурийн эсрэг оройн өнцөг

$\alpha$ бол суурьт буулгасан өндрийн уртыг ол.

Бодлого №2431

$r$ радиустай тойрогт суурь ба суурьт буулгасан өндрийнх нь нийлбэр тойргийн диаметртэй тэнцүү байх адил хажуут гурвалжин багтаав. Суурьт буулгасан өндрийг ол.

Бодлого №2435

$CE$ нь адил хажуут

$ABC$ (

$AC=CB$ ) гурвалжны өндөр.

$ABC$ гурвалжинд багтсан тойргийн төв

$O$ нь

$CE$ хэрчмийг

$CO=13$ ,

$OE=5$ байх хэрчмүүдэд хуваах бол гурвалжны талуудыг ол.

Бодлого №2437

Адил хажуут гурвалжны суурь ба түүнд буулгасан өндөр

$4$ . Багтаасан тойргийн радиусыг ол.

Бодлого №2440

Адил хажуут гурвалжны хажуу талын урт

$5$ , суурьт буулгасан өндрийн урт

$4$ бол суурийн уртыг ол.

Бодлого №2453

Тэгш өнцөгт гурвалжны катетуудын харьцаа

$3:2$ . Тэгш өнцөгөөс татсан өндөр гипотенузыг нэг нь нөгөөгөөсөө

$2$ см урт хоёр хэсэгт хуваасан бол гипотенузыг ол.

Бодлого №2457

Тэгш өнцөгт гурвалжны периметр

$10$ . Түүний гипотенузд татсан өндөр нь уг гурвалжныг нэгнийх нь периметр

$6$ байх хоёр гурвалжинд хуваав. Нөгөө гурвалжных нь периметрийг ол.

Бодлого №2470

Тэгш өнцөгт гурвалжны гипотенуз нь

$5$ см, харин түүнд татсан өндөр

$2$ см бол багтсан ба багтаасан тойргийн радиусийг ол.

Бодлого №2471

Тэгш өнцөгт гурвалжны тэгш өнцгийн оройгоос татсан өндрийг медианд нь харьцуулсан харьцаа

$2:3$ . Гурвалжны хурц өнгүүдийг ол.

Бодлого №2477

Тэгш өнцөгт гурвалжны тэгш өнцгийн оройгоос буулгасан өндөр гипотенузыг

$6$ ба

$18$ урттай хэсгүүдэд хуваах бол түүний катетуудыг ол.

Бодлого №2480

Тэгш өнцөгт гурвалжны тэгш өнцгийн оройгоос буулгасан өндөр нь гипотенузыг

$9$ ба

$16$ урттай хэсгүүдэд хуваасан бол уг гурвалжинд багтсан тойргийн радиусыг ол.

Бодлого №2481

Тэгш өнцөгт гурвалжны катетууд нь

$15$ ба

$20$ . Багтсан тойргийн төвөөс тэгш өнцгөөс татсан өндөр хүртэлх зайг ол.

Бодлого №2486

$ABC$ гурвалжны

$ACB$ тэгш өнцгөөс

$CD$ биссектрис,

$DM$ ,

$DN$ нь харгалзан

$ADC$ ба

$BDC$ гурвалжнуудын өндрүүд байв. Хэрэв

$AM=4$ ,

$BN=9$ бол

$AC$ -г ол.

Бодлого №2488

Тэгш өнцөгт гурвалжны тэгш өнцгийн оройгоос өндөр ба медиан татав. Хэрэв өндрийг медианд харьцуулсан харьцаа

$12/13$ бол гурвалжны их катетыг бага катетад харьцуулсан харьцааг ол.

Бодлого №2492

Тэгш өнцөгт гурвалжны гипотенуз нь

$125$ см, бага катет нь

$75$ cм байв. Тэгш өнцөгийн оройгоос татсан өндрийн суурь гипотенузыг 2 хэрчимд хуваах ба түүний бага хэрчмээр нь диаметрээ хийсэн тойрог татав. Уг тойргийн өгөгдсөн гурвалжны катетаас таслах хэсгийн уртыг ол.

Бодлого №2495

Тэгш өнцөгт гурвалжны тэгш өнцгийн оройгоос татсан өндөр гипотенузыг

$25,6$ ба

$14,4$ урттай хэсгүүдэд хуваах бол уг гурвалжинд багтсан тойргийн радиусыг ол.

Бодлого №2673

$ABC$ гурвалжны өндрүүдийн огтолцлолын цэгийг

$M$ гэе. Хэрэв

$M'$ цэг нь

$M$ цэгтэй гурвалжны ямар нэг талын хувьд тэгш хэмтэй цэг бол

$ABC$ гурвалжны багтаасан тойрог дээр байхыг батал.

Бодлого №2681

Гурвалжны нэг оройгоос татсан медиан ба өндөр нь оройн өнцөгөө

$3$ тэнцүү хэсэгт хуваах ба медиан нь 10 см урттай бол гурвалжны талуудыг ол.

Бодлого №2697

$ABC$ гурвалжны

$h_a, h_b, h_c$ өндрүүд мэдэгдэж байв.

$ABC$ гурвалжинд багтсан тойргийн радиусийг ол.

Бодлого №2702

$M$ ба

$N$ цэгүүд

$ABC$ гурвалжны

$AC$ тал дээр

$B$ өндрөөс 2 ба 6 гэсэн зайд байв.

$M$ ба

$N$ цэгүүдийг дайрч,

$AB$ шулууныг шүргэх тойргийн радиусыг ол.

$\angle BAC=30^\circ$ .

Бодлого №2704

$AB=14, AC=15, BC=13$ талуудтай

$ABC$ гурвалжны

$CH$ өндөрийн суурийг дайруулан

$AC$ ба

$BC$ -тэй параллель шулуун татав. Эдгээр нь

$BC$ ба

$AC$ талуудыг харгалзан

$M$ ба

$N$ цэгүүдээр огтолно.

$MN$ шулуун нь

$AB$ талын үргэлжлэлийг

$D$ цэгт огтолно.

$BD$ хэрчмийн уртыг ол.

Бодлого №2705

$BMC$ ба

$ANC$ өнцгүүд тэгш байхаар хурц өнцөгт

$ABC$ гурвалжны

$AD$ өндөр дээр

$M$ цэг,

$BP$ өндөр дээр

$N$ цэг тус тус авав.

$M$ ба

$N$ цэгүүдийн хоорондох зай

$4+2\sqrt3$ ба

$\angle MCN=30^\circ$ байв.

$CMN$ гурвалжны

$CL$ биссектрисийн уртыг ол.

Бодлого №2709

Хурц өнцөгт гурвалжны өндөрүүдийн суурийг холбож байгаа хэрчмүүдийн урт

$5, 12, 13$ . Гурвалжны талбайг ол.

Бодлого №2710

Гурвалжинд багтсан тойргийн радиус

$1$ ба түүний өндрүүд бүхэл тоо бол түүний өнцгүүдийг ол.

Бодлого №2722

Тэгш өнцөгт гурвалжны тэгш өнцгийн оройгоос буулгасан өндөр ба биссектрисийн уртууд харгалзан

$3$ ба

$4$ . Гурвалжны талбайг ол.

Бодлого №2779

Дурын

$ABC$ гурвалжны хувьд

$h_a=2p\dfrac{\sin\dfrac{B}{2}\sin\dfrac{C}{2}}{\cos\dfrac{A}{2}}$ болохыг батал.

$h_a$ ---

$A$ оройгоос татсан өндөр,

$2p$ --- гурвалжны периметр.

Бодлого №2786

$ABC$ гурвалжны

$\angle A=\dfrac{\pi}{3}$ ,

$\angle B=\dfrac{\pi}{4}$ .

$ABC$ гурвалжны өндөрүүдийн үргэлжилэл багтаасан тойргийг

$M$ ,

$N$ ба

$P$ цэгүүдээр огтолно.

$ABC$ ба

$MNP$ гурвалжнуудын талбайн харьцааг ол.

Бодлого №2787

Хурц өнцөгт

$ABC$ гурвалжны

$AD$ өндөр,

$BE$ медиан,

$CF$ биссектрис гурав

$O$ цэгт огтлолцоно. Хэрэв

$OE=2OC$ бол

$C$ өнцгийг ол.

Бодлого №2788

$ABC$ гурвалжны

$AB$ талын урт

$3$ ,

$CD$ өндөрийн урт

$3$ . Хэрэв

$AD$ хэрчмийн урт

$BC$ хэрчмийн урттай тэнцүү бол

$AC$ талын уртыг ол.

Бодлого №2792

$ABC$ гурвалжны

$C$ оройгоос татсан медиан, биссектрис ба өндөр нь харгалзан 6, 5 ба 2 гэсэн урттай.

$AB$ талын уртыг ол.

ЭЕШ 2008 E1 №15

$ABC$ гурвалжны хувьд

$BC=2$ ,

$\angle BAC=60^\circ$ ,

$\angle ABC=45^\circ$ ба орто төв нь

$H$ бол

$BH$ хэрчмийн уртыг ол.

A.

$2$ B.

$2\sqrt2$ C.

$\dfrac{\sqrt6}{2}$ D.

$\dfrac{\sqrt2}{2}$ E.

$2\sqrt{6}:3$

ЭЕШ 2008 E №17

$ABC$ гурвалжны хувьд

$AC=4$ ,

$\angle BAC=45{}^\circ ,\; \angle ABC=60{}^\circ$ ба орто төв нь

$H$ бол

$AH$ хэрчмийн уртыг ол.

A.

$\sqrt{6}$ B.

$8\sqrt{2}$ C.

$\dfrac{4\sqrt{6} }{3}$ D.

$\sqrt{2}$ E.

$\dfrac{2\sqrt{2} }{\sqrt{3} }$

$ABC$ гурвалжныг багтаасан тойргийн радиус

$2\sqrt{3}$ ба өндрүүдийн сууриар үүсгэгдэх гурвалжны периметр 9 бол

$ABC$ гурвалжны талбайг ол.

A.

$18\sqrt{3}$ B.

$9\sqrt{3}$ C.

$36\sqrt{3}$ D.

$18$ E.

$36$

Орто төв

$ABC$ гурвалжны орто төв нь

$H$ .

$\measuredangle ACB=105^\circ$ ,

$\measuredangle ABC= 30^\circ$ ба

$AH=8\sqrt2$ бол

$AC$ хэрчмийн уртыг ол.

A.

$4\sqrt2$ B.

$4\sqrt3$ C.

$7$ D.

$5\sqrt2$ E.

$8$

Гурвалжны өндөр олох

$ABC$ гурвалжны талууд

$AB=4$ ,

$AC=7$ ,

$BC=5$ байв.

$CD$ өндрийн уртыг ол.

A.

$3$ B.

$3\sqrt{3}$ C.

$2\sqrt{3}$ D.

$2\sqrt{6}$ E.

$4$

Тэгш өнцөгт гурвалжны катетуудын урт нь 10, 24. Гурвалжны тэгш өнцгийн оройгоос татсан өндрийн уртыг ол.

A.

$9\dfrac{3}{13}$ B.

$9$ C.

$10\dfrac{3}{13}$ D.

$9\dfrac{5}{13}$ E.

$10$

Гурвалжны дотор орших цэг

Гурвалжны дотор орших цэгээс талууд хүртэлх зайг, тэр талд буусан өндөрт харьцуулсан харьцааны нийлбэр хэд байх вэ?

A.

$1$ B.

$\dfrac13$ C.

$\dfrac23$ D.

$\dfrac12$ E. гурвалжны хэлбэрээс хамаарна

Гурвалжны өндрүүдийн урвуугийн нийлбэр

Гурвалжны гурван өндрийн урвуу хэмжигдэхүүний нийлбэр ямар байх вэ?

$r$ ,

$R$ нь харгалзан багтсан ба багтаасан тойргийн радиус

A.

$\dfrac1r$ B.

$\dfrac1R$ C.

$\dfrac{R}{r^2}$ D.

$\dfrac{r^2}{R}$ E. Аль нь ч биш

Гурвалжны өндөр ба талбай

$ABC$ гурвалжны

$BC,AC$ талуудад буулгасан өндөр харгалзан

$AH_1,BH_2$ бөгөөд

$BC=16$ ,

$CA=12$ ,

$BH_2-AH_1=2$ бол эдгээр өндрийн урт хэд байх вэ?

A. 3, 5 B. 8, 10 C. 6, 8 D. 5, 7 E. 7, 9

Бодлого №7692

$ABC$ гурвалжны

$AH_1,BH_2$ өндрүүд

$H$ цэгт огтлолцжээ. Хэрэв

$\measuredangle H_1HB=30^\circ$ ,

$AH_1=3\sqrt3$ ,

$BH_1=4$ ,

$\measuredangle B>\measuredangle A$ бол

$BC$ ,

$AC$ хоёр талын урт хэд хэд байх вэ?

A.

$6\sqrt3, 5$ B.

$8, 10\sqrt3$ C.

$6\sqrt3, 8$ D.

$9, 13$

Бодлого №7696

Катетууд нь

$3:7$ гэж харьцдаг тэгш өнцөгт гурвалжны гипотенузэд буулгасан өндөр 42 см бол түүний сууриар гипотенузийн хуваагдсан хэсгүүдийн урт хэд вэ?

A. 16, 100 B. 18, 98 C. 20, 96 D. 22, 94 E. 26, 90

Орто төв хүртэлх зай нь багтаасан тойргийн радиус болох гурвалжин

$ABC$ гурвалжны өндрүүдийн огтлолцол (ортотөв)

$H$ , багтаасан тойргийн радиус

$R$ ,

$CH=R$ байсан бол

$\measuredangle BCA$ ямар хэмжээтэй байх вэ?

A.

$30^\circ$ B.

$75^\circ$ C.

$45^\circ$ D.

$60^\circ$ E.

$90^\circ$

Гипотенуз нь 5, түүнд буусан өндөр 2.4 нэгж бол тэгш өнцөгт гурвалжинд багтсан тойргийн радиус аль нь вэ?

A.

$\dfrac52$ B.

$2$ C.

$\dfrac32$ D.

$1$ E.

$\dfrac12$

Тэгш өнцөгт гурвалжинд багтсан тойргийн радиус 3, гипотенузэд буусан өндөр 8 нэгж бол гипотенузийн урт аль нь вэ?

A.

$8$ B.

$4$ C.

$9$ D.

$5$ E. Ийм гурвалжин олдохгүй

Бодлого №7716

$ABC$ гурвалжинд багтсан тойрог

$BC$ ,

$CA$ ,

$AB$ талыг харгалзан

$A_1$ ,

$B_1$ ,

$C_1$ цэгт шүргэжээ. Хэрэв

$A$ оройгоос өндрүүдийн огтлолцол хүртэлх зай багтаасан тойргийн радиустай тэнцүү бол

$\begin{array}{c} [-7mm]\smile [-2mm] C_1A_1B_1\end{array}$ ямар байх вэ?

A.

$220^\circ$ B.

$240^\circ$ C.

$230^\circ$ D.

$210^\circ$

Бодлого №7723

$ABC$ гурвалжны

$AH_1$ ,

$BH_2$ өндрүүд

$H$ цэгт огтлолцсон бол

$AH:HH_1$ харьцаа аль нь вэ? үүнд:

$\measuredangle BAC=\alpha$ ,

$\measuredangle CBA=\beta$ ,

$\measuredangle ACB=\gamma$ байсан гэж бод.

A.

$\dfrac{\cos\alpha}{\sin\beta\sin\gamma}$ B.

$\dfrac{\sin\alpha}{\cos\beta\cos\gamma}$ C.

$\dfrac{\cos\alpha}{\cos\beta\cos\gamma}$ D.

$\dfrac{\sin\alpha}{\sin\beta\sin\gamma}$ E.

$1$

Бодлого №7724

$ABC$ гурвалжны

$AH_1$ ,

$BH_2$ өндрүүд

$H$ цэгт огтлолцжээ. Хэрэв дотоод өнцгүүд нь

$\alpha,\beta,\gamma$ , багтаасан тойргийн радиус

$R$ бол

$AH\cdot HH_1$ аль нь вэ?

A.

$4R^2\cos\alpha\cos\beta\cos\gamma$ B.

$3R^2\sin\alpha\cos\beta\cos\gamma$ C.

$2R^2\cos\alpha\sin\beta\sin\gamma$ D.

$R^2\sin\alpha\sin\beta\sin\gamma$

Бодлого №7726

$R$ радиустай тойрогт багтсан

$ABC$ гурвалжны

$AH_1$ өндрийн үргэлжлэл багтаасан тойрогтой

$D$ цэгт огтлолцжээ. Хэрэв орто төв нь

$H$ ,

$\measuredangle ABC=\beta$ ,

$\measuredangle BCA=\gamma$ бол

$HD$ -ийн урт аль вэ?

A.

$4R\cos\beta\cos\gamma$ B.

$4R\sin\beta\sin\gamma$ C.

$3R\sin\beta\sin\gamma$ D.

$3R\cos\beta\cos\gamma$

Медиануудаар үүсэх жижиг гурвалжны талбай

Хэрэв

$m,n$ урттай перпендикуляр хоёр медиантай гурвалжны нэг тал

$a$ урттай бол энэ талын өндрийн урт аль нь вэ?

A.

$\dfrac{mn}{2a}$ B.

$\dfrac{4mn}{3a}$ C.

$\dfrac{3mn}{4a}$ D.

$\dfrac{m^2+n^2}{2a}$ E.

$\dfrac{m^2+n^2}{4a}$

Бодлого №7732

$ABC$ гурвалжны

$B$ ,

$C$ хоёр оройгоос татсан медианы урт

$6$ ба

$4.5$ ,

$BC=5$ бол энэ талд буусан өндрийн урт аль нь вэ?

A.

$5$ B.

$4.5$ C.

$7.2$ D.

$6$ E.

$6.5$

Бодлого №7738

$ABC$ гурвалжны

$BC$ талын медианы үргэлжлэл багтаасан тойрогтой

$D$ цэгт огтлолцсон. Хэрэв медиануудын огтлолцол

$M$ ,

$S_{ABC}:S_{DBC}=3:5$ бол

$MBC$ ,

$DBC$ хоёр гурвалжны

$M,D$ оройгоос татсан өндрүүдийн харьцаа ямар байх вэ?

A.

$3:8$ B.

$1:5$ C.

$2:5$ D.

$1:3$

Бодлого №7739

Хурц өнцөгт

$ABC$ гурвалжны

$A,B$ оройгоос буулгасан өндрийн суурь

$H_1$ ,

$H_2$ байжээ. Хэрэв

$\measuredangle ACB=\arccos\frac13$ бол

$S_{ABH_1H_2}:S$ аль нь вэ?

A.

$8:9$ B. 6:7 C. 5:9 D. 4:5

Бодлого №7740

Хурц өнцөгт

$ABC$ гурвалжны өндрүүдийн суурь

$H_1$ ,

$H_2$ ,

$H_3$ , дотоод өнцгүүд нь

$\alpha,\beta,\gamma$ бол

$S_{H_1H_2H_3}:S_{ABC}$ аль нь вэ?

A.

$1:2\sin\alpha\sin\beta\sin\gamma$ B.

$2\cos\alpha\cos\beta\cos\gamma$ C.

$1:(\sin\alpha+\sin\beta+\sin\gamma)$ D.

$\cos\alpha+\cos\beta+\cos\gamma$

Тэгш өнцөгт гурвалжныг багтсан ба багтаасн тойргийн радиус

Тэгш өнцөгт гурвалжинд багтсан тойргийн радиус 4, гипотенузэд буусан өндөр 9 бол багтаасан тойргийн радиус хэд вэ?

A.

$12$ B.

$14$ C.

$16$ D.

$18$ E.

$20$

Өнцгийн котангес

Тэгш өнцөгт

$ABC$ ,

$\measuredangle C=90^\circ$ гурвалжны тэгш өнцгийн оройгоос татсан өндөр

$h$ ,

$\measuredangle A=\alpha$ , өндрийн суурь

$H$ бол

$AH=?$

A.

$\dfrac{h}{\cos\alpha}$ B.

$h\cdot\ctg\alpha$ C.

$h\cdot\tg\alpha$ D.

$\dfrac{h}{\sin\alpha}$ E.

$\dfrac{2h}{\sin2\alpha}$

ЭЕШ 2011 D №17

$ABC$ гурвалжны хувьд

$AC=8$ ,

$\angle ACB=105^\circ$ ,

$\angle ABC=30^\circ$ ба орто төв

$H$ бол

$AH$ хэрчмийн уртыг ол.

A.

$2\sqrt6$ B.

$2\sqrt2$ C.

$8\sqrt2$ D.

$8$ E.

$\dfrac{8\sqrt6}{3}$

Гурвалжны орто төв

$ABC$ гурвалжны хувьд

$\measuredangle BAC=\alpha$ ба багтаасан тойргийн радиус нь

$R$ бол

$A$ оройгоос гурвалжны ортоцентр

$H$ хүртэлх зай аль нь вэ?

A.

$R\cos\alpha$ B.

$R\sin\alpha$ C.

$R\sin2\alpha$ D.

$2R\sin\alpha$ E.

$2R\cos\alpha$

ЭЕШ 2013 A №21

$ABC$ гурвалжны

$A$ ба

$C$ оройн өндрүүд

$H$ цэгт огтлолцоно. Хэрэв

$ABC$ гурвалжныг багтаасан тойргийн радиус

$4$ нэгж ба

$\sin\angle BAH=\dfrac25$ бол

$|BH|=?$

A.

$3\dfrac56$ B.

$3\dfrac15$ C.

$3\dfrac78$ D.

$3$ E.

$3\dfrac13$

Гурвалжны өндөр

$ABC$ адил хажуут гурвалжны

$AB=AC=13$ ,

$BC=10$ байв.

$BD$ өндрийн уртыг ол.

A.

$4$ B.

$4\sqrt2$ C.

$\dfrac{17}{2}$ D.

$8$ E.

$9\dfrac{3}{13}$

Өндрүүдийн хооронд үүсэх өнцөг

$\triangle ABC$ -ийн хувьд

$\angle A=30^\circ$ ,

$\angle B=65^\circ$ байв.

$H$ нь

$ABC$ гурвалжны ортоцентр бол

$\angle AHB$ өнцөг аль нь вэ?

A.

$35^\circ$ B.

$75^\circ$ C.

$85^\circ$ D.

$95^\circ$ E.

$105^\circ$

Талбайг өндрүүдээр илэрхийлэх

Гурвалжны өндрүүд 12, 15, 20 нэгж урттай бол талбайг ол.

A.

$110$ B.

$120$ C.

$130$ D.

$140$ E.

$150$

ЭЕШ 2008 A №8

$ABC$ гурвалжны хувьд

$AB=2$ ,

$\angle BAC=45^\circ$ ,

$\angle ABC=75^\circ$ ба орто төв нь

$H$ бол

$AH$ хэрчмийн уртыг ол.

A.

$\dfrac{2\sqrt6}{3}$ B.

$\dfrac{\sqrt6}{2}$ C.

$2\sqrt2$ D.

$\dfrac{\sqrt2}{2}$ E.

$\sqrt3$

Гурвалжны өндөр ол

$\triangle ABC$ -ны

$\angle A=60^\circ, |AB|=1, |AC|=2$ бол

$A$ оройгоос буулгасан өндөр

$AA_1$ -ийн уртыг ол.

A.

$\frac1{\sqrt2}$ B.

$1$ C.

$\sqrt2$ D.

$\sqrt3$ E.

$2$

Хамгийн их талбайтай гурвалжны өндөр

Адил хажуут гурвалжны хажуу талууд нь

$24$ см. Гурвалжны өндөр ямар байхад талбай хамгийн их байх вэ?

A.

$12$ см B.

$12\sqrt{2}$ см C.

$12\sqrt{3}$ см D.

$8\sqrt{3}$ см E.

$6\sqrt{3}$ см

Gurvaljnii ondor ol

$\triangle ABC$ -ны

$\angle A=30^\circ, |AB|=\sqrt3, |AC|=2$ бол

$A$ оройгоос буулгасан өндөр

$AA_1$ -ийн уртыг ол.

A.

$\frac1{\sqrt2}$ B.

$1$ C.

$\sqrt2$ D.

$\sqrt3$ E.

$2$

Харьцаа олох

$AB=BC$ байх адил хажуут гурвалжны

$BC$ тал дээр

$BD:DC=1:4$ байх

$D$ цэг авав. Гурвалжны

$BE$ өндөр

$AD$ шулуунаар ямар харьцаанд хуваагдах вэ?

A.

$1:4$ B.

$2:3$ C.

$2:1$ D.

$1:2$ E.

$3:2$

ЭЕШ 2016 C №34

$ABC$ хурц өнцөгт гурвалжны

$BD$ ,

$AE$ өндрүүд харгалзан

$3.2$ см,

$4$ см урттай бөгөөд

$\dfrac{|BE|}{|EC|}=\dfrac13$ бол

$AC=?$

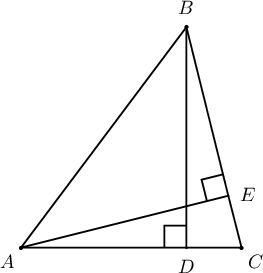
A.

$5$ B.

$4$ C.

$3$ D.

$4.5$ E.

$6$

ЭЕШ 2016 D №34

$ABC$ хурц өнцөгт гурвалжны

$BD$ ,

$AE$ өндрүүд харгалзан

$7\dfrac5{13}$ см,

$12$ см урттай бөгөөд

$\dfrac{|BE|}{|EC|}=\dfrac35$ бол

$AC=?$

A.

$13$ B.

$14$ C.

$15$ D.

$16$ E.

$18$

ЭЕШ 2016 A №34

$ABC$ хурц өнцөгт гурвалжны

$BD$ ,

$AE$ өндрүүд харгалзан

$11.2$ см,

$12$ см урттай бөгөөд

$\dfrac{|BE|}{|EC|}=\dfrac59$ бол

$AC=?$

A.

$13$ B.

$14$ C.

$15$ D.

$16$ E.

$18$

Өнцгийн тангес

Тэгш өнцөгт

$ABC$ ,

$\measuredangle C=90^\circ$ гурвалжны тэгш өнцгийн оройгоос татсан өндөр

$h$ ,

$\measuredangle A=\alpha$ , өндрийн суурь

$H$ бол

$BH=?$

A.

$\dfrac{h}{\cos\alpha}$ B.

$h\cdot\ctg\alpha$ C.

$h\cdot\tg\alpha$ D.

$\dfrac{h}{\sin\alpha}$ E.

$\dfrac{2h}{\sin2\alpha}$

ЭЕШ 2016 B №34

$ABC$ хурц өнцөгт гурвалжны

$BD$ ,

$AE$ өндрүүд харгалзан

$9\dfrac{12}{17}$ см,

$15$ см урттай бөгөөд

$\dfrac{|BE|}{|EC|}=\dfrac38$ бол

$AC=?$

A.

$13$ B.

$14$ C.

$15$ D.

$16$ E.

$17$

Гурвалжны өндрүүд ба талуудын хамаарал

$ABC$ хурц өнцөгт гурвалжны

$BD$ ,

$AE$ өндрүүд харгалзан

$11.2$ см,

$12$ см урттай бөгөөд

$\dfrac{|BE|}{|EC|}=\dfrac59$ бол

$AC=?$

A.

$13$ B.

$14$ C.

$15$ D.

$16$ E.

$18$

Өндрүүдийн огтлолцол

$ABC$ гурвалжны

$AH_1$ ,

$BH_2$ өндрүүд

$H$ цэгт огтлолцсон ба

$\measuredangle BAC=60^\circ$ ,

$\measuredangle CBA=40^\circ$ ,

$\measuredangle ACB=80^\circ$ бол

$BH:HH_2$ харьцаа аль нь вэ?

A.

$\dfrac{2\cos40^\circ}{\cos80^\circ}$ B.

$\dfrac{\cos40^\circ}{2\cos80^\circ}$ C.

$\dfrac{2}{2\cos80^\circ-1}$ D.

$\dfrac{2}{2\sin80^\circ+1}$ E.

$2.5$

ЭЕШ 2017 D №21

Гурвалжны 2 өндрийн нэг нь огтлолцлын цэгээрээ оройгоос тооцоход 8 см ба 3 см урттай хэсгүүдэд хуваагдсан байв. Хоёр дахь өндрийн огтлолцлын цэгээс суурь хүртэлх зай 2 см байсан 2 дахь өндрийн уртыг нь ол.

A. 11 см B. 12 см C. 13 см D. 14 см E. 15 см

ЭЕШ 2017 D №21

Гурвалжны 2 өндрийн нэг нь огтлолцлын цэгээрээ оройгоос тооцоход 4 см ба 3 см урттай хэсгүүдэд хуваагдсан байв. Хоёр дахь өндрийн оройгоос огтлолцлын цэг хүртэлх зай 6 см байсан бол үлдсэн хэсгийн уртыг нь ол.

A. 1 см B. 2 см C. 3 см D. 4 см E. 5 см

Тэгш өнцөгт гурвалжны катетуудын урт нь 10, 24. Гурвалжны тэгш өнцгийн оройгоос татсан өндрийн уртыг ол.

A.

$9\dfrac{3}{13}$ B.

$9$ C.

$10\dfrac{3}{13}$ D.

$9\dfrac{5}{13}$ E.

$10$

Тэгш өнцөгт гурвалжны катетуудын урт нь 5, 12. Гурвалжны тэгш өнцгийн оройгоос татсан өндрийн уртыг ол.

A.

$9\dfrac{3}{13}$ B.

$4.5$ C.

$5\dfrac{3}{13}$ D.

$4\dfrac{5}{13}$ E.

$4\dfrac{8}{13}$

Тэгш өнцөгт гурвалжныг багтсан ба багтаасн тойргийн радиус

Тэгш өнцөгт гурвалжинд багтсан тойргийн радиус 8, гипотенузэд буусан өндөр 18 бол багтаасан тойргийн радиус хэд вэ?

A.

$24$ B.

$28$ C.

$32$ D.

$36$ E.

$40$

Бодлого №15526

Катетууд нь

$1:2$ гэж харьцдаг тэгш өнцөгт гурвалжны гипотенузэд буулгасан өндөр 38 см бол түүний сууриар гипотенузийн хуваагдсан хэсгүүдийн урт хэд вэ?

A. 16, 79 B. 18, 77 C. 20, 75 D. 19, 76 E. 26, 69

$ABC$ гурвалжны талууд

$AB=12$ ,

$BC=5$ ,

$AC=13$ ба

$AB$ тал дээр

${AC_1}\colon {BC_1}={1}\colon{2}$ байх

$C_1$ цэг тэмдэглэв.

$BC$ талын дундаж нь

$A_1$ ,

$BB_1$ нь

$AC$ тал дээр буулгасан өндөр бол

$BB_1=\dfrac{\fbox{ab}}{13},$

$S_{AC_1B_1}=\dfrac{\fbox{cdef}}{13^2}$ ,

$S_{CA_1B_1}=\dfrac{\fbox{ghi}}{13^2}$ байна.

$ABC$ гурвалжны талууд

$AB=12$ ,

$BC=9$ ,

$AC=15$ ба

$AB$ тал дээр

${AC_1}\colon {BC_1}={2}$ байх

$C_1$ цэг,

$BC$ тал дээр

$BA_1\colon A_1C=1\colon 2$ байх

$A_1$ цэгийг тус тус тэмдэглэв.

$BB_1$ нь өндөр бол

$BB_1=\dfrac{\fbox{ab}}{5},$

$S_{CA_1B_1}=\dfrac{\fbox{cde}}{5^2}$ ,

$S_{BB_1C_1}=\dfrac{\fbox{fgh}}{5^2}$ байна.

Бодлого №7889

Хурц өнцөгт

$ABC$ гурвалжны талууд

$AB=2\sqrt{2}$ ,

$BC=\sqrt{5}$ ба

$\measuredangle BAC=45^{\circ}$ байв.

$AC=\fbox{a}$ болох ба

$B$ оройн өндрийн суурь

$H$ цэгээс

$AB$ ,

$BC$ талууд руу

$HD$ ,

$HE$ перепендикулярууд буулгасан бол

$DE^{2}=\dfrac{\fbox{bc}}{\fbox{d}}$ ,

$S_{DEH}=\dfrac{\fbox{e}}{\fbox{f}}$ болно.

Бодлого №7890

$ABC$ гурвалжны талууд

$AB=\sqrt{6}$ ,

$BC=\sqrt{7}$ ба

$\measuredangle BAC=45^{\circ}$ байв.

$AC=\sqrt{\fbox{a}}+\sqrt{2}$ болох ба

$B$ оройн өндрийн суурь

$H$ цэгээс

$AB$ ,

$BC$ талууд руу

$HD$ ,

$HE$ перепендикулярууд буулгасан бол

$DE^{2}=\dfrac{\fbox{bc}+8\sqrt{\fbox{d}}}{14}$ ,

$S_{BDHE}=\dfrac{\fbox{e}}{\fbox{f}}+\dfrac{\fbox{g}\sqrt{2}}{7}$ болно.

Бодлого №7893

$ABC$ гурвалжны өнцгүүд

$\measuredangle A=30^{\circ}$ ,

$\measuredangle B=120^{\circ}$ ба

$AB=10$ бол

$C$ оройгоос буулгасан өндөр

$h_{C}=\fbox{a}\sqrt{\fbox{b}}$ ,

$B$ оройн өндөр

$h_{B}=\fbox{c}$ болно.

$H$ нь

$ABC$ гурвалжны өндрүүдийн огтлолцлын цэг бол

$H$ цэгээс

$AC$ тал хүртэлх зай

$\sqrt{\fbox{de}}$ байна.

Бодлого №7894

$ABC$ гурвалжны өнцгүүд

$\alpha =30^{\circ}$ ,

$\beta =12^{\circ}$ ба

$BC=6$ бол

$h_A=\fbox{a}\sqrt{\fbox{b}}$ ,

$h_B=\fbox{c},$

$h_C=\dfrac 35\sqrt{\fbox{de}}$ .

Бодлого №7909

$ABC$ гурвалжины

$CC_1$ ,

$AA_1$ медианууд харилцан перепендикуляр бөгөөд урт нь харгалзан

$3$ ,

$4$ байв.

$AC$ талын урт

$\dfrac{\fbox{ab}}{\fbox{c}}$ ба

$BH$ өндөр нь

$\dfrac{\fbox{de}}{5}$ болно.

$ABC$ гурвалжны медиануудын огтлолцлын цэг

$M$ бол

$S_{A_1C_1M}=\fbox{f}$ байна.

Бодлого №7910

$ABC$ гурвалжны

$AA_1$ ,

$CC_1$ медианууд харилцан перепендикуляр бөгөөд урт нь харгалзан

$9$ ,

$12$ байв.

$AC$ талын урт

${\fbox{ab}}$ ба

$BH$ өндөр нь

$\dfrac{\fbox{cd}}{\fbox{e}}$ ,

$S_{BA_1C_1}=\fbox{fg}$ байна.

Бодлого №7937

$ABC$ гурвалжинд

$H$ нь өндрүүдийн огтлолцлын цэг ба

$AH=15$ ,

$BH=9$ ,

$\measuredangle AHB=120^{\circ}$ бол

$AB={\fbox{ab}}$ ,

$BC=\sqrt{3}\fbox{cd}$ ,

$AC=\sqrt{3}\fbox{ef}$ болно.

$C$ оройгоос татсан өндрийн урт

$h_c=\dfrac{\fbox{ghi}}{14}\sqrt{3}$ байна.

Бодлого №7938

$ABC$ гурвалжинд

$H$ нь өндрүүдийн огтлолцлын цэг ба

$AH=39$ ,

$BH=33$ ,

$\measuredangle AHB=60^{\circ}$ бол

$AB={\fbox{ab}}\sqrt{3}$ ,

$BC=\fbox{c}\sqrt{3}$ ,

$AC=\fbox{de}\sqrt{3}$ болно.

$C$ оройгоос татсан өндрийн урт

$h_c=\dfrac{\fbox{fg}}{\fbox{hi}}\sqrt{3}$ байна.

Ажиглах цэгээс шон хүртэлх зай

Нуурын эрэг дээр газрын гадаргаас 8 м өндөрт байрлах ажиглах цэгээс эсрэг эрэг дээр буй шонгийн орой газрын гадаргатай

$30^{\circ}$ өнцөг үүсгэн харагдаж байв. Ажиглах цэгээс нуурын мандал руу

$45^\circ$ өнцгөөр тусгасан цацраг шонгийн оройг дайрч байсан бол шонгийн өндөр

$\fbox{ab}+\fbox{c}\sqrt{\fbox{d}}$ м болох тул шон ажиглах цэгээс

$\fbox{ef} +\fbox{g}\sqrt{\fbox{h}}$ м зайтай байна.

Бодлого №7956

Нуурын эрэг дээр газрын гадаргаас 9 м өндөрт байрлах ажиглах цэгээс эсрэг эрэг дээр буй шонгийн орой газрын гадаргатай

$30^{\circ}$ өнцөг үүсгэн харагдаж байв. Ажиглах цэгээс нуурын мандал руу

$45^\circ$ өнцгөөр тусгасан цацраг шонгийн оройг дайрч байсан бол шонгийн өндөр

$\fbox{ab}+\fbox{c}\sqrt{\fbox{d}}$ м болох тул шон ажиглах цэгээс

$\fbox{ef} +\fbox{g}\sqrt{\fbox{h}}$ м зайтай байна.

Бодлого №7957

Бат 1.6 м-ийн өндөртэй ба түүнд модны орой газрын гадаргатай

$30^\circ$ -ийн өнцөг үүсгэн харагдаж байв. Мод руу чиглэж 8 м явсны дараа модны орой газрын гадаргатай

$45^\circ$ -ийн өнцөг үүсгэн харагдаж байсан бол модны өндөр

$\fbox{a} . \fbox{b}+\fbox{c}\sqrt{\fbox{d}}$ м ба анх Бат модноос

$\fbox{ef} +\fbox{g}\sqrt{\fbox{h}}$ м зайтай байжээ.

Бодлого №7958

Дорж 1,7 м өндөртэй ба түүнд модны орой газрын гадаргатай

$30^\circ$ -ийн өнцөг үүсгэн харагдаж байв. Тэрээр мод руу чиглэн 10 м явсны дараа модны орой газрын гадаргатай

$45^\circ$ -ийн өнцөг үүсгэн харагдаж байсан бол анх Дорж модноос

$\fbox{ab} +\fbox{c}\sqrt{\fbox{d}}$ м зайтай байсан ба модны өндөр

$\fbox{e}. \fbox{f} +\fbox{g}\sqrt{\fbox{h}}$ м байжээ.

Тэгш өнцөгт гурвалжны гипотенуз дээрх катетуудын проекц 25, 144 бол тэгш өнцгийн оройгоос татсан өндөр

$\fbox{ab}$ болно. Богино катет нь

$\fbox{cd}$ , урт катет нь

$\fbox{efg}$ болох бөгөөд уг гурвалжинд багтсан тойргийн радиус

$r=\fbox{hi}$ байна.

Бодлого №2311

Гурвалжны

$2$ тал нь харгалзан

$6$ см ба

$8$ см байв. Уг

$2$ талд татсан медианууд нь хоорондоо перпендикуляр бол гурвалжны талбайг ол.

Бодлого №2312

Гурвалжны суурийн урт

$26$ см, хажуу талуудад буулгасан медианууд нь харгалзан

$30$ ба

$39$ см бол гурвалжны талбайг ол.

Бодлого №2313

Гурвалжны медианууд нь

$3$ см,

$4$ см,

$5$ см урттай. Гурвалжны талбайг ол.

Бодлого №2317

Гурвалжны хоёр тал

$35$ см,

$14$ см урттай ба тэдгээрийн хоорондох өнцгийн биссектрисийн урт

$12$ см бол уг гурвалжны талбайг ол.

Бодлого №2320

Гурвалжны нэг талын урт

$20$ см ба энэ талын эсрэг орших оройг дайрсан багтаасан тойргийн шүргэгч шулуунаас уг талын үзүүрүүд хүртэлх зайнууд нь

$25$ см,

$16$ см бол гурвалжны талбайг ол.

Бодлого №2325

$ABC$ гурвалжны

$AM$ медиан нь

$BN$ медиантай перпендикуляр. Хэрэв

$AM=3$ ,

$BN=4$ бол гурвалжны талбайг ол.

Бодлого №2328

Хурц өнцөгт

$ABC$ гурвалжны

$BM$ ,

$CN$ медианууд ба

$AH$ өндрийн урт нь харгалзан

$4$ ,

$5$ ,

$6$ . Гурвалжны талбайг ол.

Бодлого №2330

Гурвалжны

$2$ талын урт нь

$1$ ба

$\sqrt {13}$ . Гурав дахь талын медиан нь

$2$ бол гурвалжны талбайг ол.

Бодлого №2332

Гурвалжны суурийн урт

$a$ . Гурвалжны суурьтай параллель, талбайг нь хагаслан хуваах хэрчмийн уртыг ол.

Бодлого №2335

Гурвалжны

$2$ тал нь

$1$ см ба

$\sqrt{15}$ см. Гурав дахь талын медиан нь

$2$ см бол гурвалжны талбайг ол.

Бодлого №2336

$ABC$ гурвалжны

$B$ оройгоос

$BD$ өндөр,

$BL$ биссектрис татав. Хэрэв

$ABC$ гурвалжны

$AB=6.5$ ,

$BC=7.5$ ,

$AC=7$ бол

$BLD$ гурвалжны талбайг ол.

Бодлого №2338

$ABC$ гурвалжны

$A$ оройгоос

$BC$ хэрчим дээр орших

$D$ цэгийг дайруулан шулуун татсан ба

$CD:BC=\alpha$ ,

$\left(\alpha< \frac{1}{2}\right)$ .

$BC$ тал дээр

$CD=DE$ байхаар

$E$ цэгийг сонгож авав. Түүнээс

$AC$ талтай параллелиар

$AB$ талыг

$F$ цэгээр огтлох шулуун татав.

$ACEF$ трапец болон

$ADC$ гурвалжны талбайн харьцааг ол.

Бодлого №2340

Гурвалжны нэг талын урт

$a$ ба уг талд налсан өнцгүүд нь

$\alpha$ ,

$\beta$ бол гурвалжны талбайг ол.

Бодлого №2341

$ABC$ гурвалжны

$BC$ ,

$AC$ ,

$AB$ талуудын урт нь харгалзан

$41$ ,

$51$ ,

$58$ . Гурвалжны талбайг ба

$B$ оройгоос буулгасан өндрийг ол.

Бодлого №2343

$ABC$ гурвалжны

$AD$ өндөр

$BC$ талаас

$4$ см-ээр бага,

$AC$ талын урт

$5$ см. Хэрвээ гурвалжны талбай нь

$16$ см.кв бол түүний периметрийг ол.

Бодлого №2344

$ABC$ гурвалжины

$AB$ тал дээр

$M, N$ цэгүүд,

$AC$ тал дээр

$D, E$ цэгүүд нь

$BC$ тал дээр

$K$ ,

$L$ цэгүүд

$AM=MN=NB$ ,

$BK=KL=LC$ ,

$AD=DE=EC$ байхаар оршиж байв. Хэрэв

$ABC$ гурвалжны талбай

$S$ бол

$ML$ ,

$NK$ ,

$BD$ ,

$BE$ шулуунуудаар үүсэх дөрвөн өнцөгтийн талбайг ол.

Бодлого №2345

Гурвалжны талын урт

$a$ түүнд налсан өнцгүүд

$\dfrac{\pi}{6}$ ,

$\dfrac{\pi}{4}$ бол гурвалжны талбайг ол.

Бодлого №2346

Гурвалжны талын урт нь

$15$ см ба түүнтэй параллель шулуун татахад үүсэх трапецийн талбай нь гурвалжны талбайн

$75\%$ болсон бол уг шулууны гурвалжны талуудын хооронд үүсэх хэсгийн уртыг ол.

Бодлого №2348

$ABC$ гурвалжин өгөгджээ.

$AC$ диаметртэй тойрог нь

$BC$ -ийн дунджийг дайрах ба

$AB$ талыг

$AD=\frac13AB$ байхаар

$D$ цэгээр отлоно. Хэрэв

$AC=1$ бол

$ABC$ гурвалжны талбайг ол.

Бодлого №2350

$\angle B=30^\circ$ ,

$AB=4$ ,

$BC=6$ байх

$ABC$ гурвалжин өгөгдөв.

$B$ өнцгийн биссектрис нь

$AC$ талыг

$D$ цэгт огтлох бол

$ABD$ гурвалжны талбайг ол.

Бодлого №2351

$AC=5$ ,

$AB=6$ ,

$BC=7$ байх

$ABC$ гурвалжин өгөгдөв.

$C$ өнцгийн биссектрис нь

$AB$ талыг

$D$ цэгт огтлох бол

$ADC$ гурвалжны талбайг ол.

Бодлого №2354

$ABC$ гурвалжны талуудыг

$FA:FC=3:1$ ,

$CN:NB=2:3$ харьцаагаар хуваах

$F, N$ цэгүүдийг сонгож авав.

$AN$ болон

$BF$ шулуунууд

$M$ цэгт огтлолцоно.

$AMB$ болон

$ANB$ гурвалжнуудын талбайн харьцааг ол.

Бодлого №2360

$AB=4$ ,

$BC=2$ ,

$AC=3$ талтай гурвалжинд тойрог багтав. Уг тойрог

$AB$ болон

$AC$ талуудыг харгалзан

$M, N$ цэгүүдээр шүргэх бол

$AMN$ гурвалжны талбайг ол.

Бодлого №2362

Хурц өнцөгт

$ABC$ гурвалжинд

$CC_1, AA_1$ өндрүүд татав. Хэрэв

$AC=1$ ,

$\angle C_1CA_1=\alpha$ .

$C_1BA_1$ гурвалжныг багтаасан тойргийн талбайг ол.

Бодлого №2363

Хурц өнцөгт

$ABC$ гурвалжинд

$CH, AH_{1}$ өндрүүд татав.

$AC=2$ ба

$HBH_{1}$ гурвалжныг багтаасан тойргийн талбай нь

$\pi/3$ .

$CH$ өндөр ба

$BC$ талуудын хоорондох өнцгийг ол.

Бодлого №2365

$AB$ диаметртэй тойргийн гадна орших

$M$ цэг нь

$AB$ цэгтэй холбогджээ.

$MA$ ба

$MB$ хэрчмүүд нь тойргийг харгалзан

$C$ ба

$D$ цэгүүдээр огтлоно.

$AMB$ гурвалжинд багтсан тойргийн талбай нь

$CMD$ гурвалжинд багтсан тойргийн талбайгаас 4 дахин их. Хэрэв нэг өнцөг нь нөгөөгөөс 2 дахин их гэж үзвэл

$AMB$ гурвалжны өнцгүүдийг ол.

Бодлого №2366

$ABC$ гурвалжны хувьд

$\angle BAC=\alpha$ ,

$\angle BCA=\gamma$ ,

$AB=c$ .

$ABC$ гурвалжны талбайг ол.

Бодлого №2368

$ABC$ гурвалжны талбай нь

$S$ ,

$\angle BAC=\alpha$ ,

$AC=b$ бол

$BC$ -г ол.

Бодлого №2370

$ABC$ гурвалжны

$AD$ медиан болон

$BE$ биссектрисүүд харилцан перпедикуляр ба

$F$ цэгт огтлолцоно.

$DEF$ гурвалжны талбай нь

$5$ бол

$ABC$ гурвалжны талбайг ол.

Бодлого №2377

$ABC$ гурвалжны талбай нь

$12$ .

$B$ оройгоос

$BD$ медианы урт

$3$ . Хэрэв

$\angle ABD=90^\circ$ бол

$AC$ талыг ол.

Бодлого №2378

$AC$ диаметртэй тойрог

$\triangle ABC$ -ны

$AB$ талыг

$AD:DB=12:5$ байх

$D$ цэгээр огтлоно.

$AC=26$ ,

$\angle ABC=45^\circ$ бол гурвалжны талбайг ол.

Бодлого №2380

$ABC$ гурвалжны талбай нь

$16$ см.кв. Хэрэв

$AC=5$ см,

$BC=8$ см,

$C$ өнцөг нь мохоо бол

$AB$ талыг ол.

Бодлого №2383

Адил хажуут

$ABC$ гурвалжны

$BC$ хажуу руу буулгасан

$AD$ өндөр нь

$ABC$ -г

$ABD$ ,

$ADC$ гурвалжнуудад хуваах ба талбайнууд нь харгалзан

$4\text{ см}^2$ ,

$2\text{ см}^2$ ба

$AC$ нь суурь бол гурвалжны талуудын уртыг ол.

Бодлого №2384

Адил хажуут

$ABC$ гурвалжны

$AD$ биссектрис нь түүнийг

$ABD$ ,

$ACD$ гурвалжнуудад хуваах ба талбай нь харгалзан

$4$ см.кв,

$2$ см.кв. Хэрэв

$AC$ нь суурь нь бол гурвалжны талуудыг ол.

Бодлого №2386

Адил хажуут

$ABC$ (

$AB=BC$ ) гурвалжинд

$AD$ биссектрис татав.

$ABD$ болон

$ADC$ гурвалжнуудын талбай харгалзан

$S_1, S_2$ . Суурийн уртыг ол.

Бодлого №2399

Адил хажуут

$ABC$ гурвалжны суурийн

$B$ ,

$C$ оройнууд ба

$A$ оройгоос буулгасан өндрийн дундаж

$M$ -ийг дайруулан 2 шулуун татав. Уг шулуунууд нь

$AC$ ,

$AB$ талуудыг харгалзан

$D, E$ цэгүүдээр огтолно. Хэрэв

$ABC$ гурвалжны талбай

$93$ бол

$AEMD$ дөрвөн өнцөгтийн талбайг ол.

Бодлого №2401

$a$ талтай зөв ABC гурвалжин дотор орших цэгээс

$AB$ ,

$BC$ ,

$CA$ талуудад перпендикуляр татав. Перпендикулярууд нь харгалзан

$m$ ,

$n$ ,

$k$ урттай.

$ABC$ гурвалжин болон перпендикуляруудын сууриудаар үүссэн гурвалжны талбайн харьцааг ол.

Бодлого №2407

Адил хажуут гурвалжинд

$r$ радиустай тойрог багтав. Багтсан тойрог нь суурьт буулгасан өндрийг оройг талаас

$1:2$ харьцаатай хэсгүүдэд хуваана. Гурвалжны талбайг ол.

Бодлого №2411

Адил хажуут гурвалжны суурь нь

$10$ ба талбай нь

$60$ . Хажуу талд буулгасан медианы уртыг ол.

Бодлого №2412

Адил хажуут гурвалжны суурь нь

$12$ , багтсан тойргийн радиус нь

$3$ бол талбайг ол.

Бодлого №2417

Адил хажуут гурвалжны суурьт буулгасан өндөр нь

$5$ , хажуу талд буулгасан өндөр нь

$6$ бол гурвалжны талбайг ол.

Бодлого №2418

Хэрэв суурьт буулгасан өндөр нь

$10$ , хажуу талд буулгасан өндөр нь

$12$ бол адил хажуут гурвалжны талбайг ол.

Бодлого №2426

Адил хажуут

$ABC$ гурвалжны

$AC$ сууриар диаметр хийсэн тойрог

$BC$ талыг

$BD:DC=3:2$ байх

$D$ цэгээр огтолно. Хэрэв

$AD=12/\sqrt{5}$ бол

$ABC$ гурвалжны талбайг ол.

Бодлого №2427

Адил хажуут гурвалжны суурийн

$B, C$ оройнуудыг

$A$ оройгоос

$BC$ талд буулгасан өндрийн дундаж цэг

$M$ -тэй хэрчмээр холбов.

$BM, CM$ хэрчмийн үргэлжлэлүүд

$AC, AB$ талуудыг харгалзан

$D, E$ цэгүүдээр огтлов. Хэрэв

$AEMD$ дөрвөн өнцөгтийн талбай

$16$ бол

$BMA$ гурвалжны талбайг ол.

Бодлого №2428

Адил хажуут гурвалжны суурьт буулгасан өндөр

$10$ см, хажуу талуудад буулгасан өндөр

$12$ см бол талбайг ол.

Бодлого №2430

Адил хажуут гурвалжны талбай

$S$ , суурийн эсрэг оройн өнцөг

$\alpha$ бол суурьт буулгасан өндрийн уртыг ол.

Бодлого №2442

Тэгш өнцөгт гурвалжны катетуудын ба гипотенуз дээрх проекцүүд нь

$m=9$ см ба

$n=16$ см бол гурвалжинд багтсан тойргийн талбайг ол.

Бодлого №2445

Тэгш өнцөгт гурвалжны гипотенуз дээр байгуулсан зөв гурвалжин түүнээс 2 дахин их талбайтай бол тэгш өнцөгт гурвалжны өнцгүүдийг ол.

Бодлого №2447

Тэгш өнцөгт гурвалжны периметр

$24$ см, талбай нь

$24\text{ см}^2$ бол багтаасан тойргийн талбайг ол.

Бодлого №2448

Тэгш өнцөгт гурвалжны катетуудын нийлбэр

$14$ см, түүнийг багтаасан тойргийн радиус

$5$ см бол өгсөн гурвалжинд багтсан тойргийн талбайг ол.

Бодлого №2450

Тэгш өнцөгт гурвалжны хурц өнцөг

$\alpha$ ба багтаасан тойргийн төвөөс нөгөө хурц өнцөгийн орой хүртлэх зай

$a$ бол гурвалжны талбайг ол.

Бодлого №2454

$ABC$ гурвалжны

$\angle C=30^\circ$ байв.

$B$ тэгш өнцгийн оройгоос татсан медиан нь

$BK$ ба

$AB$ катетын урт нь

$4$ см бол

$BCK$ гурвалжны талбайг ол.

Бодлого №2455

Тэгш өнцөгт гурвалжны бага өнцөг нь

$\alpha$ -тай тэнцүү. Бага катет ба гипотенузын дунджуудыг дайруулан гипотенузыг шүргэх тойрог татав. Тойргийн талбайг гурвалжны талбайд харьцуулсан харьцааг ол.

Бодлого №2456

$ABC$ гурвалжны

$B$ өнцөг нь тэгш.

$CB$ катет дээр

$AD, AE$ нь

$A$ өнцгийг гурван тэнцүү хуваах

$D, E$ цэгүүд авав.

$AD=a$ ,

$AE=b$ бол

$ADB$ ба

$AEB$ гурвалжинуудын талбайн харьцааг ол.

Бодлого №2462

Тэгш өнцөгт

$ABC$ гурвалжны

$BC$ катетын урт

$36$ ,

$\cos\angle BAC=\dfrac{8}{17}$ бол

$AC$ катет ба гурвалжны талбайг ол.

Бодлого №2468

Тэгш өнцөгт гурвалжны катетуудын нийлбэр

$17$ см, гипотениуз нь

$13$ см бол гурвалжны талбай ба катетуудыг ол.

Бодлого №2479

Тэгш өнцөгт гурвалжны

$\angle B=90^\circ$ ба

$A$ оройгоос татсан биссектрис нь

$BC$ талыг

$D$ цэгт огтолно.

$BD=4$ ,

$DC=6$ бол

$ADC$ гурвалжны талбайг ол.

Бодлого №2482

$ABC$ ,

$ABD$ тэгш өнцөгт гурвалжнуудын хувьд

$AB=5$ .

$C, D$ цэгүүд нь

$AB$ шулууны

$2$ талд орших ба

$BC=BD=3$ .

$E$ цэг

$AC$ тал дээр

$EC=1$ ,

$F$ цэг

$AD$ тал дээр

$FD=2$ байхаар байрлана.

$ECBDF$ таван өнцөгтийн талбайг ол.

Бодлого №2489

Тэгш өнцөгт гурвалжны тэгш өнцгийн биссектрис гипотенузыг

$3$ см,

$4$ см урттай хэрчмүүдэд хуваав. Гурвалжны талбайг ол.

Бодлого №2490

Тэгш өнцөгт гурвалжинд нэг орой нь тэгш өнцгийн оройтой давхцах квадрат багтав. Хэрэв гурвалжны нэг катет

$42$ см, квадратын тал

$24$ см бол гурвалжны талбайг ол.

Бодлого №2674

Тэгш өнцөгт гурвалжины багтсан тойргийн гипотенузыг шүргэж байгаа цэгээр гипотенузыг хуваахад үүсэх хэрчмүүдийн уртуудын үржвэр гурвалжны талбайтай тэнцүү болохыг батал.

Бодлого №2682

$ABC$ гурвалжны

$BAC$ өнцгийн биссектрис

$a$ -тай тэнцүү. Энэ биссектрисээр диаметрээ хийсэн тойрог

$AB$ ба

$BC$ талыг харгалзан

$2:1$ ба

$1:1$ харьцаагаар хуваах бол

$ABC$ гурвалжны талбайг ол.

Бодлого №2684

$ABC$ гурвалжинд багтсан тойрог

$AC$ ба

$BC$ талыг харгалзан

$M$ ба

$N$ цэгт шүргэх ба

$BD$ биссектрисийг

$P$ ба

$Q$ цэгт огтолжээ. Хэрэв

$\angle A=\pi/4$ ,

$\angle B=\pi/3$ бол

$PQM$ ба

$PQN$ гурвалжнуудын талбайн харьцааг ол.

Бодлого №2685

$ABC$ гурвалжинд багтсан тойргийн радиус

$\dfrac{10}3$ ,

$C$ өнцгийн косинус нь

$\dfrac{5}{13}$ ба талбай нь

$60$ бол гурвалжны талуудыг ол.

Бодлого №2686

$ABC$ гурвалжны

$BD$ медиан дээр

$BE=3ED$ байх

$E$ цэг авав.

$AE$ шулуун

$BC$ талыг

$M$ цэгт огтолно.

$AMC$ ба

$ABC$ гурвалжны талбайн харьцааг ол.

Бодлого №2687

$ABC$ гурвалжны талбай

$90$ см.кв,

$AD$ биссектрис нь

$BC$ талыг

$BD:CD=2:3$ харьцаагаар хуваадаг.

$BL$ хэрчим

$AD$ биссектристэй

$E$ цэгт огтлолцох ба

$L$ цэг

$AC$ хэрчмийг

$AL:CL=1:2$ байхаар хуваана.

$EDCL$ дөрвөн өнцөгтийн талбайг ол.

Бодлого №2688

$ABC$ гурвалжны талбай

$40$ см.кв,

$AD$ биссектрис

$BC$ талыг

$BD:DC=3:2$ байхаар хуваана.

$AD$ биссектрис

$BK$ медианыг

$E$ цэгт огтолно.

$EDCK$ дөрвөн өнцөгтийн талбайг ол.

Бодлого №2689

$ABC$ гурвалжны талбай

$70$ см.кв ба

$AD$ биссектрис нь

$BC$ талыг

$BD:DC=3:2$ байхаар хуваана.

$AD$ биссектрис

$BK$ хэрчмийг

$BE:EK=5:2$ харьцаагаар хувааж байхаар

$AC$ тал дээр

$K$ цэг авав.

$EDCK$ дөрвөн өнцөгтийн талбайг ол.

Бодлого №2690

$ABC$ гурвалжны

$AD$ ба

$BE$ биссектрисүүд

$O$ цэгт огтлолцоно. Хэрэв

$AC:AB:BC=4:3:2$ бол

$DOEC$ дөрвөн өнцөгтийн талбайг

$ABC$ гурвалжны талбайд харьцуулсан харьцааг ол.

Бодлого №2692

$CQ$ нь

$ABC$ гурвалжны биссектрис.

$BCQ$ гурвалжныг багтаасан тойргийн радиус

$1/3$ ба төв нь

$AC$ хэрчим дээр оршиж байв. Хэрэв

$AQ:AB=2:3$ гэвэл

$ABC$ гурвалжны талбайг ол.

Бодлого №2693

$ABC$ гурвалжин ба

$BDEF$ ромбо өгөгджээ. Ромбын бүх оройнууд

$ABC$ гурвалжны талууд дээр орших бөгөөд

$E$ оройн өнцөг нь мохоо. Хэрэв

$AE=3$ ,

$CE=7$ ба ромбод багтсан тойргийн радиус

$1$ бол

$ABC$ гурвалжны талбайг ол.

Бодлого №2695

$ABC$ гурвалжны

$AH$ биссектрис

$BE$ медианыг

$BK:KE=2$ харьцаагаар хуваах ба

$ABC$ өнцөг

$45^\circ$ байв.

$BCE$ гурвалжны талбайг энэ гурвалжныг багтаасан дугуйн талбайд харьцуулсан харьцааг ол.

Бодлого №2696

$ABC$ гурвалжны

$AB, AC$ талуудын дундаж цэгүүд харгалзан

$K, N$ .

$B$ оройг дайруулан

$AC$ талтай

$F$ цэгт,

$KN$ хэрчимтэй

$L$ цэгт огтлолцох шулуун татав.

$KL:LN=3:2$ ба

$ABC$ гурвалжны талбай

$40$ бол

$AKLF$ дөрвөн өнцөгтийн талбайг ол.

Бодлого №2707

Гурвалжны талуудын урт

$a=6$ ,

$b=8$ ба талбай нь

$S=3\sqrt 5$ байв. Гурав дахь талын урт нь уг талд буулгасан медианаас 2 дахин богино бол багтсан тойргийн радиусыг ол.

Бодлого №2708

$PQR$ гурвалжны

$Q$ оройноос татсан медианы урт

$\dfrac{3\sqrt{21}}{4}$ .

$P$ ба

$R$ орой дээр төвтэй

$5$ ба

$1$ радиустай тойргууд бие биеэ шүргэх ба

$Q$ орой нь эдгээр тойргуудын ерөнхий шүргэгч дээр байв. Хэрэв

$S< 7$ бол

$PQR$ гурвалжны талбай

$S$ -г ол.

Бодлого №2709

Хурц өнцөгт гурвалжны өндөрүүдийн суурийг холбож байгаа хэрчмүүдийн урт

$5, 12, 13$ . Гурвалжны талбайг ол.

Бодлого №2715

$\angle C=90^{\circ}$ байх адил хажуут

$ABC$ гурвалжин ба

$D$ орой нь

$AB$ тал дээр,

$E$ орой нь

$AB$ талын үргэлжлэл дээр

$A$ цэгийн талд байрлах

$DEF$ гурвалжин өгөгдөв.

$KL$ хэрчим нь

$2$ гурвалжины хоёулангийх нь дундаж шугам болдог ба

$DKLB$ дөрвөн өнцөгтийн талбай

$ABC$ гурвалжны талбайн

$5/8$ болно.

$DEF$ өнцгийг ол.

Бодлого №2716

Адил хажуут

$ABC$ (

$AB=BC$ ) гурвалжинд багтсан тойргийн төв нь

$O$ .

$AO$ шулуун нь

$BC$ хэрчимтэй

$M$ цэгт огтлолцдог.

$AO=3$ ,

$OM=27/11$ бол

$ABC$ гурвалжны талбайг ол.

Бодлого №2719

Адил хажуут

$ABC$ гурвалжны

$AC$ суурь нь уг гурвалжин дотор төвтэй тойргийн хөвч болж байв.

$B$ оройг дайрсан шулуунууд тойргийг

$D$ ба

$E$ цэгүүдэд шүргэнэ. Хэрэв

$AB=BC=2$ ,

$\angle ABC=2\arcsin\dfrac1{\sqrt5}$ ба тойргийн радиус нь

$1$ бол

$DBE$ гурвалжны талбайг ол.

Бодлого №2721

$AD$ нь тэгш өнцөгт

$ABC$ (

$\angle C=90^\circ$ ) гурвалжны биссектрис.

$\sqrt{15}$ радиустай тойрог

$A, C, D$ цэгүүдийг дайрах бөгөөд уг тойрог

$AB$ талыг

$E$ цэгт

$AE:AB=3:5$ байхаар огтолно.

$ABC$ гурвалжны талбайг ол.

Бодлого №2722

Тэгш өнцөгт гурвалжны тэгш өнцгийн оройгоос буулгасан өндөр ба биссектрисийн уртууд харгалзан

$3$ ба

$4$ . Гурвалжны талбайг ол.

Бодлого №2723

Тэгш өнцөгт

$ABC$ гурвалжны периметр

$54$ см бөгөөд

$AC$ катетын урт

$10$ см-аас их байв.

$BC$ катет дээр төвтэй

$6$ см радиустай тойрог

$AB$ ба

$AC$ шулуунуудыг шүргэх бол

$ABC$ гурвалжны талбайг ол.

Бодлого №2724

Тэгш өнцөг

$ABC$ гурвалжны гипотенуз нь

$AB$ , талбай нь

$30$ , багтсан тойргийн төв нь

$O$ байв.

$AOB$ гурвалжны талбай

$13$ бол

$ABC$ гурвалжны талуудыг ол.

Бодлого №2725

Тэгш өнцөгт

$ABC$ (

$\angle B=90^\circ$ ) гурвалжны

$AM$ медиан ба

$CD$ биссектрис

$O$ цэгт огтлолцов. Хэрэв

$CO=9$ ,

$OD=5$ гэвэл

$ABC$ гурвалжны талбайг ол.

Бодлого №2785

$ABC$ гурвалжны

$AC$ тал дээр

$AE:EC=a$ байх

$E$ цэг,

$AB$ тал дээр

$AD:DB=b$ байх

$D$ цэг авав.

$CD$ ба

$BE$ хэрчмүүд татахад үүсэх дөрвөн өнцөгтийн талбайг гурвалжны талбайд харьцуулсан харьцааг ол.

Бодлого №2786

$ABC$ гурвалжны

$\angle A=\dfrac{\pi}{3}$ ,

$\angle B=\dfrac{\pi}{4}$ .

$ABC$ гурвалжны өндөрүүдийн үргэлжилэл багтаасан тойргийг

$M$ ,

$N$ ба

$P$ цэгүүдээр огтолно.

$ABC$ ба

$MNP$ гурвалжнуудын талбайн харьцааг ол.

Бодлого №2789

$ABC$ гурвалжны

$AC$ тал дээр

$M$ цэг,

$BC$ тал дээр

$N$ цэг авав.

$AN$ ба

$BM$ хэрчимүүд

$O$ цэгт огтлолцоно. Хэрэв

$AMO$ ,

$ABO$ ,

$BNO$ гурвалжнуудын талбай харгалзан

$S_1$ ,

$S_2$ ,

$S_3$ бол

$CMN$ гурвалжны талбайг ол.

Бодлого №2791

$ABC$ гурвалжны

$AB$ ба

$BC$ тал дээр

$K$ ба

$L$ цэг авав.

$AL$ ба

$CK$ хэрчмүүдийн огтлолцлын цэг

$O$ .

$AOL$ ба

$COL$ гурвалжнуудын талбайн харьцаа

$1:8$ ба

$AOC$ гурвалжин

$BKOL$ дөрвөн өнцөгттэй хэм чацуу.

$ABC$ гурвалжны талбайг ол.

Бодлого №2800

$ABC$ гурвалжны

$AB$ тал дээр орших

$M$ ба

$N$ цэгүүдэд төвтэй 2 тойрог бие биенээ шүргэнэ. Эдгээр тойргууд

$AC$ ба

$BC$ талуудыг харгалзан

$A, P$ ба

$B, Q$ цэгүүдээр огтлох ба

$AM=PM=2$ ,

$BN=QN=5$ байв. Хэрэв

$AQN$ гурвалжны талбайг

$MPB$ гурвалжны талбайд харьцуулсан харьцаа

$15\dfrac{\sqrt{3}}{8}$ ба

$AP=\dfrac25QB\sqrt{\dfrac{2+\sqrt3}{3}}$ бол

$ABC$ гурвалжныг багтаасан тойргийн радиусыг ол.

Бодлого №2804

Төвүүд нь

$MPN$ гурвалжны

$MN$ тал дээр байрлах, бие биеэ гадаад байдлаар шүргэх тойргууд

$MP$ ба

$PN$ талуудыг харгалзан

$M, D$ ба

$N, C$ цэгүүдээр огтолно. Тойргуудын төвүүд нь харгалзан

$O_1$ ,

$O_2$ ба

$MO_1=O_1D=3$ ,

$NO_2=CO_2=6$ байв. Хэрэв

$MCO_2$ гурвалжны талбайг

$O_1DN$ гурвалжны талбайд харьцуулсан харьцаа

$\dfrac85\sqrt3$ ба

$PN=MP\sqrt{2-\sqrt3}$ бол

$MNP$ гурвалжны талбайг ол.

$R$ радиустай тойрогт багтсан адил хажуут гурвалжны талбай

Гурвалжны талуудын харьцаа

$1:2:2$ , багтаасан тойргийн радиус

$R$ бол гурвалжны талбайг ол.

A.

$\dfrac{15\sqrt{15}}{64}R^2$ B.

$\dfrac{15R^2}{64}$ C.

$15R^2$ D.

$\dfrac{\sqrt{15}R^2}{64}$ E.

$\dfrac{R^2}{64}$

ЭЕШ 2009 B1 №16

Тэгш өнцөгт гурвалжны катетууд

$2:3$ харьцаатай ба талбай нь

$12$ кв.нэгж бол түүнийг багтаасан дугуйн талбай хэдэн кв.нэгж вэ?

A.

$10\pi$ B.

$13\pi$ C.

$20\pi$ D.

$25\pi$ E.

$29\pi$

ЭЕШ 2010 A №8

$ABC$ гурвалжны хувьд

$\measuredangle ABC=90^\circ$ ,

$AB=BC$ ,

$E$ нь

$BC$ тал дээр орших бөгөөд

$\dfrac{EC}{BC}=\dfrac{1}{3}$ байх цэг,

$S_{\triangle AEC}=24$ бол

$AB=?$

A.

$6$ B.

$8$ C.

$10$ D.

$12$ E.

$14$

5, 12, 13 талуудтай гурвалжны талбайг ол.

A. 15 B. 36 C. 60 D. 18 E. 30

$ABC$ гурвалжныг багтаасан тойргийн радиус

$2\sqrt{3}$ ба өндрүүдийн сууриар үүсгэгдэх гурвалжны периметр 9 бол

$ABC$ гурвалжны талбайг ол.

A.

$18\sqrt{3}$ B.

$9\sqrt{3}$ C.

$36\sqrt{3}$ D.

$18$ E.

$36$

Медиануудаар үүсэх гурвалжин

Гурвалжны медиануудуудын урт нь 3, 4, 5 байв. Гурвалжны талбайг ол.

A.

$1$ B.

$4$ C.

$6$ D.

$8$ E.

$10$

Перпендикуляр медианууд

Гурвалжны 9, 12 урттай медианууд перпендикуляр байв. Талбайг ол.

A. 108 B. 96 C. 84 D. 72 E. 60

Гурвалжны талбай

$\sin\angle ABC=30^\circ$ ,

$AB=BC=8$ бол

$ABC$ гурвалжны талбайг ол.

A.

$32$ B.

$16$ C.

$64$ D.

$20$ E.

$25$

Гурвалжны талбай олох

$AB=3$ ,

$AC=5$ ба

$\cos\alpha=\dfrac{3}{5}$ бол

$ABC$ гурвалжны талбайг ол. Энд

$\alpha=\angle BAC$ .

A.

$6$ B.

$\dfrac{15}{2}$ C.

$\dfrac{9}{2}$ D.

$12$ E.

$8$

Ижил өндөртэй гурвалжнуудын талбайн харьцаа

$\triangle ABC$ -ийн

$AB=5$ ,

$AC=12$ ,

$BC=13$ байв. Хэрэв

$D$ нь

$A$ оройн биссектрисийн суурь бол

$ABD$ гурвалжны талбайг ол.

A.

$\dfrac{150}{17}$ B.

$8$ C.

$7$ D.

$10$ E.

$\dfrac{25}{3}$

Трапецийн талбай

$ABC$ нь тэгш өнцөгт адил хажуут гурвалжин болно. Хэрэв

$DE=3$ ба

$AB=5$ бол

$ABED$ трапецийн талбайг ол.

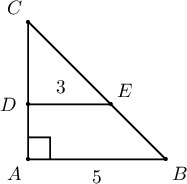
A.

$2$ B.

$4$ C.

$6$ D.

$16$ E.

$8$

Синусын теорем

$ABC$ гурвалжны

$AB=3$ ,

$\sin\measuredangle ACB=30^\circ$ бол

$ABC$ гурвалжныг багтаасан тойргоор үүсэх дугуйн талбай хэдтэй тэнцүү вэ?

A.

$4\pi$ B.

$5\pi$ C.

$8\pi$ D.

$9\pi$ E.

$16\pi$

Тэгш өнцөгт гурвалжинд багтсан тойргийн радиус 3, гипотенузэд буусан өндөр 8 нэгж бол гипотенузийн урт аль нь вэ?

A.

$8$ B.

$4$ C.

$9$ D.

$5$ E. Ийм гурвалжин олдохгүй

Гурвалжны медиан

Гурвалжны нэг тал 10 см, нөгөө хоёр талын медиан 9 см, 12 см бол талбай нь аль вэ?

A.

$36$ см.кв B.

$72$ см.кв C.

$108$ см.кв D.

$144$ см.кв E.

$150$ см.кв

Медиануудын огтлолцол

Адил хажуут гурвалжны талбай

$4.8$ , хоёр медианы урт

$3$ нэгж бол медиануудын огтлолцлоос суурийн харагдах өнцөг аль вэ?

A.

$\arcsin\frac35$ B.

$\arccos\frac35$ C.

$75^\circ$ D.

$60^\circ$ E.

$\arccos\frac35$ ,

$\pi-\arccos\frac35$

Гурвалжны медиан

$24$ см.кв талбайтай гурвалжны хоёр медиан 6 см, 8 см урт бол тэдгээрийн хоорондох өнцөг аль нь вэ?

A.

$60^\circ$ B.

$\arcsin\dfrac23$ C.

$\arcsin\dfrac34$ D.

$30^\circ$ E.

$\arccos\dfrac23$

ЭЕШ 2011 C №17

Тэгш өнцөгт гурвалжны катетууд

$2:3$ харьцаатай ба талбай нь

$156$ кв.нэгж бол түүнийг багтаасан дугуйн талбай хэдэн кв.нэгж вэ?

A.

$196\pi$ B.

$169\pi$ C.

$225\pi$ D.

$289\pi$ E.

$121\pi$

Төсөөгийн коэффициент

Гурвалжны талуудын уртыг 2 дахин ихэсгэвэл талбай нь хэд дахин ихсэх вэ?

A. 2 B. 3 C. 4 D. 5 E. 6

Героны томьёо

Талуудынх нь урт 5, 6, 7 нэгж байх гурвалжны талбай аль нь вэ?

A.

$6$ B.

$8\sqrt{2}$ C.

$3\sqrt{6}$ D.

$4\sqrt{3}$ E.

$6\sqrt6$

$ABC$ гурвалжны

$BC$ талын урт

$6$ ,

$\measuredangle BAC=120^\circ$ бол

$ABC$ гурвалжны талбай хамгийн ихдээ хэд байж болох вэ?

A.

$2\sqrt3$ B.

$3\sqrt3$ C.

$4\sqrt3$ D.

$3$ E.

$4$

ЭЕШ 2013 A №10

Адил хажуут

$ABC$ гурвалжны

$|AB|=|BC|=8$ ба суурийн өнцөг нь

$\dfrac{\pi}6$ бол гурвалжны талбайг ол.

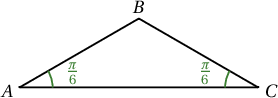
A.

$\sqrt{426}$ B.

$15\sqrt3$ C.

$16\sqrt3$ D.

$20\sqrt3$ E.

$11\sqrt3$

Төсөөтэй гурвалжнууд

Хэрвээ төсөөтэй гурвалжнуудын периметр нь

$16$ ба

$40$ см, талбайн нийлбэр нь

$87$ см.кв бол жижиг гурвалжны талбай аль нь вэ?

A.

$10$ см.кв B.

$11$ см.кв C.

$12$ см.кв D.

$13$ см.кв E.

$15$ см.кв

Талбайг өндрүүдээр илэрхийлэх

Гурвалжны өндрүүд 12, 15, 20 нэгж урттай бол талбайг ол.

A.

$110$ B.

$120$ C.

$130$ D.

$140$ E.

$150$

Хамгийн их талбайтай гурвалжны өндөр

Адил хажуут гурвалжны хажуу талууд нь

$24$ см. Гурвалжны өндөр ямар байхад талбай хамгийн их байх вэ?

A.

$12$ см B.

$12\sqrt{2}$ см C.

$12\sqrt{3}$ см D.

$8\sqrt{3}$ см E.

$6\sqrt{3}$ см

Героны томьёо

Талуудынх нь урт 10, 12, 14 нэгж байх гурвалжны талбай аль нь вэ?

A.

$24$ B.

$32\sqrt{2}$ C.

$12\sqrt{6}$ D.

$16\sqrt{3}$ E.

$24\sqrt6$

$ABC$ гурвалжныг багтаасан тойргийн радиус

$5$ ,

$\sin\angle BAC=\dfrac35$ бол

$ABC$ гурвалжны талбай хамгийн ихдээ хэдтэй тэнцүү байх вэ?

A.

$6$ B.

$20$ C.

$27$ D.

$50$ E.

$100$

$ABC$ гурвалжныг багтаасан тойргийн радиус

$10$ ,

$\sin\angle BAC=\dfrac45$ бол

$ABC$ гурвалжны талбай хамгийн ихдээ хэдтэй тэнцүү байх вэ?

A.

$48$ B.

$64$ C.

$100$ D.

$128$ E.

$256$

Дундаж шугамаар үүсэх трапецийн талбай

$ABC$ нь тэнцүү талт гурвалжин болно.

$P$ ба

$Q$ цэгүүд нь харгалзан

$AB$ ба

$BC$ талын дундаж цэгүүд. Хэрэв

$AB=4$ бол

$APQC$ -ийн талбай хэд вэ?

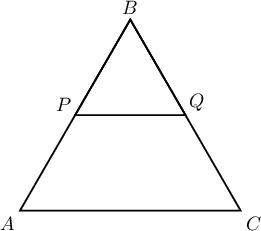
A.

$8$ B.

$\dfrac{\sqrt3}{2}$ C.

$3\sqrt3$ D.

$4$ E.

$8\sqrt3$

Адил хажуут гурвалжны талбай

10, 13, 13 талуудтай гурвалжны талбайг ол.

A. 15 B. 36 C. 60 D. 18 E. 30

$ABC$ гурвалжныг багтаасан тойргийн радиус

$4$ ба өндрүүдийн сууриар үүсгэгдэх гурвалжны периметр

$10$ бол

$ABC$ гурвалжны талбайг ол.

A.

$18\sqrt{3}$ B.

$9\sqrt{3}$ C.

$36\sqrt{3}$ D.

$18$ E.

$20$

ЭЕШ 2010 B №8

$ABC$ гурвалжны хувьд

$\measuredangle ABC=90^\circ$ ,

$AB=BC$ ,

$E$ нь

$BC$ тал дээр орших бөгөөд

$\dfrac{EC}{BC}=\dfrac{1}{3}$ байх цэг,

$S_{\triangle AEC}=54$ см.кв бол

$AB=?$

A.

$16$ B.

$18$ C.

$20$ D.

$22$ E.

$24$

Гурвалжны талбай

$\sin\angle ABC=30^\circ$ ,

$AB=BC=8$ бол

$ABC$ гурвалжны талбайг ол.

A.

$32$ B.

$16$ C.

$64$ D.

$20$ E.

$25$

Шинэ эрин 2018 А №27

$ABC$ тэгш өнцөгт гурвалжны

$B$ оройгоос эсрэг орших талыг дөрвөн тэнцүү хэсэгт хуваах хэрчмүүд татав. Будсан гурвалжны талбайг олоорой.

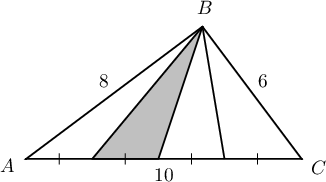
A.

$12$ B.

$24$ C.

$6$ D.

$10$ E.

$4.8$

Гурвалжны талбай олох

$AB=4$ ,

$AC=3$ ба

$\cos\alpha=\dfrac{\sqrt{3}}{2}$ бол

$ABC$ гурвалжны талбайг ол. Энд

$\alpha=\angle BAC$ .

A.

$6$ B.

$\dfrac{5}{2}$ C.

$\dfrac{7}{2}$ D.

$12$ E.

$3$

Гурвалжны талбай

Гурвалжны суурь

$a = 6 \, \text{см}$ , уг суурьт буулгасан өндөр

$h = 4 \, \text{см}$ бол талбайг ол.

A.

$9$ B.

$18$ C.

$12$ D.

$24$ E.

$10$

ЭЕШ 2011 A №25

Тэгш өнцөгт гурвалжны катетууд

$10$ ба

$15$ нэгж урттай бөгөөд түүнтэй ерөнхий тэгш өнцөгтэй, нэг орой нь гипотенуз дээр байх тэгш өнцөгтийн талбайн хамгийн их утгыг ол. Тэгш өнцөгтийн талуудыг

$x$ ,

$y$ гээд тэдгээрийн хоорондын хамаарлыг олбол

$x=\fbox{ab}-1.5y$ болно. Тэгш өнцөгтийн талбайг

$y$ -ээр илэрхийлэн уламжлал ашиглаж, түүний хамгийн их утга авах

$y$ -ийн утгыг олбол

$y=\fbox{c}$ байх ба энэ үед

$x=\fbox{d.e}$ болж талбайн хамгийн их утга нь

$S=\fbox{fg.h}$ болно.

Синусын теорем

$ABC$ гурвалжны талууд

$AB=3+\sqrt3, AC=\sqrt3+1$ ба

${\angle B=30^\circ}$ бол

$\angle C=\fbox{ab}^\circ$ , эсвэл

$\angle C=\fbox{cde}^\circ$ байна.

$\angle C=\fbox{ab}^\circ$ үед

$ABC$ гурвалжны талбай

$\sqrt3(\fbox{f}+\sqrt{\fbox{g}})$ ба

$\angle C=\fbox{cde}^\circ$ үед

$BC=\sqrt{\fbox{h}}+\fbox{i}$ болно.

Бодлого №4851

5, 12, 13 талтай тэгш өнцөгт гурвалжинд хоёр орой нь гипотенуз дээр байх тэгш өнцөгт багтаав. Тэгш өнцөгтийн талбайн хамгийн их утга нь

$\fbox{ab}$ байна. Энэ үед тэгш өнцөгтийн өргөн нь

$\dfrac{\fbox{cd}}{\fbox{ef}}$ , урт нь

$\dfrac{\fbox{gh}}{\fbox{i}}$ байна.

$ABC$ гурвалжны талууд

$AB=2$ ,

$AC=3$ ,

$BC=4$ ба

$AM_1$ медианы үргэлжлэл уг гурвалжныг багтаасан тойргийг

$A_1$ цэгт огтолдог гэе.

$M_1A_1=\dfrac{\sqrt{2}\fbox{a}}{\sqrt{\fbox{b}}}$ ба

$A_1BC$ гурвалжны периметр нь

$\fbox{c}+2\sqrt{\fbox{de}}$ байна. Мөн

$A_1BC$ гурвалжны талбай

$\dfrac{\fbox{f}\sqrt{\fbox{gh}}}{\fbox{i}}$ болно.

$ABC$ гурвалжны талууд

$AB=4$ ,

$AC=5$ ,

$BC=6$ ба

$AM$ медианы үргэлжлэл уг гурвалжныг багтаасан тойргийг

$A_1$ цэгт огтолдог гэе.

$MA_1=\dfrac{\fbox{a}}{\fbox{bc}}\sqrt{46}$ ба

$A_1C$ талын урт

$\dfrac{\fbox{de}}{\fbox{fg}}\sqrt{\fbox{46}}$ байна. Мөн

$A_1BC$ гурвалжны талбай

$\dfrac{\fbox{hij}}{46}\sqrt{7}$ болно.

Синусын теорем, Гурвалжны талбай

$ABC$ гурвалжны хувьд

$AC=4$ ,

$AB=4\sqrt{2}$ ,

$\measuredangle B=30 ^{\circ}$ бол

$\measuredangle C=\dfrac{\pi}{\fbox{a}}$ , эсвэл

$\measuredangle C=\dfrac{\fbox{b}}{\fbox{c}}\pi$ байна.

$C=\dfrac{\pi}{\fbox{a}}$ үед

$ABC$ гурвалжны талбай

$4(\sqrt{\fbox{d}}+\fbox{e} )$ ,

$\measuredangle C=\dfrac{\fbox{b}}{\fbox{c}}\pi$ үед

$BC=2(\sqrt{\fbox{f}}-\sqrt{\fbox{g}} )$ болно.

Бодлого №7896

$ABC$ гурвалжны талууд

$AC=3+\sqrt{3}$ ,

$AC=\sqrt{3}+1$ ба

$\measuredangle B=30^{\circ}$ бол

$\measuredangle C=\dfrac{\pi}{\fbox{a}}$ , эсвэл

$\measuredangle C=\dfrac{\fbox{b}}{\fbox{c}}\pi$ байна.

$C=\dfrac{\pi}{\fbox{a}}$ үед

$ABC$ гурвалжны талбай

$\sqrt{3}(\fbox{d}+\sqrt{\fbox{e}} )$ ба

$\measuredangle C=\dfrac{\fbox{b}}{\fbox{c}}\pi$ үед

$BC=\sqrt{\fbox{f}}+\fbox{g}$ болно.

Бодлого №7908

$ABC$ гурвалжны талууд

$AB=8$ ,

$BC=10$ ,

$\cos\widehat{ABC}=1/8$ байдаг гэе.

$ABC$ гурвалжны талбай $\fbox{ab}\sqrt{\fbox{7}}$ ,
$AC=\fbox{cd}$ , $\cos\widehat{ACB}=-\dfrac{\fbox{e}}{\fbox{fg}}$ ,
$AB$ талын дунджийг $M$ гээд $BC$ , $AC$ талууд дээр $PC=PM$ , $QC=QM$ байх $P, Q$ цэгүүд авахад $MP=\dfrac{\fbox{hij}}{\fbox{kl}}$ , $MQ=\dfrac{428}{\fbox{mn}}$ байна.

Бодлого №7911

Адил хажуут

$ABC$ (AC=BC) гурвалжны

$C$ өнцөгт

$\dfrac{12}{5}$ радиустай тойрог багтсан бөгөөд уг тойрог

$AC$ ,

$BC$ талуудыг харгалзан

$N$ ,

$M$ цэгт шүргэж

$AB$ талыг

$D$ ,

$E$ цэгүүдэд огтолж байв.

$BM=16/5$ ,

$\tg \beta ={3}/{4}$ ба уг тойргийн төв

$O$ бол

${MN}\colon{AB}={\fbox{a}}\colon{\fbox{bc}}$ , гурвалжны талууд

$\fbox{d}$ ,

$\fbox{e}$ болно. Мөн

$ONCM$ дөрвөн өнцөгтийн талбай

${\fbox{fgh}}{ }/{ }{\fbox{ij}}$ байна.

Бодлого №7912

Адил хажуут

$ABC$ (AB=BC) гурвалжны

$B$ өнцөгт

$6$ радиустай тойрог багтсан бөгөөд уг тойрог

$AB$ ,

$BC$ талуудыг харгалзан

$M$ ,

$N$ цэгүүдэд шүргэж

$AC$ талыг

$D$ ,

$E$ цэгүүдээр огтолж байв.

$AM=9$ ,

$\tg \alpha ={2}/{3}$ ба уг тойргийн төв

$O$ бол

${MN}\colon{AC}={\fbox{a}}\colon{\fbox{bc}}$ , гурвалжны талууд

$\fbox{de}$ ,

$\fbox{f}\sqrt{\fbox{gh}}$ болно. Мөн

$OMBN$ дөрвөн өнцөгтийн талбай

$\fbox{ij}$ байна.

Багтсан тойргийн шүргэлтийн урт

Дараахь бодлогуудыг бод.

$ABC$ гурвалжны талууд $a=3$ , $b=4$ , $c=5$ бол $\dfrac{r}{R}=\dfrac{\fbox{a}}{\fbox{b}}$ байна.
$a=3$ , $c=7$ ба $\cos \beta =1-\dfrac{r}{R}$ үед $b=\fbox{c}$ ба энэ үед гурвалжны талбай $\dfrac{\fbox{de}}{\fbox{f}}\sqrt{\fbox{g}}$ болно.

Бодлого №7914

Дараахь бодлогуудыг бод.

$ABC$ гурвалжны талууд $a=6$ , $b=8$ , $c=10$ бол $\dfrac{r}{R}=\dfrac{\fbox{a}}{\fbox{b}}$ байна.
$a=4$ , $c=6$ ба $\cos \beta =1-\dfrac{r}{R}$ бол $b=\fbox{c}$ ба энэ үед гурвалжны талбай $\dfrac{\fbox{de}}{\fbox{f}}\sqrt{\fbox{g}}$ болно.

Бодлого №7915

$ABC$ гурвалжны хувьд

$\sin^2 \alpha +\sin^2 \beta =\sin^2 \gamma$ нөхцөл биелдэг бол

$\gamma =\dfrac{\pi}{\fbox{a}}$ байна.

$AB=2\sqrt{3}$ үед

$CM$ медианы урт

$\sqrt{\fbox{b}}$ болно.

$AB=2\sqrt{3}$ талтай, эсрэг оройн өнцөг нь тогтмол

$\dfrac{\pi}{\fbox{a}}$ байх бүх гурвалжнууд дотроос хамгийн их талбайтай гурвалжны периметр

$(\fbox{c}\sqrt{\fbox{d}}+2\sqrt{3})$ байна.

Бодлого №7931

$ADE$ нь тэгш өнцөгт гурвалжин ба

$\measuredangle EAD=90^{\circ}$ ,

$\measuredangle ADE=18^{\circ}$ байв.

$B$ ,

$C$ цэгүүд нь

$AD$ тал дээр оршиж

$EC=CD=2$ ,

$EB=BC$ бол

$AC=\dfrac{\fbox{a}+\sqrt{\fbox{b}}}{\fbox{c}}$ ,

$AB=\dfrac{\fbox{d}-\sqrt{\fbox{e}}}{2}$ ба

$ADE$ гурвалжны талбай

$\dfrac{\sqrt{\fbox{fg}}}{\fbox{h}}\sqrt{5+\sqrt{5}}$ болно.

Бодлого №7932

$ABC$ нь тэгш өнцөгт гурвалжин ба

$\measuredangle BAC=90^{\circ}$ ,

$\measuredangle ACB=18^{\circ}$ байв.

$D$ ,

$E$ цэгүүд нь

$AC$ тал дээр оршиж

$BD=DE=3$ ,

$BE=EC$ бол

$BD=\dfrac{\fbox{a}\sqrt{\fbox{b}}-\fbox{c}}{4}$ ,

$AB=3\sqrt{\fbox{de}-2\sqrt{\fbox{f}}} /4$ ба

$ABC$ гурвалжны талбай

$\dfrac{\fbox{g}\sqrt{\fbox{hi}}}{16}\sqrt{5+\sqrt{5}}$ болно.

Бодлого №7969

$3$ талтай

$ABC$ зөв гурвалжны

$AB$ тал дээр

$D$ цэг,

$AC$ тал дээр

$E$ цэгийг

$AD=CE$ байхаар авчээ.

$DBCE$ дөрвөн өнцөгтийн талбайг

$S$ гэвэл

$DE\geq \dfrac{\fbox{a}}{\fbox{b}}$ болох тул

$S\geq \dfrac{\fbox{cd}}{16}\sqrt{\fbox{e}}$ байна.

Бодлого №7970

$5$ талтай

$ABC$ зөв гурвалжны

$AB$ тал дээр

$D$ цэг,

$AC$ тал дээр

$E$ цэгийг

$AD=CE$ байхаар авчээ.

$DBCE$ дөрвөн өнцөгтийн талбайг

$S$ гэвэл

$DE\geq \dfrac{\fbox{a}}{\fbox{b}}$ болох тул

$S\geq \dfrac{\fbox{cd}}{16}\sqrt{\fbox{e}}$ байна.

Бодлого №7971

$3$ талбайтай

$ABC$ гурвалжны

$AB$ ,

$BC$ ,

$AC$ талууд дээр харгалзан

$D$ ,

$E$ ,

$F$ цэгүүдийг

$\dfrac{AD}{DB}=\dfrac{t}{1-t}$ ,

$\dfrac{BE}{EC}=\dfrac{2t}{1-2t}$ ,

$\dfrac{CF}{FA}=\dfrac{3t}{1-3t}$ байхаар авчээ.

$DEF$ гурвалжны талбайг

$S$ гэвэл

$S=\fbox{ab} t^2-\fbox{cd} t+\fbox{e}$ болох ба

$t=\dfrac{3}{\fbox{fg}}$ үед

$S$ хамгийн бага

$\dfrac{\fbox{h}}{\fbox{ij}}$ утгаа авна.

Бодлого №7972

$2$ талбайтай

$ABC$ гурвалжны

$AB$ ,

$BC$ ,

$AC$ талууд дээр харгалзан

$D$ ,

$E$ ,

$F$ цэгүүдийг

$\dfrac{AD}{DB}=\dfrac{t}{1-t}$ ,

$\dfrac{BE}{EC}=\dfrac{2t}{1-2t}$ ,

$\dfrac{CF}{FA}=\dfrac{3t}{1-3t}$ байхаар авчээ.

$DEF$ гурвалжны талбайг

$S$ гэвэл

$S=\fbox{ab}t^2-\fbox{cd}t+\fbox{e}$ болох ба

$t=\dfrac{3}{\fbox{fg}}$ үед

$S$ хамгийн бага

$\dfrac{\fbox{h}}{\fbox{ij}}$ утгаа авна.

Талууд дээр оройтой гурвалжны талбай

$ABC$ гурвалжны

$AB$ ,

$BC$ ,

$AC$ талууд дээр харгалзан

$F$ ,

$E$ ,

$D$ цэгүүдийг

$\dfrac{AF}{FB}=\dfrac{BE}{EC}=\dfrac{CD}{AD}=\dfrac{2}{5}$ байхаар авчээ.

$FED$ ,

$ABC$ гурвалжнуудын талбайн харьцаа

$\dfrac{\fbox{ab}}{\fbox{cd}}$ байна.

Бодлого №7982

$ABC$ гурвалжны

$AB$ ,

$BC$ ,

$AC$ талууд дээр харгалзан

$F$ ,

$E$ ,

$D$ цэгүүдийг

$\dfrac{AF}{FB}=\dfrac{BE}{EC}=\dfrac{CD}{AD}=\dfrac{1}{4}$ байхаар авчээ.

$FED$ ,

$ABC$ гурвалжнуудын талбайн харьцаа

$\dfrac{\fbox{ab}}{\fbox{cd}}$ байна.

Гурвалжинд багтсан ромбо

$ABC$ гурвалжинд

$AC_1A_1B_1$ ромбо багтсан бөгөөд

$C_1$ ,

$A_1$ ,

$B_1$ цэгүүд нь харгалзан

$AB$ ,

$BC$ ,

$CA$ талууд дээр байрлах ба

$\dfrac{AC_1}{C_1B}=4$ ,

$B_1C=16$ бол

$AC_1=\fbox{a}$ ,

$C_1B=\fbox{b}$ байна.

$B_1C_1=4$ үед

$ABC$ гурвалжны талбай

$\fbox{cd}\sqrt{\fbox{e}}$

sin теорем

$ABC$ гурвалжны талууд

$AB=3+\sqrt3, AC=\sqrt3+1$ ба

${\angle B=30^\circ}$ бол

$\angle C=\fbox{ab}^\circ$ , эсвэл

$\angle C=\fbox{cde}^\circ$ байна.

$\angle C=\fbox{ab}^\circ$ үед

$ABC$ гурвалжны талбай

$\sqrt3(\fbox{f}+\sqrt{\fbox{g}})$ ба

$\angle C=\fbox{cde}^\circ$ үед

$BC=\sqrt{\fbox{h}}+\fbox{i}$ болно.

Төсөөгийн харьцаа

$\triangle ABC$ гурвалжны талуудын урт нь

$AB=8$ ,

$AC=12$ ,

$BC=16$ .

$D$ ,

$E$ нь харгалзан

$AB$ ба

$AC$ талууд дээр орших цэгүүд бөгөөд

$DE\parallel BC$ байв. Хэрвээ

$BD+EC=5$ бол

$DE=\fbox{ab}$ ба

$S_{\triangle ADE}=\dfrac{\fbox{cd}\sqrt{\fbox{ef}}}{\fbox{g}}$ байна.

ЭЕШ 2020, B40

$R=6$ радиустай тойрогт багтсан

$ABCDE$ таван өнцөгтийн

$AB=6\sqrt{2}$ ,

$\measuredangle ABE=45^\circ$ ,

$\measuredangle EBD=30^\circ$ ба

$BC=CD$ бол таван өнцөгтийн талбайг ол.

Бодолт. Синусын теоремоор

$AE=2R\sin45^\circ$ гэдгээс

$AE=6\sqrt{\fbox{a}}$ . Иймд

$ABE$ гурвалжны талбай

$S_1=3\fbox{b}$ . Цаашилбал

$\measuredangle BDE=\fbox{c}0^\circ$ гэдгээс

$BD=6\sqrt{\fbox{d}}$ ,

$DE=\fbox{e}$ . Иймээс

$BDE$ гурвалжны талбай

$S_2=18\sqrt{\fbox{d}}$ . Харин

$BCDE$ дөрвөн өнцөгт тойрогт багтсан гэдгээс

$C$ оройн өнцгийг тооцоолж болно. Иймд

$BCD$ гурвалжны өндөр

$CF=\fbox{f}$ ба түүний талбай

$S_3=9\sqrt{\fbox{g}}$ . Эдгээрээс таван өнцөгтийн талбай

$S=S_1+S_2+S_3$ болно.

ЭЕШ сорилго №1А, Бодлого №40

$ABCDEFGH$ зөв найман өнцөгтийн талын урт

$4$ ;

$AC$ ,

$BD$ диагоналиудын хоорондох өнцөг

$\fbox{ab.c}^\circ$ ,

$ABCDE$ таван өнцөгтийн талбай

$\fbox{de}\sqrt{2}$ ,

$ABCD$ дөрвөн өнцөгтийн талбай

$\fbox{fg}\sqrt{2}$ байна.

ЭЕШ 2020, A40

$R=4$ радиустай тойрогт багтсан

$ABCDE$ таван өнцөгтийн

$AB=4\sqrt{2}$ ,

$\measuredangle ABE=45^\circ$ ,

$\measuredangle EBD=30^\circ$ ба

$BC=CD$ бол таван өнцөгтийн талбайг ол.

Бодолт. Синусын теоремоор

$AE=2R\sin45^\circ$ гэдгээс

$AE=4\sqrt{\fbox{a}}$ . Иймд

$ABE$ гурвалжны талбай

$S_1=1\fbox{b}$ . Цаашилбал

$\measuredangle BDE=\fbox{c}0^\circ$ гэдгээс

$BD=4\sqrt{\fbox{d}}$ ,

$DE=\fbox{e}$ . Иймээс

$BDE$ гурвалжны талбай

$S_2=8\sqrt{\fbox{d}}$ . Харин

$BCDE$ дөрвөн өнцөгт тойрогт багтсан гэдгээс

$C$ оройн өнцгийг тооцоолж болно. Иймд

$BCD$ гурвалжны өндөр

$CF=\fbox{f}$ ба түүний талбай

$S_3=4\sqrt{\fbox{g}}$ . Эдгээрээс таван өнцөгтийн талбай

$S=S_1+S_2+S_3$ болно.

$ABCD$ гүдгэр дөрвөн өнцөгт өгчээ.

$AB=6$ ,

$BC=5$ ,

$CD=2$ ,

$DA=7$ ,

$AC=2x-1$ бол

$x$ -ийн бүхэл утгыг ол.

A.

$6$ B.

$5$ C.

$4$ D.

$3$ E.

$2$

Бодлого №7842

$ABCD$ гүдгэр дөрвөн өнцөгтийн

$AB\mbox{=}8$ ,

$BC\mbox{=}x$ ,

$DA\mbox{=}2x,$

$AC$ диагональ 5,

$BD=4$ бол

$x$ -ийн сондгой утга хэд вэ?

A. 6 B. 5 C. 7 D. 9 E. 4

Гурвалжны хоёр талын урт нь 5 ба 8 нэгж байв. Гурав дахь талын бүх боломжит уртын утга аль нь вэ?

A.

$]3;13[$ B.

$]0;5[$ C.

$]3;8[$ D.

$]5;8[$ E.

$]8;13[$

Гурвалжны хоёр талын урт нь 5 ба 8 нэгж байв. Доорх тоонуудын аль нь гурвалжны гурав дахь тал болж чадах вэ?

A.

$1$ B.

$3$ C.

$12$ D.

$13$ E.

$17$

Гурвалжны хоёр талын урт нь 5 ба 8 нэгж байв. Доорх тоонуудын аль нь гурвалжны гурав дахь тал болж чадахгүй вэ?

A.

$9$ B.

$10$ C.

$11$ D.

$12$ E.

$13$

Бодлого №9

Гурвалжны хоёр талын урт нь 4 ба 9 нэгж байв. Гурав дахь талын уртын бүх боломжит утга аль нь вэ?

A.

$]3;13[$ B.

$]0;5[$ C.

$]3;8[$ D.

$]5;8[$ E.

$]5;13[$

Бодлого №9

Гурвалжны хоёр талын урт нь 5 ба 9 нэгж байв. Гурав дахь талын уртын бүх боломжит утга аль нь вэ?

A.

$]3;14[$ B.

$]0;5[$ C.

$]4;14[$ D.

$]5;8[$ E.

$]5;9[$

Бодлого №2453

Тэгш өнцөгт гурвалжны катетуудын харьцаа

$3:2$ . Тэгш өнцөгөөс татсан өндөр гипотенузыг нэг нь нөгөөгөөсөө

$2$ см урт хоёр хэсэгт хуваасан бол гипотенузыг ол.

Тэгш өнцөгт гурвалжны өндөр

$\angle C=90^\circ$ ,

$CD\perp AB$ ,

$AC=15$ ,

$AD=9$ бол

$AB=?$

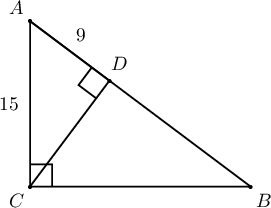
A.

$24$ B.

$20$ C.

$30$ D.

$25$ E.

$35$

$ABC$ гурвалжны талууд

$AB=12$ ,

$BC=5$ ,

$AC=13$ ба

$AB$ тал дээр

${AC_1}\colon {BC_1}={1}\colon{2}$ байх

$C_1$ цэг тэмдэглэв.

$BC$ талын дундаж нь

$A_1$ ,

$BB_1$ нь

$AC$ тал дээр буулгасан өндөр бол

$BB_1=\dfrac{\fbox{ab}}{13},$

$S_{AC_1B_1}=\dfrac{\fbox{cdef}}{13^2}$ ,

$S_{CA_1B_1}=\dfrac{\fbox{ghi}}{13^2}$ байна.

Бодлого №2315

$10, 14, 17$ талуудтай гурвалжинд мохоо өнцөг бий юу?

Бодлого №2324

$ABC$ гурвалжныг багтаасан тойргийн радиус

$R$ .

$D$ цэг багтаасан тойргийн

$BC$ нум дээр орших бөгөөд

$AD\cap BC=M$ . Хэрэв

$\angle BMD=120^\circ$ ,

$AB=R$ ,

$BM:MC=2:3$ бол

$BC$ талын уртыг ол.

Бодлого №2349

Хурц өнцөгт

$ABC$ гурвалжинд

$AD=5$ ,

$CE=3$ байх өндрүүд татжээ.

$AD$ ,

$CE$ шулуунуудын хоорондох өнцөг нь

$60^\circ$ бол

$AC$ талын уртыг ол.

Бодлого №2382

$ABC$ гурвалжны хувьд

$\angle BAC=30^\circ$ . Хэрэв

$AB=\sqrt {3}, AC=1$ бол

$BC$ талыг ол.

Бодлого №2841

Зөв дөрвөн өнцөгт пирамидын өндөр

$\sqrt3$ , хажуу ирмэгүүдийн хоорондох хавтгай өнцөг

$30^\circ$ бол пирамидын эзлэхүүн, хажуу гадаргуугийн талбайг ол.

Тойргийн нэг цэгээс

$9$ см ба

$17$ см урттай

$2$ хөвч татав. Хэрэв эдгээр хөвчүүдийн дунджууд хоорондоо

$5$ см зайтай бол тойргийн радиусыг ол.

A.

$9.75$ см B.

$\dfrac{41}4$ см C.

$12$ см D.

$10$ см E.

$\dfrac{85}8$ см

Параллель шулуунуудын хоорондох зай

$AB$ ба

$CD$ параллел шулуунууд

$60^\circ$ -ийн өнцөгөөр огтолцох хоёр хавтгайд оршино.

$A$ ба

$D$ цэгүүд огтлолцлын шулуунаас харгалзан

$a$ ба

$b$ зайд алслагдана.

$AB$ ба

$CD$ шулуунуудын хоорондох зайг ол.

A.

$a+b$ B.

$|a-b|$ C.

$\sqrt{a^2+b^2+ab}$ D.

$\dfrac13\sqrt{a^2+b^2+ab}$ E.

$\sqrt{a^2+b^2-ab}$

ЭЕШ 2010 A №3

Талууд нь 6; 9; 11 нэгж урттай гурвалжны хэлбэрийг тогтоогоорой.

A. Хурц өнцөгт гурвалжин B. Мохоо өнцөгт гурвалжин C. Тэгш өнцөгт гурвалжин D. Адил хажуут гурвалжин E. Зөв гурвалжин

Гурвалжны хэлбэр

10, 14, 17 талуудтай гурвалжны хэлбэрийг тогтоо.

A. Мохоо өнцөгт гурвалжин B. Хурц өнцөгт гурвалжин C. Тэгш өнцөгт гурвалжин D. Адил хажуут гурвалжин E. Ийм гурвалжин оршин байхгүй

Бодлого №4763

$ABC$ гурвалжинд

$BD$ медиан татжээ.

$AB=2\sqrt3$ ,

$AC=8$ ,

$\measuredangle ABD=45^\circ$ бол

$BC$ талын уртыг ол.

A.

$\sqrt6+\sqrt{10}$ B.

$4\sqrt3$ C.

$16+4\sqrt{15}$ D.

$\sqrt{52+8\sqrt{15}}$ E.

$2\sqrt{100-2\sqrt{15}}$

Бодлого №4839

$AD\parallel BC$ байх трапецийн хувьд

$AB=5$ ,

$BC=8$ ,

$BD=7$ ,

$\angle A=120^\circ$ байв. Трапецийн талбайг ол.

A.

$40$ B.

$11\sqrt3$ C.

$36$ D.

$\dfrac{67}{4}$ E.

$\dfrac{55\sqrt3}{4}$

Бодлого №4908

Гурвалжны нэг өнцгийн косинус нь

$-0.6$ байв. Дараахь өгүүлбэрүүдийн аль нь үнэн бэ?

A. Хурц өнцөгт гурвалжин B. Мохоо өнцөгт гурвалжин C. Тэгш өнцөгт гурвалжин D. Мохоо өнцөг нь

$120^\circ$ E. Уг өнцгийн синус нь

$-0.8$

Гурвалжны хамгийн бага өнцөг

$a=2\sqrt2, b=2, c=\sqrt2+\sqrt6$ талуудтай гурвалжны хамгийн бага өнцгийг ол.

A.

$90^\circ$ B.

$60^\circ$ C.

$75^\circ$ D.

$30^\circ$ E.

$45^\circ$

Адил хажуут гурвалжнууд

Адил хажуут хоёр гурвалжны хажуу талуудын урт тэнцүү байжээ. Хэрэв нэгнийх нь суурь

$12$ см, нөгөөгийн суурь, хажуу тал хоёр

$8:5$ харьцаатай, оройн өнцгүүдийн нийлбэр

$\pi$ байсан бол талуудын урт хэд хэд байх вэ?

A.

$40, 25$ B.

$24, 15$ C.

$20, 15$ D.

$32, 20$ E.

$16, 10$

Адил хажуут гурвалжны суурийн урт

$\sqrt3$ талбайтай адил хажуут гурвалжны медиануудын огтлолцлоос суурийн харагдах өнцөг

$120^\circ$ бол суурийн урт аль нь вэ?

A.

$2$ B.

$5$ C.

$6$ D.

$3$ E.

$4$

Тэгш өнцөгт трапецийн сууриудын харьцаа

Тэгш өнцөгт трапецийн

$AB$ суурь,

$AC$ диагональтай тэнцүү бөгөөд

$BC^2=AB\cdot AD$ бол бага суурийг их суурьт харьцуулсан харьцаа аль нь вэ?

A.

$3:5$ B.

$4:5$ C.

$3:8$ D.

$3:7$ E.

$2:3$

ЭЕШ 2015 D №10

$ABC$ гурвалжны

$AB=1.5$ ,

$AC=4$ ,

$\measuredangle A=60^\circ$ бол

$BC$ талын уртыг ол.

A.

$1.5$ B.

$3.5$ C.

$4$ D.

$5.5$ E.

$\sqrt{15.25}$

Гурвалжны өнцгийн косинус

Гурвалжны талуудын урт

$5$ ,

$6$ ,

$7$ нэгж бол их талын эсрэг орших өнцгийн косинус аль нь вэ?

A.

$\dfrac15$ B.

$\dfrac16$ C.

$\dfrac17$ D.

$-\dfrac15$ E.

$-\dfrac17$

ЭЕШ 2015 A №10

$ABC$ гурвалжны

$AB=3$ ,

$AC=8$ ,

$\measuredangle A=60^\circ$ бол

$BC$ талын уртыг ол.

A.

$\sqrt{61}$ B.

$7$ C.

$\sqrt{97}$ D.

$49$ E.

$\sqrt{73}$

ЭЕШ 2011 D №9

$MNP$ гурвалжинд

$MQ$ медиан татжээ. Хэрэв

$MP=2\sqrt3$ ,

$NP=8$ ,

$\measuredangle QMP=45^\circ$ бол

$MNP$ гурвалжны талбайг ол.

A.

$2\sqrt{13}$ B.

$4\sqrt{39}$ C.

$64$ D.

$\sqrt{39}$ E.

$6+\sqrt{15}$

ЭЕШ 2007 A №22

$AC=4$ нэгж,

$AB=5$ нэгж урттай

$ABC$ гурвалжны

$A$ оройн дотоод өнцгийн биссектрис

$AD=DB$ байхаар

$BC$ талтай

$D$ цэгт огтлолцсон бол

$BC$ талын уртыг ол.

A.

$6$ B.

$6.5$ C.

$7$ D.

$7.5$ E.

$8$

ЭЕШ 2015 B №10

$ABC$ гурвалжны

$AB=7.5$ ,

$AC=20$ ,

$\measuredangle A=60^\circ$ бол

$BC$ талын уртыг ол.

A.

$27.5$ B.

$7.5$ C.

$20$ D.

$10.5$ E.

$17.5$

ЭЕШ 2015 C №10

$ABC$ гурвалжны

$AB=6$ ,

$AC=16$ ,

$\measuredangle A=60^\circ$ бол

$BC$ талын уртыг ол.

A.

$\sqrt{244}$ B.

$16$ C.

$14$ D.

$8$ E.

$82$

Косинусын теорем, Өнцгийн косинус

Гурвалжны талуудын урт

$6$ ,

$7$ ,

$9$ нэгж байв. Хамгийн бага өнцгийн косинус нь хэдтэй тэнцүү вэ?

A.

$\dfrac{47}{63}$ B.

$-\dfrac{47}{63}$ C.

$\dfrac{\sqrt{17}}{36}$ D.

$-\dfrac{\sqrt{17}}{36}$ E.

$\dfrac16$

Косинусын теорем, Хажуу ирмэгийг олох

$ABC$ гурвалжны

$AB=3$ ,

$BC=7$ ба

$\measuredangle BAC=120^\circ$ байв.

$AC$ талын урт аль нь вэ?

A.

$4$ B.

$5$ C.

$6$ D.

$7$ E.

$8$

Биссектрисийн урт

$\triangle ABC$ -ийн

$AB=4$ ,

$AC=6$ ба

$\measuredangle BAC=60^\circ$ байв.

$A$ оройгоос татсан биссектрисийн уртыг ол.

A.

$\dfrac{12\sqrt3}{5}$ B.

$3\sqrt{3}$ C.

$4\sqrt3$ D.

$\dfrac{4\sqrt3}{3}$ E.

$2\sqrt{3}$

Гурвалжны их өнцөг

$\triangle ABC$ -ийн хувьд

$\dfrac{\sin\alpha}{\sqrt{7}}=\dfrac{\sin\beta}{\sqrt{3}}=\sin\gamma$ бол хамгийн их өнцгийг ол. Энд

$\alpha$ ,

$\beta$ ,

$\gamma$ нь

$\triangle ABC$ ны өнцгүүд.

A.

$75^\circ$ B.

$90^\circ$ C.

$108^\circ$ D.

$120^\circ$ E.

$150^\circ$

Трапецийн талбай

$AD\parallel BC$ байх трапецийн

$AB=5$ ,

$BC=8$ ,

$BD=7$ ,

$\angle A=120^\circ$ байв. Трапецийн талбайг ол.

A.

$\dfrac{55\sqrt3}{4}$ B.

$55$ C.

$11\sqrt{3}$ D.

$75$ E.

$26$

Медианы урт

$ABC$ гурвалжны

$AB=3$ ,

$AC=4$ ,

$BC=\sqrt{34}$ бол

$AD$ медианы урт аль нь вэ?

A.

$\dfrac12$ B.

$1$ C.

$\dfrac32$ D.

$2$ E.

$\dfrac52$

ЭЕШ 2008 A №58

Параллелограммын хоёр талын урт 2 ба 7, нэг диагоналийн урт 8 бол нөгөө диагоналийн уртыг ол.

A.

$8$ B.

$8.5$ C.

$\sqrt{42}$ D.

$10$ E.

$\sqrt{11}$

Трапецийн талбай

$AD\parallel BC$ байх

$ABCD$ трапецийн хувьд

$AB=2\sqrt{2}$ ,

$AC=2\sqrt5$ ,

$AD=8$ ,

$\measuredangle ABC=135^\circ$ бол талбайг нь ол.

A.

$5$ B.

$8$ C.

$9$ D.

$10$ E.

$12$

Гурвалжны хэлбэр

5, 7, 9 талуудтай гурвалжны хэлбэрийг тогтоо.

A. Мохоо өнцөгт гурвалжин B. Хурц өнцөгт гурвалжин C. Тэгш өнцөгт гурвалжин D. Адил хажуут гурвалжин E. Ийм гурвалжин оршин байхгүй

Бодлого №26

$ABC$ гурвалжинд

$BD$ медиан татжээ.

$AB=3$ ,

$AC=8$ ,

$\cos\measuredangle ABD=-\dfrac14$ бол

$BC$ талын уртыг ол.

A.

$4\sqrt2$ B.

$\sqrt{31}$ C.

$5$ D.

$6$ E.

$3\sqrt{5}$

Бодлого №26

$ABC$ гурвалжинд

$BD$ медиан татжээ.

$AB=2$ ,

$AC=8$ ,

$\cos\measuredangle ABD=-\dfrac14$ бол

$BC$ талын уртыг ол.

A.

$4\sqrt3$ B.

$\sqrt{46}$ C.

$5$ D.

$6$ E.

$3\sqrt{5}$

ЭЕШ 2017 D №14

$ABC$ гурвалжны

$AB=7$ ,

$BC=4$ ,

$\cos\measuredangle ACB=-0.2$ бол

$AC$ талын урт хэд вэ?

A.

$4$ B.

$5$ C.

$6$ D.

$7$ E.

$10$

ЭЕШ 2017 D №14

$ABC$ гурвалжны

$AB=14$ ,

$BC=10$ ,

$\cos\measuredangle ACB=-0.2$ бол

$AC$ талын урт хэд вэ?

A.

$8$ B.

$10$ C.

$12$ D.

$14$ E.

$13$

ЭЕШ 2010 B №3

Талууд нь 5; 12; 13 нэгж урттай гурвалжны хэлбэрийг тогтоогоорой.

A. Хурц өнцөгт гурвалжин B. Мохоо өнцөгт гурвалжин C. Зөв гурвалжин D. Адил хажуут гурвалжин E. Тэгш өнцөгт гурвалжин

Бодлого №13772

$ABC$ гурвалжинд

$BD$ медиан татжээ.

$AB=2\sqrt3$ ,

$AC=8$ ,

$\measuredangle ABD=45^\circ$ бол

$BC$ талын уртыг ол.

A.

$\sqrt6+\sqrt{10}$ B.

$4\sqrt3$ C.

$16+4\sqrt{15}$ D.

$\sqrt{52+8\sqrt{15}}$ E.

$2\sqrt{100-2\sqrt{15}}$

2021 B №23

$\frac{dy}{dx}=4x-3$ ба

$P(-1,1)$ цэгийг дайрах муруйг ол.

A.

$y=2x^2-1$ B.

$y=2x^2-3x-4$ C.

$y=4x^2-3x-6$ см D.

$y=2x^2-3x+2$ см E.

$y=4x^2-3x$ см

2019 A №23

$ABCD$ дөрвөн өнцөгт тойрогт багтжээ. Хэрэв

$BC = 12$ см,

$CD = 20$ см,

$\measuredangle BAD = 60^\circ$ бол

$BD$ хэрчмийн уртыг олно уу?

A.

$24$ см B.

$28$ см C.

$26$ см D.

$32$ см E.

$30$ см

2019 A №23

$ABCD$ дөрвөн өнцөгт тойрогт багтжээ. Хэрэв

$BC = 8$ см,

$CD = 7$ см,

$\measuredangle BAD = 60^\circ$ бол

$BD$ хэрчмийн уртыг олно уу?

A.

$13$ см B.

$11$ см C.

$10$ см D.

$12$ см E.

$14$ см

2019 B №23

$ABCD$ дөрвөн өнцөгт тойрогт багтжээ. Хэрэв

$BC = 8$ см,

$CD =7$ см,

$\measuredangle BAD = 60^\circ$ бол

$BD$ хэрчмийн уртыг олно уу?

A.

$13$ см B.

$11$ см C.

$10$ см D.

$12$ см E.

$14$ см

ЭЕШ 2007 A1 №27

Гурвалжны талуудын харьцаа

$3:7:8$ ба багтаасан тойргийн радиус нь

$\dfrac{14}{\sqrt3}$ бол

Хэмжээгээрээ дундах талын эсрэг орших өнцөг $\fbox{ab}^\circ$ байна.
Периметр нь $\fbox{cd}$ болно.
Багтсан тойргийн радиус нь $\dfrac{\fbox{e}\sqrt{\fbox{f}}}{3}$ байна.

Гурвалжин ашиглан 4 өнцөгт бодох

$O$ тойрогт багтсан

$ABCD$ дөрвөн өнцөгтийн талууд

$AB=3$ ,

$BC=7$ ,

$CD=7$ ,

$DA=5$ байв.

$ABD$ ба

$BDC$ гурвалжнуудаас косинусын теорем бичвэл

$\angle C=\fbox{ab}, BD=\fbox{c}$ болно. Тойрогт багтсан дөрвөн өнцөгтийн чанараар

$AC=\fbox{d}$ болно.

$ABCD$ дөрвөн өнцөгтийн талбай

$\fbox{ef}\sqrt{\fbox{g}}$ байна.

$O$ тойргийн радиуc

$\dfrac{\fbox{h}\sqrt{\fbox{i}}}{\fbox{j}}$ байна.

$ABD$ гурвалжинд багтсан тойргийн радиус

$\dfrac{\sqrt{\fbox{k}}}{\fbox{l}}$ байна.

$ABCD$ дөрвөн өнцөгтийн диагоналиудын огтлолцолын цэг

$E$ бол

$\sin\angle AEB=\dfrac{\fbox{m}\sqrt{\fbox{n}}}{\fbox{o}}$ байна.

Бодлого №5076

$\displaystyle ABCDS$ тэгш өнцөгт суурьтай пирамидын хувьд

$\displaystyle AB=CD=3,\ AD=BC=4$ ба хажуу ирмэгүүд нь бүгд

$\displaystyle 3$ нэгж бол

$\displaystyle \cos{\angle{ASD}}=\frac{\fbox{a}}{\fbox{b}}$ байна. Мөн пирамидын өндөр нь

$\displaystyle\frac{\sqrt{\fbox{cd}}}{\fbox{e}}$ байна.

$\dfrac{8\sqrt7}{7}$ радиустай тойрогт багтсан

$ABCD$ дөрвөн өнцөгтөд

$BC=4$ ,

$\cos\angle BAD=\dfrac18$ байв.

$BD=\fbox{a}$ , $CD=\fbox{b}$ байна.
$AB+AD=9$ бол $ABCD$ дөрвөн өнцөгтийн талбай $S=\dfrac{\fbox{cd}\sqrt{\fbox{e}}}{\fbox{f}}$ байна.

Гүдгэр 4 өнцөгтийн талуудыг бодох

$ABCD$ дөрвөн өнцөгтөд

$AB=1$ ,

$\measuredangle ABC=45^{\circ}$ ,

$\measuredangle ACB=60^{\circ}$ ,

$\measuredangle BAD=105^{\circ}$ ,

$\measuredangle ADB=45^{\circ}$ байв.

$AC$ диагоналийн урт

$\dfrac{\sqrt{\fbox{a}}}{\fbox{b}}$ ,

$\measuredangle ABD=\fbox{cd}^\circ$ ,

$AD=\dfrac{\sqrt{\fbox{e}}}{\fbox{f}}$ ,

$CD=\dfrac{\sqrt{\fbox{g}}}{\fbox{h}}$ болно.

Гүдгэр 4 өнцөгтийн талуудыг бодох

$ABCD$ дөрвөн өнцөгтөд

$AB=1$ ,

$\measuredangle ABC=60^{\circ}$ ,

$\measuredangle ACB=45^{\circ}$ ,

$\measuredangle BAD=105^{\circ}$ ,

$\measuredangle ADB=45^{\circ}$ байв.

$AC$ диагоналийн урт

$\dfrac{\sqrt{\fbox{a}}}{\fbox{b}}$ ,

$\measuredangle ABD=\fbox{cd}^\circ$ ,

$AD=\dfrac{\sqrt{\fbox{e}}}{\fbox{f}}$ ,

$CD=\dfrac{\sqrt{\fbox{g}}}{\fbox{h}}$ болно.

Гурвалжны биссектрисс ба медиан

$ABC$ гурвалжны

$AL$ биссектрисс

$CM$ медиантай

$O$ цэгт огтлолцоно.

$AC=4$ ,

$AB=6$ бол

$\dfrac{CO}{CM}=\dfrac{\fbox{a}}{\fbox{b}}$ ,

$BO$ шулууны

$AC$ талтай огтлолцох цэгийг

$N$ гэвэл

$\dfrac{ON}{BN}=\dfrac{\fbox{c}}{\fbox{d}}$ болох бөгөөд

$BL=\dfrac{12}{5}$ үед

$BN=\dfrac{\fbox{e}}{\fbox{f}}\sqrt{14}$ байна.

Хоёр тойргийн огтлолцолд үүсэх дүрс

$2(\sqrt{3}+1)$ см урттай

$AB$ хэрчмийн

$A$ цэгт төвтэй

$2\sqrt{2}$ см радиустай тойрог ба

$B$ цэгт төвтэй

$4$ см радиустай тойргууд

$C$ ,

$D$ цэгт огтлолцдог гэе.

$\measuredangle CAD =\fbox{ab}^{\circ}$ ба

$\measuredangle CBD =\dfrac{\pi}{\fbox{c}}$ , дугуйнуудын ерөнхий хэсгийн талбай нь

$\dfrac{\fbox{de}}{3}\pi-(4+4\sqrt{3})$ см

$^2$ байна.

Тойрогт багтсан

$ABCD$ дөрвөн өнцөгтийн хувьд

$AB=5$ ,

$CD=4$ ,

$AC=\dfrac{50}{7}$ ,

$BD=7$ байв.

$BC=\fbox{a}$ , $AD=\fbox{b}$ ба $AD$ тал дээр $\measuredangle BED=120^{\circ}$ байх $E$ цэг авбал $BE=\sqrt{\fbox{cd}}$ байна.
Багтаасан тойргийн радиус $\dfrac{\fbox{ef}}{\fbox{gh}}\sqrt{6}$ байна.

Косинусын теорем

$ABC$ гурвалжны талууд

$AB=5$ ,

$BC=8$ ,

$\measuredangle ABC=60^{\circ}$ байдаг гэе.

$ABC$ гурвалжны талбай $\fbox{ab}\sqrt{\fbox{c}}$ ,
$AC=\fbox{d}$ , $\cos\widehat{ACB}=\dfrac{\fbox{ef}}{\fbox{gh}}$ ,
$BC$ талын дунджийг $M$ гээд $AB$ , $AC$ талууд дээр $PA=PM$ , $QA=QM$ байх $P,Q$ цэгүүд авахад $MP=\dfrac{\fbox{i}}{\fbox{j}}$ , $MQ=\dfrac{\fbox{kl}}{\fbox{mn}}$ байна.

Мохоо өнцөгтэй байх муж

$x+2$ ,

$x+3$ ,

$x+4$ тоонууд мохоо өнцөгт гурвалжны талууд байх

$x$ -ийн утга

$]-\fbox{a};\fbox{b}[$ байна.

Бодлого №7962

$x+3$ ,

$x+4$ ,

$x+5$ тоонууд мохоо өнцөгт гурвалжны талууд байх

$x$ -ийн утга

$]-\fbox{a} \fbox{b}[$ байна.

Трапецийн талбай

$ABCD$ трапецийн хувьд

$AD$ ,

$BC$ талууд параллель ба

$|AB|=5$ ,

$|BC|=7$ ,

$|CD|=6$ ,

$|AD|=4$ байв. Трапецийн

$A$ оройгоос

$BC$ тал дээр буулгасан өндрийн урт

$\dfrac{\fbox{a}\sqrt{14}}{\fbox{b}}$ болох тул талбай нь

$\dfrac{\fbox{cd}\sqrt{\fbox{ef}}}{3}$ байна.

Призмийн огтлолын талбай

$ABCA_1B_1C_1$ зөв гурвалжин призмийн суурийн тал 4, призмийн өндөр

$\dfrac{\sqrt{42}}{7}$ байв.

$AB$ ,

$A_1C_1$ ,

$BB_1$ ирмэгүүдийн дунджийг дайрсан хавтгайгаар призмийг огтлох огтлолыг байгуулав.

Огтлолын хавтгай ба $(ABC)$ хавтгайн хоорондох өнцөг $\varphi=\arccos \sqrt{\dfrac{\fbox{a}}{\fbox{b}}}$ байна.
Огтлолын талбай $S=\dfrac{\fbox{cd}\cdot \sqrt{\fbox{e}}}{\fbox{f}}$ байна.

ЭЕШ 2007 A №28

$A$ цэгээс салаалсан, хоорондоо

$60^\circ$ өнцөг үүсгэх хоёр шулуун замын нэгэн дээр уулзвараас 300км зайд байгаа

$B$ цэгээс 60км/ц хурдтай машин, нөгөө дээр нь уулзвараас 180км зайд байгаа

$C$ цэгээс 30км/ц хурдтай машин нэгэн зэрэг уулзварын зүг хөдөлжээ.

Тэдгээрийн хоорондох зай $\fbox{a}$ цагийн дараа хамгийн бага болно. $\text{a}$ хэд вэ?
Энэ зай нь $\fbox{bc}$ км байна. $\text{b, c}$ -г ол.

Гурвалжныг бодох

$\triangle ABC$ -ийн хувьд

$a=2$ ,

$b=\sqrt2$ ,

$c=1$ байв.

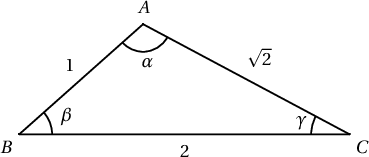
$\cos\beta=\dfrac{\fbox{a}}{4}$ , $\sin\beta=\dfrac{\sqrt{\fbox{b}}}{4}$ ;
Гурвалжны талбай нь $S_{\triangle ABC}=\dfrac{\sqrt{\fbox{c}}}{\fbox{d}}$ ;
Багтсан тойргийн радиус нь $r=\dfrac{\sqrt{7}(\fbox{e}-\sqrt{\fbox{f}})}{14}$ ;
Багтаасан тойргийн радиус нь $R=\dfrac{\fbox{g}\sqrt{14}}{\fbox{h}}$ байна.

Тойргийн нум

$O(0,0)$ цэгт төвтэй 4 радиустай тойрог ба

$(2-\sqrt3)x+y-4=0$ шулуун өгөгдөв.

Огтлолцлын цэгүүд нь $A(\fbox{a},\fbox{b})$ , $B(\fbox{c},\fbox{d}\sqrt{\fbox{e}})$
$AB$ хэрчмийн урт: $2(\sqrt{\fbox{f}}-\sqrt{\fbox{g}})$
$\measuredangle AOB$ өнцөг: $\fbox{hi}^\circ$ байна.

Гүдгэр 4 өнцөгт

Тойрогт багтсан

$ABCD$ дөрвөн өнцөгтөд

$AB=BC=4$ ,

$CD=5$ ,

$DA=9$ байв.

$\triangle ABD$ болон $\triangle BCD$ -ээс косинусын теоремоор $BD$ -г олж тэнцүүлбэл $\angle A=\fbox{ab}^\circ$ . Иймд $BD=\sqrt{\fbox{cd}}$ .
$S_{ABCD}=S_{ABD}+S_{BCD}=\fbox{ef}\cdot\sqrt{\fbox{g}}$

Ирмэгүүд дээр оройтой гурвалжны талбай

Бүх ирмэгийнх нь урт

$6$ -тай тэнцүү

$OABC$ зөв тетраэдрийн

$OA$ ,

$OB$ ,

$OC$ ирмэгүүд дээр

$OL=3$ ,

$OM=4$ ,

$ON=2$ байхаар

$L$ ,

$M$ ,

$N$ цэгүүд авав.

$LM=\sqrt{\fbox{ab}}$ , $MN=2\sqrt{\fbox{c}}$ , $NL=\sqrt{\fbox{d}}$ ;
$\sin\angle MLN=\dfrac{\fbox{e}\sqrt{\fbox{f}}}{\sqrt{91}}$ ;
$S_{\triangle LMN}=\dfrac{\fbox{h}\sqrt{3}}{\fbox{i}}$ байна.

Хоёр тойргийн огтлолцолд үүсэх дүрс

$AB=\sqrt{2}+\sqrt{6}$ байв.

$A$ цэгт төвтэй 2 радиустай тойрог,

$B$ цэгт төвтэй

$2\sqrt2$ радиустай тойрогтой

$C$ ба

$D$ цэгүүдэд огтлолцдог.

$\measuredangle CAD=\fbox{ab}^\circ$ ба

$\measuredangle CBD=\fbox{cd}^\circ$ байна. Хоёр тойргийн огтлолцолд үүсэх дүрсээр хүрээлэгдсэн дүрсийн талбай нь

$S=\dfrac{\fbox{e}}{\fbox{f}}\cdot\pi-\fbox{g}-\fbox{h}\sqrt3$

Гүдгэр 4 өнцөгт

Тойрогт багтсан

$ABCD$ дөрвөн өнцөгтөд

$AB=BC=4$ ,

$CD=5$ ,

$DA=9$ байв.

$\triangle ABD$ болон $\triangle BCD$ -ээс косинусын теоремоор $BD$ -г олж тэнцүүлбэл $\angle A=\fbox{ab}^\circ$ . Иймд $BD=\sqrt{\fbox{cd}}$ .
$S_{ABCD}=S_{ABD}+S_{BCD}=\fbox{ef}\cdot\sqrt{\fbox{g}}$

Конусын дэлгээс

$AB$ нь

$O$ оройтой конусын суурийн диаметр бөгөөд, уг конусын байгуулагч нь суурийн радиусаас 3 дахин урт байв. Хэрвээ суурийн радиус нь

$r$ ,

$P$ нь

$BP=r$ байх

$OB$ хэрчим дээрх цэг бол конусыг

$OA$ байгуулагчийн дагуу дэлгэсэн дэлгээсийн төв өнцөг нь

$\fbox{abc}^\circ$ байна.

$A$ цэгээс конусын гадаргуугийн дагуу явж

$P$ цэг хүрэх хамгийн дөт замын урт нь

$\sqrt{\fbox{d}}r$ байна.

Шонгын өндөр

Эгц босоо

$PQ$ шонгын мод 1 шулуун дээрх

$A, B, C$ цэгүүдээс харгалзан

$30^{\circ}, 45^{\circ}, 60^{\circ}$ -аар харагддаг ба

$AB=BC=20$ м бол

$PQ$ шонгын өндрийг олъё.

$CQ=\dfrac{\sqrt3}{\fbox{a}}h$ ,

$BQ=\fbox{b}h$ ,

$AQ=\sqrt{\fbox{c}}h$ болох ба

$AQB$ ба

$BQC$ гурвалжнууды

$B$ өнцгөөс косинусын теорем бичвэл

$h=\fbox{de}\sqrt{f}$ болно.

$\dfrac{8\sqrt7}{7}$ радиустай тойрогт багтсан

$ABCD$ дөрвөн өнцөгтөд

$BC=4$ ,

$\cos\angle BAD=\dfrac18$ байв.

$BD=\fbox{a}$ , $CD=\fbox{b}$ байна.
$AB+AD=9$ бол $ABCD$ дөрвөн өнцөгтийн талбай $S=\dfrac{\fbox{cd}\sqrt{\fbox{e}}}{\fbox{f}}$ байна.

Тойрогт багтсан

$ABCD$ дөрвөн өнцөгтийн хувьд

$AC=12$ ,

$BC=BD=10$ ,

$AD=3$ байв.

$AB=\fbox{a}$ байна (3 оноо).
$CD=\dfrac{\fbox{bc}}{4}$ байна (2 оноо).
Багтаасан тойргийн радиус $\dfrac{\fbox{de}}{\fbox{f}}\sqrt{7}$ байна (3 оноо).

Тойрогт багтсан

$ABCD$ дөрвөн өнцөгтийн хувьд

$AB=4$ ,

$AC=6$ ,

$BD=5$ ,

$DC=\dfrac{45}{8}$ байв.

$BC=\fbox{a}$ байна (3 оноо).
$AD=\dfrac{\fbox{b}}{\fbox{c}}$ байна (2 оноо).(Хариуг үл хураагдах бутархай хэлбэрээр бичээрэй!)
Багтаасан тойргийн радиус $\dfrac{\fbox{d}}{\fbox{e}}\sqrt{\fbox{f}}$ байна (3 оноо).

Бодлого №2319

$ABC$ гурвалжинд багтсан тойрог

$AB$ талыг

$D$ цэгээр,

$BC$ талыг

$E$ цэгээр шүргэнэ. Хэрэв

$BD:AD=1:2$ ,

$BE:CE=1:3$ бол гурвалжны өнцгүүдийг ол.

Бодлого №10584

$\triangle ABC$ -ны дотоод өнцгүүдийн хувьд

$\tg B\cdot \tg C=1$ бол

$\triangle ABC$ ямар гурвалжин бэ?

ЭЕШ 2014 A №11

Зурагт дүрсэлсэн

$x$ өнцгийг ол.

A.

$70^\circ$ B.

$60^\circ$ C.

$40^\circ$ D.

$30^\circ$ E.

$80^\circ$

Гурвалжны дотоод өнцгүүдийн нийлбэр

Гурвалжны дотоод өнцгүүд

$10^\circ, 60^\circ, x$ бол

$x=?$

A.

$10^\circ$ B.

$80^\circ$ C.

$180^\circ$ D.

$90^\circ$ E.

$110^\circ$

Бодлого №4905

Тэгш өнцөгт гурвалжны нэг хурц өнцөг нь

$20^\circ$ байв. Нөгөө хоёр өнцгийн ялгавар хэд байх вэ?

A.

$20^\circ$ B.

$30^\circ$ C.

$40^\circ$ D.

$50^\circ$ E.

$70^\circ$

Бодлого №5680

$ABC$ адил хажуут гурвалжны

$AB=AC$ ба

$\tg\angle B=3$ бол

$\cos\angle C=?$

A.

$-\dfrac{3}{\sqrt{10}}$ B.

$\dfrac{1}{\sqrt{10}}$ C.

$\dfrac{\sqrt{10}}{2}$ D.

$3\sqrt{10}$ E.

$\dfrac{3}{\sqrt5}$

Өнцөг тооцоолох

$ABC$ ,

$ADC$ гурвалжны

$AD$ ,

$BC$ талууд

$M$ цэгт огтлолцжээ. Хэрэв

$B$ ,

$D$ хоёр орой

$AC$ шулууны нэг талд орших бөгөөд

$AB=BD$ ,

$\measuredangle ABC=\measuredangle ADC=40^\circ$ ,

$\measuredangle AMC=70^\circ$ бол

$\measuredangle BCD$ ,

$\measuredangle ABD$ өнцгүүд хэдэн градус вэ?

A.

$60^\circ, 60^\circ$ B.

$70^\circ, 80^\circ$ C.

$50^\circ, 100^\circ$ D.

$30^\circ, 120^\circ$ E.

$30^\circ, 150^\circ$

ЭЕШ 2015 D №5

Тэгш өнцөгт гурвалжны нэг хурц өнцөг нь

$40^\circ$ бол нөгөө хурц өнцгийг ол.

A.

$50^\circ$ B.

$40^\circ$ C.

$180^\circ$ D.

$90^\circ$ E.

$60^\circ$

Гурвалжны өнцгүүдийн нийлбэр

Адил хажуут гурвалжны оройн өнцөг нь

$80^\circ$ бол суурийн өнцөг нь аль нь вэ?

A.

$30^\circ$ B.

$40^\circ$ C.

$50^\circ$ D.

$80^\circ$ E.

$90^\circ$

ЭЕШ 2015 A №5

Тэгш өнцөгт гурвалжны нэг хурц өнцөг нь

$20^\circ$ бол нөгөө хурц өнцгийг ол.

A.

$20^\circ$ B.

$70^\circ$ C.

$110^\circ$ D.

$90^\circ$ E.

$60^\circ$

ЭЕШ 2015 B №5

Тэгш өнцөгт гурвалжны нэг хурц өнцөг нь

$35^\circ$ бол нөгөө хурц өнцгийг ол.

A.

$65^\circ$ B.

$55^\circ$ C.

$35^\circ$ D.

$90^\circ$ E.

$115^\circ$

ЭЕШ 2015 C №5

Тэгш өнцөгт гурвалжны нэг хурц өнцөг нь

$15^\circ$ бол нөгөө хурц өнцгийг ол.

A.

$90^\circ$ B.

$75^\circ$ C.

$15^\circ$ D.

$45^\circ$ E.

$105^\circ$

ЭЕШ 2014 B №11

Зурагт дүрсэлсэн

$x$ өнцгийг ол.

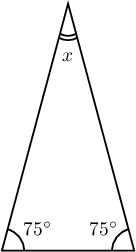
A.

$105^\circ$ B.

$75^\circ$ C.

$40^\circ$ D.

$30^\circ$ E.

$150^\circ$

Өнцөг тооцоолох

$\measuredangle BAD=45^\circ$ ,

$\measuredangle ABD=30^\circ$ бол

$\measuredangle BDC=?$

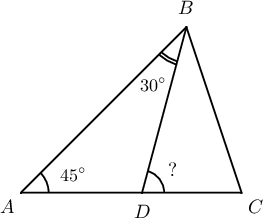
A.

$60^\circ$ B.

$75^\circ$ C.

$90^\circ$ D.

$120^\circ$ E.

$105^\circ$

Хамар өнцгүүд

Хамар хоёр өнцгийн нэг нь

$95^\circ$ бол нөгөөг ол.

A.

$85^\circ$ B.

$115^\circ$ C.

$15^\circ$ D.

$265^\circ$ E.

$105^\circ$

Хамар өнцгүүд

Хамар хоёр өнцгийн нэг нь

$75^\circ$ бол нөгөөг ол.

A.

$15^\circ$ B.

$115^\circ$ C.

$75^\circ$ D.

$150^\circ$ E.

$105^\circ$

Гурвалжны гадаад өнцгийн хэмжээ

$\alpha$ өнцгийн хэмжээг ол.

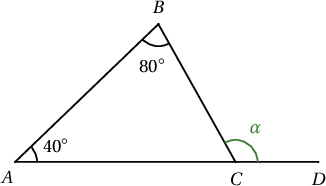
A.

$20^\circ$ B.

$50^\circ$ C.

$70^\circ$ D.

$120^\circ$ E.

$150^\circ$

Гурвалжны гадаад өнцгийн хэмжээ

$\alpha$ өнцгийн хэмжээг ол.

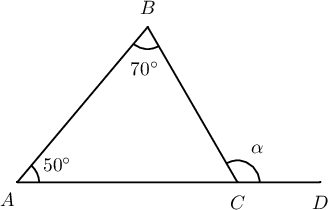
A.

$50^\circ$ B.

$70^\circ$ C.

$120^\circ$ D.

$20^\circ$ E.

$150^\circ$

Тэгш өнцөгт гурвалжны хурц өнцгийн косинус

$\angle A=90^\circ$ байх

$ABC$ тэгш өнцөгт гурвалжны хувьд

$AB=5$ ,

$AC=4$ бол

$\cos\measuredangle ABC$ аль нь вэ?

A.

$\dfrac{4}{5}$ B.

$\dfrac{4}{5}$ C.

$\dfrac{5\sqrt{41}}{41}$ D.

$\dfrac{4\sqrt{41}}{41}$ E.

$0$

Гурвалжны өнцгийн тангес

$AB=AC$ ,

$2OB=3BK$ бол

$\ctg\dfrac{\theta}{2}$ хэд байх вэ?

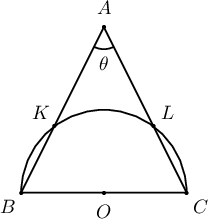
A.

$\sqrt2$ B.

$2\sqrt2$ C.

$\dfrac{1}{\sqrt2}$ D.

$\dfrac14$ E.

$4$

Өнцөг тооцоолох

Өгөгдсөн зурагт

$AK\parallel CL$ ,

$\angle A=8x$ ,

$\angle C=4x$ ,

$\angle B=132^\circ$ бол

$\angle BCL$ хэдтэй тэнцүү вэ?

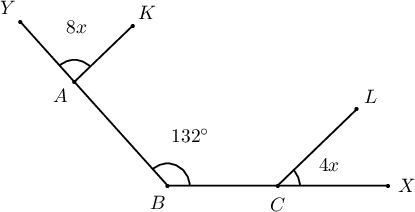
A.

$44^\circ$ B.

$88^\circ$ C.

$126^\circ$ D.

$136^\circ$ E.

$144^\circ$

2018 №A.05

Гурвалжны дотоод өнцгүүд болох гуравт аль нь вэ?

A.

$\dfrac{\pi}{5};\dfrac{2\pi}{5};\dfrac{\pi}{5}$ B.

$\dfrac{\pi}{2};\dfrac{\pi}{3};\dfrac{\pi}{6}$ C.

$\dfrac{2\pi}{3};\dfrac{\pi}{3};\dfrac{\pi}{2}$ D.

$\dfrac{\pi}{2};\dfrac{\pi}{4};\dfrac{\pi}{6}$ E.

$\dfrac{2\pi}{5};\dfrac{\pi}{10};\dfrac{\pi}{10}$

2018 №A.17

$ABC$ адил хажуут гурвалжны оройн өнцөг

$\measuredangle B=50^\circ$ бөгөөд

$AM=BM$ байхаар

$M$ цэгийг

$BC$ хажуу тал дээр авсан бол

$\measuredangle MAC$ өнцгийг ол.

A.

$25^\circ$ B.

$5^\circ$ C.

$10^\circ$ D.

$15^\circ$ E.

$20^\circ$

Гурвалжны өнцгүүдийн нийлбэр

Адил хажуут гурвалжны оройн өнцөг нь

$100^\circ$ бол суурийн өнцөг нь аль нь вэ?

A.

$30^\circ$ B.

$40^\circ$ C.

$50^\circ$ D.

$80^\circ$ E.

$90^\circ$

Өнцөг тооцоолох

$\measuredangle BAD=50^\circ$ ,

$\measuredangle BDC=70^\circ$ бол

$\measuredangle ABD=?$

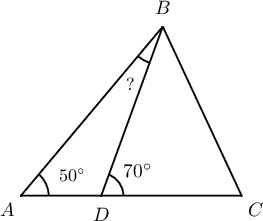
A.

$25^\circ$ B.

$45^\circ$ C.

$35^\circ$ D.

$20^\circ$ E.

$15^\circ$

Сорилго №2, 2019-2020

Гурвалжны дотоод өнцгүүд

$\angle A=20^\circ, \angle B=60^\circ, \angle C$ бол

$C$ оройн гадаад өнцөгийн хэмжээг ол.

A.

$20^\circ$ B.

$80^\circ$ C.

$40^\circ$ D.

$90^\circ$ E.

$100^\circ$

Бодлого №7916

$ABC$ гурвалжны хувьд

$\sin^2 \alpha +\sin^2 \beta =\sin^2 \gamma$ нөхцөл биелдэг бол

$\gamma =\dfrac{\pi}{\fbox{a}}$ байна.

$AB=2\sqrt{2}$ талтай, эсрэг оройн өнцөг нь тогтмол

$\dfrac{\pi}{\fbox{a}}$ байх бүх гурвалжнууд дотроос хамгийн их периметртэй гурвалжны хувьд

$AC=\fbox{b}$ ,

$\measuredangle ABC=\pi /\fbox{c}$ ба энэ үед гурвалжны периметр

$\fbox{d}+2\sqrt{2}$ болно.

Бодлого №7959

Гурвалжны

$A$ ,

$B$ ,

$C$ оройн өнцгүүд харгалзан

$\alpha$ ,

$\beta$ ,

$\gamma$ ба

$\sin \alpha \colon \sin \beta \colon \sin \gamma =6\colon 4\colon 3$ харьцаа биелдэг бол их өнцгийн косинус

$-\dfrac{\fbox{ab}}{\fbox{cd}}$ байна.

Бодлого №7960

Гурвалжны

$A$ ,

$B$ ,

$C$ оройн өнцгүүд харгалзан

$\alpha$ ,

$\beta$ ,

$\gamma$ ба

$\sin \alpha \colon \sin \beta \colon \sin \gamma =8\colon 6\colon 3$ харьцаа биелдэг бол их өнцгийн косинус

$-\dfrac{\fbox{ab}}{\fbox{cd}}$ байна.

Бодлого №2321

Гурвалжны өндөр нь

$12$ см, суурь нь

$14$ см, хоёр хажуу талын нийлбэр нь

$28$ см бол хоёр хажуу талыг нь ол.

Бодлого №2453

Тэгш өнцөгт гурвалжны катетуудын харьцаа

$3:2$ . Тэгш өнцөгөөс татсан өндөр гипотенузыг нэг нь нөгөөгөөсөө

$2$ см урт хоёр хэсэгт хуваасан бол гипотенузыг ол.

Катетууд нь

$1:3$ харьцаатай тэгш өнцөгт гурвалжины гипотенуз нь

$2\sqrt{10}$ бол гурвалжны талбайг ол.

A.

$6$ B.

$3$ C.

$2$ D.

$12$ E.

$-5$

Тэгш өнцөгт гурвалжинд багтсан тойргийн радиус 3, гипотенузэд буусан өндөр 8 нэгж бол гипотенузийн урт аль нь вэ?

A.

$8$ B.

$4$ C.

$9$ D.

$5$ E. Ийм гурвалжин олдохгүй

Бодлого №13857

Зурагт өгөгдсөн

$ABC$ гурвалжны

$BD$ өндөр бол гурвалжны периметрийг ол.

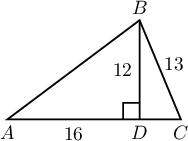
A. 54 B. 53 C. 49 D. 41 E. 60

Пифагорын теорем

Тэгш өнцөгт гурвалжны катетуудын урт

$a = 3 \, \text{см}$ ,

$b = 4 \, \text{см}$ бол гипотенузын уртыг ол.

A.

$\sqrt{7}$ B.

$5$ C.

$6$ D.

$4$ E.

$7$

Бодлого №2340

Гурвалжны нэг талын урт

$a$ ба уг талд налсан өнцгүүд нь

$\alpha$ ,

$\beta$ бол гурвалжны талбайг ол.

Бодлого №2376

$ABC$ гурвалжны хувьд

$\angle A:\angle C=3:2$ ,

$AB=28$ см,

$BC=33$ см бол

$\cos\dfrac{\angle C}{2}$ -ийг ол.

Бодлого №2437

Адил хажуут гурвалжны суурь ба түүнд буулгасан өндөр

$4$ . Багтаасан тойргийн радиусыг ол.

Бодлого №2685

$ABC$ гурвалжинд багтсан тойргийн радиус

$\dfrac{10}3$ ,

$C$ өнцгийн косинус нь

$\dfrac{5}{13}$ ба талбай нь

$60$ бол гурвалжны талуудыг ол.

ЭЕШ 2011 A №12

4 м талтай

$ABCD$ квадратын

$AB$ талын дундаж, квадратын төв,

$C$ оройг дайрсан тойргийн радиусыг ол.

A.

$4\sqrt5$ B.

$2\sqrt2$ C.

$4\sqrt2$ D.

$2\sqrt{10}$ E.

$\sqrt{10}$

Тэгш өнцөгт координатын систем ба өнцгийн синус

$A(1;1)$ ,

$B(1,6)$ ,

$C(0;4)$ бол

$\angle ACB$ өнцгийн синусыг ол.

A.

$0$ B.

$\frac{\sqrt5}{5}$ C.

$\frac{\sqrt2}{2}$ D.

$\frac{\sqrt3}{2}$ E.

$1$

Зөв гурвалжныг багтаасан тойргийн радиус

$2\sqrt3$ бол талын уртыг ол.

A.

$3$ B.

$4$ C.

$5$ D.

$6$ E.

$7$

Хамгийн их периметр

Гурвалжны 5 урттай талын эсрэг орших өнцөг нь

$60^\circ$ бол периметр нь хамгийн ихдээ хэд байх вэ?

A.

$10$ B.

$11$ C.

$12$ D.

$15$ E.

$18$

Синусын теорем

$ABC$ гурвалжныг багтаасан тойргийн радиус

$2$ ба

$\sin\alpha=\dfrac14$ бол

$BC$ талын уртыг ол.

A. 1 B. 2 C. 4 D. 8 E.

$\dfrac14$

Бодлого №5670

Хэрэв

$ABC$ гурвалжны

$\angle A=75^\circ$ ,

$\angle C=45^\circ$ ,

$AC=6\sqrt2$ бол

$BC$ талын уртыг ол.

A.

$9$ B.

$2\sqrt3+6$ C.

$2\sqrt2+6$ D.

$6\sqrt3+6$ E.

$6\sqrt2+6$

Синусын теорем

$ABC$ гурвалжны

$AB=3$ ,

$\sin\measuredangle ACB=30^\circ$ бол

$ABC$ гурвалжныг багтаасан тойргоор үүсэх дугуйн талбай хэдтэй тэнцүү вэ?

A.

$4\pi$ B.

$5\pi$ C.

$8\pi$ D.

$9\pi$ E.

$16\pi$

Гурвалжны орто төв

$ABC$ гурвалжны хувьд

$\measuredangle BAC=\alpha$ ба багтаасан тойргийн радиус нь

$R$ бол

$A$ оройгоос гурвалжны ортоцентр

$H$ хүртэлх зай аль нь вэ?

A.

$R\cos\alpha$ B.

$R\sin\alpha$ C.

$R\sin2\alpha$ D.

$2R\sin\alpha$ E.

$2R\cos\alpha$

ЭЕШ 2013 A №21

$ABC$ гурвалжны

$A$ ба

$C$ оройн өндрүүд

$H$ цэгт огтлолцоно. Хэрэв

$ABC$ гурвалжныг багтаасан тойргийн радиус

$4$ нэгж ба

$\sin\angle BAH=\dfrac25$ бол

$|BH|=?$

A.

$3\dfrac56$ B.

$3\dfrac15$ C.

$3\dfrac78$ D.

$3$ E.

$3\dfrac13$

Биссектрис

$ABC$ гурвалжныг багтаасан тойргийн радиус

$6$ ,

$\angle A=70^\circ$ ,

$\angle B=30^\circ$ бол

$\angle C$ -ийн биссектрисийн урт аль нь вэ?

A.

$3$ B.

$6$ C.

$8$ D.

$9$ E.

$10$

Бодлого №13

$ABC$ гурвалжны

$AB=3\sqrt3$ ,

$\sin\measuredangle ACB=60^\circ$ бол

$ABC$ гурвалжныг багтаасан дугуйн талбай хэдтэй тэнцүү вэ?

A.

$4\pi$ B.

$5\pi$ C.

$8\pi$ D.

$9\pi$ E.

$16\pi$

Бодлого №13

$ABC$ гурвалжны

$AB=3\sqrt2$ ,

$\sin\measuredangle ACB=45^\circ$ бол

$ABC$ гурвалжныг багтаасан дугуйн талбай хэдтэй тэнцүү вэ?

A.

$9\pi$ B.

$5\pi$ C.

$8\pi$ D.

$16\pi$ E.

$4\pi$

ЭЕШ 2017 B №14

$ABC$ гурвалжны

$\angle ABC=75^\circ$ ,

$\angle ACB=45^\circ$ ,

$BC=5$ бол

$AB$ талын уртыг ол.

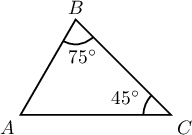
A.

$5\sqrt{\dfrac23}$ B.

$2\sqrt{\dfrac23}$ C.

$4\sqrt{\dfrac23}$ D.

$\sqrt3$ E.

$10$

ЭЕШ 2017 B №14

$ABC$ гурвалжны

$\angle ABC=75^\circ$ ,

$\angle ACB=45^\circ$ ,

$BC=3$ бол

$AB$ талын уртыг ол.

A.

$\sqrt{6}$ B.

$\sqrt{\dfrac23}$ C.

$\dfrac{\sqrt{3}}{2}$ D.

$2\sqrt3$ E.

$2\sqrt{\dfrac23}$

Синусын теорем

$ABC$ гурвалжныг багтаасан тойргийн радиус

$2$ ба

$\sin\alpha=\dfrac14$ бол

$BC$ талын уртыг ол.

A. 1 B. 2 C. 4 D. 8 E.

$\dfrac14$

Бодлого №13875

$ABC$ гурвалжны

$|BC|=\sqrt{6}, |AC|=2, \angle A= 60^\circ$ бол

$B$ оройн өндрийн уртыг ол.

A.

$\dfrac{3+\sqrt{3}}{2}$ B.

$1+\sqrt{3}$ C.

$\dfrac{2\sqrt{6}}{1+\sqrt{3}}$ D.

$2\cdot \sin 75^\circ$ E. аль нь ч биш

Зөв гурвалжныг багтаасан тойргийн радиус

$2\sqrt3$ бол талын уртыг ол.

A.

$3$ B.

$4$ C.

$5$ D.

$6$ E.

$7$

ЭЕШ 2008 E1 №22

Тойрогт багтсан

$ABCD$ дөрвөн өнцөгтийн

$AD=\sqrt3$ ,

$AB=1$ ба

$\angle ADB=30^\circ$ ,

$\angle CAD=75^\circ$ бол

багтаасан тойргийн радиус $R=\fbox{a}$ ,
$\angle BDC=\fbox{bc}^\circ$ ,
$AC^2=\fbox{d}$ байна.

Синусын теорем

$ABC$ гурвалжны талууд

$AB=3+\sqrt3, AC=\sqrt3+1$ ба

${\angle B=30^\circ}$ бол

$\angle C=\fbox{ab}^\circ$ , эсвэл

$\angle C=\fbox{cde}^\circ$ байна.

$\angle C=\fbox{ab}^\circ$ үед

$ABC$ гурвалжны талбай

$\sqrt3(\fbox{f}+\sqrt{\fbox{g}})$ ба

$\angle C=\fbox{cde}^\circ$ үед

$BC=\sqrt{\fbox{h}}+\fbox{i}$ болно.

Пирамид

Гурвалжин пирамидын суурь нь

$45^\circ$ хурц өнцөгтэй тэгш өнцөгт гурвалжин бөгөөд уг пирамидын хажуу ирмэгүүд нь тэнцүү

$4\sqrt3$ нэгж урттай ба суурийн хавтгайтай

$60^\circ$ өнцөг үүсгэдэг бол:

Пирамидын өндөр $\fbox{a}$
Суурийн гурвалжны талбай $\fbox{bc}$
Пирамидын эзлэхүүн $\fbox{de}$
Пирамидыг багтаасан бөмбөрцгийн радиус нь $\fbox{f}$ байна.

Нийлбэр ялгавар өнцгийн синусын томьёо

$\alpha$ нь I мужийн өнцөг ба

$\sin\alpha=\dfrac{5}{13}$ ,

$\beta$ нь III мужийн өнцөг ба

$\cos\beta=-\dfrac{3}{5}$ гэе.

$\sin(\alpha-\beta)=\dfrac{\fbox{ab}}{\fbox{cd}}$ ,

$\sin(\alpha+\beta)=-\dfrac{\fbox{ef}}{\fbox{gh}}$ .

Синусын теорем, илэрхийллийн хамгийн их утга

$ABC$ гурвалжны хувьд

$b\sin \beta =c\sin \gamma$ нөхцөл биелдэг бол

$b=\fbox{a} c$ болох ба

$\sin \alpha +2\cos \beta$ нийлбэр

$\alpha = \displaystyle \dfrac{\fbox{b}}{\fbox{c}}\pi$ ,

$\beta=\displaystyle\dfrac{\pi}{\fbox{d}}$ үед хамгийн их

$\dfrac{\fbox{e}\sqrt{\fbox{f}}}{2}$ утгатай байна.

Тойрогт багтсан зөв гурвалжин

Тойрогт

$5$ талтай

$ABC$ зөв гурвалжин багтжээ. Уг тойргийн

$\measuredangle BAC$ өнцөгт тулсан нум дээр

$P$ цэг авчээ.

$\measuredangle ACP =\theta$ бол

$PA+PB=\fbox{ab}\sin \Big(\theta-\dfrac{\pi}{\fbox{c}}\Big)$ болох ба

$S_{PAC}=\dfrac{\fbox{de}}{\sqrt{\fbox{f}}}\sin \Big(\dfrac{\fbox{g}}{\fbox{h}}\pi -\theta\Big)\sin \theta$ байна.

ЭЕШ 2007 A №27

$A(-6;1)$ ,

$B(2;5)$ ,

$C(3;-2)$ цэгүүдэд оройтой гурвалжин байв.

$C$ оройн медианы тэгшитгэл $y=-\fbox{a}x+1$ бол $a$ -г ол.
$\overrightarrow{AC}$ , $\overrightarrow{AB}$ векторын хоорондох өнцөг болох $A$ оройн дотоод өнцгийг $\alpha$ гэвэл $\alpha=\fbox{bc}^\circ$ байна.
Гурвалжныг багтаасан тойргийн тэгшитгэл нь $(x+\fbox{d})^2+(y-\fbox{e})^2=\fbox{f}^2$

Суурийн цэгээс хажуу ирмэг хүртэлх зай

$a$ талтай

$ABCD$ зөв тетраэдр (бүх ирмэгийн урт нь тэнцүү) өгөгдөв.

$A$ оройгоос $BCD$ талд буулгасан $AH$ өндрийн урт $\dfrac{\sqrt{\fbox{a}}}{\fbox{b}}a$ ;
$ABCD$ тетраэдрийн эзлэхүүн $\dfrac{\sqrt{\fbox{c}}}{\fbox{de}}a^3$
Өндрийн суурь $H$ цэгээс $ABC$ талс хүртэлх зай $\dfrac{\sqrt{\fbox{f}}}{\fbox{g}}a$ байна.

ЭЕШ 2008 A №62

Тойрогт багтсан

$ABCD$ дөрвөн өнцөгтийн

$AD=\sqrt3$ ,

$CD=\sqrt2$ ба

$\angle ADB=60^\circ$ ,

$\angle CAD=45^\circ$ бол

багтаасан тойргийн радиус $R=\fbox{a}$
$\angle BDC=\fbox{bc}^\circ$
$AB^2=\fbox{d}$ байна.

sin теорем

$ABC$ гурвалжны талууд

$AB=3+\sqrt3, AC=\sqrt3+1$ ба

${\angle B=30^\circ}$ бол

$\angle C=\fbox{ab}^\circ$ , эсвэл

$\angle C=\fbox{cde}^\circ$ байна.

$\angle C=\fbox{ab}^\circ$ үед

$ABC$ гурвалжны талбай

$\sqrt3(\fbox{f}+\sqrt{\fbox{g}})$ ба

$\angle C=\fbox{cde}^\circ$ үед

$BC=\sqrt{\fbox{h}}+\fbox{i}$ болно.

Багтсан дөрвөн өнцөгт

1 радиустай тойрогт багтсан

$ABCD$ дөрвөн өнцөгтийн хувьд

$\angle ABC=60^\circ, \angle DAB=105^\circ, |BC|=\sqrt3$ бол

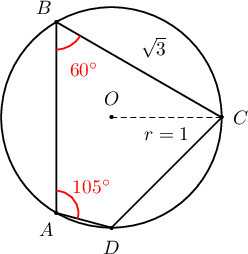
$\angle BCA=\fbox{ab}^\circ$ /1 оноо/
$\angle CAD=\fbox{cd}^\circ$ /2 оноо/
$|CD|=\sqrt{\fbox{e}}$ /2 оноо/
$|AD|=\dfrac{\sqrt{\fbox{f}}-\sqrt{\fbox{e}}}{\fbox{h}}\,\,\,$ /2 оноо/

ЭЕШ 2006 A №27

$ABC$ гурвалжны

$AB; BC; CA$ талууд дээр харгалзан

$M; N; K$ цэгүүдийг

$\dfrac{|AM|}{|MB|}=\dfrac25$ ;

$\dfrac{|BN|}{|NC|}=\dfrac{5}{6}$ ;

$\dfrac{|CK|}{|KA|}=\dfrac37$ байхаар авсан бол

$\dfrac{S_{MNK}}{S_{ABC}}=\dfrac{\fbox{ab}}{\fbox{cd}}$ байна.

ЭЕШ 2006 C №27

$ABC$ гурвалжны

$AB;BC;CA$ талууд дээр харгалзан

$M;N;K$ цэгүүдийг

$\dfrac{|AM|}{|MB|}=\dfrac{7}{19};\dfrac{|BN|}{|NC|}=\dfrac{11}{13};\dfrac{|CK|}{|KA|}=\dfrac{3}{7}$ байхаар авсан бол

$\dfrac{S_{MNK}}{S_{ABC}}=\dfrac{\fbox{ab}}{156}$

$ABC$ гурвалжны талууд

$AB=12$ ,

$BC=5$ ,

$AC=13$ ба

$AB$ тал дээр

${AC_1}\colon {BC_1}={1}\colon{2}$ байх

$C_1$ цэг тэмдэглэв.

$BC$ талын дундаж нь

$A_1$ ,

$BB_1$ нь

$AC$ тал дээр буулгасан өндөр бол

$BB_1=\dfrac{\fbox{ab}}{13},$

$S_{AC_1B_1}=\dfrac{\fbox{cdef}}{13^2}$ ,

$S_{CA_1B_1}=\dfrac{\fbox{ghi}}{13^2}$ байна.

Бодлого №2322

$10$ см,

$17$ см,

$21$ см талуудтай гурвалжинд нэг тал нь гурвалжны их тал дээр байрлах

$24$ см периметртэй тэгш өнцөгт багтав. Тэгш өнцөгтийн талуудыг ол.

Талуудын хамаарал

$ABC$ гурвалжинд

$\measuredangle BAC=2\measuredangle CBA$ бол талуудын хамаарал ямар байх вэ? (

$BC=a$ ,

$CA=b$ ,

$AB=c$ ).

A.

$a^2=b(b+c)$ B.

$a^2=c(b+c)$ C.

$b^2=a(a-c)$ D.

$2b^2=a(a+c)$ E.

$c^2=a(a+b)$

Фалесийн теорем

Зурагт үзүүлсэн

$DE\parallel BC$ ба

$AD:DB=3:4$ бол

$CE:AC$ харьцааг ол.

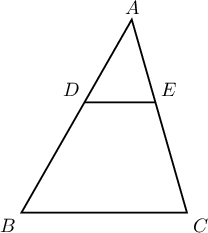
A.

$\dfrac{3}{4}$ B.

$\dfrac{4}{3}$ C.

$\dfrac{4}{7}$ D.

$\dfrac{3}{7}$ E.

$-\dfrac{3}{7}$

Параллель шулуунуудын хооронд үүсэх гурвалжнууд

$AB\parallel DE$ бол

$x=?$

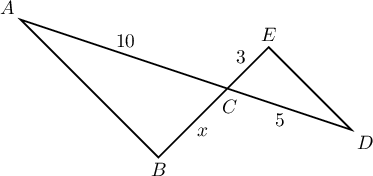
A.

$5$ B.

$6$ C.

$7$ D.

$8$ E.

$9$

Фалесийн теорем

Зурагт үзүүлсэн

$AC\parallel DK$ ба

$AD=2$ ,

$DB=3$ ,

$DK=6$ бол

$AC=?$

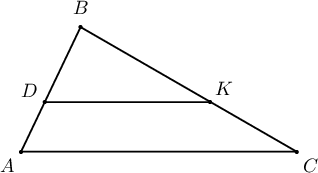
A.

$12$ B.

$14$ C.

$10$ D.

$9$ E.

$13$

10.108

Адил талт гурвалжинд нэг тал нь суурь дээр орших квадрат багтжээ. Хэрвээ квадратын тал нь

$(2-\sqrt3)\sqrt[4]{3}$ бол гурвалжны талбайг ол.

A.

$4$ B.

$0.5$ C.

$0.25$ D.

$0.7$ E.

$0.4$

Төсөөтэй гурвалжнууд

$ED$ хэрчим

$ABC$ гурвалжны

$BC$ талтай параллель,

$E$ ,

$D$ төгсгөлүүд нь харгалзан

$AB$ ,

$AC$ талууд дээр оршино. Хэрэв

$AB=8$ ,

$AC=6$ ,

$BC=7$ ба

$CD+BE=4$ бол

$DE=\fbox{a}$ ,

$S_{AED}=\dfrac{\fbox{bc}}{\fbox{de}}\sqrt{15}$ байна.

ЭЕШ 2014 A №29

Зурагт дүрсэлсэн

$ABC$ гурвалжин дотор орших

$D$ цэгийг дайруулан талуудтай параллел шулуунууд татахад 1, 16, 25 кв.нэгж талбайтай гурвалжингууд үүсэх бол

$S_{ABC}=?$

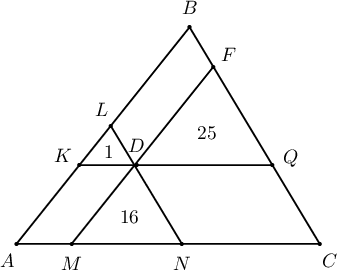
A.

$100$ B.

$42$ C.

$84$ D.

$126$ E.

$50$

Төсөөтэй гурвалжнуудын талбайн харьцаа

Адил хажуут гурвалжны суурьтай параллель шулуун хажуу талыг орой талаас нь

$5:3$ харьцаатай хэсгүүдэд хуваажээ. Хэрэв гурвалжны хуваагдсан хэсгүүдийн талбайн ялгавар

$56$ см.кв бол гурвалжны талбайг ол.

A.

$256$ см.кв B.

$220$ см.кв C.

$224$ см.кв D.

$240$ см.кв E. ийм байх боломжгүй

Төсөөтэй гурвалжнуудын талбайн харьцаа

Адил хажуут гурвалжны суурьтай нь параллель хоёр шулуун талбайг нь

$9:55:161$ харьцаатай хэсгүүдэд хуваасан бол хажуу тал нь ямар харьцаатай хэсгүүдэд хуваагдах вэ?

A.

$3:8:15$ B.

$9:64:225$ C.

$9:55:161$ D.

$5:7:9$ E.

$3:5:7$

ЭЕШ 2014 B №29

Зурагт дүрсэлсэн

$ABC$ гурвалжин дотор орших

$D$ цэгийг дайруулан талуудтай параллель шулуунууд татахад 4, 16, 25 кв.нэгж талбайтай гурвалжингууд үүсэх бол

$S_{ABC}=?$

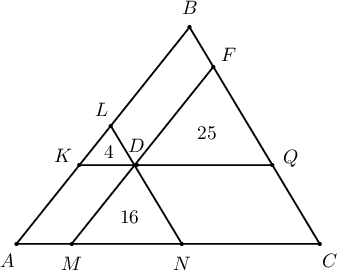
A. 121 B. 45 C. 90 D. 135 E. 111

$ABC$ гурвалжны талууд

$AB=12$ ,

$BC=5$ ,

$AC=13$ ба

$AB$ тал дээр

${AC_1}\colon {BC_1}={1}\colon{2}$ байх

$C_1$ цэг тэмдэглэв.

$BC$ талын дундаж нь

$A_1$ ,

$BB_1$ нь

$AC$ тал дээр буулгасан өндөр бол

$BB_1=\dfrac{\fbox{ab}}{13},$

$S_{AC_1B_1}=\dfrac{\fbox{cdef}}{13^2}$ ,

$S_{CA_1B_1}=\dfrac{\fbox{ghi}}{13^2}$ байна.

ЭЕШ 2014 A №35

Тэгш өнцөгт гурвалжны катетууд

$2\sqrt2$ см,

$3\sqrt2$ см урттай бол тэгш өнцгийн оройгоос татсан биссектрисийн уртыг ол.

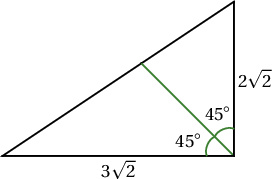
A.

$3\sqrt2$ см B.

$2.4$ см C.

$2\sqrt2$ см D.

$\sqrt{26}$ см E.

$2.6$ см

Тэгш өнцөгтийн талбай

Тэгш өнцөгт гурвалжны катетуудаар талаа хийсэн тэгш өнцөгтийн талбай 18 бол катетуудын үржвэрийг ол.

A.

$18$ B.

$9$ C.

$6$ D.

$36$ E.

$12$

Тэгш өнцөгт гурвалжны катетуудын урт нь 10, 24. Гурвалжны тэгш өнцгийн оройгоос татсан өндрийн уртыг ол.

A.

$9\dfrac{3}{13}$ B.

$9$ C.

$10\dfrac{3}{13}$ D.

$9\dfrac{5}{13}$ E.

$10$

Өнцгийн косинус

$ABC$ (

$\measuredangle ABC=90^\circ$ ) гэсэн тэгш өнцөгт гурвалжны

$\cos \measuredangle C=\dfrac{5}{13}$ ба

$AC=13$ бол

$BC$ -ийн уртыг ол.

A.

$5$ B.

$7$ C.

$9$ D.

$12$ E.

$13$

Бодлого №5733

$ABC$ тэгш өнцөгт гурвалжны

$\measuredangle BAC=90^\circ$ ,

$BC=9$ ,

$AB=6$ бол

$\cos\measuredangle ABC=?$

A.

$4/9$ B.

$1$ C.

$0$ D.

$1/2$ E.

$2/3$

Тэгш өнцөгт гурвалжны катет

$9$ нэгж, багтсан тойргийн радиус

$3$ нэгж бол өндрийн сууриар гипотенузын хуваагдсан хэсгүүд хэд хэдэн нэгж вэ?

A.

$8; 7$ B.

$\dfrac{42}5; \dfrac{33}5$ C.

$6; 9$ D.

$\dfrac{27}5; \dfrac{48}5$ E.

$7; 9$

Тэгш өнцөгт гурвалжинд багтсан тойргийн радиус 3, гипотенузэд буусан өндөр 8 нэгж бол гипотенузийн урт аль нь вэ?

A.

$8$ B.

$4$ C.

$9$ D.

$5$ E. Ийм гурвалжин олдохгүй

ЭЕШ 2015 D №5

Тэгш өнцөгт гурвалжны нэг хурц өнцөг нь

$40^\circ$ бол нөгөө хурц өнцгийг ол.

A.

$50^\circ$ B.

$40^\circ$ C.

$180^\circ$ D.

$90^\circ$ E.

$60^\circ$

ЭЕШ 2015 A №5

Тэгш өнцөгт гурвалжны нэг хурц өнцөг нь

$20^\circ$ бол нөгөө хурц өнцгийг ол.

A.

$20^\circ$ B.

$70^\circ$ C.

$110^\circ$ D.

$90^\circ$ E.

$60^\circ$

ЭЕШ 2015 B №5

Тэгш өнцөгт гурвалжны нэг хурц өнцөг нь

$35^\circ$ бол нөгөө хурц өнцгийг ол.

A.

$65^\circ$ B.

$55^\circ$ C.

$35^\circ$ D.

$90^\circ$ E.

$115^\circ$

ЭЕШ 2015 C №5

Тэгш өнцөгт гурвалжны нэг хурц өнцөг нь

$15^\circ$ бол нөгөө хурц өнцгийг ол.

A.

$90^\circ$ B.

$75^\circ$ C.

$15^\circ$ D.

$45^\circ$ E.

$105^\circ$

ЭЕШ 2014 B №35

Тэгш өнцөгт гурвалжны катетууд

$5\sqrt2$ см,

$4\sqrt2$ см урттай бол тэгш өнцгийн оройгоос татсан биссектрисийн уртыг ол.

A.

$4\dfrac{4}{9}$ см B.

$4.6$ см C.

$\dfrac{9}{40}$ см D.

$4\sqrt{6}$ см E.

$2.4$ см

Өнцгийн тангес

Тэгш өнцөгт

$ABC$ ,

$\measuredangle C=90^\circ$ гурвалжны тэгш өнцгийн оройгоос татсан өндөр

$h$ ,

$\measuredangle A=\alpha$ , өндрийн суурь

$H$ бол

$BH=?$

A.

$\dfrac{h}{\cos\alpha}$ B.

$h\cdot\ctg\alpha$ C.

$h\cdot\tg\alpha$ D.

$\dfrac{h}{\sin\alpha}$ E.

$\dfrac{2h}{\sin2\alpha}$

Тэгш өнцөгт гурвалжны периметр 12 ба нэг өнцгийн тангенс нь

$\dfrac{5}{12}$ бол энэ гурвалжныг багтаасан болон энэ гурвалжинд багтсан тойргийн радиусуудын нийлбэрийг ол.

A.

$3$ B.

$3.2$ C.

$3.3$ D.

$3.4$ E.

$4$

Тэгш өнцөгт гурвалжны катетуудын урт нь 10, 24. Гурвалжны тэгш өнцгийн оройгоос татсан өндрийн уртыг ол.

A.

$9\dfrac{3}{13}$ B.

$9$ C.

$10\dfrac{3}{13}$ D.

$9\dfrac{5}{13}$ E.

$10$

Тэгш өнцөгт гурвалжны периметр 12 ба нэг өнцгийн тангенс нь

$\dfrac{5}{12}$ бол энэ гурвалжныг багтаасан болон энэ гурвалжинд багтсан тойргийн радиусуудын нийлбэрийг ол.

A.

$3$ B.

$3.2$ C.

$3.3$ D.

$3.4$ E.

$4$

Тэгш өнцөгт гурвалжны катетуудын урт нь 5, 12. Гурвалжны тэгш өнцгийн оройгоос татсан өндрийн уртыг ол.

A.

$9\dfrac{3}{13}$ B.

$4.5$ C.

$5\dfrac{3}{13}$ D.

$4\dfrac{5}{13}$ E.

$4\dfrac{8}{13}$